Zeus: Understanding and Optimizing GPU Energy Consumption of DNN Training
Abstract
Training deep neural networks (DNNs) is becoming increasingly more resource- and energy-intensive every year. Unfortunately, existing works primarily focus on optimizing DNN training for faster completion, often without considering the impact on energy efficiency.
In this paper, we observe that common practices to improve training performance can often lead to inefficient energy usage. More importantly, we demonstrate that there is a tradeoff between energy consumption and performance optimization. To this end, we propose Zeus, an optimization framework to navigate this tradeoff by automatically finding optimal job- and GPU-level configurations for recurring DNN training jobs. Zeus uses an online exploration-exploitation approach in conjunction with just-in-time energy profiling, averting the need for expensive offline measurements, while adapting to data drifts over time. Our evaluation shows that Zeus can improve the energy efficiency of DNN training by 15.3%–75.8% for diverse workloads.
1 Introduction
Deep neural networks (DNNs) have received ubiquitous adoption in recent years across many data-driven application domains such as computer vision [20, 38, 65], natural language processing [21, 57], personalized recommendation [32, 39], and speech recognition [33]. To effectively support such growth, DNN models are predominantly trained in clusters of highly parallel and increasingly more powerful GPUs [15, 70].
However, growing demand for computation ultimately translates to greater energy demand. For instance, training the GPT-3 model [13] consumes 1,287 megawatt-hour (MWh) [75], which is equivalent to 120 years of electricity consumption for an average U.S. household [1]. This trend continues to grow: Meta reports an increasing electricity demand for AI, despite a 28.5% operational power footprint reduction [96]. Yet, existing literature on DNN training mostly ignores energy efficiency [83].
We observe that common performance optimization practices for DNN training can lead to inefficient energy usage. For example, many recent works prescribe large batch sizes for higher training throughput [29, 84]. However, we show that maximizing raw throughput may come at the cost of lower energy efficiency. Similarly, modern GPUs allow the configuration of a power limit that caps its maximum power draw, but existing solutions often ignore it. Our analysis of four generations of NVIDIA GPUs shows that none of them are entirely power proportional, and drawing maximum power gives diminishing return. Indeed, carefully choosing the right batch size and GPU power limit can reduce energy consumption by 23.8%–74.7% for diverse workloads (§2.2).
Unfortunately, reducing energy consumption is not entirely free – we discover that there is a tradeoff between energy consumption and training time for a given target accuracy (§2.3). Our characterization of the energy-time Pareto frontier highlights two notable phenomena. First, for a given training job, all Pareto-optimal configurations provide varying amounts of energy reductions in comparison to blindly using the maximum batch size and GPU power limit. Second, the amount of reduction in energy consumption often has a non-linear relationship with the increase of training time. This raises a simple question: how do we automatically identify and navigate the tradeoff between energy consumption and training time for DNN training?
In this paper, we present Zeus to address this question. Zeus is a plug-in optimization framework that automatically configures the batch size and GPU power limit to minimize the overall energy consumption and training time for DNN training jobs (§3). Unlike some recent works that only consider GPU-specific configurations [87, 11], Zeus simultaneously considers job- and GPU-related configurations. Moreover, it does not require per-job offline profiling or prediction model training [90, 101], both of which can be prohibitive in large clusters with heterogeneous hardware and time-varying workloads [94]. Instead, Zeus takes an online exploration-exploitation approach tailored to the characteristics of DNN training workflows. That is, as new data flow into the pipeline, models need to be periodically re-trained [37], manifesting itself as recurring jobs in production clusters [37, 94]. Leveraging this fact, Zeus automatically explores various configurations, measures corresponding gains or losses, and continuously adjusts its actions based on its measurements (§4).
Designing such a solution is challenging due to two sources of uncertainty in DNN training. First, due to the randomness introduced from DNN parameter initialization and data loading, the energy consumed until a DNN reaches its target accuracy varies even when training is run with the exact same configuration [82, 19]. Thus, evaluating a configuration only once does not provide sufficient information about its expected energy consumption. Second, since both DNN models and GPUs have diverse architectures and unique energy characteristics [93], offline profiling results do not easily generalize to other DNNs and GPUs. Aggravating these challenges is the large size of the possible configuration space, with each configuration taking hours or even days to evaluate.
Zeus can efficiently determine the optimal set of knobs in the configuration space by decoupling the optimization of batch size and power limit without losing optimality. Specifically, it captures the stochastic nature of DNN training by formulating the batch size optimization problem as a Multi-Armed Bandit (MAB) and runs online optimization under random observations using the Thompson Sampling policy [88]. Additionally, Zeus’s just-in-time (JIT) energy profiler finds the optimal power limit while training is running, making Zeus a completely online optimization framework.
We have implemented Zeus and integrated it with PyTorch [74] (§5). Evaluation on a diverse workload consisting of speech recognition, image classification, NLP, and recommendation tasks shows that Zeus reduces energy consumption by 15.3%–75.8% and training time by 60.6% w.r.t. simply selecting the maximum batch size and maximum GPU power limit. Zeus converges to optimal configuration among available ones quickly and can adapt to data drift effectively. Zeus’s benefits expand to multi-GPU settings as well (§6).
In summary, we make the following contributions:
-
•
To the best of our knowledge, we are the first to characterize the energy consumption vs. performance tradeoff for DNN training in terms of job- and GPU-specific configuration parameters.
-
•
We present an online optimization framework that can learn from and adapt to workload dynamics over time.
-
•
We implement and evaluate the optimizer in Zeus that integrates with existing DNN training workflows with little code change and negligible overhead, while enabling large benefits.
Zeus is open-source and available on GitHub.222https://github.com/SymbioticLab/Zeus
2 Motivation
In this section, we present an overview of energy consumption characteristics of DNN training on GPUs, opportunities for reducing energy consumption, and conclude with characterizing the tradeoff between reducing energy consumption and improving training performance.
2.1 DNN Training
Modern DNNs are trained by going over a large dataset multiple times, where each pass over the dataset is termed an epoch [28]. One epoch of training consists of thousands of iterations of gradient descent over equally sized mini-batches, with the batch size affecting model accuracy,333In this paper, we specifically consider the validation accuracy of the model, which captures how well the model generalizes to unseen data. training throughput, and energy consumption. The performance of DNN training is often measured in terms of time-to-accuracy (TTA) for a given target accuracy [19], and increasing training throughput (or precisely goodput [77]) leads to lower TTA.
2.2 Opportunities for Improving Energy Efficiency
We highlight two job and hardware configurations that can cause sizable energy inefficiency in DNN training: (1) batch size and (2) power limit of the GPU.
Impact of batch size on energy efficiency.
The size of each mini-batch during DNN training (batch size) determines how many samples are processed in one iteration. The higher it is, the faster we can go over the entire input dataset.
We observe across diverse DNN training workloads that common choices of batch size can lead to more energy consumption for the same target accuracy. Specifically, we performed a sweep over a large range of valid batch sizes (from 8 to the maximum batch size that fits in GPU memory) for six deep learning workloads including computer vision (CV), natural language processing (NLP), recommendation, and speech recognition on an NVIDIA V100 GPU (Figure 1).444We measure GPU power consumption using NVML [2]. Section 6.1 provides details on workloads and methodology. We find that the energy-optimal batch size (Batch Size Opt. in Figure 1) can lead to 3.4%–65.0% lower energy consumption than the default choice for the same target accuracy.



Impact of GPU power limit on energy efficiency.
Setting a GPU’s power limit will have the device internally trigger dynamic voltage and frequency scaling (DVFS) such that its power draw does not exceed the power limit [69]. If not set manually, the power limit is at the maximum by default. We performed a sweep over a wide range of GPU power limits555From the minimum to the maximum power limit allowed by NVIDIA System Management Interface [3]; from 100W to 250W for NVIDIA V100. for the aforementioned setup. We found that the optimal energy consumption (Power Limit Opt. in Figure 1) may happen at a lower power limit than the maximum and can reduce energy consumption by 3.0%–31.5%.
Joint optimization.
2.3 Energy-Performance Tradeoffs
Opportunities for reducing DNN training energy consumption comes with a cost. When optimized for energy efficiency, DNN training performance (time-to-accuracy, or TTA) may be impacted. In the following, we characterize this tradeoff.
We define the energy consumption of DNN training until it reaches its target accuracy as its energy-to-accuracy (ETA):
| (1) |
where denotes the GPU power limit, the batch size, and the average power consumption during training with configuration . Similar to TTA, ETA captures the end-to-end goal of DNN training.
Note that is not the same as the GPU power limit. When changes in configuration lead to an increase in TTA, ETA does not always follow because can decrease more. This motivates us to investigate the tradeoff between ETA and TTA.
Tradeoff between ETA and TTA.
We characterize and elaborate on this tradeoff using DeepSpeech2 trained on LibriSpeech as an example (Figure 2). It shows a scatter plot of (TTA, ETA) for the batch size and power limit sweep experiments in Section 2.2. We observe similar results for other workloads as well (Figure 16 in Appendix B).
Let us start with Figure 2a, where each data point denotes the (TTA, ETA) of training the model for a certain configuration.While sweeping the configurations, we focus on the boundary of all feasible (TTA, ETA) pairs. We find them to be bounded by two straight lines characterizing the average GPU power consumption. When the GPU is under heavy load, the (TTA, ETA) data points appear closer to 210W. On the other hand, when the GPU is under lighter load, its average power consumption tends closer to 90W, which is close to the GPU’s idle power consumption of 70W. More importantly, we find a curve along which all (TTA, ETA) pairs achieves Pareto optimality [16], for which we cannot improve ETA without sacrificing TTA, and vice versa.
Now let us take a closer look at the Pareto frontier in Figure 2b, with the configurations used during training annotated along each data point. We highlight two takeaways:
-
1.
These results show that baseline configurations can lead to suboptimal energy efficiency (§2). Moreover, it shows that blindly going for high batch size and power limit configurations can lead to suboptimal TTA as well.
-
2.
There exists a tradeoff between ETA and TTA, with different optimums for each. The configuration optimizing the ETA (32, 100W) is different from that optimizing TTA (48, 250W).
3 Zeus Overview
Zeus is an optimization framework that navigates the ETA-TTA tradeoff by automatically configuring the batch size and GPU power limit of recurring DNN training jobs. It enables developers to optimize energy and/or performance metrics using a single knob.
3.1 Optimization Metric
Defining a good cost metric for users to express their preference in this tradeoff is critical in designing Zeus. We propose a simple cost metric:
| (2) |
Here is the parameter specified by the user to express the relative importance of energy efficiency and training performance (throughput). When , we are only optimizing for time consumption, whereas when , we are only optimizing for energy consumption. is the maximum power limit supported by the GPU, a constant introduced to unify the units of measure in the cost metric.
3.2 Challenges in Picking the Optimal Configuration
Picking the optimal configuration(s) to minimize the energy-time cost for DNN training is challenging because the search space is large and obtaining the cost of each configuration is difficult. This is because it is hard to determine the value of both and efficiently, as explained below.
-
•
Complex power consumption model: The total energy consumption of a GPU is affected in a non-linear fashion by both the characteristics of the workload such as the number of instructions and memory accesses, as well as the GPU hardware configurations such as the frequency and voltage of the cores and memory on board [46, 6]. Existing efforts estimate GPU energy consumption based on instruction- or kernel-level information [43, 64], which are architecture-specific and workload-dependent.
-
•
Stochastic nature of DNN training: Modeling and predicting the duration for training a specific model to target accuracy (TTA) is known to be difficult [31]. Moreover, the randomness introduced during model initialization and data loading leads to variations of TTA, even when the same job is run on the same GPU with the same configuration – TTA variations can be as large as 14% [19].
3.3 Architectural Overview
At a high-level, Zeus takes an online exploration-exploitation approach to minimize the aggregate cost of recurrent DNN training jobs. Zeus addresses the aforementioned challenges with two key components:
-
1.
A just-in-time (JIT) online profiler, which efficiently profiles the energy characteristics of the training job online.
-
2.
Multi-Armed Bandit (MAB) with Thompson sampling, which allows us to embrace the stochastic nature of DL training and optimize under uncertainty while also adapting to changing workloads such as data drift.
The combination of the JIT profiler and MAB makes Zeus a fully online solution, allowing it to immediately begin optimizing for incoming jobs.

Workflow of Zeus.
Figure 3 shows an overview of the high-level workflow of Zeus. In a production environment, users submit recurrent DNN training jobs (a tuple of data, model, optimizer, and the target validation metric) to Zeus, along with a set of feasible batch sizes and power limits to explore. Zeus then predicts the optimal batch size and power limit configuration based on past execution history, and launches the training job with that configuration. During and after the training process, statistics about DNN training (e.g., validation metric) and GPU power consumption are collected and fed back to the Zeus optimizer. The Zeus optimizer learns from the feedback and adjusts its internal states. The training job will be terminated upon either reaching target metric or exceeding a stopping threshold determined by Zeus. The whole process is an automated feedback loop that minimizes the key objective of energy-time cost.
4 Zeus Algorithm Design
In this section, we delve into the details of how Zeus selects the best batch size and GPU power limit to optimize the overall cost of recurrent DNN training tasks. We first present the optimization problem formulation and how we decouple the optimizations of batch size and power limit (§4.1). Next, we show how to optimize power limit (§4.2) and batch size (§4.3) under the decoupled framework. We conclude by discussing how we address common challenging scenarios (§4.4).
4.1 Problem Formulation
The objective of Zeus is to minimize the cost of a recurring job by automatically exploring the feasible set of batch sizes and power limits . In essence, we neither want to incur too much cost searching for the optimal configuration, nor do we want to miss it. Minimizing the cumulative cost of the job over recurrences captures the implicit tradeoff between exploration and exploitation. Put formally in terms of the cost function defined by Equation 2, our objective becomes
| (4) | ||||
| s.t. |
where and respectively denote the batch size and power limit chosen at the th recurrence of the job, and and are vectors of length .
This is a challenging problem without modification, mainly because the size of the search space can be in the order of hundreds, and each value of inside the search space can only be obtained by running DNN training until it reaches the target metric. However, further expanding the cost function (Equation 3) allows us to decouple the exploration of batch size and power limit, making the problem more tractable:
| (5) | ||||
where denotes the number of epochs needed to reach the target, and epochs per second.
We find two key insights that allow the decoupling of batch size and power limit :
-
1.
Given , and can be profiled quickly during training for all possible choices of . This is due to the iterative nature of DNN training, yielding stable power and throughput estimations even with a small number of iterations.
-
2.
is not affected by the choice of as changing the power limit does not change what is computed.
This implies that the optimal power limit, given any batch size, can be determined independently based on online profiling. Moreover, since any choice of batch size is automatically accompanied by the optimal power limit, our search space is reduced to the set of batch sizes .
Formally put, we have decoupled the problem in Equation 4 into an equivalent two-level optimization problem
| (6) |
where
| (7) | ||||
4.2 Optimizing the Power Limit
We start with how Zeus determines the optimal power limit based on Equation LABEL:eq:plo-optimization, given a choice of the batch size. As highlighted earlier, we leverage the iterative nature of DNN training and the recurrent nature of jobs in production DNN training workflows.
When a job with batch size decision is submitted, our just-in-time (JIT) profiler is triggered and checks if this batch size had been profiled before. For an unseen batch size , it profiles and for all possible power limits during the first epoch of the job by partitioning the epoch into slices at iteration boundaries and dynamically changing the GPU power limit for each slice. The profile information is fed back to Zeus, and the optimal power limit of the batch size is determined by solving Equation LABEL:eq:plo-optimization. The rest of the epochs are executed with the optimal power limit. Our online JIT profiling approach consumes strictly less time and energy compared to offline profiling before running the job, because the profiling process itself contributes to training without affecting its accuracy. We show that JIT profiling incurs negligible overhead in Section 6.5.
4.3 Optimizing the Batch Size
Now we focus on how Zeus determines the batch size for each job recurrence that optimizes Equation 6. As seen in Section 4.2, is a cheap and deterministic function that identifies the optimal power limit for any batch size and returns the optimal cost of one epoch. Thus, we may limit our exploration to choosing the optimal batch size because whichever batch size we choose, the optimal power limit will accompany it.
Due to the unpredictable and stochastic nature of DNN training, picking out the optimal batch size without adequate exploration is difficult. Hence, a good solution must (1) incorporate such nature of DNN training into its exploration process, and (2) intelligently tradeoff the cost of exploring for potentially better batch sizes and the gain of exploiting batch sizes that are already known to be good.
Grid search is suboptimal.
We argue that exhaustively going through all batch sizes and selecting the one with the smallest cost is still suboptimal due to the stochastic nature of DNN training. That is, because the cost of a DNN training job can differ even when executed with the exact same configurations, it must be modeled as a cost distribution with unknown mean and variance. Although performing several trials for each batch size may yield a better estimation of the mean cost, such a strategy leads to high exploration cost because it does not quickly rule out obviously suboptimal batch sizes.
Multi-Armed Bandit formulation.
Zeus aims to explore the cost of different batch sizes and converge to the optimal batch size, while not incurring too much exploration cost.
Zeus formulates the problem as a Multi-Armed Bandit (MAB) with trials and arms, where each trial corresponds to a recurrence of the job and each arm to a batch size in . MAB is a good fit to our problem scenario in that it captures the stochasticity of DNN training by modeling the cost of each batch size as a random variable. Specifically, we choose the Gaussian distribution [81] due to its representational flexibility. The objective of the MAB formulation is to minimize the cumulative cost regret defined as
| (8) |
where the regret of choosing is defined as
| (9) | ||||
Minimizing cumulative cost regret aligns with our objective in Equation 6.
Thompson Sampling.
Belief posterior parameters and
Previous cost observations for
Belief prior parameters and
We adopt the Thompson Sampling [81] policy for the MAB formulation to tradeoff exploration and exploitation, not only because it is known to perform well in practice [17, 81] and had successful adoption recently [67, 58], but also because its modeling assumptions fit our problem scenario well.
At a high level, Thompson Sampling is an online procedure that refines its belief about the mean cost of each arm (batch size) based on experience. At each recurrence, the belief is used to pick the arm with the lowest estimated mean cost (Algorithm 1), and the belief is updated based on the actual cost observed (Algorithm 2).
Specifically, the cost distribution is modeled as a Gaussian distribution with unknown mean . Then, the belief about is modeled with its conjugate prior distribution, which is also a Gaussian distribution [24]. That is, . Here it is important to note that can be thought as of how confident the policy is in its belief about that arm, with the confidence increasing as it accumulates more observations of the cost of choosing that arm. Then, Thompson Sampling automatically balances exploration and exploitation by choosing the arm with the smallest mean cost sample (Algorithm 1). With low confidence (high variance), will be dispersed across a wider range of costs, having higher chances of getting chosen even if some of its initial observations showed high cost. In contrast, when the arms observed a lot of cost samples and the confidence is high (low variance), is likely to be centered around the mean observed cost, allowing the exploitation of arms that are known to be good. After the actual cost of an arm is observed, the belief parameters of that arm are updated using the Bayes Rule [81] (Algorithm 2).
The belief prior parameters and reflect prior belief about the mean cost of using the batch size for training and the confidence of such belief. Hence, the choice of prior parameters serve as a way to initialize the arms such that they reflect prior knowledge about the cost of each arm. If such information is not available, which is our default assumption, it is also possible to initialize the arms with a flat prior that assumes no prior knowledge – in our case, this is a Gaussian distribution with zero mean and infinite variance.
In contrast to grid search, our formulation using MAB and Thompson Sampling meets the two requirements mentioned earlier. That is, MAB inherently incorporates the stochastic nature of DNN training in that it models cost as a random variable. Moreover, Thompson Sampling can quickly rule out batch sizes that are obviously suboptimal because the probability of a smaller mean cost being sampled from an arm that observed noticeably large cost is low.
4.4 Extensions for Challenging Scenarios
Handling unknown cost variance.
Unlike conventional Gaussian Thompson Sampling applications, we may not assume that the variances of the cost of each arm are known. That is, the cost variance (i.e., how much the cost will fluctuate even when training is run with the same batch size) is not known before any observation. Moreover, the cost variance depends not only on the batch size, but also on the DNN’s robustness to the randomness in parameter initialization and data loading, making it difficult to quantify at the time the MAB is constructed. Hence, our approach is to learn the cost variance as we observe cost samples (Line 2 in Algorithm 2).

Handling stragglers during exploration.
There may be cases where an exploratory job does not reach the target metric within a reasonable amount of cost, especially during the earlier exploration stage. To handle this, we employ early stopping and pruning. The intuition is that if a batch size does not reach the target metric even after incurring an exceedingly large cost, it is highly unlikely to be the optimal one.
For early stopping, we define a cost threshold , meaning that when the cost of the current job is to exceed times the minimum cost observed so far, we stop the job and retry with another batch size. Here is a parameter to account for the stochastic nature of DL training. By default, we choose , with which we should be able to tolerate variations of TTA between different runs of the same configuration, which is usually less than the 14% [19].
Default batch size
Belief prior parameters and
For pruning, as illustrated in Figure 4, we begin with the default batch size provided by the user and first try smaller batch sizes until we meet the minimum batch size or a batch size that fails to reach the target metric before the early stopping threshold. The same process is repeated for batch sizes larger than the default batch size. Then, only the batch sizes that reached the target metric are kept in the batch size set we explore. After performing an initial round of pruning, the default batch size is updated to be the one with the smallest cost observed, and we perform pruning once more starting from the new default batch size.
The intuition behind our batch size pruning approach is the convexity we observe in the BS-ETA curve around the optimal batch size (See Figure 5). Moreover, pruning allows Zeus to quickly rule out batch sizes that are noticeably suboptimal (typically too large, leading to more training epochs and loss of accuracy [49, 27], or too small, yielding gradients that are too noisy [80]), thus cutting down the cost of exploration.
The overall process is depicted in Algorithm 3.
Handling concurrent job submissions.
Classic multi-armed bandit scenarios assume that the MAB immediately observes the cost of pulling an arm. However, in a DNN training cluster, recurring jobs may overlap in their execution when a later job starts before the completion of an earlier job. In this case, the MAB does not get to observe the cost of the earlier job at the time it has to decide the batch size for the later job. For deterministic policies like [56, 8], this leads to duplication exploration of the same batch size back-to-back, reducing the efficiency of exploration.
However, Thompson Sampling naturally mitigates this problem without modification because deciding the next batch size to explore () is a random function. That is, because Thompson Sampling samples the estimated mean cost from each arm’s belief distribution and returns the arm with the lowest sampled value, concurrent jobs can run different batch sizes even if there was no information gained between the invocations of . This is especially the case during the early stage of Thompson Sampling when the arms’ belief distributions have large variances (low confidence), losing little exploration efficiency.
During the short initial pruning phase, we run concurrent job submissions with the best-known batch size at that time. As the best batch size constantly updates throughout the exploration stage, this strategy fairly distributes the additional exploration opportunities from concurrent job submissions to batch sizes that are known to converge. We evaluate Zeus’s efficacy on handling concurrent job submissions in Section 6.3.
Handling data drift.
In production training clusters, the data on which the model is trained shifts, which is one of the reasons why re-training is triggered [63, 61]. The implication of drift in the perspective of the MAB is that the cost distribution of each arm is non-stationary.
Thompson Sampling allows a simple modification that allows us to handle non-stationary cost distributions. Since older cost observations become less and less relevant, we only operate on a window of most recent cost observations [10], and the belief distributions will not take old observations into account. Unlike exponential decay, windowing also allows the cost variance of the most recent observations to be estimated directly. When old history entries are evicted, computing the new parameters of the arm is also cheap thanks to the conjugate prior property. This way, Zeus transparently adapts to data drifts in an online manner, as we show in Section 6.4.
5 Zeus Implementation
Zeus is implemented as a Python library that can be imported into DNN training scripts. The ZeusDataLoader class integrates with PyTorch [74]. The class profiles power and throughput online by slicing epochs in iteration boundaries and invoking the NVML [2] library for power limit configuration and profiling. We have observed that five seconds of profiling for each power limit is enough to yield stable results. With the information, the optimal power limit can be automatically determined and applied. Moreover, ZeusDataLoader monitors the cost incurred by training and early stops the job if needed. Listing 1 shows an example training loop integrated with Zeus.
Observer Mode.
ZeusDataLoader supports Observer Mode, where it profiles the power consumption and throughput of each power limit and determines the optimal one, but keeps the power limit at the maximum. By doing so, without affecting time or energy consumption, ZeusDataLoader reports how much time and energy the job would have consumed if the power limit were the optimal one, allowing the user to get an idea of the impact of using Zeus. We believe that such a feature can encourage Zeus’s adoption by informing users of its potential savings.
6 Evaluation
| Task | Dataset | Model | Optimizer | Target Metric | |
|---|---|---|---|---|---|
| Speech Recognition | LibriSpeech [73] | DeepSpeech2 [33] | AdamW [62] | 192 | WER = 40.0% |
| Question Answering | SQuAD [79] | BERT (QA) [21] | AdamW [62] | 32 | F1 = 84.0 |
| Sentiment Analysis | Sentiment140 [26] | BERT (SA) [21] | AdamW [62] | 128 | Acc. = 84% |
| Image Classification | ImageNet [20] | ResNet-50 [38] | Adadelta [99] | 256 | Acc. = 65% |
| Image Classification | CIFAR-100 [53] | ShuffleNet-v2 [65] | Adadelta [99] | 1024 | Acc. = 60% |
| Recommendation | MovieLens-1M [34] | NeuMF [39] | Adam [51] | 1024 | NDCG = 0.41 |
We evaluate Zeus’s effectiveness in terms of navigating the energy-time tradeoff. Our key findings are as follows:
6.1 Experimental Setup
| Node | GPU Specification | Host Specification | ||
|---|---|---|---|---|
| HPE Apollo 6500 Gen10 Plus A40 4 | Model | A40 PCIe | CPU | AMD EPYC 7513 |
| VRAM | 48GB | RAM | 512GB DDR4-3200 | |
| mArch. | Ampere | Disk | 960GB NVMe SSD | |
| CloudLab [23] r7525 V100 2 | Model | V100 PCIe | CPU | AMD EPYC 7542 |
| VRAM | 32GB | RAM | 512GB DDR4-3200 | |
| mArch. | Volta | Disk | 2TB 7200rpm HDD | |
| Chameleon Cloud [48] RTX6000 | Model | RTX6000 | CPU | Xeon Gold 6126 |
| VRAM | 24GB | RAM | 192GB | |
| mArch. | Turing | Disk | 256GB SSD | |
| Chameleon Cloud [48] P100 2 | Model | P100 | CPU | Xeon E5-2670 v3 |
| VRAM | 16GB | RAM | 128GB | |
| mArch. | Pascal | Disk | 1TB HDD | |
Testbed Setup.
We evaluate Zeus with four generations of NVIDIA GPUs as specified in Table 2.
Workloads.
Table 1 summarizes our workloads. The default batch size () is chosen from the original model publication when available; otherwise, it is set to be the maximum batch size which consistently achieves the target accuracy.
In terms of learning rate, models trained with the Adadelta [99] optimizer do not require an initial learning rate. For optimizers that do require an initial learning rate, we made our best effort in choosing a batch size and learning rate pair that achieves reasonable accuracies by experimenting with values from the original publication of the model and those discovered by popular DL frameworks [95].
Baselines.
We compare against the following baselines:
-
1.
Default (, ). This is often the default configuration used by practitioners, where the GPU power limit is set to, or rather not changed from, the maximum. This is the most conservative baseline with no exploration.
-
2.
Grid Search with Pruning. This one tries out one configuration of for each recurrence of the job and selects the best one. We optimize naïve grid search by having it prune out batch sizes that failed to reach the target metric.
Metric.
Our primary metrics are ETA (energy consumption) and TTA (training time). Ideally, we want to reduce both; but due to their tradeoff, sometimes it may not be possible to simultaneously do both.
Defaults.
Methodology.
Due to resource constraints and environmental concerns, we cannot afford to repeatedly train all of our workloads with various configurations end-to-end hundreds of times sequentially. However, similar to how Zeus decouples the exploration of batch size and power limit, we may apply the same decoupling in our experimentation. That is, we instead take a trace-driven approach, where we collect two kinds of trace data:
-
1.
Training trace. We train all possible combinations of models and batch sizes until convergence and record the number of epochs the model took to reach its target accuracy. We repeat this with four different random seeds for every combination to capture the stochasticity in DNN training.
-
2.
Power trace. We use our JIT profiler to collect the throughput and average power consumption of all possible combinations of model, batch size, and power limit.
We then replay these traces when we need to train a model and reconstruct its TTA and ETA values in order to evaluate the decisions made by Zeus and baselines. Moreover, since we have access to all the possible choices and their outcomes, we also know the optimal choice. Therefore, with the traces, we can evaluate the regret achieved by Zeus and baselines.
Note that Zeus does not directly learn from these traces (which would be offline-profiling), but instead only learns from the replay of these traces in an online fashion.
While the aforementioned trace-driven method is used widely throughout our evaluation, we run Zeus end-to-end for the evaluation of handling data drift (§6.4) because it is more expensive to construct the trace for the drifting dataset.
6.2 Zeus Performance
In this section, we evaluate the performance of Zeus in terms of energy consumption and training time as well as the convergence characteristics of our Multi-Armed Bandit algorithm. Each experiment is run across multiple recurrences of DNN training jobs. We select the recurrence number to be , so that the Grid Search baseline finishes exploration and also has plenty of chances to exploit its choice.


Improvements in ETA.
Figure 6a shows the energy consumption (ETA) of the last five recurrences of Zeus and Grid Search w.r.t. the Default baseline, aiming to compare the final point each approach converged to. Zeus reduces energy consumption (ETA) by up to 15.3%–75.8% w.r.t. the baseline. This is also comparable to the reduction we found by exhaustively searching through all the configurations in Section 2 as well as by using Grid Search.
Tradeoff with TTA.
Figure 6b shows the time consumption (TTA) of the last five recurrences of Zeus and Grid Search w.r.t. the Default baseline. Even though Zeus reduces training time by up to 60.1%, for some workloads TTA is increased by 12.8% (Figure 6b). This is due to the tradeoff between ETA and TTA, which is the central focus of this paper. This is especially true for workloads with a tuned for minimizing training time, where there is little room for TTA improvement.


Cumulative regret.
While Zeus and Grid Search perform close to each other, Zeus uses significantly smaller amount of resources to converge. As a bandit-based solution, the effectiveness of our algorithm can be quantified via regret, the difference between the decision selected and the optimal choice (Equation 9 in Section 4.3).
Figure 7 shows the cumulative regret of Zeus and Grid Search for DeepSpeech2 and ResNet-50. The optimal configuration is identified separately by an exhaustive parameter sweep. We observe that in both workloads, Zeus is able to achieve better regret from the first job recurrence. Zeus reaches the plateau in the cumulative regret earlier than Grid Search, which means it converges to the optimal solution earlier. We observe similar results for other workload as well (Appendix D). In the worst case, Grid Search results in more cumulative regret than Zeus until convergence.
Convergence to a Pareto-optimal configuration.


Despite having no information about the application beforehand, Zeus learns the energy characteristics of it online in a few iterations. Figure 8 shows the search path of Zeus and Grid Search during training DeepSpeech2. Due to the decoupling in the optimization of power limit and batch size, Zeus explores the configuration space more efficiently and converges to the optimal configuration much faster. We observe similar results for other workloads (see Appendix E). Moreover, in Figure 8b we observe that Grid Search may not even converge to optimal configuration. This is due to the stochastic nature of DNN training, with even the same batch size yielding different energy and time consumptions. Hence, Grid Search may choose a suboptimal configuration when a suboptimal configuration luckily yields good energy and time consumptions.
6.3 Trace-Driven Simulation Using the Alibaba Trace
Here we evaluate how Zeus can save energy and time consumption for DNN training in large clusters. We run trace-driven simulation using the Alibaba GPU cluster trace [94] which contains over 1.2 million jobs spanning a period of two months. The Alibaba GPU cluster trace is suitable for our evaluation for two reasons. First, the trace identifies groups of recurring jobs, and each job is annotated with its group ID. Second, jobs within the same group show overlap in their execution, allowing us to evaluate Zeus’s capability of handling concurrent job submissions with Thompson Sampling.


In order to assign job groups to the workload (Table 1) that best resembles its runtime, we remove jobs that did not successfully terminate and run K-Means clustering [36] on the mean job runtime of each group to form six clusters. Then, we match the six clusters with our six workloads in the order of their mean runtime. When running simulation, in order to capture the intra-cluster runtime variation of each job, we scale the job runtime with the ratio of the job’s original runtime to its cluster’s mean runtime. We compare Zeus with Default and Grid Search and plot the results in Figure 9.
Figure 9a shows the cumulative energy consumption of training using all three approaches. Zeus outperforms both baselines for workloads of all types and sizes. Note that there are scenarios where the Grid Search performs worse than Default, due to it wasting too much energy and time during the exploration stage. Thanks to Zeus’s early stopping and quick online power optimization, its energy and time cost during the exploration stage is significantly reduced. Across all the models, Zeus reduces training energy usage by 7%–52%. Figure 9b shows the training time using Zeus to be increased by at most 16%, and in many cases even decreased by up to 33%. Finally, similar to earlier experiments, Zeus had significantly lower cumulative regret than Grid Search.
6.4 Handling Data Drift
While there are previous works that attempt to identify and address data drift in general ML settings [63], existing datasets are classification tasks based on small feature vectors [35, 12], completely synthetic [25, 44], or private [66].
Therefore, we create and open-source a new sentiment analysis dataset called Capriccio that is suitable for evaluating DNN models. Capriccio consists of 1.6 million tweets over three months from the Sentiment140 [26] dataset, labeled with sentiment scores and the timestamp of the tweet. We emulate data drift by capturing a sliding window of 500,000 tweets (roughly the amount of tweets in one month) at a time and moving the window forward by each day, generating 38 slices. We skip empty dates to avoid having identical slices.
We train BERT [21] on Capriccio with Zeus configured with a window size of 10, roughly corresponding to a time frame of two weeks on Twitter. We plot the selected batch size for each recurrence (slice) and its corresponding ETA and TTA of training in Figure 10. It can be seen that spikes in ETA and TTA (signaling that the current batch size may no longer be optimal) trigger the exploration of a batch size that is different from the one previously converged to.

6.5 Overhead of JIT Profiling
Measurements with the Deepspeech2 model using the default batch size show that JIT profiling results in a 0.01% increase in energy consumption and a 0.03% increase in time consumption. Such a tiny overhead is possible because the time needed to profile all power limits is very small (less than one minute) while one epoch of training spans hours (which is typical for DL workloads). Measurements on ShuffleNet-v2, which has much shorter epoch duration, show that JIT profiling results in a 0.6% increase in terms of time consumption and a 2.8% reduction in energy consumption.
6.6 Scaling to Multi-GPU
While the primary focus of this paper is on single-GPU settings, in this section, we show that Zeus can be extended to single-node multi-GPU training settings by profiling the power consumption of all GPUs that participate in training. Extensions to distributed multi-GPU setups that involve network communication is a potential future work.
Extending to multi-GPU allows us to compare our energy and time consumption with Pollux [77], a state-of-the-art distributed cluster scheduler that dynamically tunes the batch size during DNN training in order to maximize goodput. Training DeepSpeech2 on LibriSpeech on four NVIDIA A40 GPUs, Zeus consumes 12% more time but 21% less energy, comparing favorably. We especially note that while Pollux does not take energy into account, Zeus allows the user to select a different energy-time tradeoff point (e.g., speed up training but consume more energy) by selecting an appropriate .
6.7 Sensitivity Analysis and Ablation Studies
Impact of .

To characterize the impact of as defined in Equation 2, we perform a sweep of when training DeepSpeech2 and plot the resulting optimal (TTA, ETA) in Figure 11. We also plot the corresponding Pareto Front for reference. We observe that the resulting (TTA, ETA) data points fall closely to the Pareto Front. Moreover, we plot the lines along which the in Equation 2 is a constant, shown as the dotted lines. As expected, these lines form an envelope around the Pareto Front. Additional sensitivity analysis for can be found in Appendix F.
Impact of early-stopping threshold .

To study impact of the early-stopping threshold , we sweep from 1.5 to 5 and measure the cumulative ETA across all jobs. We calculate the difference in ETA relative to our default choice of , and plot the result of all jobs as well as a geometric mean across all jobs in Figure 12. The result shows that the default chosen by Zeus achieves the lowest geometric mean across all jobs. The intuition behind this is that when is too low, Zeus prematurely stops exploratory runs, reducing the effectiveness of exploration. In contrast, when is too high, it dilutes the benefit of early stopping which leads to inflated exploration cost.
Impact of individual components.
In order to show the gains from each component, we show the degradation of removing one component from Zeus: no early stopping (setting to infinity), no pruning (keeping a batch size that didn’t reach the target accuracy), and no JIT profiling (profiling each power limit in different recurrences). Figure 14 shows the slowdown relative to Zeus after disabling these components. We observe that the Zeus benefits mostly from early stopping.
Impact of GPU models.
Figure 14 shows the geometric mean of ETA normalized against Default across all jobs. Zeus achieves consistent ETA reductions across four generations of NVIDIA GPUs. See Appendix G for all results.


7 Discussion
Choice of configuration knobs.
In this paper, we pick the batch size and GPU power limit as the configuration knobs for Zeus to optimize. We choose these two to strike a balance in the tradeoff between the granularity of control and the size of the search space. For instance, one can set the frequency and voltage for individual components on the GPU for more fine-grained control and potentially higher energy efficiency, but this would result in prolonged exploration in the bigger search space. In contrast, we choose the GPU power limit, which effectively controls both frequency and voltage via DVFS and reduces the search space.
On the DL job configuration side, we pick the batch size as the knob for a similar reason. Changing the batch size has a broader impact on energy consumption of end-to-end DNN training, because it affects both the training time and the average power consumption during training. In comparison, other candidate configuration knobs such as learning rate fall short because they only affect the training time.
Hyperparameter optimization.
Hyperparameter optimization is an important workload, where many DL training jobs (trials) are submitted with specific hyperparameters chosen from a user-defined search space [9, 59, 60, 98]. If the users submit these trials with a specific batch size, they can specify the feasible batch size set to only contain that single batch size. In this case, Zeus can still reduce energy consumption by searching for the optimal GPU power limit.
Supporting distributed training.
Zeus currently only supports single-node training, but it can easily be extended to support distributed scenarios. Since the same type of GPU will have the same time and power consumption characteristics, we can apply the same power limit configuration across all GPUs to avoid stragglers. The definition of cost can be extended to sum over the time and energy consumption of all GPUs participating in training, and all other components in our solution can remain identical.
Supporting heterogeneous GPUs.
Our solution assumes that the training job runs on the same type of GPU across all of its recurrences. However, in practice, this may not always be possible due to varying resource contention or availability.
It is straightforward to add support for heterogeneous GPUs under our formulation. That is, cost values observed from one GPU can be translated to values that represent the characteristics of another GPU. As shown in Equation 6, energy-time cost can be written as the product of and . Here, the former term is independent with the choice of the GPU. Moreover, the latter term can be quickly profiled on any GPU because it consists of only and . Thus, we can obtain cost values that represent the new GPU by quickly profiling for each batch size on the new GPU and multiplying it with observed from the previous GPU. These translated cost observations can then be used to learn a new MAB that specializes on the new GPU.
8 Related Work
DNN training.
A large body of recent studies focus on creating fast kernels for tensor operations [45, 92, 100, 18], efficiently placing data and/or computation [72, 78, 97, 55], and optimizing communication [91, 76]. However, most of them optimize for TTA and are oblivious of their energy impact. These works can be applied together with Zeus, potentially accelerating training while making it energy efficient.
Another recent effort in reducing TTA (without considering energy) in multi-GPU DNN training settings is Pollux [77]. Pollux dynamically changes the batch size during training based on the Gradient Noise Scale (GNS) [68]. However, GNS does not theoretically capture the generalization of the model [68] and can only be efficiently approximated when there are more than one GPUs participating in training. Zeus, on the other hand, optimizes and trades off TTA and ETA by tuning the batch size across job recurrences and does not alter the model’s convergence characteristics.
Energy measurement for Deep Learning.
A recent line of research has analyzed the energy consumption [75] as well as the environmental impact [85, 54] for training large DNN models inside a cluster. On the device-level, benchmarking efforts have been made to understand the energy efficiency and performance of training DNN on GPUs and other accelerators [93]. Several Python frameworks have been built for measurement [40, 14] and prediction [5] of energy consumption for DNN training. Zeus takes a similar software-based approach to measure power consumption via NVML [2], in order to perform JIT profiling of DNN training jobs.
Energy optimization for Deep Learning.
Existing work has investigated energy-accuracy tradeoff in the context of DNN inference with new neural network architecture [89] and algorithm-hardware co-design [86], and training strategies such as warm-start [7] and gradient-matching-based data subset selection [50]. Other works optimize energy for DNN training on multiple GPUs with scheduling [47] and task mapping [52]. Zeus complements these solutions as it can be plugged in transparently into these frameworks.
Several works have studied the impact of GPU dynamic frequency and voltage scaling (DVFS) and power configuration on the energy consumption and performance of DNN training [101, 90, 87, 11, 52], wherein they focus on the tradeoff between the transient metric of system throughput and power consumption. While these work rely on offline modeling and profiling, Zeus focuses on a more realistic end-to-end metric of energy-to-accuracy and is fully online.
BatchSizer [71] introduces batch size as a control knob to optimize for energy efficiency of DNN inference. Zeus focuses on DNN training, and takes a holistic approach, optimizing both GPU and job configurations together.
9 Conclusion
In this work, we sought to understand and optimize the energy consumption of DNN training on GPUs. We identified the tradeoff between energy consumption and training time, and demonstrated that common practices can lead to inefficient energy usage. Zeus is an online optimization framework for recurring DNN training jobs that finds the Pareto frontier and allows users to navigate the frontier by automatically tuning the batch size and GPU power limit of their jobs. Zeus outperforms the state-of-the-art in terms of energy usage for diverse workloads and real cluster traces by continuously adapting to dynamic workload changes such as data drift. We earnestly hope that Zeus will inspire the community to consider energy as a first-class resource in DNN optimization.
Acknowledgements
Special thanks to CloudLab and Chameleon Cloud for making Zeus experiments possible. We would also like to thank the reviewers, our shepherd Jayashree Mohan, and SymbioticLab members for their insightful feedback. We also thank our colleague Rui Liu for his helpful suggestions. This work is in part supported by NSF grants CNS-1909067 and CNS-2104243 and a grant from VMWare. Jae-Won Chung is additionally supported by the Kwanjeong Educational Foundation.
References
- [1] How much electricity does an American home use? https://www.eia.gov/tools/faqs/faq.php?id=97&t=3.
- [2] NVIDIA Management Library (NVML). https://developer.nvidia.com/nvidia-management-library-nvml.
- [3] NVIDIA System Management Interface. https://developer.nvidia.com/nvidia-system-management-interface.
- [4] Thomas Anderson, Adam Belay, Mosharaf Chowdhury, Asaf Cidon, and Irene Zhang. Treehouse: A case for carbon-aware datacenter software. In HotCarbon, 2022.
- [5] Lasse F. Wolff Anthony, Benjamin Kanding, and Raghavendra Selvan. Carbontracker: Tracking and predicting the carbon footprint of training deep learning models. ICML Workshop on Challenges in Deploying and monitoring Machine Learning Systems, 2020.
- [6] Yehia Arafa, Ammar ElWazir, Abdelrahman ElKanishy, Youssef Aly, Ayatelrahman Elsayed, Abdel-Hameed Badawy, Gopinath Chennupati, Stephan Eidenbenz, and Nandakishore Santhi. Verified instruction-level energy consumption measurement for NVIDIA GPUs. In Proceedings of the 17th ACM International Conference on Computing Frontiers, 2020.
- [7] Jordan Ash and Ryan P Adams. On warm-starting neural network training. NeurIPS, 2020.
- [8] Peter Auer, Nicolo Cesa-Bianchi, and Paul Fischer. Finite-time analysis of the multiarmed bandit problem. Machine learning, 47(2):235–256, 2002.
- [9] James Bergstra, Rémi Bardenet, Yoshua Bengio, and Balázs Kégl. Algorithms for hyper-parameter optimization. NeurIPS, 2011.
- [10] Omar Besbes, Yonatan Gur, and Assaf Zeevi. Stochastic multi-armed-bandit problem with non-stationary rewards. NeurIPS, 2014.
- [11] Srikant Bharadwaj, Shomit Das, Yasuko Eckert, Mark Oskin, and Tushar Krishna. Dub: Dynamic underclocking and bypassing in NoCs for heterogeneous GPU workloads. In 2021 15th IEEE/ACM International Symposium on Networks-on-Chip (NOCS), 2021.
- [12] Albert Bifet, Geoff Holmes, Bernhard Pfahringer, Philipp Kranen, Hardy Kremer, Timm Jansen, and Thomas Seidl. Moa: Massive online analysis, a framework for stream classification and clustering. In Proceedings of the first workshop on applications of pattern analysis, 2010.
- [13] Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, Sandhini Agarwal, Ariel Herbert-Voss, Gretchen Krueger, Tom Henighan, Rewon Child, Aditya Ramesh, Daniel Ziegler, Jeffrey Wu, Clemens Winter, Chris Hesse, Mark Chen, Eric Sigler, Mateusz Litwin, Scott Gray, Benjamin Chess, Jack Clark, Christopher Berner, Sam McCandlish, Alec Radford, Ilya Sutskever, and Dario Amodei. Language models are few-shot learners. In NeurIPS, 2020.
- [14] Qingqing Cao, Aruna Balasubramanian, and Niranjan Balasubramanian. Towards accurate and reliable energy measurement of NLP models. In Proceedings of SustaiNLP: Workshop on Simple and Efficient Natural Language Processing, 2020.
- [15] Maurizio Capra, Beatrice Bussolino, Alberto Marchisio, Guido Masera, Maurizio Martina, and Muhammad Shafique. Hardware and software optimizations for accelerating deep neural networks: Survey of current trends, challenges, and the road ahead. IEEE Access, 8:225134–225180, 2020.
- [16] Yair Censor. Pareto optimality in multiobjective problems. Applied Mathematics and Optimization, 4(1):41–59, 1977.
- [17] Olivier Chapelle and Lihong Li. An empirical evaluation of thompson sampling. NeurIPS, 2011.
- [18] Tianqi Chen, Thierry Moreau, Ziheng Jiang, Lianmin Zheng, Eddie Yan, Haichen Shen, Meghan Cowan, Leyuan Wang, Yuwei Hu, Luis Ceze, et al. TVM: An automated end-to-end optimizing compiler for deep learning. In OSDI, 2018.
- [19] Cody Coleman, Daniel Kang, Deepak Narayanan, Luigi Nardi, Tian Zhao, Jian Zhang, Peter Bailis, Kunle Olukotun, Chris Ré, and Matei Zaharia. Analysis of dawnbench, a time-to-accuracy machine learning performance benchmark. ACM SIGOPS Operating Systems Review, 2019.
- [20] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. ImageNet: A large-scale hierarchical image database. In CVPR, 2009.
- [21] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics (NAACL), 2019.
- [22] Jesse Dodge, Taylor Prewitt, Remi Tachet des Combes, Erika Odmark, Roy Schwartz, Emma Strubell, Alexandra Sasha Luccioni, Noah A. Smith, Nicole DeCario, and Will Buchanan. Measuring the carbon intensity of AI in cloud instances. In ACM Conference on Fairness, Accountability, and Transparency, 2022.
- [23] Dmitry Duplyakin, Robert Ricci, Aleksander Maricq, Gary Wong, Jonathon Duerig, Eric Eide, Leigh Stoller, Mike Hibler, David Johnson, Kirk Webb, et al. The design and operation of CloudLab. In ATC, 2019.
- [24] Daniel Fink. A compendium of conjugate priors. 1997.
- [25] Joao Gama, Pedro Medas, Gladys Castillo, and Pedro Rodrigues. Learning with drift detection. In Brazilian symposium on artificial intelligence, 2004.
- [26] Alec Go, Richa Bhayani, and Lei Huang. Twitter sentiment classification using distant supervision. Stanford CS224N project report, 2009.
- [27] Noah Golmant, Nikita Vemuri, Zhewei Yao, Vladimir Feinberg, Amir Gholami, Kai Rothauge, Michael W Mahoney, and Joseph Gonzalez. On the computational inefficiency of large batch sizes for stochastic gradient descent. arXiv preprint arXiv:1811.12941, 2018.
- [28] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep learning. MIT press, 2016.
- [29] Priya Goyal, Piotr Dollár, Ross Girshick, Pieter Noordhuis, Lukasz Wesolowski, Aapo Kyrola, Andrew Tulloch, Yangqing Jia, and Kaiming He. Accurate, large minibatch SGD: Training ImageNet in 1 hour. arXiv preprint arXiv:1706.02677, 2017.
- [30] Diego Granziol, Stefan Zohren, and Stephen Roberts. Learning rates as a function of batch size: A random matrix theory approach to neural network training. Journal of Machine Learning Research, 23(173):1–65, 2022.
- [31] Juncheng Gu, Mosharaf Chowdhury, Kang G Shin, Yibo Zhu, Myeongjae Jeon, Junjie Qian, Hongqiang Liu, and Chuanxiong Guo. Tiresias: A GPU cluster manager for distributed deep learning. In NSDI, 2019.
- [32] Udit Gupta, Carole-Jean Wu, Xiaodong Wang, Maxim Naumov, Brandon Reagen, David Brooks, Bradford Cottel, Kim Hazelwood, Mark Hempstead, Bill Jia, et al. The architectural implications of facebook’s DNN-based personalized recommendation. In HPCA, 2020.
- [33] Awni Hannun, Carl Case, Jared Casper, Bryan Catanzaro, Greg Diamos, Erich Elsen, Ryan Prenger, Sanjeev Satheesh, Shubho Sengupta, Adam Coates, et al. Deep speech: Scaling up end-to-end speech recognition. arXiv preprint arXiv:1412.5567, 2014.
- [34] F Maxwell Harper and Joseph A Konstan. The movielens datasets: History and context. ACM transactions on interactive intelligent systems (TIIS), 5(4):1–19, 2015.
- [35] Michael Harries and New South Wales. Splice-2 comparative evaluation: Electricity pricing. 1999.
- [36] John A Hartigan and Manchek A Wong. Algorithm as 136: A k-means clustering algorithm. Journal of the royal statistical society. series c (applied statistics), 28(1):100–108, 1979.
- [37] Kim Hazelwood, Sarah Bird, David Brooks, Soumith Chintala, Utku Diril, Dmytro Dzhulgakov, Mohamed Fawzy, Bill Jia, Yangqing Jia, Aditya Kalro, et al. Applied machine learning at Facebook: A datacenter infrastructure perspective. In HPCA, 2018.
- [38] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
- [39] Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. Neural collaborative filtering. In Proceedings of the 26th international conference on world wide web, 2017.
- [40] Peter Henderson, Jieru Hu, Joshua Romoff, Emma Brunskill, Dan Jurafsky, and Joelle Pineau. Towards the systematic reporting of the energy and carbon footprints of machine learning. Journal of Machine Learning Research, 21(248):1–43, 2020.
- [41] Miro Hodak, Masha Gorkovenko, and Ajay Dholakia. Towards power efficiency in deep learning on data center hardware. In IEEE International Conference on Big Data, 2019.
- [42] Elad Hoffer, Itay Hubara, and Daniel Soudry. Train longer, generalize better: closing the generalization gap in large batch training of neural networks. In NeurIPS, 2017.
- [43] Sunpyo Hong and Hyesoon Kim. An integrated GPU power and performance model. In ISCA, 2010.
- [44] Geoff Hulten, Laurie Spencer, and Pedro Domingos. Mining time-changing data streams. In Proceedings of the seventh ACM international conference on Knowledge discovery and data mining (SIGKDD), 2001.
- [45] Zhihao Jia, Oded Padon, James Thomas, Todd Warszawski, Matei Zaharia, and Alex Aiken. TASO: Optimizing deep learning computation with automatic generation of graph substitutions. In SOSP, 2019.
- [46] Vijay Kandiah, Scott Peverelle, Mahmoud Khairy, Junrui Pan, Amogh Manjunath, Timothy G Rogers, Tor M Aamodt, and Nikos Hardavellas. AccelWattch: A power modeling framework for modern GPUs. In MICRO, 2021.
- [47] Dong-Ki Kang, Ki-Beom Lee, and Young-Chon Kim. Cost efficient GPU cluster management for training and inference of deep learning. Energies, 15(2):474, 2022.
- [48] Kate Keahey, Jason Anderson, Zhuo Zhen, Pierre Riteau, Paul Ruth, Dan Stanzione, Mert Cevik, Jacob Colleran, Haryadi S Gunawi, Cody Hammock, et al. Lessons learned from the chameleon testbed. In ATC, 2020.
- [49] Nitish Shirish Keskar, Dheevatsa Mudigere, Jorge Nocedal, Mikhail Smelyanskiy, and Ping Tak Peter Tang. On large-batch training for deep learning: Generalization gap and sharp minima. In ICLR, 2017.
- [50] Krishnateja Killamsetty, S Durga, Ganesh Ramakrishnan, Abir De, and Rishabh Iyer. Grad-match: Gradient matching based data subset selection for efficient deep model training. In ICML, 2021.
- [51] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In ICLR, 2015.
- [52] Toshiya Komoda, Shingo Hayashi, Takashi Nakada, Shinobu Miwa, and Hiroshi Nakamura. Power capping of CPU-GPU heterogeneous systems through coordinating DVFS and task mapping. In 2013 IEEE 31st International Conference on computer design (ICCD). IEEE, 2013.
- [53] Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
- [54] Alexandre Lacoste, Alexandra Luccioni, Victor Schmidt, and Thomas Dandres. Quantifying the carbon emissions of machine learning. arXiv preprint arXiv:1910.09700, 2019.
- [55] Fan Lai, Xiangfeng Zhu, Harsha V Madhyastha, and Mosharaf Chowdhury. Oort: Efficient federated learning via guided participant selection. In OSDI, 2021.
- [56] Tze Leung Lai, Herbert Robbins, et al. Asymptotically efficient adaptive allocation rules. Advances in applied mathematics, 6(1):4–22, 1985.
- [57] Zhenzhong Lan, Mingda Chen, Sebastian Goodman, Kevin Gimpel, Piyush Sharma, and Radu Soricut. ALBERT: A lite BERT for self-supervised learning of language representations. ICLR, 2020.
- [58] Sebastien Levy, Randolph Yao, Youjiang Wu, Yingnong Dang, Peng Huang, Zheng Mu, Pu Zhao, Tarun Ramani, Naga Govindaraju, Xukun Li, et al. Predictive and adaptive failure mitigation to avert production cloud VM interruptions. In OSDI, 2020.
- [59] Liam Li, Kevin Jamieson, Afshin Rostamizadeh, Ekaterina Gonina, Jonathan Ben-Tzur, Moritz Hardt, Benjamin Recht, and Ameet Talwalkar. A system for massively parallel hyperparameter tuning. Proceedings of Machine Learning and Systems, 2:230–246, 2020.
- [60] Lisha Li, Kevin Jamieson, Giulia DeSalvo, Afshin Rostamizadeh, and Ameet Talwalkar. Hyperband: A novel bandit-based approach to hyperparameter optimization. The Journal of Machine Learning Research, 18(1):6765–6816, 2017.
- [61] Weixin Liang and James Zou. Metashift: A dataset of datasets for evaluating contextual distribution shifts and training conflicts. arXiv preprint arXiv:2202.06523, 2022.
- [62] Ilya Loshchilov and Frank Hutter. Decoupled weight decay regularization. In ICLR, 2019.
- [63] Jie Lu, Anjin Liu, Fan Dong, Feng Gu, Joao Gama, and Guangquan Zhang. Learning under concept drift: A review. IEEE Transactions on Knowledge and Data Engineering, 31(12):2346–2363, 2018.
- [64] Cheng Luo and Reiji Suda. A performance and energy consumption analytical model for GPU. In 2011 IEEE ninth international conference on dependable, autonomic and secure computing, 2011.
- [65] Ningning Ma, Xiangyu Zhang, Hai-Tao Zheng, and Jian Sun. Shufflenet v2: Practical guidelines for efficient CNN architecture design. In ECCV, 2018.
- [66] Ankur Mallick, Kevin Hsieh, Behnaz Arzani, and Gauri Joshi. Matchmaker: Data drift mitigation in machine learning for large-scale systems. In MLSys, 2022.
- [67] Ryan Marcus, Parimarjan Negi, Hongzi Mao, Nesime Tatbul, Mohammad Alizadeh, and Tim Kraska. Bao: Making learned query optimization practical. In SIGMOD, 2021.
- [68] Sam McCandlish, Jared Kaplan, Dario Amodei, and OpenAI Dota Team. An empirical model of large-batch training. arXiv preprint arXiv:1812.06162, 2018.
- [69] Xinxin Mei, Qiang Wang, and Xiaowen Chu. A survey and measurement study of GPU DVFS on energy conservation. Digital Communications and Networks, 3(2):89–100, 2017.
- [70] Sparsh Mittal and Sumanth Umesh. A survey on hardware accelerators and optimization techniques for RNNs. Journal of Systems Architecture, 112:101839, 2021.
- [71] Seyed Morteza Nabavinejad, Sherief Reda, and Masoumeh Ebrahimi. Batchsizer: Power-performance tradeoff for DNN inference. In Proceedings of the 26th Asia and South Pacific Design Automation Conference, 2021.
- [72] Deepak Narayanan, Aaron Harlap, Amar Phanishayee, Vivek Seshadri, Nikhil R Devanur, Gregory R Ganger, Phillip B Gibbons, and Matei Zaharia. Pipedream: generalized pipeline parallelism for DNN training. In SOSP, 2019.
- [73] Vassil Panayotov, Guoguo Chen, Daniel Povey, and Sanjeev Khudanpur. Librispeech: an ASR corpus based on public domain audio books. In IEEE international conference on acoustics, speech and signal processing (ICASSP), 2015.
- [74] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. NeurIPS, 2019.
- [75] David Patterson, Joseph Gonzalez, Quoc Le, Chen Liang, Lluis-Miquel Munguia, Daniel Rothchild, David So, Maud Texier, and Jeff Dean. Carbon emissions and large neural network training. arXiv preprint arXiv:2104.10350, 2021.
- [76] Yanghua Peng, Yibo Zhu, Yangrui Chen, Yixin Bao, Bairen Yi, Chang Lan, Chuan Wu, and Chuanxiong Guo. A generic communication scheduler for distributed DNN training acceleration. In SOSP, 2019.
- [77] Aurick Qiao, Sang Keun Choe, Suhas Jayaram Subramanya, Willie Neiswanger, Qirong Ho, Hao Zhang, Gregory R Ganger, and Eric P Xing. Pollux: Co-adaptive cluster scheduling for goodput-optimized deep learning. In OSDI, 2021.
- [78] Samyam Rajbhandari, Jeff Rasley, Olatunji Ruwase, and Yuxiong He. ZeRO: Memory optimizations toward training trillion parameter models. In International Conference for High Performance Computing, Networking, Storage and Analysis (SC), 2020.
- [79] Pranav Rajpurkar, Jian Zhang, Konstantin Lopyrev, and Percy Liang. SQuAD: 100,000+ questions for machine comprehension of text. In EMNLP, 2016.
- [80] Sebastian Ruder. An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747, 2016.
- [81] Daniel J Russo, Benjamin Van Roy, Abbas Kazerouni, Ian Osband, Zheng Wen, et al. A tutorial on thompson sampling. Foundations and Trends® in Machine Learning, 11(1):1–96, 2018.
- [82] Simone Scardapane and Dianhui Wang. Randomness in neural networks: an overview. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 7(2):e1200, 2017.
- [83] Roy Schwartz, Jesse Dodge, Noah A. Smith, and Oren Etzioni. Green AI. Commun. ACM, 63(12):54–63, 2020.
- [84] Samuel L Smith, Pieter-Jan Kindermans, Chris Ying, and Quoc V Le. Don’t decay the learning rate, increase the batch size. In ICLR, 2018.
- [85] Emma Strubell, Ananya Ganesh, and Andrew McCallum. Energy and policy considerations for deep learning in NLP. Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 2019.
- [86] Thierry Tambe, Coleman Hooper, Lillian Pentecost, Tianyu Jia, En-Yu Yang, Marco Donato, Victor Sanh, Paul Whatmough, Alexander M Rush, David Brooks, et al. EdgeBERT: Sentence-level energy optimizations for latency-aware multi-task NLP inference. In MICRO, 2021.
- [87] Zhenheng Tang, Yuxin Wang, Qiang Wang, and Xiaowen Chu. The impact of GPU DVFS on the energy and performance of deep learning: An empirical study. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, 2019.
- [88] William R Thompson. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika, 25(3-4):285–294, 1933.
- [89] Chengcheng Wan, Muhammad Santriaji, Eri Rogers, Henry Hoffmann, Michael Maire, and Shan Lu. ALERT: Accurate learning for energy and timeliness. In ATC, 2020.
- [90] Farui Wang, Weizhe Zhang, Shichao Lai, Meng Hao, and Zheng Wang. Dynamic GPU energy optimization for machine learning training workloads. IEEE Transactions on Parallel and Distributed Systems, 2021.
- [91] Guanhua Wang, Shivaram Venkataraman, Amar Phanishayee, Nikhil Devanur, Jorgen Thelin, and Ion Stoica. Blink: Fast and generic collectives for distributed ML. In Proceedings of Machine Learning and Systems, 2020.
- [92] Haojie Wang, Jidong Zhai, Mingyu Gao, Zixuan Ma, Shizhi Tang, Liyan Zheng, Yuanzhi Li, Kaiyuan Rong, Yuanyong Chen, and Zhihao Jia. PET: Optimizing tensor programs with partially equivalent transformations and automated corrections. In OSDI, 2021.
- [93] Yuxin Wang, Qiang Wang, Shaohuai Shi, Xin He, Zhenheng Tang, Kaiyong Zhao, and Xiaowen Chu. Benchmarking the performance and energy efficiency of AI accelerators for AI training. In 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID), 2020.
- [94] Qizhen Weng, Wencong Xiao, Yinghao Yu, Wei Wang, Cheng Wang, Jian He, Yong Li, Liping Zhang, Wei Lin, and Yu Ding. MLaaS in the wild: Workload analysis and scheduling in large-scale heterogeneous GPU clusters. In NSDI, 2022.
- [95] Thomas Wolf, Lysandre Debut, Victor Sanh, Julien Chaumond, Clement Delangue, Anthony Moi, Pierric Cistac, Tim Rault, Remi Louf, Morgan Funtowicz, Joe Davison, Sam Shleifer, Patrick von Platen, Clara Ma, Yacine Jernite, Julien Plu, Canwen Xu, Teven Le Scao, Sylvain Gugger, Mariama Drame, Quentin Lhoest, and Alexander Rush. Transformers: State-of-the-art natural language processing. In EMNLP, 2020.
- [96] Carole-Jean Wu, Ramya Raghavendra, Udit Gupta, Bilge Acun, Newsha Ardalani, Kiwan Maeng, Gloria Chang, Fiona Aga, Jinshi Huang, Charles Bai, Michael Gschwind, Anurag Gupta, Myle Ott, Anastasia Melnikov, Salvatore Candido, David Brooks, Geeta Chauhan, Benjamin Lee, Hsien-Hsin Lee, Bugra Akyildiz, Maximilian Balandat, Joe Spisak, Ravi Jain, Mike Rabbat, and Kim Hazelwood. Sustainable AI: Environmental implications, challenges and opportunities. In Proceedings of Machine Learning and Systems, 2022.
- [97] Yuanzhong Xu, HyoukJoong Lee, Dehao Chen, Blake Hechtman, Yanping Huang, Rahul Joshi, Maxim Krikun, Dmitry Lepikhin, Andy Ly, Marcello Maggioni, et al. GSPMD: general and scalable parallelization for ML computation graphs. arXiv preprint arXiv:2105.04663, 2021.
- [98] Peifeng Yu, Jiachen Liu, and Mosharaf Chowdhury. Fluid: Resource-aware hyperparameter tuning engine. MLSys, 2021.
- [99] Matthew D Zeiler. Adadelta: an adaptive learning rate method. arXiv preprint arXiv:1212.5701, 2012.
- [100] Lianmin Zheng, Chengfan Jia, Minmin Sun, Zhao Wu, Cody Hao Yu, Ameer Haj-Ali, Yida Wang, Jun Yang, Danyang Zhuo, Koushik Sen, Joseph E. Gonzalez, and Ion Stoica. Ansor: Generating high-performance tensor programs for deep learning. In OSDI, 2020.
- [101] Pengfei Zou, Ang Li, Kevin Barker, and Rong Ge. Indicator-directed dynamic power management for iterative workloads on GPU-accelerated systems. In 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID). IEEE, 2020.
Appendix A Energy Savings Potential on GPUs




Figure 15 shows the potential for energy savings on four different generations of NVIDIA GPUs: Ampere (A40), Volta (V100), Turing (RTX6000), and Pascal (P100). All four generations show that there are sufficient potential for energy savings, motivating Zeus.
Appendix B TTA vs. ETA for All Workloads






Figure 16 plots the Pareto Front for all six workloads and the baseline (default batch size and maximum power limit) is shown as a red triangle. Note that the axes do not start from zero in order to zoom into the Pareto Front. Data points were gathered on an NVIDIA V100 GPU.
Appendix C ETA w.r.t. Configurations for All Workloads











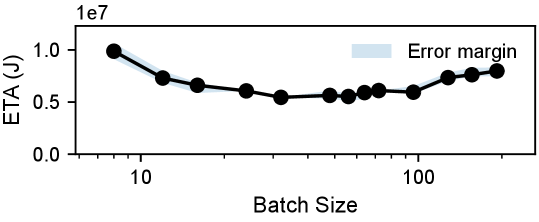
Appendix D Cumulative Regret of All Workloads





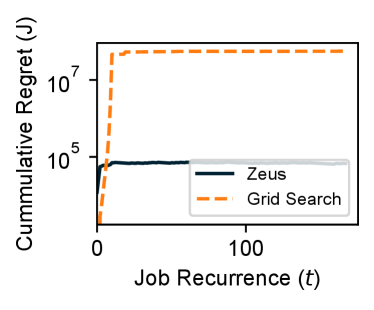
Figure 19 shows the cumulative regret of Zeus and Grid Search over job recurrences for all six workloads. In general, Zeus converges to a better knob than Grid Search while being faster.
Appendix E Search Paths for All Workloads

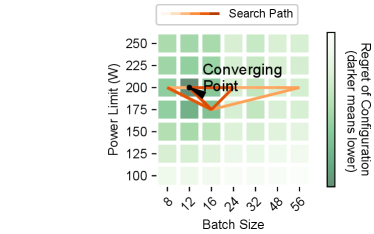










Figures 20 and 21 respectively show the search path of Zeus and Grid Search in the 2D configuration space. Thanks to the decoupling of batch size and power limit, Zeus is able to more efficiently navigate the search space and converge to a knob while consuming less energy and time during exploration.
Appendix F Additional Sensitivity Analysis

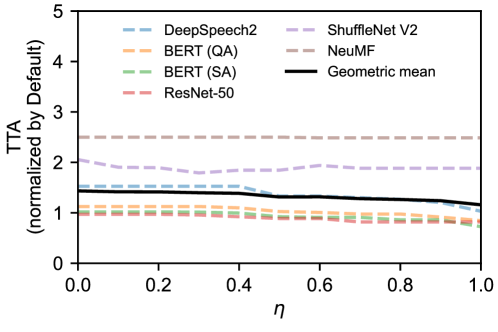
Figure 22 compares both the energy consumption and training time for Zeus against Default. We also calculate and plot the geometric mean across all jobs. The result shows that with higher , Zeus prioritizes reducing energy consumption over time, leading to higher improvement factor of energy, and vice versa.
Appendix G Performance of Zeus on All GPUs








Figure 23 presents the energy and time consumption of all workloads on four different generations NVIDIA GPUs: Ampere (A40), Volta (V100), Turing (RTX6000), and Pascal (P100). The overall trends hold for all GPUs.