Zero-field composite Fermi liquid in twisted semiconductor bilayers

Introduction. Recently, signatures of fractional quantum anomalous Hall (FQAH) states at zero magnetic field have been observed by optical measurements on twisted bilayer MoTe₂ ($t$MoTe₂) at fractional fillings of the moiré unit cell $n=\frac{2}{3}$ and $\frac{3}{5}$ [1]. In a separate work, the charge gap of the putative FQAH state at $n=\frac{2}{3}$ was measured [2]. FQAH states in twisted homobilayers of transition metal dichalcogenides (TMD) were theoretically predicted as a consequence of topological moiré bands [3], spontaneous ferromagnetism, and strong correlations [4, 5, 6, 7]. These recent observations provide new motivation to explore the phenomenology and phase diagram of partially filled Chern bands in $t$MoTe₂ and beyond [8, 9].

Unlike Landau levels, Chern band systems can exhibit competition between incompressible FQAH states  [10, 11, 12, 13, 14, 15, 16, 17, 18] and more conventional broken symmetry phases enabled by the presence of a periodic lattice structure, such as charge ordered phases [19, 20, 21] and generalized Wigner crystals [22, 23, 24, 25], or conducting phases [26, 27, 28] like Fermi liquids and even superconductors. Exotic quantum critical phases have also been shown to appear in half-filled flat Chern bands [29]. As a result, the global phase diagram of partially filled Chern bands is potentially much richer than that of Landau levels, calling for systematic study.

In this work, we focus on the physics of twisted TMD bilayers at even-denominator filling factors, which have not yet received attention. We present numerical evidence from continuum model exact diagonalization (ED) calculations of gapless metallic states at filling factors $n=\frac{1}{2}$ and $\frac{3}{4}$. Remarkably, depending on the twist angle, two types of ferromagnetic metals with full spin/valley polarization are found. At larger twist angle, the ground state is a Fermi liquid. In contrast, at smaller twist angles where strong interaction effect induces odd-denominator FQAH states, we find non-Fermi liquid metals of composite fermions at $n=\frac{1}{2}$ and $\frac{3}{4}$. These states share features with the composite Fermi liquid (CFL) at high magnetic fields [30, 31], but are “enriched” by the underlying moiré superlattice. We dub these zero-field non-Fermi liquid states “anomalous composite Fermi liquids” (ACFLs).

Synonymously with the CFL phases in Landau level systems, we propose the ACFL as the parent state of the FQAH phase diagram at $B=0$ [32, 33, 34]. Indeed, based on our ED study, we argue that the prominent FQAH states at $n=\frac{2}{3}$ and $\frac{3}{5}$ in twisted TMD homobilayers are descendants of the ACFL state at $n=\frac{1}{2}$. These states fall along a Jain sequence of FQAH states, which we show emerges by doping the ACFL.

We further reveal the unique phenomenology of the ACFL state itself. Perhaps most strikingly, the ACFL resistivity and thermodynamic properties experience intrinsic commensurability oscillations as a function of density, $\rho_{e}$, at $B=0$. This behavior contrasts both with an ordinary Fermi liquid and a CFL in a Landau level [35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45]. Close to the ACFL state, we find the oscillations are periodic in $1/\delta\rho_{e}$ and occur at large integers $j$ satisfying

$\displaystyle\frac{1}{\delta\rho_{e}}\propto\frac{j+\phi}{k_{F}\,Q}\,,$

(1)

where $\delta\rho_{e}\equiv\rho_{e}-\overline{\rho}$ is the doping density from half filling, $Q$ is the moiré superlattice wave vector, $k_{F}=\sqrt{4\pi\overline{\rho}}$ is the composite Fermi wave vector, and $\phi$ is a phase shift. For the ACFL state at a particular even-denominator filling fraction such as $\overline{n}=\frac{1}{2}$, $k_{F}$ is proportional to $Q$, meaning that the doping density, $\delta\rho_{e}$, associated with the commensurability oscillation is inversely proportional to the moiré unit cell area. As a result, the corresponding filling fraction, $n=\overline{n}+\delta n$, is universal.

Eq. (1) is both a consequence of the attachment of flux to charge in the ACFL – which causes the composite fermions to feel an effective magnetic field upon doping – and the system’s intrinstic moiré potential. In contrast, commensurability oscillations in CFLs in Landau level systems require an externally supplied periodic potential. In addition to commensurability oscillations, a distinguishing feature of a CFL (at zero or finite field) is a large DC Hall angle, ${\theta_{H}=\arctan(\sigma_{xy}/\sigma_{xx})}$, which approaches $\pi/2$ in the clean limit [30].

CFL phases are expected to exhibit non-Fermi liquid observable features, some of which may be accessible as new platforms are developed realizing the ACFL. For example, the thermodynamic entropy of the ACFL state can be measured from the change in chemical potential with temperature through a Maxwell relation  [46, 47]. In the clean limit, because gauge fluctuations lead to a logarithmic mass enhancement of composite fermions, the entropy of ACFL state should also be enhanced [48], ${s(T)/T\sim m_{*}(T)\sim\log T}$ [30], compared to the linear temperature dependence of an ordinary Fermi liquid, ${s(T)/T\sim\,}$constant. In systems where the electronic Coulomb interaction is screened by a nearby metallic gate, this enhancement becomes a power law, ${s(T)/T\sim T^{-1/3}}$.

Motivation. In ordinary Landau level quantum Hall systems, the existence of a CFL phase can be understood through flux attachment. At even-denominator filling ${\nu=2\pi\rho_{e}/B=\frac{1}{2q}}$, where $q$ is an integer, $\rho_{e}$ is the electron density, and $B$ is the external magnetic field, attaching $2q$ flux quanta to each electron completely screens the magnetic field, leading to an effective system of composite fermions in effective magnetic field $b_{*}=B-2q(2\pi\rho_{e})=0$. As a result, the composite fermions form a Fermi surface strongly coupled to an emergent gauge field [30]. Upon doping away from $\nu=\frac{1}{2q}$, the composite fermions feel a nonvanishing magnetic field and fill Landau levels, leading to the Jain sequence of observed fractional quantum Hall phases,

$\displaystyle\nu_{\mathrm{Jain}}$

$\displaystyle=\frac{p}{2q\,p-1}\,,$

(2)

where $p$ is the number of filled composite fermion Landau levels [32, 33].

A similar picture should be applicable to twisted TMD bilayers in the absence of a physical magnetic field, when (1) interactions spontaneously drive all carriers into the Chern band of one valley; (2) the Coulomb Hamiltonian projected to the Chern band sufficiently resembles that of the lowest Landau level (LLL); and (3) the band dispersion is small relative to the system’s characteristic interaction energy scale $\sim e^{2}/(\epsilon a_{M})$. When these conditions are satisfied, the problem can be approximately mapped to that of a partially filled Landau level. One might therefore expect that any of the quantum Hall phases in a Landau level at filling $\nu$ should be possible in a flat $C=1$ band at the same filling. The challenge is to find situations in which such physics succeeds over other phases that are not possible in Landau levels. Hence, once a material is known to exhibit the FQAH effect, it is natural to anticipate that other essential features of the fractional quantum Hall phase diagram also occur in the same material, such as the convergence of Jain sequence FQAH phases into a metallic CFL at half-filling.

Numerical evidence for ACFL. We now provide numerical evidence for the ACFL in $t$MoTe₂. The nontrivial layer pseudospin structure of this system’s Bloch wavefunctions endows its moiré bands with topological character [3]. In particular, the first moiré valence band in each valley has $|C|=1$, with opposite signs in opposite valleys due to time-reversal symmetry. We study the continuum model of $t$MoTe₂ with Coulomb interaction $U(r)=\frac{e^{2}}{\epsilon r}$ projected to the lowest moiré band, using finite size ED with torus geometry [8]. Further details of the model and methodology are provided in the Supplemental Material.

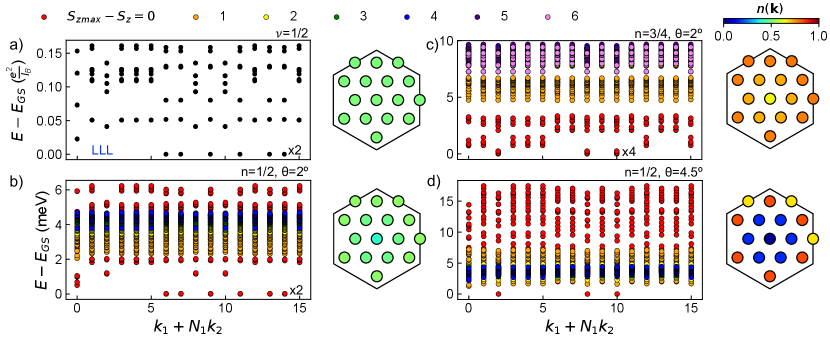
To establish a benchmark for a CFL on a finite-size torus, we show the low-lying many-body spectrum of the half-filled LLL on a torus with 16 flux quanta in Fig. 1(a). Given our system geometry, the spectrum features 12 exactly degenerate ground states with 2 in each of 6 momentum sectors. The momentum quantum numbers of the degenerate ground states reflect the most compact possible composite Fermi sea configurations [14]. There are 6 such configurations – one composite fermion is accounted for by occupying the state at the center of the Brillouin zone, 6 more by occupying the set of closest points, and the final one by occupying any one of the 6 next closest points. The additional factor of 2 in the overall ground state degeneracy is enforced by the non-commuting center-of-mass magnetic translations  [49]. We also show the momentum space occupation numbers of electron Bloch states averaged over the ground state manifold. The Bloch state occupation is uniform despite the presence of a composite Fermi sea.

Next, in Fig. 1(b), we show the many-body spectrum of the $\theta=2^{\circ}$ lowest $t$MoTe₂ band at filling $n=\frac{1}{2}$ on the corresponding 16-unit-cell torus across all possible $S_{z}\geq 0$ sectors. First, we observe that the lowest-lying states have $S_{z}=S_{z,\mathrm{max}}=4$, indicating spontaneous, full spin/valley polarization. Moreover, these states have the same momentum quantum numbers as their partners in the LLL, providing evidence for a composite Fermi sea. The momentum space occupation numbers are nearly uniform as in the LLL, demonstrating that the system is not a ferromagnetic Fermi liquid. In Fig. 1(c), we show an ED spectrum at $n=\frac{3}{4}$ that exhibits full valley polarization and similarly resembles its partner in the LLL, which is shown in the Supplemental Material.

In Fig. 1(d), we contrast these findings with $n=\frac{1}{2}$ at a larger twist angle $\theta=4.5^{\circ}$. Here, the lowest-energy states are still fully spin/valley polarized, but their many-body momenta are those expected from simply occupying the moiré band Bloch states with lowest energy, indicating a Fermi liquid phase. Moreover, the Bloch state occupation numbers in Fig. 1(c) exhibit a sharp drop across the Fermi surface expected for non-interacting, spin-polarized holes.

Effective theory of the ACFL. With this motivation, we propose a long wavelength effective theory of the ACFL in a Chern band at half-filling, $n=\frac{1}{2}$,

	$\displaystyle\mathcal{L}_{\mathrm{ACFL}}$	$\displaystyle=\psi^{\dagger}\Big{[}i\partial_{t}+a_{t}+A_{t}+\mathcal{V}(\bm{x})\Big{]}\,\psi$
		$\displaystyle\qquad-\frac{1}{2m_{*}}\left|(i\partial_{i}+a_{i}+A_{i})\psi\right|^{2}-V(\rho_{e})$
		$\displaystyle\qquad-\frac{1}{2}\frac{1}{4\pi}\,\varepsilon_{\mu\nu\lambda}\,a_{\mu}\partial_{\nu}a_{\lambda}-a_{t}\,\overline{\rho}\,.$		(3)

Here $\psi$ is the composite fermion field, $m_{*}$ is an effective mass; $V(\rho_{e})$ is the density-density interaction potential; ${a_{\mu}=(a_{t},a_{x},a_{y})}$ is a fluctuating Chern-Simons statistical gauge field; and ${A_{\mu}=(A_{t},A_{x},A_{y})}$ is the background electromagnetic gauge field. We denote the value of the charge density at half filling by $\overline{\rho}$, such that the charge per unit cell is ${\overline{n}\equiv\overline{\rho}\times(\textrm{unit cell area})=\frac{1}{2}}$. Importantly, although we focus on $n=\frac{1}{2}$ here, the theory for the ACFL at $n=\frac{3}{4}$ is easily obtained by attaching $4$ flux quanta and acting with a particle-hole transformation (subtracting a filled $C=1$ band). We expect its universal properties to be essentially the same as the ACFL at $n=\frac{1}{2}$. In the Supplemental Material, we discuss how Eq. (Zero-field composite Fermi liquid in twisted semiconductor bilayers ) can be constructed from a parton mean field construction along similar lines to Ref. [27], which also considered ACFL type phases in flat Chern bands (we note here that the Supplemental Material also includes the additional Refs. [50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66]).

The theory in Eq. (Zero-field composite Fermi liquid in twisted semiconductor bilayers ) closely resembles the Halperin-Lee-Read (HLR) theory of half-filled Landau levels [30]. This is not surprising: the $|C|=1$ Chern band in twisted TMD bilayers can be thought of as carrying an emergent magnetic flux of one flux quantum per unit cell, which arises from the skrymion lattice configuration of “Zeeman” field acting on the layer pseudospin  [3]. Nevertheless, there are two major differences with the standard HLR theory for a half-filled Landau level. The first is the final term, which alters the usual flux attachment constraint. Using the equation of motion for $a_{t}$,

$\displaystyle\rho_{e}=\overline{\rho}+\frac{1}{2}\frac{1}{2\pi}(\bm{\nabla}\times\bm{a})\,,$

(4)

where we have used the fact that the physical electron density consides with that of the composite fermions, ${\rho_{e}=\delta\mathcal{L}_{\mathrm{ACFL}}/\delta A_{t}=\psi^{\dagger}\psi}$, and boldface denotes spatial vectors. At half-filling of the Chern band, $n=\overline{n}=\frac{1}{2}$, meaning that by Eq. (4) the gauge flux per unit cell must vanish, and the composite fermions form a Fermi surface (as above, we use $n$ to denote charge per unit cell).

The second difference is that Eq. (Zero-field composite Fermi liquid in twisted semiconductor bilayers ) includes the effect of the moiré superlattice, in the form of a periodic scalar potential,

$\displaystyle\mathcal{V}(\bm{x})=\mathcal{V}_{0}\sum_{n=1}^{3}\cos\left(\bm{Q}_{n}\cdot\bm{x}\right)\,,$

(5)

where $\bm{Q}_{n}$ are the moiré superlattice wave vectors (see Supplemental Material). The full scalar potential felt by the composite fermions is therefore $\mathcal{V}(\bm{x})+A_{t}$, where $A_{t}$ includes any additional probe fields. We will see that the presence of this term leads to commensurability oscillations which are unique to the ACFL.

Although the theory in Eq. (Zero-field composite Fermi liquid in twisted semiconductor bilayers ) should correctly reproduce long wavelength, universal observable properties, we emphasize that this theory is not meant to completely incorporate microscopic details. For example, it does not give the correct algebra of density operators, nor does it incorporate the composite fermion dipole moment. Rather, we expect that should a complete, band-projected theory be constructed, then Eq. (Zero-field composite Fermi liquid in twisted semiconductor bilayers ) could be understood as its long wavelength limit. For recent efforts to develop band-projected composite fermion theories in the context of the LLL, see Refs. [67, 68, 69, 70].

FQAH sequence. Doping away from half-filling by tuning charge density or applied magnetic field causes the composite fermions to feel a net magnetic field and fill Landau levels. As a result, we can immediately predict a Jain sequence of FQAH states in $t$MoTe₂ corresponding to integer quantum Hall states of composite fermions. Like fractional Chern insulator states developed earlier [71, 16, 17, 18, 72], these FQAH phases are topological orders enriched with (super)lattice symmetry. Say that the composite fermions fill $p$ Landau levels,

$\displaystyle\nu_{\psi}=2\pi\frac{\langle\psi^{\dagger}\psi\rangle}{b_{*}}=p$

$\displaystyle,\qquad b_{*}=\bm{\nabla}\times(\bm{a}+\bm{A})\,,$

(6)

where $b_{*}$ is the total magnetic field felt by the composite fermions. Combining the flux attachment constraint, Eq. (4), with Eq. (6), we can relate the electron density to the applied magnetic field, ${B=\bm{\nabla}\times\bm{A}}$,

$\displaystyle\rho_{e}(B)$

$\displaystyle=\frac{p}{2p-1}\left(2\overline{\rho}-\frac{B}{2\pi}\right)\,.$

(7)

The Streda formula then implies that one will measure Landau fans extending to $B=0$, with slopes that fall on the Jain sequence (see Fig. 3),

$\displaystyle\frac{d\rho_{e}}{dB}=\sigma_{xy}=-\frac{p}{2p-1}\,.$

(8)

For the FQAH sequence proximate to $n=\frac{3}{4}$, one obtains FQAH states on the sequence, $n=1-\frac{p}{4p-1}$.

It is instructive to multiply Eq. (7) on both sides by the superlattice unit cell area to obtain the simple expression,

$\displaystyle n=\frac{p}{2p-1}\left(1-n_{\Phi}\right)\,,$

(9)

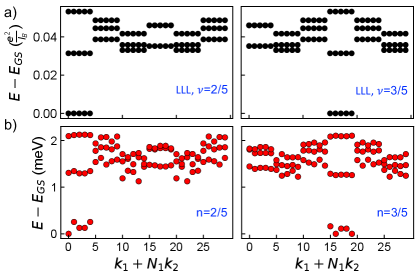
where $n_{\Phi}$ is the flux per unit cell. The FQAH Jain sequence includes the observed state at filling $\frac{2}{3}$ in $t$MoTe₂, which has also been studied numerically [8, 9]. In Fig. 2 we present ED evidence for additional Jain FQAH states in $t$MoTe₂ at $n=\frac{2}{5}$ and its particle-hole conjugate at $n=\frac{3}{5}$.

Intrinsic commensurability oscillations at zero field. We now explore the host of phenomena arising from an interplay of flux attachment with the presence of the moiré superlattice potential. Indeed, due to the periodic modulation intrinsic to moiré materials, we find that both commensurability oscillations [73, 74, 75, 76, 77] and Hofstadter subgaps can be accessed by tuning density alone.

Commensurability oscillations occur when the cyclotron radius and the modulation period are commensurate. More precisely, magnetoresistance minima and compressibility maxima are expected when a system in a spatially modulated potential with wave vector $Q$ satisfies the electronic flat band conditions,

$$2k_{F}Q\,\ell^{2}=2\pi(j+\phi)\,,$$

(10)

where $j$ is a positive integer, $\ell$ is the effective magnetic length felt by the electric charges, and $\phi$ is a phase shift. This condition is derived in the Supplemental Material from both perturbative and semiclassical approaches.

Again focusing on the $n=\frac{1}{2}$ ACFL, if the system is doped from half-filling by density, $\delta\rho_{e}=\rho_{e}-\overline{\rho}$, the composite fermions feel a magnetic field $b_{*}=4\pi\,\delta\rho_{e}$ by the flux attachment constraint in Eq. (4). As in the HLR approach, the composite Fermi wave vector of the ACFL described by Eq. (Zero-field composite Fermi liquid in twisted semiconductor bilayers ) is set by the electric charge density, ${k_{F}=\sqrt{4\pi\overline{\rho}}}$. We then find that commensurability oscillations occur at densities

$$\delta\rho_{e}=\frac{k_{F}\,Q}{(2\pi)^{2}}\frac{1}{j+\phi}$$

(11)

at large $j$ where $\delta\rho_{e}$ is small compared to $\overline{\rho}$. For the $n=1/2$ ACFL, we have $k_{F}Q=(4\pi^{3/2}/\sqrt[4]{3})/A$ ($A$ is the moiré unit cell area) so that the oscillations correspond to filling fractions, ${n=\frac{1}{2}+\delta n}$, where

$$\delta n=\frac{1}{\sqrt[4]{3}\sqrt{\pi}}\frac{1}{j+\phi}\approx\frac{0.43}{j+\phi}\,.$$

(12)

Close to $n=1/2$, the oscillations therefore have period $\Delta(1/\delta n)\approx 2.3$.

We emphasize that in the ACFL these commensurability oscillations occur in the absence of any external magnetic field. They coexist with SdH oscillations coming from filling integer Landau levels of composite fermions, which realize Jain states in a clean system. Additionally, tuning density and external field together allows full access of the magnetic spectrum of composite fermions near half-filling of the Chern band.

Discussion. Starting from a band-projected continuum model for $t$MoTe₂, we have presented exact diagonalization evidence for compressible, non-Fermi liquid states at zero magnetic field, which we dub the anomalous composite Fermi liquid. Much as in conventional fractional quantum Hall systems, we argue that the ACFL picture offers a powerful organizing perspective for understanding fractional quantum anomalous Hall states. Indeed, all of the states for which there currently exists theoretical or experimental evidence fall on the celebrated Jain sequence. We furthermore developed an effective theory capturing the universal properties of the ACFL offering concrete, observable signatures, including commensurability oscillations and Jain sequence FQAH states themselves.

Interestingly, in the recent experiment on $t$MoTe₂ [1], the coercive field is found to be enhanced at $n=\frac{3}{4}$, in addition to $n=\frac{2}{3}$. Unlike the $n=\frac{2}{3}$ state, which is incompressible, the $n=\frac{3}{4}$ state appears to be compressible. Our theory offers a potential explanation of the observed $n=\frac{3}{4}$ state as the ACFL.

Finally, the emergence of an ACFL state suggests the possibility of new quantum phase transitions not possible at finite field. For example, while our analysis here focuses on zero displacement field, it should be possible to induce a phase transition between ACFL and ferromagnetic Fermi liquid phases by tuning displacement field. Continuous transitions between CFLs and Fermi liquids have been proposed in the past [27, 28]. We leave study of such phase transitions to future work.

Note added. Recently, an independent work by Dong et al. [78] appeared, which has some overlapping conclusions with the present study.

Acknowledgements. We are grateful to Xiaodong Xu and Ady Stern for interesting discussions. HG also thanks Jennifer Cano, Mike Mulligan, Sri Raghu, T. Senthil, Raman Sohal, Alex Thomson, and Cenke Xu for conversations on related topics. This work was supported by the Air Force Office of Scientific Research (AFOSR) under award FA9550-22-1-0432 and the David and Lucile Packard Foundation. HG is supported by the Gordon and Betty Moore Foundation EPiQS Initiative through Grant No. GBMF8684 at the Massachusetts Institute of Technology. The authors acknowledge the MIT SuperCloud and Lincoln Laboratory Supercomputing Center for providing HPC resources that have contributed to the research results reported within this paper.