Zeptosecond dynamics in atoms: fact or fiction?

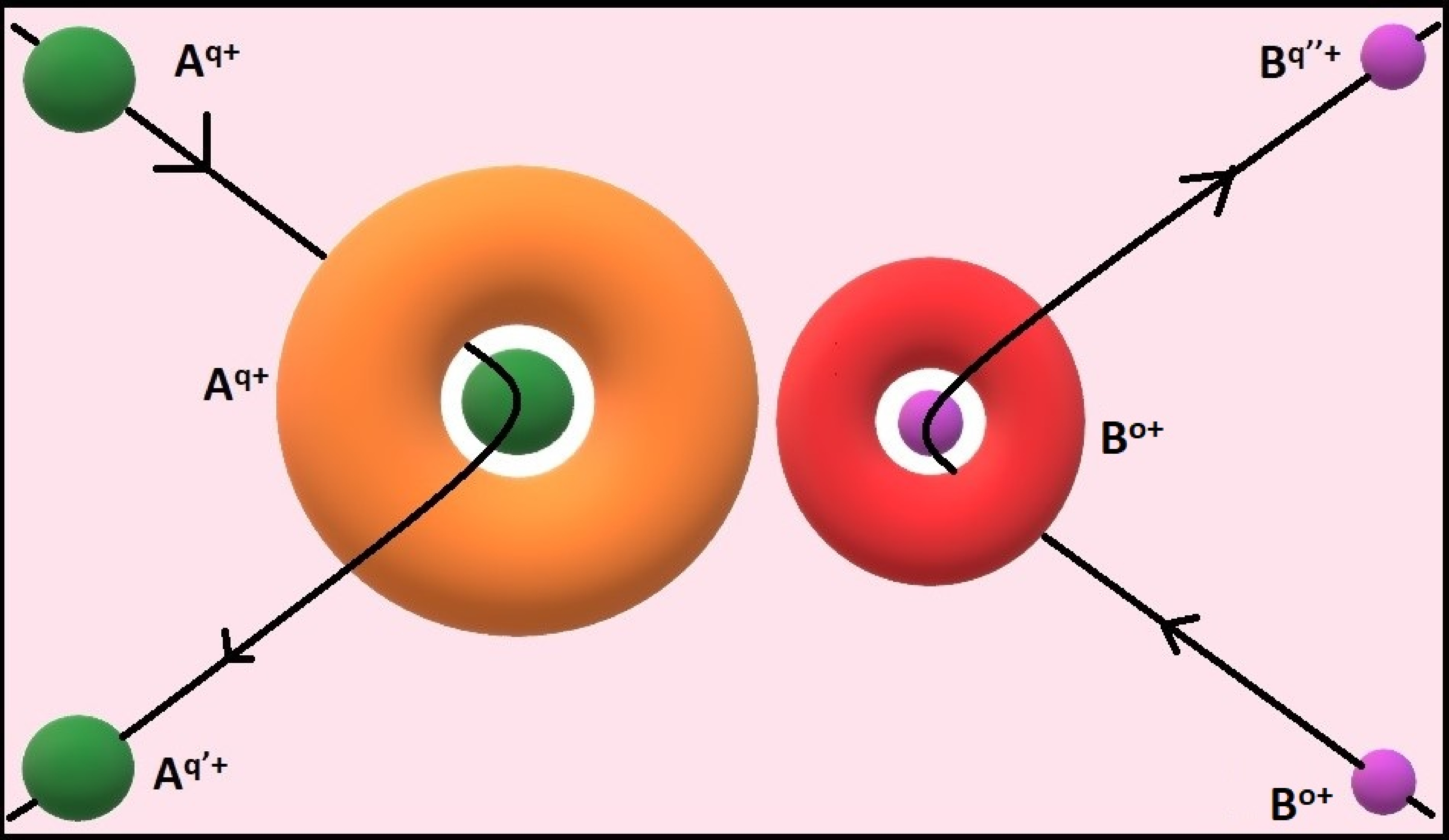
Nuclear Coulomb excitation can take place during the heavy-ion collisions at intermediate energy [18] and even at the relativistic energy [19]. The origin of nuclear Coulomb excitation is as follows: While the projectile approaching the target nucleus, it faces the nuclear interaction barrier potential [20] and thus it is retarded, which originates Lienard-Wiechert potential to emit electromagnetic radiation [21] or nuclear bremsstrahlung. A conceptual schematic diagram is shown in Fig.1. The power is radiated in a doughnut about the direction of spontaneous deceleration of the projectile or target nuclei, not in the forward or backward direction. It can be absorbed by the projectile ion or the target atom and total power radiated ($P$) by the projectile (target) can be calculated from the famous Larmor formula [21] in center of mass frame as

$$P=\frac{\mu_{0}q^{2}f^{2}}{6\pi c}$$

(1)

here $\mu_{0}$ the permeability in vacuum, $q$ the nuclear charge of the projectile (target), $c$ the velocity of light, and $f$ the deceleration of the projectile or target is obtained by the change of velocity of the projectile or target occurring in collision time $\tau_{coll}$. Two limits of $\tau_{coll}$ are

$$\tau^{max}_{Coll}=\frac{a}{v}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \text{and}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \tau^{min}_{Coll}=\frac{a\sin{(\theta_{cm}/2)}}{v}.$$

(2)

here the symmetrized parameter $a=Z_{1}Z_{2}e^{2}/(m_{0}v)$, $m_{0}$ is the reduced mass, $v$ is projectile ion velocity, and $\theta_{cm}$ is the grazing angle. Note that $\tau^{max}_{Coll}$ causes the minimum power and $\tau^{min}_{Coll}$ the maximum as $f$ varies with inverse squared of the collision time. Since $\theta_{cm}$ is close to 180^∘ at $\leq$ fusion barrier, we get $\tau^{min}_{Coll}=\tau^{max}_{Coll}$ at the sub-barrier energies. This condition holds good for the resonance energy also, which is quite lower than the fusion barrier energy. Resonance energy, interaction barrier, change of velocity of the projectile ion due to its encounter with the interaction barrier, $\tau^{max}_{Coll}$, and total energy radiated ($P\times\tau^{max}_{Coll}$) in the projectile system are listed in Table I.

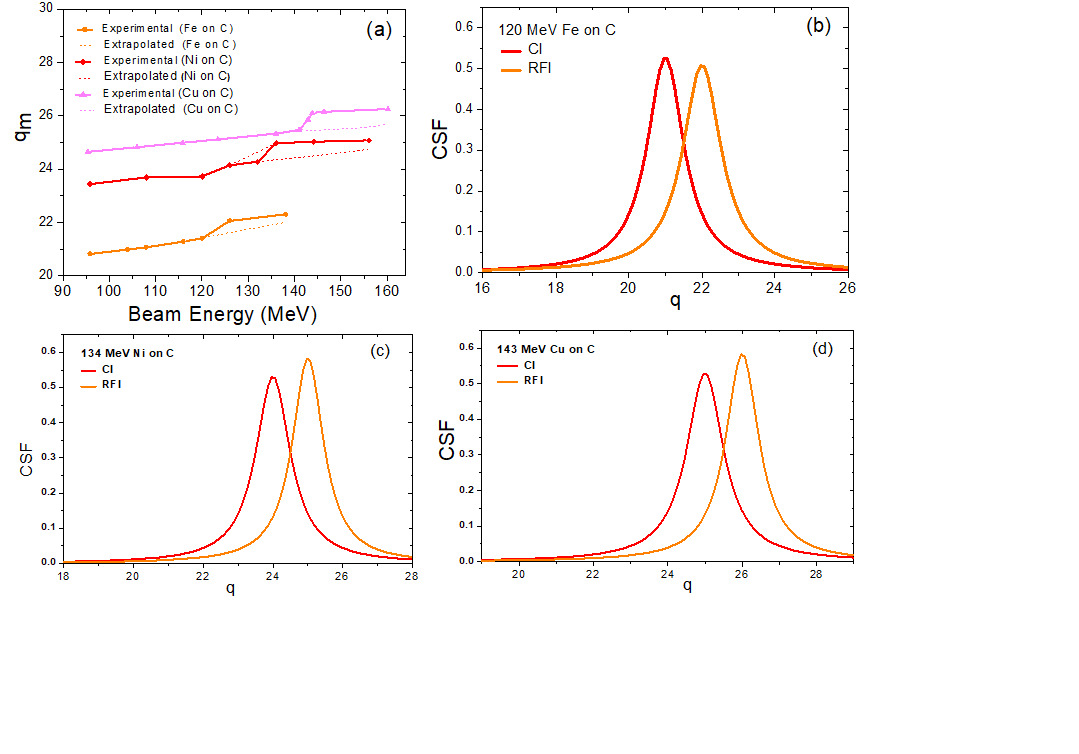
We can notice in Table I that the energy radiated is quite high. Let us see what degree of ionization can be caused from this energy in the projectile and target systems. The ionization energies vary with the ionic state and these data are readily available in NIST data base [22]. The charge states used for Fe beam of 120 MeV, Ni beam of 134 MeV, and Cu beam of 143 MeV were 9⁺, 10⁺, and 11⁺, respectively [23]. The radiation energy in every system can ionize it up to the bare ionic stage if we consider the full energy is absorbed in the system. If that is not the case, still high ionic state is achievable because of the fact that the s-electron is ionized faster than the p-electron [24]. The absorbed energy can create 1s and 2s shell fully ionized before the p-electrons and the K x-ray spectra can exhibit up to H-like lines. Exactly this fact is experimentally seen as shown in Fig. 2. Fig. 2(a) displays the variation of mean charge states (q_m) with beam energies. We can notice that the q_m vary quite smoothly till the resonance occurs at a certain beam energy. This trend signifies that till the resonance point only the Coulomb ionization (CI) is responsible but from this point on wards the nuclear bremsstrahlung being into action. If we fit the q_m data up to the resonance energy with a line and extrapolate it to the higher energies, we get an idea how the q_m would have varied in the post resonance regime in absence of the nuclear bremsstrahlung. This nature is shown by the dotted line in Fig. 2(a). Having gotten the q_m and the fact that the charge state distribution (CSD) inside the foil follows the Lorentzian distribution [23], we can numerically obtain the CSD, i.e., a plot of charge state fraction $F(q)$ versus the charge state $q$, due to the CI as well as radiation field ionization (RFI) at the resonance energy as follows

$$F(q)=\frac{1}{\pi}\frac{\frac{\Gamma}{2}}{(q-q_{m})^{2}-(\frac{\Gamma}{2})^{2}}$$

(3)

Here distribution width $\Gamma$ is taken from Novikov and Teplova [25], as follows

$$\centering\Gamma(x)=C[1-exp(-(x)^{\alpha})][1-exp(-(1-x)^{\beta})]\@add@centering$$

(4)

where $x=q_{m}/z$, $\alpha=0.23$, $\beta=0.32$, and $C=2.669-0.0098×Z_{2}+0.058×Z_{1}+0.00048×Z_{1}×Z_{2}$. Where

$$\Gamma^{2}=[1-(\frac{q_{m}}{Z})^{\frac{5}{3}}]\frac{q_{m}}{4}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \text{and}\leavevmode\nobreak\ \leavevmode\nobreak\ \leavevmode\nobreak\ \sum_{q}F(q)=1.$$

(5)

Here, the width $\Gamma$ is taken from the work of Novikov and Teplova [25]. Note that $q_{m}$ being different for CI and RFI. The CSDs so obtained are shown in Fig. 2(b-d). One can see clearly that the higher charge states are produced due to the RFI from resonance energy on wards. Though both the RFI and CI are the manifestation of the electromagnetic interaction, but they occur through the photons and charge particles, respectively. It implies that the RFI is faster than the CI. If RFI causes the higher charge state in advance, the CI cannot have any role to play on this charge changing process. Thus, the two processes are never in action together.
To know the difference between the nuclear and atomic timescales for the systems considered, we estimate the characteristic time ($t_{0}$) for the atomic states from the ratio of the expectation values of electronic radius ($\langle{r}\rangle$) and velocity ($\langle{v}\rangle$) of the corresponding state and it turns out to be in attoseconds. According to the measured x-ray spectra [12], on the average the exit channel occurs with the Li-like ions (mean charge state). Considering Li-like $1s2s2p$ ${}^{2,4}P^{o}_{1/2,3/2,5/2}$ levels in Fe, Ni, and Cu are mostly populated at the resonance energies. To evaluate $t_{0}$ for these levels, we have computed $\langle{r}\rangle$ and $\langle{v}\rangle$ by the multi-configuration Dirac-Fock formalism using GRASP2K [26]. The value of $t_{0}$ for the three systems mentioned in Table I is found to be 0.383, 0.328, and 0.306 $as$, respectively, which are at least two orders of magnitude larger than the nuclear collision times ($zs$ timescale) when the RFI is taking place. It thus raises a fundamental question: how does then the RFI transcend into the atomic regime ($as$ timescale)?

The above mentioned radiative power may cause both the excitation and ionization in the ions in the short nuclear collision timescales ($zs$). The ionization will give rise to free electrons leaving the ion in ground state, whereas the excitation can lead to autoionization in the multielectron atomic systems. This process may result in excited state that relaxes in to ground state by emitting with higher x-ray energy, as shown in Fig. 2. The autoionization process does not occur instantly as the electron has to move from the interaction regime to an interaction free regime, which introduces a time delay because of the difference between the density of states of the two regions [27]. The energy-integral of time delay is an adiabatic invariant in quantum scattering theory and it provides a quantization condition for resonances [28]. The delay in the autoionization process, called as the Eisenbud-Wigner-Smith (EWS) time delay [29, 30], has been measured in a recent experiment [24]. To estimate the EWS time delay as well as the photoionization cross-section, we have employed the nonrelativistic versions of the random-phase approximation with exchange (RPAE) and Hartree-Fock (HF) methods [31]. The partial photoionization cross-section for the transition from an occupied state $n_{i}l_{i}$ to the photoelectron continuum state $kl$ is calculated as

$$\sigma_{n_{i}l_{i}\to kl}(\omega)=\frac{4}{3}\pi^{2}\alpha a_{0}^{2}\omega\left|\langle kl\,\|\,\hat{D}\,\|n_{i}l_{i}\rangle\right|^{2}\,$$

(6)

where $\omega$ being the photon energy, $\alpha$ the fine structure constant and $a_{0}$ the Bohr radius are used in atomic units $e=m=\hbar=1$. In the independent electron Hartree-Fock (HF) approximation, the reduced dipole matrix element is evaluated as a radial integral given below

$$\langle kl\|\,\hat{D}\,\|n_{i}l_{i}\rangle=[l][l_{i}]\left(\begin{array}[]{rrr}l&1&l_{i}\\ 0&0&0\\ \end{array}\right)\\ \int r^{2}dr\,R_{kl}(r)\,r\,R_{n_{i}l_{i}}(r)\,$$

(7)

where the notation $[l]=\sqrt{2l+1}$ is used. The basis of occupied atomic states $\|n_{i}l_{i}\rangle$ is defined by the self-consistent HF method and calculated using the computer code [32]. The continuum electron orbitals $\langle kl\|$ are defined within the frozen-core HF approximation and evaluated using the computer code [33].
In the RPAE, the reduced dipole matrix element is found by summing an infinite sequence of Coulomb interactions between the photoelectron and the hole in the ionized shell. A virtual excitation in the shell $j$ to the ionized electron state ${\bm{k}}^{\prime}$ may affect the final ionization channel from the shell $i$. This way RPAE accounts for the effect of inter-shell $i\leftrightarrow j$ correlation, also known as inter-channel coupling. It is important to note that, within the RPAE framework, the reduced dipole matrix element is complex and, thereby, adds to the phase of the dipole amplitude.
The photoelectron group delay, which is the energy derivative of the phase of the complex photoionization amplitude, is evaluated as

$$\tau={d\over dE}\arg f(E)\equiv{\rm Im}\Big{[}f^{\prime}(E)/f(E)\Big{]}.$$

(8)

Here $f(E)$ is used as a shortcut for the amplitude $\langle\psi^{(-)}_{\bm{k}}|\hat{z}|\phi_{i}\rangle$ evaluated for $E=k^{2}/2$ and $\hat{\bm{k}}\parallel{\bm{z}}$, where $\psi^{(-)}_{\bm{k}}$ is an incoming scattering state with the given photoelectron momentum ${\bm{k}}$ [34].
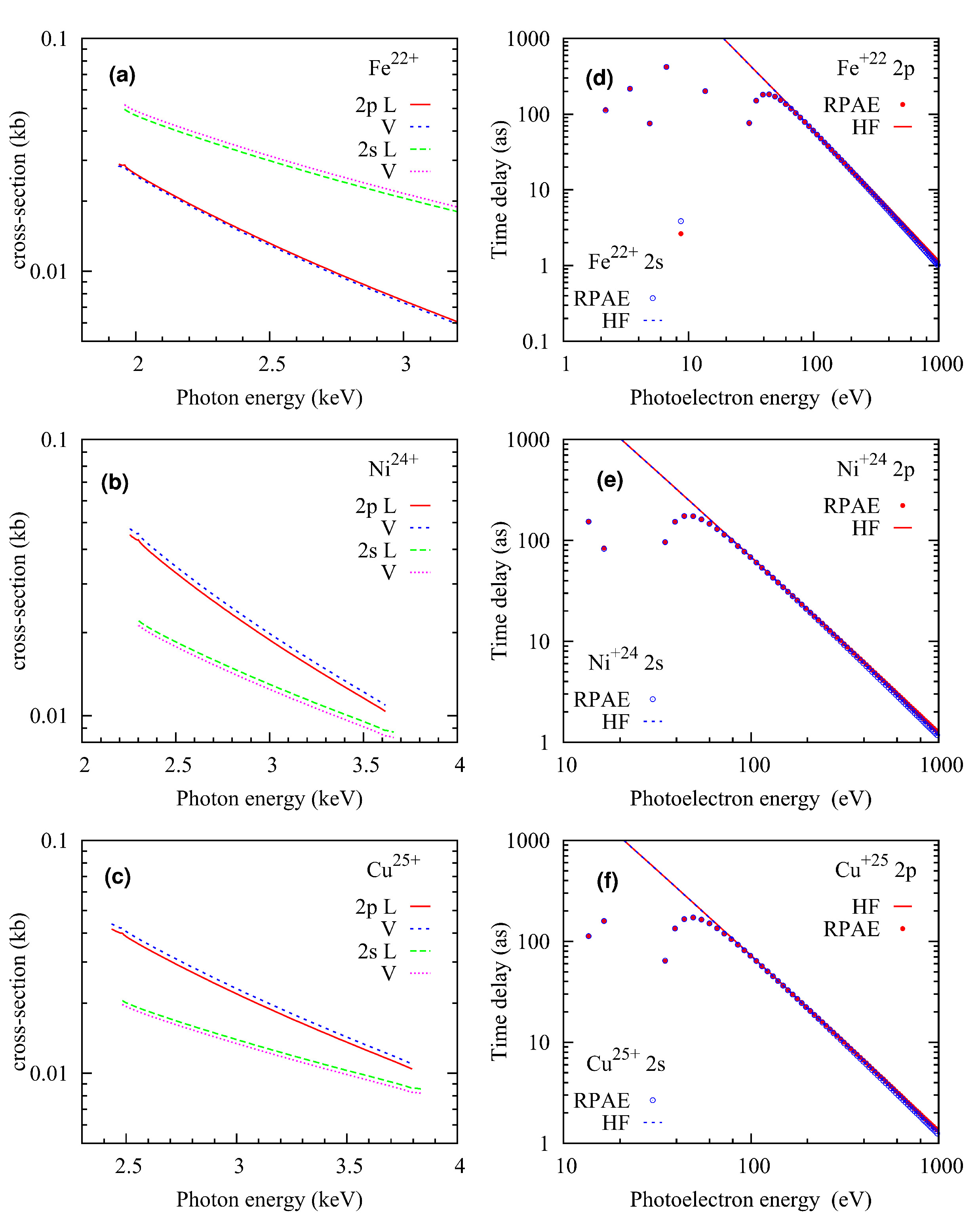
For the photoionization and time delay calculations, we have considered the charge species Fe²²⁺, Ni²⁴⁺, and Cu²⁵⁺ for the systems ⁵⁶Fe + ¹²C, ⁵⁸Ni + ¹²C, and ⁶³Cu + ¹²C, respectively, as the Li-like ions are observed [13] after the autoionizaion. It is found that the EWS time delay, $\tau$, is proportional to $\varepsilon^{-3/2}ln(1/\varepsilon$), where $\varepsilon$ is the photon energy and the elastic scattering phase, $\sigma$ ($\approx$ $\eta$ $ln{|\eta|}$, $\eta=-Z/\sqrt{2\varepsilon}$) are divergent near the threshold because of the Coulomb singularity [31]. To remove this singularity, we have cut off the low energy photoelectrons for time delay calculations in present computations. The results of the computations are presented in Fig.3 and the photoionization cross-sections are very close for the length (L) and velocity (V) gauges. The photoionization cross-sections for 2p electron in Ni²⁴⁺ and Cu²⁵⁺ are higher than that of 2s electron for all photon energies. Whereas, for Fe²²⁺, the photoionization cross-sections for 2s electron is higher than the 2p electron.
Dissociation of the excited state can only occur in $as$ or greater timescale because no atomic states exist with lifetime shorter than an $as$. This sort of occurrence is due to the fact that the emission of an electron from an excited state is delayed by $as$ due to electron correlation effects [35]. For example, photoemission of an electron is delayed up to six attoseconds [36]. Laser induced photoionization of different states in Ne are delayed differently. The 2p state is 21$\pm 5$ $as$ more delayed than the 2s state in Ne because of multi electron-correlation dynamics [24]. This picture has been theoretically reproduced using above mentioned approach and the same is applied for three test cases.