Zeno Regime of Collective Emission: Non-Markovianity beyond Retardation
Abstract
To build up a collective emission, the atoms in an ensemble must coordinate their behavior by exchanging virtual photons. We study this non-Markovian process in a subwavelength atom chain coupled to a one-dimensional (1D) waveguide and find that retardation is not the only cause of non-Markovianity. The other factor is the memory of the photonic environment, for which a single excited atom needs a finite time, the Zeno regime, to transition from quadratic decay to exponential decay. In the waveguide setup, this crossover has a time scale longer than the retardation, thus impacting the development of collective behavior. By comparing a full quantum treatment with an approach incorporating only the retardation effect, we find that the field memory effect, characterized by the population of atomic excitation, is much more pronounced in collective emissions than that in the decay of a single atom. Our results maybe useful for the dissipation engineering of quantum information processings based on compact atom arrays.
It is well known since the 1960s [1, 2] that the short-time dynamics of an excited atom differs significantly from the exponential decay based on the Weisskopf-Wigner formalism [3]. The finite memory of the photonic reservoir leads to a growth in the decay rate from zero that is quadratic in time [4, 5]. It has inspired attempts to prevent decay by quickly repeating measurements [6, 7, 8, 9], i.e., the Zeno effect. Actually, the duration of the non-exponential decay, characterized by the Zeno time , is typically many orders of magnitude shorter than the lifetime, rendering the field memory effect undetectable. For example, an optimal estimation of the 2P-1S transition of the hydrogen atom reads [10]. Instead of the decay of a single atom, in this Letter, we study atom ensembles [11], especially the subwavelength atom arrays, where the separation between two adjacent atoms, , is shorter than the resonant wavelength , and reveal the prominent memory effect in the Zeno regime.
The long-time collective emissions from an atomic ensemble are well described by Lehmberg’s formalism based on the Markov approximation [12, 13]. For example, it predicts a power-law scaling with the number of atoms for the subradiant states of a subwavelength atom array [14, 15, 16, 17]. However, Markovian theories are not able to answer how the collective behaviors are built up. This process must be non-Markovian because the atoms are organized by the retarded photon-mediated interactions. Instead, we may upgrade the Markovian description minimally by including delayed feedback: Every atom starts from exponential decay independently but adjusts its decay rate in response to the signal from another atom. This physical picture has been analytically studied for two atoms with the photonic reservoir being 3D free space [18] or 1D waveguide [19, 20, 21]. Retardation effects of waveguide quantum electrodynamics (QED) are also studied in Refs. [22, 23, 24, 25, 26, 27].
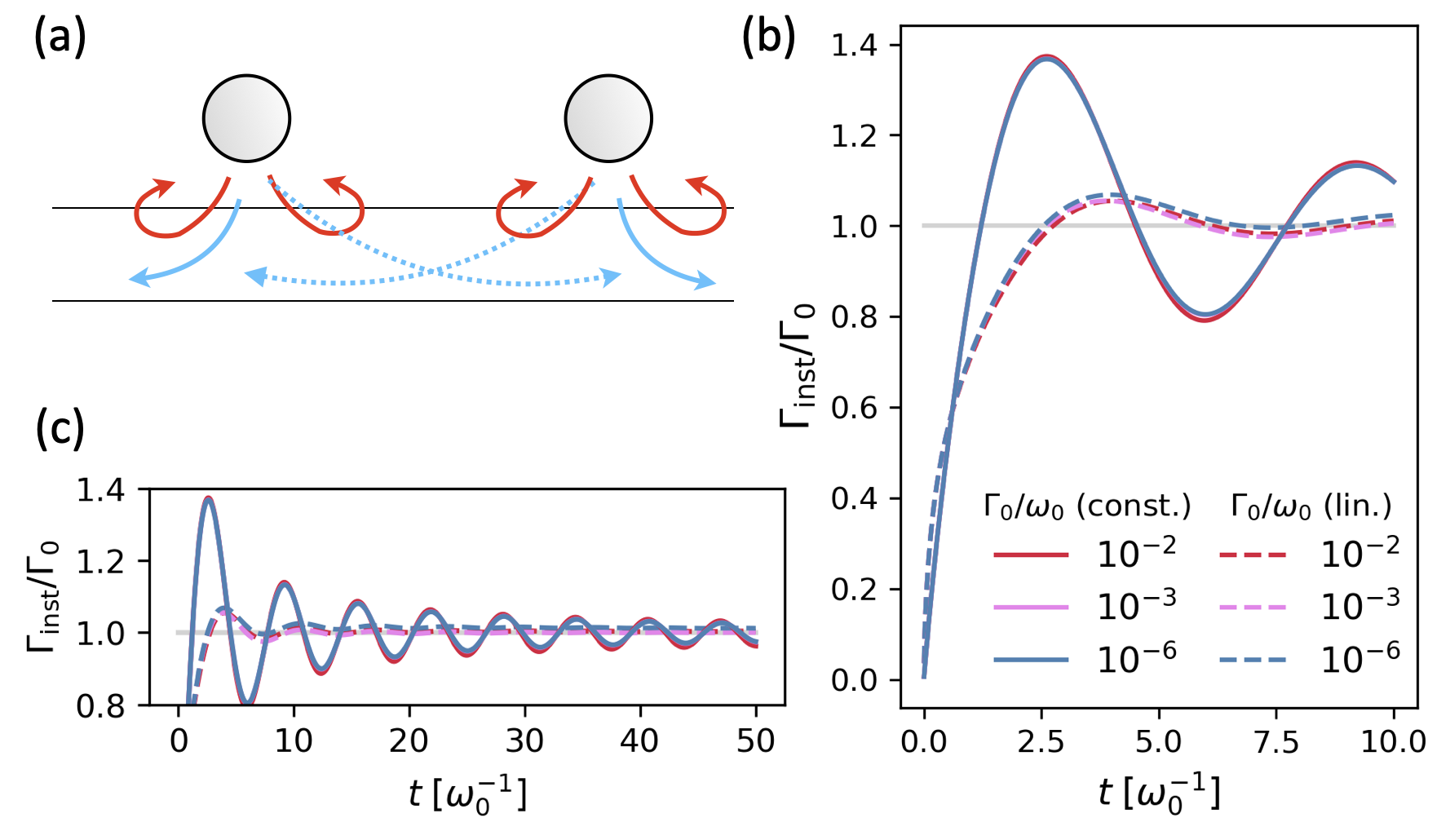
But how does the Zeno regime come into effect? The Zeno time, exemplified by the the 2P-1S transition of the hydrogen atom satisfies [10]. In a subwavelength atom array, the minimal retardation time , with the speed of light, fulfills that . It means that the virtual photons sent from an atom have already passed many other atoms, building up cooperativeness to a certain extent, while an isolated atom has not yet entered exponential decay. Thus, the development of the full collective emission and the reduction to Markovian behavior are two simultaneous processes highly intertwined. As illustrated in Fig. 1(a), the above-mentioned retardation-only picture studied in Refs. [19, 20, 21, 22, 23, 24, 25, 26, 27] does not apply to compact atom ensembles, i.e., there are memory effects beyond retardation.
To show the memory effect beyond retardation, we shall compare the retardation-only picture with a full quantum treatment. Their difference is displayed by the evolution of instantaneous decay rates and excited state populations. Our findings indicate that this memory effect in collective emissions is much more pronounced than that in the decay of a single atom, making subwavelength atom array a better platform to detect the non-Markovianity in the Zeno regime. In this Letter, we shall concentrate on the setup of waveguide QED. Experimental feasibilities and memory effect of free space radiation field will also be discussed.
Zeno Time of the Waveguide QED.
The waveguide QED setup consists of two-level atoms with the ground state and the excited state , and a 1D continuum of bosonic modes. The annihilation and generation operator of the waveguide mode with wavenumber are denoted by and , respectively. They satisfy the bosonic commutation relation . Hamiltonian of the system is conventionally written in analogy with the multipolar gauge Hamiltonian of quantum optics, colloquially the “” Hamiltonian [28, 29, 30], though the bosons field may not be photonic, e.g. it could be surface acoustic waves [31, 32] and matter waves [33, 34], etc.,
| (1) | ||||
where , , denotes the coordinate of atom , is the cutoff of wavenumber. The coupling strength will be specified below. Here we assume a linear dispersion relation for the waveguide, , where is the group velocity of the guided modes. (The Zeno time of a setup with non-linear dispersion relation is found qualitatively the same [35].) The atomic transition frequency defines a resonant wavenumber . We assume so that the non-Markovianity induced by reservoir band edges [36] is irrelevant.
The counter-rotating terms of Hamiltonian (1) cannot be ignored for short-time dynamics [10]. Moreover, they are found to lead to non-linearity at the single-photon level [37]. Fortunately, theoretical difficulties brought by them can be avoided by turning to the gauge introduced by Drummond [38], which is also called the Jaynes-Cummings (JC) gauge [39, 40]. The transformation from the multipolar gauge to the JC gauge reads , where
| (2) |
At the first order of , we obtain
| (3) | ||||
where . The neglected terms at the order of give corrections to the atom and waveguide self-energies, while corrections to their couplings occur at the order of [10, 41, 42].
The absence of counter-rotating terms grants (3) a nice property that its ground state is identical to that of its free part , an atom-field product state, where denotes the field vacuum. Then, the physical state of exciting an atom from the overall ground state, , is also a product state. This kind of physical states are exactly the initial states interested by us. With respect to the multipolar gauge , the same physical state is written as , which is, however, an entangled state between the atoms and the field. Recall that initial states in the product form can greatly simply the theoretical analysis and are essential for theories of open quantum system [43, 44, 45]. Thus, we choose to work with instead of .
Next, let us specify the coupling strength . In the literature of waveguide QED, a localized atom-field interaction is often assumed [46] so that is a -independent constant [46, 28, 29, 30]. It can be spelled by the Markovian decay rate as . Another option for is , the same as the multipolar Hamiltonian of atoms in free space [30] (recall that an atom does not couple to the full displacement field but only its transverse component, which is a nonlocal field [47]). In this case, we have . The above two choices for correspond to a constant and a linear spectral density, hence will be denoted by “const-wQED” and “lin-wQED”, respectively.
We are now in a position to calculate the Zeno time. Given an initial state and a Hamiltonian , the Zeno time is defined from the short-time expansion of the non-decay probability
| (4) |
The Zeno time is a characterization to the duration of non-exponential decay, but not an exact measure. Nevertheless, we substitute and with into Eq. (4) and obtain
| (5) |
Remarkably, of const-wQED is independent of the cutoff , which is introduced in Eq. (1). This is not seen elsewhere. The above result implies that , hence , is valid if (for const-wQED) or (for lin-wQED). Such weak atom-field couplings are satisfied commonly. Zeno time for is discussed in Ref. [35].
Equation of Motion.
Suppose that the system is initialized with only one atomic excitation. Note that preserves the number of excitations, thanks to the absence of counter-rotating terms. Thus, the evolution is captured by the singly-excited ansatz
| (6) |
where and are superposition coefficients to be determined. The Schrödinger equation in the interaction picture implies the integro-differential equation
| (7) | ||||
This equation is further transformed into an integral equation and solved numerically [35].
The above equation will be compared with the following one embodying only the non-Markovianity caused by retardation [20, 21]
| (8) |
where and for and vanishes otherwise. It can be derived from Eq. (7) via an approximation introduced in Ref. [18], see also Ref. [35]. Note that while the right-hand-side of Eq. (7) incorporates the entire history , the right-hand-side of Eq. (8) includes only a distance-dependent delay. Ignoring this delay immediately aligns it with the Markovian effective non-Hermitian Hamiltonian of waveguide QED [30]. Hereafter, data produced by Eq. (8) will be labeled by “retard.”
We shall characterize the non-exponential decay by instantaneous decay rate and population in excited state of the whole chain:
| (9) |
These two quantities can also be defined for every individual atom in an apparent way.
Individual decay.
Let us start from the decay of a single atom. We plot in units of in Figs. 1(b,c) for both const-wQED (solid curves) and lin-wQED (dashed curves). Either one is calculated with three values of , (red), (pink) and (blue). The cutoff is set at . For either const-wQED or lin-wQED, curves belonging to the three almost overlap; for each value of , of lin-wQED increases faster at first () but soon becomes more gradual than that of const-wQED. The latter increases to roughly and turns to oscillating around with a waning amplitude. The non-Markovianity of const-wQED is more pronounced, as what we learn from its Zeno time (5). It is shown in Fig. 1(c) that the oscillation of the curves of const-wQED is still visible at , equivalent to a distance of eight wavelengths for photon propagation.
Although the curves of clearly demonstrate the non-exponential decay, it is defined as the derivative with respect to time so that producing the curves requires a high temporal resolution () of measuring . This is of course experimentally challenging. The requirement of temporal resolution might be relaxed if the non-Markovianity can be manifested by itself, or equivalently, . Unfortunately, we will see in Fig. 2(e) that it is not the case for : is averaged out to the memory-less Markovian result quickly. But fortunately, it would be possible for subwavelength atom arrays ().
Superradiance.
We consider a chain of atoms initialized in the timed-Dicke state
| (10) |
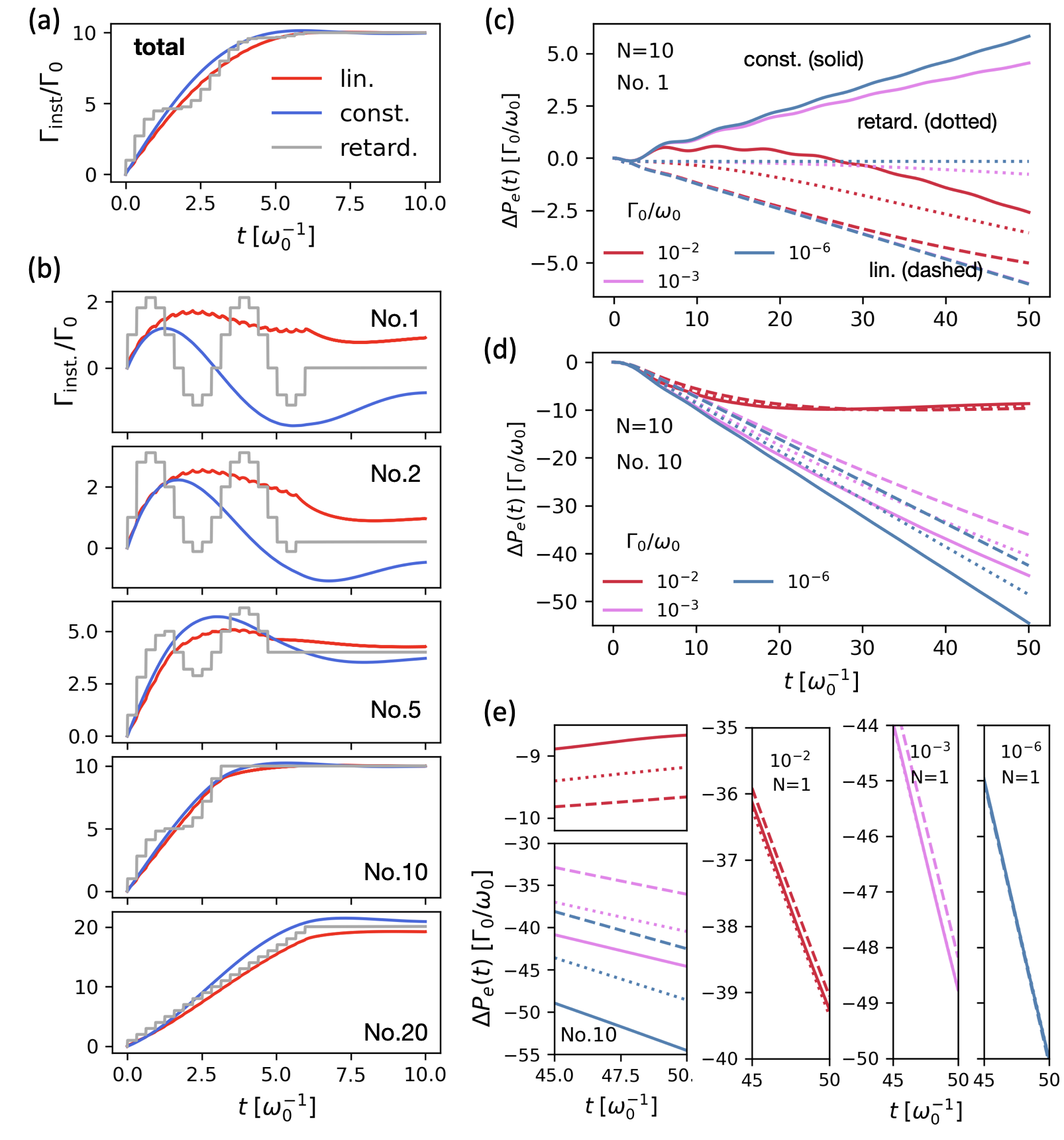
This kind of states are experimentally accessible [48, 49]. State (10) with are the single-photon superradiant state [50]. We substitute with , , and atom-atom separation (see results of in [35]) into into Eqs. (7) and (8) and show the results of in Fig. 2(a) for . Curves of Eq. (7) (red for lin-wQED and blue for const-wQED) show continuous growth while that of Eq. (8) (grey) gives a step-like increase. They agree well after .
Next, we pick five atoms, No. 1, 2, 5, 10, 20 ( if ), and plot the individual instantaneous decay rate, in Fig. 2(b). It shows that the atoms decay at different rates. Atom 1 decays slowly while Atom 20 accelerates to (the opposite is obtained if we choose with ). The three curves (const-wQED, lin-wQED and retard.) agree better for atoms in the middle, i.e., atom 10. In particular, for atom 1, significant derivations between three curves of are visible: the grey curve (retard.) shows two cycles of emission and absorption, the red curve (const-wQED) shows only emission while absorption is dominant for the blue curve (lin-wQED).
Such discrepancy inspires us to look at the change of individual population , where for state (10). In Fig. 2(c), we plot it for atom 1 of a shorter chain () within a longer time window . To compare with Fig. 1, we apply the same three values of and the same coloring as in Fig. 1. Figure 2(c) shows that for (pink) and (blue) there is a gap of between const-wQED (solid curves) and lin-wQED (dashed curves), while the predictions of Eq. (8) (dotted curves) are roughly in the middle. For stronger atom-waveguide coupling , the curves of const-wQED (red solid) and that of Eq. (8) (red dotted) have a tendency toward getting closer. We also plot for the last atom (No. 10) in Fig. 2(d). It shows gaps between const-wQED (solid) and lin-wQED (dashed) of roughly the same scale as atom 1, except for the case of . A zoom-in view for is shown in the left-most panel of Fig. 2(e).
To compare, we plot for the case of in the right three panels of Fig. 2(e), each for one choice of . We find that predictions of the three models (solid, dashed and dotted curves) are almost indistinguishable for . Thus, in terms of , the non-Markovian effect in the Zeno regime is much more prominent in collective emissions than in the decay of a single atom. And it is reasonable to conclude that the requirement of temporal resolution is significantly relaxed to the level of .
Subradiance.
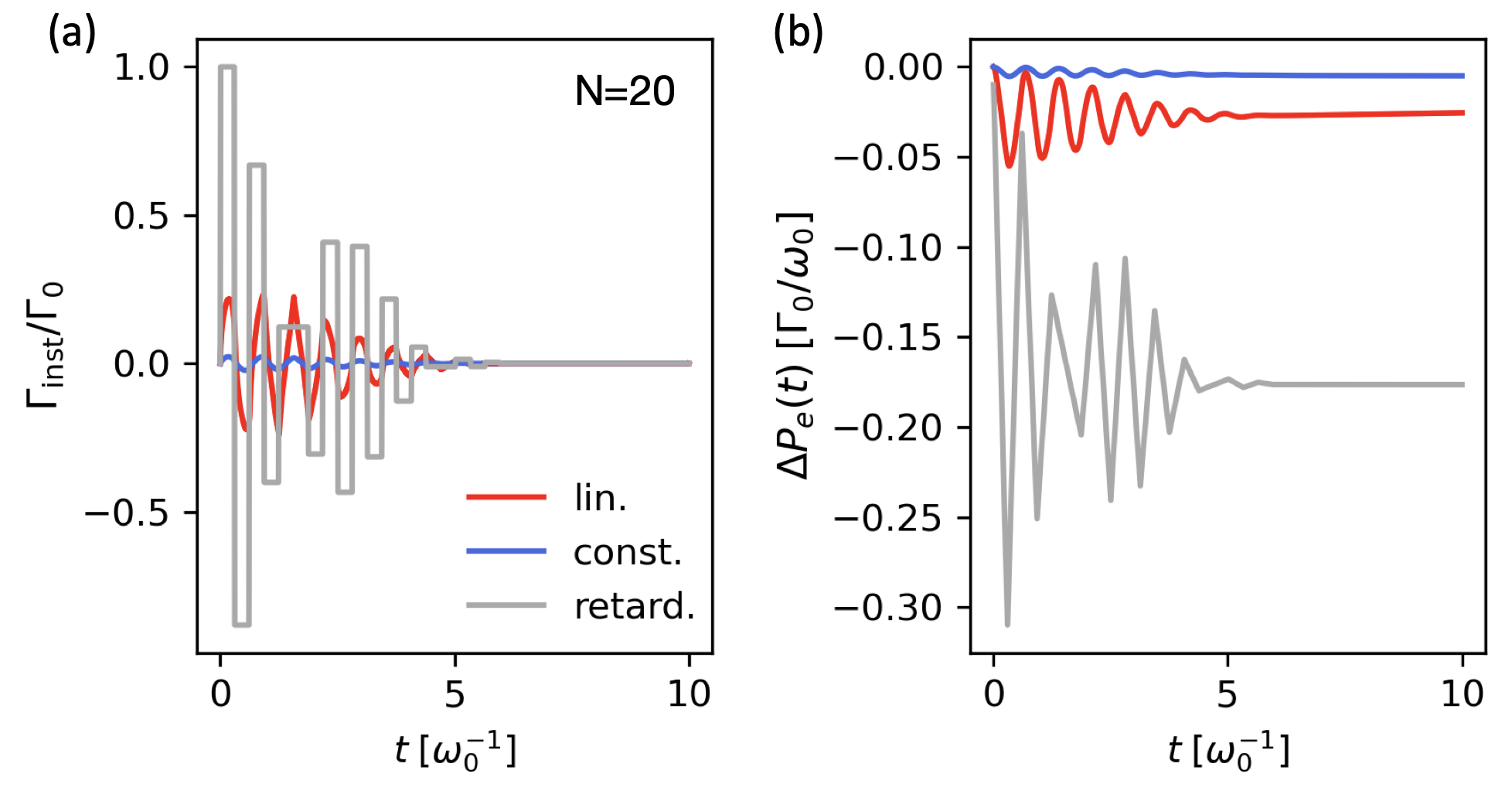
The effective Hamiltonian of waveguide QED defines a subradiant eigenstate approximated by with [14, 15, 16]. We suppose the same parameters as in Fig. 2(a,b) and plot for a chain initialized in in Fig. 3(a). In all cases, the subradiance is built through quick oscillations between emissions and absorptions. But the amplitudes are different: The piecewise curve predicted by Eq. (8) has the largest amplitudes. In Fig. 3(b), we plot of the whole chain. It also shows apparent relative discrepancies between the three predictions.
Discussions.
It is of fundamental interest to extend the theory to atoms in free space. However, a controversial issue is that on which Hamiltonian all calculations should be based. Most works chose the Coulomb gauge ( interaction) disregarding the term, see, e.g., Refs. [51, 52, 53, 54, 55]. Taking the counter-rotating terms into account, it has been found that [10], the same as lin-wQED. Thus, we expect the same non-Markovianity, or perhaps even more pronounced, because the resonant dipole-dipole interaction in free space diverges as for short distances, resulting in strong photon blockade [56]. But recently Hamiltonians of quantum optics is revisited by causal perturbation theory [57]. In this sense, non-Markovianity beyond retardation might be viewed as a probe to determine which theory better captures the true physics.
For experimental tests, our plots show that temporal resolution at the scale of is favorable. Among various platforms of waveguide QED, superconducting circuits have the highest coupling efficiency [30] and fabricating the transmon qubits into a subwavelength chain is straightforward [58]. The transition frequency is in the GHz regime so that temporal resolution at nanosecond is sufficient. Subwavelength atom arrays can also be realized by trapping Sr atoms in optical lattices [59]. The wavelength of transition is so the temporal resolution should be . Scenarios where the boson fields are surface acoustic waves [31, 32] and matter waves [33, 34] need further studies.
Conclusions.
We have studied the Zeno regime of the decay of subwavelength atom arrays coupled to a 1D waveguide. Non-markovianity beyond retardation, characterized by instantaneous decay rates and population in the excited states, is addressed by comparing the full quantum treatment Eq. (7) with Eq. (8), which includes only the retardation effect. Specifically, the evolution of excited state population (in the single-photon superradiant state) manifests reservoir memory effect with a significantly relaxed temporal resolution. Our results might be useful for protecting the quantum information stored in compact atom ensembles [14, 60] via dissipation engineering [61], and studying the correlated noise in quantum computing processors [62], etc. For future works, one may explore such possibilities using the theoretical tools of non-Markovian open systems [43, 44, 45].
Acknowledgements.
The author thanks Klaus Mølmer for careful reading of the manuscript and for providing valuable comments. The author acknowledges the financial support from CAS Project for Young Scientists in Basic Research (YSBR-100), National Natural Science Foundation of China (Grant No. 12375024), Innovation Program for Quantum Science and Technology (Grant No. 2-6), and the startup grant of IOP-CAS.References
- Winter [1961] R. G. Winter, Evolution of a quasi-stationary state, Phys. Rev. 123, 1503 (1961).
- Newton [1961] R. G. Newton, The exponential decay law of unstable systems, Annals of Physics 14, 333 (1961).
- Weisskopf and Wigner [1930] V. Weisskopf and E. Wigner, Berechnung der natürlichen linienbreite auf grund der diracschen lichttheorie, Zeitschrift für Physik 63, 54 (1930).
- Wilkinson et al. [1997] S. R. Wilkinson, C. F. Bharucha, M. C. Fischer, K. W. Madison, P. R. Morrow, Q. Niu, B. Sundaram, and M. G. Raizen, Experimental evidence for non-exponential decay in quantum tunnelling, Nature 387, 575 (1997).
- Crespi et al. [2019] A. Crespi, F. V. Pepe, P. Facchi, F. Sciarrino, P. Mataloni, H. Nakazato, S. Pascazio, and R. Osellame, Experimental investigation of quantum decay at short, intermediate, and long times via integrated photonics, Phys. Rev. Lett. 122, 130401 (2019).
- Chiu et al. [1977] C. B. Chiu, E. C. G. Sudarshan, and B. Misra, Time evolution of unstable quantum states and a resolution of zeno’s paradox, Phys. Rev. D 16, 520 (1977).
- Misra and Sudarshan [1977] B. Misra and E. C. G. Sudarshan, The zeno’s paradox in quantum theory, Journal of Mathematical Physics 18, 756 (1977).
- Itano et al. [1990] W. M. Itano, D. J. Heinzen, J. J. Bollinger, and D. J. Wineland, Quantum zeno effect, Phys. Rev. A 41, 2295 (1990).
- Presilla et al. [1996] C. Presilla, R. Onofrio, and U. Tambini, Measurement quantum mechanics and experiments on quantum zeno effect, Annals of Physics 248, 95 (1996).
- Zheng et al. [2008] H. Zheng, S. Y. Zhu, and M. S. Zubairy, Quantum zeno and anti-zeno effects: Without the rotating-wave approximation, Phys. Rev. Lett. 101, 200404 (2008).
- Dicke [1954] R. H. Dicke, Coherence in spontaneous radiation processes, Phys. Rev. 93, 99 (1954).
- Lehmberg [1970a] R. H. Lehmberg, Radiation from an -atom system. i. general formalism, Phys. Rev. A 2, 883 (1970a).
- Lehmberg [1970b] R. H. Lehmberg, Radiation from an -atom system. ii. spontaneous emission from a pair of atoms, Phys. Rev. A 2, 889 (1970b).
- Asenjo-Garcia et al. [2017] A. Asenjo-Garcia, M. Moreno-Cardoner, A. Albrecht, H. J. Kimble, and D. E. Chang, Exponential improvement in photon storage fidelities using subradiance and “selective radiance” in atomic arrays, Phys. Rev. X 7, 031024 (2017).
- Zhang and Mølmer [2019] Y.-X. Zhang and K. Mølmer, Theory of subradiant states of a one-dimensional two-level atom chain, Phys. Rev. Lett. 122, 203605 (2019).
- Zhang and Mølmer [2020] Y.-X. Zhang and K. Mølmer, Subradiant emission from regular atomic arrays: Universal scaling of decay rates from the generalized bloch theorem, Phys. Rev. Lett. 125, 253601 (2020).
- Kornovan et al. [2019] D. F. Kornovan, N. V. Corzo, J. Laurat, and A. S. Sheremet, Extremely subradiant states in a periodic one-dimensional atomic array, Phys. Rev. A 100, 063832 (2019).
- Milonni and Knight [1974] P. W. Milonni and P. L. Knight, Retardation in the resonant interaction of two identical atoms, Phys. Rev. A 10, 1096 (1974).
- Gonzalez-Ballestero et al. [2013] C. Gonzalez-Ballestero, F. J. García-Vidal, and E. Moreno, Non-markovian effects in waveguide-mediated entanglement, New Journal of Physics 15, 073015 (2013).
- Sinha et al. [2020a] K. Sinha, P. Meystre, E. A. Goldschmidt, F. K. Fatemi, S. L. Rolston, and P. Solano, Non-markovian collective emission from macroscopically separated emitters, Phys. Rev. Lett. 124, 043603 (2020a).
- Sinha et al. [2020b] K. Sinha, A. González-Tudela, Y. Lu, and P. Solano, Collective radiation from distant emitters, Phys. Rev. A 102, 043718 (2020b).
- Dinc and Brańczyk [2019] F. Dinc and A. M. Brańczyk, Non-markovian super-superradiance in a linear chain of up to 100 qubits, Phys. Rev. Res. 1, 032042 (2019).
- Shen et al. [2019] H. Z. Shen, S. Xu, H. T. Cui, and X. X. Yi, Non-markovian dynamics of a system of two-level atoms coupled to a structured environment, Phys. Rev. A 99, 032101 (2019).
- Carmele et al. [2020] A. Carmele, N. Nemet, V. Canela, and S. Parkins, Pronounced non-markovian features in multiply excited, multiple emitter waveguide qed: Retardation induced anomalous population trapping, Phys. Rev. Res. 2, 013238 (2020).
- Arranz Regidor et al. [2021] S. Arranz Regidor, G. Crowder, H. Carmichael, and S. Hughes, Modeling quantum light-matter interactions in waveguide qed with retardation, nonlinear interactions, and a time-delayed feedback: Matrix product states versus a space-discretized waveguide model, Phys. Rev. Res. 3, 023030 (2021).
- Trivedi et al. [2021] R. Trivedi, D. Malz, S. Sun, S. Fan, and J. Vučković, Optimal two-photon excitation of bound states in non-markovian waveguide qed, Phys. Rev. A 104, 013705 (2021).
- Barkemeyer et al. [2022] K. Barkemeyer, A. Knorr, and A. Carmele, Heisenberg treatment of multiphoton pulses in waveguide qed with time-delayed feedback, Phys. Rev. A 106, 023708 (2022).
- Roy et al. [2017] D. Roy, C. M. Wilson, and O. Firstenberg, Colloquium: Strongly interacting photons in one-dimensional continuum, Rev. Mod. Phys. 89, 021001 (2017).
- Chang et al. [2018] D. E. Chang, J. S. Douglas, A. González-Tudela, C.-L. Hung, and H. J. Kimble, Colloquium: Quantum matter built from nanoscopic lattices of atoms and photons, Rev. Mod. Phys. 90, 031002 (2018).
- Sheremet et al. [2023] A. S. Sheremet, M. I. Petrov, I. V. Iorsh, A. V. Poshakinskiy, and A. N. Poddubny, Waveguide quantum electrodynamics: Collective radiance and photon-photon correlations, Rev. Mod. Phys. 95, 015002 (2023).
- Gustafsson et al. [2014] M. V. Gustafsson, T. Aref, A. F. Kockum, M. K. Ekström, G. Johansson, and P. Delsing, Propagating phonons coupled to an artificial atom, Science 346, 207 (2014).
- Guo et al. [2017] L. Guo, A. Grimsmo, A. F. Kockum, M. Pletyukhov, and G. Johansson, Giant acoustic atom: A single quantum system with a deterministic time delay, Phys. Rev. A 95, 053821 (2017).
- de Vega et al. [2008] I. de Vega, D. Porras, and J. Ignacio Cirac, Matter-wave emission in optical lattices: Single particle and collective effects, Phys. Rev. Lett. 101, 260404 (2008).
- Krinner et al. [2018] L. Krinner, M. Stewart, A. Pazmiño, J. Kwon, and D. Schneble, Spontaneous emission of matter waves from a tunable open quantum system, Nature 559, 589 (2018).
- [35] See Supplemental Material for additional discussions about Zeno time, detailed calculations and extra plots, which inlcudes Refs. [18, 40, 15, 63].
- Vats and John [1998] N. Vats and S. John, Non-markovian quantum fluctuations and superradiance near a photonic band edge, Phys. Rev. A 58, 4168 (1998).
- Jacobs et al. [2023] K. Jacobs, S. Krastanov, M. Heuck, and D. R. Englund, Quantum theory of single-photon nonlinearities generated by ensembles of emitters (2023), arXiv:2307.01375 [quant-ph] .
- Drummond [1987] P. D. Drummond, Unifying the pa and de interactions in photodetector theory, Phys. Rev. A 35, 4253 (1987).
- Stokes and Nazir [2019] A. Stokes and A. Nazir, Gauge ambiguities imply jaynes-cummings physics remains valid in ultrastrong coupling QED, Nature Communications 10, 10.1038/s41467-018-08101-0 (2019).
- Stokes and Nazir [2022] A. Stokes and A. Nazir, Implications of gauge freedom for nonrelativistic quantum electrodynamics, Rev. Mod. Phys. 94, 045003 (2022).
- Wang et al. [2010] D.-w. Wang, Z.-h. Li, H. Zheng, and S.-y. Zhu, Time evolution, lamb shift, and emission spectra of spontaneous emission of two identical atoms, Phys. Rev. A 81, 043819 (2010).
- Li et al. [2012] Y. Li, J. Evers, H. Zheng, and S.-Y. Zhu, Collective spontaneous emission beyond the rotating-wave approximation, Phys. Rev. A 85, 053830 (2012).
- Rivas et al. [2014] Á . Rivas, S. F. Huelga, and M. B. Plenio, Quantum non-markovianity: characterization, quantification and detection, Reports on Progress in Physics 77, 094001 (2014).
- Breuer et al. [2016] H.-P. Breuer, E.-M. Laine, J. Piilo, and B. Vacchini, Colloquium: Non-markovian dynamics in open quantum systems, Rev. Mod. Phys. 88, 021002 (2016).
- de Vega and Alonso [2017] I. de Vega and D. Alonso, Dynamics of non-markovian open quantum systems, Rev. Mod. Phys. 89, 015001 (2017).
- Shen and Fan [2005] J.-T. Shen and S. Fan, Coherent single photon transport in a one-dimensional waveguide coupled with superconducting quantum bits, Phys. Rev. Lett. 95, 213001 (2005).
- Cohen-Tannoudji et al. [1997] C. Cohen-Tannoudji, J. Dupont-Roc, and G. Grynberg, Photons and Atoms: Introduction to Quantum Electrodynamics, 1st ed. (Wiley-VCH, 1997).
- Röhlsberger et al. [2010] R. Röhlsberger, K. Schlage, B. Sahoo, S. Couet, and R. Rüffer, Collective lamb shift in single-photon superradiance, Science 328, 1248 (2010).
- Corzo et al. [2019] N. V. Corzo, J. Raskop, A. Chandra, A. S. Sheremet, B. Gouraud, and J. Laurat, Waveguide-coupled single collective excitation of atomic arrays, Nature 566, 359 (2019).
- Scully et al. [2006] M. O. Scully, E. S. Fry, C. H. R. Ooi, and K. Wódkiewicz, Directed spontaneous emission from an extended ensemble of atoms: Timing is everything, Phys. Rev. Lett. 96, 010501 (2006).
- Moses [1973] H. E. Moses, Photon wave functions and the exact electromagnetic matrix elements for hydrogenic atoms, Phys. Rev. A 8, 1710 (1973).
- Wódkiewicz and Eberly [1976] K. Wódkiewicz and J. Eberly, Markovian and non-markovian behavior in two-level atom fluorescence, Annals of Physics 101, 574 (1976).
- Seke and Herfort [1988] J. Seke and W. N. Herfort, Deviations from exponential decay in the case of spontaneous emission from a two-level atom, Phys. Rev. A 38, 833 (1988).
- Facchi and Pascazio [1998] P. Facchi and S. Pascazio, Temporal behavior and quantum zeno time of an excited state of the hydrogen atom, Physics Letters A 241, 139 (1998).
- Berman and Ford [2010] P. R. Berman and G. W. Ford, Spectrum in spontaneous emission: Beyond the weisskopf-wigner approximation, Phys. Rev. A 82, 023818 (2010).
- Cidrim et al. [2020] A. Cidrim, T. S. do Espirito Santo, J. Schachenmayer, R. Kaiser, and R. Bachelard, Photon blockade with ground-state neutral atoms, Phys. Rev. Lett. 125, 073601 (2020).
- Marzlin and Fitzgerald [2018] K.-P. Marzlin and B. Fitzgerald, Spontaneous emission and atomic line shift in causal perturbation theory, Journal of Mathematical Physics 59, 042103 (2018).
- Mirhosseini et al. [2019] M. Mirhosseini, E. Kim, X. Zhang, A. Sipahigil, P. B. Dieterle, A. J. Keller, A. Asenjo-Garcia, D. E. Chang, and O. Painter, Cavity quantum electrodynamics with atom-like mirrors, Nature 569, 692 (2019).
- Olmos et al. [2013] B. Olmos, D. Yu, Y. Singh, F. Schreck, K. Bongs, and I. Lesanovsky, Long-range interacting many-body systems with alkaline-earth-metal atoms, Phys. Rev. Lett. 110, 143602 (2013).
- Manzoni et al. [2018] M. T. Manzoni, M. Moreno-Cardoner, A. Asenjo-Garcia, J. V. Porto, A. V. Gorshkov, and D. E. Chang, Optimization of photon storage fidelity in ordered atomic arrays, New Journal of Physics 20, 083048 (2018).
- Harrington et al. [2022] P. M. Harrington, E. J. Mueller, and K. W. Murch, Engineered dissipation for quantum information science, Nature Reviews Physics 4, 660 (2022).
- Singh et al. [2023] K. Singh, C. E. Bradley, S. Anand, V. Ramesh, R. White, and H. Bernien, Mid-circuit correction of correlated phase errors using an array of spectator qubits, Science 380, 1265 (2023).
- Zhang et al. [2021] Y.-X. Zhang, C. R. i Carceller, M. Kjaergaard, and A. S. Sørensen, Charge-noise insensitive chiral photonic interface for waveguide circuit qed, Phys. Rev. Lett. 127, 233601 (2021).