Worldline master formulas for the dressed electron propagator, part 2: On-shell amplitudes
Abstract
In the first part of this series, we employed the second-order formalism and the “symbol” map to construct a particle path-integral representation of the electron propagator in a background electromagnetic field, suitable for open fermion-line calculations. Its main advantages are the avoidance of long products of Dirac matrices, and its ability to unify whole sets of Feynman diagrams related by permutation of photon legs along the fermion lines. We obtained a Bern-Kosower type master formula for the fermion propagator, dressed with photons, in terms of the “-photon kernel,” where this kernel appears also in “subleading” terms involving only of the photons.
In this sequel, we focus on the application of the formalism to the calculation of on-shell amplitudes and cross sections. Universal formulas are obtained for the fully polarised matrix elements of the fermion propagator dressed with an arbitrary number of photons, as well as for the corresponding spin-averaged cross sections. A major simplification of the on-shell case is that the subleading terms drop out, but we also pinpoint other, less obvious simplifications.
We use integration by parts to achieve manifest transversality of these amplitudes at the integrand level and exploit this property using the spinor helicity technique. We give a simple proof of the vanishing of the matrix element for “all ” photon helicities in the massless case, and find a novel relation between the scalar and spinor spin-averaged cross sections in the massive case. Testing the formalism on the standard linear Compton scattering process, we find that it reproduces the known results with remarkable efficiency. Further applications and generalisations are pointed out.
1 Introduction
In the first part of this series 130 , simply to be called ‘I’ in the following, we developed a novel path-integral representation of the electron propagator in an external electromagnetic field suitable for practical calculations in the worldline approach to QED feynman:pr80 ; feynman:pr84 ; polyakovbook ; strassler1 ; strassler2 ; 5 ; 15 ; 41 ; UsRep , in particular for tree-level amplitudes involving multiple photons and related quantities. In contrast to the standard first-order Dirac formalism, it is based on the less-known but equivalent second order fermion approach to spinor QED feygel ; hostler ; berdun ; morgan . Let us briefly retrace the main steps of this derivation, referring the reader to I for the details.
1.1 Short review of the formalism
The starting point in the second-order formalism is the following factorisation of the -space Dirac propagator in a Maxwell background (we suppress spin indices for brevity),
| (1) |
where , is the covariant derivative and we introduced the matrix elements111See appendix A for our conventions.
| (2) |
where . For this “kernel” function, following fragit , we then derived the following path integral representation:
| (3) | |||||
Here is the straight-line path between the endpoints, is an external Grassmann Lorentz vector, and the inverse of the “symbol map” symb converts products of ’s into fully antisymmetrised products of Dirac matrices,
| (4) |
When working in four dimensions, this reduces to the three cases
| (5) | |||||
| (6) | |||||
| (7) |
We then performed the usual projection onto an -photon background of fixed momenta and polarisations, and used Gaussian integration on both the orbital path integral, , and spin path integral, , to derive Bern-Kosower type master formulas for the -photon kernel both in configuration and in momentum space. We also showed a convenient way to decompose these amplitudes into contributions with a fixed number of orbital and spin interactions, which we refer to as a spin-orbit decomposition.
As in I, in our applications here we will focus entirely on momentum-space amplitudes. Fourier transforming the starting identity (1) to momentum space, and projecting it onto the -photon sector, it turns into
| (8) | |||||
Here in the second term the ‘hat’ on and means omission. The terms involving are called “subleading” and arise because one of the photons could be taken from the appearing in the covariant derivative in the factor in (1). An important advantage of the “worldline representation” is that it automatically takes care of the permutations over the photons, and thus avoids the break-up of the amplitude into individual Feynman diagrams. This may not seem very relevant at the tree-level, but becomes an important issue when tree-level amplitudes are used for the construction of multiloop amplitudes by sewing 15 ; 41 ; 100 .
1.2 The on-shell case
In I our focus was on the use of the off-shell amplitudes as a building block for loop amplitudes, which we exemplified by a recalculation of the one-loop electron self-energy in an arbitrary gauge and dimension. Now, our objective is to explore the simplifications which can be achieved in the on-shell case, both for the amplitudes themselves as well as for the linear () and non-linear () Compton scattering cross sections that can be constructed out of them. Thus our principal object of interest is the on-shell matrix element corresponding to the dressed electron propagator with fixed spins . In its construction we must remember that the second-order representation of the dressed electron propagator still contains the external propagators, which must be removed before going on-shell. Thus the matrix element has to be written as
| (9) |
where the spinors satisfy the on-shell relations
| (10) |
Thus these zeroes must be cancelled by corresponding poles to get a non-vanishing matrix element, which is the fermionic version of the LSZ theorem. Looking at the decomposition (8), we can see how this works for the leading term: as explained in part I, is, in the second-order formalism, built from untruncated Feynman diagrams involving only scalar propagators. Thus it contains a factor , which led us to the redefinition (I. 5.11),
| (11) |
Since , the cancellation of the poles can then be made explicit:
| (12) |
The same does not work for the subleading terms, , since in those the pole has been shifted to . Thus they can be omitted in the calculation of on-shell matrix elements, and our final formula for the matrix elements of the -photon dressed electron propagator becomes
| (13) |
As is clear from (7), in the Dirac matrix structure of is (I 5.11),
| (14) |
with . Moreover, from the spin-orbit decomposition it is clear that can be split as
| (15) |
where is, up to the coupling constant factor, the truncated scalar propagator (see (I.1.2) for its path integral representation),
| (16) |
while terms in involve the spin interaction at least once.
On-shell matrix elements in QED are guaranteed to be transversal in the photon polarisations, implying that it must be possible to write the amplitude entirely in terms of photon field-strength tensors, defined by
| (17) |
for a photon of momentum with polarisation vector . Although this fact is even stated in some textbooks on QFT (see, e.g., peskinschroeder-book ), in the standard Feynman diagram approach it is by no means trivial to actually achieve this rewriting explicitly for an arbitrary number of photons (see, e.g., felihu ). Here we will show both for the dressed scalar propagator as well as for the kernel of the dressed electron propagator how this manifest transversality can be achieved at the integrand level by a simple integration-by-parts algorithm. We will also develop some useful formulas for the application of the standard spinor helicity technique to expressions where all polarisation vectors are contained in field-strength tensors.
A less obvious simplification concerning the coefficients is that there are useful relations between them whenever both and are on-shell. We will see that, for ( is the dual to ),
| (18) | |||||
| (19) |
so that in principle the full information on the matrix element is already contained in .
Our goal of obtaining general expressions for the fully polarised matrix elements, valid for any without the explicit knowledge of the coefficient functions , made it necessary to dispose of explicit formulas for the Dirac bilinears appearing when (14) is put into (13). To our surprise, we could not find in the literature explicit formulas for those bilinears valid for general , and arbitrary spin axes. We have therefore derived suitable formulas ourselves, based on an algorithm proposed recently in olpozp (see section 5).
After summing over electron spins, which we are still able to do for arbitrary and photon helicity assignments, further simplification is possible, leading to the following very compact representation for the spin-averaged cross sections:
| (20) |
We then apply all this machinery to the case, performing a complete recalculation of the fully polarised matrix elements for Compton scattering, as well as the spin-averaged and the fully unpolarised cross sections, and recover the known results with relatively little effort.
The organisation of part 2 is as follows. Sections 2 - 6 are preparatory: in section 2 we explain the on-shell IBP procedure leading to the “R-representation” of the integrands of the on-shell photon-dressed scalar and electron propagator. Section 3 contains a collection of formulas involving the fixed-helicity field-strength tensors . As a warm-up, in section 4 we apply the formalism to the scalar QED case, obtaining the matrix elements and demonstrating the well-known vanishing of the “all +” amplitudes in the massless limit. Section 5 is devoted to the construction of Dirac bilinears, section 6 to the study of the coefficient functions . The central section of this paper is 7, which contains the construction of the fully polarised matrix elements as well as the spin-averaged cross sections, for arbitrary photon number and helicity assignments. Section 8 deals with the “all +” case, which exhibits some further interesting simplifications related to the well-known connections between helicity, self-duality and supersymmetry thooft ; dadda ; brolee ; dufish1 ; dufish2 ; 51 . In section 9 we apply all these developments to the ordinary Compton scattering case. Our conclusions and directions of future work are offered in section 10.
There are four appendices. In appendix A we summarise our conventions; contrary to I, where Euclidean conventions were used throughout, for the computation of on-shell quantities it is, as usual, preferable to Wick rotate from Euclidean to Minkowski space. Apart from changing the metric from to , this will also induce a factor of for each propagator and a factor of for each vertex. This amounts to a global factor of for the dressed scalar or spinor propagators or , but a factor for their truncated versions and , defined by
| (21) | |||||
| (22) |
Thus in Minkowski space we have and .
In appendix B we provide explicit formulas for the Dirac bilinears of section 5 for the two most standard choices of electron polarisations, projection of the spin on the direction of motion or on the -axis in the electron’s rest frame. Appendix C derives recursion formulas for the coefficient functions that provide an alternative algorithm for their determination. Finally some simplifications peculiar to the massless limit are discussed in appendix D.
2 Manifest transversality at the integrand level
An essential feature of the worldline formalism is the option of using integration-by-parts (‘IBP’) strassler1 ; strassler2 ; 41 ; 26 ; 91 to improve on the integrand of parameter integrals before their actual calculation. For the prototypical case, the one-loop -photon amplitudes, one can hope to reduce significantly the number of terms in the integrand, to achieve manifest gauge invariance at the integrand level, eliminate spurious UV divergences (for the case), and realise the unification of the scalar and spinor QED cases through the “Bern-Kosower cycle replacement rule” berkosPRL ; berkosNPB . Although similar manipulations could also be done using Feynman diagrams, they would usually become much more cumbersome as well as harder to find since they do not involve individual Feynman diagrams but rather whole sets of them.
For general , two different IBP algorithms have already been developed: “symmetric IBP” 26 ; 41 which leads to the “Q-representation,” well-suited to the application of the “cycle replacement rule,” and the algorithm of 91 resulting in the “R-representation,” which provides manifest gauge invariance (it is also possible to combine the two 91 ).
Here in the open-line case, this becomes a matter of “off-shell” vs. “on-shell,” since the IBPs leading to the R-representation generate boundary terms that in the on-shell case can be omitted due to the LSZ theorem, but would be messy to deal with in the off-shell case; this is why in part I we focused on “symmetric IBP,” while for our present on-shell purposes we prefer to work with the R-representation. Thus we will now derive this representation, starting with the scalar line and then using the spin-orbit decomposition to extend it to the spinor line.
2.1 Manifestly transversal representation of the dressed scalar propagator
The basic idea of the R-representation has been explained already in section 2.3 of I. The electromagnetic potential is specialised to a sum of plane waves, , and we project onto the contribution to the kernel that is multi-linear in the . The photons inserted along the line are then represented by vertex operators,
| (23) |
The simplest way of achieving manifest transversality of photonic amplitudes is to rewrite each vertex operator from the beginning in terms of the photon field-strength tensor. In scalar QED one can do this by adding to the vertex operator a total-derivative term supplying the “missing half” of that tensor:
| (24) |
Here is a “reference vector” that is arbitrary except for the constraint . In the open-line case, adding this term causes non-vanishing boundary terms, but these do not have both of the poles necessary for contributing to the on-shell matrix element , defined by the on-shell limit of . Thus, as far as the calculation of is concerned, the -photon dressed scalar propagator could as well be used with the replacement
| (25) |
throughout. Thus, in particular, the master formula (I. 2.25) (originally due to dashsu and ahmbassch-16 ),
can then as well be written purely in terms of the field strength tensors of the photons in the form
even though the right-hand sides of (LABEL:master-dss) and (LABEL:linemastercov) are not actually equal.
The result of expanding out the exponential factor in (LABEL:linemastercov) will be named , where was already introduced in part I,
| (28) | |||||
The on-shell master formula (LABEL:linemastercov) can then be rewritten as
| (29) |
For use below let us also write down the first two polynomials :
| (30) | ||||
To obtain additional simplifications, we observe that the most complicated term in is always given by the product
| (31) |
which, upon choosing222Excluding the case when , since here on-shell. for , turns into
| (32) |
For every ordering of the variables , there is a such that the th term in the product is given by
| (33) |
Thus the term in question can be made to vanish by this choice of reference momenta, leaving only those contributions in that involve at least one of the (these -functions generate the seagull vertex of scalar QED).
However, it is important to stress that the reference momenta cannot be chosen term-by-term, but rather have to be fixed globally. Their role is, in fact, very similar to the reference momenta of the spinor helicity formalism to be used below, except that they are not restricted to be null vectors.
2.2 Manifestly transversal representation of the N-photon kernel
Proceeding to the spinor-line case, in section 6 of part I we had seen that the -photon kernel can be decomposed naturally as
| (34) |
since in the representation (3) after specialising to an -photon background a certain number of photons have to be taken out of the spin path integral , and the remaining ones out of the coordinate (orbital) path integral . The former ones are by convention associated to the variables , and since the spin path integral couples to the background field only through the field-strength tensor , manifest transversality in those indices is automatic, as is also borne out by our explicit formula for these terms, written in terms of functions , (6.8) of part I (some of these are given below). Thus only the transversality of the orbital part has to be taken care of, and here it is obvious that the only change necessary in the final formula for , (I. 6.10), is to replace the orbital prefactor polynomials by the corresponding objects of the R representation, defined by (compare (LABEL:linemastercov) and (I.6.11))
| (35) |
Thus we arrive at the following manifestly transversal version of the spin-orbit decomposition (compare with (I 6.10)):
where the sum runs over all choices of out of the variables, and was given in (28).
For example, the spin-orbit decomposition of the two-photon kernel will now, instead of (I.6.13), take the form
| (37) |
Here was given in (30), while
| (38) | ||||
and
| (39) | ||||
We shall use these explicit results below when we recover the standard Compton cross section.
3 Photon polarisations and spinor helicity
As is usual in the high-energy physics context, we will fix the on-shell photon polarisations using a basis of helicity eigenstates, and employ the spinor helicity formalism for the construction of these states. Following the conventions of srednicki-book ; elvhua-book , they are given by
| (40) |
where denotes the photon momentum and the reference vector. Since in our representation all polarisation vectors are already absorbed into field-strength tensors, let us also collect here a number of formulas involving field strength tensors of on-shell photons with fixed circular polarisations,
| (41) |
(some but not all of these formulas were already given in 56 ).
First, since the are transversal they should be independent of the reference momentum . And indeed, one can show that they can be written purely in terms of as follows,
| (42) |
The following matrix identities can then easily be established:
-
•
Hermitian conjugation:
(43) -
•
(Anti-) self duality:
(44) where is the dual field-strength tensor.
-
•
Products:
(45) (46) (47) Here and in the following we will often follow the usual notation of replacing a by inside spinorial expressions.
-
•
Anticommutators:
(48) (49) -
•
Factorisation of traces:
(50) -
•
Same-helicity traces:
(51) (52)
Finally, let us also write down spinor helicity expressions for and for the case where the are null vectors:
| (53) |
| (54) | |||
| (55) |
| (56) | |||
| (57) |
4 Some scalar-line calculations
As a warm-up, let us illustrate the use the formalism by rederiving some known results in scalar QED.
4.1 Vanishing of the “all +” amplitudes for the massless scalar line
For starters, let us rederive the fact that the scalar propagator dressed with any number of equal-helicity photons gives a vanishing amplitude in the limit of vanishing scalar mass (see, amongst others, Bernicot ).
This fact we can see most directly from the scalar master formula in its “first alternative version,” equation (I.2.23):
| (58) |
If the scalar is massless, is a null vector on-shell, so we can take it as the reference vector for all the photons. This removes the terms proportional to in the exponent. Then if all the photons have the same helicity, the identity
| (59) |
removes all the terms in the exponent involving . The only terms left are of the form
| (60) |
Now we apply a similar argument to the one given below (30): for any given ordering of the there will be one with the largest value, so that , which makes the whole term vanish (taking also into account that on-shell we cannot have since ). This completes the proof of the vanishing of this amplitude.
4.2 N=2 amplitudes for the massive scalar line
Next, let us have a look at the massive scalar line. In this case the vanishing theorem does not hold, so let us calculate the two independent matrix elements for the case, and .
For the case, we use the on-shell master formula (29) together with (30) and the observation that setting removes the first term in , leading to
| (61) | |||||
The integrals simply give the propagators associated to the external legs,
| (62) |
since there is no internal propagator when the two photons meet at the same point along the line. Therefore
| (63) |
Now we can use the identity (48):
| (64) |
so that the final result becomes
| (65) |
in which we have further introduced the notation
| (66) |
Turning now to the component, we refine our choice of reference momenta according to
| (67) |
These reference momenta are equally good as for removing the first term in as in (32), but have the advantage of being null vectors. Thus we can now apply (56) to write, in the second term,
| (68) |
leading to the compact form for the amplitude
| (69) |
This should be independent of the choice of reference momentum, and indeed it is easy to see that it can be rewritten as
| (70) |
5 Electron polarisations and Dirac bilinears
In this section we develop some general formulae for Dirac bilinears that will be central in arriving at universal formulae for fully polarised amplitudes without the need to have explicit knowledge of the coefficients , and or of the number or helicity of the photons participating in the scattering process. The on-shell electron polarisations can be fixed by imposing the following conditions srednicki-book ,
| (71) |
with spin labels , and where the vectors and , which define the directions for measuring the particle spins, satisfy and . Using the approach outlined in olpozp , we introduce a set of -vectors with which we can construct quantities that span the space of the Dirac bilinears , and appearing in (13) for the polarised amplitudes.
To achieve this we introduce the null vector and its conjugate given with respect to the physical outgoing momentum , as
| (72) | ||||
These vectors are orthogonal to and and the set forms a basis in the space of four-vectors. We further define the following four scalars,
| (73) | ||||
and the normalisation factor
| (74) |
One can now decompose the spinor as a linear combination of the and their Dirac adjoints whose coefficients can be written in terms of the . The Dirac bilinears (scalar), and (pseudoscalar) can then be expressed in terms of these same scalars as follows,
| (75) |
Similarly, we can obtain the tensor bilinears decomposed in terms of antisymmetric combinations of the basis constructed above as
| (76) | |||||
where
| (77) |
In appendix B we compute the coefficients explicitly for the two most common choices of the spin axes (i) along the -axis in the rest frame of the electron (ii) along the direction of motion.
6 Relations between the functions
Evaluating the dressed electron propagator between on-shell spinors allows us to exhibit hidden relations between the coefficient functions that hold whenever both electrons are on-shell. This works in the following way. Rather than factorising from the left, as we did in (8), we could as well have used the “reversed” identity (see (I.7.2))
| (78) | |||||
We equate the two expressions for , multiply by , and then take on-shell. This is sufficient to make the subleading terms drop out, since they all lack one of the two poles. Using (11), (14) we get the identity
| (79) |
which by a comparison of the terms linear and cubic in Dirac matrices yields the identities
| (80) | |||||
| (81) |
Here we found it convenient to further introduce the dual tensor . Contracting these with either or we obtain scalar relations,
| (82) | |||||
| (83) |
We see that knowledge of is sufficient to reconstruct the other coefficients. Note further that (82) implies that for , while (83) implies that for .
Aside from the identities presented here between coefficients at fixed , there are some useful recurrence relations between coefficients for different numbers of photons: for brevity these are derived in Appendix C.
7 On-shell matrix elements for the dressed electron propagator
We are now ready for our main task, namely the construction of the on-shell matrix elements corresponding to the fermion line dressed with photons. We will treat these matrix elements in full generality - the fully polarised matrix elements, the spin-averaged polarised cross sections and the totally unpolarised cross section - albeit only for the electron-electron case; the electron-positron, positron-electron and positron-positron cases can be obtained from this by crossing as usual.
7.1 Fully polarised spinor-line matrix element
Using (13), (14) and formulas (75), (76) for the Dirac bilinears, we get the following universal formulas for the polarised matrix elements , independently of the photon number and helicity assignments (we recall that the fermion spins are defined with respect to the vectors and that enter the expressions for the coefficients above):
| (84) |
7.2 Summing over electron spins
For the construction of the spin-averaged cross section, we could either sum over the polarised matrix elements,
| (85) |
using our results (84), or start directly from (13), (14). In either case the result reads, after simple algebra,
| (86) | |||||
However, this expression can still be drastically simplified using the relations (80), (81). For this purpose, we start with rewriting (omitting now the subscript ‘’)
| (87) |
From (80) we have
| (88) |
For the other term, we can use to show
| (89) |
and then use (81) to write
| (90) |
Using these various relations in (86) together with (82), (83) and their complex conjugates, it can be transformed into the surprisingly compact form that we wrote down already in the introduction, equation (20):
| (91) |
7.3 Summing over photon polarisations
Finally, summing over photon polarisations can be done using
| (92) |
Here it should be remembered that, in the spinor-helicity formalism, this completeness relation normally would involve additional longitudinal terms on the right-hand-side,
| (93) |
(with the reference momentum of ) but here they can be omitted due to the on-shell transversality of the coefficients .
8 The “all +” helicity case
Finally, let us have a closer look at the “all +” case. Here we can expect something special to happen because of the well-known connections between helicity, duality, and supersymmetry thooft ; dadda ; brolee ; dufish1 ; dufish2 ; 51 . A background field consisting of photons with only “+” helicities is self dual, which in our present conventions means (compare (44))
| (94) |
This relation can equivalently be expressed as
| (95) |
which is also a step towards exhibiting the associated supersymmetry of the Dirac operator in a self-dual background thooft ; dufish1 ; dufish2 . From the definition (2) of the kernel , and the fact that it reduces to in the absence of the term, we conclude (e.g. by expanding in that term) that in the all case
| (96) |
leading to the following relations for the coefficient functions , and :
| (97) | |||||
| (98) |
Since , the first of these relations can also be written as
| (99) |
Combining the second relation (98) with (82) and (83), we get a further relation
| (100) |
and combining this equation with (99) enables us to express in terms of :
| (101) |
Turning our attention now to the spin-averaged cross section, further simplification follows from the fact that in Minkowski space
| (102) |
Combined with the self-duality relation (98) this leads to the vanishing of . Thus (91) now reduces to
| (103) |
which furthermore by (99) and (101) can be expressed entirely in terms of the scalar coefficient :
| (104) |
Therefore by (16) we are getting a relation between the scalar and spinor cross sections,
| (105) |
This relation is, to the best of our knowledge, new. Note that it becomes equality for ,
| (106) |
a clear manifestation of the underlying supersymmetry.
Note that equation (104) cannot be used in the massless limit. Instead, we can conclude directly from (100) that, for , , leading to the vanishing of (103) for the massless fermion line, and thus of the matrix elements themselves, in agreement with DeCaus ; StirlingSH ; Ozeren ; Badger2 (we also show this directly at the level of the amplitudes in appendix D).
9 Compton scattering
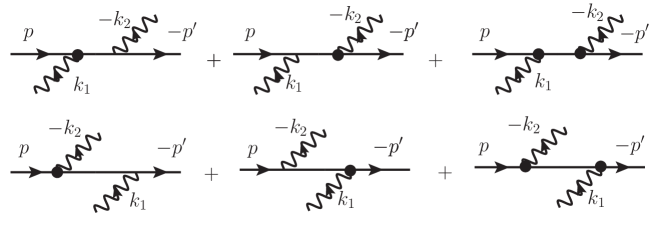
Let us now test our formalism on a recalculation of the Compton scattering amplitude and cross section in spinor QED. We would like to stress once more here that the underlying Feynman rules are not the standard Dirac ones, but second-order rules as explained in part I. As such they contain the diagrams that exist already in scalar QED, depicted in Fig. 1, and other ones involving at least one (spin) interaction, shown in Fig.2.

9.1 The N=2 case
For , we already calculated the coefficient functions off-shell in part I using the fermion line master formula, leading to (I 5.19), and we could use these expressions with on-shell conditions, whereafter it is possible to rewrite them in terms of field-strength tensors. Instead, it is more convenient to follow our present approach and get the on-shell coefficient functions using the spin-orbit decomposition from I and the -representation.
Using at first the same reference momenta of our scalar calculation above, (67), we find, using (37), (30), and (I 6.9), after simple algebra, the coefficients
At this stage it becomes clear that the part of each of the reference vectors (67) proportional to their photon’s momentum drops out of the scalar products in each coefficient. As such, we could at this stage replace the by without losing information (since this does not invalidate our removal of the more complicated term in ) – the same is true for scalar QED as is clear from (69) and its correspondence with .
Below we shall make use of both representations of the coefficients. In general it is useful to keep the null vectors, for use with the spinor helicity representation (section 3). However, it turns out that for calculating the amplitude in a particular reference frame, it is more convenient to take advantage of the freedom to use , since the explicit construction of the spinors , etc, is complicated by their dependence on the photon momenta. On the other hand, at the level of the cross section, spinor products turn into (-vector) scalar products and here the vector form of the can be applied directly.
9.2 The functions with fixed helicities
We begin by providing the coefficients in (LABEL:ABCfinal) in an arbitrary Lorentz frame for the construction of the fully polarised amplitudes in (84) for . Since also the vectors and are defined for an arbitrary frame (likewise and can be chosen with any direction in this frame), this achieves a representation of the polarised amplitudes valid for a general system of reference.
We will denote the polarised amplitudes by , suppressing the superscript ‘’ and as above denoting the helicity of photon by . For the calculation of , we require the coefficients
| (108) |
(recall that ). With these coefficients one readily verifies the general results of sections 6 (equations (82) and (83)) and 8 (equations (99)–(101)). In particular, we shall use the important result below. For the amplitudes we find
| (109) |
Again, these results satisfy the relations given in section 6. These coefficients can be substituted directly into (84) to find the fully polarised amplitudes in any reference frame (we detail the determination of the coefficients in the following subsection).
9.3 The fully polarised amplitudes
We now further specialise to the centre-of-mass frame, where
| (110) |
with
| (111) |
Measuring the particle spins along their direction of motion (“helicity basis”), we can use the general formulas derived in appendix B with and . From (140), (144) and (145) we get
| (112) | ||||||
and the coefficients can be read off from (146):
| (113) |
When written in terms of the Mandelstam variables
| (114) |
the non-zero coefficients turn into
| (115) |
We shall again provide the amplitudes and using (LABEL:ABCfinal) and (84) in this frame. Since in the coefficients and we represent the field strength tensors in terms of spinor helicity variables, we need the explicit components of the spinors related to the vector and ,
| (116) |
For the actual calculation of the coefficients, however, it is now more convenient to replace the to avoid having to determine the explicit form of the spinors for the reference vectors in this frame. Doing this in (LABEL:ABCfinal), we obtain,
| (117) | ||||||
| (118) |
and we can express the remaining scalars in terms of these:
| (119) | |||||
| (120) | |||||
| (121) | |||||
| (122) |
Using (84), and the above equations, the fully polarised amplitudes read as,
| (123) |
Likewise for the amplitudes we find
| (124) | ||||||
| (125) | ||||||
| (126) |
along with
| (127) | |||||
| (128) |
which lead to
| (129) |
All these matrix elements agree, up to signs due to differing conventions, with the results presented by Denner and Dittmaier Denner (to be precise, our corresponds to their , with a relative sign ). For historical discussion and derivation of Compton scattering from density matrix and operator techniques, and using the Stokes parameters for the description of polarisation, we refer the reader to fano ; mcmaster .
9.4 Polarised photons, unpolarised electrons
Moving on to the cross section, we can complete the electron spin sums whilst leaving the photon helicities arbitrary. For this calculation, it is useful to use (108) and (109) as they stand (rather than replacing the by ), since upon multiplication of the coefficients with their complex conjugates, the spinor products are turned into -vector scalar products. We begin with the amplitudes for the helicity assignment. Noting that
| (130) |
we find, after simple algebra,
| (131) |
so that (91) provides
| (132) |
Note that we could have obtained this result more easily using (65) and (105).
Similarly for the helicity amplitude we find
| (133) |
giving in total
| (134) |
Writing these results in terms of the usual Mandelstam variables introduced above we arrive at
| (135) | ||||
In the massless limit, this gives the well-known results
| (136) | ||||
Note that, in our conventions, the amplitude is the helicity violating one, correctly vanishing in the massless case. In the present formalism, it is clear from (131) that this comes about by a cancellation between the and terms. We discuss some aspects of the massless amplitudes in greater detail in appendix D.
9.5 The unpolarised Compton cross section
Finally, let us also sum over photon polarisations to write down the unpolarised cross section:
This is again in agreement, of course, with the standard textbook result, see, for example, eq. (5.87) in peskinschroeder-book .
10 Conclusions and Outlook
In the second part of this series of papers, we have worked out the simplifications that can be achieved using the new, first-quantised worldline representation of the fermion propagator developed in part 1 for the photon-dressed fermion line, when both the fermion legs as well as all photons are taken on-shell (although it should be emphasised that many of the formulas presented here would still be valid if only the fermions were taken on-shell, not the photons). For general kinematics and helicity assignments, we have found three types of simplifications:
-
1.
Most importantly, the “subleading” contributions to the dressed propagator can be omitted.
-
2.
The coefficient functions become manifestly transversal and can be rewritten in terms of photon field-strength tensors in a systematic way.
-
3.
There exist -independent relations between those coefficient functions. As a consequence, all on-shell information is contained in the coefficient .
Further simplifications have been exhibited for special kinematics () or helicity assignments (the “all +” case). We have also derived recursion formulas for the functions that may become useful as an alternative to the direct calculation methods of I.
On a technical level, we have provided a number of useful relations involving the fixed-helicity photon field-strength tensors, and we have derived explicit formulas for all the relevant Dirac bilinears, for arbitray on-shell momenta and spin vectors . These formulas have allowed us to give expressions for the fully polarised amplitudes valid in an arbitrary Lorentz frame in terms of a canonical set of numerical coefficients and reference vectors defined in that frame. For the fixed-helicity but spin-summed cross sections we have found that the result can be derived purely from the squared moduli of the coefficients.
Applying this machinery to the linear Compton scattering process we have found it to lead to significant simplifications over the standard calculation in the first-order Dirac formalism333R. Stora once told one of the authors (C.S.) that V. Weisskopf was so dissatisfied with the standard textbook calculation of the Compton cross section that he asked not only him, but several others of his PhD students to look for a better way to get the simple final result.. The reasons are easy to pinpoint: first, the encoding of the Dirac algebra structure in the Grassmann path integral replaces the “partially antisymmetric” (in the Lorentz indices) Dirac matrices by the “fully antisymmetric” vectors , and therefore in leads effectively to an early projection on the Clifford basis, avoiding the appearance of products of more than four Dirac matrices. We find it curious that, although this representation including the “symbol map” have in principle been known for decades fradkin ; fragit , this attractive feature has apparently never been noted. This also implies an early disentanglement of the photon polarisations and fermion spins, allowing them to be treated completely independently. In particular it makes it possible to perform the average over the latter without having to fix the photon number or helicity assignments.
Thus we expect the formalism to be very well-suited for future calculations of non-linear Compton scattering King1 ; Boca1 ; Heinzl1 ; Seipt1 ; Seipt2 ; Boca2 ; King2 , including at higher orders, as well as its crossed process, multiple photon Bremsstrahlung (see, for example, Haug ; Gupta ; Majumdae ; Nadzhafov ; DeCausmaeckerI ; BerendsII ; BerendsIV ; BerendsVI ) and electron-positron annihilation into several photons acfpc ; eidkur ; berkle ; lee-epannihilation . This will, of course, require a computer algebra implementation, which is in progress.
Another very natural application would be to multiloop contributions to the QED anomalous magnetic moment of the type shown in Fig. 3.
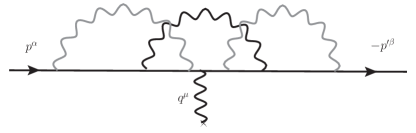
A version of this formalism taylored to this specific purpose (, one photon taken at low energy, the remaining ones taken off-shell and sewn off in pairs) will be presented elsewhere. As an additional attractive feature, the formalism makes it relatively easy to extract the form factor .
In the forthcoming third part of this series, we extend the formalism to the construction of the dressed electron propagator in a constant external field, a case where the absence of a practicable extension of the worldline formalism to open fermion lines had been particularly felt (partial results of the third part have already been published in 113 ).
However, there are many other possible generalisations, let us mention here only a few:
- •
-
•
Dressing the electron line with gravitons, which would generalise previous work on closed scalar and fermion loops Bastianelli:2004zp ; Bastianelli:2007jv ; 87 as well as on open scalar lines 125 . This is of current interest considering the recent application of the worldline formalism to classical black-hole scattering plefka ; jmps1 ; jmps2 .
-
•
Dressing a quark line with gluons, where the color degrees of freedom can be treated very similarly to the spin ones using Grassmann variables Balachandran:1976ya ; Barducci:1976xq ; Bastianelli:2013pta ; Ahmadiniaz:2015xoa ; JO1 ; JO2 .
-
•
Going to finite temperature (see, e.g., sato:therm ; mckeon:therm ; venwir ).
As a final remark, let us emphasise that although here we have focused on the implementation of the formalism in terms of path integrals, nowadays often simply called the “worldline formalism,” we could also have worked more directly with the Feynman diagrams of the second-order formalism. However, such an approach would obscure some of the important advantages of the formalism, such as its ability to combine Feynman diagrams that differ only by the position of the photon legs along the fermion line, and the flexibility provided by IBP in the proper-time parameters.
Acknowledgements.
We thank P. Cvitanović, G.V. Dunne and A. Ilderton for useful conversations and correspondence. CS and JPE thank CONACYT for support through project Ciencias Basicas 2014 No. 242461. JPE further acknowledges financial support from UMSNH through CiC project #483224-2019. VMBG received support from PRODEP project 511-6/19-4990 for part of this work.Appendix A Conventions
On the side of the worldline formalism, we work in Euclidean space with metric , and use Dirac matrices fulfilling . On the field theory side, we Wick rotate to Minkowski space with metric , and use . We further define and . These Minkowski space conventions coincide with the textbook of Srednicki srednicki-book except for the sign of the electric charge, and the fact that we use all ingoing momenta in Feynman diagrams instead of all outgoing ones.
Appendix B Special cases of Dirac bilinears
In this appendix, which supplements section 5, we compute the coefficients explicitly for the electron-electron case and for the two most common choices of the spin-axis vectors and , corresponding to a projection on the electron’s direction of motion (the helicity basis) or on the direction corresponding to the -axis in its rest frame. As an overall convention, we take the ingoing electron to move along the axis and the outgoing one in the - plane. Thus we can write their four-vectors as
| (138) |
B.1 Standard basis
If we use the most common definition of the electron polarizations, the vectors and are taken as in the respective rest frames, and then subjected to the same Lorentz boost that brings their electron up to speed. With our convention (138) this results in
| (139) | ||||
| (140) |
Finally, the null vector (72)
| (141) |
must be constructed using the corresponding spinorial Lorentz boost. This gives, after a lengthy but simple calculation,
| (142) |
This is all we need for the evaluation of (73). One finds, after substantial cancellations,
| (143) |
B.2 Helicity basis
Due to our convention of the incoming particle moving in the direction, changing to the helicity basis leaves unchanged. The vectors and become simpler:
| (144) | |||||
| (145) |
The coefficients also simplify,
| (146) |
Note that in the case of forward scattering, , both bases coincide. If the scattering is forward and elastic, , the coefficients become trivial, .
Appendix C Recursion relations for kernel coefficients
Various relations between the coefficients, , and have been presented in the main text. Here we follow a different path, taking advantage of the definition of the kernel as the inverse of a Klein-Gordon-like operator, to derive some recursive identities that hold between coefficients for different numbers of photons. These could be useful if one had already determined the coefficients up to a given , since they can be used to produce the coefficients at order and higher.
Scalar QED
Beginning with scalar QED the full scalar propagator, , is the inverse of the Klein-Gordon operator in position space so that it satisfies the defining equation:
| (147) |
Our path integral representation of the -photon dressed propagator, (I.2.1) and (LABEL:linemastercov) is an inverse for this operator projected onto the subspace multi-linear in photon polarisations. Thus, writing the propagator as a sum over photon numbers,
| (148) |
where the term is taken multi-linear in , the defining equation (147) in momentum space becomes
| (149) |
where we truncate at some multi-linear order. Defining the amputated propagator via
| (150) |
we extract the contribution to find a recursion relation,
| (151) |
where as usual the hat indicates that the variable is removed. The terms in brackets represent the addition of extra (scalar QED) vertices glued on to a sum of - and -photon amplitudes to “promote” them to an -photon amplitude.
In the case of on-shell photons, we can simplify the recursion relation by replacing the polarisation vectors according to
| (152) |
in the recursion relation, which then turns into
| (153) |
So if we use the -representation of the amplitude, (29), then we produce the -photon propagator already written in a manifestly gauge invariant way.
Spinor QED
For the spinor case we proceed analogously, but with respect to the kernel , (2) which is a Green function for the Klein-Gordon plus spin coupling operator,
| (154) |
Going to momentum space and projecting onto terms multi-linear in photon polarisation leads to the requirement that
| (155) |
If we now also use the identification (11)
| (156) |
then we can solve the relation for the , for :
| (157) |
This equation is analogous to (151), but with the inclusion of the additional spin vertex present in the second order Feynman rules. Now we decompose the matrix structure as in (14) and find three recursion relations between the coefficients. Firstly for ,
| (158) |
then for :
| (159) |
and finally for ,
| (160) |
These can be used to convert the coefficients presented in the main text into the coefficients for and greater numbers of photons.
There are two simplification that can be made on-shell. Firstly, the relations between coefficients, (80) and (82), allow for the right hand sides of the recursion relations to be written entirely in terms of the and . Secondly, since are transversal on-shell, we can again substitute , to rewrite the relations in terms of the field strength tensors of the photons. Since all on-shell information is contained in , it suffices to give this coefficient. For , we have
| (161) |
with
| (162) |
In the general case, ()
| (163) |
Now we have a manifestly gauge invariant recursion relation that can be used to determine the coefficients at order from those of lower order.
Appendix D Helicity amplitudes in the massless limit
In the worldline formalism the massless fermion amplitudes corresponding to (9) can be obtained in two ways. One of them is using the formula (13) and computing the limit when ,
| (164) |
The second way is by setting first in (9), and then taking the limit when . With the aid of equations (8) and (11), we arrive at
where the spinors in the subleading contribution satisfy the massless on-shell relations in (10).
The leading contribution in (LABEL:am_massless_prev) is equivalent to
| (166) |
Then, from (164) and (LABEL:am_massless_prev), we obtain the second formula to compute the massless amplitude,
| (167) |
that now comes only from the subleading piece that depends upon the kernel with photons. Let us corroborate that both (164) and (167) give the correct amplitude for . According to (I 5.13), (I 5.14), and (I 5.20), we obtain that,
| (168) | |||||
| (169) | |||||
| (170) | |||||
Using the formula (164), the amplitude for is calculated as,
| (171) | |||||
where before the limiting process we have used the on-shell relations (10). The result in (171) is the same as the one computed from the standard formalism using Feynman diagrams. Similarly for , we obtain that
| (172) | |||||
where we have recovered again the result from the standard formalism in the massless case.
Let us compute now the amplitudes with the formula (167), using (168) and (169) and the massless on-shell relation in (10). In doing so, we arrive at,
| (173) | |||||
| (174) | |||||
which give the correct amplitudes.
One of the advantages of working with the formula (167) is that, instead of the coefficients for the kernel , we need only those for which are simpler. In the decomposition (14), the formula (167) reads as,
| (175) | |||||
where in the last line, we have used the antisymmetry of , and the equation,
| (176) |
On the other hand in the derivation of the second formula for the massless amplitude, we could have used the reversed identity (78). In this case (175) becomes,
| (177) | |||||
Now, in the spinor helicity formalism the photon polarisation vectors are given by equation (40), and the fermion spinors by srednicki-book ; elvhua-book ,
| (178) |
Then, from either (175) or (177), the amplitudes when the ingoing and the outgoing fermion have different physical helicities vanish since
| (179) |
Furthermore, if all photons have the same helicities as the incoming fermion, or the opposite helicity of the outgoing one, the amplitude also vanishes since, choosing the reference momenta of the polarisation vectors to be or , we have that srednicki-book ,
| (180) |
These all imply that when all photons have the same helicities, the corresponding tree level amplitude with one incoming and one outgoing massless fermion must vanishes, which agrees with the results of section 8.
Now, to calculate the non-zero massless amplitudes, we can choose the reference momenta for the photon polarisations such that the terms in (175), or equivalently in (177), do not contribute to the amplitude. Then, we only need to calculate the terms with the coefficient .
For the amplitudes where the incoming and outgoing fermion have negative physical helicity, we choose the reference momenta for the polarisation vectors with negative helicity, and for the polarisation vectors with positive helicities. Then, the amplitude, according to (175), reads as
| (181) |
where we have used the identity
| (182) |
and with the sum running only over photons with negative helicity.
For the amplitudes , we choose the reference momenta to be for the polarisation vectors with positive helicity, and for the polarisation vectors with negative helicities. Then, the amplitude, according to (177), reads as,
| (183) |
As an example, let us compute the unpolarised-electron cross section for . According to (169), the coefficient is given by,
| (184) |
Therefore, from (181), we obtain that
| (185) | |||||
Similarly, from (183) we find
| (186) |
Thus the unpolarised-electron cross section turns into
| (187) | |||||
This agrees with (LABEL:comptonunpol) in the massless limit.
References
- (1) N. Ahmadiniaz, V. M. Banda Guzmán, F. Bastianelli, O. Corradini, J. P. Edwards and C. Schubert, Worldline master formulas for the dressed electron propagator. Part I. Off-shell amplitudes, JHEP 08 (2020) 049, arXiv:2004.01391 [hep-th].
- (2) R. P. Feynman, Mathematical formulation of the quantum theory of electromagnetic interaction, Phys. Rev. 80 (1950) 440.
- (3) R. P. Feynman, An operator calculus having applications in quantum electrodynamics, Phys. Rev. 84 (1951) 108.
- (4) A. M. Polyakov, Gauge Fields and Strings, Harwood (1987).
- (5) M. J. Strassler, Field theory without Feynman diagrams: One-loop effective actions, Nucl. Phys. B 385 (1992) 145, arXiv:hep-ph/9205205 [hep-ph].
- (6) M. J. Strassler, Field theory without Feynman diagrams: a demonstration using actions induced by heavy particles, SLAC-PUB-5978 (1992) (unpublished).
- (7) M. G. Schmidt and C. Schubert, On the calculation of effective actions by string methods, Phys. Lett. B 318 (1993) 438, arXiv:hep-th/9309055 [hep-th].
- (8) M. G. Schmidt and C. Schubert, Multiloop calculations in the string-inspired formalism: the single spinor-loop in QED, Phys. Rev. D 53 (1996) 2150, arXiv:hep-th/9410100 [hep-th].
- (9) C. Schubert, Perturbative quantum field theory in the string inspired formalism, Phys. Rep. 355 (2001) 73, arXiv:hep-th/0101036 [hep-th].
- (10) J. P. Edwards and C. Schubert, Quantum mechanical path integrals in the first quantised approach to quantum field theory, Technical Report to be published in the proceedings of the workshop “Path Integration in Complex Dynamical Systems,” Leiden, 6 Feb - 10 Feb 2017. arXiv:1912.10004 [hep-th].
- (11) R. P. Feynman and M. Gell-Mann, Theory of Fermi interaction, Phys. Rev. 109 (1958) 193.
- (12) L. C. Hostler, Scalar formalism for quantum electrodynamics, J. Math. Phys. 26 (1985) 1348.
- (13) Z. Bern and D. C. Dunbar, A mapping between Feynman and string motivated one loop rules in gauge theories, Nucl. Phys. B 379 (1992) 562.
- (14) A. Morgan, Second order fermions in gauge theories, Phys. Lett. B 351 (1995) 249, arXiv:hep-ph/9502230 [hep-ph].
- (15) E. S. Fradkin and D. M. Gitman, Path integral representation for the relativistic particle propagators and BFV quantization, Phys. Rev. D 44 (1991) 3230.
- (16) F. Bastianelli, A. Huet, C. Schubert, R. Thakur and A. Weber, Integral representations combining ladders and crossed ladders, JHEP 1407 (2014) 066, arXiv:1405.7770 [hep-ph].
- (17) M. E. Peskin and D. V. Schroeder, Introduction to Quantum Field Theory, Addison-Wesley 1995.
- (18) B. Feng, X. D. Li and R. Huang, Expansion of EYM Amplitudes in Gauge Invariant Vector Space, Chin. Phys. C 44 (2020) no.12, 123104, arXiv:2005.06287 [hep-th].
- (19) M. A. Olpak and A. Ozpineci, On the calculation of covariant expressions for Dirac bilinears, arXiv:1905.10470 [hep-th].
- (20) G. ’t Hooft, Computation of the quantum effects due to a four-dimensional pseudoparticle, Phys. Rev. D 14 (1976) 3432.
- (21) A. D’Adda and P. Di Vecchia, Supersymmetry and instantons, Phys. Lett. B 73 (1978) 162.
- (22) L. S. Brown and C. Lee, Massive propagators in instanton fields, Phys. Rev. D 18 (1978) 2180.
- (23) M. J. Duff and C. J. Isham, Selfduality, Helicity, and Supersymmetry: The Scattering of Light by Light, Phys. Lett. B 86 (1979) 157.
- (24) M. J. Duff and C. J. Isham, Selfduality, Helicity, and Coherent States in Nonabelian Gauge Theories, Nucl. Phys. B 162 (1980) 271.
- (25) G. V. Dunne and C. Schubert, Two-loop self-dual Euler-Heisenberg Lagrangians. I: Real part and helicity amplitudes, JHEP 0208 (2002) 053, arXiv:hep-th/0205004 [hep-th].
- (26) C. Schubert, The structure of the Bern-Kosower integrand for the N-gluon amplitude, Eur. Phys. J. C 5 (1998) 693, arXiv:hep-th/9710067 [hep-th].
- (27) N. Ahmadiniaz, C. Schubert and V. M. Villanueva, String-inspired representations of photon/gluon amplitudes, JHEP 1301 (2013) 312, arXiv:1211.1821 [hep-th].
- (28) Z. Bern and D. A. Kosower, Efficient calculation of one loop QCD amplitudes, Phys. Rev. Lett. 66 (1991) 1669.
- (29) Z. Bern and D. A. Kosower, The computation of loop amplitudes in gauge theory, Nucl. Phys. B 379 (1992) 451.
- (30) K. Daikouji, M. Shino, Y. Sumino, Bern-Kosower rule for scalar QED, Phys. Rev. D 53 (1996) 4598, arXiv:hep-ph/9508377 [hep-ph].
- (31) N. Ahmadiniaz, A. Bashir and C. Schubert, Multiphoton amplitudes and generalized Landau-Khalatnikov-Fradkin transformation in scalar QED, Phys. Rev. D 93 (2016) 045023, arXiv: 1511.05087 [hep-ph].
- (32) M. Srednicki, Quantum Field Theory, Cambridge University Press (2007).
- (33) H. Elvang and Y.-T. Huang, Scattering amplitudes in gauge theory and gravity, Cambridge University Press (2015).
- (34) L. C. Martin, C. Schubert and V. M. Villanueva Sandoval, On the low-energy limit of the QED N - photon amplitudes, Nucl. Phys. B 668 (2003) 335, arXiv:hepth/0301022 [hep-th].
- (35) C. Bernicot and J.-Ph Guillet, Six-photon amplitudes in scalar QED, JHEP 0801 (2008) 059, arXiv:0711.4713 [hep-ph].
- (36) A. Denner and S. Dittmaier, Complete O(alpha) QED corrections to polarised Compton scattering, Nucl. Phys. B 540 (1999) 58-86, arXiv:hep-ph/9805443.
- (37) U. Fano, Description of States in Quantum Mechanics by Density Matrix and Operator Techniques, Rev. Mod. Phys. 29 (1957) 75.
- (38) W. McMaster, Matrix Representation of Polarization, Rev. Mod. Phys. 33 (1961) 8.
- (39) P. De Causmaecker, R. Gastmans, W. Troost and T. T. Wu, Helicity amplitudes for massless QED, Phys. Lett. B105 (1981) 215.
- (40) R. Kleiss and W. J. Stirling, Cross sections for the production of an arbitrary number of photons in electron-positron annihilation, Phys. Lett. B 179 (1986) 159.
- (41) K. J. Ozeren and W. J. Stirling, MHV techniques for QED processes, JHEP 0511 (2005) 016, arXiv:hep-th/0509063 [hep-th].
- (42) S. Badger, N. E. J. Bjerrum-Bohr and P. Vanhove, Simplicity in the Structure of QED and Gravity Amplitudes, JHEP 0902 (2009) 038, arXiv:0811.3405 [hep-th].
- (43) E.S. Fradkin, Application of functional methods in quantum field theory and quantum statistics (II), Nucl. Phys. 76 (1966) 588.
- (44) B. King and S. Tang, Nonlinear Compton scattering of polarized photons in plane-wave backgrounds, Phys. Rev. A 102 (2020) 022809, arXiv:2003.01749 [hep-ph].
- (45) M. Boca and V. Florescu, Nonlinear Compton scattering with a laser pulse, Phys. Rev. A 80 (2009) 053403
- (46) T. Heinzl, D. Seipt, D. and B. Kampfer, Beam-Shape Effects in Nonlinear Compton and Thomson Scattering, Phys. Rev. A 81 (2010) 022125, arXiv:0911.1622 [hep-ph].
- (47) D. Seipt and B. Kampfer, Non-linear Compton scattering of ultrahigh-intensity laser pulses, arXiv:1111.0188 [hep-ph].
- (48) D. Seipt and B. Kampfer, Non-Linear Compton Scattering of Ultrashort and Ultraintense Laser Pulses, Phys. Rev. A 83 (2011) 022101.
- (49) M. Boca, V. Dinu and V. Florescu, Electron distributions in nonlinear Compton scattering, Phys. Rev. A 86 (2012) 013414, arXiv:1206.6971 [physics.atom-ph].
- (50) B. King, Double Compton scattering in a constant crossed field, Phys. Rev. A 91 (2015) 033415, arXiv:1410.5478 [hep-ph].
- (51) E. Haug, and W. Nakel, The elementary process of Bremsstrahlung, World Scientific, N.J., (2004)
- (52) S. N. Gupta, Multiple Bremsstrahlung, Phys. Rev. 99 (1955) 1015.
- (53) R. C. Majumdae, V. S. Mathur and J. Dhar, Multiple photon production in Compton scattering and bremsstrahlung, Il Nuov. Cim. 12 (1959) 97.
- (54) I. M. Nadzhafov, Multiphoton bremsstrahlung, Sov. Phys. Jour. 13 (1970) 114.
- (55) P. De Causmaecker, R. Gastmans, W. Troost and T. T. Wu, Multiple bremsstrahlung in gauge theories at high energies (I). General formalism for quantum electrodynamics, Nucl. Phys. B 206 (1982) 53.
- (56) F. A. Berends, R. Kleiss, P. De Causmaecker, R. Gastmans, W. Troost and T. T. Wu, Multiple bremsstrahlung in gauge theories at high energies (II). Single bremsstrahlung, Nucl. Phys. B 206 (1982) 61.
- (57) F. A. Berends, P. De Causmaecker, R. Gastmans, R. Kleiss, W. Troost and T. T. Wu, Multiple bremsstrahlung in gauge theories at high energies: (IV). The process e+e, Nucl. Phys. B 239 (1984) 395.
- (58) F. A. Berends, P. De Causmaecker, R. Gastmans, R. Kleiss, W. Troost and T. T. Wu, Multiple bremsstrahlung in gauge theories at high energies: (IV). The process e+e e+e, Nucl. Phys. B 264 (1986) 265.
- (59) G. Andreassi, G. Calucci, G. Furlan, G. Peressutti, and P. Cazzola, Radiative corrections to the total cross section for annihilation of a pair into photons, Phys. Rev. 128 (1962) 1425.
- (60) S. Eidelman and E. Kuraev, e+ e- annihilation into two and three photons at high energy, Nucl. Phys. B 143 (1978) 353.
- (61) F. A. Berends and R. Kleiss, Distributions for electron-positron annihilation into two and three photons, Nucl. Phys. B 186 (1981) 22.
- (62) R. N. Lee, Electron-positron annihilation to photons at revisited, Nucl. Phys. B 960 (2020) 115200, arXiv:2006.11082 [hep-ph].
- (63) N. Ahmadiniaz, F. Bastianelli, O. Corradini, J. P. Edwards and C. Schubert, One-particle reducible contribution to the one-loop spinor propagator in a constant field, Nucl. Phys. B 924 (2017) 377, arXiv:1704.05040 [hep-th].
- (64) M. Mondragón, L. Nellen, M. G. Schmidt and C. Schubert, Yukawa couplings for the spinning particle and the worldline formalism, Phys. Lett. B 351 (1995) 200, arXiv:hep-th/9502125 [hep-th].
- (65) M. Mondragón, L. Nellen, M. G. Schmidt and C. Schubert, Axial couplings on the worldline, Phys. Lett. B 366 (1996) 212, arXiv:hep-th/9510036 [hep-th].
- (66) E. D’ Hoker, D. G. Gagné, Worldline path integrals for fermions with scalar, pseudoscalar and vector couplings, Nucl. Phys. B 467 (1996) 272, arXiv:hep-th/9508131 [hep-th].
- (67) E. D’ Hoker, D. G. Gagné, Worldline path integrals for fermions with general couplings, Nucl. Phys. B 467 (1996) 297, arXiv:hep-th/9512080 [hep-th].
- (68) D. G. C. McKeon, C. Schubert, A New approach to axial vector model calculations, Phys. Lett. B 440 (1998) 101, arXiv:hep-th/9807072 [hep-th].
- (69) F. A. Dilkes, D. G. C. McKeon, C. Schubert, A New approach to axial vector model calculations. 2., JHEP 9903 (1999) 022, arXiv:hep-th/9812213 [hep-th].
- (70) F. Bastianelli and C. Schubert, One loop photon-graviton mixing in an electromagnetic field: Part 1, JHEP 0502 (2005) 069, gr-qc/0412095.
- (71) F. Bastianelli, U. Nucamendi, C. Schubert and V. M. Villanueva, One loop photon-graviton mixing in an electromagnetic field: Part 2, JHEP 0711 (2007) 099, arXiv:0710.5572 [gr-qc].
- (72) F. Bastianelli, O. Corradini, J. M. Dávila and C. Schubert, On the low energy limit of one loop photon-graviton amplitudes, Phys. Lett. B 716, 345 (2012), arXiv:1202.4502 [hep-th].
- (73) N. Ahmadiniaz, F. M. Balli, O. Corradini, J. M. Dávila and C. Schubert, Compton-like scattering of a scalar particle with N photons and one graviton, Nucl. Phys. B 950 (2020) 114877, arXiv:1908.03425 [hep-th] .
- (74) G. Mogull, J. Plefka and J. Steinhoff, Classical black hole scattering from a worldline quantum field theory, JHEP 2102 (2021) 048, arXiv:2010.02865 [hep-th].
- (75) G. U. Jakobsen, G. Mogull, J. Plefka and J. Steinhoff, Classical Gravitational Bremsstrahlung from a Worldline Quantum Field Theory, Phys. Rev. Lett. 126 (2021) 201103, arXiv:2101.12688 [gr-qc].
- (76) G. U. Jakobsen, G. Mogull, J. Plefka and J. Steinhoff, Gravitational Bremsstrahlung and Hidden Supersymmetry of Spinning Bodies, arXiv:2106.10256 [hep-th].
- (77) A. P. Balachandran, P. Salomonson, B. S. Skagerstam and J. O. Winnberg, Classical Description of Particle Interacting with Nonabelian Gauge Field, Phys. Rev. D 15 (1977) 2308.
- (78) A. Barducci, R. Casalbuoni and L. Lusanna, Classical Scalar and Spinning Particles Interacting with External Yang-Mills Fields, Nucl. Phys. B 124 (1977) 93.
- (79) F. Bastianelli, R. Bonezzi, O. Corradini and E. Latini, Particles with non abelian charges, JHEP 1310 (2013) 098, arXiv:1309.1608 [hep-th].
- (80) N. Ahmadiniaz, F. Bastianelli and O. Corradini, Dressed scalar propagator in a non-Abelian background from the worldline formalism, Phys. Rev. D 93 (2016) 025035, Addendum: Phys. Rev. D 93 (2016) 049904, arXiv:1508.05144 [hep-th].
- (81) O. Corradini and J. P. Edwards, Mixed symmetry tensors in the worldline formalism, JHEP 1605 (2016) 056, arXiv:1603.07929 [hep-th].
- (82) J. P. Edwards and O. Corradini, Mixed symmetry Wilson-loop interactions in the worldline formalism, JHEP 1609 (2016) 081, arXiv:1607.04230 [hep-th].
- (83) H.-T. Sato, Integral representations of thermodynamic 1PI Green functions in the worldline formalism, J. Math. Phys. 40 (1999) 6407, arXiv:hep-th/9809053 [hep-th].
- (84) D. G. C. McKeon, Thermal Vacuum Polarization Using the Quantum Mechanical Path Integral, Int. J. Mod. Phys A 12 (1997) 5387.
- (85) R. Venugopalan and J. Wirstam, Hard thermal loops and beyond in the finite temperature worldline formulation of QED, Phys. Rev. D 63 (2001) 125022, arXiv:hep-th/0102029 [hep-th].