What does the Milky Way look like?
Abstract
In spite of much work, the overall spiral structure morphology of the Milky Way remains somewhat uncertain. In the last two decades, accurate distance measurements have provided us with an opportunity to solve this issue. Using the precise locations of very young objects, for the first time, we propose that our Galaxy has a multiple-arm morphology that consists of two-arm symmetry (the Perseus and Norma Arms) in the inner parts and that extends to the outer parts, where there are several long, irregular arms (the Centaurus, Sagittarius, Carina, Outer, and Local Arms).
1 Introduction
Determining the detailed spiral structure of the Milky Way (MW) has long been a difficult issue in astronomy. Since we are deeply embedded in the Galactic disk, there are always multiple structural features superimposed along the observational line of sight. For a spiral galaxy, there may be two different components of spiral arms (Dobbs & Baba, 2014, and references therein). One is composed of a spiral pattern indicated by the distribution of the older stellar population, and the other is a spiral picture traced by diffuse or dense interstellar gas and young objects, e.g., high-mass star-forming regions (HMSFRs), massive O–B stars, Hii regions, young open clusters (YOCs), etc.
Pioneering work was made by Morgan and his colleagues in the 1950s. They found three short spiral-arm segments in the solar neighborhood using spectroscopic parallaxes of high-mass stars (Morgan et al., 1952, 1953). Soon after, larger-scale spiral structure, extending almost across the entire Galactic disk, was mapped with HI survey data using kinematic methods (e.g., van de Hulst et al., 1954; Kerr et al., 1957; Bok, 1959; Burton & Shane, 1970). Later, however, the distances of HI clouds, derived from kinematic methods, were found to have large uncertainties due to noncircular (peculiar) motions. Thus, the HI results in these early studies are not very reliable. Photometric methods are much more accurate than kinematic methods, although they can only be used to determine objects at distances up to 2 kpc, i.e., much smaller than the size of the MW. For this reason, kinematic methods are still widely used to study the entire MW. By analyzing a number of Hii regions with photometric and/or improved kinematic distances, a paradigmatic map of the Galaxy’s spiral arms was made by Georgelin & Georgelin (1976). They first proposed that the MW has four major arms. This picture was then frequently updated by using other spiral tracers, such as molecular clouds (e.g., Burton & Gordon, 1978; Dame et al., 1987, 2001; Sun et al., 2015; Du et al., 2016), star-forming complexes (Russeil, 2003), a larger sample of Hii regions (e.g., Paladini et al., 2004; Hou & Han, 2014), HI gas (e.g., Levine et al., 2006), etc., most of which relied on kinematic methods.
Although kinematic methods are being improved all the time, they sometimes cause significant uncertainties in the locations of sources. Therefore, the debate continues over such basic facts as the existence of some spiral arms, the number of arms, and the size of the MW. Measuring distances as accurately as possible using spiral tracers is key to settling these disputes and correctly uncovering the Galaxy’s spiral structure. Recently, substantial progress in tracing the Galactic structure using young objects has been achieved. On the one hand, Very Long Baseline Interferometry (VLBI) can yield trigonometric parallax accuracies down to a few as (e.g., Xu et al., 2006; Hachisuka et al., 2006; Sanna et al., 2017), allowing precise distance measurements toward masers associated with HMSFRs throughout the Galaxy. Focusing on mapping the MW, the Bar and Spiral Structure Legacy (BeSSeL) Survey (Brunthaler et al., 2011) and the VLBI Exploration of Radio Astrometry (VERA) array (VERA Collaboration et al., 2020) have measured accurate distances for up to 200 masers. These measurements indicate that the MW is a four-arm spiral, with some extra arm segments and spurs (Reid et al., 2019, hereafter R19). On the other hand, a large amount of young stars provided by the Gaia mission has densified the spiral-arm segments traced by masers, which also help determine the Galactic spiral structure in the solar neighborhood (Xu et al., 2018a, b, 2021a; Hao et al., 2021; Hou, 2021; Poggio et al., 2021).
External spiral galaxies can also act as a mirror to help us understand Galactic morphology better as the MW is one of trillions of galaxies in the observable universe. Pictures of external spiral galaxies show that there are largely three distinct types of morphology. In two extreme cases, grand-design spiral galaxies are highly symmetric, characterized by clear, long, and symmetric spiral arms, whereas flocculent ones are fragmented, consisting of many short, irregular, and patchy segments. An intermediate type lies in between, so-called multiple-arm spiral galaxies whose main characteristic is an inner two-arm symmetry and several irregular arms in the outer parts (Elmegreen & Elmegreen, 2014). Different from flocculent galaxies, both grand-design and multiple-arm galaxies have two prominent, symmetric arms in their inner regions, and almost no external galaxies present four spirals extending from their centers to their outer regions (Elmegreen & Elmegreen, 1982, 1987, 1995). Today, it is widely accepted that the MW galaxy has four continuous spiral arms extending outward from the inner Galaxy to distant outer regions (e.g., Georgelin & Georgelin, 1976; Reid et al., 2019; Minniti et al., 2021). If that is the case, the MW may be an atypical galaxy in the universe.
In the past few years, the number of young objects in the MW with precisely measured distances has increased significantly. It would be constructive to combine these high-quality data together to provide a better understanding the MW’s spiral structure. In this contribution, largely following the previously developed spiral-arm-fitting approach presented by R19, we have synthesized the available data set of spiral tracers with precisely measured distances, including the parallax measurements of HMSFR masers from VLBI observations, massive O–B2-type stars, and YOCs from the Gaia mission, aiming to uncover the real image of our archetypal Galaxy.
2 Data
Currently, VLBI maser parallax measurements are mainly carried out in the Northern Hemisphere, with uncertainties of typically 20as, while a number of observations have uncertainties down to 10as or better, allowing reliable distances to be determined for objects located at the Galactic Center (GC) and beyond (Zhang et al., 2013; Sanna et al., 2017; Reid et al., 2019; Xu et al., 2021b). On the other hand, Gaia Data Release 3 (DR3) data have uncertainties of order 20–30 as, which enable us to reveal the spiral structure within 5 kpc of the Sun. In addition to using these distances to trace the spiral structure directly, ascertaining arm tangencies are also a good way to determine the locations of spiral arms, which are identified from the distributions of stars, interstellar gas, dust, and star-formation sites in the Galactic plane (Hou & Han, 2015).
2.1 Masers
VLBI at radio wavelengths has been used to detect a large amount of masers associated with HMSFRs, and they can be used to map the spiral structure of the MW from the solar neighborhood to the GC and beyond. Table 1 lists the coordinates and parallaxes of 204 HMSFR masers measured with VLBI techniques, including the National Radio Astronomy Observatory’s Very Long Baseline Array, the Japanese VLBI Exploration of Radio Astrometry project, the European VLBI Network, and the Australian Long Baseline Array. For the masers listed in Table 1, 199 were summarized by R19, and five have been newly reported by Xu et al. (2021b) and Bian et al. (2022) in the past two years. The typical parallax accuracy of the masers is 20 as, and 19 of them even have accuracies of 10 as or better.
2.2 O–B2-type stars
High-mass stars are generally located near their birthplaces, and thus they can also be used to trace the Galactic spiral structure. Employing the same method as used by Gaia Collaboration et al. (2022), we adopted the effective temperature, spectral type, distance from the galactic plane, and the astrometric fidelity indicator, (Rybizki et al., 2022), to select O–B-type star candidates from Gaia DR3 (Gaia Collaboration et al., 2022). We only use stars with a parallax precision better than 20%, i.e., parallax_over_error 5. After applying this criterion, we obtained a total of 495 965 O–B stars.
Then, RR-Lyrae stars identified by vari_rryrae in Gaia DR3 were removed. Next, we filter the tangential velocity with km s-1, the same as Gaia Collaboration et al. (2018), where and are the proper motions in the R.A. and decl., respectively, is the parallax, and = 4.74 km yr s-1. After filtering based on the above criteria, 488 449 O–B-type stars are left. In this work, we only consider stars hotter than 20 000 K, which corresponds to O–B2-type stars whose typical ages are younger than 20 Myr (Chen et al., 2013). The final sample is composed of 23 807 O–B2 stars. We perform a parallax zero-point correction for all O–B2-type stars in the sample, as indicated by (Lindegren et al., 2021). The median standard error of the parallaxes of the O–B2-type stars is 17 as.
2.3 Open clusters
Since YOCs ( 20 Myr) can trace the spiral arms well (Hao et al., 2021), we only use OCs younger than 20 Myr as tracers in this work. In recent years, taking full advantage of the high-precision astrometric data provided by Gaia, numerous studies have identified thousands of OCs in the MW, and their ages cover a wide range, from several megayears to a few gigyears. Based on many previous works, Hao et al. (2021) compiled a catalog containing more than 3 700 OCs using Gaia Early Data Release 3. Soon after, 704 and 628 newly found OCs in the Gaia area were reported by Hao et al. (2022) and Castro-Ginard et al. (2022), respectively. In this work, we have synthesized the above three catalogs and obtained a large sample of 5 021 OCs, of which 1 011 OCs have ages younger than 20 Myr. We apply a parallax zero-point correction for the member stars of each OC, and then use the average parallax of all members as the OC’s parallax (Lindegren et al., 2021). Similar to the O–B2-type star sample, we only use YOCs with parallax accuracies better than 20%, resulting in a final number of 981 YOCs. The median standard error of parallax of YOCs is 23 as.
3 Objects Assigned to Spiral Arms
3.1 Masers
The spiral arms of the MW show quasi-continuous structure in CO and HI in Galactic longitude–local standard of rest (LSR) velocity (–) maps. We initially assign masers to spiral arms by comparing the positions of the sources with the loci of arm segments provided by Reid et al. (2016). Although a plan view of the MW from – plots cannot accurately place HMSFR masers into spiral arms, one can, in most cases, assign HMSFR masers to spiral arms by their association with CO and HI emission features. In addition, the Galactic latitudes and parallax distances can be helpful for confirming the arm assignments of HMSFR masers and avoiding any anomalous kinematic effects.
In Figure 1, we have overlaid the HMSFR masers on the – plot of HI emission. Figure 2 shows the Galactic longitude–latitude positions of the maser sources, and Figure 3 presents a plan view of the MW. In these three figures, the white dots indicate spurs or sources for which the arm assignments are unclear. The arm assignments for most sources, in terms of the matches, are clear and consistent with the parallax distances. It is worth mentioning that the maser sources assigned to the Norma and Scutum Arms in previous work (R19) are mixed together in the –, –, and – plots (as shown by the zoomed-in subfigures in Figures 1, 2, and 3), respectively. Therefore, in this work, these sources are assigned to the same arm, namely the Norma Arm. Besides, R19 indicated that the Sagittarius Arm has a 2 kpc long gap centered at ∘ near (, ) = (2, 6) kpc (see Figure 3), and the arm segment on the left of the gap belongs to the Sagittarius Arm. As this arm segment is connected to the Carina Arm, here we have assigned the masers to the Carina Arm.



Since the radial velocities () of different spiral arms are almost equal to 0 km s-1 in the direction of the GC (340∘ 20∘) and anti-GC (160∘ 200∘), the Galactic latitudes and parallax distances are used as the primary indicators for arm assignment. For sources within 5 kpc of the Sun, their arm assignments can be determined confidently based on their accurate parallax distances. However, for some distant sources, their parallax distances may be consistent with two or even three spiral arms within their 1 uncertainties, so their Galactic latitudes can provide strong evidence to resolve this issue. G019.6000.23 is a good example of this situation. Around ∘, and of the Sagittarius and Perseus Arms are (0.08∘, 39 km s-1) and (0.08∘, 26 km s-1), respectively (Reid et al., 2016). Near (, ) = (4, 4) kpc, G019.6000.23 has a velocity of 41 km s-1, implying it may belong to either the Sagittarius Arm or the Perseus Arm judging from the match in Figure 1 and the (, ) match in Figure 3. Considering that the Galactic latitude of G019.6000.23 is 0.23∘, we rule out assigning this maser to the Perseus Arm based on the latitude difference of 0.31∘ (-height of 70 pc at a distance of 13 kpc). The Sagittarius Arm matches this maser in both latitude and , and thus we assign G019.6000.23 to the Sagittarius Arm. The same technique for arm assignment is also adopted for the sources G229.5700.15 and G240.3100.07, whose Galactic latitudes are 0.15∘ and 0.07∘, respectively. From the – plot (Figure 1) and the plan view of the MW (Figure 3), they could be in either the Perseus Arm or the Outer Arm. At ∘ and ∘, the Galactic latitudes of the Perseus Arm are 2.10∘ and 2.44∘ (Reid et al., 2019), and the corresponding values are 0.17∘ and 0.19∘ for the Outer Arm (Reid et al., 2019). Hence, the differences of 2.25∘ and 2.51∘ (-height of 200 pc at a distance of 5 kpc) in the Galactic latitude rule out the sources as belonging to the Perseus Arm, and instead they likely reside in the Outer Arm. The arm assignment of each source is listed in Table 1, and the numbers of the sources in the spiral arms are listed in Table 2.
3.2 Young Objects
The high-precision parallaxes of young stars provided by Gaia are excellent tracers, and can be used to map the spiral structure near the Sun. To reveal the MW’s spiral structure better, we use a bivariate kernel density estimator (Feigelson & Babu, 2012) to outline the stellar density structures around the Sun. Meanwhile, considering the exponential distribution of stars in the Galactic disk, we adopt a weight related to the Galactocentric radius, which is set as . Here, is the constant factor and is the disk scale, assumed to be 3 kpc (Binney & Tremaine, 2008). Assuming that the weight at solar circle is 1, we simply set . Adopting a local bandwidth of 0.4 kpc, which is similar to Poggio et al. (2021), the density structures indicated by the O–B2-type stars (color background) and YOCs (contours) are shown in Figure 4. The color backgrounds and contours are concordant. The distributions of the O–B2-type stars and YOCs are highly structured rather than homogeneous.

Owing to a lack of radial velocities of many O–B2-type stars, we could not assign them to spiral arms based on the Galactic – maps as masers. Instead, we adopt a new method to judge which spiral arm an O–B2-type star belongs to according to the probability of the O–B2-type star being located in one of the spiral arms shown in the plan view of the MW. Here, the probability is calculated by a Gaussian function, i.e.,
| (1) |
where is the distance to the spiral arm, is the uncertainty of the distance, and is the arm width, which defaults to 0.3 kpc in this work. Finally, we only select stars with probabilities larger than 10%, corresponding to them being less than 1.7 away from the nearest spiral arm.
3.3 Spiral-arm-fitting Function
We fit a spiral pattern to the spiral-arm segments by adopting a log-periodic spiral, defined as,
| (2) |
where is the Galactocentric radius at the Galactocentric azimuth, , (defined as 0 toward the Sun and increasing in the direction of Galactic rotation) for an arm with radius at reference azimuth , and pitch angle . We fit a straight line to using a Bayesian Markov Chain Monte Carlo (MCMC) procedure to estimate the parameters and .
The test is employed to evaluate the fitted result of the spiral arms, i.e.,
| (3) |
Here, the subscripts “obs” and “mod” on the , respectively mean the radius gleaned from the observational data and from the model, respectively; the subscript represents the th source, is the radius dispersion for , and is the number of sources.
Each log-periodic spiral arm has been depicted by the locations of the masers using the method described by R19. We also constrain the fitted arms to pass the observed arm tangencies (Hou & Han, 2015). After assigning the O–B2-type stars to the spiral arms in the solar neighborhood (the Outer, Perseus, Local, and Carina Arms) based on their probabilities of being located in the referenced spiral arm, we fit the arm parameters ( and ) using Eq. 2. The referenced azimuth, , is arbitrarily set to zero when using the O–B2-type stars to fit the spiral arms. Since the structures indicated by the O–B2-type stars seem to be consistent with those inferred by the masers, we use the spiral arms traced by the masers as the initial reference. Afterward, we assign the O–B2-type stars to the fitted arms and repeat the above procedures until the fitted spiral arms converge. The best-fitting parameters of the masers and O–B2-type stars are listed in Table 2. Figure 3 presents the spiral arms depicted by the masers as well as the arm tangencies, and Figure 4 shows the spiral arms depicted by the O–B2-type stars.
4 The Morphology of the MW
4.1 The MW as a Multiple-arm Galaxy

The precise locations of the masers, O–B2-type stars, and YOCs have revealed the spiral structure of the MW. As shown in Figure 5, the Norma Arm traced by these masers passes the arm tangency at 30.6∘ in the first Galactic quadrant. Due to a lack of masers and young stars in the fourth Galactic quadrant, we adopt a constant pitch angle to extend the Norma Arm outward and it passes through the arm tangency at 305.5∘; the conjectural arm is depicted by the dotted line in Figure 5. There is an additional arm tangency at 311.5∘ near the tangency of the Norma Arm (305.5∘). Two adjacent tangencies are likely created by one spiral arm dividing into two spiral arms (Minniti et al., 2021). Therefore, near the direction of 310∘–340∘, the Norma Arm likely bifurcates out of the Centaurus Arm. Owing to a lack of high-precision data, the Centaurus Arm has been inferred by using the arm tangency at 311.5∘, as depicted by the dotted line in Figure 5. After extending the Perseus Arm inward with a constant pitch angle, it naturally meets the arm tangency at 328.8∘, which is symmetric with the Norma Arm, as shown by the dotted line in Figure 5. Employing the best-fitting pitch angle (see Table 2), the Sagittarius Arm is expected to intersect with the Perseus Arm in the direction of 10∘–30∘ and extend upwards passing the arm tangency at 49.3∘. Around 10∘–30∘, in fact, the masers in the Sagittarius and Perseus Arms exhibit consistent trend in the – and – plots, which could provide support for the above intersection. To sum up, the Norma and Perseus Arms are likely the two symmetric arms in the inner MW. As they extend from the inner Galaxy to the outer parts, they bifurcate, and connect to the Centaurus and Sagittarius Arms, respectively.
In addition to the Perseus Arm, the masers also trace several other spiral arms in the outer Galaxy region, including the Outer, Local, Carina, and Sagittarius Arms. The Outer, Perseus, Local, and Carina Arms are confirmed by O–B2-type stars and YOCs, which also densify and complement the spiral arms depicted by the masers. In Figure 5, the spiral arms depicted by the O–B2-type stars have been indicated by black solid lines. The Local Arm has a propensity to bend down in the third quadrant and may extend forward. Due to a lack of data, we are currently unable to determine whether the Outer Arm is connected to one of the inner arms. As shown in Figure 5, the Carina Arm may be not connected to the Sagittarius Arm. Using masers and the arm tangency at 283.5∘, we have depicted the Carina Arm and inferred its structure in the fourth quadrant, which is confirmed by the fitted result of the young objects in the Gaia data. On the whole, the spiral structure in the solar neighborhood traced by the multifarious young objects nearly agrees with the structure depicted by R19. Considering the inner two symmetric arms and several arm segments in the outer Galaxy regions, the MW should be considered as a multiple-arm spiral galaxy.
Previous studies have indicated that there are slight offsets between the spiral arms traced by objects of different ages (e.g., Vallée, 2014; Hou & Han, 2015). Indeed, as shown in Figure 5, there is a similar situation between the spiral arms drawn by masers and those by young objects; however, these differences are not expected to have an effect on the overall Galactic morphology determined in this work. The consistency of the spiral arms indicated by the various tracers also reinforces the validity of these arms. According to previous research on external galaxies, the pitch angle of a long spiral arm can be variable (Honig & Reid, 2015). Although a constant pitch angle is typically adopted to depict the Perseus Arm, if it is not constant, it is not likely to change the global structure of the MW when considering the widespread distribution of the masers related to the Perseus Arm.
4.2 Comparing the Galactic Morphology Here with That of R19
In the solar neighborhood, the multiple spiral arms of the MW depicted by the masers, O–B2 stars, and YOCs are almost concordant with the results outlined by R19, and the young objects observed by Gaia densify and extend the spiral structure constructed by using the VLBI maser data alone. In the inner region of the Galaxy, R19 proposed that our Galaxy has four major spiral arms, namely the Norma, Scutum, Sagittarius, and Perseus Arms, while this work suggests that there are two major spiral arms, the Norma and Perseus Arms. Since the HMSFR masers assigned to the Norma and Scutum Arms in R19 are mixed together, these sources are considered as belonging to the same arm, i.e., the Norma Arm. After extending inward into the inner regions of the MW, the Sagittarius and Perseus Arms are expected to intersect in the direction of 10∘–30∘, instead of being two spiral arms separated from each other. Therefore, the Sagittarius Arm in this work is considered to be a bifurcation of the Perseus Arm.
4.3 Properties of MW-like Galaxies
Considering that the MW is a typical SBbc- or SBc-type galaxy (Binney & Tremaine, 2008), we select 185 external galaxies with morphologies identified as SBbc- and SBc-type from the SIMBAD database, and compare their morphologies with that of the MW. For more details, please see Appendix B. The properties of the sample of external MW-like galaxies, which contains 73 (40%) flocculent, 99 (54%) multiple-arm, 12 (6%) grand-design, and one unidentified case, have been visually inspected. For multiple-arm galaxies, we have also counted the number of their inner spiral arms, as shown in Figure 6. Statistically, only 2% of the multiple-arm galaxies have four inner arms. But relatively speaking, 83% of the multiple-arm galaxies clearly present two inner arms. As mentioned above, the MW galaxy likely has two inner symmetric arms and several arm segments in the outer regions, showing a multiple-arm morphology. So, in this case, the morphology of the MW is similar to those of most multiple-arm galaxies in the universe.
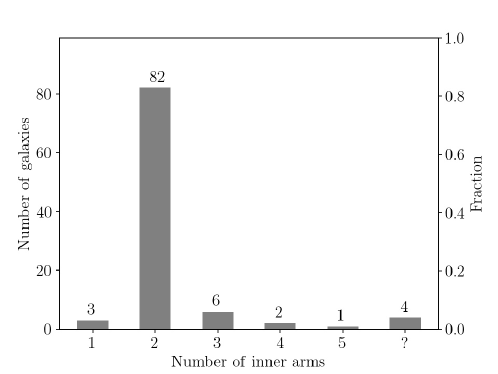
In most multiple-arm galaxies, there is usually a change in the appearance of the spirals midway out in the disk because of symmetric bifurcations or broadenings of the inner spiral arms. Generally, the inner spiral arms of a galaxy are considered to be within 0.5 or twice the radius of galactic bar, where is the radius at which the surface brightness is 25 mag arcsec-2 (Elmegreen & Elmegreen, 1995). The value of the MW is about 11.5 kpc (de Vaucouleurs & Pence, 1978), and recent research has reported that the radius of the Galactic bar is 3.1 kpc (Hilmi et al., 2020). Since the nearly symmetric bifurcations of the inner two arms of the MW are situated at distances of 5.0–6.5 kpc from the GC, the features of the inner two arms of our Galaxy are concordant with the statistical patterns of external galaxies. Additionally, we find that the inner two arms of 73% of the external multiple-arm, barred galaxies start from the ends of the galactic bars. Because there are not enough young objects observed in the Galactocentric region, it is still not possible to determine whether or not the Norma and Perseus Arms start at the ends of the Galactic bar. The potential connections are depicted by chain lines in Figure 5.
5 Summary
High-precision data of various young objects have suggested that the MW is a multiple-arm galaxy, which provides a possible alternative for future studies of the Galactic structure. However, more details of the MW are expected to be revealed using VLBI parallax measurements in the southern sky and Gaia’s upgraded data set. Likewise, in the near future, the SKA and ngVLA will assist in obtaining maser measurements on the far side of the Galactic disk, allowing us to understand the spiral structure of our Galaxy more deeply.
| Source | R.A. | Decl. | Parallax | x | y | Spiral Arm1 | |
|---|---|---|---|---|---|---|---|
| (hh:mm:ss) | (dd:mm:ss) | (mas) | (mas yr-1) | (mas yr-1) | (km s-1) | ||
| G305.2000.01 | 13:11:16.8912 | 62:45:55.008 | 0.250 0.050 | 6.90 0.33 | 0.52 0.33 | 38 5 | Nor |
| G339.8801.25 | 16:52:04.6776 | 46:08:34.404 | 0.480 0.080 | 1.60 0.52 | 1.90 0.52 | 34 3 | Nor |
| G348.7001.04 | 17:20:04.0360 | 38:58:30.920 | 0.296 0.026 | 0.73 0.31 | 2.83 0.59 | 9 5 | Nor |
| G359.6100.24 | 17:45:39.0697 | 29:23:30.265 | 0.375 0.021 | 1.00 0.40 | 1.50 0.50 | 21 5 | Nor |
| G007.4700.05 | 18:02:13.1823 | 22:27:58.981 | 0.049 0.006 | 2.43 0.10 | 4.43 0.16 | 14 10 | Nor |
| G000.3100.20 | 17:47:09.1092 | 28:46:16.278 | 0.342 0.042 | 0.21 0.39 | 1.76 0.64 | 18 3 | Nor |
| G005.8800.39 | 18:00:30.2801 | 24:04:04.576 | 0.334 0.020 | 0.18 0.34 | 2.26 0.34 | 9 5 | Nor |
| G009.2100.20 | 18:06:52.8421 | 21:04:27.878 | 0.303 0.096 | 0.41 0.45 | 1.69 0.50 | 43 5 | Nor |
| G010.3200.15 | 18:09:01.4549 | 20:05:07.854 | 0.343 0.035 | 1.03 0.36 | 2.42 0.50 | 10 5 | Nor |
| G011.1000.11 | 18:10:28.2470 | 19:22:30.216 | 0.246 0.014 | 0.23 0.38 | 2.01 0.41 | 29 5 | Nor |
| G011.9100.61 | 18:13:58.1205 | 18:54:20.278 | 0.297 0.050 | 0.66 0.69 | 1.36 0.75 | 37 5 | Nor |
| G012.6800.18 | 18:13:54.7457 | 18:01:46.588 | 0.416 0.028 | 1.00 0.95 | 2.85 0.95 | 58 10 | Nor |
| … |
| Spiral Arm | Range | Width | Tangency | Tracer | |||||
|---|---|---|---|---|---|---|---|---|---|
| (deg) | (kpc) | (deg) | (deg) | (kpc) | (deg) | ||||
| Outer | 12 | 25 70 | 12.05 0.39 | 17.9 1.94 | 3.6 4.1 | 0.96 0.18 | – | 1.08 | masers |
| 231 | 30 5 | 11.75 0.02 | 0 (–) | 3.9 0.5 | 0.41 (–) | – | 1.08 | O–B2 stars | |
| 626 | 5 30 | 11.79 0.05 | 0 (–) | 1.1 1.4 | 0.41 (–) | – | 1.02 | O–B2 stars | |
| Perseus | 39 | 10 160 | 9.50 0.09 | 18.78 2.26 | 11.0 1.1 | 0.41 0.10 | – | 1.00 | masers |
| 5 797 | 30 40 | 9.90 0.01 | 0 (–) | 1.9 0.3 | 0.28 (–) | – | 1.00 | O–B2 stars | |
| Local | 28 | 10 40 | 8.29 0.08 | 8.95 2.12 | 11.3 1.9 | 0.30 0.03 | – | 1.04 | masers |
| 2 363 | 20 40 | 8.40 0.16 | 0 (–) | 10.0 2.5 | 0.26 (–) | – | 1.09 | O–B2 stars | |
| Carina | 17 | 5 20 | 6.35 0.11 | 9.93 1.88 | 21.4 4.6 | 0.29 0.06 | – | 1.00 | masers |
| 6 330 | 40 20 | 6.65 0.02 | 0 (–) | 17.5 0.9 | 0.26 (–) | – | 1.06 | O–B2 stars | |
| Sagittarius | 24 | 26 150 | 6.02 0.65 | 119.11 2.03 | 1.3 5.1 | 0.47 0.60 | 49.3 | 1.03 | masers |
| Norma | 53 | 0 120 | 4.96 0.02 | 13.07 2.79 | 15.0 1.1 | 0.36 0.06 | 30.6, 305.5 | 1.01 | masers |
Appendix A Additional figures
Figure A1 displays the distributions of the O–B2 stars and YOCs projected onto the Galactic plane.


Appendix B MW-like Galaxies
The contribution of the O–B-type stars to the total MW intensity is only 15% in the near-infrared, compared with 65% in bluer filters (Schweizer, 1976). In order to reveal the spiral morphology of young objects, we use blue images (defined below) in this work. Here, the imaging data of the selected galaxies were obtained from the Sloan Digital Sky Survey (SDSS) DR7 in the band or Digitized Sky Survey (DSS) in the blue band.
After excluding galaxies with small angular sizes (minor diameter smaller than 30 arcsec) and large inclinations (inclinations larger than 60∘), we obtain a sample of 185 external MW-like galaxies. The spiral-arm classification method we adopt is from Elmegreen & Elmegreen (1987). First, a flocculent galaxy lacks bimodal symmetry and has a spiral-like structure composed only of small pieces. Second, a multiple-arm galaxy generally has two inner arms branching midway out in the disk, and there are other arms as well. Third, a grand-design galaxy has a two-arm symmetry, and the arms are long and continuous at least over part of the galaxy. We identify the spiral-arm classifications of the selected 185 external MW-like galaxies, as listed in Table A1, where the flocculent, multiple-arm, and grand-design galaxies are symbolized as F, M, and G, respectively. Figure A2 presents some examples of the flocculent, grand-design, and multiple-arm galaxies.



Using the high-resolution -band images provided by the Palomar Observatory Sky Survey, spiral-arm classifications were made for more than 700 external galaxies with various types by classified (Elmegreen & Elmegreen, 1987). Table A2 presents the classifications of 29 galaxies that appear in this work and in that of Elmegreen & Elmegreen (1987), in which 24 galaxies have the same spiral-arm classes, and five galaxies are classified as multiple-arm galaxies in this work, as shown in Figure A3. Three of the five galaxies, i.e., NGC 289, NGC 1300, and NGC 2441, which were classified as grand-design galaxies by Elmegreen & Elmegreen (1987), tend to be multiple-arm galaxies due to their bifurcate or noncontinuous inner spiral arms. Several spiral arms of another two spiral galaxies, i.e., NGC 3145 and NGC 3687, also show that they are multiple-arm galaxies, rather than flocculent galaxies, as classified by Elmegreen & Elmegreen (1987).





| Name | Morphological Type | Survey | EE Type | Inner Two Arms | Arm Start From Bar | EE87 | ||
|---|---|---|---|---|---|---|---|---|
| (arcmin) | (arcmin) | (Y/N) | (Y/N) | |||||
| ESO 60-18 | SBc | 0.73 | 0.61 | DSS | G | Y | Y | – |
| ESO 61-6 | SBc | 0.85 | 0.51 | DSS | F | – | – | – |
| ESO 69-9 | SBc: | 1.86 | 1.32 | DSS | M | Y | Y | – |
| ESO 72-12 | SBc | 1.15 | 0.65 | DSS | M | Y | Y | – |
| ESO 76-22 | SBc | 0.93 | 0.68 | DSS | M | Y | Y | – |
| ESO 85-5 | SBc | 1.15 | 0.71 | DSS | M | Y | Y | – |
| ESO 109-34 | SBc | 1.05 | 0.68 | DSS | M | Y | N | – |
| ESO 111-15 | SBc/Ir | 0.76 | 0.68 | DSS | F | – | – | – |
| ESO 142-4 | SBc: | 0.95 | 0.60 | DSS | G | Y | Y | – |
| ESO 193-6 | SBc | 1.23 | 1.05 | DSS | M | Y | Y | – |
| ESO 217-32 | SBc | 1.07 | 0.79 | DSS | G | Y | Y | – |
| ESO 221-14 | SB:c/I… | 0.95 | 0.76 | DSS | M | Y | Y | – |
| … |
| F | M | G | |
|---|---|---|---|
| F | 9 | 0 | 0 |
| M | 2 | 14 | 3 |
| G | 0 | 0 | 1 |
References
- Bian et al. (2022) Bian, S. B., Xu, Y., Li, J. J., et al. 2022, AJ, 163, 54, doi: 10.3847/1538-3881/ac3d90
- Binney & Tremaine (2008) Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press)
- Bok (1959) Bok, B. J. 1959, The Observatory, 79, 58
- Brunthaler et al. (2011) Brunthaler, A., Reid, M. J., Menten, K. M., et al. 2011, \an, 332, 461, doi: 10.1002/asna.201111560
- Burton & Gordon (1978) Burton, W. B., & Gordon, M. A. 1978, A&A, 63, 7
- Burton & Shane (1970) Burton, W. B., & Shane, W. W. 1970, in The Spiral Structure of our Galaxy, ed. W. Becker & G. I. Kontopoulos, Vol. 38, 397
- Castro-Ginard et al. (2022) Castro-Ginard, A., Jordi, C., Luri, X., et al. 2022, A&A, 661, A118, doi: 10.1051/0004-6361/202142568
- Chen et al. (2013) Chen, Y., Zhou, P., & Chu, Y.-H. 2013, ApJ, 769, L16, doi: 10.1088/2041-8205/769/1/L16
- Dame et al. (2001) Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792, doi: 10.1086/318388
- Dame et al. (1987) Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706, doi: 10.1086/165766
- de Vaucouleurs & Pence (1978) de Vaucouleurs, G., & Pence, W. D. 1978, AJ, 83, 1163, doi: 10.1086/112305
- Dobbs & Baba (2014) Dobbs, C., & Baba, J. 2014, PASA, 31, e035, doi: 10.1017/pasa.2014.31
- Du et al. (2016) Du, X., Xu, Y., Yang, J., et al. 2016, ApJS, 224, 7, doi: 10.3847/0067-0049/224/1/7
- Elmegreen & Elmegreen (1982) Elmegreen, D. M., & Elmegreen, B. G. 1982, MNRAS, 201, 1021, doi: 10.1093/mnras/201.4.1021
- Elmegreen & Elmegreen (1987) —. 1987, ApJ, 314, 3, doi: 10.1086/165034
- Elmegreen & Elmegreen (1995) —. 1995, ApJ, 445, 591, doi: 10.1086/175723
- Elmegreen & Elmegreen (2014) —. 2014, ApJ, 781, 11, doi: 10.1088/0004-637X/781/1/11
- Feigelson & Babu (2012) Feigelson, E. D., & Babu, G. J. 2012, Modern Statistical Methods for Astronomy: With R Applications (Cambridge University Press), doi: 10.1017/CBO9781139015653
- Gaia Collaboration et al. (2018) Gaia Collaboration, Babusiaux, C., van Leeuwen, F., et al. 2018, A&A, 616, A10, doi: 10.1051/0004-6361/201832843
- Gaia Collaboration et al. (2022) Gaia Collaboration, Drimmel, R., Romero-Gomez, M., et al. 2022, arXiv e-prints, arXiv:2206.06207. https://arxiv.org/abs/2206.06207
- Georgelin & Georgelin (1976) Georgelin, Y. M., & Georgelin, Y. P. 1976, A&A, 49, 57
- Hachisuka et al. (2006) Hachisuka, K., Brunthaler, A., Menten, K. M., et al. 2006, ApJ, 645, 337, doi: 10.1086/502962
- Hao et al. (2022) Hao, C. J., Xu, Y., Wu, Z. Y., et al. 2022, A&A, 660, A4, doi: 10.1051/0004-6361/202243091
- Hao et al. (2021) Hao, C. J., Xu, Y., Hou, L. G., et al. 2021, A&A, 652, A102, doi: 10.1051/0004-6361/202140608
- HI4PI Collaboration et al. (2016) HI4PI Collaboration, Ben Bekhti, N., Flöer, L., et al. 2016, A&A, 594, A116, doi: 10.1051/0004-6361/201629178
- Hilmi et al. (2020) Hilmi, T., Minchev, I., Buck, T., et al. 2020, MNRAS, 497, 933, doi: 10.1093/mnras/staa1934
- Honig & Reid (2015) Honig, Z. N., & Reid, M. J. 2015, ApJ, 800, 53, doi: 10.1088/0004-637X/800/1/53
- Hou (2021) Hou, L. G. 2021, \frass, 8, 103, doi: 10.3389/fspas.2021.671670
- Hou & Han (2014) Hou, L. G., & Han, J. L. 2014, A&A, 569, A125, doi: 10.1051/0004-6361/201424039
- Hou & Han (2015) —. 2015, MNRAS, 454, 626, doi: 10.1093/mnras/stv1904
- Kerr et al. (1957) Kerr, F. J., Hindman, J. V., & Carpenter, M. S. 1957, Nature, 180, 677, doi: 10.1038/180677a0
- Levine et al. (2006) Levine, E. S., Blitz, L., & Heiles, C. 2006, Sci, 312, 1773, doi: 10.1126/science.1128455
- Lindegren et al. (2021) Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2, doi: 10.1051/0004-6361/202039709
- Minniti et al. (2021) Minniti, J. H., Zoccali, M., Rojas-Arriagada, A., et al. 2021, A&A, 654, A138, doi: 10.1051/0004-6361/202039512
- Morgan et al. (1952) Morgan, W. W., Sharpless, S., & Osterbrock, D. 1952, AJ, 57, 3, doi: 10.1086/106673
- Morgan et al. (1953) Morgan, W. W., Whitford, A. E., & Code, A. D. 1953, ApJ, 118, 318, doi: 10.1086/145754
- Paladini et al. (2004) Paladini, R., Davies, R. D., & De Zotti, G. 2004, MNRAS, 347, 237, doi: 10.1111/j.1365-2966.2004.07210.x
- Poggio et al. (2021) Poggio, E., Drimmel, R., Cantat-Gaudin, T., et al. 2021, A&A, 651, A104, doi: 10.1051/0004-6361/202140687
- Reid et al. (2016) Reid, M. J., Dame, T. M., Menten, K. M., & Brunthaler, A. 2016, ApJ, 823, 77, doi: 10.3847/0004-637X/823/2/77
- Reid et al. (2019) Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131, doi: 10.3847/1538-4357/ab4a11
- Russeil (2003) Russeil, D. 2003, A&A, 397, 133, doi: 10.1051/0004-6361:20021504
- Rybizki et al. (2022) Rybizki, J., Green, G. M., Rix, H.-W., et al. 2022, MNRAS, 510, 2597, doi: 10.1093/mnras/stab3588
- Sanna et al. (2017) Sanna, A., Reid, M. J., Dame, T. M., Menten, K. M., & Brunthaler, A. 2017, Sci, 358, 227, doi: 10.1126/science.aan5452
- Schweizer (1976) Schweizer, F. 1976, ApJS, 31, 313, doi: 10.1086/190384
- Sun et al. (2015) Sun, Y., Xu, Y., Yang, J., et al. 2015, ApJ, 798, L27, doi: 10.1088/2041-8205/798/2/L27
- Vallée (2014) Vallée, J. P. 2014, AJ, 148, 5, doi: 10.1088/0004-6256/148/1/5
- van de Hulst et al. (1954) van de Hulst, H. C., Muller, C. A., & Oort, J. H. 1954, Bull. Astron. Inst. Netherlands, 12, 117
- VERA Collaboration et al. (2020) VERA Collaboration, Hirota, T., Nagayama, T., et al. 2020, PASJ, 72, 50, doi: 10.1093/pasj/psaa018
- Xu et al. (2021a) Xu, Y., Hou, L. G., Bian, S. B., et al. 2021a, A&A, 645, L8, doi: 10.1051/0004-6361/202040103
- Xu et al. (2018a) Xu, Y., Hou, L.-G., & Wu, Y.-W. 2018a, RAA, 18, 146, doi: 10.1088/1674-4527/18/12/146
- Xu et al. (2006) Xu, Y., Reid, M. J., Zheng, X. W., & Menten, K. M. 2006, Sci, 311, 54, doi: 10.1126/science.1120914
- Xu et al. (2018b) Xu, Y., Bian, S. B., Reid, M. J., et al. 2018b, A&A, 616, L15, doi: 10.1051/0004-6361/201833407
- Xu et al. (2021b) —. 2021b, ApJS, 253, 1, doi: 10.3847/1538-4365/abd8cf
- Zhang et al. (2013) Zhang, B., Reid, M. J., Menten, K. M., et al. 2013, ApJ, 775, 79, doi: 10.1088/0004-637X/775/1/79