WfChef: Automated Generation of Accurate Scientific Workflow Generators

The basis for our approach is the identification of particular sub-DAGS in workflow instances for a particular application. Let us first define the concept of a type hash:

Figure 1 shows an example for a simple 4-task diamond workflow, where $TD$, $TU$, and $TH$ strings are shown for each vertex. The type hash of each vertex in a workflow encodes information regarding the vertex’s role in the structures and sub-structures of the workflow. From now on, we assume that each vertex is annotated with its type hash. Given a workflow $w$, we define the type hash of $w$, denoted as $TH(w)$, as the set of unique type hashes of $w$’s vertices. $TH(w)$ can be computed in $O(|w|^{2}\log(|w|))$.

The basis of our approach is the observation that, given a workflow, sub-DAGs of it that have the same type hash are representative of the same application-specific pattern (i.e., groups of vertices of certain types with certain dependency structures, but not necessarily the same size). We formalize the concept of a pattern occurrence as follows:

Figure 2 shows an example workflow, where vertex types are once again indicated by colors. Based on the above definitions, this workflow contains 6 POs, each shown within a rectangular box. The two POs in the red boxes have the same type hash, and we say that they correspond to the same pattern. But note that although they correspond to the same pattern, they do not have the same number of vertices. POs can occur within POs, as is the case for the POs in the green boxes in this example. Note that a sub-DAG of the rightmost POs (the three-task PO in the red box) has the same type hash as the POs in the green boxes. In fact, it is identical to those POs (i.e., a blue vertex followed by a green vertex). But this subgraph is not a PO because it does not have a common ancestor with any of the other POs with similar type hashes.

WfChef consists of two main algorithms, WfChefRecipe and WfChefGenerate. The former is invoked only once and takes as input a set of workflow instances for a particular application, $W$, and outputs a “recipe”, i.e., a data structure that encodes relevant information extracted from the workflow instances. The latter is invoked each time a synthetic workflow instance needs to be generated. It takes as input a recipe and a desired number of vertices (as well as a seeded pseudo-random number generator), and outputs a synthetic workflow instance. Both these algorithms have polynomial complexity and implement several heuristics, as described hereafter.

The pseudo-code for WfChefRecipe is shown in Algorithm 1. Lines 2 to 16 are devoted to detecting all POs in $W$. For each $w$ in $W$, the algorithm visits $w$’s vertices (Lines 5-15). An arbitrary unvisited vertex $v$ is visited, and another arbitrary unvisited vertex $v^{\prime}$ is found, if it exists, that has the same type-hash as $v$ (Lines 6-7). If no such $v^{\prime}$ exists then the algorithm visits another vertex $v$ (Line 8). Otherwise, it marks $v^{\prime}$ as visited (Line 9) and computes the set of closest common ancestor and successor vertices for $v$ and $v^{\prime}$ (Lines 10-11). The pseudo-code of the ClosestCommonAncestors and ClosestCommonDescendants functions is not shown as they are simple DAG traversals. If $v$ and $v^{\prime}$ do not have at least one common ancestor and one common descendant, then the algorithm visits another vertex $v$ (Line 12). Otherwise, two POs have been found, which are constructed and appended to the list of POs that occur in $w$ at Lines 13 and 14. The pseudo-code for function SubDAG is not shown. It takes as input a vertex in a DAG, a set of ancestors of that vertex, and a set of descendants of that vertex. It returns a DAG that contains all paths from all ancestors to all descendants to traverse $v$, but from which the ancestors and descendants have been removed (along with their outgoing and incoming edges).

Lines 17 to 23 are devoted to computing a set of “errors” resulting from using a particular (smaller) base workflow to generate a larger (synthetic) workflow. The WfChef approach consists in replicating POs in a base workflow to scale up its number of vertices while retaining a realistic structure. Therefore, when needing to generate a synthetic workflow at a particular scale, it is necessary to choose a base workflow as a starting point. To provide some basis for this choice, for each $w\in W$, the algorithm generates a synthetic workflow with $|w|$ vertices using as a base each workflow in $W$ with fewer vertices than $w$ (Lines 12-22). The ReplicatePOs function replicates POs in a base workflow to generate a larger synthetic workflow (it is described at the end of this section). The error, that is the discrepancy between the generated workflow and $w$, is quantified via some error metric (the Error function) and recorded at Line 21 (in our implementation we use the THF metric described in Section V-B). The way in which these recorded errors are used in our approach is explained in the description of WfChefGenerate hereafter. Finally, at Line 24, the algorithm returns a recipe, i.e., a data structure that contains the workflow instances ($W$), the discovered pattern occurrences ($POs$), and the above errors ($Errors$).

The pseudo-code for WfChefGenerate is shown in Algorithm 2. It takes as input a recipe ($rcp$) and a desired number of vertices $n$. At Line 2, the algorithm determines the workflow in $W$ that has the numbers of vertices closest to $n$. This workflow is called $closest$. At Line 3, the algorithm finds the workflow in $W$ that, when used as a base for generating a synthetic workflow with $|closest|$ vertices, leads to the lowest error. The intent here is to pick the best base workflow for generating a synthetic workflow with $n$ vertices. No workflow in $W$ may have exactly $n$ vertices. As a heuristic, we choose the best base workflow for generating a synthetic workflow with $|closest|$ vertices, based on the errors computed at Lines 17 to 23 in Algorithm 1. The synthetic workflow is generated by calling function ReplicatePOs at Line 4, and returned at Line 5.

The pseudo-code for ReplicatePOs is shown in Algorithm 3. It takes as input a desired number of vertices ($n$), a base workflow ($base$), the list of POs in the base workflow ($bPOs$), and the list of POs in the workflow whose number of vertices is the closest to $n$ ($cPOs$). The intent is to replicate POs in the base workflow, picking which pattern to replicate based on the frequency of POs for that pattern in the closest workflow. At Line 2, the algorithm first sets the generated workflow to be the base workflow. Lines 4-9 are devoted to computing a probability distribution. More specifically, for each PO in $bPOs$, the algorithm computes the probability with which this PO should be replicated. Given a PO in $bPOs$, $nc$ is the number of POs for that same pattern in $cPOs$ (Line 5) and $tc$ is the total number of POs in $cPOs$. Thus, $nc/tc$ is the probability that a PO in $cPOs$ is for that same pattern. $nb$ is the number of POs in $bPOs$ for that same pattern (Line 7). The probability of picking one of these POs in $bPO$ for replication is thus computed as $((nc/tc)/nb)$ (Line 8). Note that this probability could be zero since $nc$ could be zero. The algorithm then iteratively adds one PO from the base graph to the generated graph (while loop at Lines 10 to 13). At each iteration, a PO $po$ in $bPO$ is picked randomly with probability $prob[po]$ (Line 11), and this pattern is added to $g$ (Line 12). The function AddPO operates as follows. Given a workflow, $g$, and a to-be-added PO, $po$, for a specific pattern, it: (i) randomly picks in $g$ one existing PO for that same pattern, $po^{\prime}$; (ii) adds $po$ to the workflow, connecting its entry, resp. exit, vertices to the parent, resp. children, vertices of the corresponding entry, resp. exit, vertices of $po^{\prime}$.

The pseudo-code in this section is designed for clarity. Our actual implementation, described in the next section, is more efficient and avoids all unnecessary re-computations (e.g., the probabilities computed in WfChefGenerate).

We have implemented our approach in a Python package called wfchef. Specifically, this package defines a Recipe class. The constructor for that class takes as input a list of workflow instances and implements algorithm WfChefRecipe. The workflow instances are provided as files in the WfCommons JSON format ⁴⁴4https://github.com/wfcommons/workflow-schema. The class has a public method duplicate that implements the WfChefGenerate algorithm, and a private method duplicate_nodes that implements the ReplicatePOs algorithm. This Python package is available on GitHub⁵⁵5https://github.com/tainagdcoleman/wfchef.

We compare the realism of the synthetic workflow instances generated by WfChef generators to that of instances generated with the original workflow generator in [4], which is called WorkflowGenerator, and with the more recent generator proposed in [5], which is called WorkflowHub. Recall that both WorkflowGenerator and WorkflowHub are hand-crafted, while WfChef generators and automatically produced.

We consider workflow instances from two scientific applications: (i) Epigenomics, a bioinformatics workflow [16]; and (ii) Montage, an astronomy workflow [17]. We choose these two applications because they are well-known and used in production. But also, WorkflowGenerator and WorkflowHub can generate synthetic workflow instances for both of these applications, which makes it possible to compare our approach to previous work. Note that both these previously proposed generators support several scientific workflow applications. However, the only ones they have in common are Epigenomics and Montage. Two other applications are supported by WorkflowGenerator and also by WorkflowHub. Unfortunately, WorkflowGenerator generates synthetic workflow structures that are no longer valid with respect to the current versions of these applications. Therefore, they are incorrect and not comparable to real workflow instances or to synthetic workflows generated by WorkflowHub.

Our ground truth consists of real Montage and Epigenomics workflow instances. These instances are publicly available on the WorkflowHub repository [5]. They were obtained based on logs of application executions with the Pegasus Workflow Management System [18] on the Chameleon academic cloud testbed [19]. Specifically, we consider 14 Montage workflow instances with between 105 and 9807 tasks, and 25 Epigenomics workflow instances with between 75 and 1697 tasks.

We generate synthetic workflow instances with the same number of tasks as real workflow instances, so as to compare synthetic instances to real instances. Both WorkflowGenerator and WorkflowHub encode application-specific knowledge to produce synthetic workflow instances for any desired number of tasks, $n$. Instead, WfChef generators rely on training data, i.e., real workflow instances. We use a simple “training and testing” approach. That is, for generating a synthetic workflow instance with $n$ tasks, we invoke WfChefRecipe with all real workflow instances with $<n$ tasks. For instance, say we want to use WfChef to generate an Epigenomics workflow with 127 tasks. We have real Epigenomics instances for 75, 121, and 127 tasks. We invoke WfChefRecipe with the 75- and 121-tasks instances to generate the recipe. We then invoke WfChefGenerate, passing to it this receipt and asking it to generate a 127-tasks instance.

We use two graph metrics to quantify the realism of generated workflows, as described hereafter.

Figure 3 shows AED results for Epigenomics (top) and Montage (bottom) workflow instances, for WfChef, WorkflowGenerator, and WorkflowHub. WorkflowHub and WfChef use randomization in their heuristics. Therefore, for each number tasks we generated 10 sample synthetic workflow with each tool. The heights of the bars in Figure 3 correspond to average AED values, and we show error bars that represent the range between the third quartile (Q3) and the first quartile (Q1), in which 50 percent of the results lie. Error bars also show minimum and maximum values. Note that error bars, minimum, and maximum values are not shown for WorkflowGenerator as it generates synthetic workflow structures deterministically.

The key observation from Figure 3 is that in most cases WfChef leads to lower average AED values than its competitors. For Epigenomics, WorkflowGenerator leads to the worst results for all workflow sizes, being significantly outperformed by WorkflowHub. WorkflowHub is itself outperformed by WfChef for all workflow sizes. On average over all Epigenomics instances, WorkflowGenerator, WorkflowHub, and WfChef lead to an AED of 2.039, 1.473, and 1.086, respectively. For Montage workflows (Figure 3-bottom), WorkflowGenerator outperforms WorkflowHub for all workflow instances, and both are outperformed by WfChef. On average over all Montage instances, WorkflowGenerator, WorkflowHub, and WfChef lead to an AED of 1.694, 2.216, and 1.111, respectively.

The good results obtained by WfChef are due to it being able to generated instances that are closer in size and that are more faithful to real workflow instances. Note that the AED metric values are quite high overall, often above 1. Although the synthetic instances may have a structure that is overall similar to that of the real instances, making the two workflows absolutely identical requires a large number of edits. For this reason, hereafter we present results for a second metric.

Figure 4 shows THF results for Epigenomics (top) and Montage (bottom). More results are shown than in Figure 3 since we can evaluate the THF metric for larger workflow instances. Like in Figure 3, bar heights represent averages and error bars, minimum, and maximum values are shown for WorkflowHub and WfChef.

Results are mostly in line with AED results. For Epigenomics, WorkflowGenerator leads to the worst average results for all workflow sizes. WfChef leads to significantly better results on average than WorkflowHub in all but two cases. For 349- and 423-task workflows, although WfChef leads to better average results, error bars for WfChef and WorkflowHub have a large amount of overlap. Note that the length of the error bars for the WfChef results show a fair amount of variation, with short error bars for one workflow size and significantly longer error bars for the next size up (e.g., going from 265 tasks to 349 tasks). This behavior is due to “jumps” in structure between workflows of certain scales. In other words, for a given application, it is common for smaller workflows to contain only a subset of the patterns that occur in larger workflows. On average over all Epigenomics instances, WorkflowGenerator, WorkflowHub, and WfChef lead to a THF of 0.097, 0.021, and 0.004, respectively. For Montage, WorkflowGenerator leads to better average results than WorkflowHub for all workflow sizes, and WfChef leads to strictly better results than its competitors for all workflow sizes. On average over all Montage instances, WorkflowGenerator, WorkflowHub, and WfChef lead to a THF of 0.211, 0.252, and 0.040, respectively.

We conclude that generators produced by WfChef generate synthetic workflow instances with structures that are significantly more realistic than that of workflows generated by WorkflowGenerator and WorkflowHub.

Synthetic workflow instances are typically used in the literature to drive simulations of workflow executions. A pragmatic way to evaluate the realism of synthetic workflow instances is thus to quantify the discrepancy between their simulated executions to that of their real counterparts, for executions simulated for the same compute platform using the same Workflow Management System (WMS). To do so, we use a simulator [20] of a the state-of-the-art Pegasus WMS [18]. The simulator is built using WRENCH [21], a framework for implementing simulators of WMSs that are accurate and can run scalably on a single computer. In [22], it was demonstrated that WRENCH provides high simulation accuracy for workflow executions using Pegasus. To ensure accurate and coherent comparisons, all simulation results in this section are obtained for the same simulated platform specification as that of the real-world platforms that was used to obtain the real workflow instances (based on execution logs): 4 compute nodes each with 48 processors on the Chameleon testbed [19].

We quantify the discrepancies between the simulated execution of a synthetic workflow instance and that of a real workflow instance with the same number of vertices, using two metrics. The first metric is the absolute relative difference between the simulated makespans (i.e., overall execution times in seconds). The second metric is the Root Mean Square Percentage Error (RMSPE) of workflow task start dates. The former metric is simpler (and used often in the literature to quantify simulation error), but the latter captures more detailed information about the temporal structure of the simulated executions.

Figure 5 shows makespans of simulated executions for real workflow instance and synthetic instances generated by WorkflowGenerator, WorkflowHub, and WfChef, for Epigenomics (top) and Montage (bottom). Note that, unlike for the results in the previous section, error bars are shown for WorkflowGenerator. Although it generates workflows with deterministic structure, it samples task characteristics (i.e., task runtimes, input/output data sizes) from particular random distribution. Both WorkflowHub and WfChef do a similar sampling, but from distributions determined via statistical analysis of real workflow instances.

Overall, we find that the execution of synthetic workflows generated by WorkflowGenerator leads to the least accurate makespans. WorkflowHub and WfChef lead to better results, with a small advantage for WorkflowHub. On average over all Epigenomics instances, the average relative differences between makespans of the real workflow instances and of the synthetic instances generated by WorkflowGenerator, WorkflowHub, and WfChef are 75.73%, 15.21%, and 15.50%, respectively. For Montage instances, these averages are 135.12%, 32.61%, and 25.59%.

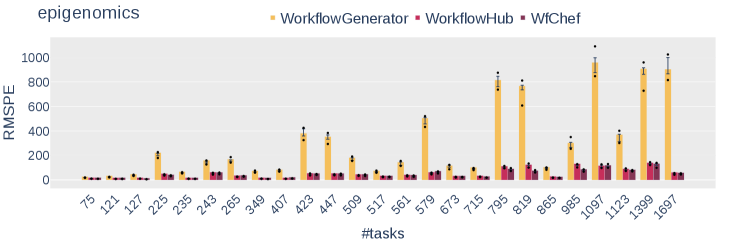
Figure 6 shows results for the RMSPE of workflow task start dates. Here again, we find that the synthetic workflow instances generated by WorkflowGenerator lead to unrealistic simulated execution. WorkflowHub and WfChef lead to more similar results, with a small advantage to WfChef. On average over all Epigenomics instances, the RMSPE of workflow task completion dates for synthetic Epigenomics instances generated by WorkflowGenerator, WorkflowHub, and WfChef are 294.70%, 46.08%, and 40.49%, respectively. For Montage instances, these averages are 558.93%, 64.29%, and 55.42%.

We conclude that WfChef generators produce synthetic workflow instances that lead to simulated executions that are drastically more realistic than that of synthetic workflows generated by WorkflowGenerator. In fact, it is fair to say that WorkflowGenerator does not make it possible to obtain realistic simulation results (which is a concern given its popularity and commonplace use in the literature). WfChef generators lead to results that are similar but typically more accurate than WorkflowHub. And yet, WfChef generators are automatically generated meaning that, and very much unlike WorkflowGenerator and WorkflowHub, require zero implementation effort.