Weyl excitations via helicon-phonon mixing in conducting materials

Introduction. The tremendous recent interest in Weyl materials Wan et al. (2011); Armitage et al. (2018); Xu et al. (2015a); Lv et al. (2015a, b); Xu et al. (2015b, c); Yang et al. (2015); Xu et al. (2016); Hasan et al. (2017) is owed, in large part, to a plethora of fundamental and novel topological phenomena they can display: the chiral anomaly Burkov (2015, 2018), topological surface states Wan et al. (2011); Armitage et al. (2018), unconventional regimes of transport Son and Spivak (2013); Syzranov and Radzihovsky (2018); Moll et al. (2016); Potter et al. (2014); Skinner (2014), etc. Numerous predictions and observations of Weyl-related topological phenomena have motivated researchers to look for Weyl excitations not only in electronic but also in magnetic, photonic and acoustic systems.

Excitations with Weyl dispersion may generically be engineered via the hybridisation of two other types of excitations with similar energies if the interactions between them vanishes along a certain direction of momentum. Such interactions lead to a degeneracy between the two bands of the hybridised excitations at the respective wave vectors and a gap for other wave vectors. For example, the hybridization between different types of plasma waves Kaner and Skobov (1968); Morgan (1967) has been shown to lead to Weyl excitations in photonic metamaterials Yang et al. (2017); Guo et al. (2017); Li et al. (2021) and magnetized electron gases Gao et al. (2016); Parker et al. (2020); Fu and Qin (2021); Parker (2021). This mechanism of the formation of Weyl excitations is similar to the emergence of 2D topological excitations due to the hybridization between phonons and spin-waves Okamoto et al. (2020); Park and Yang (2019); Shen and Kim (2020); Takahashi and Nagaosa (2016); Zhang et al. (2019); Go et al. (2019); Zhang et al. (2020); Neumann et al. (2022), spin- and plasma-waves Efimkin and Kargarian (2021), as well as excitons and cavity photons Karzig et al. (2015); Nalitov et al. (2015).

In this Letter, we demonstrate that conducting materials in magnetic fields generically host Weyl excitation due to the hybridisation of phonons with helicons Kaner and Skobov (1968); Morgan (1967), collective neutral modes of electrons interacting with electromagnetic waves propagating in the material. Such Weyl excitations emerge generically due to the hybridisation of helicons with longitudinal acoustic phonons. In polar crystals, Weyl excitations are also created by the interactions of helicons with longitudinal optical phonons.

The predicted Weyl excitations can be detected in, e.g., Raman-spectroscopy experiments. Weyl excitations involving optical phonons in the bulk of the material also lead to the formation of topologically protected arc states on its surfaces, which can be observed via the surface plasmon resonance.

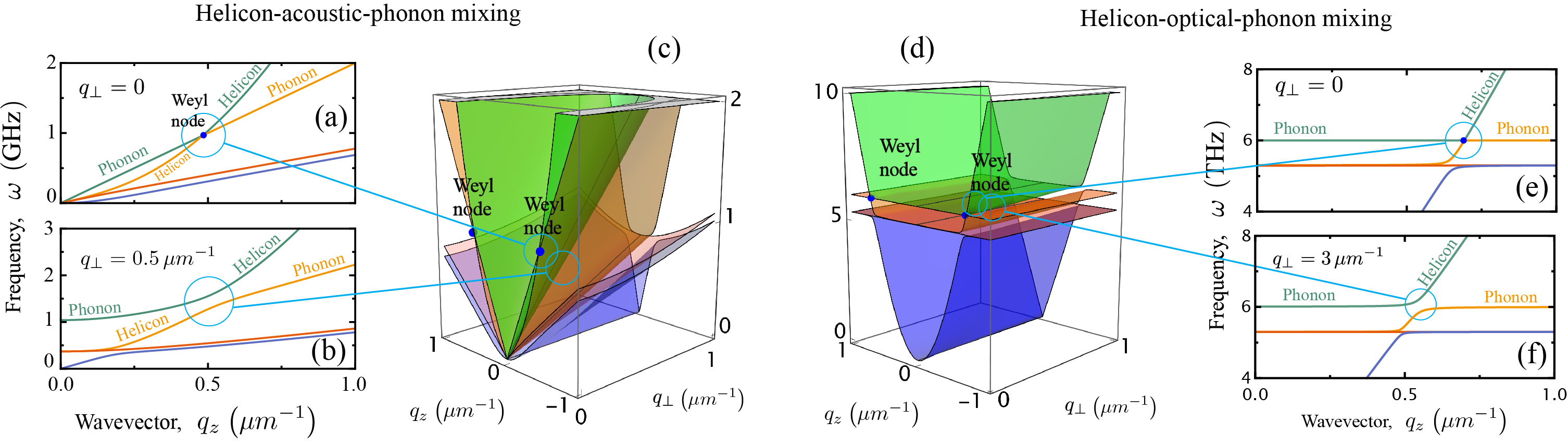
Heuristic argument for the emergence of Weyl nodes. A conductor in a magnetic field hosts excitations called helicons Kaner and Skobov (1968) that exhibit the anisotropic dispersion $\propto|{\mathbf{q}}|({\mathbf{B}}\cdot{\mathbf{q}})$ at small wave vectors ${\mathbf{q}}$. If helicon-phonon interactions are neglected, the helicon dispersion intersects along a line with the phonon dispersion. Such an intersection always exists for acoustic phonons (see Fig. 1c), which are linearly dispersive for small ${\mathbf{q}}$. It also exists for optical phonons, which are gapped, if the magnetic field (cyclotron frequency $\omega_{c}$) is sufficiently large (see Fig. 1d).

Unless wavevector $\mathbf{q}$ is aligned with the direction of the magnetic field $\mathbf{B}$, helicons involve both transverse and longitudinal oscillations of electric current and electromagnetic fields. As a result, they interact with both longitudinal and transverse phonon modes and the mixed helicon-phonon excitations are separated by a gap (as shown in Figs. 1b and f). In contrast, helicons propagating along the magnetic field $\mathbf{B}$ are purely transverse circularly polarized waves (these corkscrew-shaped oscillations motivated the term “helicon”) and their coupling with the longitudinal phonon mode vanishes (cf. Figs. 1a and e). As a result, dispersion relations for the mixed helicon-phonon excitations intersect at two selected points in reciprocal space and are of the Weyl nature in their vicinity.

The intersections of the dispersion relations for the mixed modes involving acoustic phonons and helicons have been known previously Kaner and Skobov (1968). In this Letter, we demonstrate that they are of the Weyl nature and that such excitations also emerge for optical phonons. Furthermore, we show that Weyl excitations created by optical-phonon-Weyl hybridisation can be readily observed in experiments and favor the emergence of arc surface modes.

Helicon waves. In the absence of phonons, the propagation of the helicon waves is described by the linearized hydrodynamics equation

where $e$ is the absolute value of the electron charge; $n$ is the electron density; $m$ is the effective mass and $c$ is the speed of light in vacuum. The magnetic field includes both the large external magnetic field $\mathbf{B}=B\mathbf{e}_{\mathrm{z}}$ and a small oscillating component $\mathbf{H}(\mathbf{r},t)$ created by propagating current density oscillations. For simplicity, we assume that the medium is non-magnetic, i.e. has the magnetic permeability $\mu=1$.

The helicon dispersion can be obtained from Eqs. (1a)-(1b) as a solution of the eigenvalue problem $\omega\psi_{\mathrm{pl}}=\hat{\mathcal{H}}_{\mathrm{pl}}(\mathbf{q})\psi_{\mathrm{pl}}$ Gao et al. (2016); Parker et al. (2020); Fu and Qin (2021); Parker (2021) with the $9$-component vector $\psi_{\mathrm{pl}}=\{\sqrt{\epsilon_{\infty}}\mathbf{E}(\mathbf{q}),\mathbf{H}(\mathbf{q}),4\pi\mathbf{j}(\mathbf{q})/\omega_{\mathrm{p}}\sqrt{\epsilon_{\infty}}\}^{T}$, where $\omega_{\mathrm{p}}=\sqrt{4\pi ne^{2}/m\varepsilon_{\infty}}$ is the plasma frequency and $\varepsilon_{\infty}$ is the contribution of the electronic shells of the atoms to the dielectirc constants {at GHz and higher frequencies, $\mathbf{D}(\mathbf{r},t)=\epsilon_{\infty}\mathbf{E}(\mathbf{r},t)$}. The matrix $\hat{\mathcal{H}}_{\mathrm{pl}}$ is given by

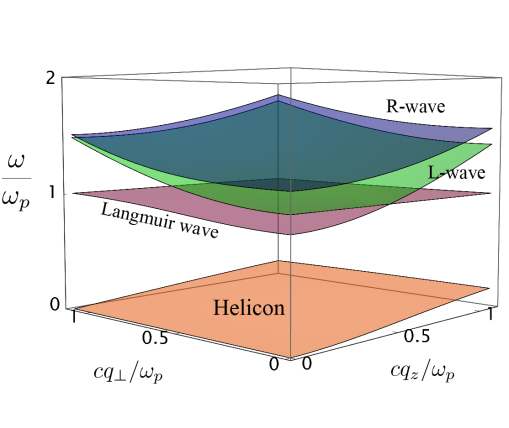
The dispersion of the magnetoplasma modes is given by the positive ($\omega>0$) eigenvalues of the “Hamiltonian” (2a). They include three gapped dispersion branches (longitudinal Langmuir waves and transverse circularly polarized L- and R-waves) with the gap of the order of the plasma frequency $\omega_{p}$ and a gapless branch, helicons (sometimes referred to as whistlers Swanson (2003), cf. Fig. 2), on which we focus in the rest of the paper.

For small ratios $\omega_{c}/\omega_{p}$ of the cyclotron to plasma frequencies, corresponding to realistic materials, the high-frequency modes can be excluded (see Supplemental Material SM for details) and the dynamics of helicons can be conveniently described using the three-component vector $\psi_{\mathrm{hel}}=\left\{(B_{x}-iB_{y})/\sqrt{2},-B_{z},(-B_{x}-iB_{y})/\sqrt{2}\right\}$. The dispersion $\omega(\mathbf{q})$ of the low-energy excitations is given by the eigenvalue problem $\omega(\mathbf{q})\psi_{\mathrm{hel}}=\hat{\mathcal{H}}_{\mathrm{hel}}(\mathbf{q})\psi_{\mathrm{hel}}$ with the matrix $\hat{\mathcal{H}}_{\mathrm{hel}}(\mathbf{q})$ given by

where $\alpha=\omega_{\mathrm{c}}\bar{c}^{2}/\omega_{\mathrm{p}}^{2}=Bc/4\pi ne$.

By introducing the effective spin-$1$ operator $\bf\hat{s}$ in the space of vectors $\psi_{\mathrm{H}}$, the operator (3) can be rewritten in the form $\hat{\mathcal{H}}_{\mathrm{hel}}(\mathbf{q})=\alpha q_{z}\left({\bf\hat{s}}\cdot\mathbf{q}\right)$ similar to the dispersion $\hat{H}_{\text{Weyl}}=v\left({\bf\hat{s}}\cdot\mathbf{q}\right)$ of a spin-$1$ Weyl semimetal Bradlyn et al. (2016). The topological properties of the low-energy helicons are similar to those of spin-$1$ Weyl fermions. The operator (3) describes the helicon dispersion for small wave vectors $|\mathbf{q}|\ll\omega_{p}/c$. At larger wave vectors, the dispersion $\omega(\mathbf{q})$ with nonvanishing transverse wave vectors saturates to $\omega_{c}$.

We note that helicons propagating (anti-)parallel to the magnetic field ${\mathbf{B}}$ have circular polarization in the plane perpendicular to ${\mathbf{B}}$. As we discuss below, the transverse polarization of helicons leads to the vanishing of the helicon-phonon interaction for both longitudinal acoustic and longitudinal optical phonons.

Interactions between helicons and acoustic phonons. In the absence of electrons, the dynamics of long-wave acoustic phonons is universally described in terms of the lattice displacement ${\mathbf{u}}({\mathbf{r}},t)$ by the equation of motion Landau and Lifshitz (1959)

where $\hat{W}^{\mathrm{ac}}_{\mathbf{q}}$, $\mathbf{u}(\mathbf{q},t)$ and $\mathbf{p}(\mathbf{q},t)$ are the Fourier-transforms of, respectively, $\hat{W}^{\mathrm{ac}}_{{\mathbf{r}}-{\mathbf{r}}^{\prime}}$, $\mathbf{u}(\mathbf{r},t)$ and $\mathbf{p}(\mathbf{r},t)$. The momentum ${\mathbf{p}}$ is the momentum canonically conjugate to the displacement ${\mathbf{u}}$; $s_{\mathrm{l}}$ and $s_{\mathrm{t}}$ are the velocities of, respectively, longitudinal and transverse phonons; the matrix $\hat{W}^{\mathrm{ac}}_{\mathbf{q}}$ (dynamical matrix) describes the energy

of elastic deformations of the crystal where $\rho$ is the its mass density (see SM SM for an explicit derivation of the dynamical matrix). The equations Eq. 4a and b can also be written as the eigenvalue problem $\omega\psi_{\mathrm{ac}}=\hat{\mathcal{H}}_{\mathrm{ac}}(\mathbf{q})\psi_{\mathrm{ac}}$ with the 6-component vector $\psi_{\mathrm{ac}}=\{\mathbf{p},\hat{W}_{\mathbf{q}}^{\mathrm{ac}}\mathbf{u}\}$ and the matrix $\hat{\mathcal{H}}_{\mathrm{ac}}(\mathbf{q})$ given by

The interactions between helicons and acoustic phonons come from relativistic effects (“inductive coupling” Kaner and Skobov (1968)). On the one hand, the dynamics of the crystalline lattice lead to the modification

of the electric field ${\mathbf{E}}$ in the reference frame of the displaced atoms, where, in the long-wave limit under consideration, the displacement ${\mathbf{u}}({\mathbf{r}},t)$ varies smoothly compared to atomic length scales. The currents ${\mathbf{j}}({\mathbf{r}},t)$ in the helicon waves also lead the forces

(per unit volume) acting on the lattice of the crystal and thus contributing to the displacements ${\mathbf{u}}({\mathbf{r}},t)$. Equations (7) and (8) describe the interactions between the electromagnetic field and the deformations of the lattice and thus account for the interactions between helicons and phonons.

The dynamics of coupled helicons and phonons is conveniently described by the $15$-component vector $\psi_{\mathrm{pl-ac}}=\{\sqrt{\varepsilon_{\infty}}\mathbf{E},\mathbf{H},4\pi\mathbf{j}/\omega_{\mathrm{p}}\sqrt{\varepsilon_{\infty}},\sqrt{4\pi\rho}\mathbf{p},\sqrt{4\pi\rho}\hat{W}_{\mathbf{q}}^{\mathrm{ac}}\mathbf{u}\}^{\mathrm{T}}$, where the first three vectors describe helicons [cf. Eqs. (1a)-(1c)] and the last two vectors describe the phonon degrees of freedom. The collective dispersion of coupled helicons and phonons is given by the solution of the eigenvalue problem $\omega\psi_{\mathrm{pl-ac}}(\mathbf{q})=\hat{\mathcal{H}}_{\mathrm{pl-ac}}(\mathbf{q})\psi_{\mathrm{pl-ac}}(\mathbf{q})$ with the “Hamiltonian” $\hat{\mathcal{H}}_{\mathrm{pl-ac}}$ given by

where the frequency $\gamma_{\mathrm{ac}}=\omega_{\mathrm{c}}\sqrt{nm/\rho}$ describes the strength of the coupling between helicons and acoustic phonons.

The structure of the matrix (9) can be understood as follows. The top left $3\times 3$ block (whose each element is a $3\times 3$ matrix) matches the matrix (2a) that describes the helicon degrees of freedom in the absence of phonons. The bottom right $2\times 2$ block describes the dynamics of phonons and has eigenvectors that correspond to the harmonic modes of the crystal. The other terms describe the helicon-phonon coupling and are obtained from Eqs. (7) and (8) taking into account that $\partial_{t}{\mathbf{u}}({\mathbf{q}},t)={\mathbf{p}}({\mathbf{q}},t)$.

The dispersions of the hybridized helicon-phonon excitations, given by the eigenvalues of the matrix (9), are plotted in Figs. 1a-c for a crystal of potassium in the magnetic field $B=20\;\hbox{T}$. The character of helicon-phonon hybridisation is qualitatively different for different branches of the dispersion of acoustic phonons. Helicons do not interact with the antisymmetric combination of two transverse phonon modes. The interaction between helicons and the symmetric combination of the transverse phonon modes leads to a gap in the dispersion of the resulting excitations at all wave vectors.

By contrast, the interaction of longitudinal phonons with helicons vanishes for ${\mathbf{q}}\parallel{\mathbf{B}}$ and is finite for other wave vectors. Their hybridisation leads to the formation of two dispersion bands that intersect at the wave vectors ${\mathbf{q}}_{\text{Weyl}}^{\pm}=\pm{\bf e}_{z}s_{l}/\alpha$, at which the frequencies of phonons and helicons match ($s_{l}|{\mathbf{q}}|=|\alpha q_{z}{\mathbf{q}}|$) and which are parallel to the magnetic field ${\mathbf{B}}$. The interactions lead to the splitting between the bands at all other wave vectors. Therefore, the interaction between helicons and the longitudinal phonons leads to the formation of Weyl excitations near the wave vectors ${\mathbf{q}}_{\text{Weyl}}^{\pm}$.

Near the Weyl points, the Hamiltonian of the Weyl excitations as a function of the wave vector ${\mathbf{k}}={\mathbf{q}}-{\mathbf{q}}_{\text{Weyl}}^{\pm}$ measured from the Weyl points is given by

where $k_{\pm}=k_{x}\pm ik_{y}$ and the matrix acts in the space of the phonon and helicon bands that are being hybridized. The transverse velocity of the Weyl excitations $s_{\perp}^{\mathrm{ac}}=\gamma_{\mathrm{ac}}\bar{c}/2\omega_{\mathrm{p}}$ is determined by the strength of the helicon-phonons interactions. The Weyl nodes near the wave vectors ${\mathbf{q}}_{\text{Weyl}}^{\pm}$ have topological Chern numbers Burkov (2018) $C^{\pm}=\frac{1}{2\pi}\int_{S}{\boldsymbol{\nabla}}_{\mathbf{k}}\times\langle\psi_{+}({\mathbf{k}})|i{\boldsymbol{\nabla}}_{\mathbf{k}}|\psi_{+}({\mathbf{k}})\rangle\,d{\mathbf{S}}=\mp 1$, where $\psi_{+}({\mathbf{k}})$ is the eigenvector of the Hamiltonian (10) that describes the quasiparticle state with the wavevector $\mathbf{k}$ and $S$ is an arbitrary closed surface in reciprocal space surrounding the Weyl node.

Interaction between helicons and optical phonons. In certain materials, such as polar crystals or ionic semimetals, the elementary cell consists of positively and negatively charged ions, and electric polarization may be caused by a relative displacement of the atoms within the cell. This leads to strong interactions of helicons with optical phonons, which, unlike the case of acoustic phonons, are non-relativistic in nature. Such interactions lead to the emergence of additional pairs of Weyl excitations, distinct from those generated by the interactions of helicons with acoustic phonons.

In what follows, we consider a crystal with two ions in the elementary cell and introduce the relative displacement ${\mathbf{w}}({\mathbf{r}},t)$ between the ions. Our results can be generalized to the case of an arbitrary number of atoms in the elementary cell.

Due to a change in the electric polarization, the displacement ${\mathbf{w}}$ affects the electric induction

in the crystal, where $\varepsilon_{\infty}$ is determined by the polarization of the electron shells of the atoms in an electric field, and the quantity $\chi$ describes the response of the polarization to ${\mathbf{w}}$ ¹¹1For polar crystals, $\chi=\omega_{l}\sqrt{(\epsilon_{0}-\epsilon_{\infty})/4\pi}$ is usually parametrized in terms of the static dielectric constant $\epsilon_{0}$ and its value $\epsilon_{\infty}$ in the high-frequency limit. In the absence of helicons, the long-wave dynamics of displacement ${\mathbf{w}}({\mathbf{r}},t)$ are governed by the equation of motion Huang (1951)

where the dynamical matrix $\hat{W}^{\mathrm{op}}_{\mathbf{q}}$ determines the dispersion of optical phonons (see Supplemental Material SM for a specific form of $\hat{W}^{\mathrm{op}}_{\mathbf{q}}$) in the absence of phonon interaction with the electromagnetic fields.

Similarly to the case of acoustic phonons, the collective modes of helicons interacting with optical phonons can be obtained as a solution of the eigenvalues problem $\hat{\mathcal{H}}_{\mathrm{pl}-\mathrm{op}}\psi_{\mathrm{pl-op}}=\omega\psi_{\mathrm{pl-op}}$, where $\psi_{\mathrm{pl-op}}=\{\sqrt{\varepsilon_{\infty}}\mathbf{E},\mathbf{H},4\pi\mathbf{j}/\omega_{\mathrm{p}}\sqrt{\varepsilon_{\infty}},\sqrt{4\pi}\mathbf{p},\sqrt{4\pi}\hat{W}_{\mathbf{q}}^{\mathrm{op}}\mathbf{u}\}^{\mathrm{T}}$. The resulting effective Hamiltonian $H_{\mathrm{pl-op}}$ is given by

where $\gamma_{\mathrm{op}}=\chi\sqrt{4\pi/\epsilon_{\infty}}$ describes the strength of the coupling between helicons and optical phonons. The off-diagonal blocks in the matrix $\hat{\mathcal{H}}_{\mathrm{pl-ac}}$ and $\hat{\mathcal{H}}_{\mathrm{pl-op}}$, given by Eqs. (9) and (13), have different structure that reflects the distinct physical mechanisms of helicon interactions with acoustic and optical phonons.

In what follows, we neglect the dispersion of longitudinal and transverse optical phonons, i.e. assume that their frequencies $\omega_{l}$ and $\omega_{t}$ are momentum-independent, which provides a good approximation for realistic crystals. Also, we assume that the frequencies $\omega_{l}$ and $\omega_{t}$ are of the same order of magnitude but differ. These assumptions are satisfied for semiconductors with the anisotropic wurtzite crystalline structure (e.g. CdSe, AlN, InN, etc) ²²2We also assume that the external magnetic field is directed along the c-axis of the crystal or in semiconductors with the zincblend structure (e.g. InAs, InSb, etc) in the presence of a uniaxial strain. We also assume that the semiconductor crystal is heavily doped $\omega_{\mathrm{l}},\omega_{\mathrm{c}}\ll\omega_{\mathrm{p}}$ that implies dispersion curves for both helicons and optical phonons are well separated from the ones for high-frequency plasma Langmuir, R- and L- waves ³³3We note that the emergence of the Weyl helicon-phonon waves does not rely on this assumption. Instead, it ensures that the renormalization of phonon dispersion curves due to their interactions with the three gapped high-frequency magnetoplasma modes can be safely neglected and simplifies the analysis of the dispersion relations for the mixed excitations.

The dispersion relations of excitations obtained as the eigenvalues of the matrix $\hat{\mathcal{H}}_{\mathrm{pl-op}}$ are shown in Fig. 1d-f, with the numerical values of frequencies and wave vectors given for heavily doped CdSe for the magnetic field $B=45\;\hbox{T}$ and electron concentration $n=4\cdot 10^{19}\;\hbox{cm}^{-3}$ (see Supplemental Material SM for the details of the estimates).

Similarly to the case of acoustic phonons, the dispersions of non-interacting helicons and longitudinal optical phonons intersect along 2D lines, which for optical phonons are given by $\omega_{l}/\alpha=|q_{z}q|$. Interactions split these intersecting branches at all wave vectors other than ${\mathbf{q}}^{\pm}_{\text{Weyl}}=\pm{\bf e_{z}}\sqrt{\omega_{l}/\alpha}$ parallel to the magnetic field. Indeed, for this direction of wave vector, the electric field of helicon waves is orthogonal to the polarisation and displacement of longitudinal phonons, and the helicon-phonon interaction vanishes. As a result, the hybridised helicon-phonon excitations have two bands that touch at the Weyl points at the wave vectors ${\mathbf{q}}^{\pm}_{\text{Weyl}}$. As a function of small deviations ${\mathbf{k}}={\mathbf{q}}-{\mathbf{q}}^{\pm}_{\text{Weyl}}$ of momentum from Weyl points, the Hamiltonian of the Weyl excitations is given by

where $s_{\perp}^{\mathrm{op}}=\gamma_{\mathrm{op}}\omega_{\mathrm{c}}c/2\omega_{\mathrm{p}}^{2}$ is the transverse velocity of Weyl excitations. The Weyl nodes near wave vectors ${\mathbf{q}}_{\text{Weyl}}^{\pm}$ have topological Chern numbers $C^{\pm}=\mp 1$.

Discussion. A prominent manifestation of the Weyl spectrum topology is a possible presence of protected surface arc states Burkov (2018); Hasan et al. (2017); Wan et al. (2011); Armitage et al. (2018). The existence of such arcs on the surface of a crystal requires that the excitations have a global gap in the reciprocal-space plane perpendicular to the surface. Provided that the global gap is present, the presence of the arc states is dictated by the bulk-edge correspondence Armitage et al. (2018).

In the case of acoustic phonos, the derived above Weyl excitations do not have such a gap and, therefore, lack arc surface states. By contrast, the dispersion of the mixed modes involving optical phonons has the global gap for any reciprocal-space section between the Weyl nodes. As for the other sections, the global gap naturally appears if the optical phonons are dispersive (that is not captured by the hydrodynamic scheme we employ in this Letter). We can get insights into the behavior of the arc states if we consider the evolution of the mixed modes spectra with the longitudinal optical phonons frequency $\omega_{\mathrm{l}}$ treated as a free parameter. If $\omega_{\mathrm{l}}$ exceeds $\omega_{\mathrm{c}}$, longitudinal phonons and helicons do not intersect, and the Weyl nodes do not emerge. If $\omega_{\mathrm{l}}$ crosses $\omega_{\mathrm{c}}$ and further decreases, the pair of Weyl nodes emerges at the infinity ($q_{z}\rightarrow\pm\infty$) and then moves towards $q_{z}=0$. Thus, the surface arc states connect the projections of Weyl nodes in different Brillouin zones to the surface. The exact shape of the arcs away from their ends is non-universal and depends on the details of the phonon and helicon dispersion in the entire Brillouin zone.

The characteristic wavevectors and frequencies of Weyl excitations are very different in the cases of acoustic and optical phonons. For acoustic phonons, their mixing with helions has been reported in potassium Grimes and Buchsbaum (1964); Libchaber and Grimes (1969a); Blaney (1967), aluminium Larsen and Saermark (1967), indium Gudkov (1982), lead telluride Schilz (1968) and cadmium arsenide Rosenman (1965), is prominent within the MHz$\sim$GHz range and can be tuned by an external magnetic field. In the case of optical phonons, the frequencies of the Weyl excitations are determined by the frequencies of optical phonons that typically lie in the THz range. Good material candidates would have: (i) low frequencies of optical phonons and at least a moderate splitting between their longitudinal and transverse modes; (ii) high mobilities of charge carriers. Among semiconductors extensively studied in the context of optoelectronics and plasmonics Caldwell et al. (2015), these conditions are well satisfied for CdSe and strained InSb.

The discussed phonon-helicon excitations is a rather favourable playground for Weyl physics and observing associated fundamental phenomena. The predicted Weyl excitations are highly tunable, with the dispersion curves that can be tuned by the external magnetic field, strain, electric currents, etc. The relatively small momenta of these excitations allow for them to be readily excited by electromagnetic pulses in the THz and GHz ranges. The discussed systems present time-reversal-symmetry-breaking Weyl semimetals Armitage et al. (2018) (effectively, Weyl semimetal with only two symmetric Weyl cones, as opposed to the so-called inversion-symmetry-breaking Weyl semimetals, in which the Weyl nodes lie, in general, at different energies). Such Weyl semimetals are extremely rare in solid-state materials and have not been observed until recently Ma et al. (2019); Morali et al. (2019).

The predicted Weyl excitations and the surface arc states can be probed by phononic techiques (Raman and inelastic X-ray scattering experiments), as well as various techniques designed for plasmon-polaritons, including angle-resolved reflection experiment Gao et al. (2016); Wang et al. (2019). The unidirectional nature of the topological-surface-arc excitations is promising for applications in the context of topological and non-reciprical plasmonics Shastri et al. (2021).

Conclusion and outlook. We have shown that a generic conductor in a magnetic field hosts Weyl excitations, which emerge as a result of the hybridisation of helicon waves and phonons. Such Weyl excitations exist generically due to the interactions of helicons with acoustic phonons. In polar crystals, additional Weyl excitations may emerge due to the interactions of helicons with optical phonons.

In this paper, we considered the emergence of Weyl excitations in topologically trivial materials. Our approach can be extended to doped topological insulators and Weyl semimetals, in which helicons are impacted by anomalous electronic responses as well as axion electrodynamic effects Pellegrino et al. (2015); Gorbar et al. (2017)

In this paper, we neglected the effects of dissipation on the considered excitations, assuming quasiparticle and phonon scattering rates to be sufficiently smaller than the characteristic frequencies, which corresponds to realistic experimental conditions SM . In principle, dissipation effects may not only result in the broadening of Weyl nodes but lead to new intriguing phenomena. It has been predicted, for example, that in plasmonic and photonic crystals, non-Hermitian perturbations of the effective Hamiltonian can make Weyl nodes evolve into nodal discs Wang et al. (2020) and nodal rings Cerjan et al. (2019). We leave the studies of such effects and the conditions necessary for realising them for future studies.

Acknowledgments. We acknowledge support from the Australian Research Council Centre of Excellence in Future Low-Energy Electronics Technologies (CE170100039).