Weakly coupled alternating chains in the distorted honeycomb lattice compound Na2Cu2TeO6
Abstract
Spin-1/2 chains with alternating antiferromagnetic (AF) and ferromagnetic (FM) couplings exhibit quantum entanglement like the integer-spin Haldane chains and might be similarly utilized for quantum computations. Such alternating AF-FM chains have been proposed to be realized in the distorted honeycomb-lattice compound Na2Cu2TeO6, but to confirm this picture a comprehensive understanding of the exchange interactions including terms outside of the idealized model is required. Here we employ neutron scattering to study the spin dynamics in Na2Cu2TeO6 and accurately determine the coupling strengths through the random phase approximation and density functional theory (DFT) approaches. We find the AF and FM intrachain couplings are the dominant terms in the spin Hamiltonian, while the interchain couplings are AF but perturbative. This hierarchy in the coupling strengths and the alternating signs of the intrachain couplings can be understood through their different exchange paths. Our results establish Na2Cu2TeO6 as a weakly-coupled alternating AF-FM chain compound and reveal the robustness of the gapped ground state in alternating chains under weak interchain couplings.
pacs:
Introduction. Spin-1/2 chains with alternating AF and FM couplings are known to exhibit gapped excitations and exponentially decaying correlations [1, 2], which are different from those of the spin-1/2 Bethe chains with uniform couplings [3] but more similar to the spectrum of integer-spin Haldane chains [4, 4]. Assuming alternating couplings of (AF) and (), the Hamiltonian of an alternating chain can be written as . In the special case of , an alternating chain can be viewed as disconnected spin dimers, and the local singlet-triplet (triplon) excitations over the dimers account for the excitation gap in the spectrum. Non-zero couplings will introduce dispersion for the triplon excitations. At , one recovers the gapless character of a Bethe chain. In the whole range of , theoretical calculations have revealed a hidden string order that is protected by the global rotation symmetry [6, 7], showing that the gapped ground state of alternating chains is a symmetry-protected topological state of the same type as that of Haldane chains [8]. Considering the prospect of Haldane chains as the resource ground state for measurement-based quantum computation [9], the additional degrees of freedom in alternating chains may be important to explore further flexibility in qubit operations.
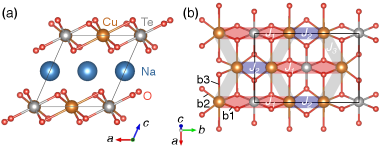
Experimental realizations of alternating AF-FM chains are limited to a few compounds, including CuNb2O6 [10], DMACuCl3 [11], Na3Cu2SbO6 [12], and BaCu2V2O8 [13] where the exchange couplings have been accurately determined through neutron scattering. Recently, a new candidate compound, Na2Cu2TeO6, was proposed [14, 15, 16, 17, 18]. Similar to Na3Cu2SbO6, the Cu2+ ions () in Na2Cu2TeO6 form a distorted honeycomb lattice in the plane, which are separated by the Na+ layers along the axis (see Fig. 1). Magnetic susceptibility measurements on a powder sample of Na2Cu2TeO6 revealed a spin gap K [14], which has been attributed to strong AF couplings in the DFT calculations [14, 16, 17, 18]. However, controversy remains as to the sign of the intrachain coupling : magnetic susceptibility data can be fitted equally well by the FM or AF model [15], and this ambiguity is not resolved by contradictory DFT results that support either AF [14, 16] or FM [17, 18] couplings. The magnitude of also remains to be determined, as comparable and couplings might invalidate a spin chain scenario.
To establish whether Na2Cu2TeO6 represents a rare realization of the alternating AF-FM spin chains, here we perform inelastic neutron scattering (INS) experiments on a single crystal sample of Na2Cu2TeO6 to determine the exchange coupling strengths. We confirm the spin gap originates from the dominant AF coupling (22.8 meV), and the interchain coupling is found to be much weaker (1.3 meV). Most importantly, we reveal the intrachain coupling to be FM with a strength ( meV) that is much higher than , thus establishing Na2Cu2TeO6 as a weakly-coupled alternating AF-FM chain compound. Through the DFT calculations, the alternating signs of the interchain couplings can be attributed to their different exchange paths.
Experimental Details. Polycrystalline Na2Cu2TeO6 was utilized as a source material for crystal growth in a flux based on TeO2 and Na2CO3. Details for the polycrystal synthesis and characterization can be found in the Supplemental Materials [19]. Powders of these materials in a ratio of 2(Na2Cu2TeO6):1(Na2CO3):4(TeO2) were mixed and loaded into a Pt crucible that was covered with a Pt lid. The crucible was heated rapidly to 900 ∘C where the melt was homogenized for 12 h in air. The furnace was then cooled at 2 ∘C/h to 500 ∘C at which point it was turned off to cool. The translucent green crystals were recovered by boiling the product-filled crucible in a hot aqueous solution of potassium hydroxide, followed by additional rinsing in deionized water.
INS experiments on Na2Cu2TeO6 were performed on the fine-resolution Fermi chopper spectrometer SEQUOIA at the SNS of the ORNL. A single crystal (mass 140 mg) was aligned with the (001) vector vertical. A closed cycle refrigerator (CCR) was employed to reach temperatures down to 5 K. The incident neutron energy was meV, and the Fermi chopper frequency of 180 Hz and 420 Hz was selected in the high-intensity and high-resolution modes, respectively. Data were acquired by rotating the sample in 1∘ steps, covering a total range of 200∘ at 5 K and 100∘ at higher temperatures. Data reductions and projections were performed using MANTID [20] and HORACE softwares [21].
First-principles calculations using the projector augmented wave (PAW) method were performed based on the DFT as implemented in the Vienna ab initio Simulation Package (VASP) code [22, 23, 24]. The generalized gradient approximation (GGA) and the revised Perdew-Burke-Ernzerhof (PBEsol) function were used to treat the electron exchange-correlation potential [25, 26]. Based on the ab initio ground-state wave function, the Cu-site centered Wannier functions (WFs) with orbital were constructed using the WANNIER90 code [27, 28].
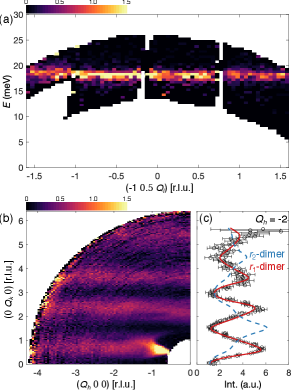
Results. As shown in Fig. 1(a), the large separation of Å between the honeycomb layers indicates likely negligible interlayer couplings. This is immediately confirmed in our single-crystal INS experiment. Figure 2(a) plots a representative slice of the measured spectrum along the direction that is perpendicular to the plane. A single excitation mode is observed at meV, which is flat within the instrument resolution (1.6 meV at the elastic line). In contrast, strong dispersion in the energy range of [17, 28] meV are observed in the plane as summarized in Fig. 3(a-d), thus confirming all the related couplings to be within the honeycomb layers.
The lack of dispersion out of the plane allows us to integrate data along for better statistics. Fig. 2b plots the scattering intensity integrated in the range of in [-2, 2] (r.l.u.) and in [17, 28] meV. Along the direction, intensity is strongly modulated with a periodicity of (r.l.u.). For dimer systems, it is established that intensity of the triplon excitations is modulated by the dimer structure factor , where is the vector that connects the two spin sites within the dimer [29, 30, 31]. Therefore, the modulation along indicates that dimers in Na2Cu2TeO6 are forming along the axis, and its periodicity tells the bond distance within the dimers. As shown in Fig. 2(c), the model that assumes dimers forming over the bonds with a distance of accurately describes the intensity modulation, thus confirming the couplings to be AF and dominant as proposed by the DFT calculations [15, 16, 17, 18].
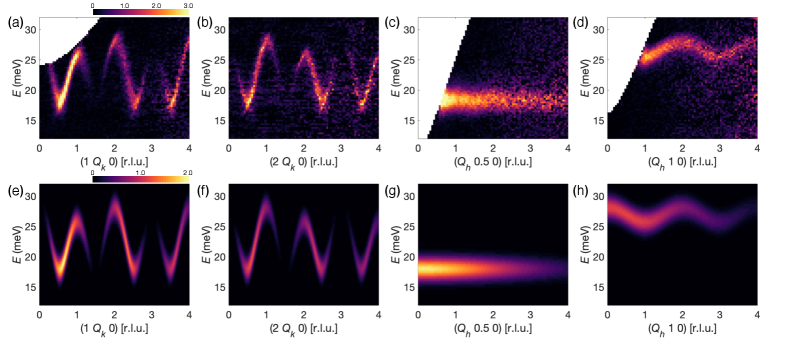
Figure 3(a-d) summarizes the dispersion along and in the plane. Along the chain direction (), the triplon band reaches its lowest energy of meV at with integer , indicating the FM character of the interdimer couplings [32, 11]. Different from the conventional chain compounds, the top of the dispersion varies at successive integer positions, which might arise from the interchain couplings. As compared in Fig. 3(c) and (d), although the triplon band looks flat along ( 0.5 0) at the bottom of the band, dispersion with a bandwidth of meV is observed along ( 1 0) at the top of the band, which suggests weak but non-negligible couplings.
The triplon dispersion in dimer systems can often be analyzed through the random phase approximation [33, 29, 34, 35, 36]. Under this approximation, the dispersion relation can be written as
| (1) |
where describes the population difference between the singlet and triplet states [29, 34] and for Na2Cu2TeO6 can be approximated by 1 at K due to the large excitation gap. is the Fourier sum of interactions beyond dimer exchange:
| (2) |
Experimental dispersion values were extracted from Gaussian fits to constant scans at 140 points throughout the measured reciprocal space volume, which were then fitted by the dispersion relation in Eq. (1). The fitted coupling strengths are meV, meV, and meV. The calculated spectra are summarized in Fig. 3(e-h) for comparison with the experimental data. The FM character of the couplings is thus unambiguously established, and the weakness of the interchain justifies the description of Na2Cu2TeO6 as a weakly-coupled alternating AF-FM chain compound.
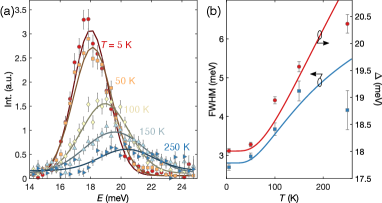
In Haldane chains the existence of a spin gap is known to protect the spin entanglement [37]. Na2Cu2TeO6 can serve as a model system to test that the same ideas are valid for alternating spin chains. In long-range ordered magnets, the excitation gap often decreases at higher due to reduced ordering moments. As a contrast, the gap of Haldane chains increases with due to the reduction in the coherent length and the consequent finite-size effect [38, 39]. The scans at (1, 0.5, 0) shown in Fig. 4(a) indeed reveal an increased gap at elevated . We parameterize the lineshape using a Gaussian function that is independently fit at each temperature, and the value of is the centroid of the Gaussian peak. As summarized in Fig. 4(b), in a large range below K, the fitted gap size and full width at half maximum (FWHM) exhibit an activated behavior that are characteristic of Haldane chains [40, 41]:
| (3) |
where , , and are fitting parameters, is the gap size at 0 K and is fixed at 18.0 meV. The validity of the activated behavior further confirms the similarity between the alternating AF-FM chains and the integer-spin Haldane chains, thus revealing the robustness of the topological ground state against weak interchain couplings.
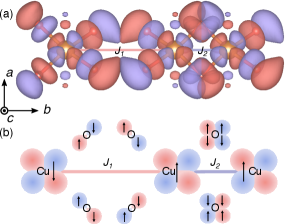
Discussion. The emergence of spin chains in Na2Cu2TeO6 can be ascribed to the distortion of the honeycomb lattice. As shown in Fig. 1(b), the exchange paths of involve the longest Cu-O bonds b3 of the distorted octahedra. Therefore, the couplings are expected to be weak as the unoccupied Cu orbitals disfavor the elongated bond direction, which reduces the electron hopping between the chains.
The sign of the interchain couplings is more subtle, and different scenarios exist in the previous DFT calculations [14, 16, 17, 18]. As summarized in the Supplemental Materials, our DFT calculations confirm the alternating FM and AF intrachain couplings in agreement with the experiment. The contrasting and couplings can be understood through the Wannier functions (WFs) as plotted in Fig. 5(a). Due to the contributions from the O states, the WFs overlap directly over the paths but are almost orthogonal over the path. Therefore, the path, in spite of its longer distance, develops a stronger coupling than that over the path. Based on the WFs, the signs of the couplings can be understood through the Goodenough-Kanamori-Anderson rules [42, 43, 44, 45] as shown in Fig. 5(b). For the couplings, the Cu-OO-Cu super-superexchange leads to an AF interaction between the Cu2+ spins. While for the couplings, the interaction become FM as the angle of ∠Cu-O-Cu is close to , which means a pair of orthogonal O orbitals with parallel spins are involved in the virtual electron hopping.
Conclusions. Neutron scattering experiments have been performed on the honeycomb-lattice compound Na2Cu2TeO6 to study its spin correlations. A triplon excitation mode was observed, which exhibits strong dispersion along the chain but weak dispersion perpendicular to the chain. Under the random phase approximation, the intrachain couplings were found to be alternating AF and FM, and a weak interchain coupling was also established. The emergence of spin chains in Na2Cu2TeO6 was ascribed to the distortion of the honeycomb lattice, and the alternating intrachain couplings were understood through the DFT calculations. Our works establish the existence of weakly-coupled alternating AF-FM spin-1/2 chains in Na2Cu2TeO6 and reveal a robust gapped ground state that is similar to that of the integer-spin Haldane chains.
Acknowledgments. We acknowledge helpful discussions with Jyong-Hao Chen, Tong Chen, and Tao Hong. This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. This research used resources at the Spallation Neutron Source (SNS), a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory (ORNL).
References
- Hida [1992a] K. Hida, Ground-state phase diagram of the spin-1/2 ferromagnetic-antiferromagnetic alternating heisenberg chain with anisotropy, Phys. Rev. B 46, 8268 (1992a).
- Hida [1994] K. Hida, Excitation spectrum of the spin-1/2 ferromagnetic-antiferromagnetic alternating Heisenberg chain, J. Phys. Soc. Jpn 63, 2514 (1994).
- Bethe [1931] H. Bethe, Zur Theorie der Metalle. I. Eigenwerte und Eigenfunktionen der linearen Atomkette, Z. Phys. 71, 205 (1931).
- Haldane [1983] F. D. M. Haldane, Nonlinear field theory of large-spin Heisenberg antiferromagnets: Semiclassically quantized solitons of the one-dimensional easy-axis Néel state, Phys. Rev. Lett. 50, 1153 (1983).
- Affleck et al. [1987] I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki, Rigorous results on valence-bond ground states in antiferromagnets, Phys. Rev. Lett. 59, 799 (1987).
- Hida [1992b] K. Hida, Crossover between the Haldane-gap phase and the dimer phase in the spin-1/2 alternating Heisenberg chain, Phys. Rev. B 45, 2207 (1992b).
- Kohmoto and Tasaki [1992] M. Kohmoto and H. Tasaki, Hidden ZZ2 symmetry breaking and the Haldane phase in the quantum spin chain with bond alternation, Phys. Rev. B 46, 3486 (1992).
- Pollmann et al. [2010] F. Pollmann, A. M. Turner, E. Berg, and M. Oshikawa, Entanglement spectrum of a topological phase in one dimension, Phys. Rev. B 81, 064439 (2010).
- Miyake [2010] A. Miyake, Quantum computation on the edge of a symmetry-protected topological order, Phys. Rev. Lett. 105, 040501 (2010).
- Kodama et al. [1999] K. Kodama, H. Harashina, H. Sasaki, M. Kato, M. Sato, K. Kakurai, and M. Nishi, Neutron scattering study on the quasi-one-dimensional spin-gap system CuNb2O6, J. Phys. Soc. Jpn 68, 237 (1999).
- Stone et al. [2007] M. B. Stone, W. Tian, M. D. Lumsden, G. E. Granroth, D. Mandrus, J.-H. Chung, N. Harrison, and S. E. Nagler, Quantum spin correlations in an organometallic alternating-sign chain, Phys. Rev. Lett. 99, 087204 (2007).
- Miura et al. [2008] Y. Miura, Y. Yasui, T. Moyoshi, M. Sato, and K. Kakurai, Magnetic excitations of spin-gap system Na3Cu2SbO6 with distorted honeycomb structure, J. Phys. Soc. Jpn 77, 104709 (2008).
- Klyushina et al. [2018] E. S. Klyushina, A. T. M. N. Islam, J. T. Park, E. A. Goremychkin, E. Wheeler, B. Klemke, and B. Lake, dimerized antiferromagnetic-ferromagnetic quantum spin chain BaCu2V2O8, Phys. Rev. B 98, 104413 (2018).
- Xu et al. [2005] J. Xu, A. Assoud, N. Soheilnia, S. Derakhshan, H. L. Cuthbert, J. E. Greedan, M. H. Whangbo, and H. Kleinke, Synthesis, structure, and magnetic properties of the layered copper(II) oxide Na2Cu2TeO6, Inorg. Chem. 44, 5042 (2005).
- Miura et al. [2006] Y. Miura, R. Hirai, Y. Kobayashi, and M. Sato, Spin-gap behavior of Na3Cu2SbO6 with distorted honeycomb structure, J Phys. Soc. Jpn. 75, 084707 (2006).
- Derakhshan et al. [2007] S. Derakhshan, H. L. Cuthbert, J. E. Greedan, B. Rahaman, and T. Saha-Dasgupta, Electronic structures and low-dimensional magnetic properties of the ordered rocksalt oxides Na3Cu2SbO6 and Na2Cu2TeO6, Phys. Rev. B 76, 104403 (2007).
- Koo and Whangbo [2008] H.-J. Koo and M.-H. Whangbo, Analysis of the spin lattice model for the spin-gapped layered compounds Na3Cu2SbO6 and Na2Cu2TeO6 on the basis of electronic structure calculations, Inorg. Chem. 47, 128 (2008).
- Schmitt et al. [2014] M. Schmitt, O. Janson, S. Golbs, M. Schmidt, W. Schnelle, J. Richter, and H. Rosner, Microscopic magnetic modeling for the Na3Cu2SbO6 and Na2Cu2TeO6, Phys. Rev. B 89, 174403 (2014).
- [19] See Supplemental Materials for details on the preparation and characterizations of the powder sample and the DFT calculations.
- Arnold et al. [2014] O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou, and J. Zikovsky, Mantid—Data analysis and visualization package for neutron scattering and SR experiments, Nucl. Instr. Methods Phys. Res. Sec. A 764, 156 (2014).
- Ewings et al. [2016] R. Ewings, A. Buts, M. Le, J. van Duijn, I. Bustinduy, and T. Perring, Horace: Software for the analysis of data from single crystal spectroscopy experiments at time-of-flight neutron instruments, Nucl. Instrum. Methods Phys. Res. A 834, 132 (2016).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
- Kresse and Joubert [1999] G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B 59, 1758 (1999).
- Blöchl [1994] P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B 50, 17953 (1994).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Perdew et al. [2008] J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou, and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett. 100, 136406 (2008).
- Marzari and Vanderbilt [1997] N. Marzari and D. Vanderbilt, Maximally localized generalized wannier functions for composite energy bands, Phys. Rev. B 56, 12847 (1997).
- Mostofi et al. [2008] A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt, and N. Marzari, wannier90: A tool for obtaining maximally-localised wannier functions, Comput. Phys. Commun. 178, 685 (2008).
- Leuenberger et al. [1984] B. Leuenberger, A. Stebler, H. U. Güdel, A. Furrer, R. Feile, and J. K. Kjems, Spin dynamics of an isotropic singlet-ground-state antiferromagnet with alternating strong and weak interactions: An inelastic-neutron-scattering study of the dimer compound Cs3Cr2Br9, Phys. Rev. B 30, 6300 (1984).
- Xu et al. [2000] G. Xu, C. Broholm, D. H. Reich, and M. A. Adams, Triplet waves in a quantum spin liquid, Phys. Rev. Lett. 84, 4465 (2000).
- Cavadini et al. [2001] N. Cavadini, G. Heigold, W. Henggeler, A. Furrer, H.-U. Güdel, K. Krämer, and H. Mutka, Magnetic excitations in the quantum spin system TlCuCl3, Phys. Rev. B 63, 172414 (2001).
- Tennant et al. [2003] D. A. Tennant, C. Broholm, D. H. Reich, S. E. Nagler, G. E. Granroth, T. Barnes, K. Damle, G. Xu, Y. Chen, and B. C. Sales, Neutron scattering study of two-magnon states in the quantum magnet copper nitrate, Phys. Rev. B 67, 054414 (2003).
- Haley and Erdös [1972] S. B. Haley and P. Erdös, Standard-basis operator method in the Green’s-function technique of many-body systems with an application to ferromagnetism, Phys. Rev. B 5, 1106 (1972).
- Stone et al. [2008a] M. B. Stone, M. D. Lumsden, S. Chang, E. C. Samulon, C. D. Batista, and I. R. Fisher, Singlet-triplet dispersion reveals additional frustration in the triangular-lattice dimer Ba3Mn2O8, Phys. Rev. Lett. 100, 237201 (2008a).
- Stone et al. [2008b] M. B. Stone, M. D. Lumsden, Y. Qiu, E. C. Samulon, C. D. Batista, and I. R. Fisher, Dispersive magnetic excitations in the antiferromagnet Ba3Mn2O8, Phys. Rev. B 77, 134406 (2008b), publisher: American Physical Society.
- Allenspach et al. [2020] S. Allenspach, A. Biffin, U. Stuhr, G. S. Tucker, S. Ohira-Kawamura, M. Kofu, D. J. Voneshen, M. Boehm, B. Normand, N. Laflorencie, F. Mila, and C. Rüegg, Multiple magnetic bilayers and unconventional criticality without frustration in BaCuSi2O6, Phys. Rev. Lett. 124, 177205 (2020).
- Wierschem and Sengupta [2014] K. Wierschem and P. Sengupta, Characterizing the haldane phase in quasi-one-dimensional spin-1 heisenberg antiferromagnets, Mod. Phys. Lett. B 28, 1430017 (2014).
- Jolicœur and Golinelli [1994] T. Jolicœur and O. Golinelli, model study of Haldane-gap antiferromagnets, Phys. Rev. B 50, 9265 (1994).
- Nightingale and Blöte [1986] M. P. Nightingale and H. W. J. Blöte, Gap of the linear spin-1 Heisenberg antiferromagnet: A Monte Carlo calculation, Phys. Rev. B 33, 659 (1986).
- Zheludev et al. [1996] A. Zheludev, S. E. Nagler, S. M. Shapiro, L. K. Chou, D. R. Talham, and M. W. Meisel, Spin dynamics in the linear-chain =1 antiferromagnet Ni(C3H10N2)2N3(ClO4), Phys. Rev. B 53, 15004 (1996).
- Bera et al. [2015] A. K. Bera, B. Lake, A. T. M. N. Islam, and A. Schneidewind, Critical properties of coupled anisotropic Haldane spin chains in a magnetic field, Phys. Rev. B 92, 060412(R) (2015).
- Anderson [1950] P. W. Anderson, Antiferromagnetism. Theory of superexchange interaction, Phys. Rev. 79, 350 (1950).
- Goodenough [1955] J. B. Goodenough, Theory of the role of covalence in the perovskite-type manganites [La, (II)]MnO3, Phys. Rev. 100, 564 (1955).
- Goodenough [1958] J. B. Goodenough, An interpretation of the magnetic properties of the perovskite-type mixed crystals La1-xSrxCoO3-λ, J. Phys. Chem. Solids 6, 287 (1958).
- Moskvin et al. [1975] A. S. Moskvin, N. S. Ovanesyan, and V. A. Trukhtanov, Angular dependence of the superexchange interaction Fe3+-O2--Cr3+, Hyperfine Interactions 1, 265 (1975).
Weakly-coupled alternating chains in the distorted honeycomb-lattice compound Na2Cu2TeO6
Supplementary Information
I Polycrystal synthesis and characterization
Polycrystalline samples of Na2Cu2TeO6 were prepared using a solid-state method. Powders of Na2CO3 (99.997, Alfa Aesar), TeO2 (99.99, Beantown Chemical) and CuO (99.995, Alfa Aesar) were mixed in a molar ratio of 1.03:1:2. The mixed powders were ground thoroughly in air and pressed into pellets with diameter. A furnace was preheated to 660 ∘C before the pellets were loaded in the furnace to minimize the loss of Na2CO3. The temperature was held at 660 ∘C for 8 hours before cooling down to room temperature.
Neutron diffraction experiments on a powder sample of Na2Cu2TeO6 were performed on the time-of-flight powder diffractometer POWGEN at the Spallation Neutron Source (SNS) of the Oak Ridge National Laboratory (ORNL). The powder (mass 8.4 g) was placed in a vanadium can. Data were acquired at 300 K and 20 K using the 1.5 Å instrumental configuration with an incoming neutron wavelength band of 0.9672.033 Å. Rietveld refinements of the neutron diffraction data were performed using the FULLPROF program [1].
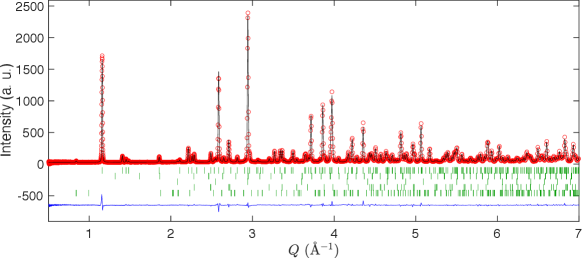
Figure S1 summarizes the refinement results for the powder neutron diffraction data collected at K, which is far below the K gap revealed in magnetic susceptibility. The Na2Cu2TeO6 phase (fractional weight %) can be refined using the monoclinic space group with lattice parameters Å, Å, Å, and , which are consistent with the previous report [2]. About deficiency was observed at the Na sites. The Cu ions occupy the sites at [0, 0.665(1), 0], leading to distances of Å and Å for the and bonds, respectively. Minority phases of Cu3TeO6 ( %), Cu2O ( %), and CuO ( %) were detected in the powder sample. The magnetic phase of CuO was also included in the refinement [3], which contributes to the weak reflection at Å-1. The overall goodness-of-fit parameters are , , and . Most importantly, no magnetic reflection of Na2Cu2TeO6 can be discerned in our diffraction data at K, which confirms the quantum disordered ground state of the gapped spin system [4].
II DFT calculations
To better understand the magnetic properties of Na2Cu2TeO6, we introduced the electron correlation by using GGA plus () with the Dudarev format on the Cu site [5]. As shown in Fig. S2, we considered four different antiferromagnetic (AF) configurations together with the ferromagnetic (FM) state.
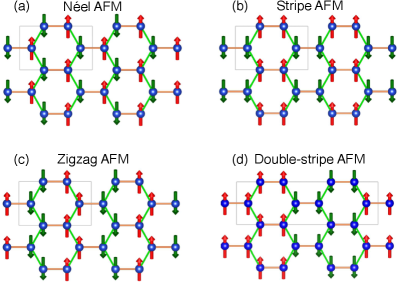
Using the experimental crystal structure, we calculated the energies of five magnetic configurations as a function of , 2, 4, 6, and 8 eV in Table S1. The exchange interactions can be estimated by mapping the calculated total energies for each magnetic state to the classical Heisenberg model. Four AFM equations are used to calculate four unknown parameters and the extracted spin exchange parameters can be found in Table S2.
| Confg. | Energy equations | Energy (meV) | ||||
|---|---|---|---|---|---|---|
| (eV)= 0 | 2 | 4 | 6 | 8 | ||
| FM | 269 | 172 | 116 | 77 | 49 | |
| N-AFM | 38 | 33 | 28 | 22 | 16 | |
| S-AFM | 252 | 160 | 107 | 71 | 44 | |
| Z-AFM | 55 | 46 | 38 | 29 | 21 | |
| D-AFM | 0 | 0 | 0 | 0 | 0 | |
| Coupling | (eV) = 0 | 2 | 4 | 6 | 8 |
|---|---|---|---|---|---|
| 130.3 | 83.3 | 56.0 | 37.3 | 23.3 | |
| -23.3 | -19.8 | -16.3 | -12.8 | -9.3 | |
| 4.3 | 3.3 | 2.5 | 1.8 | 1.3 |
For all of the values of employed here, the super-superexchange coupling is AF, and its coupling strength is several times higher than that of the FM coupling . The coupling is AF and is much weaker in strength than and . Thus, the two strongest spin exchange couplings and form alternating chains, which is consistent with the experimental results in the main text. With in the range of [0, 8] eV, the ratio of has maximum value of and a minimum value of , covering the experimentally determined value of . The calculated value of has a maximum value of 0.056 and a minimum value of 0.033. The experimentally determined ratio of was found to be 0.059(1), which is close to the upper limit of the calculated value.
All our present DFT results show good agreement with the previous theoretical works [6, 7]. As explained in Ref. [6], the DFT calculations in Ref. [2] neglects the ferromagnetic contributions to the exchange coupling, thus predicting the wrong sign for when the coupling strength is weak [8]. While in Ref. [9], although the authors emphasized that the coupling should be AF by comparing their total energy with different spin arrangements, not sufficient information about the details of the calculation, such as energies or spin arrangements used, were presented in that publication. By contrast, all the details of the energies and mapping equations for different magnetic configurations are listed clearly in the present work.
References
- Rodriguez-Carvajal [1993] J. Rodriguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Physica B: Conden. Matter 192, 55 (1993).
- Xu et al. [2005] J. Xu, A. Assoud, N. Soheilnia, S. Derakhshan, H. L. Cuthbert, J. E. Greedan, M. H. Whangbo, and H. Kleinke, Synthesis, structure, and magnetic properties of the layered copper(II) oxide Na2Cu2TeO6, Inorg. Chem. 44, 5042 (2005).
- Wang et al. [2016] Z. Wang, N. Qureshi, S. Yasin, A. Mukhin, E. Ressouche, S. Zherlitsyn, Y. Skourski, J. Geshev, V. Ivanov, M. Gospodinov, and V. Skumryev, Magnetoelectric effect and phase transitions in CuO in external magnetic fields, Nat. Commun. 7, 10295 (2016).
- Affleck et al. [1987] I. Affleck, T. Kennedy, E. H. Lieb, and H. Tasaki, Rigorous results on valence-bond ground states in antiferromagnets, Phys. Rev. Lett. 59, 799 (1987).
- Dudarev et al. [1998] S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys, and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B 57, 1505 (1998).
- Koo and Whangbo [2008] H.-J. Koo and M.-H. Whangbo, Analysis of the spin lattice model for the spin-gapped layered compounds Na3Cu2SbO6 and Na2Cu2TeO6 on the basis of electronic structure calculations, Inorg. Chem. 47, 128 (2008).
- Schmitt et al. [2014] M. Schmitt, O. Janson, S. Golbs, M. Schmidt, W. Schnelle, J. Richter, and H. Rosner, Microscopic magnetic modeling for the Na3Cu2SbO6 and Na2Cu2TeO6, Phys. Rev. B 89, 174403 (2014).
- Whangbo et al. [2003] M.-H. Whangbo, H.-J. Koo, and D. Dai, Spin exchange interactions and magnetic structures of extended magnetic solids with localized spins: theoretical descriptions on formal, quantitative and qualitative levels, J. Solid State Chem. 176, 417 (2003).
- Derakhshan et al. [2007] S. Derakhshan, H. L. Cuthbert, J. E. Greedan, B. Rahaman, and T. Saha-Dasgupta, Electronic structures and low-dimensional magnetic properties of the ordered rocksalt oxides Na3Cu2SbO6 and Na2Cu2TeO6, Phys. Rev. B 76, 104403 (2007).