Weak Localization Correction to Linear Absorption in Conventional Superconductors

Takanobu Jujo E-mail address: [email protected] of Materials ScienceDivision of Materials Science Graduate School of Science and Technology Graduate School of Science and Technology Nara Institute of Science and Technology Nara Institute of Science and Technology Ikoma Ikoma Nara 630-0101 Nara 630-0101 Japan Japan

Abstract

The weak localization effect on a linear absorption spectrum is investigated for disordered s-wave superconductors. The vertex correction is incorporated into the response function in a way that is consistent with the weak localization correction to a one-particle spectrum. The effect of interactions between electrons enhanced by their diffusive motion makes a major contribution to the correction term. Numerical calculations show that the weak localization effect suppresses the absorption by the excitation across the gap to a greater extent than that by thermal excitation, which is a similar tendency to the results of experiments. The ratio of the linear absorption with vertex corrections to that without the corrections shows a large variation at the frequency that is around twice the energy of the superconducting gap. This behavior represents a relationship between the weak localization effect on the linear absorption and that on the one-particle spectrum.

1 Introduction

The weak localization effect has so far been studied mainly in the normal state. In the case of the noninteracting electron systems, a correction term in conductivity arises from the coherent backscattering by impurities. [1] The motion of electrons becomes diffusive in the presence of the impurity scattering, and electron–electron interactions such as the screened Coulomb interaction are modified. [2, 3, 4] This effect also gives a weak localization correction to the dc and ac conductivities. [4, 5, 6]

Through the same effect, the superconducting transition temperature $T_{c}$ is lowered because the interactions between electrons change owing to the impurity scattering. [7, 8, 9] In the case of the superconducting state, there have been few studies on weak localization effect other than the correction to $T_{c}$ . For example, superfluid density is calculated considering only the effect of backscattering by impurities. [10] As for the conductivity, the influence of superconducting fluctuation becomes strong near the transition temperature. [11, 12, 13] This fluctuation effect on ac conductivity has been investigated in the normal state, [14, 15, 16, 17] but the effect of the Coulomb interaction has not been taken into account in these studies.

In the presence of the superconducting gap ( $\Delta$ ) (when the temperature is below the transition temperature), the real part of ac conductivity takes finite values at a frequency ( $\omega$ ) lower than twice the superconducting gap owing to thermally excited quasiparticles. In the case of $\omega>2\Delta$ , there exists a finite absorption even at absolute zero owing to the excitation across the gap. [18, 19] This behavior of ac conductivity is described by the Mattis–Bardeen (MB) formula.

In recent years, deviations from the MB formula have been observed experimentally in strongly disordered systems. [20, 21, 22] These studies show that the absorption for $\omega<2\Delta$ is large and the spectrum at the gap edge ( $\omega\simeq 2\Delta$ ) becomes blurred as compared with that obtained on the basis of the MB theory. This phenomenon has been interpreted with several ideas, such as the pair-breaking effect by nonuniformity, [23] collective excitation modes, [24] or the existence of a normal (Drude) component. [21] These systems are considered to be situated near the superconductor–insulator transition and have inhomogeneities. It is yet unknown whether these systems reflect the weak localization effect partly because there is no theory about this correction effect in the superconducting state.

In this study, we show how the weak localization effect appears in the ac conductivity of superconductors in a homogeneously disordered system. The conductivity including vertex corrections is calculated in a three-dimensional system, in which the expansion parameter is $1/(k_{F}l)^{2}$ where $k_{F}$ is the Fermi wave number and $l=v_{F}\tau$ is the mean free path ( $v_{F}$ and $\tau$ being the Fermi velocity and the relaxation time, respectively). We derive vertex corrections from the functional derivative of self-energy. The latter gives a weak localization correction to a one-particle spectrum in the superconducting state. [25] According to the calculated results, it is found that the weak localization correction is larger for $\omega>2\Delta$ is larger than for $\omega<2\Delta$ . Taking the ratio of the correction term to the MB conductivity clarifies how the correction effect on the linear absorption is related to that on the one-particle spectrum.

The structure of this paper is as follows. Section 2 gives a formulation for calculating response functions including the impurity scattering and interactions between electrons. In Sect. 3, a formula for the conductivity including vertex corrections that give a weak localization effect is obtained. Section 4 gives the results of numerical calculations on the basis of obtained expressions for the conductivity.

2 Formulation

We calculate the ac conductivity $\sigma_{q}$ by Keldysh’s method [26] with the use of the functional integral. [27] The absorption spectrum is given by the real part of the ac conductivity, and it is written as

{\rm Re}\sigma_{q}=-\frac{{\rm Im}K_{q}}{\omega}.

(1)

“ ${\rm Re}$ ” and “ ${\rm Im}$ ” indicate the real and imaginary parts, respectively. $q=(\mib q,\omega)$ with $\mib q$ being the wave number vector in three dimensions. We consider only the uniform case $(\mib q=\mib 0)$ and finite frequencies ( $\omega\neq 0$ ), and set $\hbar=c=1$ in this paper. $K_{q}$ is a response function and defined with the current density $J_{q}$ as

J_{q}=-K_{q}A_{q},

(2)

where $A_{q}$ is the vector potential. We consider an isotropic system and omit indices of vectors. The current density is derived from the functional derivative of the action ( $S$ ) by the vector potential:

J_{q}=\left.\frac{-i}{\sqrt{2}}\frac{\delta{\rm ln}\langle{\rm e}^{iS}\rangle_{e,p,i}}{\delta A_{-q}^{qu}}\right|_{A^{qu}\to 0}.

(3)

Here, $A^{qu}_{q}$ is the Fourier transform of $A^{qu}_{\mib q,t}:=(A^{+}_{\mib q,t}-A^{-}_{\mib q,t})/\sqrt{2}$ with $A^{+(-)}_{\mib q,t}$ being the vector potential in the forward (backward) direction in time. [27] The vector potential in Eq. (2) is given by the Fourier transform of $(A^{+}_{\mib q,t}+A^{-}_{\mib q,t})/2$ $(=:A^{cl}_{\mib q,t}/\sqrt{2})$ . We consider the following action:

\begin{split}S=&\int_{\cal C}dt\{\sum_{\mib k,\sigma}\bar{\psi}_{\mib k,\sigma,t}(i\partial_{t}-\xi_{\mib k})\psi_{\mib k,\sigma,t}-(2N^{3})^{-1}\sum_{\mib k,\mib k^{\prime},\mib q,\sigma,\sigma^{\prime}}v_{\mib q}^{C}\bar{\psi}_{\mib k,\sigma,t}\psi_{\mib k+\mib q,\sigma,t}\bar{\psi}_{\mib k^{\prime},\sigma^{\prime},t}\psi_{\mib k^{\prime}-\mib q,\sigma^{\prime},t}\\ &+\sum_{\mib q}\bar{b}_{\mib q,t}(i\partial_{t}-\omega_{\mib q})b_{\mib q,t}+(N^{3})^{-1/2}\sum_{\mib k,\mib q,\sigma}\bar{\psi}_{\mib k+\mib q,\sigma,t}[e{\mib A}_{\mib q,t}\cdot{\mib v}_{\mib k+\mib q/2}-g_{ph}\phi_{\mib q,t}-u_{\mib q}]\psi_{\mib k,\sigma,t}\}.\end{split}

(4)

(The integration $\int_{\cal C}dt$ is taken over the forward and backward time contour. [27] $\xi_{\mib k}$ and $\omega_{\mib q}$ are dispersions of electrons and phonons, respectively. The terms including $v^{C}_{\mib q}=4\pi e^{2}/{\mib q}^{2}$ , $g_{ph}$ , and $u_{\mib q}$ describe the Coulomb interaction between electrons, the electron–phonon coupling, and the impurity scattering, respectively. We take into account only the first order of the external field ${\mib A}_{q}$ because we consider the linear absorption. $N^{3}$ is the number of sites, and ${\mib v}_{\mib k}=\partial\xi_{\mib k}/\partial{\mib k}$ . $\phi_{\mib q,t}:=b_{\mib q,t}+\bar{b}_{-\mib q,t}$ .) $\langle\cdot\rangle_{e,p,i}$ means the integrations over the degrees of freedom of electrons and phonons and averaging over the impurities.

Firstly, we integrate out the electronic degrees of freedom ( $\langle{\rm e}^{iS}\rangle_{e,p,i}=\langle{\rm e}^{iS^{\prime}}\rangle_{\varphi,p,i}$ ). Here,

\begin{split}iS^{\prime}=&\frac{1}{2}\sum_{\mib q}\int d\omega\sum_{l,l^{\prime}=cl,qu}\left[\frac{-i\omega_{E}}{2}\phi^{l}_{-q}m^{ph}_{l,l^{\prime}}\phi^{l^{\prime}}_{q}+\frac{-ie^{2}}{v^{C}_{\mib q}}\varphi^{l}_{-q}m^{v}_{l,l^{\prime}}\varphi^{l^{\prime}}_{q}\right]+\sum_{n=1}^{\infty}\frac{(-1)^{n-1}}{n}{\rm tr}(GV)^{n}.\end{split}

(5)

The first term describes the phonon degrees of freedom, and the second term is obtained from the Hubbard–Stratonovich transformation of the Coulomb interaction between electrons. [28] $cl$ $(qu)$ means a sum (difference) of the forward and backward paths in time divided by $\sqrt{2}$ (this definition is different from that in Ref. 27 by a factor of $\sqrt{2}$ ). $m^{ph}_{l,l^{\prime}}=m^{v}_{l,l^{\prime}}=1$ for $(l,l^{\prime})=(cl,qu)$ and $(qu,cl)$ , and $m^{ph}_{l,l^{\prime}}=m^{v}_{l,l^{\prime}}=0$ for $(l,l^{\prime})=(cl,cl)$ and $(qu,qu)$ . In Eq. (5), we adapted approximations that the dispersion of phonons takes a constant value ( $\omega_{E}$ ) and the electron–phonon interaction is weak coupling (the effect of retardation is omitted: $\omega-\omega_{E}\simeq-\omega_{E}$ ). $G$ is Green’s function of electrons and $V$ describes interaction effects. $V$ and $G$ are written as $4\times 4$ matrices (the product of Keldysh and Nambu spaces). ${\rm tr}[\;\cdot\;]$ indicates the trace over $4\times 4$ matrices and includes the summation over wave numbers and integration over frequencies. $\hat{\;\cdot\;}$ and ${\rm Tr}[\;\cdot\;]$ given below indicate $2\times 2$ Nambu matrices and the trace over these matrices, respectively.

G=\begin{pmatrix}\hat{G}^{+}_{k}&\hat{G}^{K}_{k}\\ \hat{0}&\hat{G}^{-}_{k}\end{pmatrix}

(6)

with $G^{+(-)}_{k}$ being the retarded (advanced) Green’s function and

\hat{G}^{K}_{k}={\rm tanh}\left(\frac{\epsilon}{2T}\right)\left(\hat{G}^{+}_{k}-\hat{G}^{-}_{k}\right),

(7)

where $T$ is the temperature and $k=({\mib k},\epsilon)$ .

We consider that $G$ includes the mean-field superconducting gap ( $\Delta$ ) given by the electron–phonon interaction and the effect of the isotropic impurity scattering with the Born approximation, and $V$ describes other interaction effects. The one-particle Green’s function is written as [29, 30]

\hat{G}^{\pm}_{k}=\frac{\eta_{\epsilon}^{\pm}\epsilon\hat{\tau}_{0}+\xi_{\mib k}\hat{\tau}_{3}+\eta_{\epsilon}^{\pm}\Delta\hat{\tau}_{1}}{(\eta_{\epsilon}^{\pm}\epsilon)^{2}-\xi_{\mib k}^{2}-(\eta_{\epsilon}^{\pm}\Delta)^{2}}.

(8)

Here, $\hat{\tau}_{0}=\left(\begin{smallmatrix}1&0\\ 0&1\end{smallmatrix}\right)$ , $\hat{\tau}_{3}=\left(\begin{smallmatrix}1&0\\ 0&-1\end{smallmatrix}\right)$ , $\hat{\tau}_{1}=\left(\begin{smallmatrix}0&1\\ 1&0\end{smallmatrix}\right)$ , and $\Delta$ is determined by the gap equation

\Delta\hat{\tau}_{1}=\frac{g_{ph}^{2}}{\omega_{E}N^{3}}\sum_{\mib k}\int\frac{d\epsilon}{2\pi i}\hat{\tau}_{3}\hat{G}^{K}_{k}\hat{\tau}_{3}.

(9)

$\eta_{\epsilon}^{\pm}$ is given by the following equation including the impurity scattering:

\eta_{\epsilon}^{\pm}\epsilon\hat{\tau}_{0}-\eta_{\epsilon}^{\pm}\Delta\hat{\tau}_{1}=\epsilon\hat{\tau}_{0}-\Delta\hat{\tau}_{1}-\frac{n_{i}u^{2}}{N^{3}}\sum_{\mib k}\hat{\tau}_{3}\hat{G}^{\pm}_{k}\hat{\tau}_{3},

(10)

and is written as

\eta_{\epsilon}^{\pm}=1+\frac{\alpha}{\zeta_{\epsilon}^{\pm}}.

(11)

$\alpha:=n_{i}u^{2}mk_{F}/2\pi=1/2\tau$ with $n_{i}$ and $m$ being the concentration of impurities and the mass of quasiparticles, respectively, with

\zeta^{\pm}_{\epsilon}=-i{\rm sgn}(\epsilon)\sqrt{\epsilon^{2}-\Delta^{2}}\theta(|\epsilon|-\Delta)+\sqrt{\Delta^{2}-\epsilon^{2}}\theta(\Delta-|\epsilon|).

(12)

$\theta(\cdot)$ is a step function. $V=V_{A}+V_{i}+V_{C}+V_{p}$ describes the coupling to the external field ( $V_{A}$ ) and vertex corrections in the conductivity. $V_{C}$ , $V_{p}$ , and $V_{i}$ represent the Coulomb interaction between electrons, the electron–phonon interaction, and the scattering by impurities, respectively. These are written as

V_{A}=\frac{e{\mib v}_{(\mib k+\mib k^{\prime})/2}}{\sqrt{2}\sqrt{2\pi N^{3}}}\cdot\begin{pmatrix}\hat{\tau}_{0}\mib{A}^{cl}_{k-k^{\prime}}&\hat{\tau}_{0}\mib{A}^{qu}_{k-k^{\prime}}\\ \hat{\tau}_{0}\mib{A}^{qu}_{k-k^{\prime}}&\hat{\tau}_{0}\mib{A}^{cl}_{k-k^{\prime}}\end{pmatrix},

(13)

V_{C}=\frac{-ie}{\sqrt{2}\sqrt{2\pi N^{3}}}\begin{pmatrix}\hat{\tau}_{3}\varphi^{cl}_{k-k^{\prime}}&\hat{\tau}_{3}\varphi^{qu}_{k-k^{\prime}}\\ \hat{\tau}_{3}\varphi^{qu}_{k-k^{\prime}}&\hat{\tau}_{3}\varphi^{cl}_{k-k^{\prime}}\end{pmatrix},

(14)

V_{p}=\frac{-g_{ph}}{\sqrt{2}\sqrt{2\pi N^{3}}}\begin{pmatrix}\hat{\tau}_{3}\phi^{cl}_{k-k^{\prime}}&\hat{\tau}_{3}\phi^{qu}_{k-k^{\prime}}\\ \hat{\tau}_{3}\phi^{qu}_{k-k^{\prime}}&\hat{\tau}_{3}\phi^{cl}_{k-k^{\prime}}\end{pmatrix},

(15)

and

V_{i}=\frac{-u_{\mib k-\mib k^{\prime}}}{\sqrt{2\pi N^{3}}}\begin{pmatrix}\hat{\tau}_{3}&\hat{0}\\ \hat{0}&\hat{\tau}_{3}\end{pmatrix}\sqrt{2\pi}\delta(\epsilon-\epsilon^{\prime}).

(16)

$\delta(\cdot)$ is a delta function.

3 Expressions for Correction Terms

In this section, we show expressions for the linear absorption including vertex corrections. A detailed derivation of these expressions is given in Appendix. The following subsection shows a method of calculating four-point interaction vertices.

3.1 Vertex corrections

The coefficient of $A^{cl}_{q}A^{qu}_{-q}$ in $\langle exp[\sum_{n}(-1)^{n}{\rm tr}(GV)^{n}/n]\rangle_{\varphi,p,i}$ gives the linear response including vertex corrections. We take this vertex correction to be consistent with the weak localization correction to the one-particle spectrum. [25] The diagram of the latter correction is shown in Fig. 1.

Refer to caption — Figure 1: (a) Diagram of the weak localization correction to the one-particle spectrum. The effect of interactions is included in the shaded square (the interaction vertex). The solid lines indicate the one-particle Green function [Eqs. (6)-(8)]. (b) Diagram of the interaction vertex, which includes the screened Coulomb interaction, superconducting fluctuation, and diffuson. The arrow in the square specifies the direction of the interaction vertex. (c) The bare interaction vertex consists of the bare Coulomb interaction (wavy line), electron–phonon interaction (dashed line), and impurity scattering (dotted line with a cross).

The weak localization effect mainly arises from the screened Coulomb interaction corrected by the diffuson. The superconducting fluctuation is taken into account because of the coupling between the electron density and the phase of the superconducting order parameter.

The vertex corrections to the response function are given by the functional derivative of the self-energy by the one-particle Green function. [31] These four-point interaction vertices are obtained by cutting the lines specified by the arrows in the self-energy in Fig. 2(a), which is equivalent to Fig. 1(a).

The arrow numbers indicate the corresponding vertex corrections. When we cut the solid lines with arrow numbers “1”, “2”, “3”, and “4”, we obtain the four-point interaction vertices corresponding to the Maki–Thompson (MT) term, the MT term corrected by the diffuson, the density of states (DOS) term, and the Aslamazov–Larkin (AL) term, respectively. These are written as “ $MT0$ ”, “ $MT$ ”, “ $DOS$ ”, and “ $AL$ ” below, respectively.

The four-point interaction vertex obtained in this way is called an irreducible four-point interaction vertex. The reducible four-point interaction vertex is obtained by the ladder-type summation of the irreducible vertex. As the number of rungs of the ladder increases, the exponent $n$ of $1/(k_{F}l)^{2n}$ (the coefficient of the correction term) increases. Thus, we take account of only the lowest order of $1/(k_{F}l)^{2}$ . [32] This perturbation method is consistent with an approximation that the one-particle Green’s function [Eqs. (6)–(8)] does not include the weak localization effect, [29] and it is necessary to calculate the self-energy term in Sect. 3.2.2 [Fig. 4(a)] below because of this approximation.

3.2 Expressions of correction terms for linear absorption

3.2.1 Maki–Thompson terms

The diagrams of the MT terms are shown in Fig. 3.

As derived in Appendix A.1, the expression for one of the MT terms [Fig. 3(a)] is written as

\frac{{\rm Re}\sigma^{MT0}_{\omega}}{\sigma_{0}}=\frac{-3\sqrt{3\tau}}{\omega(4\pi k_{F}l)^{2}}\int dx\sqrt{x}\int d\epsilon\int d\omega^{\prime}{\rm Im}Q^{MT0}_{\epsilon,\omega^{\prime},x}(\omega)

(17)

( $x=Dq^{\prime 2}$ with $D=v_{F}^{2}\tau/3$ being the diffusion constant and $\sigma_{0}=e^{2}n_{e}\tau/m$ with $n_{e}=k_{F}^{3}/3\pi^{2}$ ). Here,

\begin{split}Q^{MT0}_{\epsilon,\omega^{\prime},x}(\omega)=&\sum_{i=0,1,2,3,4}2\Gamma_{i}(q^{\prime})\{C^{t}_{\omega^{\prime}}\sum_{s=\pm}s(T^{h}_{\epsilon_{4}}{\cal N}_{i}^{+++s}+T^{h}_{\epsilon_{3}}{\cal N}_{i}^{++s-}+T^{h}_{\epsilon_{2}}{\cal N}_{i}^{+s--}+T^{h}_{\epsilon_{1}}{\cal N}_{i}^{s---})\\ &+\sum_{s,s^{\prime}=\pm}ss^{\prime}(T^{h}_{\epsilon_{3}}T^{h}_{\epsilon_{4}}{\cal N}_{i}^{++ss^{\prime}}+T^{h}_{\epsilon_{2}}T^{h}_{\epsilon_{4}}{\cal N}_{i}^{+s-s^{\prime}})+{\cal N}_{i}^{+++-}+{\cal N}_{i}^{---+}\}\end{split}

(18)

with $C^{t}_{\omega}={\rm coth}(\omega/2T)$ , $T^{h}_{\epsilon}={\rm tanh}(\epsilon/2T)$ , $\epsilon_{1}=\epsilon+(\omega+\omega^{\prime})/2$ , $\epsilon_{2}=\epsilon+(\omega-\omega^{\prime})/2$ , $\epsilon_{3}=\epsilon-(\omega+\omega^{\prime})/2$ , and $\epsilon_{4}=\epsilon-(\omega-\omega^{\prime})/2$ .

{\cal N}_{i}^{s_{1}s_{2}s_{3}s_{4}}=\frac{{\rm Tr}[(\hat{\tau}_{0}+s\hat{\tau}_{j}\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}})(\hat{\tau}_{0}+s\hat{g}^{s_{3}}_{\epsilon_{3}}\hat{\tau}_{j}\hat{g}^{s_{4}}_{\epsilon_{4}}\hat{\tau}_{j})]}{2(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{3}}+\zeta^{s_{4}}_{\epsilon_{4}})}

(19)

for $i=0,1,2,3$ $\left[s=\left\{\begin{smallmatrix}1&(i=0,3)\\ -1&(i=1,2)\end{smallmatrix}\right.\text{ and }j=\left\{\begin{smallmatrix}3&(i=2,3)\\ 0&(i=0,1)\end{smallmatrix}\right.\right]$ and

{\cal N}_{4}^{s_{1}s_{2}s_{3}s_{4}}=\frac{-{\rm Tr}[\hat{\tau}_{1}\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{g}^{s_{3}}_{\epsilon_{3}}\hat{\tau}_{j}\hat{g}^{s_{4}}_{\epsilon_{4}}]}{(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{3}}+\zeta^{s_{4}}_{\epsilon_{4}})}

(20)

with $\hat{g}_{\epsilon}^{\pm}:=g_{\epsilon}^{\pm}\hat{\tau}_{0}+f_{\epsilon}^{\pm}\hat{\tau}_{1}$ ( $g_{\epsilon}^{\pm}=-\epsilon/\zeta^{\pm}_{\epsilon}$ and $f_{\epsilon}^{\pm}=-\Delta/\zeta^{\pm}_{\epsilon}$ ). $\Gamma_{i=0,1,2,3,4}$ represent the screened Coulomb interaction and the superconducting fluctuation [33] and are written as

\begin{pmatrix}\Gamma_{3}(q)\\ \Gamma_{2}(q)\\ \Gamma_{4}(q)\end{pmatrix}=\frac{1}{(1/p+\chi_{2})[1-(p+c_{q})\chi_{3}]+4(p+c_{q})(\chi^{\prime})^{2}}\begin{pmatrix}(p+c_{q})(1/p+\chi_{2})/2\\ -[1-(p+c_{q})\chi_{3}]/2\\ -(p+c_{q})\chi^{\prime}\end{pmatrix},

(21)

\Gamma_{0}(q)=\frac{p/2}{1-p\chi_{0}},

(22)

and

\Gamma_{1}(q)=\frac{-1/2}{1/p+\chi_{1}}

(23)

with $p:=(\pi\rho_{0}/2)(g_{ph}^{2}/\omega_{E})$ and $c_{q}:=(\pi\rho_{0}/2)v^{C}_{\mib q}$ ( $\rho_{0}:=mk_{F}/\pi^{2}$ ).

\chi_{i}=\sum_{s=\pm}s\int\frac{d\epsilon}{2\pi i}{\rm Tr}\left[\frac{T^{h}_{\epsilon}X_{\epsilon+\omega,\epsilon}^{+s}\hat{\tau}_{i}(h_{i}\hat{\tau}_{i}+\hat{g}^{+}_{\epsilon+\omega}\hat{\tau}_{i}\hat{g}^{s}_{\epsilon})}{2\alpha(1-2X_{\epsilon+\omega,\epsilon}^{+s})}+\frac{T^{h}_{\epsilon+\omega}X_{\epsilon+\omega,\epsilon}^{s-}\hat{\tau}_{i}(h_{i}\hat{\tau}_{i}+\hat{g}^{s}_{\epsilon+\omega}\hat{\tau}_{i}\hat{g}^{-}_{\epsilon})}{2\alpha(1-2X_{\epsilon+\omega,\epsilon}^{s-})}\right]-\frac{2}{\pi}h_{i}^{\prime\prime}

(24)

for $i=0,1,2,3$ $\left[h_{i}=\left\{\begin{smallmatrix}1&(i=0,3)\\ -1&(i=1,2)\end{smallmatrix}\right.\text{ and }h^{\prime\prime}_{i}=\left\{\begin{smallmatrix}1&(i=0,3)\\ 0&(i=1,2)\end{smallmatrix}\right.\right]$ , and

\chi{{}^{\prime}}=\sum_{s=\pm}s\int\frac{d\epsilon}{2\pi i}{\rm Tr}\left[\frac{T^{h}_{\epsilon}X_{\epsilon+\omega,\epsilon}^{+s}(-i\hat{\tau}_{2})\hat{g}^{+}_{\epsilon+\omega}\hat{\tau}_{3}\hat{g}^{s}_{\epsilon}}{4\alpha(1-2X_{\epsilon+\omega,\epsilon}^{+s})}+\frac{T^{h}_{\epsilon+\omega}X_{\epsilon+\omega,\epsilon}^{s-}(-i\hat{\tau}_{2})\hat{g}^{s}_{\epsilon+\omega}\hat{\tau}_{3}\hat{g}^{-}_{\epsilon}}{4\alpha(1-2X_{\epsilon+\omega,\epsilon}^{s-})}\right]

(25)

[ $\hat{\tau}_{2}=\left(\begin{smallmatrix}0&-i\\ i&0\end{smallmatrix}\right)$ ].

The expression of the real part of the conductivity corresponding to Fig. 3(b) (the MT term with an additional diffuson) is given by the following equation, the derivation of which is given in Appendix A.1:

\frac{{\rm Re}\sigma^{MT}_{\omega}}{\sigma_{0}}=\frac{\sqrt{3\tau}}{\omega(4\pi k_{F}l)^{2}}\int dxx^{3/2}\int d\epsilon\int d\omega^{\prime}{\rm Im}Q^{MT}_{\epsilon,\omega^{\prime},x}(\omega).

(26)

$Q^{MT}_{\epsilon,\omega^{\prime},x}(\omega)$ is given by Eq. (18) with ${\cal N}$ replaced by the following ${\cal M}$ :

\begin{split}{\cal M}_{i}^{s_{1}s_{2}s_{3}s_{4}}=&\frac{1}{(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{3}}+\zeta^{s_{4}}_{\epsilon_{4}})}\left(\frac{1}{x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{3}}_{\epsilon_{3}}}+\frac{1}{x+\zeta^{s_{2}}_{\epsilon_{2}}+\zeta^{s_{4}}_{\epsilon_{4}}}\right)\\ &\times\frac{1}{2}{\rm Tr}[(\hat{\tau}_{0}+s\hat{\tau}_{j}\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}})(\hat{\tau}_{0}+s\hat{g}^{s_{3}}_{\epsilon_{3}}\hat{\tau}_{j}\hat{g}^{s_{4}}_{\epsilon_{4}}\hat{\tau}_{j})+(\hat{\tau}_{j^{\prime}}\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j^{\prime}}-s\hat{g}^{s_{2}}_{\epsilon_{2}})(s\hat{g}^{s_{3}}_{\epsilon_{3}}-\hat{\tau}_{j^{\prime}}\hat{g}^{s_{4}}_{\epsilon_{4}}\hat{\tau}_{j^{\prime}})]\end{split}

(27)

for $i=0,1,2,3$ $\left[s=\left\{\begin{smallmatrix}1&(i=0,3)\\ -1&(i=1,2)\end{smallmatrix}\right.,\text{ }j=\left\{\begin{smallmatrix}3&(i=2,3)\\ 0&(i=0,1)\end{smallmatrix}\right.\text{ and }j^{\prime}=\left\{\begin{smallmatrix}0&(i=2,3)\\ 3&(i=0,1)\end{smallmatrix}\right.\right]$ and

{\cal M}_{4}^{s_{1}s_{2}s_{3}s_{4}}=\frac{{\rm Tr}[\hat{\tau}_{1}(\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{g}^{s_{4}}_{\epsilon_{4}}-\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{g}^{s_{3}}_{\epsilon_{3}}-\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{g}^{s_{3}}_{\epsilon_{3}}\hat{\tau}_{j}\hat{g}^{s_{4}}_{\epsilon_{4}})]}{(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{3}}+\zeta^{s_{4}}_{\epsilon_{4}})}\left(\frac{1}{x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{3}}_{\epsilon_{3}}}+\frac{1}{x+\zeta^{s_{2}}_{\epsilon_{2}}+\zeta^{s_{4}}_{\epsilon_{4}}}\right).

(28)

3.2.2 Density of states terms

The diagrams of the DOS terms are shown in Fig. 4.

As derived in Appendix A.2, the result of the self-energy term [Fig. 4(a)] is written as

\frac{{\rm Re}\sigma^{DOS0}_{\omega}}{\sigma_{0}}=\frac{-3\sqrt{3\tau}}{\omega(8\pi k_{F}l)^{2}}\int dx\sqrt{x}\int d\epsilon\int d\omega^{\prime}{\rm Im}Q^{DOS0}_{\epsilon,\omega^{\prime},x}(\omega)

(29)

with

\begin{split}&Q^{DOS0}_{\epsilon,\omega^{\prime},x}(\omega)=\sum_{i=0,1,2,3,4}2\{C^{t}_{\omega^{\prime}}[\Gamma_{i}(q^{\prime})-\Gamma_{i}^{*}(q^{\prime})]\sum_{s=\pm}s(T^{h}_{\epsilon_{4}}{\cal S}_{i}^{+++s}+T^{h}_{\epsilon_{1}}{\cal S}_{i}^{sss-})\\ &+\Gamma_{i}(q^{\prime})(\sum_{s,s^{\prime}=\pm}ss^{\prime}T^{h}_{\epsilon_{2}}T^{h}_{\epsilon_{4}}{\cal S}_{i}^{+s+s^{\prime}}+\sum_{s=\pm}sT^{h}_{\epsilon_{2}}T^{h}_{\epsilon_{1}}{\cal S}_{i}^{+s+-})-\Gamma_{i}^{*}(q^{\prime})\sum_{s=\pm}sT^{h}_{\epsilon_{1}}T^{h}_{\epsilon_{2}}{\cal S}_{i}^{-s--}\},\end{split}

(30)

where $\Gamma^{*}$ means the complex conjugate of $\Gamma$ . Here,

{\cal S}_{i}^{s_{1}s_{2}s_{3}s_{4}}=\frac{{\rm Tr}[s\hat{\tau}_{0}+\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j}-s\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{\tau}_{3}+\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{\tau}_{j}+3(s\hat{g}^{s_{1}}_{\epsilon_{1}}-\hat{\tau}_{j^{\prime}}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j^{\prime}}+s\hat{g}^{s_{3}}_{\epsilon_{1}}+\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j}\hat{g}^{s_{3}}_{\epsilon_{1}})\hat{g}^{s_{4}}_{\epsilon_{4}}]}{2(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})}

(31)

for $i=0,1,2,3$ [the values of $s$ , $j$ , and $j^{\prime}$ are the same as those in ${\cal M}$ below Eq. (27)] and

{\cal S}_{4}^{s_{1}s_{2}s_{3}s_{4}}=\frac{-{\rm Tr}[\hat{\tau}_{1}(\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{3}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{3}-\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{\tau}_{3}+3\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{g}^{s_{4}}_{\epsilon_{4}}+3\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{3}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{g}^{s_{4}}_{\epsilon_{4}})]}{(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})}.

(32)

The expression of the DOS term shown in Fig. 4(b) is given by the following equation:

\frac{{\rm Re}\sigma^{DOS}_{\omega}}{\sigma_{0}}=\frac{-\sqrt{3\tau}}{\omega(4\pi k_{F}l)^{2}}\int dxx^{3/2}\int d\epsilon\int d\omega^{\prime}{\rm Im}Q^{DOS}_{\epsilon,\omega^{\prime},x}(\omega).

(33)

$Q^{DOS}_{\epsilon,\omega^{\prime},x}(\omega)$ is given by Eq. (30) with ${\cal S}$ replaced by the following ${\cal D}$ :

{\cal D}_{i}^{s_{1}s_{2}s_{3}s_{4}}=\frac{{\rm Tr}[s\hat{\tau}_{0}+\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j}-s\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{\tau}_{3}+\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{\tau}_{j}-(s\hat{g}^{s_{1}}_{\epsilon_{1}}-\hat{\tau}_{j^{\prime}}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j^{\prime}}+s\hat{g}^{s_{3}}_{\epsilon_{1}}+\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{j}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{j}\hat{g}^{s_{3}}_{\epsilon_{1}})\hat{g}^{s_{4}}_{\epsilon_{4}}]}{2(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{4}}_{\epsilon_{4}}+\zeta^{s_{2}}_{\epsilon_{2}})}

(34)

for $i=0,1,2,3$ (the values of $s$ , $j$ , and $j^{\prime}$ are the same as those in the cases of ${\cal M}$ and ${\cal S}$ above) and

{\cal D}_{4}^{s_{1}s_{2}s_{3}s_{4}}=\frac{-{\rm Tr}[\hat{\tau}_{1}(\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{3}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{3}-\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{\tau}_{3}-\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{g}^{s_{4}}_{\epsilon_{4}}-\hat{g}^{s_{1}}_{\epsilon_{1}}\hat{\tau}_{3}\hat{g}^{s_{2}}_{\epsilon_{2}}\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon_{1}}\hat{g}^{s_{4}}_{\epsilon_{4}})]}{(x+\zeta^{s_{1}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{3}}_{\epsilon_{1}}+\zeta^{s_{2}}_{\epsilon_{2}})(x+\zeta^{s_{4}}_{\epsilon_{4}}+\zeta^{s_{2}}_{\epsilon_{2}})}.

(35)

3.2.3 Aslamazov–Larkin term

The diagram of the AL term is shown in Fig. 5.

The result of the AL term ( $\sigma^{AL}_{\omega}=\sigma^{AL1}_{\omega}+\sigma^{AL2}_{\omega}$ ) is given by the following equation, the derivation of which is given in Appendix A.3:

\frac{{\rm Re}\sigma^{AL}_{\omega}}{\sigma_{0}}=\frac{\sqrt{3\tau}}{2\pi^{3}\omega(k_{F}l)^{2}}\int d\omega^{\prime}\int dxx^{3/2}{\rm Re}Q^{AL}_{\omega^{\prime},x}(\omega)

(36)

with

\begin{split}Q^{AL}_{\omega^{\prime},x}(\omega)=&\sum_{i=3,2}\{\Gamma_{1}(q-q^{\prime})[C^{t}_{\omega^{\prime}}\Gamma_{i}(q^{\prime})({\cal A}^{(1)}_{i,1})^{2}+(C^{t}_{\omega}-C^{t}_{\omega^{\prime}})\Gamma^{*}_{i}(q^{\prime})({\cal A}^{(2)}_{i,1})^{2}-C^{t}_{\omega}\Gamma^{*}_{i}(q^{\prime}){\cal A}^{(2)}_{i,1}{\cal A}^{(3)}_{i,1}]\\ &+\Gamma_{i}(q-q^{\prime})[C^{t}_{\omega^{\prime}}\Gamma_{1}(q^{\prime})({\cal A}^{(1)}_{i,2})^{2}+(C^{t}_{\omega}-C^{t}_{\omega^{\prime}})\Gamma^{*}_{1}(q^{\prime})({\cal A}^{(2)}_{i,2})^{2}-C^{t}_{\omega}\Gamma^{*}_{1}(q^{\prime}){\cal A}^{(2)}_{i,2}{\cal A}^{(3)}_{i,2}]\}\\ &+\Gamma_{1}(q-q^{\prime})[2C^{t}_{\omega^{\prime}}\Gamma_{4}(q^{\prime}){\cal A}^{(1)}_{2,1}{\cal A}^{(1)}_{3,1}+2(C^{t}_{\omega}-C^{t}_{\omega^{\prime}})\Gamma^{*}_{4}(q^{\prime}){\cal A}^{(2)}_{2,1}{\cal A}^{(2)}_{3,1}-C^{t}_{\omega}\Gamma^{*}_{4}(q^{\prime})({\cal A}^{(2)}_{2,1}{\cal A}^{(3)}_{3,1}+{\cal A}^{(2)}_{3,1}{\cal A}^{(3)}_{2,1})]\\ &-\Gamma_{4}(q-q^{\prime})[2C^{t}_{\omega^{\prime}}\Gamma_{1}(q^{\prime}){\cal A}^{(1)}_{2,2}{\cal A}^{(1)}_{3,2}+2(C^{t}_{\omega}-C^{t}_{\omega^{\prime}})\Gamma^{*}_{1}(q^{\prime}){\cal A}^{(2)}_{2,2}{\cal A}^{(2)}_{3,2}-C^{t}_{\omega}\Gamma^{*}_{1}(q^{\prime})({\cal A}^{(2)}_{2,2}{\cal A}^{(3)}_{3,2}+{\cal A}^{(2)}_{3,2}{\cal A}^{(3)}_{2,2})].\end{split}

(37)

Here,

{\cal A}^{(1)}_{i,j}=\sum_{s=\pm}s\int d\epsilon(T^{h}_{\epsilon}{\cal L}_{i,j}^{+s+}+T^{h}_{\epsilon+\omega^{\prime}}{\cal L}_{i,j}^{+-s}+T^{h}_{\epsilon+\omega}{\cal L}_{i,j}^{s--}),

(38)

{\cal A}^{(2)}_{i,j}=\sum_{s=\pm}s\int d\epsilon(T^{h}_{\epsilon+\omega^{\prime}}{\cal L}_{i,j}^{++s}+T^{h}_{\epsilon}{\cal L}_{i,j}^{+s-}+T^{h}_{\epsilon+\omega}{\cal L}_{i,j}^{s--}),

(39)

and

{\cal A}^{(3)}_{i,j}=\sum_{s=\pm}s\int d\epsilon(T^{h}_{\epsilon+\omega^{\prime}}{\cal L}_{i,j}^{++s}+T^{h}_{\epsilon+\omega}{\cal L}_{i,j}^{s+-}+T^{h}_{\epsilon}{\cal L}_{i,j}^{-s-})

(40)

with

{\cal L}_{2,j}^{s_{1}s_{2}s_{3}}=\frac{{\rm Tr}[\hat{\tau}_{0}-\hat{g}^{s_{1}}_{\epsilon+\omega}\hat{g}^{s_{2}}_{\epsilon}-\hat{\tau}_{l}\hat{g}^{s_{1}}_{\epsilon+\omega}\hat{\tau}_{l}\hat{g}^{s_{3}}_{\epsilon+\omega^{\prime}}-\hat{\tau}_{l^{\prime}}\hat{g}^{s_{2}}_{\epsilon}\hat{\tau}_{l^{\prime}}\hat{g}^{s_{3}}_{\epsilon+\omega^{\prime}}]}{2(x+\zeta^{s_{1}}_{\epsilon+\omega}+\zeta^{s_{3}}_{\epsilon+\omega^{\prime}})(x+\zeta^{s_{2}}_{\epsilon}+\zeta^{s_{3}}_{\epsilon+\omega^{\prime}})}

(41)

and

{\cal L}_{3,j}^{s_{1}s_{2}s_{3}}=\frac{{\rm Tr}[\hat{\tau_{1}}(\hat{\tau}_{0}-\hat{g}^{s_{1}}_{\epsilon+\omega}\hat{g}^{s_{2}}_{\epsilon}+\hat{\tau}_{l}\hat{g}^{s_{1}}_{\epsilon+\omega}\hat{\tau}_{l}\hat{g}^{s_{3}}_{\epsilon+\omega^{\prime}}+\hat{\tau}_{l^{\prime}}\hat{g}^{s_{2}}_{\epsilon}\hat{\tau}_{l^{\prime}}\hat{g}^{s_{3}}_{\epsilon+\omega^{\prime}})]}{2(x+\zeta^{s_{1}}_{\epsilon+\omega}+\zeta^{s_{3}}_{\epsilon+\omega^{\prime}})(x+\zeta^{s_{2}}_{\epsilon}+\zeta^{s_{3}}_{\epsilon+\omega^{\prime}})}.

(42)

$(l,l^{\prime})=(0,3)$ and $(3,0)$ for $j=1$ and $2$ , respectively. The result in the case of the normal state [14] is obtained by setting $\Delta=0$ in the above equations.

3.2.4 Maximally crossed term

The maximally crossed (MC) term is the vertex correction, which does not include the screened Coulomb interaction and the superconducting fluctuation explicitly, but gives a weak localization correction to the conductivity by the coherent backscattering effect. [1, 10] (The contribution of this term to the one-particle spectrum vanishes and is not included in Figs. 1 and 2.) The diagram of this term is shown in Fig. 6(b).

As derived in Appendix A.4, the linear absorption by the maximally crossed term is written as

\frac{{\rm Re}\sigma^{MC}_{\omega}}{\sigma_{0}}=\frac{3\sqrt{3\tau}}{8\pi\omega(k_{F}l)^{2}}\int dx\sqrt{x}\int d\epsilon(T^{h}_{\epsilon+\omega}-T^{h}_{\epsilon}){\rm Re}\sum_{s=\pm}s\frac{{\rm Tr}[\hat{\tau}_{0}+\hat{g}^{+}_{\epsilon+\omega}\hat{g}^{s}_{\epsilon}]}{2(x+\zeta_{\epsilon+\omega}^{+}+\zeta_{\epsilon}^{s})}.

(43)

4 Results

4.1 Numerical calculations

In this section, we numerically evaluate Eqs. (17), (26), (29), (33), (36), and (43). The ranges of integrations over $x=Dq^{2}$ , $\epsilon$ , and $\omega^{\prime}$ in these equation are $x<1/\tau$ , $|\epsilon|$ , and $|\omega^{\prime}|<1/\tau$ , in which the approximation Eq. (50) holds. (The low-energy properties are given by this range.) We make the variables symmetrical in advance, such as $\epsilon_{1\textendash 4}$ below Eq. (18). The superconducting gap at $T=0$ is taken to be the unit of energy ( $\Delta_{0}=1$ ), and the electron–phonon coupling $p$ is determined by the gap equation. $c_{q}$ ( $=\pi\omega_{p}^{2}\tau/2Dq^{2}\gg p$ with $\omega_{p}=\sqrt{4\pi n_{e}e^{2}/m}$ the plasma frequency) in the denominator and the numerator of $\Gamma_{3,2,4}(q)$ cancel out each other as in Eqs. (45)–(47) in Ref. 25. (The effective interaction becomes independent of $e^{2}$ . [34]) The relation between $\alpha=1/2\tau$ and $k_{F}l$ is fixed to $k_{F}l/2\tau=E_{F}=300\Delta_{0}$ , where $E_{F}$ is the Fermi energy.

The calculated results of $\Gamma_{i}(q)$ at $T=0$ are given in Ref. 25, in which it is shown that terms including the Coulomb interaction ( $\Gamma_{3,2,4}$ ) are larger than other terms ( $\Gamma_{0,1}$ ). In the case of the absorption spectrum, it can also be shown that terms including the Coulomb interaction predominantly contribute to the correction term. We will not show correction terms decomposed for each vertex ( $\Gamma_{i}$ ) explicitly below.

The dependence of ${\rm Re}\sigma_{\omega}/\sigma_{0}$ on $\omega$ for several values of $T/T_{c}$ is shown in Fig. 7.

Here, $\sigma_{\omega}=\sigma^{(0)}_{\omega}+\sigma^{\rm vc}_{\omega}$ with $\sigma^{\rm vc}_{\omega}=\sigma^{MT0}_{\omega}+\sigma^{MT}_{\omega}+\sigma^{DOS0}_{\omega}+\sigma^{DOS}_{\omega}+\sigma^{AL}_{\omega}+\sigma^{MC}_{\omega}$ [ ${\rm Re}\sigma_{\omega}={\rm Re}\sigma_{\omega}^{(0)}\left(1+{\rm Re}\sigma^{\rm vc}_{\omega}/{\rm Re}\sigma_{\omega}^{(0)}\right)$ ]. ${\rm Re}\sigma^{(0)}_{\omega}$ is the real part of the conductivity given by the MB theory (i.e., the linear absorption without vertex corrections) and is written as

\frac{{\rm Re}\sigma^{(0)}_{\omega}}{\sigma_{0}}=\frac{-1}{2\omega}\int d\epsilon(T^{h}_{\epsilon+\omega}-T^{h}_{\epsilon}){\rm Re}\sum_{s=\pm}s\frac{1}{2}{\rm Tr}[\hat{g}^{+}_{\epsilon+\omega}\hat{g}^{s}_{\epsilon}].

(44)

The comparison of ${\rm Re}\sigma_{\omega}/\sigma_{0}$ with the MB formula ${\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}$ is shown in Fig. 7. In this figure, $(0)\times c_{0}$ represents the result of $c_{0}\times{\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}$ . $c_{0}$ is chosen such that $c_{0}\times{\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}$ overlaps ${\rm Re}\sigma_{\omega}/\sigma_{0}$ in the range of $\omega\lessapprox 2\Delta$ . This result shows that ${\rm Re}\sigma_{\omega}/\sigma_{0}$ is not proportional to the MB conductivity. The suppression of the conductivity by vertex corrections is larger at $\omega>2\Delta$ than at $\omega<2\Delta$ for low temperatures. As a result, the excitations below $2\Delta$ (i.e., thermal excitations) seem to be relatively enhanced as compared with the behavior of the MB conductivity.

The ratio of vertex corrections to the MB conductivity, ${\rm Re}\sigma^{\rm vc}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}$ , is shown in Fig. 8.

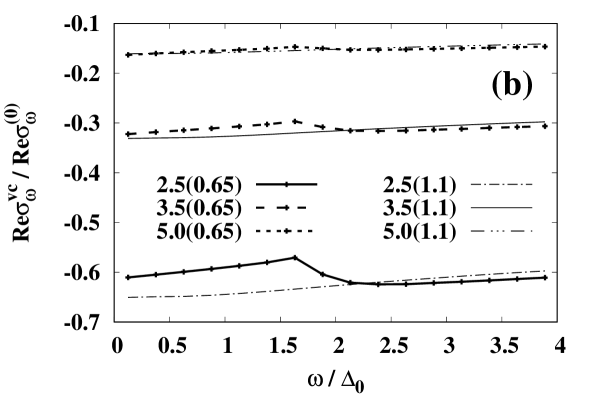
Figure 8(a) shows that the difference in ${\rm Re}\sigma^{\rm vc}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}$ between $\omega>2\Delta$ and $\omega<2\Delta$ becomes significant at low temperatures. The suppression of ${\rm Re}\sigma_{\omega}$ by vertex corrections is larger (smaller) than that in the normal state ( $T/T_{c}=1.1$ ) for $\omega>2\Delta$ ( $\omega<2\Delta$ ). The vertex correction is less effective for the thermal excitation ( $\omega<2\Delta$ ). Figure 8(b) shows that the absolute value of ${\rm Re}\sigma^{\rm vc}_{\omega}$ is roughly proportional to $1/(k_{F}l)^{2}$ , as expected from the analytical expressions in the previous section. There also exists a difference between $\omega>2\Delta$ and $\omega<2\Delta$ for other values of $k_{F}l$ , which is similar to the case of $k_{F}l=2.5$ .

The components of ${\rm Re}\sigma^{\rm vc}_{\omega}/\sigma_{0}$ are shown in Fig. 9.

Figure 9 shows that ${\rm Re}\sigma^{MT,DOS0,MC}_{\omega}/\sigma_{0}$ ( ${\rm Re}\sigma^{MT0,DOS,AL}_{\omega}/\sigma_{0}$ ) takes a negative (positive) value. These vertex corrections are seemingly proportional to the MB conductivity. The comparison between vertex corrections and $c_{0}\times{\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}$ shows that this is not the case. Here, $c_{0}$ is chosen in the same way as in Fig. 7. In the cases of ${\rm Re}\sigma^{MT,MT0,DOS,DOS0}_{\omega}$ , the deviations from the MB conductivity show a similar $\omega$ -dependence with each other. When we choose $c_{0}$ so that $c_{0}\times{\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}$ overlaps ${\rm Re}\sigma^{MT,MT0,DOS,DOS0}_{\omega}$ around $\omega\lessapprox 2\Delta$ , each of $|{\rm Re}\sigma^{MT,MT0,DOS,DOS0}_{\omega}|$ takes values larger than $|c_{0}\times{\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}|$ for $\omega>2\Delta$ . This indicates that these four terms give larger corrections in ${\rm Re}\sigma_{\omega}$ for $\omega>2\Delta$ than for $\omega<2\Delta$ . The maximally crossed term shows an opposite tendency. The correction by the thermal excitation is larger than that by the excitation above $2\Delta$ in the case of $|{\rm Re}\sigma^{MC}_{\omega}|$ . The AL term is smaller than other terms and negligible in the superconducting state, although ${\rm Re}\sigma^{AL}_{\omega}$ in the normal state is enhanced for small $\omega$ by the superconducting fluctuation near $T_{c}$ . This smallness of the AL term originates from the fact that one of two fluctuation modes is the amplitude mode ( $\Gamma_{1}$ ), as shown in Eq. (37). Note that $\Gamma_{1}$ does not include the Coulomb interaction effect.

The ratios of components of vertex corrections to the MB conductivity are shown in Fig. 10.

The relationship between the sizes of vertex corrections in the superconducting state is similar to that in the normal state. For $T/T_{c}=0.45$ , the absolute values of the MT and DOS terms are smaller for $\omega<2\Delta$ than for $\omega>2\Delta$ , and show a variation around $\omega\simeq 2\Delta$ . The comparison of the absolute values between vertex corrections shows that ${\rm Re}\sigma^{DOS0}_{\omega}$ gives a predominant contribution in ${\rm Re}\sigma_{\omega}$ , although there is a cancellation among vertex corrections. Thus, the difference in ${\rm Re}\sigma^{DOS0}_{\omega}$ between $\omega<2\Delta$ and $\omega>2\Delta$ mainly leads to the deviation of ${\rm Re}\sigma_{\omega}$ from the MB-like behavior. For $T/T_{c}=1.1$ , ${\rm Re}\sigma^{DOS0}_{\omega}$ is suppressed at small values of $\omega$ , which causes a suppression of ${\rm Re}\sigma_{\omega}$ at low frequencies, as shown in Fig. 7.

4.2 Origin of the variation of the correction term around $\omega=2\Delta$

In this subsection, we show that the variation of the ratio ${\rm Re}\sigma^{\rm vc}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}$ around $\omega\simeq 2\Delta$ is related to the correction to the one-particle spectrum. Equation (44) is rewritten as ${\rm Re}\sigma^{(0)}_{\omega}/\sigma_{0}=({\rm Re}\sigma^{(0)a}_{\omega}+{\rm Re}\sigma^{(0)b}_{\omega})/\sigma_{0}$ with ${\rm Re}\sigma^{(0)a}_{\omega}/\sigma_{0}=\int_{\Delta+\omega/2}^{\infty}d\epsilon h_{\epsilon,\omega}$ and ${\rm Re}\sigma^{(0)b}_{\omega}/\sigma_{0}=-\int_{0}^{\omega/2-\Delta}d\epsilon\theta(\omega-2\Delta)h_{\epsilon,\omega}$ for $\omega>0$ . Here, $h_{\epsilon,\omega}=(T^{h}_{\epsilon+\omega/2}-T^{h}_{\epsilon-\omega/2}){\rm Tr}[{\rm Im}\hat{g}^{+}_{\epsilon+\omega/2}{\rm Im}\hat{g}^{+}_{\epsilon-\omega/2}]/\omega$ . ${\rm Re}\sigma_{\omega}^{(0)a}$ is a decreasing function with respect to $\omega$ and ${\rm Re}\sigma_{\omega}^{(0)b}$ takes finite values only for $\omega>2\Delta$ . The weak localization effect on the one-particle spectrum is approximately taken into account as ${\rm Im}\hat{g}^{+}_{\epsilon}\times[1-(1-s^{\prime}\sqrt{(|\epsilon|-\Delta)\tau})/(k_{F}l)^{2}]=:{\rm Im}\hat{g^{\prime}}^{+}_{\epsilon}$ . $s^{\prime}=+$ $(-)$ means that the suppression of the density of states is large close to (apart from) the gap edge. Here, the case of $s^{\prime}=-$ is used for comparison and does not correspond to the real system. We calculate the conductivity including this effect ( ${\rm Re}\sigma^{\prime}_{\omega}={\rm Re}\sigma^{{}^{\prime}a}_{\omega}+{\rm Re}\sigma^{{}^{\prime}b}_{\omega}$ ) by replacing $\hat{g}^{+}_{\epsilon}$ by $\hat{g^{\prime}}^{+}_{\epsilon}$ in the above $h_{\epsilon,\omega}$ . The correction part of the conductivity ${\rm Re}\sigma^{\prime}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}-1$ is shown in Fig. 11.

The large variation of ${\rm Re}\sigma^{{}^{\prime}}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}-1$ occurs around $\omega\simeq 2\Delta$ with the same (opposite) tendency for $s^{\prime}=+$ $(-)$ as that of ${\rm Re}\sigma^{\rm vc}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}$ .

In ${\rm Re}\sigma^{{}^{\prime}a}_{\omega}$ , which is given by the thermal excitations, $\epsilon+\omega/2\simeq 3\Delta$ and $\epsilon-\omega/2\simeq\Delta$ for $\omega\simeq 2\Delta$ (the contribution from $\epsilon\simeq\Delta+\omega/2$ is large in the integration at low temperatures), and then only ${\rm Im}\hat{g^{\prime}}^{+}_{\epsilon-\omega/2}$ is put on the gap edge. On the other hand, in ${\rm Re}\sigma^{{}^{\prime}b}_{\omega}$ , which is given by excitations across the gap with $\omega\gtrsim 2\Delta$ , $\epsilon+\omega/2\simeq\Delta$ and $\epsilon-\omega/2\simeq-\Delta$ for $\omega\simeq 2\Delta$ , and then both ${\rm Im}\hat{g^{\prime}}^{+}_{\epsilon\pm\omega/2}$ are put on the gap edge. Thus, ${\rm Re}\sigma^{{}^{\prime}b}_{\omega}$ is more sensitive to the values of the density of states near the gap edge than ${\rm Re}\sigma^{{}^{\prime}a}_{\omega}$ in the case of $\omega\simeq 2\Delta$ . When the suppression of the density of states is larger near the gap edge than apart from the gap edge (corresponding to the case of $s^{\prime}=+$ ), the correction part of $|{\rm Re}\sigma^{{}^{\prime}b}_{\omega}|$ for $\omega\gtrsim 2\Delta$ is larger than that of $|{\rm Re}\sigma^{{}^{\prime}a}_{\omega}|$ for $\omega\lesssim 2\Delta$ . This leads to the negative slope of ${\rm Re}\sigma^{\prime}_{\omega}/{\rm Re}\sigma^{(0)}_{\omega}-1$ around $\omega\simeq 2\Delta$ , as shown in Fig. 11.

5 Summary and Discussion

In this study, we calculated the weak localization correction to the linear absorption of three-dimensional s-wave superconductors. This correction is caused by the coherent backscattering and the interaction effect (Coulomb interaction and superconducting fluctuations) enhanced by the diffusion term. Numerical calculations show that the correction effect is greater on the excitations across the gap ( $\omega>2\Delta$ ) than on the thermal excitations ( $\omega<2\Delta$ ). This tendency is shown to be related to the weak localization correction to the one-particle spectrum. The latter is known as the Altshuler–Aronov effect, which was confirmed in experiments [35, 36].

We showed that the weak localization effect can be made clear by taking the ratio of the correction term to the MB formula. The dependence of this ratio on the frequency shows a large variation near $\omega\simeq 2\Delta$ . This variation indicates that the correction term relatively enhances the absorption by the thermal excitations as compared with that by the excitations across the gap and blurs the absorption edge in the spectrum. The experimental result in a strongly disordered system shows a qualitatively similar tendency. [20] The quantitative result is not explained by our calculation because this system is outside the range of the weak localization.

Even in the case of less disordered systems, by taking the ratio of the absorption spectrum to the MB formula, the weak localization effect should be visible as a variation of this ratio around $\omega\simeq 2\Delta$ . We consider that this ratio can be used as a sign of the weak localization.

In order to deal with a more disordered system (i.e., outside the weak localization regime) such as some experiments, [20, 21, 22] the following should be considered theoretically as future issues. Since the calculations in this paper are based on the perturbation theory, one way to improve the calculation is to take account of higher-order terms. This is needed when we consider the metal-insulator transition. As another possibility, it is conceivable to change the treatment of the impurity scattering, for example, by considering an inhomogeneous case. [23, 37] In this study, we considered a homogeneously disordered system, but it is meaningful to see how the Coulomb interaction (a predominant factor in the weak localization effect) is incorporated in the case of inhomogeneous systems. [38]

Acknowledgment

The numerical computation in this work was carried out at the Yukawa Institute Computer Facility.

Appendix A Derivation of Correction Terms for Linear Absorption

In this Appendix, we give a detailed derivation of the results shown in Sect. 3.2. We obtain expressions of correction terms Eqs. (17), (26), (29), (33), (36), and (43) by calculating Eqs. (3)–(5) with the use of Eqs. (6)–(16). The calculation is performed by expanding $e^{iS^{\prime}}$ in accordance with Figs. 3–6, and we incorporate the effects of interactions (i.e., the screened Coulomb interaction, superconducting fluctuation, and scattering by impurities) in accordance with Fig. 1. In the following subsections, we show the equations obtained by this process.

A.1 Maki–Thompson term

The real part of the conductivity shown in Fig. 3(a) is written as

\begin{split}{\rm Re}\sigma^{MT0}_{\omega}=&\frac{e^{2}}{2\omega N^{3}}\sum_{\mib q^{\prime}}\int\frac{d\omega^{\prime}}{2\pi i}\int\frac{d\epsilon}{2\pi i}{\rm Im}\Bigl{\{}\left(\frac{\pi\rho_{0}}{2}\right)^{-1}\\ &\times\sum_{i=0,1,2,3,4}\left(\sum_{{\cal S}_{1}}C^{t}_{\omega^{\prime}}[\Gamma_{i}(q^{\prime})-\Gamma^{*}_{i}(q^{\prime})]+\sum_{{\cal S}_{2}}\Gamma_{i}(q^{\prime})+\sum_{{\cal S}_{3}}\Gamma^{*}_{i}(q^{\prime})\right)\\ &\times\frac{1}{N^{3}}\sum_{\mib k}{\rm Tr}[\hat{I}^{s_{4},b^{\prime}}_{\epsilon+\omega^{\prime}}\hat{G}_{k+q^{\prime}}^{s_{4}}v_{k+q^{\prime}}\hat{G}_{k+q+q^{\prime}}^{s_{1}}\hat{I}^{s_{1},a}_{\epsilon+\omega+\omega^{\prime}}\hat{Y}_{i}\hat{I}^{s_{2},a^{\prime}}_{\epsilon+\omega}\hat{G}_{k+q}^{s_{2}}v_{k}\hat{G}_{k}^{s_{3}}\hat{I}^{s_{3},b}_{\epsilon}\hat{Y}^{\prime}_{i}]\Bigr{\}}.\end{split}

(45)

$\Gamma_{i=0,1,2,3,4}$ indicate the interaction effects [Eqs. (21)–(23)], and the derivation of these equations is given in Ref. 25. $\sum_{{\cal S}_{1,2,3}}$ indicate the summations taken over $(s_{1},s_{2},s_{3},s_{4})$ with

(s_{1},s_{2},s_{3},s_{4})=\left\{\begin{matrix}(+,+,+,K),(+,+,K,-),(+,K,-,-),(K,-,-,-)&\text{for }{\cal S}_{1}\\ (+,+,K,K),(+,K,-,K),(+,+,+,-),(-,-,-,+)&\text{for }{\cal S}_{2}\\ (K,+,K,-),(K,K,-,-),(+,-,-,-),(-,+,+,+)&\text{for }{\cal S}_{3}.\end{matrix}\right.

(46)

$(\hat{I})(\hat{I}^{\prime})$ represents the vertex correction by the impurity scattering, and it is written as

(\hat{I}^{s_{1},x}_{\epsilon})(\hat{I}^{s_{2},x^{\prime}}_{\epsilon-\omega^{\prime}})=(\hat{\tau}_{0})(\hat{\tau}_{0})+\frac{n_{i}u^{2}}{N^{3}}\sum_{\mib k}(\hat{\tau}_{3}\hat{G}_{k}^{s_{1}})(\hat{G}_{k-q^{\prime}}^{s_{2}}\hat{\tau}_{3})+\left(\frac{n_{i}u^{2}}{N^{3}}\right)^{2}\sum_{\mib k,\mib k^{\prime}}(\hat{\tau}_{3}\hat{G}_{k}^{s_{1}}\hat{\tau}_{3}\hat{G}_{k^{\prime}}^{s_{1}})(\hat{G}_{k^{\prime}-q^{\prime}}^{s_{2}}\hat{\tau}_{3}\hat{G}_{k-q^{\prime}}^{s_{2}}\hat{\tau}_{3})+\cdots

(47)

( $x=a,b$ ). $(\hat{\;\;})(\hat{\;\;})$ represents a combination of matrices and does not mean a product of matrices [ $(\hat{A})(\hat{B})\neq\hat{A}\hat{B}$ ]. The summation taken over $\mib k$ results in the following expression:

(\hat{I}^{s_{1},x}_{\epsilon})(\hat{I}^{s_{2},x^{\prime}}_{\epsilon-\omega^{\prime}})=(\hat{\tau}_{0})(\hat{\tau}_{0})+\frac{X^{s_{1},s_{2}}_{\epsilon,\epsilon-\omega^{\prime}}}{1-2X^{s_{1},s_{2}}_{\epsilon,\epsilon-\omega^{\prime}}}[(\hat{\tau}_{3}\hat{g}_{\epsilon}^{s_{1}})(\hat{g}_{\epsilon-\omega^{\prime}}^{s_{2}}\hat{\tau}_{3})+(\hat{\tau}_{0})(\hat{\tau}_{0})]

(48)

with

X^{s_{1},s_{2}}_{\epsilon,\epsilon-\omega^{\prime}}=\alpha\int_{-1}^{1}\frac{d({\rm cos}\theta)}{2}\frac{2\alpha+\zeta_{\epsilon}^{s_{1}}+\zeta_{\epsilon-\omega^{\prime}}^{s_{2}}}{(2\alpha+\zeta_{\epsilon}^{s_{1}}+\zeta_{\epsilon-\omega^{\prime}}^{s_{2}})^{2}+(v_{F}q^{\prime}{\rm cos}\theta)^{2}}.

(49)

This expression describes the diffusion at a low energy:

\frac{X^{s_{1},s_{2}}_{\epsilon,\epsilon-\omega^{\prime}}/\alpha}{1-2X^{s_{1},s_{2}}_{\epsilon,\epsilon-\omega^{\prime}}}\simeq\frac{1}{Dq^{\prime 2}+\zeta^{s_{1}}_{\epsilon}+\zeta^{s_{2}}_{\epsilon-\omega^{\prime}}}.

(50)

$(\hat{Y}_{i})(\hat{Y}^{\prime}_{i})$ indicates the vertices of interactions $\Gamma_{i}$ . $(\hat{Y}_{i})(\hat{Y}^{\prime}_{i})=(\hat{\tau}_{i})(\hat{\tau}_{i})$ for $i=0,1,2,3$ , and $(\hat{Y}_{i})(\hat{Y}^{\prime}_{i})=(\hat{\tau}_{3})(-i\hat{\tau}_{2})+(i\hat{\tau}_{2})(\hat{\tau}_{3})$ for $i=4$ .

In the dirty limit ( $\Delta\tau\ll 1$ ), the following approximation holds for the summation over ${\mib k}$ :

\begin{split}&\frac{1}{N^{3}}\sum_{\mib k}(\hat{G}_{k+q^{\prime}}^{s_{4}}v_{k+q^{\prime}}\hat{G}_{k+q+q^{\prime}}^{s_{1}})(\hat{G}_{k+q}^{s_{2}}v_{k}\hat{G}_{k}^{s_{3}})\simeq\frac{\pi\rho_{0}\tau^{3}}{4}\int_{FS}v_{k}^{2}\{4(\hat{g}^{s_{4}}_{\epsilon+\omega^{\prime}}\hat{g}^{s_{1}}_{\epsilon+\omega+\omega^{\prime}})(\hat{g}^{s_{2}}_{\epsilon+\omega}\hat{g}^{s_{3}}_{\epsilon})\\ &+[(\hat{g}^{s_{4}}_{\epsilon+\omega^{\prime}}\hat{g}^{s_{1}}_{\epsilon+\omega+\omega^{\prime}})+(\hat{\tau}_{0})][(\hat{g}^{s_{2}}_{\epsilon+\omega}\hat{g}^{s_{3}}_{\epsilon})+(\hat{\tau}_{0})]+[(\hat{g}^{s_{4}}_{\epsilon+\omega^{\prime}}\hat{\tau}_{3})+(\hat{\tau}_{3}\hat{g}^{s_{1}}_{\epsilon+\omega+\omega^{\prime}})][(\hat{g}^{s_{2}}_{\epsilon+\omega}\hat{\tau}_{3})+(\hat{\tau}_{3}\hat{g}^{s_{3}}_{\epsilon})]\},\end{split}

(51)

where $\int_{FS}$ is the integration over the Fermi surface. Using the above expressions, we obtain the result for the MT0 term [Eq. (17)].

The real part of the conductivity shown in Fig. 3(b) is given by Eq. (45) with $(1/N^{3})\sum_{\mib k}{\rm Tr}[\;\cdot\;]$ replaced by

\begin{split}&n_{i}u^{2}\left(\frac{1}{N^{3}}\right)^{2}\sum_{\mib k,\mib k^{\prime}}{\rm Tr}[\\ &\hat{I}^{s_{4},b^{\prime}}_{\epsilon+\omega^{\prime}}\hat{G}_{k^{\prime}+q^{\prime}}^{s_{4}}v_{k^{\prime}+q^{\prime}}\hat{G}_{k^{\prime}+q+q^{\prime}}^{s_{1}}\hat{I}^{s_{1},c}_{\epsilon+\omega+\omega^{\prime}}\hat{\tau}_{3}\hat{G}^{s_{1}}_{k+q+q^{\prime}}\hat{I}^{s_{1},a}_{\epsilon+\omega+\omega^{\prime}}\hat{Y}_{i}\hat{I}^{s_{2},a^{\prime}}_{\epsilon+\omega}\hat{G}^{s_{2}}_{k+q}v_{k}\hat{G}^{s_{3}}_{k}\hat{\tau}_{3}\hat{I}^{s_{3},c^{\prime}}_{\epsilon}\hat{G}^{s_{3}}_{k^{\prime}}\hat{I}^{s_{3},b}_{\epsilon}\hat{Y}^{\prime}_{i}\\ &+\hat{I}^{s_{4},c}_{\epsilon+\omega^{\prime}}\hat{\tau}_{3}\hat{G}_{k^{\prime}+q^{\prime}}^{s_{4}}v_{k^{\prime}+q^{\prime}}\hat{G}_{k^{\prime}+q+q^{\prime}}^{s_{1}}\hat{I}^{s_{1},a}_{\epsilon+\omega+\omega^{\prime}}\hat{Y}_{i}\hat{I}^{s_{2},a^{\prime}}_{\epsilon+\omega}\hat{G}^{s_{2}}_{k^{\prime}+q}\hat{\tau}_{3}\hat{I}^{s_{2},c^{\prime}}_{\epsilon+\omega}\hat{G}^{s_{2}}_{k+q}v_{k}\hat{G}^{s_{3}}_{k}\hat{I}^{s_{3},b}_{\epsilon}\hat{Y}^{\prime}_{i}\hat{I}^{s_{4},b^{\prime}}_{\epsilon+\omega^{\prime}}\hat{G}^{s_{4}}_{k+q^{\prime}}].\end{split}

(52)

Using the same approximation as in Ref. 34 we obtain

\begin{split}\frac{1}{N^{3}}\sum_{\mib k}(\hat{G}_{k+q^{\prime}}^{s_{4}}v_{k+q^{\prime}}\hat{G}_{k+q+q^{\prime}}^{s_{1}})(\hat{G}^{s_{3}}_{k})\simeq&\frac{\pi\rho_{0}\tau^{3}}{2}\int_{FS}v_{k}(\mib v_{k}\cdot\mib q^{\prime})[2(\hat{g}^{s_{4}}_{\epsilon+\omega^{\prime}}\hat{g}^{s_{1}}_{\epsilon+\omega+\omega^{\prime}})(\hat{\tau}_{3})-(\hat{g}^{s_{4}}_{\epsilon+\omega^{\prime}}\hat{\tau}_{3})(\hat{g}^{s_{3}}_{\epsilon})\\ &-(\hat{\tau}_{3}\hat{g}^{s_{1}}_{\epsilon+\omega+\omega^{\prime}})(\hat{g}^{s_{3}}_{\epsilon})],\end{split}

(53)

and $(1/N^{3})\sum_{\mib k}(\hat{G}^{s_{1}}_{k+q+q^{\prime}})(\hat{G}^{s_{2}}_{k+q}v_{k}\hat{G}^{s_{3}}_{k})$ is calculated in the same way. Using these expressions and

\frac{e^{2}}{2\alpha^{2}N^{3}}\sum_{\mib q}\left(\int_{FS}v_{k}({\mib v}_{k}\cdot{\mib q})\right)^{2}=\frac{\sigma_{0}\sqrt{3\tau}}{2(k_{F}l)^{2}}\int d(Dq^{2})(Dq^{2})^{3/2},

(54)

we obtain the result of the MT term with an additional diffuson [Eq. (26)].

A.2 Density of states term

The expression of the self-energy correction term [Fig. 4(a)] is given by

\begin{split}{\rm Re}\sigma^{DOS0}_{\omega}=&\frac{e^{2}}{\omega N^{3}}\sum_{\mib q^{\prime}}\int\frac{d\omega^{\prime}}{2\pi i}\int\frac{d\epsilon}{2\pi i}{\rm Im}\Bigl{\{}\left(\frac{\pi\rho_{0}}{2}\right)^{-1}\\ &\times\sum_{i=0,1,2,3,4}\left(\sum_{{\cal S}_{1}}C^{t}_{\omega^{\prime}}[\Gamma_{i}(q^{\prime})-\Gamma^{*}_{i}(q^{\prime})]+\sum_{{\cal S}_{2}}\Gamma_{i}(q^{\prime})+\sum_{{\cal S}_{3}}\Gamma^{*}_{i}(q^{\prime})\right)\\ &\times\frac{1}{N^{3}}\sum_{\mib k}{\rm Tr}[\hat{I}^{s_{3},b^{\prime}}_{\epsilon}\hat{G}_{k}^{s_{3}}v_{k}\hat{G}_{k-q}^{s_{4}}v_{k}\hat{G}_{k}^{s_{1}}\hat{I}^{s_{1},a}_{\epsilon}\hat{Y}_{i}\hat{I}^{s_{2},a^{\prime}}_{\epsilon-\omega^{\prime}}\hat{G}_{k-q^{\prime}}^{s_{2}}\hat{I}^{s_{2},b}_{\epsilon-\omega^{\prime}}\hat{Y}^{\prime}_{i}]\Bigr{\}}\end{split}

(55)

[two diagrams in Fig. 4(a) give the same expression by transforming the variables]. ${\cal S}_{1}$ indicates the summation taken over $(s_{1},s_{2},s_{3},s_{4})=(+,+,+,K)$ , $(+,+,K,-)$ , $(+,K,-,-)$ , and $(K,-,-,-)$ . In the same way, $(+,K,+,K)$ , $(+,K,K,-)$ , and $(+,+,-,-)$ for ${\cal S}_{2}$ , and $(K,K,-,-)$ and $(+,-,-,-)$ for ${\cal S}_{3}$ . As in the case of the MT term, in the dirty limit, the summation over ${\mib k}$ results in the following expression:

\begin{split}&\frac{1}{N^{3}}\sum_{\mib k}(\hat{G}_{k}^{s_{3}}v_{k}\hat{G}_{k-q}^{s_{4}}v_{k}\hat{G}_{k}^{s_{1}})(\hat{G}_{k-q^{\prime}}^{s_{2}})\simeq\frac{\pi\rho_{0}\tau^{3}}{4}\int_{FS}v_{k}^{2}\{4(\hat{g}_{\epsilon}^{s_{3}}\hat{g}_{\epsilon-\omega}^{s_{4}}\hat{g}_{\epsilon}^{s_{1}})(\hat{g}_{\epsilon-\omega^{\prime}}^{s_{2}})\\ &+[(\hat{g}_{\epsilon}^{s_{3}}\hat{g}_{\epsilon-\omega}^{s_{4}}\hat{\tau}_{3})+(\hat{g}_{\epsilon}^{s_{3}}\hat{\tau}_{3}\hat{g}_{\epsilon}^{s_{1}})+(\hat{\tau}_{3}\hat{g}_{\epsilon-\omega}^{s_{4}}\hat{g}_{\epsilon}^{s_{1}})+(\hat{\tau}_{3})](\hat{\tau}_{3})+[(\hat{g}_{\epsilon}^{s_{3}}\hat{g}_{\epsilon-\omega}^{s_{4}}\hat{g}_{\epsilon}^{s_{1}})+(\hat{g}_{\epsilon}^{s_{3}})+(\hat{\tau}_{3}\hat{g}_{\epsilon-\omega}^{s_{4}}\hat{\tau}_{3})+(\hat{g}_{\epsilon}^{s_{1}})](\hat{g}_{\epsilon-\omega^{\prime}}^{s_{2}})\}.\end{split}

(56)

Then, the result of the self-energy term is given by Eq. (29).

The real part of the conductivity by the DOS term shown in Fig. 4(b) is given by Eq. (55) with $(1/N^{3})\sum_{\mib k}{\rm Tr}[\;\cdot\;]$ replaced by

\begin{split}n_{i}u^{2}\left(\frac{1}{N^{3}}\right)^{2}\sum_{\mib k,\mib k^{\prime}}{\rm Tr}[\hat{I}^{s_{3},b^{\prime}}_{\epsilon}\hat{G}_{k^{\prime}}^{s_{3}}v_{k^{\prime}}\hat{G}_{k^{\prime}-q}^{s_{4}}\hat{\tau}_{3}\hat{I}^{s_{4},c^{\prime}}_{\epsilon-\omega}\hat{G}_{k-q}^{s_{4}}v_{k}\hat{G}_{k}^{s_{1}}\hat{I}^{s_{1},a}_{\epsilon}\hat{Y}_{i}\hat{I}^{s_{2},a^{\prime}}_{\epsilon-\omega^{\prime}}\hat{G}_{k-q^{\prime}}^{s_{2}}\hat{I}^{s_{2},c}_{\epsilon-\omega^{\prime}}\hat{\tau}_{3}\hat{G}_{k^{\prime}-q^{\prime}}^{s_{2}}\hat{I}^{s_{2},b}_{\epsilon-\omega^{\prime}}\hat{Y}^{\prime}_{i}].\end{split}

(57)

We calculate this expression with the use of the same approximation as in Eq. (53). The result for the DOS term is given by Eq. (33).

A.3 Aslamazov–Larkin term

The real part of the conductivity for the left diagram in Fig. 5 is given by the following expression:

\begin{split}{\rm Re}\sigma^{AL1}_{\omega}=&\frac{e^{2}}{2\omega N^{3}}\sum_{\mib q^{\prime}}\int\frac{d\omega^{\prime}}{2\pi}\sum_{i,j=0,1,2,3,4}{\rm Re}\{(C^{t}_{\omega^{\prime}}+C^{t}_{\omega-\omega^{\prime}})\Gamma_{i}(q^{\prime})\Gamma_{j}(q-q^{\prime}){\cal R}^{(1)}_{i,j}{\cal Q}^{(1)}_{i,j}\\ &+(C^{t}_{\omega}-C^{t}_{\omega^{\prime}})\Gamma^{*}_{i}(q^{\prime})\Gamma_{j}(q-q^{\prime}){\cal R}^{(2)}_{i,j}{\cal Q}^{(2)}_{i,j}+(C^{t}_{\omega}-C^{t}_{\omega-\omega^{\prime}})\Gamma_{i}(q^{\prime})\Gamma^{*}_{j}(q-q^{\prime}){\cal R}^{(3)}_{i,j}{\cal Q}^{(3)}_{i,j}\\ &-C^{t}_{\omega}\Gamma^{*}_{i}(q^{\prime})\Gamma_{j}(q-q^{\prime}){\cal R}^{(2)}_{i,j}{\cal Q}^{(4)}_{i,j}-C^{t}_{\omega}\Gamma_{i}(q^{\prime})\Gamma^{*}_{j}(q-q^{\prime}){\cal R}^{(3)}_{i,j}{\cal Q}^{(5)}_{i,j}\}\end{split}

(58)

with

{\cal R}^{(x)}_{i,j}=\sum_{{\cal S}_{x}}\int\frac{d\epsilon}{2\pi}\frac{1}{N^{3}}\sum_{\mib k}{\rm Tr}[\hat{G}^{s_{1}}_{k+q}v_{k}\hat{G}^{s_{2}}_{k}\hat{I}^{s_{2},a}_{\epsilon}\hat{Y}^{\prime}_{i}\hat{I}^{s_{3},a^{\prime}}_{\epsilon+\omega^{\prime}}\hat{G}^{s_{3}}_{k+q^{\prime}}\hat{I}^{s_{3},b}_{\epsilon+\omega^{\prime}}\hat{Y}^{\prime}_{j}\hat{I}^{s_{1},b^{\prime}}_{\epsilon+\omega}]

(59)

and

{\cal Q}^{(x)}_{i,j}=\sum_{{\cal S}_{x}}\int\frac{d\epsilon}{2\pi}\frac{1}{N^{3}}\sum_{\mib k}{\rm Tr}[\hat{G}^{s_{2}}_{k}v_{k}\hat{G}^{s_{1}}_{k+q}\hat{I}^{s_{1},b}_{\epsilon+\omega}\hat{Y}_{j}\hat{I}^{s_{3},b^{\prime}}_{\epsilon+\omega^{\prime}}\hat{G}^{s_{3}}_{k+q^{\prime}}\hat{I}^{s_{3},a}_{\epsilon+\omega^{\prime}}\hat{Y}_{i}\hat{I}^{s_{2},a^{\prime}}_{\epsilon}].

(60)

$\sum_{{\cal S}_{x}}$ indicates that the summation is taken over $(s_{1},s_{2},s_{3})$ with

(s_{1},s_{2},s_{3})=\left\{\begin{matrix}(+,K,+),(+,-,K),(K,-,-)&(x=1),\\ (+,+,K),(+,K,-),(K,-,-)&(x=2),\\ (+,K,+),(K,-,+),(-,-,K)&(x=3),\\ (+,+,K),(K,+,-),(-,K,-)&(x=4),\\ (K,+,+),(-,K,+),(-,-,K)&(x=5).\end{matrix}\right.

(61)

$(1/N^{3})\sum_{\mib k}(\hat{G}^{s_{2}}_{k}v_{k}\hat{G}^{s_{1}}_{k+q})(\hat{G}^{s_{3}}_{k+q^{\prime}})$ and $(1/N^{3})\sum_{\mib k}(\hat{G}^{s_{1}}_{k+q}v_{k}\hat{G}^{s_{2}}_{k})(\hat{G}^{s_{3}}_{k+q^{\prime}})$ are calculated in the same way as in Eq. (53). In the same way, the real part of the conductivity for the right diagram of Fig. 5 ( ${\rm Re}\sigma^{AL2}_{\omega}$ ) is calculated, and it is given by Eq. (58) with ${\cal R}^{(1)}_{i,j}$ , ${\cal R}^{(2)}_{i,j}$ , and ${\cal R}^{(3)}_{i,j}$ replaced by ${\cal R}^{{}^{\prime}(1)}_{i,j}$ , ${\cal R}^{{}^{\prime}(3)}_{i,j}$ , and ${\cal R}^{{}^{\prime}(3)}_{i,j}$ , respectively. Here,

{\cal R}^{{}^{\prime}(x)}_{i,j}=\sum_{{\cal S}_{x}}\int\frac{d\epsilon}{2\pi}\frac{1}{N^{3}}\sum_{\mib k}{\rm Tr}[\hat{G}^{s_{1}}_{k+q}v_{k}\hat{G}^{s_{2}}_{k}\hat{I}^{s_{2},a}_{\epsilon}\hat{Y}^{\prime}_{j}\hat{I}^{s_{3},a^{\prime}}_{\epsilon+\omega-\omega^{\prime}}\hat{G}^{s_{3}}_{k+q-q^{\prime}}\hat{I}^{s_{3},b}_{\epsilon+\omega-\omega^{\prime}}\hat{Y}^{\prime}_{i}\hat{I}^{s_{1},b^{\prime}}_{\epsilon+\omega}].

(62)

The summation over $\mib k$ in $(1/N^{3})\sum_{\mib k}(\hat{G}^{s_{1}}_{k+q}v_{k}\hat{G}^{s_{2}}_{k})(\hat{G}^{s_{3}}_{k+q-q^{\prime}})$ is performed in the same way as in the above calculations.

Using the above expressions, we find that ${\cal R}$ , ${\cal Q}$ , and ${\cal R}^{\prime}$ have the following properties: ${\cal R}^{(x)}_{i,j}={\cal Q}^{(x)}_{i,j}={\cal R}^{{}^{\prime}(x)}_{i,j}=0$ for $i=j=0,1,2,3$ and $(i,j)=(0,1),(1,0),(2,3),(3,2)$ with $x=1,2,3$ . ${\cal R}^{(1,2,3)}_{i,j}={\cal R}^{{}^{\prime}(1,3,2)}_{i,j}$ for $(i,j)=(1,2),(2,1),(1,3),(3,1)$ , and ${\cal R}^{(1,2,3)}_{i,j}=-{\cal R}^{{}^{\prime}(1,3,2)}_{i,j}$ for $(i,j)=(0,2),(2,0),(0,3),(3,0)$ . Then, the sum of ${\rm Re}\sigma^{AL1}_{\omega}$ and ${\rm Re}\sigma^{AL2}_{\omega}$ includes only the terms of $\Gamma^{(*)}_{i}(q^{\prime})\Gamma^{(*)}_{j}(q-q^{\prime})$ with $(i,j)=(1,3)$ , $(3,1)$ , $(1,2)$ , $(2,1)$ , $(1,4)$ , and $(4,1)$ . The result of the AL term ( $\sigma^{AL}_{\omega}=\sigma^{AL1}_{\omega}+\sigma^{AL2}_{\omega}$ ) is given by Eq. (36).

A.4 Maximally crossed term

The real part of the conductivity given in Fig. 6(b) is expressed as

\begin{split}{\rm Re}\sigma^{MC}_{\omega}=&\frac{-e^{2}}{2\omega N^{3}}\sum_{\mib q^{\prime}}\sum_{s=\pm}s\int\frac{d\epsilon}{2\pi}(T^{h}_{\epsilon+\omega}-T^{h}_{\epsilon})\frac{1}{N^{3}}\sum_{\mib k}v_{\mib k}v_{\mib q^{\prime}-\mib k}\sum_{n=1}^{\infty}n_{i}u^{2}\left(\frac{n_{i}u^{2}}{N^{3}}\right)^{n}\sum_{\mib k_{1},\cdots,\mib k_{n}}{\rm Tr}[\\ &\hat{G}^{s}_{\mib q^{\prime}-\mib k,\epsilon}\hat{G}^{+}_{\mib q^{\prime}-\mib k,\epsilon+\omega}\hat{\tau}_{3}\hat{G}^{+}_{\mib k_{n},\epsilon+\omega}\cdots\hat{\tau}_{3}\hat{G}^{+}_{\mib k_{1},\epsilon+\omega}\hat{\tau}_{3}\hat{G}^{+}_{\mib k,\epsilon+\omega}\hat{G}^{s}_{\mib q^{\prime}-\mib k,\epsilon}\hat{\tau}_{3}\hat{G}^{s}_{\mib q^{\prime}-\mib k_{n},\epsilon}\cdots\hat{\tau}_{3}\hat{G}^{s}_{\mib q^{\prime}-\mib k_{1},\epsilon}\hat{\tau}_{3}].\end{split}

(63)

$(1/N^{3})\sum_{\mib k}v_{\mib k}v_{\mib q^{\prime}-\mib k}(\hat{G}^{s}_{\mib q^{\prime}-\mib k,\epsilon}\hat{G}^{+}_{\mib q^{\prime}-\mib k,\epsilon+\omega})(\hat{G}^{+}_{\mib k,\epsilon+\omega}\hat{G}^{s}_{\mib q^{\prime}-\mib k,\epsilon})$ is calculated in the same way as in Eq. (51). The calculation similar to Eq. (48) shows that

\sum_{n=1}^{\infty}\left(\frac{n_{i}u^{2}}{N^{3}}\right)^{n}\sum_{\mib k_{1},\cdots,\mib k_{n}}(\hat{G}^{+}_{\mib k_{n},\epsilon+\omega}\cdots\hat{\tau}_{3}\hat{G}^{+}_{\mib k_{1},\epsilon+\omega})(\hat{G}^{s}_{\mib q^{\prime}-\mib k_{n},\epsilon}\cdots\hat{\tau}_{3}\hat{G}^{s}_{\mib q^{\prime}-\mib k_{1},\epsilon})\simeq\frac{X^{+s}_{\epsilon+\omega,\epsilon}[(\hat{g}^{+}_{\epsilon+\omega})(\hat{g}^{s}_{\epsilon})+(\hat{\tau}_{3})(\hat{\tau}_{3})]}{1-2X^{+s}_{\epsilon+\omega,\epsilon}}.

(64)

Then, the real part of the conductivity for this term is given by Eq. (43).

References

[1] L. P. Gor’kov, A. I. Larkin, and D. E. Khmel’nitskii, JETP Lett. 30, 228 (1979).
[2] A. Schmid, Z. Physik 271, 251 (1974).
[3] B. L. Al’tshuler and A. G. Aronov, Solid State Commun. 30, 115 (1979).
[4] B. L. Al’tshuler and A. G. Aronov, Sov. Phys. JETP 50, 968 (1979).
[5] H. Fukuyama, J. Phys. Soc. Jpn 48, 2169 (1980).
[6] B. L. Altshuler, A. G. Aronov, and P. A. Lee, Phys. Rev. Lett. 44, 1288 (1980).
[7] Yu. N. Ovchinnikov, Sov. Phys. JETP 37, 366 (1973).
[8] S. Maekawa and H. Fukuyama, J. Phys. Soc. Jpn 51, 1380 (1981).
[9] H. Takagi and Y. Kuroda, Solid State Commun. 41, 643 (1982).
[10] R. A. Smith and V. Ambegaokar, Phys. Rev. B 45, 2463 (1992).
[11] L. G. Aslamazov and A. I. Larkin, Sov. Phys. Solid State 10, 875 (1968).
[12] K. Maki, Prog. Theor. Phys. 40, 193 (1968).
[13] R. S. Thompson, Phys. Rev. B 1, 327 (1970).
[14] H. Schmidt, Z. Physik 216, 336 (1968).
[15] L. G. Aslamasov and A. A. Varlamov, J. Low Temp. Phys. 38, 223 (1980).
[16] F. Federici and A. A. Varlamov, Phys. Rev. B 55, 6070 (1997).
[17] A. Petković and V. M. Vinokur, J. Phys.: Condens. Matter 25, 355701 (2013).
[18] D. C. Mattis and J. Bardeen, Phys. Rev. 111, 412 (1958).
[19] A. A. Abrikosov and L. P. Gor’kov, Sov. Phys. JETP 8, 1090 (1959).
[20] B. Cheng, L. Wu, N. J. Laurita, H. Singh, M. Chand, P. Raychaudhuri, and N. P. Armitage, Phys. Rev. B 93, 180511 (2016).
[21] J. Simmendinger, U. S. Pracht, L. Daschke, T. Proslier, J. A. Klug, M. Dressel, and M. Scheffler, Phys. Rev. B 94, 064506 (2016).
[22] U. S. Pracht, N. Bachar, L. Benfatto, G. Deutcher, E. Farber, M. Dressel, and M. Scheffler, Phys. Rev. B 93, 100503 (2016).
[23] A. I. Larkin and Yu. N. Ovchinnikov, Sov. Phys. JETP 34, 1144 (1972).
[24] U. S. Pracht, T. Cea, N. Bachar, G. Deutcher, E. Farber, M. Dressel, M. Scheffler, C. Castellani, A. M. García-García, and L. Benfatto, Phys. Rev. B 96, 094514 (2017).
[25] T. Jujo, J. Phys. Soc. Jpn 88, 104701 (2019).
[26] L. V. Keldysh, Sov. Phys. JETP 20, 1018 (1965).
[27] A. Kamenev and A. Levchenko, Adv. Phys. 58, 197 (2009).
[28] The following relation is obtained by the Hubbard–Stratonovich transformation: $exp(-i\int_{\cal C}dt\sum_{\mib k,\mib k^{\prime},\mib q,\sigma,\sigma^{\prime}}v_{\mib q}^{C}\bar{\psi}_{\mib k,\sigma,t}\psi_{\mib k+\mib q,\sigma,t}\bar{\psi}_{\mib k^{\prime},\sigma^{\prime},t}\psi_{\mib k^{\prime}-\mib q,\sigma^{\prime},t}/2N^{3})=\int{\cal D}[\varphi]exp(-i\int_{\cal C}dt\sum_{\mib q}[\varphi_{\mib q,t}\varphi_{-\mib q,t}e^{2}/2v^{C}_{\mib q}+ie\varphi_{\mib q,t}\sum_{\mib k,\sigma}\bar{\psi}_{\mib k,\sigma,t}\psi_{\mib k-\mib q,\sigma,t}/\sqrt{N^{3}}])$ . Using $\int_{\cal C}dt\varphi_{\mib q,t}\varphi_{-\mib q,t}=\int_{-\infty}^{\infty}dt(\varphi^{+}_{\mib q,t}\varphi^{+}_{-\mib q,t}-\varphi^{-}_{\mib q,t}\varphi^{-}_{-\mib q,t})=\int_{-\infty}^{\infty}dt(\varphi^{cl}_{\mib q,t}\varphi^{qu}_{-\mib q,t}+\varphi^{qu}_{\mib q,t}\varphi^{cl}_{-\mib q,t})$ , we obtain the second term of Eq. (5). Here, the superscript $+$ $(-)$ in $\varphi_{\mib q,t}^{\pm}$ indicates that the field $\varphi_{\mib q,t}$ resides on the forward (backward) branch. A calculation of the term $\int_{\cal C}dt\varphi_{\mib q,t}\bar{\psi}_{\mib k,\sigma,t}\psi_{\mib k-\mib q,\sigma,t}$ is performed in a similar way. [27]
[29] We use this one-particle Green’s function to perturbatively calculate the weak localization correction to the linear absorption. In this calculation, the weak localization effect is not included in a self-consistent way in the one-particle state of electrons. This method of calculation is the same as that previously used in the case of the normal state, [3, 4, 5, 6, 7, 8, 9, 14, 15, 16, 17, 34] and is considered to be valid also in the superconducting state. This is because the excitation energy of the superconducting phase fluctuation is pushed up to the plasma frequency, and the effect of fluctuation becomes small in a three-dimensional system.
[30] In the superconducting state, the weak localization effect lowers $T_{c}$ and reduces the superconducting gap $\Delta$ . [39] In this perturbative calculation, the value of $\Delta$ itself does not affect the spectrum qualitatively ( $\Delta$ at $T=0$ is set to be the unit of energy). The validity of this method of calculation is related to the behavior of the spectrum around the gap edge. For example, when the effect of paramagnetic impurities on the spectrum is considered perturbatively (Sect. 4 in Ref. 25), the perturbation term diverges at the gap edge. In this case, the spectrum should be calculated consistently with the values of $\Delta$ . On the other hand, in the weak localization correction, the perturbation term for the spectrum is finite, and then the behavior of the spectrum can be discussed independently of the size of the superconducting gap.
[31] G. Baym and L. P. Kadanoff, Phys. Rev. 124, 287 (1961).
[32] In a three-dimensional system, the higher-order terms are proportional to $1/(k_{F}l)^{2n}$ ( $n$ is the number of the irreducible four-point interaction vertices included in the conductivity) for all the cases of “MT0”, “MT”, “DOS0”, “DOS”, “AL”, and “MC” in the dirty limit $\Delta\tau\ll 1$ (the mean free path is shorter than the coherence length). Our calculation is valid in the case of $(k_{F}l)^{2}\gg 1$ . On the other hand, in the case of a (quasi-)two-dimensional system, the $n$ -th order term in ${\rm Re}\sigma_{\omega}$ is proportional to $1/(k_{F}l)^{n}$ . Then, in a thin film, the higher-order terms are more effective than in a three-dimensional case, and the approximation used in this study is valid in the latter case for a wide range of values of $k_{F}l$ .
[33] The subscripts $i=0,1,2,3$ in $\chi_{i}$ and $\Gamma_{i}$ are related to those of Pauli matrices ( $\hat{\tau}_{i}$ ) in the Nambu space. For example, $\hat{\tau}_{3}$ and $\hat{\tau}_{2}$ indicate the density fluctuation and the superconducting phase fluctuation, respectively, as noted in Ref. 25. $\Gamma_{4}(q)$ originates from the mixing term $\chi^{\prime}$ , which couples the above two fluctuations.
[34] B. L. Altshuler, D. Khmel’nitzkii, A. I. Larkin, and P. A. Lee, Phys. Rev. B 22, 5142 (1980).
[35] B. Sacépé, C. Chapelier, T. I. Baturina, V. M. Vinokur, M. R. Bakanov, and M. Sanquer, Phys. Rev. Lett. 101, 157006 (2008).
[36] M. Chand, G. Saraswat, A. Kamlapure, M. Mondal, S. Kumar, J. Jesudasan, V. Bagwe, L. Benfatto, V. Tripathi, and P. Raychaudhuri, Phys. Rev. B 85, 014508 (2012).
[37] A. Ghosal, M. Randeria, and N. Trivedi, Phys. Rev. B 65, 014501 (2001).
[38] G. Seibold, L. Benfatto, and C. Castellani, Phys. Rev. B 96, 144507 (2017).
[39] R. A. Smith, M. Yu. Reizer, and J. W. Wilkins, Phys. Rev. B 51, 6470 (1995).

Weak Localization Correction to Linear Absorption in Conventional Superconductors

Abstract

1 Introduction

2 Formulation

3 Expressions for Correction Terms

3.1 Vertex corrections

3.2 Expressions of correction terms for linear absorption

3.2.1 Maki–Thompson terms

3.2.2 Density of states terms

3.2.3 Aslamazov–Larkin term

3.2.4 Maximally crossed term

4 Results

4.1 Numerical calculations

4.2 Origin of the variation of the correction term around ω=2​Δ\omega=2\Delta

5 Summary and Discussion

Acknowledgment

Appendix A Derivation of Correction Terms for Linear Absorption

A.1 Maki–Thompson term

A.2 Density of states term

A.3 Aslamazov–Larkin term

A.4 Maximally crossed term

References

4.2 Origin of the variation of the correction term around $\omega=2\Delta$