Weak localization competes with the quantum oscillations in a natural electronic superlattice: the case of Na_1.5(PO₂)₄(WO₃)₂₀

The unfading interest in low dimensional conducting materials originates from their remarkable electronic properties. High critical temperature in superconductors Kharkov and Sushkov (2016); Cyr-Choinière et al. (2017), improved thermoelectric properties Xie et al. (2009); Mao et al. (2016); Kolincio et al. (2016a); Molina-Valdovinos et al. (2018), instability of the electron gas into a charge density wave (CDW) Monceau (2012); Grüner (1988), are consequences of a pronounced structural and electronic anisotropy. In particular, quasi 1D or 2D conductors exhibit a partial Fermi surface (FS) reconstruction at a CDW transition, accompanied by strong reduction of free electron density, increase of the remaining carriers mobilities, and enhanced magnetoresistance Yasuzuka et al. (1999); Schlenker et al. (1985).

In addition, quantum corrections may strongly impact the low temperature transport properties. Weak localization (WL) phenomenon is a well known example. Another characteristic of low temperature magnetoresistance effects in metals, especially of those with high carrier mobility, is the existence of Shubnikov de Haas (SdH) quantum oscillations. They originate from the quantization of electron density of states into Landau levels when exposed to a magnetic field, and are observed in high purity samples in the limit $\omega_{c}\tau\gg$ 1, where $\omega_{c}=\frac{eB}{m^{*}}$ is the cyclotron frequency, $m^{*}$ the effective mass of carriers, and $\tau$ the elastic scattering time). WL and SdH effects are a priori antagonistic because they are respectively favored and limited by disorder. However, due to the decrease of the WL contribution with magnetic field and with the restricted condition $\omega_{c}\tau\leq(k_{F}\ell)^{-1}$ ($k_{F}$ is the Fermi momentum and $l$ the electronic mean free path), a crossover can be observed between these two quantum processes, whose magnetic field range has been related to interaction effects Sedrakyan and Raikh (2008). This crossover has been previously observed in rare systems showing strong 2D characteristics: 2D electron gas heterostructures with high mobilities Wang et al. (2018), quantum wells Sedrakyan and Raikh (2008); Tayari et al. (2015); Sarcan et al. (2018), and graphene Heer et al. (2010); et al. (2014). We show here that both WL and SdH are for the first time observed in a single crystal whose 2D character arises from the carriers confinement in conducting layers with a thickness of few atomic planes. The sample under study belongs to the monophosphate tungsten bronze (MPTB) family A_x(PO₄)₂(WO₃)_2m (A = K, Na or Pb). In this family, carriers originate from the PO₄ groups, and are delocalized in the middle of WO₃ layers, giving a pronounced anisotropic electronic structure Roussel et al. (2001); Foury-Leylekian and Pouget (2002). The carrier density can be tuned by changing $m$ due to the increase of unit cell for constant carrier numbers and/or by the insertion of A cations with metallic character Roussel et al. (2000). These A cations are inserted in hexagonal tunnels to give A_x(PO₄)₂(WO₃)_2mDomengés et al. (1988). Supplemental interest of this bronze family is that most of the investigated members have shown CDW transitions that have been explained using the hidden nesting concept Canadell and Whangbo (1991); Kolincio et al. (2016b).

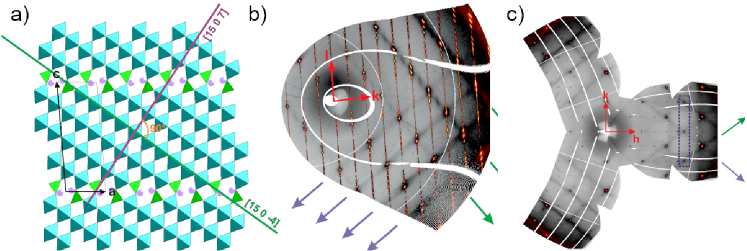
X-ray diffraction investigations performed at room temperature reveal that the whole pattern can be described using a monoclinic cell ($a=6.5483(6)$Å, $b=5.2893(5)$Å, $c=18.0789(15)$Å, $\beta=94.7000(4)^{\circ}$) and the space group $P2_{1}/m$; these cell parameters are in agreement with those reported for Pb_xP₄W₂₀O₆₈  on the basis of a pattern matching analysis performed on powder diffraction data Roussel et al. (1998). The final agreement factor for our data is 4.7% and the refined chemical composition is Na_1.49(8)P₄W₂₀O₆₈; Na sites are partly occupied. For details of the data collection, refinement and the atomic structure parameters see the Supplementary Material sup .

A projection along the b axis is shown in Figure 1a. The main structural characteristics expected for the MPTB family in the fundamental state are observed. Slabs of the (WO₆) edge sharing octahedra alternate with slices of (PO₄) tetraehdra; at the junction, hexagonal tunnels host Na atoms. Two orthogonal directions [15 0 7] and [15 0 -4] can be highlighted; they correspond to chains of 10 and 5 edge sharing (WO₆) octahedra respectively (see Figure  1a).

To check the possibility of a CDW transition, full data collections were performed at RT and 130 K on the ID28 beamline at ESRF synchrotron. There is no evidence for additional scattering signal at RT but at 130K diffuse scattering can be observed on different experimental frames. An accurate study of the (hk0)* plane (see Figures 1c) reveals an enhancement of the diffuse signal at the intersection of two diffuse planes for the $\frac{1}{2}$a* wave vector. An analysis of the shift between the positions of the diffuse scattering in subsequent (0kl)*, (1kl)*, (2kl)* reciprocal layers, reveals that the diffuse sheets intersecting them run along the direction [15 0 7] (see Supplementary Material sup for details).

The planes running along [15 0 7] are perpendicular to [-7 0 15]*; but [-7 0 15]* and [15 0 -4] fortuitously correspond to the same direction (see Supplementary Materials sup ) the direction of the chain of 10 octahedra. Then the observation of the diffuse scattering can be correlated with an ordering within the longest (WO₆) chain but with a loss of order both along b and along [15 0 -4] i.e. with a loss of order with the adjacent chains. The existence of diffuse scattering planes evidences the 1D ordering, possibly associated to CDW. Nevertheless, the absence of their condensation to sharp reflections shows that this ordering shows at T = 130 K a moderate coherence length, instead of establishing a long range order.

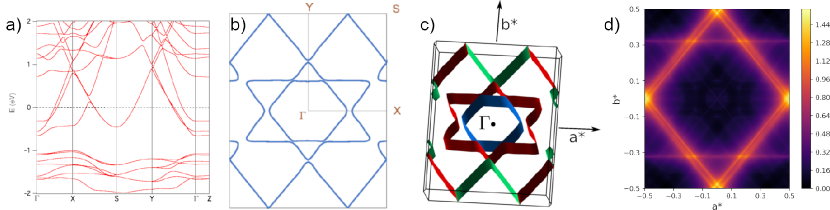
Having established the crystalographic parameters, we studied the electronic structure of Na_1.5(PO₂)₄(WO₃)₂₀. The results of band calculations performed with Generalised Gradient Approximation (GGA) (see supplementary material for details sup ) are shown in Fig. 2. There are large similarities between the studied compound and other MPTB members showing CDW Wang et al. (1989); Canadell and Whangbo (1991). As seen in Fig. 2a, three bands are crossing the Fermi level resulting in FS composed of three quasi 1D elements: three pairs of parallel planes running along $(a^{*}+b^{*})$, $(a^{*}-b^{*})$, and $b^{*}$ directions with almost no dispersion along $c^{*}$ as shown in Figures 2a) and c). While the presence of similar flat regions in MPTB hosting CDW gives a rise to hidden 1D nesting Wang et al. (1989); Canadell and Whangbo (1991), their almost perfect alignment in Na_1.5(PO₂)₄(WO₃)₂₀ additionally enhances the susceptibility for such a scenario. The relevance of this mechanism is additionally supported by the calculation of a Linhard function (Fig. 2d). In particular three very intense features are near the a*/2 wave vector suggest that large parts of the Fermi surface are susceptible to destruction by either an inherent instability of the Fermi surface or coupling with another type of instability of the lattice with this wave vector.

Fig. 3a shows the thermal variation of resistivity $\rho$ of a Na_1.5(PO₂)₄(WO₃)₂₀ single crystal. Metallic behavior ($\frac{d\rho}{dT}<0$) is observed from 400 K down to 10 K, where a smooth increase of resistivity appears. The electronic resistivity follows a -ln$T$ variation at low temperature, and this experimental observation suggests a WL contribution. The expression of the WL correction to conductance for non interacting electrons is Bergmann (1984):

where $p$ describes the temperature dependence of the inelastic scattering rate $\tau_{i}\propto T^{-p}$. p is equal to 1 for phase breaking dominated by Coulomb interactions and to 3 for electron-phonon scattering Lee and Ramakrishnan (1985). Fitting the low temperature part gives $\frac{dG}{dlnT}$ = 0.0517 $\Omega^{-1}$, to compare with $\frac{e^{2}p}{2\pi\hbar}$ = 1.23 10^-5 $\Omega^{-1}$ expected for a 2D WL contribution. The large difference between these values can be explained if our sample is considered as a superlattice of N independent and non-interacting 2D layers, giving rise to a multilayered WL effect Moyle et al. (1987); Stormer et al. (1986); Szott et al. (1989a, b, 1992). Dividing the measured conductivity by the theoretical WL conductivity of a single layer gives N $\approx$ 4300, considering a value p = 1, as expected for electron scattering in d-electron systems. Multiplying N by a thickness of the W-O conducting layer - approximately equal to the c lattice constant, we obtain $\approx$ 10 $\mu$m, comparable to the thickness of the sample. The weak disorder causing WL can originate from a weakly nonuniform distribution of Na atoms in the tunnels Kolincio et al. (2016b), stacking faults reported for MPTB with high $m$ parameter Domengés et al. (1983) or can be contributed by the short order of charge density waves state.

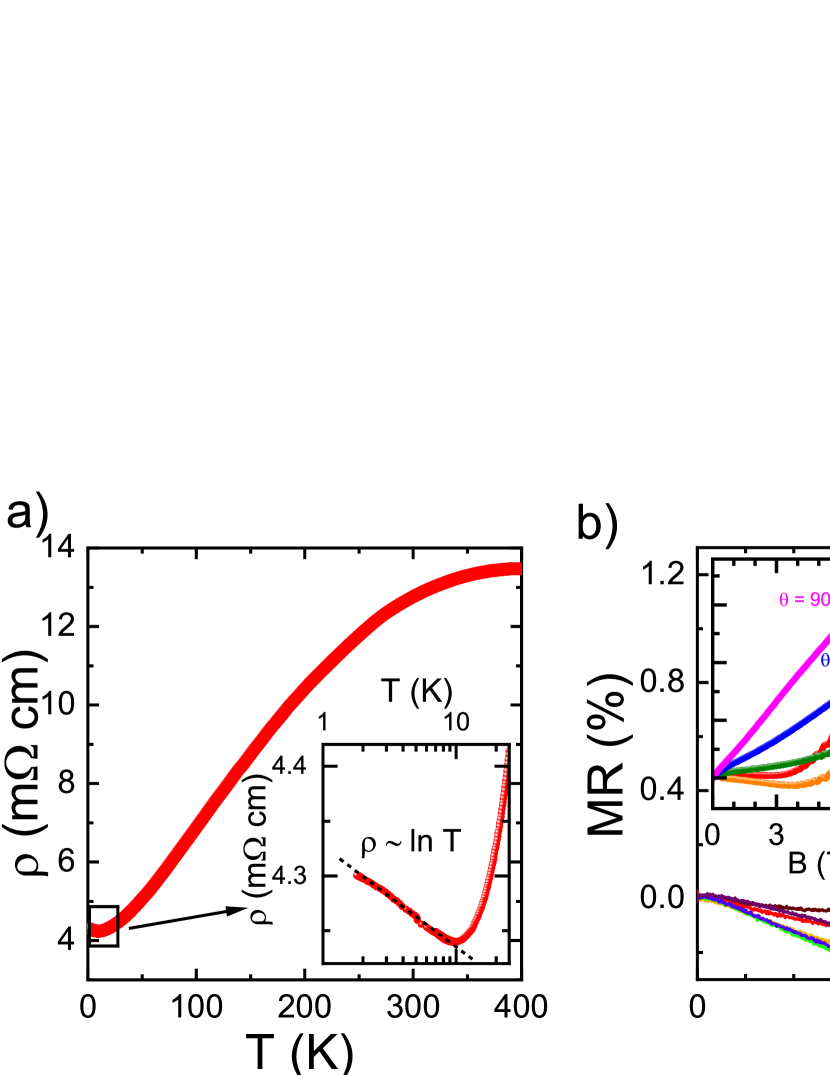
Since other mechanisms can lead to a logarithmic increase of resistivity at low temperature (Kondo scattering, strong Coulomb interaction), we analyzed the magnetoresistance ($MR=\frac{\rho(B)-\rho(0)}{\rho(0)}\cdot 100\%$) in order to confirm the underlying mechanism. The low temperature magnetoresistance depicted in Figure 3b is non-monotonic. It is negative for moderate $B$, and upon increasing the magnetic field, it shows a minimum followed by a notable increase. For T $\leq$ 18 K, large oscillations of the resistance can be observed in the increasing part of $MR(B)$.

As a strong argument for WL, we observe a negative MR for B perpendicular to the conducting plane ($\theta$ = 0^o) but it disappears in the parallel configuration ($\theta$ = 90^o) - see inset of Fig. 3b. This is precisely what is expected in the 2D WL regime, where the orbital effect responsible for the MR is suppressed for parallel fields Meyer et al. (2002). The low field magnetoconductance $\Delta G=G(B)-G(0)$ in the WL regime, can be described by the Hikami-Larkin-Nagaoka (HKN) expression Hikami et al. (1980); Lee and Ramakrishnan (1985):

where $\psi$ is the digamma function and $A$ = $\frac{4eD\tau_{i}B}{\hbar}$. To show the increase of magnetoconductance in the magnetic field, we have quantified and removed the classical $\sim$ B² magnetoresistance component. Then, we fit the low field curves with the WL expression considering the number of 4300 independent layers as found from the thermal dependence of conductivity. As shown in Fig. 3c, the fits show good agreement with the experimental data. The diffusion length of localization (Thouless length) L_ϕ = (D$\tau_{i}$)^1/2 was extracted from the fitting parameter and reported in the Fig. 4a. It is worth noting that L_ϕ is larger than the thickness of the conducting layer and approximately equal to the periodicity along the $c$ axis, confirming the regime of 2D coherence. When increasing the magnetic field, the dephasing regime emerges for L_B = $\left(\frac{2\hbar}{eB_{\phi}}\right)^{1/2}\geq L_{\phi}$. The effect of the magnetic field is then no longer relevant for WL and a negative contribution disappears. We have compared the value of $B_{\phi}$ extracted from the fitting with the condition L = L_B and the magnetic field value B^∗ where the G(B) ceases to grow with B and where quantum oscillations immediately emerge. We find that these values are very close to each other (for example for 4, 8 and 10 K the values obtained from the fits yield 5.27 T, 5.36 T, and 5.49 T respectively to compare with observed B^∗ = 5.45 T, 5.31 T and 5.53 T, respectively). For lowest temperatures, $L_{\phi}$ ceases to grow as the temperature is lowered, and even drops for 1.8 K, where the negative MR term also starts to decrease. A plausible explanation for this effect is the further crossover from weak localization to weak antilocalization (WAL)Lang et al. (2013); Liu et al. (2012) due to strong spin-orbit effects observed in tungsten rich compounds Sheng et al. (2017); McCormick et al. (2017). This scenario is also supported by the emergence of sharp cusp-like features in the low field limit of magnetoresistance (see Supplementary Materials), which is characteristic for WAL regimeBergmann (1984); Thomas et al. (2016). A further examination of this term, to obtain reliable HKN fit with the introduction of the antilocalization component will require the transport measurements at temperatures below 1.8 K.

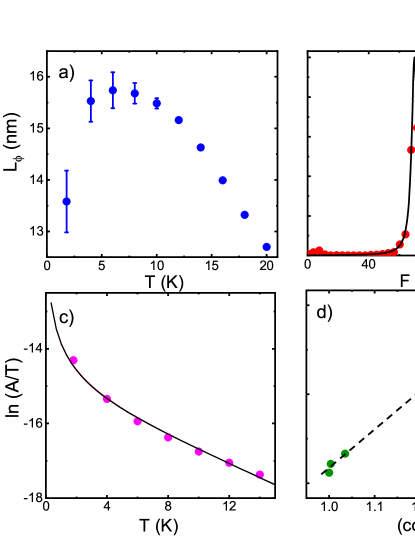
The oscillations in magnetoresistance emerge immediately after the negative WL term is suppressed, as evidenced in Fig. 3c. They are periodic as a function of 1/B, as expected for Shubnikov-de Haas quantum oscillations. We have used the Lifshitz-Kosevich (LK) theory to extract the electronic parameters Lifshitz and Kosevich (1956). The Fourier transform of the oscillating part of magnetoresistance gives the power spectrum shown in Fig. 4b. A peak can be observed at the frequency $F_{1}$= 69 T for $\theta$ = 0^o. This value yields the area $A_{1}$ of an extremal Fermi surface cross section that is perpendicular to B, through the Onsager relation Shoenberg (1984) $A_{i}=2\pi eF_{i}/\hbar$. It corresponds to a FS cross section $A_{1}$= 0.68 nm^-2, i.e. to a very small part ($\approx$ 0.5 %) of the first Brillouin zone, estimated to be 110 nm^-2. A plausible explanation for the presence of such a small pocket is the Fermi surface decomposition associated with charge density wave. This scenario is supported by the X-ray diffuse scattering and electronic structure calculations showing a potential for strong nesting around a*/2, which most likely occurs at high temperature as for other high m values of the MPTB family Ottolenghi, Alberto and Pouget, Jean-Paul (1996). The temperature dependence of the quantum oscillations amplitude is depicted in Fig. 4c. It can be related to the effective mass of quasi-particles m^∗ through the temperature damping factor. We find m^∗= 0.83 m_e with m_e being the free electron mass, indicating that the electron-electron interactions are moderate as theoretically predicted for the WL-SdH crossoverSedrakyan and Raikh (2008). The field dependence of the quantum oscillations allows to estimate the Dingle temperature T_D $\approx$ 6 K, corresponding to an electronic mean free path $l\approx$ 62 nm. Since the Fermi momentum is $k_{F}\approx(A_{1}/\pi)^{1/2}$ = 0.47 nm^-1, it leads to $k_{F}l\approx$ 29$\gg$ 1 confirming the diffusive regime Minkov et al. (2002); Pusep et al. (2004). The angle $\theta$ between $B$ and the $c$ axis was varied from 0 to 90^o and the SdH oscillations can be observed within experimental resolution up to $\theta\approx$ 50^o. The frequency of the SdH oscillations clearly shifts to larger values as $\theta$ is increased, with an approximate 1/cos$\theta$ variation, as depicted in the inset of Figure 4b. This is expected for quasi-2D Fermi surface topology and is also consistent with the angular dependence of magnetoresistance shown in the inset of figure 3b. For $B$ perpendicular to the conducting plane, MR initially attenuated by the negative contribution, steeply increases with $\sim B^{2}$ in the high field limit, where the WL phase coherence is broken, while for in-plane orientation MR is sublinear with $B$ which gives a tendency for saturation as $B\rightarrow\infty$. Such a behavior is characteristic for open and closed orbits, respectively, expected for a cylinder-like FSPippard (2009).

Such a reduced, cylindrical Fermi surface is a characteristic feature of 2D systems, as high mobility ultrathin films and heterostructures Wu et al. (2017); Gillgren et al. (2014); Kozuka et al. (2009); Li et al. (2015) and unparalleled cases of pure Bi and graphene, where the FS covers only 10^-5 and 10^-6 of the Brillouin zone, respectively Soule et al. (1964); Bhargava (1967); Behnia et al. (2007); Édel’man (1976). The renormalization of the Na_1.5(PO₂)₄(WO₃)₂₀ electronic structure driven by the charge density wave, causing the lowering of the Fermi wavevectors brings this bulk system close to a natural superlattice, with reduced number of carriers and/or reduced Fermi energy, which promotes the quantum phenomena.

In conclusion, we report the structural and transport properties of the monophosphate tungsten bronze Na_1.5(PO₂)₄(WO₃)₂₀. We demonstrate that this single crystal shows multilayered 2D weak localization effects. As soon as the dephasing by magnetic field dominates and breaks the WL contribution, there is a sudden crossover to the large quantum oscillations regime. This shows that natural crystals with 2D characteristics and reduced carriers density possibly due to a CDW condensation can be used as promising systems for investigating enhanced quantum transport properties.