22institutetext: Department of Physics, Tezpur University, Tezpur 784028, India
33institutetext: Solar Physics and Space Plasma Research Centre (SP2RC), School of Mathematics and Statistics, University of Sheffield, Hounsfield Road, Hicks Building, Sheffield, S3 7RH, UK
44institutetext: Department of Astronomy, Eötvös Loránd University, Budapest, Pázmány P. sétány 1/A, H-1117, Hungary
55institutetext: Physical Research Laboratory, Udaipur Solar Observatory, Devali, Badi Road, Udaipur 313001, India
55email: aish@iucaa.in, sharmaaishawnnya@gmail.com
Wave amplitude modulation in fan loops as observed by AIA/SDO
Abstract
Aims. To perform a detailed analysis to understand the evolution and dynamics of propagating intensity disturbances observed in a fan loop system.
Methods. We perform multiwavelength time-distance analysis of a fan loop system anchored in an isolated sunspot region (AR 12553). The active region was observed by the Atmospheric Imaging Assembly on-board the Solar Dynamics Observatory. We measure the phase speeds of the propagating intensity disturbances by employing cross-correlation analysis, as well as by obtaining the slopes in xt-plots. We obtain original as well as de-trended light curves at different heights of the time-distance maps and characterize them by performing Fouriér and Wavelet analysis, respectively.
Results. The time-distance maps reveal clear propagation of intensity oscillations in all the coronal EUV channels except AIA 94 and 335 Å. We determine the nature of the intensity disturbances as slow magneto-acoustic waves by measuring their phase speeds. The time-distance maps, as well as the de-trended light curves, show an increase and decrease in the amplitude of propagating 3-min oscillations over time. The amplitude variations appear most prominent in AIA 171 Å, though other EUV channels also show such signatures. Fouriér power spectrum yield the presence of significant powers with several nearby frequencies between 2–3 minutes (5–8 mHz), along with many other smaller peaks between 2–4 minutes. Wavelet analysis shows an increase and decrease of oscillating power around 3-min simultaneous to the amplitude variations. We obtain the modulation period to be in the range of 20–30 minutes.
Conclusions. Our results provide the viability of occurrence of phenomenon like ‘Beat’ among the nearby frequencies giving rise to the observed amplitude modulation. However, we can not at this stage rule out the possibility that the modulation may be driven by variability of an underlying unknown source.
Key Words.:
Sun: atmosphere — Sun: corona — Sun: UV radiation — Sun: oscillations — waves1 Introduction
Identification and characterization of magnetohydrodynamic (MHD) waves and oscillations are major thrust areas of research in the field of solar plasma-astrophysics. MHD waves are considered to be an important candidate for heating of the solar atmosphere (Erdélyi, 2004; Ofman, 2005; Taroyan & Erdélyi, 2009; Rajaguru et al., 2019; Liu et al., 2019). They may have significant roles in triggering of jets (De Pontieu et al., 2004; Chandra et al., 2015) as well as in the acceleration of fast solar wind (Cranmer, 2009).
One of the wave modes observed in the solar corona is slow mode magneto-acoustic waves. The propagation of this wave mode is largely confined to the magnetic field direction. They are compressional in nature, and propagate with speed that is less than the local sound speed in the solar corona. Such waves are often observed as fluctuations in intensity as well as in Doppler velocity (Wang et al., 2009; Gupta et al., 2012). These waves were first reported as propagating intensity disturbances (PIDs) by Ofman et al. (1997) in coronal plumes in off-limb observations recorded by the UltraViolet Coronagraph Spectrometer (UVCS, Kohl et al., 1995) on-board the Solar and Heliospheric Observatory (SOHO). Similar intensity oscillations in coronal fan loops were first detected by Berghmans & Clette (1999) using the Extreme-ultraviolet Imaging Telescope (EIT, Delaboudinière et al., 1995) on board SOHO in 195 Å channel, and later confirmed by De Moortel et al. (2000) in the observations recorded by Transition Region and Coronal Explorer (TRACE, Handy et al., 1999) in the 171 Å channel. Fan loops are magnetic plasma structures in the corona with temperature between 0.6–1 MK (Reale, 2010; Ghosh et al., 2017). They are found at the edges of active regions, and are mostly rooted in the umbra and umbra-penumbra boundaries of sunspots. They also remain anchored to the penumbra and non-sunspot (such as, plage) regions. From a statistical study, Kiddie et al. (2012) concluded that PIDs of sunspot origin are temperature dependent and have subsonic propagation speed.
Since the discovery of PIDs in coronal fan loops, a number of theoretical and observational studies have been performed to unravel their characteristics, propagation and dissipation and also their counterparts in the lower solar atmosphere (see, e.g., Nakariakov et al., 2000; De Moortel et al., 2002a, c; Roberts, 2006; De Moortel, 2009; Bogdan, 2000; Bogdan & Judge, 2006; Khomenko & Collados, 2015). Using wavelet analysis, De Moortel et al. (2002b) found that the periods of the PID are of the order of s. However, careful observation of their footpoint locations showed that the coronal fan loops rooted in sunspot regions have a dominant period of s, and the loops rooted in non-sunspot regions, such as plages are dominant in s period oscillations. This distinction was explained in terms of the underlying driver at the photospheric level, exciting the loop footpoints.
In addition to the regular 3-min and 5-min oscillation, few studies have reported longer-period oscillations in the fan loops. Wang et al. (2009) has reported longer-period propagating waves at around 12 and 25 minutes along a fan-like coronal structure in the intensity (see also Marsh et al., 2009) and Doppler shift of the Fe XII 195 Å line using EUV Imaging Spectrometer (EIS, Culhane et al., 2007) on-board HINODE (Kosugi et al., 2007). Stenborg et al. (2011) showed the presence of waves in multiples of 8 minutes in coronal fan loops such as, in 16-min, 24-min, 40-min etc. It was speculated that the presence of the 8-min period could be attributed to beat phenomenon, which may occur due to the superposition of ubiquitous 3-min chromospheric and 5-min photospheric oscillations that leak into the corona through the inclined guide field that is provided by fan loops. However, they did not emphasise the excitation mechanisms of other longer-period oscillations that they detected in their observations.
In this paper, we perform a detailed analysis of intensity perturbations propagating along a fan loop system anchored within a sunspot. We track the evolution of these intensity oscillations by using the high spatially and temporally resolved data recorded by the Atmospheric Imaging Assembly (AIA, Lemen et al., 2012) on-board the Solar Dynamic Observatory (SDO, Pesnell et al., 2012). Our motivation is to understand how intensity oscillations with a range of periodicities interact, and affect the propagation characteristics of most dominant 3-min oscillations along fan loops. The rest of the paper is structured as follows. In Section 2, we describe the observations obtained for this study and briefly address the data reduction and preparation. We present the details of the different analyses acquired in this study, such as time-distance maps, Fouriér analysis, wavelet analysis and respective results in Section 3. Finally, we summarise our findings and conclude in Section 4.
2 Observations

The main aim of this work is to perform a multi-wavelength study of the dynamics of a fan loop system. For this purpose we have utilised the observations recorded by AIA using its UV channel, AIA 1600 Å and all the EUV channels, AIA 304 Å, 171 Å, 131 Å, 193 Å, 211 Å, 335 Å, and 94 Å. These channels are dominated with different spectral lines formed in a range of temperatures. For more information on the temperature sensitivity of different channels see O’Dwyer et al. (2010), Del Zanna et al. (2011), and Boerner et al. (2012). AIA provides full disk images with a cadence of 12 s in EUV and 24 s in UV. In addition, for contextual purpose, we use continuum data obtained using the Helioseismic and Magnetic Imager (HMI, Schou et al., 2012a, b), also on-board SDO. The AIA and HMI data are processed using standard processing software provided in the solar software (SSW; Freeland & Handy, 1998) distribution. The processed level 1.5 AIA and HMI data provides a pixel resolution of 0.6″.


The fan loop system, which is studied here, belongs to the active region NOAA AR 12553 observed on June 16, 2016. We have analysed the AIA observations recorded between 07:30:10 to 10:30:10 UT. We note that all the observations taken in different channels are rotated/de-rotated to the reference time at 9:15:00 UT for further analysis. Panel (a) in Fig. 1 displays a portion of the Sun’s disk image including AR 12553 observed in 171 Å passband. The yellow box encloses the fan loop system named as region of interest, a zoom-up of which is shown in panel (b).
3 Data Analysis and Results
In Fig. 2, we plot the regions of interest observed from HMI and AIA. Panels (a) and (b) show the HMI intensity and line-of-sight [LOS] magnetogram, respectively. The magnetogram is displayed within the magnetic field range of G (with white indicating positive polarity and black indicating negative polarity). Panel (c) to (i) are taken by AIA in passband as labelled. The over-plotted cyan inner and yellow outer contours are plotted to visualise the umbra-penumbra and penumbra-plage boundaries, respectively. The umbra-penumbra contour is at the level of 38000 DN, whereas the penumbra-plage boundary is at the level of 53000 DN based on HMI continuum image. These contours are further over-plotted on the UV and EUV intensity images obtained in 1600 Å and 171 Å, shown in panels (c) and (e). Panel (e) reveals that some fan loops are rooted deep inside the umbra, and some are at the umbra-penumbra boundary.
Since our primary motivation is to study the wave dynamics of steady fan loops, we focus on the region that does not suffer from any flaring activity. With this condition in mind, we located three different regions on the fan loop system with white boxes, as shown in the panel (a) of Fig. 3 and studied the corresponding light curves over the following three-hour period. The resultant light curves are shown in panel (b) of Fig.3. The light curves are normalized with respect to the maximum intensities of each curve. The light curves conspicuously give the impression that the fan loop system does not show evolution more than 10% from the mean. Therefore, these could be considered for our study. The blue light curve taken from a location along fan loop 3 indicates some background intensity enhancement from time to time.
In order to study the existence and propagation of intensity disturbances along the fan loops, we employ time-distance analysis and construct artificial slits (slits 1, 2 and 3) along the three fan loops as shown in panel (a) of Fig. 3. We choose 171 Å image for the identification of fan loops as they are best seen at temperature of (e.g., Brooks et al., 2011; Ghosh et al., 2017). We note that each slit is four pixels wide. We further emphasise that this analysis could be performed using one slit. However, to check the consistency of the results, we have used three different slits along different fan loops anchored in the umbra of the sunspot (see panel (a) in Fig. 3). We describe the results for slit 1 in the following, and provide the results for slits 2 and 3 in the Appendix for brevity.
3.1 Time-distance maps


Fig. 4 displays the time-distance map observed along slit 1 in 171 Å. The time-distance map reveals clear propagation of intensity disturbances in the form of dark and bright ridges. These ridges are observed up to a distance of 8-10 (5.90-7.35 Mm) along the slit.
Fig. 5 displays the time-distance maps obtained along slit 1 from other AIA EUV channels as labelled. The PIDs are clearly discernible in all the EUV channels of AIA except for channels like 335 Å, and 94 Å, which are formed above a temperature of 2.5 MK. In AIA 193 Å, the PIDs are observed up to a distance of 8-10 (5.9-7.35 Mm) similar to 171 Å channel of AIA. However, in channels such as 131 Å, and 211 Å the PIDs are only seen upto a distance of around 4 (2.9 Mm). The time-distance maps also reveal a decrease in the signal strength of the propagating features as they travel along the loops, which indicates a reduction in their amplitude of oscillations ( 10% to 5%).
To perform a quantitative analysis on the propagation of the intensity disturbances, we obtain light curves at different projected heights from the origin of the slit. The yellow dashed lines in Figs. 4 and 5 highlight the locations chosen to receive the light curves. We denote the locations by L1, L2, L3, and L4 that correspond to , , , and , respectively. We note that the light curves are obtained from the absolute, unprocessed time-distance maps. We show such light curves in 171 Å for a few projected heights in Fig. 6 (left column). In the right column of Fig. 6, we plot corresponding de-trended light curves. The over-plotted blue lines on the original light curves indicate the background trends, which are obtained from a running average over 30 minutes. We see that 30-min running average describe the low-frequency background very well. We then, subtract the background trends from the respective original light curves to obtain the de-trended light curves. The de-trended light curves provide a very clear, evident, and unperturbed evolution of the intensity. We use the de-trended light curves for further studies.
3.2 Phase speeds of the Propagating Intensity Oscillations


| AIA EUV channel | Time lag | Phase speed from cross-correlation analysis | Phase speed from time-distance ridges |
|---|---|---|---|
| Å | sec. | km s-1 | km s-1 |
| 171 | 24.3 | 54.44 | 50.0 |
| 131 | 24.4 | 54.22 | 50.0 |
| 193 | 24.4 | 54.22 | 57.7 |
| 211 | 35.55 | 37.21 | 49.0 |
Before going into the details of the analysis, we intend to characterize the PIDs in terms of their phase speeds, as its measurements play a vital role in understanding their nature. To obtain the phase speeds, we employ two methods. In one method, we obtain the phase speeds by obtaining the slopes of the ridges observed in the time-distance plots. We draw multiple slopes (more than 20) along the propagating ridges by visual inspection and obtained the average propagation speed. The over-plotted yellow and white slanted lines in Figs. 4 and 5 indicate the slopes used to measure the average projected phase speeds of the PIDs. We obtain the average projected phase speeds along slit 1 as km s-1 for 171 Å, km s-1 for 131 Å, km s-1 for 193 Å, and km s-1 for 211 Å. The noted errors are the standard deviation obtained using multiple slopes.
Although the phase speeds obtained above by manually drawing slopes provides a feasible estimate of the phase speeds, it is subjected to errors due to its user-dependent nature. Therefore, in order to avoid the human bias associated with this method, we employ a technique that provides phase speeds by cross-correlating the light curves obtained at different heights (e.g., Gupta et al., 2010; Kiddie et al., 2012). The cross-correlation yields the time lag corresponding to the maximum cross-correlation coefficient and thereby the phase speeds. We carry out this analysis by using the standard IDL routine . For this purpose, we consider the de-trended light curves obtained at locations L1 and L2 (marked by yellow dashed lines in Figs. 4 and 5). We emphasise that the analysis carried out with the original light curves also gives similar time lags.
The cross-correlation curves obtained for different AIA EUV channels are shown in Fig. 7. The obtained phase speeds are given in Table 1 against different time-lags observed in different EUV channels. For comparison, we have also listed the phase speeds achieved using the ridges of time-distance maps. We note that the obtained phase speeds using both the methods are in agreement within the errors.
The obtained phase speeds are not the true speed but projected speeds in the plane of sky, as mentioned earlier. In order to measure the true phase speed, we need an estimate of the inclination angle (the angle between the line of sight and the guided magnetic field along which the wave propagates). The true phase speed is then obtained from the measured projected phase speed divided by the sine of the inclination angle. Since we do not have direct measurement of the inclination angle of the guide field, we consider a range of possible angles varying between to and estimate the respective true phase speeds for different AIA channels. Our findings show that the true phase speeds remain close to the sound speed in corona111The speed of sound in the solar corona is given by km s-1 with measured in kelvin [K] (see Aschwanden, 2004). The sound speed for 1 MK coronal plasma is around 140 km s-1. As an example, we discuss the estimated true phase speeds of the PIDs in AIA 171 Å channel considering different inclination angles in the Appendix A. The phase speeds of the PIDs closer to the speed of sound suggest that they are slow mode magneto-acoustic waves.
3.3 Amplitude modulation observed in AIA 171 Å
The de-trended light curves in 171 Å (Fig. 6) reveal a peculiar oscillatory pattern. We find the clear presence of an amplitude modulation with an overall increase and decrease of the wave pattern over time. The modulation is discernible even in the time-distance map shown in Fig. 4 in terms of brightness.
In order to understand the modulation in more details, we have obtained the frequency components responsible for such patterns using Fouriér analysis and studied their evolution using wavelet analysis (Torrence & Compo, 1998).
3.3.1 Fouriér Analysis

Fig. 8 displays the normalised Fouriér power spectra derived from the original light curves for the locations L1 – L4 in Fig. 4 (marked by yellow dashed lines). The power in the panels is normalised with respect to the maximum power obtained at location L1. The power spectra of all the locations indicate three dominant peaks within 5 – 6 mHz (3.33 – 2.78 minutes). They are at around 5.26 mHz (3.17-min, marked as f2 in Fig. 8), 5.56 mHz (3.00-min, marked as f3), and 5.83 mHz (2.85-min, marked as f4). In addition, there are other smaller peaks identified at around 4.99 mHz (3.34-min, f1), 6.11 mHz (2.72-min, f5), 6.84 mHz (2.44-min, f6) and 7.42 mHz (2.24-min, f7). The vertical dashed black lines mark these peaks. We also observe a decrease in the power of the frequency peaks as we go away from the footpoint of the fan loop.
The observations of several nearby frequencies in the power spectra led us to postulate that the phenomenon of beat may play a role to generate the amplitude modulation. The beat is a phenomenon which occurs when two waves of slightly different frequencies, say, f1 and f2, interfere giving rise to a resulting wave undergoing amplitude modulations with frequency, fb = f1-f2. We call this frequency, ‘fb’, as beat frequency. In the current observations, assuming the interaction of the three dominant frequency components (f2, f3, and f4) observed in Fig. 8, we find that for frequency components 5.26 mHz (f2) and 5.83 mHz (f4), there is a beat frequency fb = 0.57 mHz, i.e., 29-min. We note that the 29-min is close to the modulation period that we obtain from a simple visual inspection of the detrended light curves in Fig. 6 (see also section 3.3.2).
The other combinations give us fb = 0.30 mHz ( 55-min) for 5.26 mHz (f2) and 5.56 mHz (f3) and fb = 0.27 mHz ( 61.70-min) for 5.56 mHz (f3) and 5.83 mHz (f4). Similarly, the interference of the dominant frequency around 5.56 mHz (3-min.) with those of frequencies at around 4.99 mHz (f1), 6.11 mHz (f5), 6.84 mHz (f6), and 7.42 mHz (f7), give rise to beat frequencies of around 0.57 mHz (29-min), 0.55 mHz (30-min), 1.28 mHz (13-min), and 1.86 mHz (8.96-min), respectively. However, we note that in the dynamic and complex solar atmosphere, it is difficult to explain the observed period of amplitude modulation in terms of a particular beat period as the propagation becomes affected by all the frequency components. Krishna Prasad et al. (2015) observed amplitude modulation in the Fouriér-filtered light curves with a mean period of 20 – 27 minutes, and reported the possibility of occurrence of the beat. We note that large-period oscillations with periods of around 8-min, 12-min, 24-min, 40-min, 63.4-min in coronal fan loops have also been reported before by Wang et al. (2009); Stenborg et al. (2011). However, no observational pieces of evidence were provided to answer their origin.
3.3.2 Wavelet Analysis









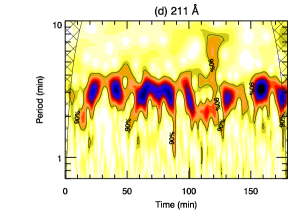
To study the temporal variation of the frequency, we perform wavelet analysis on the 30-min de-trended 171 Å light curves obtained at locations marked in Fig. 4. For this purpose, we use the Morlet wavelet as the basis function, which is a plane wave multiplied by a gaussian, and convolve it with the light curves (Torrence & Compo, 1998). In Fig. 9, we plot the wavelet results for the light curves obtained at locations, L1 (left panel) and L3 (right panel). Each wavelet plot consists of three panels. The de-trended light curve used for wavelet analysis is displayed on top panel (a). The wavelet power spectrum that shows the variation of power at different periods with time is plotted in the bottom left panel (b). The global wavelet power spectrum, obtained by taking the average over the time domain of the wavelet transform, is plotted in the bottom right panel (c). In each wavelet spectrum (lower left panel), we denote a cross-hatched region called the cone-of-influence (COI). The COI region appears because of the edge effects which arises due to the finite-length of time series. Any estimate of the oscillation period in this region becomes unreliable. The horizontal dashed lines in the global wavelet panels show the longest period that can be detected due to COI. We mention the first two power peaks (P1 and P2) obtained from the global wavelet at the right top corner of the wavelet plots.
In the wavelet spectrum panels, we find that most of the oscillating power lies in the range 2–4 minutes throughout the observed duration. We also observe an increase and decrease in the wavelet power, which is co-temporal with the appearance and disappearance of the modulations observed in the corresponding light curves. As expected, the global wavelet spectra show the presence of dominant power peak (P1) at around 3-min period for all the locations. We obtain second power peaks (P2) around 57.68-min. and 44.48-min. for locations L1 and L2, and at 28.84-min and 20.30-min for locations L3 and L4, respectively. We see that these second power peaks are below the 99% confidence level, therefore unreliable.
To quantify the modulation period, we follow a particular approach (Krishna Prasad et al., 2015; Sharma et al., 2017). We see that it is the 3-min wave amplitude that is modulated. The Fouriér Power Spectrums (Fig. 8) also illustrate significant power within 2 to 4 minutes, with dominant peaks around 3-min. Inspecting the power within 2 to 4 minutes, we measure the wavelet oscillatory power averaged within this period range. This oscillatory power will essentially mimic an amplitude variation that would be caused by all the waves having periods within the 2 and 4-minute range (Sharma et al., 2017; Krishna Prasad et al., 2015; Sych et al., 2012). Then, we apply wavelet to the obtained amplitude variation to estimate the dominant period of amplitude modulation. Fig. 10 shows wavelet power spectrums obtained in such way for AIA 171 Å for locations, as done for Fig. 9. We obtain the dominant/first power peaks (P1) around 34.30-min, 20.39-min, 22.24-min, and 26.45-min for locations L1, L2, L3, and L4, respectively. We find the longer-period power peaks above the 99% confidence level for all the marked locations of Fig. 4. We emphasise that we find similar results with the unfiltered, original light curves.
3.4 Amplitude modulation in other AIA EUV channels
For completeness, we study the light curves obtained from other AIA EUV channels at the locations shown by over-plotted yellow dashed lines of Fig. 5. We de-trended the light curves in a similar way as was done for those obtained from 171 Å and performed further analysis. In Fig. 11, we present the wavelet analysis results obtained using light curve at L1 for 193 Å (left panels) and 211 Å (right panels). The power is concentrated at a period (P1) around 3-min, and undergo an increase and decrease over time, as can be seen in the panels (b) of Fig. 11. To quantify the modulation period, we approached the similar method as done for AIA 171 Å (described in the last paragraph of 3.3.2). We obtain the dominant power peaks (P1) around 22.24-min, 20.39-min for 193 Å and 211 Å respectively The analysis of 131 Å showed similar behaviour and provided the dominant modulation period around 22.24-min However, we emphasize that the modulation is best seen in AIA 171 Å.
3.5 AIA 1600 Å and 304 Å observations at the footpoint of the fanloop
To investigate the origin of the modulation shown by the propagating slow MHD waves in AIA EUV channels, we study the footpoint of the fan loop in AIA 1600 Å and 304 Å. Fig. 12 shows an AIA 1600 Å image with the footpoint of the fan loop obtained from AIA 171 Å traced by slit 1. A yellow box bounds the footpoint location situated in the sunspot umbra. The size of the box is 44 in pixel scale. We obtain the light curves averaged over the region and de-trend it over 30 minutes and performed wavelet analysis. The wavelet results for 1600 Å (left panel) and 304 Å (right panel) are shown in Fig. 13. In the wavelet power map, we do not observe a clear pattern in 1600 Å, whereas in 304 Å, there is clear modulation around 3-min. We obtain the modulation period around 22.24-min in the similar way as obtained for 171 Å (described in last paragraph of 3.3.2).
3.6 Observation of high frequency component
Besides the modulation, we observe some high-frequency oscillations around 1.5-min ( 11 mHz) in the wavelet power maps (panel b). We show zoomed up versions of the wavelet power panels (b) in Fig. 14 for different AIA channels as labelled. Such powers are observed at the footpoint of the fan loop in the sunspot umbra (Fig. 12) at 304 Å, and at location L1 of the fan loops for the coronal channels 171 Å, 193 Å, and 211 Å. However, they are not present throughout the time-series. Besides, we note that we detect the high-frequency components in 90% confidence level. Therefore further observational work is required to establish the viability of this finding.



4 Summary and Conclusions
In this work, we have studied the nature of PIDs observed in an active region fan loop system rooted in a sunspot umbra using AIA/SDO observations. We find that the PIDs are best observed in 171 Å data. The PIDs were also seen in other channels of AIA except for 335 Å and 94 Å. We have measured the phase speeds of the PIDs in all the AIA channels and found that the phase speeds are subsonic. This is suggestive that these are slow mode magneto-acoustic waves. We further found that the phase speeds measured in different channels are not dependent on temperature. This is in contradiction with the results obtained by, e.g., Banerjee et al. (2009); Krishna Prasad et al. (2012); Kiddie et al. (2012); Gupta (2014). A possible reason for this may be the broad temperature response of the AIA channels. Fan loops are structures of typically 1 MK; therefore it may be that the emissions from the lower-temperature components are contributing to these different AIA EUV emissions (Ghosh et al., 2017), thereby giving similar phase speeds.
Our result shows that the PIDs have longer detection length ( Mm) in 171 Å and 193 Å, whereas a shorter detection length ( Mm) in 131 Å and 211 Å. The similar detection length in 171 and 193 Å could be due to the similar temperature range covered by both these channels. We note that AIA 131 Å has a peak formation temperature closer to that of 171 Å in quiet conditions. Therefore, the shorter detection length observed in 131 Å may be due to the weaker signal-to-noise ratio (SNR) (¡ 10) than that of 171 Å (¿ 65). The shorter detection length observed in 211 Å channel may also be related to its SNR, which we find to be less than 20.
The light curves obtained at multiple locations along the loops show an increase and decrease in the amplitude of oscillations over time. Such variation is better seen in the de-trended light curves (see Fig. 6). Fouriér analysis on the original light curves reveals that there are several nearby frequencies within 5–8 mHz. The findings obtained here suggest that beat may be a possibility behind the observed amplitude modulation that are very likely created due to the interference of the nearby frequency components. We observe similar frequency peaks in all the AIA EUV coronal (except AIA 335 Å and 94 Å) as well as chromospheric channels. Lites (1986) has reported the various frequencies peaks identified in our study in chromospheric umbra, and Fludra (2001) reported them in transition region sunspot plumes. Centeno et al. (2006, 2009); Krishna Prasad et al. (2015) observed the presence of amplitude modulations in Fouríer filtered light curves and measured a modulation period of 20-27 minutes (Krishna Prasad et al., 2015). However, in our study, the amplitude modulations were prominent enough to detect them prior to any filtration (Fig. 6), which to our knowledge is the first such observational finding. Wavelet analysis also reveals an increase and decrease of the oscillation power around 3-min simultaneous to the observed amplitude modulation. We obtain the modulation period to be in the range 20-30 minutes.
Observation of similar amplitude variation at the lower solar atmosphere (right panels of Fig. 13) as observed by AIA 304 Å (log [T/K] = 4.7, Lemen et al. (2012)) supports one more possibility that may be the amplitude variability is caused by the underlying driver. Photospheric p-modes are, in general, assumed to be the cause of propagating slow magnetoacoustic waves observed in the corona (De Pontieu et al., 2005; Krishna Prasad et al., 2015; Zhao et al., 2016). Hence, the amplitude variability of the p-mode may affect and give rise to the particular amplitude variation of the propagating intensity waves observed along the fan loop. Observational studies have shown the effect oscillatory phenomenon in the lower solar atmosphere on the propagation of slow-magnetoacoustic waves along coronal fanloops (Jess et al., 2012; Sharma et al., 2017). However, further study is required both observationally and theoretically to understand the origin of such amplitude modulation in time series.
In addition to the amplitude modulation, we see presence of low period (high frequency) oscillations around 1.5-min (11 mHz) (see Fig. 14) in this study. We observe these high-frequency oscillations both at the chromospheric and coronal heights. Wang et al. (2018) first observed high-frequency oscillations by imaging observations at different heights above sunspot umbra in the range 10 – 14 mHz (around 1-min.). They related such high-frequency modes at coronal heights to perturbations at photospheric umbra. Krishna Prasad et al. (2017) reported frequencies around 13 mHz using IRIS 2796 Å in chromospheric sunspot umbra. We note that the observed high-frequency around 11 mHz is close to the double of the dominant (fundamental) frequency at around 5.56 mHz, and hence is similar to the second harmonics. However, one needs to be cautious to associate the high-frequency modes observed in our study to second harmonics, as harmonics are so far, observed in standing waves in coronal closed loops (Srivastava & Dwivedi, 2010). Verwichte et al. (2004) reported the detection of higher harmonics in coronal kink wave oscillations with a deviation in the frequency ratio of second to first harmonics from its canonical value of 2 in a homogeneous medium. Andries et al. (2005); Erdélyi & Verth (2007); Luna-Cardozo et al. (2012) proposed that such deviation may occur because of longitudinal density and or magnetic stratification along stratified expanding flux tubes like those in the corona, and therefore can be used as a seismological tool to measure the density scale height.
Acknowledgements.
The authors are thankful to the referee for relevant suggestions on improving the manuscript. A.S. and D.T. acknowledge the Max-Planck Partner Group of the Max-Planck Institute for Solar System Research, Göttingen at IUCAA. R.E. is grateful to Science and Technology Facilities Council (STFC grant nr ST/M000826/1) UK and to Chinese Academy of Sciences President’s International Fellowship Initiative, Grant No. 2019VMA0052 for the support received. G.A. Ahmed acknowledges the visiting associateship of IUCAA. AIA and HMI data used here, are courtesy of SDO (NASA).References
- Andries et al. (2005) Andries, J., Arregui, I., & Goossens, M. 2005, The Astrophysical Journal, 624, L57
- Aschwanden (2004) Aschwanden, M. J. 2004, Physics of the Solar Corona. An Introduction (Praxis Publishing Ltd)
- Banerjee et al. (2009) Banerjee, D., Teriaca, L., Gupta, G. R., et al. 2009, A&A, 499, L29
- Berghmans & Clette (1999) Berghmans, D. & Clette, F. 1999, Sol. Phys., 186, 207
- Boerner et al. (2012) Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41
- Bogdan (2000) Bogdan, T. J. 2000, Sol. Phys., 192, 373
- Bogdan & Judge (2006) Bogdan, T. J. & Judge, P. G. 2006, Philosophical Transactions of the Royal Society of London Series A, 364, 313
- Brooks et al. (2011) Brooks, D. H., Warren, H. P., & Young, P. R. 2011, ApJ, 730, 85
- Centeno et al. (2006) Centeno, R., Collados, M., & Trujillo Bueno, J. 2006, ApJ, 640, 1153
- Centeno et al. (2009) Centeno, R., Collados, M., & Trujillo Bueno, J. 2009, ApJ, 692, 1211
- Chandra et al. (2015) Chandra, R., Gupta, G. R., Mulay, S., & Tripathi, D. 2015, MNRAS, 446, 3741
- Cranmer (2009) Cranmer, S. R. 2009, Living Reviews in Solar Physics, 6, 3
- Culhane et al. (2007) Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19
- De Moortel (2009) De Moortel, I. 2009, Space Sci. Rev., 149, 65
- De Moortel et al. (2002a) De Moortel, I., Hood, A. W., Ireland, J., & Walsh, R. W. 2002a, Sol. Phys., 209, 89
- De Moortel et al. (2002b) De Moortel, I., Ireland, J., Hood, A. W., & Walsh, R. W. 2002b, A&A, 387, L13
- De Moortel et al. (2000) De Moortel, I., Ireland, J., & Walsh, R. W. 2000, A&A, 355, L23
- De Moortel et al. (2002c) De Moortel, I., Ireland, J., Walsh, R. W., & Hood, A. W. 2002c, Sol. Phys., 209, 61
- De Pontieu et al. (2005) De Pontieu, B., Erdélyi, R., & De Moortel, I. 2005, ApJ, 624, L61
- De Pontieu et al. (2004) De Pontieu, B., Erdélyi, R., & James, S. P. 2004, Nature, 430, 536
- Del Zanna et al. (2011) Del Zanna, G., O’Dwyer, B., & Mason, H. E. 2011, A&A, 535, A46
- Delaboudinière et al. (1995) Delaboudinière, J., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291
- Erdélyi (2004) Erdélyi, R. 2004, Astronomy and Geophysics, 45, 4.34
- Erdélyi & Verth (2007) Erdélyi, R. & Verth, G. 2007, A&A, 462, 743
- Fludra (2001) Fludra, A. 2001, A&A, 368, 639
- Freeland & Handy (1998) Freeland, S. L. & Handy, B. N. 1998, Sol. Phys., 182, 497
- Ghosh et al. (2017) Ghosh, A., Tripathi, D., Gupta, G. R., et al. 2017, ApJ, 835, 244
- Gupta (2014) Gupta, G. R. 2014, A&A, 568, A96
- Gupta et al. (2010) Gupta, G. R., Banerjee, D., Teriaca, L., Imada, S., & Solanki, S. 2010, ApJ, 718, 11
- Gupta et al. (2012) Gupta, G. R., Teriaca, L., Marsch, E., Solanki, S. K., & Banerjee, D. 2012, A&A, 546, A93
- Handy et al. (1999) Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999, Sol. Phys., 187, 229
- Jess et al. (2012) Jess, D. B., De Moortel, I., Mathioudakis, M., et al. 2012, ApJ, 757, 160
- Khomenko & Collados (2015) Khomenko, E. & Collados, M. 2015, Living Reviews in Solar Physics, 12
- Kiddie et al. (2012) Kiddie, G., De Moortel, I., Del Zanna, G., McIntosh, S. W., & Whittaker, I. 2012, Sol. Phys., 279, 427
- Kohl et al. (1995) Kohl, J. L., Esser, R., Gardner, L. D., et al. 1995, Sol. Phys., 162, 313
- Kosugi et al. (2007) Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3
- Krishna Prasad et al. (2012) Krishna Prasad, S., Banerjee, D., & Singh, J. 2012, Solar Physics, 281, 67
- Krishna Prasad et al. (2015) Krishna Prasad, S., Jess, D. B., & Khomenko, E. 2015, ApJ, 812, L15
- Krishna Prasad et al. (2017) Krishna Prasad, S., Jess, D. B., Van Doorsselaere, T., et al. 2017, ApJ, 847, 5
- Lemen et al. (2012) Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17
- Lites (1986) Lites, B. W. 1986, ApJ, 301, 992
- Liu et al. (2019) Liu, J., Nelson, C., Snow, B., Wang, Y., & Erdélyi, R. 2019, Nature Communications, 10
- Luna-Cardozo et al. (2012) Luna-Cardozo, M., Verth, G., & Erdélyi, R. 2012, ApJ, 748, 110
- Marsh et al. (2009) Marsh, M. S., Walsh, R. W., & Plunkett, S. 2009, ApJ, 697, 1674
- Nakariakov et al. (2000) Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000, A&A, 362, 1151
- O’Dwyer et al. (2010) O’Dwyer, B., Del Zanna, G., Mason, H. E., Weber, M. A., & Tripathi, D. 2010, A&A, 521, A21
- Ofman (2005) Ofman, L. 2005, Space Science Reviews, 120, 67
- Ofman et al. (1997) Ofman, L., Romoli, M., Poletto, G., Noci, G., & Kohl, J. L. 1997, ApJ, 491, L111+
- Pesnell et al. (2012) Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3
- Rajaguru et al. (2019) Rajaguru, S. P., Sangeetha, C. R., & Tripathi, D. 2019, ApJ, 871, 155
- Reale (2010) Reale, F. 2010, Living Reviews in Solar Physics, 7, 5
- Roberts (2006) Roberts, B. 2006, Philosophical Transactions of the Royal Society of London Series A, 364, 447
- Schou et al. (2012a) Schou, J., Borrero, J. M., Norton, A. A., et al. 2012a, Sol. Phys., 275, 327
- Schou et al. (2012b) Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012b, Sol. Phys., 275, 229
- Sharma et al. (2017) Sharma, A., Gupta, G. R., Tripathi, D., Kashyap, V., & Pathak, A. 2017, ApJ, 850, 206
- Srivastava & Dwivedi (2010) Srivastava, A. K. & Dwivedi, B. N. 2010, New A, 15, 8
- Stenborg et al. (2011) Stenborg, G., Marsch, E., Vourlidas, A., Howard, R., & Baldwin, K. 2011, A&A, 526, A58
- Sych et al. (2012) Sych, R., Zaqarashvili, T. V., Nakariakov, V. M., et al. 2012, A&A, 539, A23
- Taroyan & Erdélyi (2009) Taroyan, Y. & Erdélyi, R. 2009, Space Science Reviews, 149, 229
- Torrence & Compo (1998) Torrence, C. & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61
- Verwichte et al. (2004) Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77
- Wang et al. (2018) Wang, F., Deng, H., Li, B., et al. 2018, The Astrophysical Journal, 856, L16
- Wang et al. (2009) Wang, T. J., Ofman, L., Davila, J. M., & Mariska, J. T. 2009, A&A, 503, L25
- Zhao et al. (2016) Zhao, J., Felipe, T., Chen, R., & Khomenko, E. 2016, ApJ, 830, L17
Appendix A : True phase speeds of PIDs in AIA 171 Å
| Projected Phase speed | Inclination angle | Probable true |
| in AIA 171 Å | Phase speeds | |
| v [km s-1] | [] | [km s-1] |
| 10 | 304.6 | |
| 20 | 154.66 | |
| 52.9 | 30 | 105.8 |
| 40 | 82.29 | |
| 50 | 69.05 | |
| 60 | 61.08 | |
| 70 | 56.29 | |
| 80 | 53.71 | |
| 90 | 52.9 |
Appendix B : PIDs along slits 2 and 3
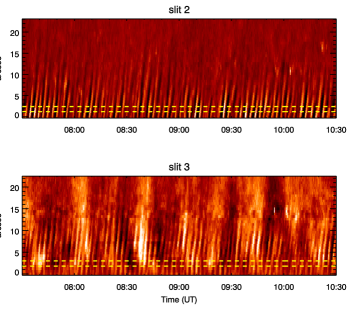


We analyze the evolution of intensity disturbances propagating along slits 2 and 3 (shown in Figure 3-a). We find the 3-min propagating intensity oscillations along slits 2 and 3 undergoing amplitude modulations. However, modulations were not strong enough as observed for slit 1. Figures 16 and 17 present the increase and decrease of wavelet power of the 3-min oscillations representing the modulations.