Watch Your Head: Assembling Projection Heads to Save the Reliability of Federated Models
Abstract
Federated learning encounters substantial challenges with heterogeneous data, leading to performance degradation and convergence issues. While considerable progress has been achieved in mitigating such an impact, the reliability aspect of federated models has been largely disregarded. In this study, we conduct extensive experiments to investigate the reliability of both generic and personalized federated models. Our exploration uncovers a significant finding: federated models exhibit unreliability when faced with heterogeneous data, demonstrating poor calibration on in-distribution test data and low uncertainty levels on out-of-distribution data. This unreliability is primarily attributed to the presence of biased projection heads, which introduce miscalibration into the federated models. Inspired by this observation, we propose the ”Assembled Projection Heads” (APH) method for enhancing the reliability of federated models. By treating the existing projection head parameters as priors, APH randomly samples multiple initialized parameters of projection heads from the prior and further performs targeted fine-tuning on locally available data under varying learning rates. Such a head ensemble introduces parameter diversity into the deterministic model, eliminating the bias and producing reliable predictions via head averaging. We evaluate the effectiveness of the proposed APH method across three prominent federated benchmarks. Experimental results validate the efficacy of APH in model calibration and uncertainty estimation. Notably, APH can be seamlessly integrated into various federated approaches but only requires less than 30% additional computation cost for 100 inferences within large models.
Introduction
Federated learning is a training paradigm that holds promise for privacy preservation (McMahan et al. 2017; Wei et al. 2020). This approach does not require the central server to collect clients’ data. Instead, clients train their local models and upload the parameters to the server for aggregation. In addition to privacy concerns, the reliability of neural networks has also garnered considerable attention, given their deployment in numerous critical scenarios (Levinson et al. 2011; Miotto et al. 2016). Recent research has shown that modern neural networks tend to exhibit overconfidence (Guo et al. 2017). This issue is far from trivial, especially in classification networks, where overconfidence can lead to higher predicted confidence in the sample than the actual probability of its assigned class. Even for the out-of-distribution sample, the model will assign it to a specific class with high confidence (i.e. low uncertainty) attached. Such discrepancies have grave implications for decision-making and significantly harms the model’s reliability, rendering softmax outputs unsuitable as uncertainty indicators.

Privacy protection and reliability guarantees have a large cross field in practical application scenarios. Taking smart healthcare for example, it’s always impractical to collect the private data of patients to a central server for the training of a diagnostic classification model, and thus leads to the broad application of federated learning. However, privacy is not all we are after. In such important application scenarios, it is natural to chase for the reliability of the model, expecting it to output low confidence in misclassified diagnoses and refuses to make decisions with unknown diagnoses. So here comes the natural question: Whether the federated model is reliable? Is it well-calibrated and sensitive to the out-of-distribution data?
Unfortunately, the answer to this question still remains unclear. Despite the numerous challenges associated with federated learning (Kairouz et al. 2021; Li et al. 2020a), the issue of reliability has received less attention, although the problem could be even worse (refer to Section 3). In federated learning, the complex data distribution among different clients often makes the basic I.I.D assumption invalid, resulting in poor convergence and performance degradation of the global model. To address these issues, a great number of methods have been proposed to alleviate the impact of the Non-IID data (Karimireddy et al. 2020; Li, He, and Song 2021; Li et al. 2020b). However, none of these methods attempts to assess how the federated framework affects the model’s reliability, much less improve it.
What’s worse, most existing calibration and uncertainty estimation methods, which can improve the reliability of models, can not be applied to the federated models directly. MCDropout (Gal and Ghahramani 2016) requires the presence of dropout layers in the network, which are rarely used in current network designs because of the discrepancy between dropout and BatchNorm layers (Li et al. 2019). Deep Ensembles (Riquelme, Tucker, and Snoek 2018) is also an empirical but effective method of uncertainty estimation. However, it requires training the networks with different random initializations multiple times, which is costly and impractical in federated learning. It is also impractical to convert the model structure into the Bayesian model for the application of the Bayesian-based uncertainty estimation methods. Except for these classic methods, the latest SOTA uncertainty estimation methods always require additional data operation (Thiagarajan et al. 2022), updating of global class centroids (Van Amersfoort et al. 2020), well-trained checkpoints (Maddox et al. 2019), etc, making these effective methods not applicable to federated frameworks.
In this paper, by conducting extensive experiments on the popular benchmark dataset, we provide a systematic investigation of the reliability of the federated model. We uncover the fact that the federated model is unreliable compared to the model of centralized training. Generic federated models tend to be more miscalibrated while personalized federated models exhibit lower uncertainty (i.e. less insensitive) to the OOD data. Experimental results illustrate that data heterogeneity cooperated with partial participation significantly harms the model’s reliability while the impact of other factors is trivial. We further demonstrate that the biased projection head is one of the main causes of the reliability degradation. Motivated by this observation, we proposed a lightweight but effective uncertainty estimation method named APH for federated learning to improve the federated model’s reliability. By randomly permuting the obtained federated parameter of the projection head as initialization, APH fine-tunes multiple projection heads with various learning rates to explore its parameter space and introduce parameter diversity, producing reliable predictions through head assembling and averaging.
The contributions of this paper are delivered as follows:
1) We provide a systematic analysis of the reliability of the federated model. We uncover the fact that the federated model is unreliable compared with the centralized training model and further investigate its impact factors.
2) We propose a lightweight but effective federated uncertainty estimation method named APH. APH can be seamlessly integrated into most SOTA methods to improve the performance and reliability of federated models.
3) We validate the effectiveness of APH on prominent federated benchmarks with models of various sizes, showing its effectiveness and efficiency in improving reliability.


Background and Related Work
Problem Setup
We consider a practical horizontal federated scenario (Yang et al. 2019) with the Non-IID data distribution among clients. In this paper, we mainly focus on the skewness in label distribution and the quantity skewness (Li et al. 2022; Zhu et al. 2021). The skewness of the feature distribution is out of the scope of our paper as it is usually what vertical federated learning is concerned with.
Assume that there are independent clients. Each client has their own local training data . The aim of federated learning is to utilize this distributed dataset to train a generic model or a set of personalized models in communication rounds for the -classification problem. We denote as the participation ratio. In each communication round , we first select clients and get the participated client set . For each client , we distribute the current global model parameter to client , and update its local model parameter . Typically, in FedAvg, we set . Then each client utilize its local data to update its local model parameter for epochs. All the updated model parameter of client in will be uploaded to the server and used to get the global model .




Non-IID Data

IID Data
Evaluation Metrics of Model Uncertainty
Expected Calibration Error(ECE) measures the discrepancy between prediction probability and empirical accuracy, providing an important tool to assess model calibration (Naeini, Cooper, and Hauskrecht 2015).
Negative Log-Likelihood(NLL) is a proper scoring rule for measuring the accuracy of predicted probabilities and evaluating the quality of uncertainty (Ovadia et al. 2019).
Entropy of the predictive distribution is a common metric to evaluate the model’s reliability when facing OOD data (Ovadia et al. 2019). The histogram of the predictive entropy is always used to compare the uncertainty quality.
Related Work
Uncertainty Estimation. Uncertainty estimation is the most common way to improve a model’s reliability in practical scenarios. It aims to produce the accurate uncertainty or confidence of the given sample, reflecting the possibility of fault judgment and indicating whether the sample is out of the knowledge scope of the model. The most common approach for uncertainty estimation is using softmax output in the last layer. However, it is always overconfident in modern neural networks(Guo et al. 2017). Existed uncertainty estimation methods can be roughly divided into Bayesian and Non-Bayesian methods. Bayesian methods (Louizos and Welling 2016; Riquelme, Tucker, and Snoek 2018) always involve the computation of the posterior distribution of parameters, which is computationally intractable due to numerous non-linear operations in the network forward passes. A variety of approximation methods has been developed, including variational inference (Graves 2011), Monte Carlo Markov Chain (Welling and Teh 2011), MCDropout (Gal and Ghahramani 2016), etc. Though the Bayesian model could estimate model uncertainty through parameter posterior distribution, most of these methods can not be applied to modern networks due to their complexity. Different from Bayesian methods, ensemble-based methods do not put a distribution over model parameters (Lakshminarayanan, Pritzel, and Blundell 2017). Instead, they train several independent models with different random initializations on the same dataset. -UQ (Thiagarajan et al. 2022) utilizes the NTK (Jacot, Gabriel, and Hongler 2018) to approximate the training procedure of the ensembles to estimate uncertainty. During inference, the ensemble will average the outputs to form the prediction, which introduces additional computation costs. Different from the ensemble-based methods, EDL (Sensoy, Kaplan, and Kandemir 2018) and DUQ (Van Amersfoort et al. 2020) can estimate uncertainty in a single forward pass.
Federated Learning. Current SOTA federated learning methods can be divided into generic federated learning (G-FL) methods and personalized federated learning (P-FL) methods. The typical algorithm of the former G-FL methods is the FedAvg (McMahan et al. 2017), which aims to train a single generic model for all clients. However, heterogeneity greatly hinders the performance and the generalization ability of the federated global model. To tackle this issue, numerous methods have been proposed from the perspectives of local drift mitigation (Gao et al. 2022; Li et al. 2020c), gradient revision (Hsu, Qi, and Brown 2019; Acar et al. 2021), knowledge preservation (Lin et al. 2020; Lee et al. 2022), etc. Though improvement has been achieved, there is still a significant performance gap between the federated model and the centralized training model. Different from the single generic model, P-FL methods expect to train each client in a personalized model to fit their unique data distribution. It preserves the distribute-and-aggregate schema of the classic federated learning and regularizes the personalized model with generic information. The idea of the P-FL is first proposed in Smith et al. (2017), and further formally extended by Arivazhagan et al. (2019). Inspired by these pioneer work, a great number of P-FL methods with different strategies have been proposed, such as fine-tuning the global model (Fallah, Mokhtari, and Ozdaglar 2020), splitting and fine-tuning the client-specific head (Collins et al. 2021), learning additional personalized models (T Dinh, Tran, and Nguyen 2020; Li et al. 2021), aggregating with personalized strategies (Huang et al. 2021; Zhang et al. 2020, 2023).

Reliability of the Federated Models
To explore how the federated optimization influences the reliability of the obtained model, we conduct a systematic experiment on different SOTA federated methods. We use the Dirichlet distribution to assign the proportion of class from Cifar10 to each client. The total client number is 20, and the default local epoch is set to 10. To get a more comprehensive view of the reliability, we use different SOTA federated frameworks to train federated models, including FedAvg (McMahan et al. 2017), FedProx (Li et al. 2020c), FedDyn (Acar et al. 2021), MOON (Li, He, and Song 2021), FedNTD (Lee et al. 2022) for G-FL, and FedFOMO (Zhang et al. 2020), FedALA (Zhang et al. 2023), FedPAC (Xu, Tong, and Huang 2022) for P-FL.
Generic Federated Models are Not Reliable
To investigate the influence of federated optimization on the model’s reliability, we first consider exploring the calibration on in-domain test data by measuring the F-ECE of the obtained federated model. The larger the F-ECE, the more miscalibrated and thus less reliable the model is. To unify the comparison between G-FL and P-FL methods, we propose to measure the federated expected calibration error for both generic and personalized federated models.
Definition 1.
Consider a federated learning framework with clients for a -class classification problem. Each client has its own test and model parameter . Given the partitions , the federated expected calibration error (F-ECE) is defined as:
| (1) |
| (2) |
| (3) |
, where , and are the assigned class and confidence of predicted by model .



We train the generic federated models with different SOTA methods on heterogeneous Cifar10 and explore their F-ECE on in-domain test data and predictive distribution entropy on OOD test data. The experimental results are displayed in Fig. 2. Experimental results demonstrate that all models obtained from G-FL methods demonstrate a higher F-ECE on in-domain test data and lower predictive entropy on OOD test data than the traditional centralized training model, which indicates significant overconfidence and severe unreliability problems of generic federated models. Figure 3(a) further demonstrates that such loss of reliability is not caused by the degradation of the accuracy.
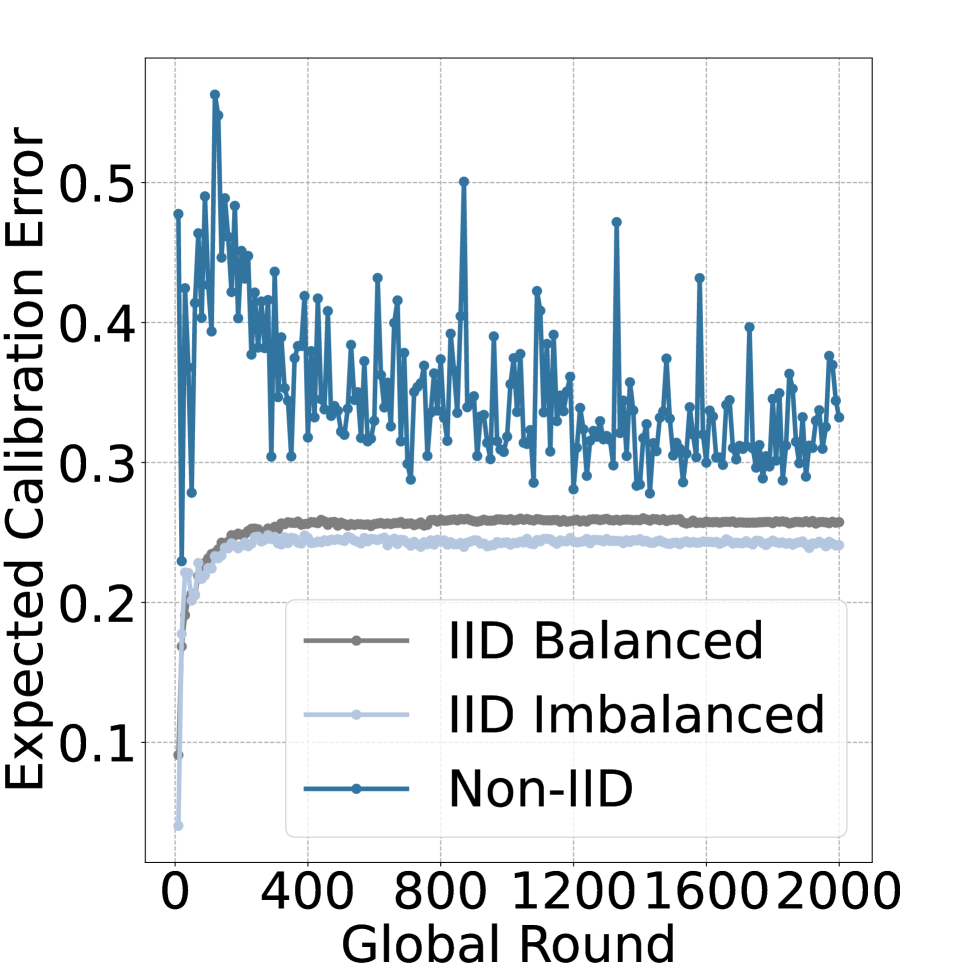
We further explore the related impact factors on the reliability of generic federated models. Without loss of generality, we choose FedAvg as the federated framework in the following experiments. We investigate the F-ECE under different federated settings, e.g. local epoch number, partial participation ratio, data quantity imbalance, and severity of Non-IID distribution. The experimental results are shown in Fig. 3. As demonstrated in Fig. 3(b), 3(c) and 3(e), data quantity, local epochs, as well as partial participation under IID data have a trivial impact on the reliability of the generic federated model. However, the Non-IID severity significantly harms the federated model’s reliability, and the low participation ratio magnifies such impact (See Fig. 3(d) and 3(e)).
Personalized Federated Models are Not Solutions
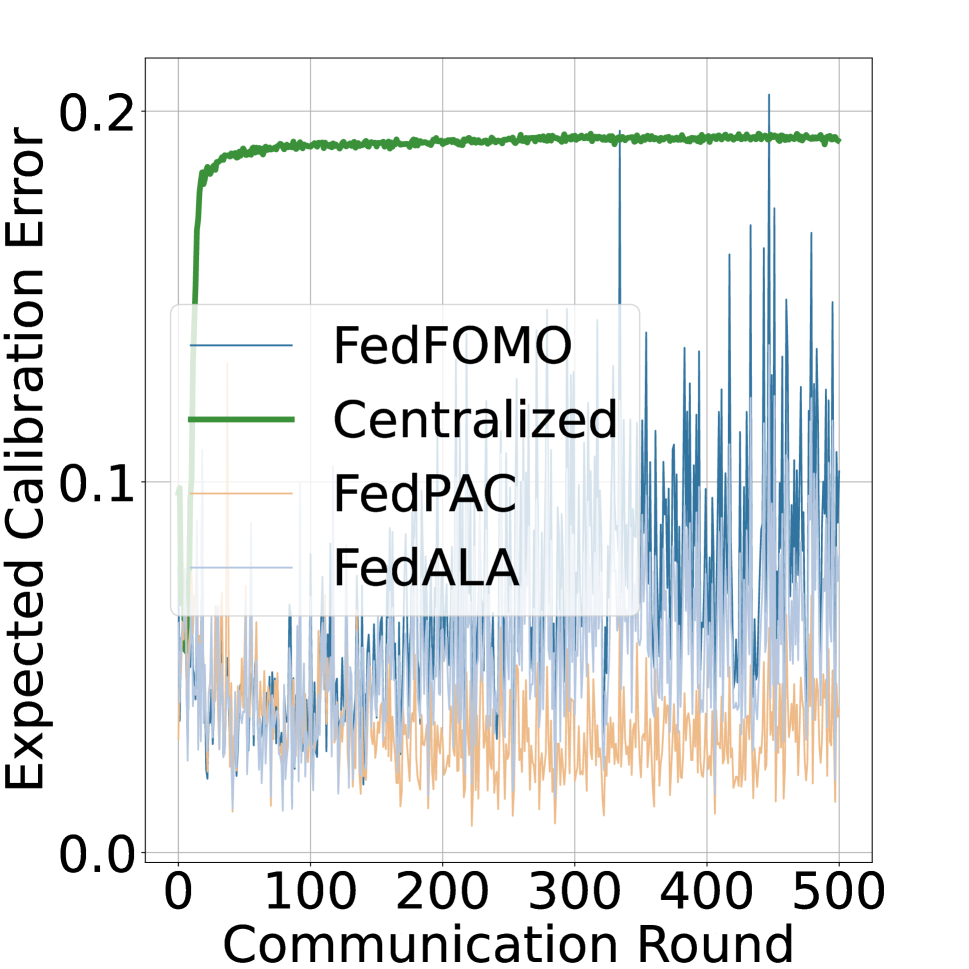
We further turn our gaze to the personalized federated models. Similarly, we train the personalized federated model utilizing SOTA personalized federated methods on Cifar10 with practical settings. The F-ECE on in-domain test data and the predictive entropy are evaluated to measure the reliability of the obtained personalized federated models. We report the experimental results of FedPAC (Xu, Tong, and Huang 2022), FedALA (Zhang et al. 2023), and FedFOMO (Zhang et al. 2020) compared with the centralized training schema in Fig. 4. Results demonstrate that the personalized federated model is more calibrated than the centralized training model, while still exhibiting lower uncertainty to OOD test samples, indicating that personalized federated models are not the solution for reliable federated learning.
Projection Head Bias is the Primary Cause
Although the conclusion is depressing, we further conduct an interesting experiment motivated by CCVR (Luo et al. 2021) and FedRoD (Chen and Chao 2021), in which they point out that the classifier of the federated model is biased and local updated models of FedAvg are naturally well-personalized federated models respectively. Our experiment revolves around the single question: Whether the projection heads of federated models are the main cause of the degradation of reliability? To answer this question, we fine-tune the projection head of local models by utilizing their local dataset while keeping the feature extractors frozen. After the fine-tuning of the projection head, we further evaluate its F-ECE on in-domain test data and predictive entropy on OOD data. Results are displayed in Fig. 5.
Specifically, we adopt two strategies that fine-tune the last fully connected layer and the whole projection head respectively. As demonstrated in Fig. 5, the generic federated model achieves lower F-ECE than the centralized training model with the same accuracy after only one round of full-head fine-tuning. It further gets a significant F-ECE decrease after only 5 fine-tuning rounds. Oppositely, the result of the last layer fine-tuning is not satisfying but still gets a decrease on F-ECE. Moreover, we observe that the histograms of predictive entropy on the OOD samples of the head fine-tuned models are almost the same as the generic model’s, indicating nearly no improvement in the uncertainty estimation obtained from the fine-tuning of the projection head.
Such an observation validates our conjecture: the biased projection head is one of the main causes of the degradation of model reliability. Intuitively, the data heterogeneity and partial participation strategies always lead to inconsistency of the averaged gradients, causing severe overfitting of projection heads. The success of model calibration and the failure of model uncertainty of the head fine-tuning strategy demonstrate that it is not enough to deal with projection heads alone, parameter diversity must be obtained to actually improve the reliability of the federated model.
| Cifar10 | Cifar100 | Tiny-ImageNet | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Accuracy | F-ECE | NLL | Accuracy | F-ECE | NLL | Accuracy | F-ECE | NLL | |
| FedAvg | 0.615 | 0.168 | 1.454 | 0.284 | 0.458 | 5.586 | 0.098 | 0.395 | 6.200 |
| FedDropout | 0.619 | 0.138 | 1.333 | 0.282 | 0.458 | 6.091 | 0.115 | 0.290 | 5.115 |
| Client Ensembles | 0.601 | 0.130 | 1.252 | 0.286 | 0.395 | 5.194 | 0.127 | 0.081 | 4.717 |
| FedAvg + FineTune | 0.784 | 0.073 | 0.823 | 0.323 | 0.426 | 5.094 | 0.239 | 0.275 | 4.459 |
| FedAvg + APH | 0.902 | 0.036 | 0.311 | 0.484 | 0.091 | 2.747 | 0.294 | 0.089 | 3.671 |
| Method | FedProx | FedDyn | FedNTD | FedALA | FedFOMO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| With/Without APH | Without | With | Without | With | Without | With | Without | With | Without | With | |
| Cifar10 | Acc | 0.556 | 0.897 | 0.559 | 0.861 | 0.553 | 0.900 | 0.894 | 0.899 | 0.877 | 0.881 |
| F-ECE | 0.226 | 0.066 | 0.102 | 0.034 | 0.263 | 0.033 | 0.065 | 0.047 | 0.090 | 0.064 | |
| NLL | 1.662 | 0.344 | 9.333 | 0.464 | 2.028 | 0.326 | 0.460 | 0.325 | 0.916 | 0.397 | |
| Cifar100 | Acc | 0.197 | 0.275 | 0.225 | 0.486 | 0.298 | 0.485 | 0.416 | 0.427 | 0.315 | 0.303 |
| F-ECE | 0.41 | 0.078 | 0.616 | 0.102 | 0.449 | 0.128 | 0.396 | 0.090 | 0.337 | 0.114 | |
| NLL | 5.215 | 3.679 | 10.602 | 3.800 | 5.444 | 2.823 | 4.833 | 3.135 | 3.452 | 2.918 | |
| Tiny-ImageNet | Acc | 0.083 | 0.166 | 0.089 | 0.121 | 0.114 | 0.338 | 0.293 | 0.298 | 0.215 | 0.210 |
| F-ECE | 0.238 | 0.108 | 0.602 | 0.073 | 0.351 | 0.149 | 0.326 | 0.105 | 0.201 | 0.112 | |
| NLL | 5.439 | 4.517 | 10.496 | 13.769 | 5.678 | 3.149 | 4.098 | 3.797 | 4.034 | 3.742 | |
Assembling Projection Heads to Make Federated Model Reliable Again
As discussed before, fine-tuning the projection head is not sufficient to encounter the overconfidence problem of deep neural networks, leading to a higher accuracy but still bad reliability performance. While single fine-tuning is struggling, we borrow the idea from the deep ensemble (Lakshminarayanan, Pritzel, and Blundell 2017) to introduce the parameter diversity into the model inference by fine-tuning multiple projection heads with different initialization.
We now propose Assembled Projection Heads (APH). Specifically, for model of the client which is obtained by either generic or personalized federated methods after rounds, APH splits the model into two parts, i.e. feature extractor and projection head . Freezing the feature extractor, APH treats the parameter of the projection head as the prior, and further samples from the Gaussian distribution to permute the prior to get multiple initialized parameters. The initialized parameter of the projection head of client is given as:
, where , is the hyper-parameter which controls the magnitude of , is an identity matrix whose trace equals the parameter number in . After getting the initialized heads, APH fine-tunes these projection heads on the local dataset for epochs respectively with various learning rates to get the fine-tuned projection heads . The learning rate is sampled from an uniform distribution . The final prediction of in client is given as
The proposed APH method can be easily applied to most generic and personalized federated frameworks to improve the model’s reliability. Different from ensemble-based methods which require inference time for runs, APH only involves additional computation in multiple projection heads, which is a quite small fraction in the total computation cost of inference. For large models such as ResNet-50, the computational overhead of the projection head is only around 0.3% of the whole inference process. Thus even for the APH method which possesses 100 projection heads, the additional computation cost is still less than 30%.



Experiments
The Setup
In this section, we will briefly introduce the details and related settings of our experiments. Due to the limited spaces, more experimental settings and results (Ablation study, Robustness on hyper-parameters) can be found in Appendix.
Dataset. We conduct experiments on popular federated dataset Cifar10, Cifar100 (Krizhevsky, Hinton et al. 2009). To further validate the effectiveness of the proposed APH on large datasets, we also conduct experiments on the Tiny-ImageNet dataset (Le and Yang 2015). We partition each of the datasets into 10 clients with the default heterogeneous setting. The participation strategy is the same as the experiment in Section 3. For OOD dataset, we use SVHN (Netzer et al. 2011) for Cifar10/100, and ImageNet-O (Hendrycks et al. 2021) for Tiny-ImageNet.
Methods. We evaluate the effectiveness of our method compared with the simple baseline MC-Dropout, deep ensembles of personalized client models. Other calibration and uncertainty estimation methods are not applicable due to the federated training schema (See Appendix for details). To validate the effectiveness and the compatibility of proposed APH with other SOTA federated methods, we also apply APH to SOTA generic federated methods FedProx, FedDyn, FedNTD and personalized methods FedFOMO, FedALA.
Models. We train a CNN on the Cifar10 dataset, and further validate the effectiveness on large models by training ResNet-50 on the Cifar100 and Tiny-ImageNet datasets.
Hyperparameters. For federated methods, we set the global communication round to 100 for Cifar10/100, and 20 for Tiny-ImageNet. The local epoch number is set to 10. For the dropout ratio in FedDrop, we select the best result from . For the used in APH, we select the from , where is the magnitude of the order of the mean value of the parameter. For the lower bound of learning rate, we set the to 0.001. For the upper bound , we choose the best result from .
| Parameter | Accuracy | F-ECE | |||
|---|---|---|---|---|---|
| Without | With | Without | With | ||
| 0.05 | 0.578 | 0.947 | 0.123 | 0.015 | |
| 0.1 | 0.598 | 0.900 | 0.162 | 0.041 | |
| 0.5 | 0.667 | 0.763 | 0.241 | 0.106 | |
| 0.2 | 0.420 | 0.885 | 0.280 | 0.041 | |
| 0.6 | 0.597 | 0.901 | 0.173 | 0.038 | |
| 1 | 0.598 | 0.900 | 0.162 | 0.041 | |
| 10 | 0.598 | 0.900 | 0.162 | 0.041 | |
| 20 | 0.606 | 0.899 | 0.175 | 0.041 | |
| 40 | 0.592 | 0.896 | 0.205 | 0.042 | |
| 10 | 0.598 | 0.900 | 0.162 | 0.041 | |
| 50 | 0.569 | 0.889 | 0.183 | 0.056 | |
| 100 | 0.588 | 0.909 | 0.123 | 0.054 | |
| Without | 10 | 50 | 100 | |
|---|---|---|---|---|
| Accuracy | 0.284 | 0.484 | 0.501 | 0.503 |
| F-ECE | 0.458 | 0.091 | 0.077 | 0.071 |
| NLL | 5.586 | 2.747 | 2.188 | 2.056 |
| Additional Cost | 0.00% | 2.44% | 12.25% | 24.49% |
Reliability On In-domain Test Data
For the reliability of in-domain test data, we report the F-ECE and NLL as calibration metrics. Results of unbiased metric (i.e. F-KDE-ECE (Popordanoska, Sayer, and Blaschko 2022)) can be found in Appendix.
Effectiveness on Calibration. We first evaluate the effectiveness of APH compared with other available SOTA calibration and uncertainty estimation methods. Experimental results are displayed in the Table 1. As can be seen from the table, the proposed APH significantly reduces the F-ECE of the given model and largely improves its accuracy through multiple projection head assembling.
Compatibility on SOTA Methods. We further conduct experiments to validate the compatibility and effectiveness of the proposed APH combined with other SOTA generic and personalized federated methods. We display the experimental results in Table 2. Experimental results demonstrate that the proposed APH can be seamlessly integrated into SOTA federated methods and still performs well in accuracy improvement and model calibration.
Robustness on Federated Hyperparameters. We now validate the robustness of APH under the various federated settings. We mainly focus on the crucial hyper-parameters, i.e. client participation ratio , the severity level of data heterogeneity , local epoch , and client number . We report the experimental results in Table 3. As can be seen from the table, APH is robust to federated hyper-parameters.
Reliability On Out-Of-Distribution Test Data
In this section, we evaluate the effectiveness of APH in improving model reliability on the OOD dataset. For clarity, we here report the result of the first client. Detailed results of all clients with various federated methods can be found in the Appendix. As can be seen in Fig. 7, APH can significantly improve the uncertainty level of both generic and personalized federated methods on various datasets, showing its effectiveness in improving reliability to OOD samples. We also evaluate the effectiveness of APH under domain shifts on Cifar-C (Hendrycks and Dietterich 2019) in Appendix.
Analysis on Computation Efficiency
Computation cost is always the key concern in uncertainty estimation. We here conduct experiments to validate the computation efficiency of APH. We set the various numbers of projection heads and report the results in Table 4. The computation cost is calculated using floating point operation numbers. As demonstrated in the table, APH achieves significant improvement with only 10 heads. Even for 100 heads, APH requires less than additional computational cost.
Conclusion
In this paper, we conduct a systematic experiment about the reliability of federated models. We uncover the fact that federated models are not reliable under heterogeneous data. We further investigate the impact factors and point out biased projection head is one of the main causes of reliability degradation. Motivated by the observation, we propose APH, a lightweight but effective uncertainty estimation framework for federated models. By treating the existing projection head parameters as priors, APH randomly samples multiple initialized parameters of projection heads from the prior and further performs targeted fine-tuning on locally available data under varying learning rates. Such a head ensemble introduces parameter diversity into the deterministic model, producing reliable predictions via head averaging. Experiments conducted on Cifar10, Cifar100, and Tiny-ImageNet validate the efficacy of APH in improving reliability by model calibration and uncertainty estimation.
Acknowledgements
This work is supported in part by the National Key Research and Development Program of China under Grant 2020AAA0109602; by the National Natural Science Foundation of China under Grant 62306074.
References
- Acar et al. (2021) Acar, D. A. E.; Zhao, Y.; Navarro, R. M.; Mattina, M.; Whatmough, P. N.; and Saligrama, V. 2021. Federated learning based on dynamic regularization. arXiv preprint arXiv:2111.04263.
- Arivazhagan et al. (2019) Arivazhagan, M. G.; Aggarwal, V.; Singh, A. K.; and Choudhary, S. 2019. Federated learning with personalization layers. arXiv preprint arXiv:1912.00818.
- Chen and Chao (2021) Chen, H.-Y.; and Chao, W.-L. 2021. On Bridging Generic and Personalized Federated Learning for Image Classification. In International Conference on Learning Representations.
- Collins et al. (2021) Collins, L.; Hassani, H.; Mokhtari, A.; and Shakkottai, S. 2021. Exploiting shared representations for personalized federated learning. In International conference on machine learning, 2089–2099. PMLR.
- Fallah, Mokhtari, and Ozdaglar (2020) Fallah, A.; Mokhtari, A.; and Ozdaglar, A. 2020. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach. Advances in Neural Information Processing Systems, 33: 3557–3568.
- Gal and Ghahramani (2016) Gal, Y.; and Ghahramani, Z. 2016. Dropout as a bayesian approximation: Representing model uncertainty in deep learning. In international conference on machine learning, 1050–1059. PMLR.
- Gao et al. (2022) Gao, L.; Fu, H.; Li, L.; Chen, Y.; Xu, M.; and Xu, C.-Z. 2022. Feddc: Federated learning with non-iid data via local drift decoupling and correction. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 10112–10121.
- Graves (2011) Graves, A. 2011. Practical variational inference for neural networks. Advances in neural information processing systems, 24.
- Guo et al. (2017) Guo, C.; Pleiss, G.; Sun, Y.; and Weinberger, K. Q. 2017. On calibration of modern neural networks. In International conference on machine learning, 1321–1330. PMLR.
- Hendrycks and Dietterich (2019) Hendrycks, D.; and Dietterich, T. 2019. Benchmarking neural network robustness to common corruptions and perturbations. arXiv preprint arXiv:1903.12261.
- Hendrycks et al. (2021) Hendrycks, D.; Zhao, K.; Basart, S.; Steinhardt, J.; and Song, D. 2021. Natural adversarial examples. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 15262–15271.
- Hsu, Qi, and Brown (2019) Hsu, T.-M. H.; Qi, H.; and Brown, M. 2019. Measuring the effects of non-identical data distribution for federated visual classification. arXiv preprint arXiv:1909.06335.
- Huang et al. (2021) Huang, Y.; Chu, L.; Zhou, Z.; Wang, L.; Liu, J.; Pei, J.; and Zhang, Y. 2021. Personalized cross-silo federated learning on non-iid data. In Proceedings of the AAAI conference on artificial intelligence, volume 35, 7865–7873.
- Jacot, Gabriel, and Hongler (2018) Jacot, A.; Gabriel, F.; and Hongler, C. 2018. Neural tangent kernel: Convergence and generalization in neural networks. Advances in neural information processing systems, 31.
- Kairouz et al. (2021) Kairouz, P.; McMahan, H. B.; Avent, B.; Bellet, A.; Bennis, M.; Bhagoji, A. N.; Bonawitz, K.; Charles, Z.; Cormode, G.; Cummings, R.; et al. 2021. Advances and open problems in federated learning. Foundations and Trends® in Machine Learning, 14(1–2): 1–210.
- Karimireddy et al. (2020) Karimireddy, S. P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; and Suresh, A. T. 2020. Scaffold: Stochastic controlled averaging for federated learning. In International Conference on Machine Learning, 5132–5143. PMLR.
- Krizhevsky, Hinton et al. (2009) Krizhevsky, A.; Hinton, G.; et al. 2009. Learning multiple layers of features from tiny images.
- Lakshminarayanan, Pritzel, and Blundell (2017) Lakshminarayanan, B.; Pritzel, A.; and Blundell, C. 2017. Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in neural information processing systems, 30.
- Le and Yang (2015) Le, Y.; and Yang, X. 2015. Tiny imagenet visual recognition challenge. CS 231N, 7(7): 3.
- Lee et al. (2022) Lee, G.; Jeong, M.; Shin, Y.; Bae, S.; and Yun, S.-Y. 2022. Preservation of the global knowledge by not-true distillation in federated learning. Advances in Neural Information Processing Systems, 35: 38461–38474.
- Levinson et al. (2011) Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J. Z.; Langer, D.; Pink, O.; Pratt, V.; et al. 2011. Towards fully autonomous driving: Systems and algorithms. In 2011 IEEE intelligent vehicles symposium (IV), 163–168. IEEE.
- Li et al. (2022) Li, Q.; Diao, Y.; Chen, Q.; and He, B. 2022. Federated learning on non-iid data silos: An experimental study. In 2022 IEEE 38th International Conference on Data Engineering (ICDE), 965–978. IEEE.
- Li, He, and Song (2021) Li, Q.; He, B.; and Song, D. 2021. Model-contrastive federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 10713–10722.
- Li et al. (2021) Li, T.; Hu, S.; Beirami, A.; and Smith, V. 2021. Ditto: Fair and robust federated learning through personalization. In International Conference on Machine Learning, 6357–6368. PMLR.
- Li et al. (2020a) Li, T.; Sahu, A. K.; Talwalkar, A.; and Smith, V. 2020a. Federated learning: Challenges, methods, and future directions. IEEE signal processing magazine, 37(3): 50–60.
- Li et al. (2020b) Li, T.; Sahu, A. K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; and Smith, V. 2020b. Federated optimization in heterogeneous networks. Proceedings of Machine Learning and Systems, 2: 429–450.
- Li et al. (2020c) Li, T.; Sahu, A. K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; and Smith, V. 2020c. Federated optimization in heterogeneous networks. Proceedings of Machine learning and systems, 2: 429–450.
- Li et al. (2019) Li, X.; Chen, S.; Hu, X.; and Yang, J. 2019. Understanding the disharmony between dropout and batch normalization by variance shift. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2682–2690.
- Lin et al. (2020) Lin, T.; Kong, L.; Stich, S. U.; and Jaggi, M. 2020. Ensemble distillation for robust model fusion in federated learning. Advances in Neural Information Processing Systems, 33: 2351–2363.
- Louizos and Welling (2016) Louizos, C.; and Welling, M. 2016. Structured and efficient variational deep learning with matrix gaussian posteriors. In International conference on machine learning, 1708–1716. PMLR.
- Luo et al. (2021) Luo, M.; Chen, F.; Hu, D.; Zhang, Y.; Liang, J.; and Feng, J. 2021. No fear of heterogeneity: Classifier calibration for federated learning with non-iid data. Advances in Neural Information Processing Systems, 34: 5972–5984.
- Maddox et al. (2019) Maddox, W. J.; Izmailov, P.; Garipov, T.; Vetrov, D. P.; and Wilson, A. G. 2019. A simple baseline for bayesian uncertainty in deep learning. Advances in neural information processing systems, 32.
- McMahan et al. (2017) McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; and y Arcas, B. A. 2017. Communication-efficient learning of deep networks from decentralized data. In Artificial intelligence and statistics, 1273–1282. PMLR.
- Miotto et al. (2016) Miotto, R.; Li, L.; Kidd, B. A.; and Dudley, J. T. 2016. Deep patient: an unsupervised representation to predict the future of patients from the electronic health records. Scientific reports, 6(1): 1–10.
- Naeini, Cooper, and Hauskrecht (2015) Naeini, M. P.; Cooper, G.; and Hauskrecht, M. 2015. Obtaining well calibrated probabilities using bayesian binning. In Proceedings of the AAAI conference on artificial intelligence, volume 29.
- Netzer et al. (2011) Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; and Ng, A. Y. 2011. Reading digits in natural images with unsupervised feature learning.
- Ovadia et al. (2019) Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.; Lakshminarayanan, B.; and Snoek, J. 2019. Can you trust your model’s uncertainty? evaluating predictive uncertainty under dataset shift. Advances in neural information processing systems, 32.
- Popordanoska, Sayer, and Blaschko (2022) Popordanoska, T.; Sayer, R.; and Blaschko, M. B. 2022. A Consistent and Differentiable Canonical Calibration Error Estimator. In Advances in Neural Information Processing Systems.
- Riquelme, Tucker, and Snoek (2018) Riquelme, C.; Tucker, G.; and Snoek, J. 2018. Deep bayesian bandits showdown: An empirical comparison of bayesian deep networks for thompson sampling. arXiv preprint arXiv:1802.09127.
- Sensoy, Kaplan, and Kandemir (2018) Sensoy, M.; Kaplan, L.; and Kandemir, M. 2018. Evidential deep learning to quantify classification uncertainty. Advances in neural information processing systems, 31.
- Smith et al. (2017) Smith, V.; Chiang, C.-K.; Sanjabi, M.; and Talwalkar, A. S. 2017. Federated multi-task learning. Advances in neural information processing systems, 30.
- T Dinh, Tran, and Nguyen (2020) T Dinh, C.; Tran, N.; and Nguyen, J. 2020. Personalized federated learning with moreau envelopes. Advances in Neural Information Processing Systems, 33: 21394–21405.
- Thiagarajan et al. (2022) Thiagarajan, J.; Anirudh, R.; Narayanaswamy, V. S.; and Bremer, T. 2022. Single model uncertainty estimation via stochastic data centering. Advances in Neural Information Processing Systems, 35: 8662–8674.
- Van Amersfoort et al. (2020) Van Amersfoort, J.; Smith, L.; Teh, Y. W.; and Gal, Y. 2020. Uncertainty estimation using a single deep deterministic neural network. In International conference on machine learning, 9690–9700. PMLR.
- Wei et al. (2020) Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H. H.; Farokhi, F.; Jin, S.; Quek, T. Q.; and Poor, H. V. 2020. Federated learning with differential privacy: Algorithms and performance analysis. IEEE Transactions on Information Forensics and Security, 15: 3454–3469.
- Welling and Teh (2011) Welling, M.; and Teh, Y. W. 2011. Bayesian learning via stochastic gradient Langevin dynamics. In Proceedings of the 28th international conference on machine learning (ICML-11), 681–688.
- Xu, Tong, and Huang (2022) Xu, J.; Tong, X.; and Huang, S.-L. 2022. Personalized Federated Learning with Feature Alignment and Classifier Collaboration. In The Eleventh International Conference on Learning Representations.
- Yang et al. (2019) Yang, Q.; Liu, Y.; Chen, T.; and Tong, Y. 2019. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology (TIST), 10(2): 1–19.
- Zhang et al. (2023) Zhang, J.; Hua, Y.; Wang, H.; Song, T.; Xue, Z.; Ma, R.; and Guan, H. 2023. Fedala: Adaptive local aggregation for personalized federated learning. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 37, 11237–11244.
- Zhang et al. (2020) Zhang, M.; Sapra, K.; Fidler, S.; Yeung, S.; and Alvarez, J. M. 2020. Personalized Federated Learning with First Order Model Optimization. In International Conference on Learning Representations.
- Zhu et al. (2021) Zhu, H.; Xu, J.; Liu, S.; and Jin, Y. 2021. Federated learning on non-IID data: A survey. Neurocomputing, 465: 371–390.