Wasserstein Generative Adversarial Networks for Online Test Generation for Cyber Physical Systems
Abstract.
We propose a novel online test generation algorithm WOGAN based on Wasserstein Generative Adversarial Networks. WOGAN is a general-purpose black-box test generator applicable to any system under test having a fitness function for determining failing tests. As a proof of concept, we evaluate WOGAN by generating roads such that a lane assistance system of a car fails to stay on the designated lane. We find that our algorithm has a competitive performance respect to previously published algorithms.
1. Introduction
Safety validation is the process of establishing the correctness and safety of a system operating in an environment (Corso et al., 2021). Validation is necessary to ensure that a system works as expected before it is taken into production. This is especially important with safety properties of cyber-physical systems (CPS), where a fault can lead to severe damage to property or even death.
System validation is a challenging and open problem. While there is a large body of knowledge on the subject, the size, complexity, and requirements for software-intensive systems have grown over time. There is a need for cost and time efficient approaches that support system-level verification and validation of complex systems including program code, machine learning models, and hardware components.
In this article, we present a novel test generation algorithm for the CPS testing competition organized in 2022 within the 14th International Search-Based Software Testing Workshop (SBST 2022).
The system under test (SUT) is the lane assist feature of a car. This is a feature that aims to maintain a car safely within the boundaries of its driving lane without human assistance. If working properly, it can help to avoid an accident due to a distracted or tired driver. On the other hand, a faulty implementation may fail to avoid an accident or even actively cause one.
The main safety requirement for the lane assist feature is described as an upper bound on the percentage of the body of the car that is out of the boundaries of its lane () at any given moment. We can formalize this in signal temporal logic (Donzé, 2013) as . The goal of the test generator is to falsify this requirement.


We do not have access to any kind of specification, design document, or source code of the SUT. Instead, we are provided an implementation that can be executed in a simulated environment and a specification of the inputs and outputs of this simulator. The input of the simulator is a driving scenario defined as a road with the car as the only traffic. The output of a test is the maximum observed during the simulation, which we denote by . Based on this premise, our approach is in essence a system-level, black-box online test generator. It produces roads as inputs, observes the system outputs, and uses these observation to decide what should be the next test to execute. The goal is to find a failing test, i.e., a test whose fitness satisfies . In order to appreciate how difficult the task is, we included in Figure 1 two roads defined by points which are visually similar but have very different fitnesses. This also shows that humans have hard time estimating the lane assist performance: a human driver would perform equally well on both roads.
There are two main quality criteria for our test generator. First, our generator should aim to generate as many failing tests as possible within a given time budget. Executing a simulation is a time consuming process and the testing process is limited by a budget given as a time limit. The second goal is to generate failing tests that are as diverse as possible. The hypothesis is that a set of diverse failing tests can improve the process of determining the root cause of the observed errors. These are two conflicting criteria since a test generator may generate many failing tests by exploiting previously found positives instead of exploring the input space for more diverse tests.
The test generation algorithm presented in this article is based on a novel approach to the falsification of CPS. While most existing approaches use a known metaheuristic such as a genetic algorithm to search for tests with high fitness, our algorithm uses a Wasserstein generative adversarial network (WGAN) (Arjovsky et al., 2017) as a generator for such tests. Our algorithm starts tabula rasa and interacts with the system to learn how to generate high-fitness tests. The algorithm has no domain knowledge about the SUT except for the representation of the input space to facilitate random search and learning by a neural network. Minimal usage of domain knowledge makes our algorithm general-purpose, i.e., it is easily adjusted for other SUTs. Our experimental results indicate that our algorithm has competitive performance when compared with the previously published algorithms (Panichella et al., 2021).
We remark that our algorithm shares ideas with the algorithm of the paper (Porres et al., 2021) which is inspired by GANs. The algorithm of (Porres et al., 2021) does not train a GAN in the sense of the original GAN paper (Goodfellow et al., 2014) as it trains a generator neural network whose outputs achieve a large value when fed through a discriminator neural network. While this approach can achieve good results (Porres et al., 2021), it is a viable strategy for the generator to always generate a single good test. In such a case, the resulting test generator would not fulfill the second quality criterion. In order to work around this potential problem, our algorithm trains a proper GAN. In fact, we train a WGAN, and WGANs are known to be able to produce varied samples from their target distributions (Arjovsky et al., 2017).
2. A Novel Algorithm
2.1. Feature Representation
The input to the simulator is a sequence of points in the plane which the provided simulator interface interpolates to a road. See Figure 1 for roads defined by points. Not all sequences are valid: intersecting roads and roads with steep turns are disallowed. Moreover, a road must fit in a map of units. An efficient black-box validator for candidate roads is provided by the SBST 2021 CPS competition (Panichella et al., 2021).
Generating valid tests by randomly choosing sequences of plane points is difficult, so we opted to use the feature representation described in (et al., 2021). For us, a test is a vector in whose components are curvature values in the range . Given a test, we fix the initial point to be the bottom midpoint of the map and the initial direction to be directly up. Then we numerically integrate the curvature values with a fixed step length to obtain more points. Fixing the initial point and direction is justified by noting that the test fitness (maximum ) should be translation and rotation invariant.
This feature representation makes random search of valid roads more feasible. In our experiments, we set and we estimated that then the probability of a test being valid equals . On the other hand, we estimated that a sequence of plane points with components chosen uniformly randomly in corresponds to a valid road with probability . For both estimates, we generated random roads.
2.2. Overview of Models and Their Training
Let be the set of failing tests in the test space . Our aim is to learn online a mapping from a latent space to the test space such that uniform sampling of the latent space yields samples of via the map . To achieve this, we train this generator as a WGAN (Arjovsky et al., 2017). In this setting, is a neural network and it is trained to minimize the Wasserstein distance between the distribution of and the real data distribution . This is accomplished with the help of a critic (also a neural network) which, informally speaking, is trained to distinguish between tests in and outside of it.
Training the WGAN traditionally requires having a training data sample from in advance. Since we do not have such data, an alternative approach is needed. We propose to begin from a set of random valid tests and update it using an analyzer (also trained online). We execute the tests of on the SUT to know for all . We use this data to train (a neural network) to approximate the mapping . We may now use the generator to produce valid tests and estimate their fitness by without consulting the SUT (recall that a validator is available). When we have found a valid test which is estimated by to have high fitness, we execute it on the SUT and add the test and its outcome to .
Training the WGAN directly on treats all tests equally which is counterproductive as can contain many low-fitness tests. We propose to create a training batch from which is biased towards high-fitness tests and train the WGAN on it. Ideally becomes more able to generate high-fitness tests and gets more accurate as more data is available. The analyzer does not need to be perfect; it just needs to drive the training towards high-fitness tests.
It has been observed that WGANs, like GANs, can produce novel variations of their training data (Arjovsky et al., 2017) so, whenever the fitness function is well-behaved on the test space (e.g., it is locally continuous) and the random search is representative enough, the generator should eventually produce high-fitness tests, some of which belong to . Failing this could be taken as an indication that faults do not exist.
Our experiments confirm that Algorithm 1 can expose many faults of the SUT of the SBST 2021 CPS testing competition showing empirically the validity of the above ideas. This achieves the first quality criterion of a test generator. WGANs have been shown to avoid the so-called GAN mode collapse in which a generator produces the same output over and over (Arjovsky et al., 2017). We observe this in our experiments as we typically find clusters of failing tests that are largely different from each other. This achieves the second quality criterion.
2.3. The Algorithm
Let us explain the pseudocode of our WOGAN algorithm Algorithm 1. Its main structure is similar to the OGAN algorithm of (Porres et al., 2021). Initially a population of random tests is created and executed on the SUT. On each round of the outer loop, the analyzer is trained on the current tests and their fitnesses , and the WGAN consisting of the generator and the critic is trained on a biased batch of samples from (see the next paragraph). Then candidate tests are produced by in the inner loop until a valid test whose fitness estimates to be high enough has been produced. The acceptance threshold is lowered on each iteration in order to find suitable candidates reasonably fast. The accepted test is added to the test suite along with its fitness. Finally a parameter controlling the biased batching is updated. The algorithm terminates when the time budget is exhausted.
Let us then describe how the biased batches are formed. Partition the interval (the range of ) into contiguous bins of length . Put each test in to a bin according to its fitness. We weight the bins and sample bins ( is the batch size) according to this weighting. The biased batch is formed by choosing a test uniformly randomly (without replacement) from each sampled bin. The weights are chosen according to a shifted sigmoid function . The parameter increases linearly from to during the execution. Thus initially low-fitness tests have a chance of being selected, encouraging exploration, whereas later only high-fitness tests are likely to be sampled.
3. Experimental Results
In this section we compare our WOGAN algorithm to two other algorithms: random search (to establish a baseline) and the Frenetic algorithm (et al., 2021), a genetic algorithm whose performance was deemed to be among the best of the SBST 2021 CPS testing competition entries (Panichella et al., 2021).
3.1. Experiment Setup
The goal of the test generation is to generate a test suite with as many failing tests as possible within a time budget of hours. A test is considered failed if its fitness (maximum ) exceeds . No speed limit is imposed on the simulator AI. We report the results of repeated experiments for each algorithm.
We use the version of the BeamNG.tech simulator as in the current 2022 iteration of the competition. The
lane assist AI used is the one provided by BeamNG.tech. The data was collected on a desktop PC running Windows 10
Education with Intel i9-10900X CPU, Nvidia GeForce RTX 3080 GPU, and 64 GB of RAM.
WOGAN. We produce roads with points, i.e., we set . This is an arbitrary decision driven by the fact that it is challenging to train neural networks with limited training data of high dimensionality. We set , so the latent space has dimension . In Algorithm 1, we set (approximately of the roads that can be tested in the given time budget) and target_reducer . We use ( bins) and (batch size ) in the WOGAN batch sampling. Our random search produces tests , as described in Subsection 2.1, such that for all . Frenetic uses the same procedure.
We train the WGAN using gradient penalty as in (Gulrajani et al., 2017). The critic and generator both use a dense neural network
of two hidden layers with neurons and ReLU activations. The analyzer has two hidden layers with neurons and
ReLU activations. The WGAN is trained with the default settings of (Gulrajani et al., 2017) and learning rate as
suggested in (Arjovsky
et al., 2017). The analyzer is trained with the Adam optimizer with learning rate and beta
parameters and . These settings yielded good performance, but we did not attempt to determine the best
parameters empirically.
Frenetic. Frenetic (et al., 2021) is a genetic algorithm that uses, in our opinion, domain-specific mutators to generate new solutions. A remarkable feature in Frenetic is the use of two sets of mutators depending on if an individual represents a passed or a failed test. Mutators for passed tests are used to explore the solution space while the mutators for failed tests exploit the failure to generate new high-fitness roads. The mutators for failed test mutators are: reversing the cartesian representation of a road, reversing its curvature values, splitting the road in two halves and swapping them, and mirroring the road. These mutators create new roads that are diverse by construction under many similarity measures and may lead to tests with high-fitness.
We updated the Frenetic algorithm to use the latest version of the simulator. We also set the number of roads for the initial random search to which is the same as in WOGAN. Due to the changes, we consider that the version of Frenetic used in this article is not equivalent to the one presented in (et al., 2021) and its results are not comparable.
Notice that Frenetic produces roads defined by variable number of points. Its random search builds roads with
points and the genetic algorithm rules can change this number. As stated above, WOGAN considers only roads
defined by points which is a much lower number. We opted not to change Frenetic in order to keep our modified
Frenetic as close as possible to the original.
Random. This algorithm simply generates uniformly randomly tests as described in Subsection 2.1 (that is, we generate roads of points).
3.2. Results

| Random | WOGAN | Frenetic | |
|---|---|---|---|
| mean executed tests | |||
| SD executed tests | |||
| mean failing tests | |||
| SD failing tests | |||
| mean fitness final | |||
| SD fitness final | |||
| mean fitness final | |||
| SD fitness final | |||
| mean diversity | |||
| SD diversity |
Number of Failing Tests. See Figure 2 for box plots for the number of failing tests in each of the experiments per algorithm. See also Table 1 for key statistics. Evidently both WOGAN and Frenetic beat the random search which can only find failing tests on average out of an average of tests executed per experiment. WOGAN is statistically different from Frenetic (at significance level ): the Wilcoxon signed-rank test reports a -value of under the null hypothesis that the median of differences is . In Table 1, we also include the means of average fitnesses of the final and final of the test suites. Thus WOGAN and Frenetic manage not only to find failing tests but high-fitness tests in general.
The results indicate that our approach can achieve performance comparable to an
algorithm using more domain-specific knowledge. Thus we have experimentally validated that our WOGAN algorithm fulfills the first quality criterion of
finding many failing tests.
Generation Time.
We define the generation time of a test being the time elapsed between two executions of a valid test. Average
generation times are (SD ), (SD , and
(SD ) for Random, WOGAN, and Frenetic respectively. However, generation time is
mostly spent on testing if a candidate test is valid. The remaining time is
negligible for Random and on average (SD ) and (SD
) for WOGAN and Frenetic respectively. WOGAN uses this time mainly for model training. All times
reported are measured in real time. Observe that WOGAN manages to execute more tests than Frenetic (see Table 1)
even though it uses more time for generation. This is explained by noting that Frenetic produces longer roads which
require longer simulation time.
Failing Test Diversity. It is an open problem how to measure if the failing tests are “diverse”. The SBST 2021 CPS testing competition (Panichella et al., 2021) used a certain notion of sparseness to measure this, but here we opt for the following simpler measure. For each test, we find its interpolation to a road (this is what is actually fed to the simulator) and evenly reduce it to obtain a sequence of plane points of length (the minimum length we observed). These points are rotated in such a way that the initial direction is always directly up. Then we transform the point sequence to angles between two consecutive points to obtain a vector in . For a complete test suite, we define its diversity to be the median of the pairwise Euclidean distances of these vectors for failing tests. Small diversity value indicates that the failing tests are not diverse.
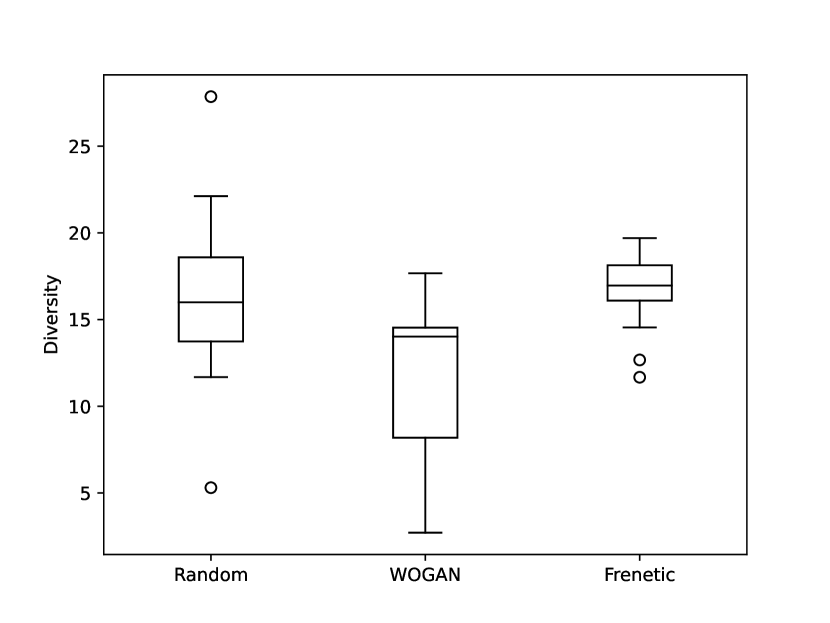
The diversities of the test suites are reported in Figure 3 and additional statistics are found in Table 1. Intuitively the set of failing tests for random search should be diverse. Therefore Figure 3 indicates that WOGAN and Frenetic both succeed at producing reasonably diverse failing tests according to the selected diversity measure. The diversity values for WOGAN and Frenetic are statistically different (at significance level ): the Wilcoxon signed-rank test reports a -value of under the null hypothesis that the median of differences is . We remark that the roads generated by Frenetic are based on a higher number of plane points, so they are by nature more varied. We conclude that we have shown evidence that WOGAN fulfills the second quality criterion of being able to generate diverse failing tests. It is true that the data suggests that WOGAN removes diversity, but accurately assessing the situation would require a deeper study of the tradeoffs between our conflicting quality criteria.
4. Conclusions
We have presented a novel online black-box test generation algorithm based on ideas from generative adversarial networks. The algorithm uses no explicit domain knowledge except in the choice of problem feature representation. Additionally, the algorithm learns a generator which can be thought of as a model for high-fitness tests for the SUT. Further examination of this model could prove useful in studying the SUT in more detail.
We have shown experimentally that our WOGAN algorithm can achieve a performance comparable to previous competitive algorithms. Not only is WOGAN able to find faults of the SUT, but it can produce a varied set of failing tests. However, we remark that our evaluation is based on a single experiment and that the merits of the WOGAN algorithm should be examined independently in the context of the SBST 2022 CPS testing competition.111Note added in proof: The competition report is available at (Gambi et al., 2022). See also (Peltomäki et al., 2022) for a brief note on WOGAN’s performance in the competition.
In the future, we aim to write a more complete subsequent work providing full details, additional experiments, and actual code.
Acknowledgements.
This research work has received funding from the ECSEL Joint Undertaking (JU) under grant agreement No 101007350. The JU receives support from the European Union’s Horizon 2020 research and innovation programme and Sweden, Austria, Czech Republic, Finland, France, Italy, Spain.References
- (1)
- Arjovsky et al. (2017) M. Arjovsky, S. Chintala, and L. Bottou. 2017. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 70). PMLR, 214–223.
- Corso et al. (2021) A. Corso, R. J. Moss, M. Koren, R. Lee, and M. J. Kochenderfer. 2021. A survey of algorithms for black-box safety validation of cyber-physical systems. J. Artif. Intell. Res. 72 (2021), 377–428. https://doi.org/10.1613/jair.1.12716
- Donzé (2013) A. Donzé. 2013. On signal temporal logic. In Runtime Verification - 4th International Conference, RV 2013 (Lecture Notes in Computer Science, Vol. 8174). Springer, 382–383. https://doi.org/10.1007/978-3-642-40787-1_27
- et al. (2021) E. Castellano et al. 2021. Frenetic at the SBST 2021 Tool Competition. In 2021 IEEE/ACM 14th International Workshop on Search-Based Software Testing (SBST). 36–37. https://doi.org/10.1109/SBST52555.2021.00016
- Gambi et al. (2022) A. Gambi, G. Jahangirova, V. Riccio, and F. Zampetti. 2022. SBST tool competition 2022. In 15th IEEE/ACM International Workshop on Search-Based Software Testing, SBST 2022.
- Goodfellow et al. (2014) I. J. Goodfellow, J. P.-A., M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio. 2014. Generative adversarial networks. CoRR abs/1406.2661 (2014). arXiv:1406.2661
- Gulrajani et al. (2017) I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, and A. Courville. 2017. Improved training of Wasserstein GANs. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17). Curran Associates Inc., 5769–5779.
- Panichella et al. (2021) S. Panichella, A. Gambi, F. Zampetti, and V. Riccio. 2021. SBST Tool Competition 2021. In 14th IEEE/ACM International Workshop on Search-Based Software Testing, SBST 2021. IEEE, 20–27. https://doi.org/10.1109/SBST52555.2021.00011
- Peltomäki et al. (2022) J. Peltomäki, F. Spencer, and I. Porres. 2022. WOGAN at the SBST 2022 CPS tool competition. In 15th IEEE/ACM International Workshop on Search-Based Software Testing, SBST 2022. https://doi.org/10.1145/3526072.3527535
- Porres et al. (2021) I. Porres, H. Rexha, and S. Lafond. 2021. Online GANs for automatic performance testing. In IEEE International Conference on Software Testing, Verification and Validation Workshops (ICSTW 2021). 95–100. https://doi.org/10.1109/ICSTW52544.2021.00027