Waist inequality for 3-manifolds
with positive scalar curvature

For (a)-(c), see [MN12, Proposition A.1]. For (d), consider Gauss’ equation:

So that:

By Yau [Yau87], since $\Sigma$ is two-sided and has index 1:

where $F$ is conformal map from $\Sigma$ to $n$-sphere $S^{n}$ and $g$ is a conformal automorphism of $S^{n}$.

Finally, by Li-Yau [LY82]: $\inf_{n}V_{c}(n,\Sigma)=V_{c}(\mathbb{RP}^{2})=6\pi$. Thus:

∎

Part $(a)$ follows directly from the diameter estimate in (2.3).

Part $(b)$ also follows from (2.3), as in [LZ16, Proposition 2.2]. Indeed, we can pick two points $p$ and $q$ at a distance $\operatorname{diam}(\Sigma)$ and consider a geodesic ball $B_{r}(p)$ with $r=\frac{\operatorname{diam}(\Sigma)}{2}$. Since $\Sigma$ has index $1$ either the connected component of $\Sigma\setminus\partial B_{r}(p)$ that contains $p$ or the connected component that contains $q$ must be stable. Then the result follows from the estimate for the filling radius. ∎

Since the scalar curvature is positive the only orientable two-sided stable minimal surfaces in $M$ are 2-spheres. Let $S_{1}^{1},\ldots,S_{k_{1}}^{1}$ be a maximal collection of pairwise disjoint two-sided stable minimal 2-spheres and projective planes. Since the metric is bumpy the set of such spheres and projective planes is finite (possibly empty).

Each connected component $K_{l}$ of $M\setminus\bigcup_{i=1}^{k_{1}}S_{i}^{1}$ is irreducible, since otherwise we could find a stable minimal sphere in its interior by [MSY82].

First consider orientable components $K_{l}$. By classification of 3-manifolds of positive scalar curvature it follows that each orientable component $K_{l}$ is a spherical space form with possibly some balls removed (all the boundary components are stable minimal 2-spheres).

If $K_{l}\cong\mathbb{RP}^{3}$ with some balls removed, then by [KLS19, Theorem 17] either there is an index $1$ minimal Heegaard torus, or there is a stable minimal $\mathbb{RP}^{2}$ with stable double cover (note that although [KLS19, Theorem 17] is stated for closed manifolds the proof applies to the case of a manifold with boundary consisting of stable minimal spheres). In the second case we cut $K_{l}$ along the minimal stable $S^{2}_{l}\cong\mathbb{RP}^{2}$ to obtain a 3-sphere with some balls removed and such that all boundary components are stable. Applying min-max argument we obtain an index $1$ 2-sphere $S^{3}_{l}$ in the interior of $K_{l}\setminus S^{2}_{l}$.

It follows from Thurston’s Elliptization Conjecture proved by Perelman that every orientable irreducible 3-manifold of positive scalar curvature is a Seifert fiber space with at most $3$ exceptional fibers and therefore admits a Heegaard splitting of genus less than or equal to $2$ (see [Mor88], [BCZ91]).

Suppose $K_{l}\not\cong\mathbb{RP}^{3}$ is homeomorphic to a spherical space form with some balls removed. We have that the Heegaard genus $g_{K_{l}}$ of $K_{l}$ satisfies $g_{K_{l}}\leq 2$. By [KLS19, Theorem 17] there exists a minimal surface $S^{3}_{l}\subset K_{l}$ of Morse index 1 that is isotopic to the Heegaard splitting of $K_{l}$.

Now consider non-orientable components. If $K_{l}$ is not orientable then it must be homeomorphic to $\mathbb{RP}^{2}\times S^{1}$ with some balls removed by [Eps61, Theorem 5.1]. In this case we cut along a maximal collection of disjoint stable and index 1 projective planes and 2-spheres to obtain a collection $K_{l,j}$ each homeomorphic to $\mathbb{RP}^{2}\times[0,1]$ with some balls removed or $S^{3}$ with some balls removed. If $K_{l,j}$ is homeomorphic to $S^{3}$ with some balls removed, then it is geometrically prime. We claim that if $K_{l,j}$ is homeomorphic to $\mathbb{RP}^{2}\times[0,1]$ with some balls removed then it is non-orientable geometrically prime. Indeed, if it has an index $1$ two-sphere as one of the boundary components, then we can minimize in the isotopy class ([MSY82]) to obtain a stable minimal 2-sphere in the interior. Similarly, if it has two or more index 1 projective planes as boundary components, then we can obtain a stable minimal projective plane in the interior. If all boundary components are stable then by the min-max construction of [KLS19] there exists an index $1$ minimal $\mathbb{RP}^{2}$ in the interior of $K_{l,j}$. This contradicts maximality of the collection of minimal spheres and projective planes.

Hence, each connected component $K$ has exactly one boundary component $S\subset\partial K$ that is a minimal surface of index $1$. We claim that $K$ now has no minimal surfaces in its interior. Consider a mean convex surface $\Sigma$ obtained by small perturbation of $S$ to the inside of $K$. Then the level set flow applied to $\Sigma$ will either become extinct in finite time or will converge to a disjoint collection of finitely many stable minimal surfaces as $t\rightarrow\infty$ by the result of White [Whi00]. Since $K$ is homeomorphic to a handle body or $\mathbb{RP}^{2}\times[0,1]$ with some balls removed and we already cut the manifold along a maximal collection of disjoint stable minimal spheres and projective planes we have that the flow converges to $\partial K\setminus S$. By the Maximum Principle [Ilm92] $K$ has no smooth embedded minimal surfaces in its interior. ∎

Our argument is in the vein of Theorem 8.1 in [HK19]. Let us first consider the case when $l=0$, that is, $\partial N=\Sigma$. Since there are no closed stable minimal surfaces in the interior of $N$, by a result of White [Whi00], the level-set flow must become extinct in finite time, say $T$; that is, $K_{T}=\emptyset$. Because any mean curvature flow with surgery starting at $K_{0}$ is also a family of closed sets that is a set-theoretic subsolution for the level-set flow, in the terminology of Ilmanem [Ilm94], and the level-set flow $M_{t}$ is the maximal set-theoretic subsolution, we get an a priori bound $T<\infty$ for the extinction time of any mean curvature flow with surgeries starting at $K_{0}$. Thus, given $\varepsilon>0$, we may select $\delta<<1$ and $H_{\text{\rm trig}}>>H_{\text{\rm neck}}>>H_{\text{\rm thick}}>>1$ so that the $(\mathbb{\alpha},\delta,\mathbb{H})$-flow $K_{t}$ starting at $\partial K_{0}=K$ will be sufficiently close to the level-set flow in the Hausdorff sense so that all the discarded regions by the flow will have area summing up to at most $\varepsilon$.

Now, we assume $l\geq 1$. We fill in $N$ by gluing three-disks to the boundaries $\Sigma_{2},\ldots,\Sigma_{l}$ while maintaining their minimality and stability. By doing this we obtain a domain $M$ with mean-convex boundary $\partial M=\Sigma_{0}$ which contains stable minimal surfaces $\Sigma_{1},\Sigma_{2},\ldots,\Sigma_{l}$, but no other stable minimal surfaces in the region between $\Sigma_{0}$ and $\Sigma_{1},\Sigma_{2},\ldots,\Sigma_{l}$. Consider the level-set flow ([CGG91, ES91]) $\{M_{t}\}_{t\geq 0}$ starting at $M_{0}=M$ and let

By the barrier principle, since $\Sigma_{1},\Sigma_{2},\ldots,\Sigma_{l}$ are minimal, they will be contained in $M_{t}$ for all $t\geq 0$ and thus in $M_{\infty}$. Additionally, by Theorem 11.1 of White [Whi00], $M_{\infty}$ has finitely many connected components and the boundary of each one of them is a stable minimal surface. Since there is no stable minimal surface in region between of $\partial M$, and $\Sigma_{1},\Sigma_{2},\ldots,\Sigma_{l}$, we conclude that

By the same theorem of White [Whi00], the convergence of $\partial M_{t}$ to $\partial M_{\infty}=\Sigma_{1}\cup\Sigma_{2}\cup\cdots\cup\Sigma_{l}$ is smooth as $t\nearrow\infty$.

Thus, given $\varepsilon>0$, we may pick $T>0$ such that $\partial M_{T}$ consists of a union of graphical surfaces on a $\varepsilon/2$-neighborhood of $\partial M_{\infty}=\Sigma_{1}\cup\Sigma_{2}\cup\cdots\cup\Sigma_{l}$. We consider a sequence of $(\mathbb{\alpha},\delta_{n},\mathbb{H}_{n})$-flows $M^{n}_{t}$ on $[0,T]$ with initial condition $\partial M^{n}_{0}=\partial M=\Sigma_{0}$, $\delta_{n},\nearrow\infty$ and thick curvature thresholds $H^{n}_{\text{\rm thick}}\nearrow\infty$.

Since the initial domain is kept fixed and the thick curvatures tend to infinity as $n\rightarrow\infty$, by the work of Lauer [Lau13], we have that the above sequence of flows with surgery converge to the level set flow in the Hausdorff sense. Thus, picking $n$ sufficiently large, we have an $(\mathbb{\alpha},\delta_{n},\mathbb{H}_{n})$-flow that satisfy the desired hypothesis. ∎

We will start by proving slightly weaker version of the proposition: $(\ast)$ Given $\varepsilon>0$, there exists a tree foliation $\{\Sigma_{x}\}_{x\in G}$, such that

1. (1)

   $\operatorname{genus}(\Sigma_{x})\leq\operatorname{genus}(\Sigma)$

2. (2)

   $\operatorname{Area}(\Sigma_{x})\leq\operatorname{Area}(S)+\varepsilon$

which is mean convex on $[0,T]\setminus B$ for an $\varepsilon$-small set $B$.

The proof follows essentially by flowing the large component $\Sigma$ of $\partial N$ by mean curvature flow, which is area-decreasing and does not increase genus (even after surgeries). Because of potential surgeries and components getting discarded, we will need to introduce a procedure to foliate the surgery and discarded regions (without increasing the genus or area by more than $\varepsilon$).

First, let’s set up the mean curvature flow with surgeries. We use the notation and apply the existence results of Section 3.2 on mean curvature flow with surgeries starting at the large component of $\partial N$. Let $\{K^{i}_{t}\}$, $i=1,\ldots,k+1$, be the smooth flows that comprise the flow with surgeries $K_{t}$ (Definition 3.1) and $0<t_{1}<...<t_{k}<T-\varepsilon$ the respective surgery times. We may assume $\varepsilon$ is sufficiently small and $T$ is chosen sufficiently large so that $\partial K_{T-\varepsilon}\setminus\partial N$ is a disjoint union of spheres, each lying in a small tubular neighborhood and being graphical over a stable minimal surface in $\partial N\setminus\Sigma$. We may extend the family to the interval $[T-\varepsilon,T]$ by defining a smooth isotopy of each connected component of $\partial K^{k}_{T-\varepsilon}\setminus\partial N$ to the corresponding minimal surface $\Sigma_{1},\ldots,\Sigma_{l}$.

We now give an informal description of how we derive the foliation $\{\Sigma_{x}\}_{x\in G}$. First consider $t\in[0,T]$ outside of small neighborhood of surgery times $t_{i}$. For each family $\{\partial K_{t}^{i}\}$, we let $\{\Sigma_{x}\}$ to be smooth families of connected components of $\partial K_{t}^{i}\setminus\partial N$ parametrized by a disjoint union of intervals $E_{1}^{i},...,E_{n_{i}}^{i}$. From these intervals we start building edges of the graph $G$, which for the moment are disconnected.

At a surgery time, the replacement of a neck with two standard caps occurs in a small ball, where the metric is nearly Euclidean and the neck is close to a standard cylinder. For each such replacement we add a vertex $v$ to the graph $G$ and define surface $\Sigma_{v}$ that is equal to the the union of the connected component that contains the neck and a small disc $D$ in the middle of the neck/cylinder. This process starts connecting the edges of the graph $G$ corresponding to the intervals $E_{1}^{i},...,E_{n_{i}}^{i}$: we define deformations of the unions of each of the half-cylinders with $D$ into the corresponding standard cap. Proceeding this way for each neck-caps replacement we obtain the union of connected components of $\partial K^{i+1}_{t}$ for some $t$ slightly larger than $t_{i}$ and discarded components of $\partial K^{i}_{t}$. For each connected component of the discarded part we define a tree foliation that ends in a collection of points. This can be done since the discarded part has very small area.

Note that in this procedure, depending on whether the neck-caps surgery disconnects a component of $\partial K_{t}^{i}$, the vertex $v$ will be of degree bigger than 1, and potentially great than 3. To account for this and to have only vertices with degree at most 3, we will change the above procedure slightly by hand by gluing only one disk $D$ at a time for every surgery time where several neck-caps replacements take place. We describe the construction in more detail below.

Let $\sigma>0$ be a small constant sufficiently smaller than $\varepsilon$. Define maps $p_{i}:K_{t_{i}}^{+}\setminus K_{t_{i-1}+\sigma}^{i}\rightarrow\bigcup_{j}E^{i}_{j}$, so that the fibers $\{p_{i}^{-1}(t)\}$, $t\in E^{i}_{j}=[t_{i-1}+\sigma,t_{i}]$, are a smooth family of connected surfaces evolving by mean curvature flow. The map $s:\bigcup_{j}E^{i}_{j}\longrightarrow[t_{i-1}+\sigma,t_{i}]$ is defined so that $\partial K_{t}^{i}\setminus\partial N=(s\circ p)^{-1}(t)$.

It remains to describe the family of surfaces $(s\circ p)^{-1}(t)$ for $t\in B=\bigcup_{i=1}^{k}[t_{i},t_{i}+\sigma]$, that is, as the family goes through a surgery. These surgeries can be of two types: neck-caps replacements or discarding components.

Vertices corresponding to neck-caps surgeries. We define vertices corresponding to surgeries of the mean curvature flow and the families of surfaces parametrized by neighborhoods of the vertices in the tree $G$. Fix a surgery time $t_{i}$. Let $\{B_{j}\}_{j=1}^{m_{i}}$ be the set of disjoint balls so that $K^{\sharp}_{t_{i}}$ is obtained by replacing $\delta$-necks in balls $B_{j}$ by pairs of standard caps. $K^{i+1}_{t_{i}}$ is then obtained from $K^{\sharp}_{t_{i}}$ by discarding small connected components.

To ensure the graph $G$ only has vertices with degree at most 3, we will deal with each $B_{j}$ separately. We pick a separation time $\tau_{i}\in(0,\frac{\sigma}{2})$ sufficiently small so that the evolution of smooth mean curvature flow of $K^{i}_{t}$ and $K^{i+1}_{t}$ exists for $t\in[t_{i},t_{i}+\tau_{i}]$ and it is graphical over $K^{i}_{t_{i}}$ and $K^{i+1}_{t_{i}}$, correspondingly. By Remark 3.5, for each $j=1,...,m_{i}$, we have maps $\Phi_{j}:B_{j}\rightarrow\mathbb{R}^{3}$, such that:

1. (1)

   $\Phi_{j}$ is a $2$-bilipschitz diffeomorphism onto its image in $\mathbb{R}^{3}$;

2. (2)

   the images of the $\delta$-necks in $\Phi_{j}(\partial K^{i}_{t}\cap B_{j})$ are contained in $C_{t}^{j}$, where $C_{t}^{j}$ is a family of concentric infinite cylinders in $\mathbb{R}^{3}$ for $t\in[t_{i},t_{i}+\tau_{i}]$;

3. (3)

   the images of the caps in $\Phi_{j}(\partial K^{i+1}_{t}\cap B_{j})$ are contained in $S_{t}^{j,1}+S^{j,2}_{t}$, where $S^{j,1}_{t}$ and $S^{j,2}_{t}$ are two families of concentric spheres in $\mathbb{R}^{3}$ for $t\in[t_{i},t_{i}+\tau_{i}]$.

Let $t_{i,j}=t_{i}+\frac{(j-1)\tau_{i}}{2m_{i}}$. At $t_{i,1}=t_{i}$, we focus on the neck replacement taking place in $B_{1}$. Let $\Gamma$ denote the limiting surface of $(s\circ p)^{-1}(t)$ as $t\rightarrow t^{-}_{i,1}$ and let $C^{1}=\Phi_{1}(\Gamma\cap B_{1})$, which is a cylinder by construction (Remark 3.5). Let $D$ denote a flat disc in $\mathbb{R}^{3}$ that is perpendicular to the axis of $C^{1}$ and is equidistant from the two boundary curves of $C^{1}$. We define a vertex $v_{i,1}$ in the tree $G$ and surface $\Sigma_{v_{i,1}}=p^{-1}(v_{i,1})$ to be the union of $\Phi_{1}^{-1}(D)$ and the connected component of $\Gamma$ that intersects $B_{1}$.

The disc $D$ separates the cylinder $C^{1}$ into two components, $C_{1}^{1}$ and $C_{2}^{1}$. For $t\in[t_{i,1},t_{i,1}+\tau_{i}]$ and $l=1,2$ we define a family of discs $D^{l,1}_{t}$ with the following properties:

1. (1)

   $D^{l,1}_{t_{i,1}}=C^{1}_{l}\cup D$;

2. (2)

   $\partial D^{l,1}_{t}=\partial S^{l}_{t}$;

3. (3)

   $\{D^{l}_{t}\}$ is a family of smooth discs foliating the region between $C^{1}_{l}\cup D$ and $S^{l}_{t_{i,1}+\tau_{i}}$.

Finally, for $t\in[t_{i,1},t_{i,1}+\tau_{i}]=[t_{i,1},t_{i,2}]$, let $\Gamma_{t}$ denote the evolution by mean curvature flow of the union of one or two connected components of $\partial\left((s\circ p)^{-1}(t_{i})\right)$ that were obtained from $\Gamma$ by the neck-caps replacement. Then family

is the desired family of surfaces parametrized by a small neighborhood of vertex $v_{i,1}$ in the graph $G$. For components that belong to the thick part (that is, the part that is not discarded in the MCF with surgery) we extend the family forward in time using MCF until they join up with families parametrized by edges $E^{i}_{1},E^{i}_{2},\ldots,E^{i}_{n_{i}}$.

We then repeat the above process for $t\in[t_{i,2},t_{i,3}]$ focusing on the neck-caps replacements in $B_{2}$ and so on.

Contracting discarded components. As noted in Remark 3.5, the discarded components are either a convex sphere of controlled geometry, a capped-off chain of $\varepsilon$-necks, or an $\varepsilon$-loop and have areas $\rightarrow 0$ as $\varepsilon\rightarrow 0$.

By coarea inequality we can cover each discarded component $S$ by balls $B_{l}$, such that $B_{l}$ is $2$-bilipschitz diffeomorphic to a small ball in $\mathbb{R}^{3}$, and $\partial B$ intersects $S$ in a finite union of small loops. We start filling these loops by minimal discs one by one in a way similar to the procedure described above. Eventually, we obtain a collection of disjoint spheres each contained in a small ball $B_{l}$. Then by Lemma [CL20a, Lemma 4.1] there exists a Morse foliation contracting the sphere to a point. The argument in Lemma [CL20a, Lemma 4.1] can be slightly modified to give a tree foliation instead of a Morse foliation.

Finally, observe that the foliation is mean convex on $[0,T]\setminus B$. Moreover, we may assume that parameters of the $(\mathbb{\alpha},\delta,\mathbb{H})$-flow have been chosen so that $K_{t_{i}}^{i}\subset N_{\varepsilon/2}(K_{t_{i}}^{i-1})$ and so for $\sigma$ sufficiently small we have that the set $B$ is $\varepsilon$-small.

End of the proof. We now show how to finish the argument for Proposition 3.10 from its weaker version $(\ast)$. Given a geometrically prime or non-orientable geometrically manifold $N$ with large component $\Sigma$, we flow $\Sigma$ by smooth mean curvature flow for a short time $[0,t_{0}]$ and, by mean convexity, me may assume:

for some small real number $\alpha$. We then discard the region of $N$ bounded by $\Sigma$ and $\Sigma_{t_{0}}$, obtaining a new geometrically prime manifold $N^{\prime}$ with large component $\Sigma_{t_{0}}$. Proposition 3.10 then follows by applying its weaker version $(\ast)$ to $N^{\prime}$ with a choice of $\varepsilon<\alpha$. ∎

By [Whi91] we can make an arbitrary small perturbation to make the metric on $M$ bumpy. For an arbitrarily small $\varepsilon>0$ we will construct a foliation for the perturbed bumpy metric, so that the bounds on the area and diameter in the original metric are worse by at most $\varepsilon$.

When $M$ is homeomorphic to $S^{3}$ we apply Theorem 2.7 to decompose $M$ into a union of geometrically prime regions that have an index 1 minimal sphere as their large boundary component. From Proposition 3.10 we obtain a tree-foliation of each geometrically prime region by a family of 2-spheres. The areas of these spheres are at most $\frac{24\pi}{\Lambda_{0}}$ by Theorem 2.1. We can assemble these foliations together to obtain a map $\tilde{f}:M\rightarrow G$. Note that $G$ must be a tree. Fix a map $g:G\rightarrow\mathbb{R}$, such that the restriction of $g$ to any edge is linear and non-singular. The map $\tilde{f}\circ g$ can then be perturbed to a Morse function from $M$ to $\mathbb{R}$ with desired properties. The details of this perturbation are postponed until the proof of Theorem 1.1, where it is done in a more general setting.

If $M$ is homeomorphic to $S^{2}\times S^{1}$ we consider manifold $M^{\prime}\cong S^{2}\times[0,1]$ obtained by cutting $M$ along a minimal sphere that minimizes area in the isotopy class of $S^{2}\times\{0\}$. Applying Proposition 3.10 as above we obtain a map $\tilde{f}:M^{\prime}\rightarrow G$ onto a tree $G$ with vertices $v_{1}$, $v_{2}$ of $G$ corresponding to two stable boundary spheres of $M^{\prime}$. Let $g:G\rightarrow S^{1}$ be a map with $g(v_{1})=g(v_{2})$ and such that the restriction of $g$ to each edge is non-singular. A perturbation of $\tilde{f}\circ g$ then gives the desired Morse function on $M$.

Finally, case (c) follows by Proposition 3.10. ∎

Let $f:M\rightarrow G$ be the map from $M$ to a graph $G$ from part (c) of Theorem 1.3. Recall that graph $G$ has vertices of degree at most $3$.

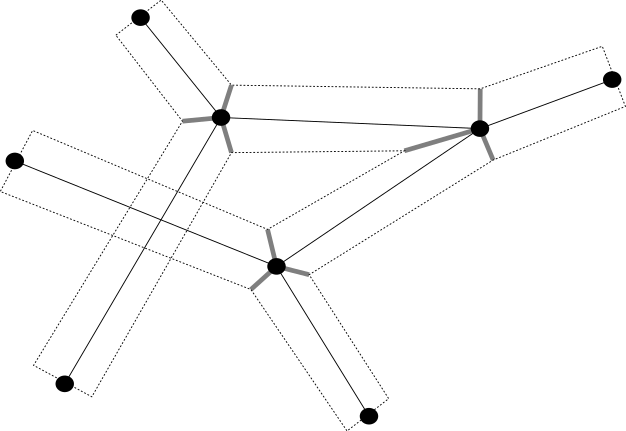
Consider a general position smooth immersion of $G$ in $\mathbb{R}^{2}$. In particular, vertices are disjoint and every edge $E$ of $G$ in $\mathbb{R}^{2}$ intersects at most finitely many other edges. Moreover, let $\{U_{E_{i}}\}$ denote the set of $\varepsilon$-neighborhoods of edges of $G$, then for $\varepsilon>0$ sufficiently small we may assume that each point $x\in\mathbb{R}^{2}$ is contained in at most two distinct $U_{E_{i}}$, $U_{E_{k}}$ if $x$ lies at a distance $>\varepsilon$ from the vertices of $G$. If $x\in B_{\varepsilon}(v)$ for some vertex $v$ of $G$, then it may lie in at most three sets $U_{E_{i_{1}}},U_{E_{i_{2}}},U_{E_{i_{3}}}$ corresponding to edges $E_{i_{1}},E_{i_{2}},E_{i_{3}}$ adjacent to the vertex $v$.

First we define map $F$ in the neighborhood of a degree $3$ vertex of $G$. Let $T_{v}=l_{1}\cup l_{2}\cup l_{3}$ denote a “tripod”, a union of three arcs emanating from vertex $v$ to the boundary of $\varepsilon$-neighborhood of $G$, each $l_{i}$ bisecting the angle between two edges of $E$ (see Fig. 1). Recall from the proof of Theorem 3.10 that $f^{-1}(v)$ is a union of a surface $\Sigma$ and a disc $\Sigma_{1}$ intersecting $\Sigma$ in a closed curve $\gamma$ that separates $\Sigma$, $\Sigma\setminus\gamma=\Sigma_{2}\cup\Sigma_{3}$. For each $\Sigma_{i}$ there exists a Morse function $f_{i}:\Sigma_{i}\rightarrow[0,1]$ with $f_{i}^{-1}(0)=\gamma$ and satisfying

for $t\in[0,1]$ ([GAL17]). (Recall from the proof of Theorem 3.10 that the length of curve $\gamma$ can be assumed to be arbitrarily small). Hence, we can define map $F$ from $\Sigma_{1}\cup\Sigma$ to the tripod $T$ with the desired length bounds.

In an analogous way we define $F$ near all other vertices. It remains to define an interpolation that will take values in the neighborhood of each edge. Existence of such an interpolation, with controlled length of pre-images, follows by Proposition 4.3 and Theorem 4.2 from [LZ16].

We now discuss the value of constant $C$. Surfaces $\{f^{-1}(x)\}$ have areas bounded by $\frac{32\pi}{\Lambda}$ and genus $\leq 2$. If we plug that into the estimate from Theorem 4.2 in [LZ16] for parametric sweepouts, keeping in mind that graph $G$ can have double points in $\mathbb{R}^{2}$, we obtain that the length is bounded by $\textrm{length}(F^{-1})\leq\frac{70000}{\sqrt{\Lambda}}$. A better estimate can be obtained if we cut genus 2 surface along short curves and then apply a better bound for the lengths of curves in a sweepout of a surface that is diffeomorphic to a sphere with holes from [Lio14].

We briefly describe how to cut a genus 2 surface $\Sigma$. First we find a non-contractible curve $\gamma$ of length at most $\sqrt{\frac{2}{\sqrt{3}}}\sqrt{Area(\Sigma)}$ ([KS06]). Cutting $\Sigma$ along $\gamma$ we obtain either one or two genus 1 surfaces and glue in two spherical caps along $\gamma$ each of area $\textrm{length}(\gamma)^{2}/2\pi$. We then subdivide the resulting surface (or surfaces) using systolic inequality for the torus and slide the subdividing curve (or curves) into the interior of the original surface $\Sigma$ without affecting its length. In the end we obtain one or two surfaces with boundary diffeomorphic to a sphere with holes. Using the bounds from [Lio14] we obtain that there exists a sweepout of $\Sigma$ with curves of length $<\frac{1000}{\sqrt{\Lambda_{0}}}$. By Proposition 4.3 [LZ16] we can construct a family of sweepouts for the 1-parameter family of surfaces corresponding to an edge of $G$ with lengths $<\frac{2000}{\sqrt{\Lambda_{0}}}$. Hence, we can take $C=4000$. ∎