Vorticity-strain rate dynamics and the smallest scales of turbulence

A defining property of fluid turbulence is the presence of a wide range of dynamically interacting scales – bounded from above by the largest scales, which are of the order of flow dimension, and from below by the smallest scales, determined by the diffusive action of molecular viscosity. The largest scales transport the bulk of the flow energy and momentum, whereas the smallest scales are responsible for dissipating the flow energy into heat. The net transfer of energy from large to small-scales (onto viscous dissipation) occurs via an energy cascade, which renders the averaged energy dissipation-rate $\langle\epsilon\rangle$ to become independent of (kinematic) viscosity $\nu$ – which is also termed dissipative anomaly. This phenomenology, first proposed by Kolmogorov (1941) Kolmogorov (1941a, b) (K41 henceforth), identifies the smallest scales in the flow as:

$\displaystyle\eta_{\rm K}=\left(\nu^{3}/\langle\epsilon\rangle\right)^{1/4}\ \ ;\ \ \tau_{\rm K}=\left(\nu/\langle\epsilon\rangle\right)^{1/2}$

(1)

where $\eta_{\rm K}$ and $\tau_{\rm K}$ are the Kolmogorov length and time-scale respectively.

While dissipative anomaly has been widely confirmed Sreenivasan (1984, 1998); Pearson et al. (2002); Kaneda et al. (2003), the overall mean-field description of K41 has been invalidated Frisch (1995); Sreenivasan and Antonia (1997). This is because the fluctuations of dissipation-rate, and velocity gradients in general, exhibit a high-degree of spatial and temporal intermittency, with large non-Gaussian excursions from its mean, which become increasingly stronger with the Reynolds number Meneveau and Sreenivasan (1991); Buaria et al. (2019); Elsinga et al. (2020). Such extreme events play a crucial role in numerous physical processes Falkovich et al. (2002); Sreenivasan (2004); Vergassola et al. (2007); Hamlington et al. (2012) and are at the center of turbulence theories and models Frisch (1995); Sreenivasan and Antonia (1997); Meneveau (2011). Simultaneously, it follows that the smallest scales in the flow, putatively corresponding to the extreme events, would be smaller than the Kolmogorov scales defined by Eq. (1) Paladin and Vulpiani (1987); Sreenivasan and Meneveau (1988); Nelkin (1990); Yakhot and Sreenivasan (2005); Buaria et al. (2019).

Several phenomenological models have been proposed to describe intermittency, with reasonable success in characterizing the statistics of velocity increments for inertial-scales Frisch (1995); Sreenivasan and Antonia (1997). However, an accurate description of the the smallest scales has remained elusive for two reasons. The first limitation is the insufficiency of well-resolved data across a wide range of Reynolds numbers, since capturing extreme events requires a very stringent small-scale resolution Donzis et al. (2008); Yeung et al. (2018); Buaria et al. (2019). The second limitation is that of phenomenological models, which typically appeal to adjustable parameters without a clear connection to the dynamics of the Navier-Stokes equations. For instance, it is well-known that extreme gradients are structurally arranged in tube-like vortices Douady et al. (1991); Jiménez et al. (1993); Ishihara et al. (2009); Buaria et al. (2019); however, prevailing intermittency theories neither predict this feature nor take it into account in a precise manner.

In this Letter, overcoming the aforementioned limitations, we propose a simple framework to characterize the smallest scales of turbulence based on vortical flow structures while also directly connecting to the underlying Navier-Stokes dynamics. Our predictions are validated with data from state-of-the-art direct numerical simulations (DNS) of the incompressible Navier-Stokes equations, demonstrating excellent agreement. We additionally show that predictions from prior intermittency models are recovered as a limiting case of our framework, and discuss the root of this discrepancy.

The DNS data utilized here correspond to the canonical setup of forced stationary isotropic turbulence in a periodic domain Ishihara et al. (2009), enabling the use of highly accurate Fourier pseudo-spectral methods Rogallo (1981). The key novelty of our data is that we have simultaneously achieved both very high Reynolds number and the prescribed small-scale resolution to accurately resolve the extreme events Yeung et al. (2018); Buaria et al. (2019). The data correspond to the same Taylor-scale Reynolds number ${R_{\lambda}}$ range of $140-1300$ as attained in recent studies (Buaria and Sreenivasan, 2020; Buaria et al., 2020a, b; Buaria and Pumir, 2021; Buaria et al., 2022; Buaria and Yeung, 2017). However, the run at ${R_{\lambda}}=1300$ is extended to a grid of $18432^{3}$ points (see Yeung and Ravikumar (2020)) – the largest DNS run to date – presenting a substantial improvement on any previous work investigating the smallest scales Schumacher (2007); Donzis et al. (2008); Buaria et al. (2019). The resolution is $k_{\rm{max}}\eta_{\rm K}\approx 6$ for ${R_{\lambda}}\leq 650$, and $k_{\rm{max}}\eta_{\rm K}\approx 4.5$ for ${R_{\lambda}}=1300$, where $k_{\rm{max}}=\sqrt{2}N/3$, is the maximum resolved wavenumber on a $N^{3}$ grid. Convergence with respect to resolution and statistical sampling has been thoroughly established in previous works (Yeung et al., 2018; Buaria et al., 2019; Yeung and Ravikumar, 2020).

We first identify the intrinsic features of Navier-Stokes dynamics that are essential to characterize the small-scales. From the velocity gradient tensor $A_{ij}=\partial u_{i}/\partial x_{j}$, two important descriptors of small-scale motions can be identified, viz., the strain-rate tensor $S_{ij}=(A_{ij}+A_{ji})/2$, and the vorticity vector $\omega_{i}=\epsilon_{ijk}A_{jk}$ ($\epsilon_{ijk}$ being the Levi-Civita symbol). We utilize their square-norms:

$\displaystyle\Sigma=2S_{ij}S_{ij}\ ,\ \ \ \Omega=\omega_{i}\omega_{i}\ ,$

(2)

the former being the dissipation-rate without the viscosity, i.e., $\Sigma=\epsilon/\nu$, and $\Omega$ being the enstrophy. From statistical homogeneity and the definition of $\tau_{\rm K}$, it follows $\langle\Omega\rangle=\langle\Sigma\rangle=1/\tau_{\rm K}^{2}$. It is well-known that the interaction of strain and vorticity plays a direct role in generating extreme gradients in the flow and hence the smallest scales Jiménez et al. (1993); Tsinober (2009). Understanding the salient properties of this interaction constitutes the first step of our analysis.

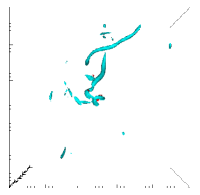
Figure 1 shows the structure of extreme events at the highest ${R_{\lambda}}$ ($=1300$), via visualization of isosurfaces of strain and vorticity. Figure 1a corresponds to a moderately large threshold and illustrates the well-known picture of intense gradients corresponding to vortical filaments, surrounded by sheet-like regions of intense strain Jiménez et al. (1993); Moisy and Jiménez (2004); Ishihara et al. (2009); Buaria et al. (2019). In Fig. 1b, a substantially larger threshold is chosen, and remarkably vortical filaments still prevail.

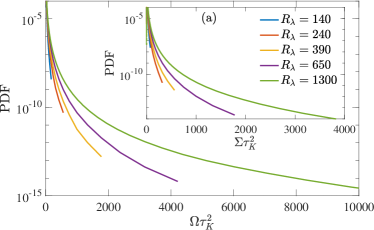
Although $\Omega$ and $\Sigma$ have the same mean, it is well-known that $\Omega$ is more intermittent Kerr (1985); Ishihara et al. (2009); Buaria et al. (2019) – likely due to the disparate role of vortex stretching in amplifying vorticity and simultaneously depleting strain Tsinober (2009); Buaria et al. (2022). This is reflected in their probability density functions (PDFs) in Fig. 2a, which firmly establishes that this difference is not a low-${R_{\lambda}}$ effect as previously believed He et al. (1998); Nelkin (1999); Donzis et al. (2008). The local interrelationship between strain and vorticity can be better understood by considering their mutual conditional expectations as shown in Fig. 2b (and also have been studied previously in various contexts Donzis et al. (2008); Buaria et al. (2019); Buaria and Pumir (2021)). The main observation is that while large $\Sigma$ is accompanied by proportionately large $\Omega$, i.e., $\langle\Omega|\Sigma\rangle\sim\Sigma$, the converse is not true. Instead, the strain in regions of intense vorticity is considerably weaker, and empirically described by the power-law:

$\displaystyle\langle\Sigma|\Omega\rangle\tau_{\rm K}^{2}\sim(\Omega\tau_{\rm K}^{2})^{\gamma}\ \ ,\ 0<\gamma<1$

(3)

where the exponent $\gamma$ slowly increases with ${R_{\lambda}}$ (see inset of Fig. 2b). Notably, existing intermittency models neither predict this, nor take it into account when characterizing the smallest scales.

With the knowledge of vortical flow structures and the asymmetry between the behavior of strain and vorticity (reflected in the exponent $\gamma$), we now formulate the framework to quantify the smallest scales in the flow. From a physical standpoint, the smallest length-scale in the flow corresponds to the smallest dimension of vortical structures, as obtained from a balance between viscosity and some effective strain $S_{\rm e}\simeq\Sigma_{\rm e}^{1/2}$ acting on the particular structure Burgers (1948):

$\displaystyle\eta=(\nu^{2}/\Sigma_{\rm e})^{1/4}$

(4)

which can be rewritten as

$\displaystyle\eta/\eta_{\rm K}=(\Sigma_{\rm e}\tau_{\rm K}^{2})^{-1/4}$

(5)

The classical Kolmogorov result in Eq. (1) is obtained for $\Sigma_{\rm e}$ corresponding to the mean-field, i.e., $\Sigma_{\rm e}=\langle\epsilon\rangle/\nu=1/\tau_{\rm K}^{2}$. Instead, the observation in Fig. 2 suggests utilizing the conditional relation in Eq. (3), leading to

$\displaystyle\eta/\eta_{\rm K}=(\Omega\tau_{\rm K}^{2})^{-\gamma/4}$

(6)

Introducing the length-scale $\eta_{\rm{ext}}$ as the size associated with vortex structures corresponding to $\Omega_{\rm{max}}$, which in turn corresponds to the smallest time-scale $\tau_{\rm{ext}}$, i.e., $\Omega_{\rm{max}}\sim\tau_{\rm{ext}}^{-2}$, leads to

$\displaystyle\eta_{\rm{ext}}/\eta_{\rm K}=(\tau_{\rm{ext}}/\tau_{\rm K})^{\gamma/2}$

(7)

Keeping in mind the growth of PDF tails with ${R_{\lambda}}$ (when normalized by $\tau_{\rm K}$), we can write:

$\displaystyle\eta_{\rm{ext}}=\eta_{\rm K}\times{R_{\lambda}}^{-\alpha}\ ,\ \ \ \tau_{\rm{ext}}=\tau_{\rm K}\times{R_{\lambda}}^{-\beta}\ ,$

(8)

where $\alpha,\beta>0$ are to be determined. Substituting these in Eq. (7) leads to

$\displaystyle 2\alpha=\gamma\beta\ ,$

(9)

giving first direct relation between $\alpha$ and $\beta$.

We now recall that velocity gradients in the flow simply correspond to velocity increments across the smallest length-scale. Hence, the strongest gradient simply corresponds to the largest velocity increment, say $\delta u_{\rm{max}}$ over $\eta_{\rm{ext}}$:

$\displaystyle 1/\tau_{\rm{ext}}\sim\delta u_{\rm{max}}/\eta_{\rm{ext}}\ .$

(10)

Based on earlier works Paladin and Vulpiani (1987); Jiménez et al. (1993); Buaria et al. (2019) (see also sup ):

$\displaystyle\delta u_{\rm{max}}\sim u^{\prime}\ ,$

(11)

where $u^{\prime}$ is the r.m.s. of velocity; which upon substitution in Eq. (10) gives

$\displaystyle\beta=\alpha+1/2\ ,$

(12)

Here, we have used the standard estimate $u^{\prime}/u_{\rm K}\sim{R_{\lambda}}^{1/2}$, where $u_{\rm K}=\eta_{\rm K}/\tau_{\rm K}$. Finally, solving Eqs. (9) and (12) allows us to obtain $\alpha$ and $\beta$ in terms of $\gamma$:

$\displaystyle\beta=\frac{1}{2-\gamma}\ ,\ \ \alpha=\frac{\gamma}{2(2-\gamma)}\ .$

(13)

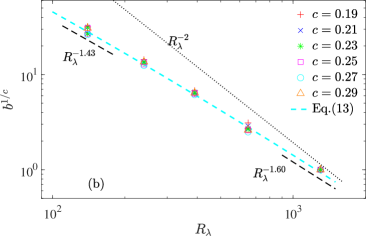
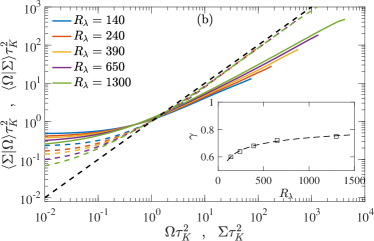
To first validate the result for $\beta$, we return to the PDFs shown in Fig. 2a, with the expectation that rescaling them with $\tau_{\rm{ext}}$ should collapse the tails. Figure 3a shows this result, with $\beta$ (and $\tau_{\rm{ext}}$) defined based on $\gamma$ obtained in Fig. 2b – demonstrating excellent agreement. It should be noted that a similar collapse was also obtained in Buaria et al. (2019) at lower ${R_{\lambda}}$ and for a fixed value of $\beta=0.775$. However, the current data at significantly higher ${R_{\lambda}}$ negate a fixed value of $\beta$. Hence, the ${R_{\lambda}}$-dependence of $\beta$ (arising from $\gamma$) is a crucial ingredient of the current approach and imperative for obtaining an accurate description. This expectation and the quantitative variation of $\beta$ are also consistent with recent results of Elsinga et al. (2020), which characterize the scaling of extreme dissipation events based on underlying shear-layer structures.

While the arguments leading to Eq. (13) utilize the physical picture of intense vorticity tubes, the collapse in Fig. 3a remarkably indicates that both extreme vorticity and strain scale with $\tau_{ext}$ – though these extrema arise from different spatial locations. This suggests that the amplification of vorticity and strain occurs simultaneously with the same time-scale, albeit non-locally ¹¹1 note, vorticity and strain are coupled non-locally via the Biot-Savart relation Buaria et al. (2020b); Buaria and Pumir (2021), inducing the asymmetry in their local correlation as observed in Fig. 2b. Thus, the exponent $\gamma<1$, which captures this asymmetry, also captures the non-locality of vorticity-strain interaction. In fact, as demonstrated later, this is also the key reason for our framework’s success over prior intermittency models.

The collapse in Fig. 3a can be additionally verified by noting that the tails of PDFs of $\Sigma$ and $\Omega$ (and velocity gradients in general) are well fitted by stretched-exponential functions Meneveau and Sreenivasan (1991); Benzi et al. (1991); Kailasnath et al. (1992); Zeff et al. (2003); Donzis et al. (2008); Buaria et al. (2019):

$\displaystyle f_{X}(x)\approx a\exp(-b\ x^{c})\ ,$

(14)

where $x=\Omega\tau_{\rm K}^{2}$ or $\Sigma\tau_{\rm K}^{2}$. Applying a change of variable $x_{\rm e}=x(\tau_{\rm K}/\tau_{\rm{ext}})^{2}$ will lead to the transformation $b\rightarrow b^{\prime}=b\times{R_{\lambda}}^{2\beta c}$. A necessary condition to collapse the tails would imply that $b^{\prime}$ is independent of ${R_{\lambda}}$, leading to the expectation that $b^{1/c}\sim{R_{\lambda}}^{-2\beta}$ (for any given value of $c$).

Figure 3b shows the plot of $b^{1/c}$ as a function of ${R_{\lambda}}$, for various $c$ values (comprehensive details about the fitting procedure, and the chosen range of $c$ are discussed in the Supplementary sup ). We compare the slope of the data points for $b^{1/c}$ with the result for $\beta$ in Eq. (13) by utilizing the $\gamma$ obtained earlier from Fig. 2b (note $\gamma$ varies from $0.60-0.75$ for ${R_{\lambda}}=140-1300$) – once again, demonstrating excellent agreement. It is worth iterating that the collapse obtained in Fig. 3a does not depend on the curve fitting procedure. Nevertheless, this fitting procedure independently reaffirms the robustness of our result and rules out any ambiguity.

While the result for $\tau_{\rm{ext}}$ (and $\beta$) was readily verified using the PDF tails, verifying $\eta_{\rm{ext}}$ (and $\alpha$) presents an inherent difficulty. A simple approach would be to evaluate the PDF of the coarse-grained gradient $\delta u_{r}/r$, where $\delta u_{r}$ is the velocity increment over some scale $r$, and successively make $r$ smaller until the PDF of $\delta u_{r}/r$ collapses to the PDF of velocity gradient for $r\leq\eta_{\rm{ext}}$. However, DNS data only provides discrete values of $r$ (in integer multiples of the grid spacing $\Delta x$), making it impractical to precisely identify the exact $r/\eta_{\rm{ext}}$ without invoking some interpolation or approximate analysis. Instead, we devise a simple alternative by characterizing the deviations of $\delta u_{r}/r$ from the actual gradient. Note, the velocity increment can be longitudinal or transverse, i.e., corresponding to velocity component parallel or perpendicular (respectively) to the separation vector, but it will be evident that this choice is immaterial.

From the Taylor-series expansion of $\delta u_{r}$, it follows:

$\displaystyle\frac{\delta u_{r}}{r}=\frac{\partial u}{\partial x}+\frac{\partial^{2}u}{\partial x^{2}}\frac{r}{2!}+\frac{\partial^{3}u}{\partial x^{3}}\frac{r^{2}}{3!}+...$

(15)

For $r\leq\eta_{\rm{ext}}$, the r.h.s. converges to $\partial u/\partial x$, whereas for $r>\eta_{\rm{ext}}$ deviations are expected due to the higher-order corrections. For the most extreme gradients, we can nominally write: $\partial^{n}u/\partial x^{n}\simeq c_{n}u^{\prime}/\eta_{\rm{ext}}^{n}$, where $c_{n}$ are independent of ${R_{\lambda}}$. Together with $u^{\prime}\sim\eta_{\rm{ext}}/\tau_{\rm{ext}}$, this gives:

$\displaystyle\frac{\delta u_{r}\tau_{\rm{ext}}}{r}\simeq c_{1}+\frac{c_{2}}{2!}\left(\frac{r}{\eta_{\rm{ext}}}\right)+\frac{c_{3}}{3!}\left(\frac{r}{\eta_{\rm{ext}}}\right)^{2}+...\ ,$

(16)

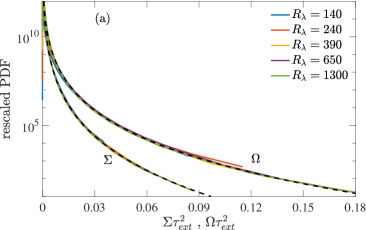
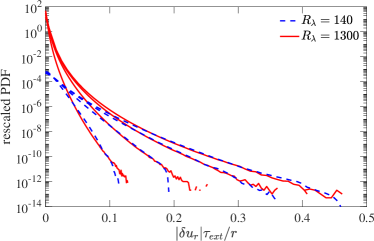
leading to expectation that the tails of PDFs of $\delta u_{r}\tau_{\rm{ext}}/r$ can be collapsed at different ${R_{\lambda}}$ by matching the $r/\eta_{\rm{ext}}$, thus providing a simpler test with DNS data. We notice that $\eta_{\rm K}/\eta_{\rm{ext}}$ at ${R_{\lambda}}=140$ is approximately $2$ times than that at ${R_{\lambda}}=1300$. Fig. 4 shows the rescaled PDF of $\delta u_{r}\tau_{\rm{ext}}/r$, for $r/\eta_{\rm K}=1,2,4,8$ at ${R_{\lambda}}=1300$, and $r/\eta_{\rm K}=2,4,8,16$ at ${R_{\lambda}}=140$, showing a remarkably good collapse of the tails, providing a strong confirmation of our approach. Similarly, for ${R_{\lambda}}=140$ and ${R_{\lambda}}=650$, the ratio of their $\eta_{\rm K}/\eta_{\rm{ext}}$ is approximately $1.5$, and a similar collapse is obtained (see sup ).

The framework developed in this work differs from previous phenomenological models, which ignore important features of the Navier-Stokes dynamics. In this regard, the commonly utilized notion is that the viscous cutoff scale is defined by the phenomenological criteria of local Reynolds number being unity Paladin and Vulpiani (1987); Nelkin (1990); Frisch (1995); Yakhot and Sreenivasan (2005); Schumacher (2007):

$\displaystyle\delta u_{r}\ r/\nu\simeq 1\ .$

(17)

This is essentially an ad-hoc extension of the K41 phenomenology, since $u_{\rm K}\eta_{\rm K}/\nu=1$. The velocity increment $\delta u_{r}$ is assumed to be Hölder continuous, akin to multifractility Frisch (1995):

$\displaystyle\delta u_{r}/u^{\prime}\sim(r/L)^{h}\ ,$

(18)

where $L$ is the large-eddy length and $h$ is the local Hölder exponent. It trivially follows that the smallest scales correspond to the minimum Hölder exponent $h_{min}$. Since $\delta u_{r}\sim u^{\prime}$ for the smallest scales, or equivalently $h_{min}=0$ Paladin and Vulpiani (1987); Nelkin (1990); Frisch (1995), it can be shown that sup :

$\displaystyle\beta=2\alpha\ ,\ \ \beta=\alpha+\frac{1}{2}\ ,$

(19)

giving $\beta=1$ and $\alpha=1/2$, in line with previous predictions Paladin and Vulpiani (1987); Sreenivasan and Meneveau (1988); Nelkin (1990); Yakhot and Sreenivasan (2005).

It can be readily seen that the result in Eq. (19) differs from our results in Eqs. (9) and (12) only by the factor $\gamma$, both being the same if $\gamma=1$, i.e. when strain and vorticity are locally commensurate. While the numerical results clearly demonstrate that $\gamma<1$, the weak increase in $\gamma$ with ${R_{\lambda}}$ (inset of Fig. 2b) is suggestive of a slow approach to $\gamma=1$ when ${R_{\lambda}}\to\infty$. However, a nominal extrapolation of the data in Fig. 2b suggests that this limit will be reached at extremely large ${R_{\lambda}}$, beyond what can be achieved experimentally or numerically sup . In fact, this is in line with previous and recent results which independently reaffirm the shortcomings of the multifractal model Jiménez et al. (1993); Buaria and Sreenivasan (2020); Elsinga et al. (2020).

Since the result in Eq. (18) (for $h=0$, giving $\delta u_{r}\sim u^{\prime}$) is consistent across all descriptions, the noted discrepancy arises from the criterion in Eq. (17). For vortex tubes, the smallest scale as set by Eq. (4) is qualitatively similar to the criteria in Eq. (17). However, it does not provide any constraint on the circulation of the vortex, $\Gamma$, implying that the local Reynolds number defined as $R_{\Gamma}=\Gamma/\nu$ is not necessarily unity. Instead, our results indicate $R_{\Gamma}\simeq{R_{\lambda}}^{1-\beta}$, in qualitative agreement with the results of Jiménez et al. (1993). Note, for ${R_{\lambda}}\to\infty$, the expectation $\gamma,\beta\to 1$ implies that $R_{\Gamma}\to$ constant. Thus, the crucial misstep in prevailing intermittency models appears to be its inability in distinguishing longitudinal and transverse components and utilizing their local correlation. In fact, previous and recent results have shown that this shortcoming also extends to inertial range, where longitudinal and transverse structure functions exhibit different scaling exponents, contrary to the prediction from the multifractal model Dhruva et al. (1997); Shen and Warhaft (2002); Gotoh et al. (2002); Grauer et al. (2012).

In conclusion, we have developed a simple framework to characterize the smallest scales of turbulence, which utilizes the underlying asymmetry between strain and vorticity dynamics of Navier-Stokes equations. We have demonstrated excellent agreement of DNS data with predictions, and shown that our parametrization reduces to predictions from existing intermittency models when the symmetry between strain and vorticity is restored, albeit at extremely large ${R_{\lambda}}$, which are unattainable on Earth. In this regard, understanding the asymmetry between vorticity and strain appears to be a crucial component to understand intermittency in turbulence for all practical situations of interest, suggestive of a new avenue of investigation. It would also be pertinent to extend the current framework to turbulent mixing of scalars, where recent results have suggested that the smallest scales in the scalar field also deviate from classical predictions Buaria et al. (2021a, b).