Volume effect on the extraction of sound velocity in high-energy nucleus-nucleus collisions

Jing-An Sun [email protected] Institute of Modern Physics, Fudan University, Shanghai 200433, China Department of Physics, McGill University 3600 rue University Montreal, QC Canada H3A 2T8 Li Yan [email protected] Institute of Modern Physics, Fudan University, Shanghai 200433, China Key Laboratory of Nuclear Physics and Ion-beam Application (MOE), Fudan University, Shanghai 200433, China

Abstract

The determination of the speed of sound in quark-gluon plasma is a crucial aspect of understanding the properties of strongly interacting matter created in relativistic heavy-ion collisions. In this study, we investigate the impact of initial-state fluctuations on the extraction of the speed of sound in a quark-gluon plasma in the ultra-central collisions. By employing the T_RENTo model for simulating initial conditions, we demonstrate that these fluctuations lead to sizable volume effect, which in turn corrects the measured values of the sound velocity. With respect to realistic conditions of high-energy heavy-ion experiments, we provide quantitative estimate of these corrections.

I introduction

The speed of sound, $c_{s}$ , defined as the ratio of the variation of pressure to that of energy density, relies on certain thermodynamic conditions,

c_{s}^{2}\equiv\frac{dP}{de}\Big{|}_{X}\,.

(1)

For instance, with respect to a quantum chromodynamic (QCD) system in thermal equilibrium, the solution of sound velocity from the lattice calculations of QCD implicitly assumes adiabatic condition Bazavov et al. (2014).

Speed of sound can be measured in experiments. Consider, for instance, ideally a thermal system in equilibrium is constrained in a box with fixed volume. As one warms up the system by generating entropy adiabatically, effectively the increase of temperature, $\Delta T$ , and entropy $\Delta S$ , can be used to estimate the sound velocity. By definition and the thermodynamic relations Van Hove (1982); Campanini and Ferri (2011),

c_{s}^{2}\equiv\frac{dP}{de}=\frac{sdT}{Tds}=\frac{\Delta T/T}{\Delta S/S}\,.

(2)

In obtaining the last equation, one has taken into account the property of spatial homogeneity owing to the global thermal equilibrium condition, and the fixed volume condition: $\Delta V/\Delta S=0$ .

Recently, in spirit of Eq. (2), the measurement of the speed of sound of a thermal QCD system has been proposed Gardim et al. (2020a) and carried out via the high-energy ultra-central collisions at the Large Hadron Collider (LHC) Hayrapetyan et al. (2024); Nielsen (2024). In these ultra-central collisions, system volume approaches maximum, while event-by-event quantum fluctuations from nucleon-nucleon collisions provide a means of entropy production adiabatically. In Eq. (2), the condition of thermal equilibrium is essential, although in realistic high-energy heavy-ion collisions, thermal equilibrium in the produced quark-gluon plasmas (QGP) is expected only locally, and even approximately, leading to a dissipative fluid description of the system expansion Shen and Yan (2020). Accordingly, the conservation of energy and entropy allows one to effectively convert the system into a homogenous QGP with volume $V_{\rm eff}$ and temperature $T_{\rm eff}$ . Regarding final-state observables, hydrodynamic response relations are introduced to further relate the effective temperature $T_{\rm eff}$ to the mean value of the transverse momentum of the produced particles $\langle p_{T}\rangle$ : $T_{\rm eff}\propto\langle p_{T}\rangle$ , and the total entropy to the charged particle multiplicity: $S\propto dN_{\rm ch}/dy$ . Eventually, the conjecture Gardim et al. (2020a) states that sound velocity in QGP can be measured in experiments from the ultra-central collisions by

\displaystyle(c_{s}^{0})^{2}=\frac{\Delta\ln T_{\rm eff}}{\Delta\ln S}=\frac{\Delta\ln\langle p_{T}\rangle}{\Delta\ln(dN_{\rm ch}/dy)}\,.

(3)

To avoid confusion, in Eq. (3) and the following, we denote the extracted sound velocity from the ratio of relative change of the effective temperature to that of the total entropy by $c_{s}^{0}$ .

To validate this conjecture, several theoretical analyses have been performed Gardim et al. (2020b, 2024); Soares Rocha et al. (2024); Nijs and van der Schee (2024). In this work, assuming the well-established hydrodynamic response relations, we examine the extraction of sound velocity with respect to the fluctuating initial state of realistic heavy-ion collisions. On the first sight, it might seem trivial because the first equation in Eq. (3) follows simply the thermodynamic relation in Eq. (2). However, on an event-by-event basis, initial state density with fluctuations is neither homogeneous, nor sufficiently large that variation of the effective volume can be negligible. As a consequence, finite-volume effect arises which corrects the extracted sound velocity from Eq. (3), leading to,

c_{s}^{2}=\frac{dP}{de}=\left(1-\frac{\Delta\ln V_{\rm eff}}{\Delta\ln S}\right)^{-1}\frac{\Delta\ln T_{\rm eff}}{\Delta\ln S}\,.

(4)

Here, the ratio between the relative change of volume and total entropy $\Delta\ln V_{\rm eff}/\Delta\ln S$ , characterizes the response of the system volume as entropy is produced, which is not necessarily vanishing as one converts a fluctuating system to a homogeneous one. In fact, imposing the condition that $\Delta\ln V_{\rm eff}/\Delta\ln S=0$ induces violation of adiabiticity.

II Effective modeling of initial state

Let us first briefly review the T_RENTo model that we shall use. T_RENTo Model Moreland et al. (2015) provides one of the state-of-the-art numerical modelings of the initial stage of relativistic nucleus-nucleus collisions, with several parameters that represent different physics aspects. There are three substantial ingredients in the model,

•

A Gaussian beam-integrated proton density function with width $w$ ,

$\int dz\rho(x,y)\sim\exp\left(-\frac{x^{2}+y^{2}}{2w^{2}}\right)\,.$ (5)

In principle, the width captures the size of a proton as it participates the collisions.
•

A fluctuating thickness function for each proton, $T_{A,B}(x,y)\sim\alpha_{A,B}\int dz\rho$ , with $A$ ( $B$ ) labeling the pair of projectiles and $\alpha_{A,B}$ random weights satisfying a gamma distribution with unit mean,

$P_{k}(\alpha)=\frac{k^{k}}{\Gamma(k)}\alpha^{k-1}e^{-k\alpha}\,.$ (6)

Here, the fluctuating parameter $k$ is also inversely proportional to the variance. Owing to the appearance of the random weights, the resulted multiplicity receives extra fluctuations. Larger fluctuations are realized via smaller values of the fluctuation parameter $k$ , and vice versa.
•

A reduced thickness function that characterizes initial state entropy density,

$s(\tau_{0},x,y)=CT_{R}(x,y)=\left(\frac{T_{A}^{p}+T_{B}^{p}}{2}\right)^{1/p}\,,$ (7)

where the generalized mean parameter $p$ , is introduced to effectively average the thickness functions from the two colliding nucleons. The overall factor $C$ can be adjusted, according to the total multiplicity in collisions.

The three parameters, width $w$ , fluctuation parameter $k$ , and the generalized mean $p$ , are allowed to vary to reproduce the initial entropy density profile of a thermalized QGP, on different grounds. For instance, $p=1$ gives rise to arithmetic average in Eq. (7), which leads to the Monte Carlo wounded nucleon ansatz Miller et al. (2007) and deposits a blob of entropy for each nucleon. For $p=0$ , entropy is deposited around the center of the nucleon-nucleon collision, and the resulted density profile approximates that obtained in the IP-Glasma model Schenke et al. (2012). With respect to a number of observables in experiments, these parameters have been determined based on Bayesian analyses Everett et al. (2021), with the most probable values found in ranges, $p\in[0.063,0.139]$ , $w\in[0.81,1.19]$ fm and $k\in[0.98,1.05]$ . In the current study, we consider $w=1$ fm, $k=1$ , and $p=0$ as the most probable values.

III Extraction of sound velocity

Refer to caption — Figure 1: (Color online) The initial-state parameter dependent relations between $T_{\rm eff}$ and $S$ , and $V_{\rm eff}$ and $S$ . Left panels ((a) and (b)): variation of width parameter $w$ , with $p$ and $k$ fixed. Middle panels ((c) and (d)): variation of the fluctuation parameter $k$ , with $p$ and $w$ fixed. Right panels ((e) and (f)): variation of the fluctuation parameter $p$ , with $k$ and $w$ fixed.

The procedure of extracting sound velocity in the QGP medium starts with solving the effective temperature and effective volume Gardim et al. (2020a) from the equations,


	$\displaystyle E=E_{\rm final}=e(T_{\rm eff})V_{\rm eff}\,,$		(8a)
	$\displaystyle S=S_{\rm final}=s(T_{\rm eff})V_{\rm eff}\,,$		(8b)

where the final-state total energy and entropy are estimated from particles emitted from the freeze-out hyper-surface. We employ a parameterized lattice equation of state (LEOS) that interpolates between the hadron resonance gas at low temperatures to the lattice results of QCD at high temperatures. With same parameters as those used in Bazavov et al. (2014), the effective parameterization of the LEOS has been widely applied in many hydrodynamic calculations.

With respect to the conservation of energy and entropy, the equations can be imposed as well if the total energy and entropy are given by the initial states,


$\displaystyle E=E_{\rm initial}$	$\displaystyle=\tau_{0}\int d\vec{x}_{\perp}d\eta_{s}e(\tau_{0},\vec{x}_{\perp},\eta_{s})\,,$	(9a)
$\displaystyle S=S_{\rm initial}$	$\displaystyle=\tau_{0}\int d\vec{x}_{\perp}d\eta_{s}s(\tau_{0},\vec{x}_{\perp},\eta_{s})\,,$	(9b)

where the initial energy density is achieved by converting the entropy density using the LEOS, $e=e(s)$ ¹¹1 An alternative procedure is to relate the reduced thickness $T_{R}(x,y)$ to the initial energy density profile, then entropy density is obtained by a conversion via LEOS $s=s(e)$ Everett et al. (2021). . The initial proper time $\tau_{0}$ in hydrodynamic modeling is often considered with respect to a quick thermalization assumption, with $\tau_{0}\leq 1$ fm/c. In our analysis, the exact value of $\tau_{0}$ is irrelevant to the extraction of the speed of sound. The dependence on the space-time rapidity, $\eta_{s}={\rm arctanh}(z/t)$ , reflects the breaking of boost invariance in high-energy collisions, which is necessary for the conservation of energy during medium expansion. In this work, we consider a factorized density and a two-parameter function $s(\tau_{0},\vec{x}_{\perp},\eta_{s})=s(\tau_{0},\vec{x}_{\perp})\times w(\eta_{s})$ for the longitudinal density profile Chatterjee and Bożek (2018),

w(\eta_{s})=\exp\left(-\theta(|\eta_{s}|-\eta_{M})\frac{(|\eta_{s}|-\eta_{M})^{2}}{2\sigma_{\eta}^{2}}\right)\,.

(10)

Varying the parameters, $\eta_{M}$ and $\sigma_{\eta}$ , the shape of the longitudinal distribution can be adjusted accordingly. In particular, the shape affects the entropy and energy in the mid-rapidity region, $\eta_{s}\in[-0.5,0.5]$ , and potentially plays a role in the rapidity selection in the extraction of the speed of sound in experiments Nijs and van der Schee (2024); Nielsen (2024). We nevertheless leave the discussion on the $\eta_{s}$ dependence to future works.

Ideally, with respect to the energy and entropy conservation, Eq. (8) and Eq. (9) are equivalent. However, it should be emphasized that, due to the finite dissipative effect in realistic QGP, from Eq. (9) the resulted relation between the effective temperature and entropy is not expected comparable to the relation between the mean transverse momentum and charged particle multiplicity in experiements²²2 Finite viscous effects lead to entropy production and a change in the mean transverse momentum. Accordingly, in the ultra-central collisions, the distributions of the mean transverse momentum and the charged particle multiplicity, are supposed to be distorted, in comparion to the distribution of $T_{\rm eff}$ and $S$ solved from Eq. (9). .

By imposing these identities in Eq. (8), as well in Eq. (9), the medium from realistic heavy-ion collisions is effectively converted to a homogeneous QGP in equilibrium, with volume $V_{\rm eff}$ and temperature $T_{\rm eff}$ . In order to solve a sound velocity that is consistent with LEOS, the conversion must be adiabatic. Accordingly, volume between the two systems must differ. For instance, for inhomogeneous systems extra entropy is produced during the conversion, similar to the thermalization process. If there is no change of volume between the realistic QGP and the homogeneous QGP, without work there must be heat flow out of the system according to the first law of thermodynamics, thus adiabaticity condition is violated.

III.1 Dependence on initial state model parameters

Without solving the entire medium evolution towards particlization, it is significantly simplified to extract the sound velocity from Eq. (9) on an event-by-event basis. In particular, the effect of initial state fluctuations on the extraction of the speed of sound can be studied. For each set of parameters in the T_RENTo model, $(w,k,p)$ , we select and simulate roughly five million events across the 0% to 5% centrality class of Pb-Pb collisions. We also vary the overall constant $C$ in Eq. (7), in order to scan a wider range of effective temperatures Gardim et al. (2024).

We first fix the fluctuation parameter $k$ and the generalized mean $p$ by their most probable values, and vary the effective nucleon width around $w=1.0$ fm, results are shown in the left panels of Fig. 1 ((a) and (d)). In analogy to the measurements of mean transverse momentum and multiplicity in experiments, we plot the effective temperature normalized by its average value in these ultra-central events, $T_{\rm eff}/T_{\rm eff}^{0}$ , as a function of the total entropy scaled by its corresponding average, $S/S^{0}$ . As shown in Fig. 1 (a), these are data points solved within approximately 40 bins in the 0%-5% centrality class. Statistical errors of these points are estimated with respect to their standard deviation. At $S>S^{0}$ , the system size tends to saturate with a vanishing impact parameter, one observes a perfect linear relation between $T_{\rm eff}/T_{\rm eff}^{0}$ and $S/S^{0}$ , with the slope corresponding to $c_{s}^{0}$ that can be extracted following Eq. (3). Note that, unlike the mean transverse momentum, from event-by-event simulations of initial states, there is no plateau and dip observed below $S^{0}$ in the effective temperature Nielsen (2024); Hayrapetyan et al. (2024); Nijs and van der Schee (2024). With the width growing from $w=0.5$ fm (blue points), to $w=1.0$ fm (brown points), to $w=1.5$ fm (green points), the resulted effective temperature decreases, but the slope increases.

In Fig. 1 (d), the variation of the effective volume is plotted similarly, as a function of total entropy, for the ultra-central collisions events. We notice that although the original size of the collision system saturates, as the impact parameter approaches zero for $S>S^{0}$ , the effective volume grows linearly. The slope of these lines, which we indicate as $\alpha=\Delta\ln V_{\rm eff}/\Delta\ln S$ , exhibits a systematic decrease as the width increases from $0.5$ fm to $1.5$ fm.

We next focus on the effect of the fluctuation parameter $k$ . Analogously, we scan $k$ around its most probable values, while $w$ and $p$ are fixed. The corresponding results are shown in the middle panels of Fig. 1 ((b) and (e)). We notice that variation of $k$ does not change the effective temperature, neither the total entropy. Consequently, the linear relation between $T_{\rm eff}$ and $S$ is barely affected by $k$ . Unless for the small value, $k=0.5$ , namely, large multiplicity fluctuations, the effect of $k$ on the effective volume is negible as well. With respect to the variation of $k$ , the linearity between $V_{\rm eff}$ and $S$ in the ultra-central events is weakly affected.

The results in Fig. 1 (c) and (f) are associated with the effect of $p$ , for which we repeat the simulations with fixed values of both $k=1.0$ and $w=1.0$ fm, but vary $p$ from -1 to 1. The increase of $p$ does not impact the effective temperature, but does lead to a significant enhancement in the total entropy and the effective volume. Accordingly, the extracted slope $c_{s}^{0}$ increases, and $\alpha$ decreases, as $p$ increases.

Interestingly, if one takes into account the linear relations $T_{\rm eff}\propto\langle p_{T}\rangle$ and $S\propto dN_{\rm ch}/dy$ , the parameter dependence of $T_{\rm eff}$ and $S$ found in our simulations are consistent to the observations from the Bayesian analyses of full hydrodynamic calculations Everett et al. (2021). First, the width parameter $w$ has a negative correlation to the effective temperature (or $\langle p_{T}\rangle$ ), and a positive correlation to the total entropy (or $dN_{\rm ch}/dy$ ). The fluctuation parameter $k$ is barely correlated to both the effective temperature (or $\langle p_{T}\rangle$ ) and the total entropy (or $dN_{\rm ch}/dy$ ). The generalized mean $p$ is positively correlated to the total entropy (or $dN_{\rm ch}/dy$ ), while it has negligible effect on the effective temperature (or $\langle p_{T}\rangle$ ).

III.2 Volume effect

One immediately deduces that $c_{s}^{0}$ barely relies on the fluctuation parameter $k$ , as both $T_{\rm eff}$ and $S$ are not affected by the variation of $k$ . However, the correlations of $T_{\rm eff}$ and $S$ to $w$ and $p$ , result in strong initial-state parameter dependence of the extracted sound velocity $c_{s}^{0}$ from the event-by-event simulations. As shown in the top panels of Fig. 2, $c_{s}^{0}$ , the slope extracted directed from the linearity between $T_{\rm eff}$ and $S$ , captures to a large extent the physical speed of sound, as comparing to the input values from LEoS. However, the exacted values of $c_{s}^{2}$ can deviate from the physical speed of sound, depending on $p$ and $w$ . For instance, at $T_{\rm eff}=225$ MeV, corresponding to the ultra-central PbPb collisions at $\sqrt{s_{NN}}=$ 5.02 TeV, small value of $p=-1$ gives rise to an underestimate of the speed of sound, while large $p$ leads to overestimation. In fact, one notices positive correlations between $(c_{s}^{0})^{2}$ , and $p$ and $w$ .

To extract the physical values of the speed of sound, $c_{s}$ , a volume effect correction is required in addition to $c_{s}^{0}$ . To some extent, the volume effect arising from the event-by-event simulations is rooted in the spatial inhomogeneity of the initial state density profile. Fig. 3 illustrates four typical initial-state density profiles generated by the T_RENTo model. With both $p$ and $w$ increase (from (a) to (d)), instead of being discrete, the density distribution tends to be more smooth and connected. On the other hand, recall that the ratio $\alpha$ grows monotonically from being negative towards being positive, as $p$ and $w$ increase. In fact, it can be shown as in the Appendix, with respect to an inhomogeneous density, the change of the effective volume with respect to entropy production can be positive, if the density distribution is extremely discrete (as in panel (a) and (b) in Fig. 3), and can be negative if the density distribution is more connected (as in panel (c) and (d) in Fig. 3). Moreover, the absolute change of the effective volume is large when the entropy production leads to larger spatial inhomogeneity.

Because the effective volume $V_{\rm eff}$ varies as the entropy increases, corrections due to the volume effect must be taken into account. According to Eq. (4), the speed of sound extracted with respect to different parameters, $w$ , $k$ , and $p$ are shown in the lower panel of Fig. 2. With the volume effect correction, improvement is remarkable comparing to the LEoS results. It is worth noticing that, with the volume effect correction, the extraction also precisely captures the non-monotonic increase of the speed of sound at low temperatures, where the system becomes a hadron gas. Moreover, after the volume effect correction, parameter dependence of the extracted speed of sound becomes negligible. This is important, because the physical value of the extracted speed of sound must be independent of the initial-state parameters, as $c_{s}$ reflects only the thermodynamic nature of the medium.

We now estimate the ratio $\Delta\ln V_{\rm eff}/\Delta\ln S$ for realistic high-energy heavy-ion experiments. Regarding the variation of $p$ or $k$ in the calculations, the effective temperatures $T_{\rm eff}$ can be determined with certain values. For all these fixed effective temperatures, the corresponding ratio $\Delta\ln V_{\rm eff}/\Delta\ln S$ exhibits linear correlation with the total entropy. Given the relation between the total entropy and the charged particle multiplicity, namely, $6.7\times dN_{\rm ch}/dy=dS/d\eta_{s}$ Hanus et al. (2019), these linear correlations are shown in Fig. 4. Replacing also $T_{\rm eff}=\langle p_{T}\rangle/3$ , We find a formula that parameterizes all these lines,

\frac{\Delta\ln V_{\rm eff}}{\Delta\ln S}=a-\exp\left[-\left(b_{0}+b_{1}\langle p_{T}\rangle+b_{2}\langle p_{T}\rangle^{2}\right)\right]N_{\rm ch}\,,

(11)

with the constant coefficients: $a=1$ , $b_{0}=-3.54$ , $b_{1}=26.97$ GeV^-1 and $b_{2}=-45.67$ GeV^-2. Here, $a=1$ should be understood as the relative ratio in the thermodynamic limit where $dS/dV=S/V$ . Given Eq. (11), the measured mean transverse momentum and the charged particle multiplicity in the ultra-central collisions allow one to estimate the volume effect. The formula Eq. (11) should be valid for all the ultra-central nucleus-nucleus collisions carried out at the LHC and the top energy at the Relativistic Heavy-Ion Collider at the Brookhaven National Laboratory. In particular, for the measured effective temperature ( $T_{\rm eff}=220$ MeV) and charged particle multiplicity ( $dN_{\rm ch}/dy=1943\pm 54$ Adam et al. (2016)) regarding the ultra-central PbPb collisions at $\sqrt{s_{NN}}=$ 5.02 TeV at the LHC, Eq. (11) yields $\Delta\ln V_{\rm eff}/\Delta\ln S=0.065\pm 0.025$ . Therefore, the measured value of the speed of sound Hayrapetyan et al. (2024); Nielsen (2024) is expected slightly smaller than the physical one.

IV Summary and discussion

With the help of the T_RENTo modeling of initial states, we are able to investigate the effect of event-by-event fluctuations on the extraction of the sound velocity proposed in Ref. Gardim et al. (2020a). On one hand, these event-by-event fluctuations are crucial as they provide a means of variation of entropy in the systems created in ultra-central nucleus-nucleus collisions adiabatically. On the other hand, however, spatial inhomogeneity induced by these fluctuations results in variation of the effective volume. Accordingly, the extraction formula, which relates the speed of sound in QGP to the ratio of the relative change of mean transverse momentum and the relative change of the charged particle multiplicity, must receive corrections from the volume effect.

In fact, the variation of the effective volume is inevitable, as the conversion from an inhomogeneous density distribution to a fixed-volume QGP system can not be realized adiabaticity, it thus affects the extraction of the speed of sound nonetheless. With the correction from the volume effect, the extracted speed of sound from our simulations appears physical, as they are not only quantitatively consistent with the LEOS results, but also independent of initial-state parameters.

Although the precise volume effect can only be calculated via model simulations, we propose an empirical formula (Eq. (11)) that can be used for realistic experiments, provided the mean transverse momentum and the charged particle multiplicity.

Acknowledgements.

We are grateful to Jean-Yves Ollitrault and Wei Li for helpful discussions. Jing-An Sun also thanks the hospitality of the nuclear theory group at McGill University, especially for the useful conversations with Charles Gale, Sangyong Jeon, Lipei Du, Xiangyu Wu, and Nicolas Miro Fortier. The computations are made on the Beluga supercomputer system at McGill University, managed by Calcul Québec and the Digital Research Alliance of Canada. This work is supported by the National Natural Science Foundation of China under Grant No. 12375133 and 12147101.

Appendix A Inhomogeneity and $\Delta\ln V_{\rm eff}/\Delta\ln S$

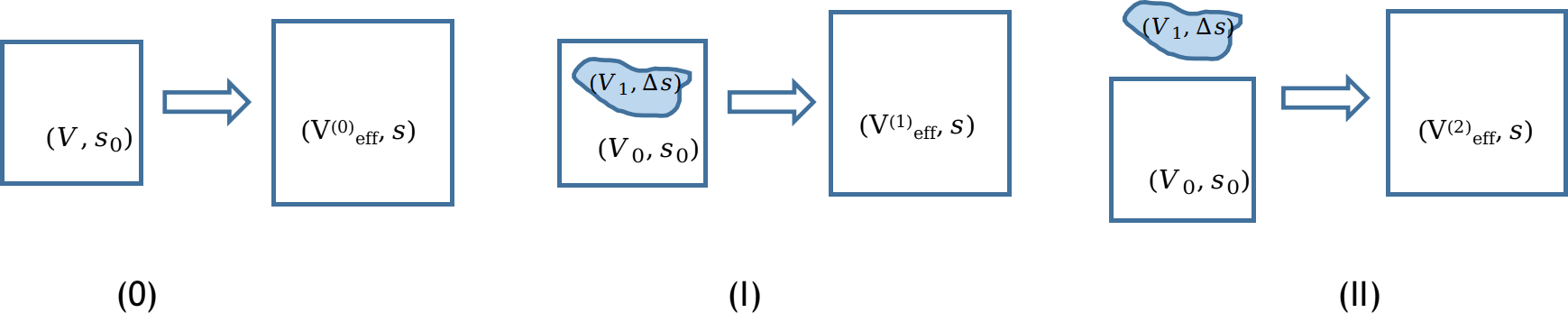
To illustrate the role of spatial inhomogeneity due to the quantum fluctuation of the entropy production in the ultra-central high-energy heavy-ion collisions in the volume effect, we consider a toy model, as shown in Fig. 5.

Let us start with a trivial conversion of a homogeneous system with volume $V$ and entropy density $s_{0}=s(e_{0})$ according to the equation of state, corresponding to the case (0). Conversoin with respect to the identification of total energy and entropy gives rise to an identical system, especially, $V_{\rm eff}^{(0)}=V$ . One may treat the case (0) as the background system without extra entropy production.

Case (I): The quantum nature of the initial-state fluctuations in heavy-ion collisions implies inhomogeneous entropy production. For simplicity, to see the variation of the effective volume as a consequence of the entropy increase from quantum fluctuations, we simply consider a subsystem inside the original homogeneous QGP with $V_{1}<V$ , in which energy density $e_{1}=e_{0}+\Delta e$ corresponding to the extra entropy produced in this subsystem, namely, $s_{1}=s_{0}+\Delta s$ , as in Fig. 5. The rest of the system, where entropy density stays the same, has a volume $V_{0}=V-V_{1}$ . The identification of total energy and entropy leads to an equation,

s(X_{0}e_{0}+X_{1}e_{1})=X_{0}s(e_{0})+X_{1}s(e_{1})\,,

(12)

with $X_{0}=V_{0}/V_{\rm eff}$ and $X_{1}=V_{1}/V_{\rm eff}$ . Note that $(X_{0}+X_{1})^{-1}=V_{\rm eff}^{(1)}/V=V_{\rm eff}^{(1)}/V_{\rm eff}^{(0)}=1+\Delta\ln V_{\rm eff}$ . With respect to a parameterization of the equation of state, $s(e)\propto e^{\kappa}$ , with $\kappa$ a constant, Eq. (12) can be solved analytically. By introducing $\varepsilon=\Delta e/e=\Delta\ln e$ and $v=V_{1}/(V_{0}+V_{1})$ to quantify the inhomogeneity in the system due to the entropy production, one finds the solution,

\Delta\ln V_{\rm eff}=\left(\frac{1-v+v(1+\varepsilon)^{\kappa}}{(1+v\varepsilon)^{\kappa}}\right)^{-\frac{1}{\kappa-1}}-1

(13)

Except $\kappa=1$ , for which the change of the effective volume becomes undetermined by $v$ , for a small increase of entropy or energy, $\varepsilon>0$ , as the inhomogeneity vanishes as $v=0$ or $v=1$ , the change of the effective volume approaches zero, as expected. For arbitrary finite $v$ , Eq. (13) results in $\Delta\ln V_{\rm eff}<0$ , and reaches maximum with respect to the largest inhomogeneity, i.e., $v=1/2$ .

Case (II): We consider a different scenario of entropy production due to initial-state fluctuations, that the quantum fluctuation results in entropy (or energy) produced outside the original system. We keep the same notions as in Case (I), namely, the volume in which the entropy is produced is $V_{1}$ such that $v=V_{1}/V$ , and $\Delta e/e=\varepsilon$ corresponds to the extra energy density produced outside the original volume, as shown in Fig. 5. Note that now $V_{0}=V_{\rm eff}^{(0)}$ , and $\Delta\ln V_{\rm eff}=1/X_{0}-1$ , yields,

\Delta\ln V_{\rm eff}=\left(\frac{1+v\varepsilon^{\kappa}}{(1+v\varepsilon)^{\kappa}}\right)^{-\frac{1}{\kappa-1}}-1

(14)

For absolute homogeneity, namely, $\varepsilon=0$ or $v=0$ , $\Delta\ln V_{\rm eff}=0$ . It is easy to show that with respect to a small entropy production, $\Delta\ln V_{\rm eff}>0$ for arbitrary $0<v<1$ , and the change of effective volume becomes maximum as $v=1$ , at which the system becomes most inhomogeneous.

For the realistic initial state density distributions, as shown in Fig. 3, case (I) applies to systems which are more smooth and connected, so that the extra entropy is likely to be generated inside the original volume, while case (II) characterizes the entropy production in a system that is created initially with a more discrete profile.

References

Bazavov et al. (2014) A. Bazavov et al. (HotQCD), Phys. Rev. D 90, 094503 (2014), arXiv:1407.6387 [hep-lat] .
Van Hove (1982) L. Van Hove, Physics Letters B 118, 138 (1982).
Campanini and Ferri (2011) R. Campanini and G. Ferri, Phys. Lett. B 703, 237 (2011), arXiv:1106.2008 [hep-ph] .
Gardim et al. (2020a) F. G. Gardim, G. Giacalone, M. Luzum, and J.-Y. Ollitrault, Nature Phys. 16, 615 (2020a), arXiv:1908.09728 [nucl-th] .
Hayrapetyan et al. (2024) A. Hayrapetyan et al. (CMS), (2024), arXiv:2401.06896 [nucl-ex] .
Nielsen (2024) E. G. Nielsen, (2024), SQM2024 Abstract.
Shen and Yan (2020) C. Shen and L. Yan, Nucl. Sci. Tech. 31, 122 (2020), arXiv:2010.12377 [nucl-th] .
Gardim et al. (2020b) F. G. Gardim, G. Giacalone, and J.-Y. Ollitrault, Phys. Lett. B 809, 135749 (2020b), arXiv:1909.11609 [nucl-th] .
Gardim et al. (2024) F. G. Gardim, A. V. Giannini, and J.-Y. Ollitrault, (2024), arXiv:2403.06052 [nucl-th] .
Soares Rocha et al. (2024) G. Soares Rocha, L. Gavassino, M. Singh, and J.-F. Paquet, (2024), arXiv:2405.10401 [hep-ph] .
Nijs and van der Schee (2024) G. Nijs and W. van der Schee, Phys. Lett. B 853, 138636 (2024), arXiv:2312.04623 [nucl-th] .
Moreland et al. (2015) J. S. Moreland, J. E. Bernhard, and S. A. Bass, Phys. Rev. C 92, 011901 (2015), arXiv:1412.4708 [nucl-th] .
Miller et al. (2007) M. L. Miller, K. Reygers, S. J. Sanders, and P. Steinberg, Ann. Rev. Nucl. Part. Sci. 57, 205 (2007), arXiv:nucl-ex/0701025 .
Schenke et al. (2012) B. Schenke, P. Tribedy, and R. Venugopalan, Phys. Rev. Lett. 108, 252301 (2012), arXiv:1202.6646 [nucl-th] .
Everett et al. (2021) D. Everett et al. (JETSCAPE), Phys. Rev. C 103, 054904 (2021), arXiv:2011.01430 [hep-ph] .
Chatterjee and Bożek (2018) S. Chatterjee and P. Bożek, Phys. Rev. Lett. 120, 192301 (2018), arXiv:1712.01189 [nucl-th] .
Hanus et al. (2019) P. Hanus, A. Mazeliauskas, and K. Reygers, Phys. Rev. C 100, 064903 (2019), arXiv:1908.02792 [hep-ph] .
Adam et al. (2016) J. Adam et al. (ALICE), Phys. Rev. Lett. 116, 222302 (2016), arXiv:1512.06104 [nucl-ex] .