Visualizing Similarity of Pathline Dynamics in 2D Flow Fields

Localized FTLE was introduced by Kasten et al. [18] and is an alternative to computing FTLE [12] using flow maps. Flow maps are constructed by advecting particles in the flow forward (or backward) in time. The flow map maps the initial positions of the tracer particles to their end positions after a specified integration time. The map gradient then describes the deformation gradient used for computing the right Cauchy-Green deformation tensor. Its spectral norm normalized by the integration time results in the FTLE field. In contrast, localized FTLE is based on the local deviation of the neighborhood along a pathline and allows the pathlines to be processed individually.

With the velocity field $\mathbf{v}(\mathbf{x},t)$ and a pathline $p(\mathbf{x}_{0},t_{0};\tau)$, the deviation of infinitely close particles is governed by the spatial gradient of the velocity field along the pathline. We denote an infinitely close perturbed particle as $\mathbf{y}:=\mathbf{x}_{0}+\sigma(t)$, with the time-varying perturbation vector $\sigma(t)\in\mathbb{R}^{3}$. At $t_{0}$, $\|\sigma(0)\|$ is close to zero. Kasten et al. then approximated the temporal evolution of the deviation $\sigma(t)$, by considering very short advection times. The solution of the differential equation for short advection times is then $\sigma(t)=\mbox{exp}(\nabla_{0}t)\sigma(0)$, where $\nabla_{0}=\nabla\mathbf{v}(p(0),t_{0})$

Kasten et al. [18] applied this approximation for short time intervals along the pathline $p(\mathbf{x}_{0},t_{0};\tau)$. Note that the samples are equidistant in time. They obtain the following description for the cumulative deviation along a pathline $\sigma(\tau)=\Psi_{t_{0}}^{t_{0}+\tau}(\mathbf{x}_{0})\sigma(0)$, where the matrix:

maps the neighborhood of the point $\mathbf{x_{0}}$ to the deviation after advection over the advection time $\tau$. $N$ is the number of discrete time steps, and $\Delta_{t}$ is the (small) temporal sample distance. The integration time satisfies $\tau=\Delta_{t}\cdot N$. $\Psi_{t_{0}}^{t_{0}+\tau}(\mathbf{x}_{0})$ can be treated analogously to the flow map gradient. Although we will not apply localized FTLE directly, we will utilize the idea of computing the deformation gradient along pathlines by accumulating small deviations.

The Jensen-Shannon divergence (JSD) [20] is an information-theoretic divergence measure based on Jensen’s inequality [16] and the Shannon entropy [26]. It is similar to the common Kullback-Leibler divergence [19], which measures the divergence between statistical populations.

The Kullback-Leibler divergence is defined as follows:

where $\xi_{1}$ and $\xi_{2}$ are discrete probability distributions defined in the same probability space $X$. The Kullback-Leibler divergence is always larger than zero. As $KL(\xi_{1}|\xi_{2})\neq KL(\xi_{2}|\xi_{1})$ applies, this measure is not symmetric. Note that it can be made symmetric by defining the measure $J=KL(\xi_{1}|\xi_{2})+KL(\xi_{2}|\xi_{1})$. The most significant drawback for our purposes is that the Kullback-Leibler divergence requires absolute continuity: $\xi_{2}(x)=0\implies\xi_{1}(x)=0$. In our approach, absolute continuity is not guaranteed.

In our method, we apply the closely related Jensen-Shannon divergence:

where $m=\frac{1}{2}\xi_{1}+\frac{1}{2}\xi_{2}$. The JSD is a symmetric divergence measure that does not require absolute continuity, as $m(x)=0\implies\xi_{1}(x)=0\land\xi_{2}(x)=0$ applies by definition.

The finite-strain tensor is a common tensor in continuum mechanics and closely related to the right Cauchy-Green tensor. It is defined as $E=\frac{1}{2}[F^{T}F-I]=\frac{1}{2}[C-I]$, where $F\in\mathbb{R}^{2\times 2}$ is the deformation gradient, $C\in\mathbb{R}^{2\times 2}$ is the right Cauchy-Green tensor, and $I\in\mathbb{R}^{2\times 2}$ is the identity. Analogously to the Cauchy-Green tensor, it describes the deformation of a fluid volume from a reference configuration and captures nonlinear dynamics.

Note that the product integral described in Equation 1 computes the product of matrices. As matrix multiplication is not commutative, the gradient for short advection times must be applied in the correct order. By directly constructing and utilizing a distribution from the deformation gradients for short integration times that contribute to $\Psi$, we lose information on the correct order. Our goal is to construct a distribution based on (short) deformation gradients without order dependence, and thus without matrix multiplication. In order to describe the deformation dynamics as a distribution, we first require a description of the nonlinear strain tensor using summation, which is commutative.

After computing the pathlines (using the Dormand-Prince method [6]), we construct an infinitesimal strain tensor by applying the localized concept for short advection times. The deformation gradient for a short advection time is described and approximated by omitting the higher order terms of the Taylor series: $F_{\Delta}=\mbox{exp}(\nabla_{0}\Delta_{t}))\approx I+\nabla_{0}\Delta_{t}$, where $\Delta_{t}\in\mathbb{R}$ is the (small) advection time, and $\nabla_{0}$ is the spatial gradient of the velocity field at the corresponding position in space and time.

We can now calculate the finite strain for short advection times by inserting $F_{\Delta}$ into the equation of $E$ and rearranging the equation to: $E_{\Delta}=\frac{1}{2}[\Delta_{t}\nabla_{0}+\Delta_{t}\nabla_{0}^{T}+\Delta_{t}^{2}\nabla_{0}^{T}\nabla_{0}]$. We choose the advection time to be very short ($\Delta_{t}\ll 1$), so that $\|\Delta_{t}\nabla_{0}\|$ is also small. We can then omit $\Delta_{t}^{2}\nabla_{0}^{T}\nabla_{0}$, as $\Delta_{t}^{2}\ll\Delta_{t}$. This results in the so-called infinitesimal strain tensor, a common tensor from continuum mechanics: $\mathbf{\epsilon}=\frac{1}{2}[\Delta_{t}\nabla_{0}+\Delta_{t}\nabla_{0}^{T}]\approx E_{\Delta}$.

We now briefly show that the sum of infinitesimal strains along a pathline is a viable approximation for the finite strain tensor. Two consecutive transformations $\mbox{exp}(\nabla_{0}\Delta_{t}))$ and $\mbox{exp}(\nabla_{1}\Delta_{t}))$ result in the deformation gradient $F_{2}=\mbox{exp}(\nabla_{1}\Delta_{t}))\mbox{exp}(\nabla_{0}\Delta_{t}))$. When inserting $F_{2}$ into the equation for the finite-strain tensor, substituting for the approximation, and omitting the matrix products as shown in the equation for $E_{\Delta}$ and $\mathbf{\epsilon}$, we obtain the following equation:

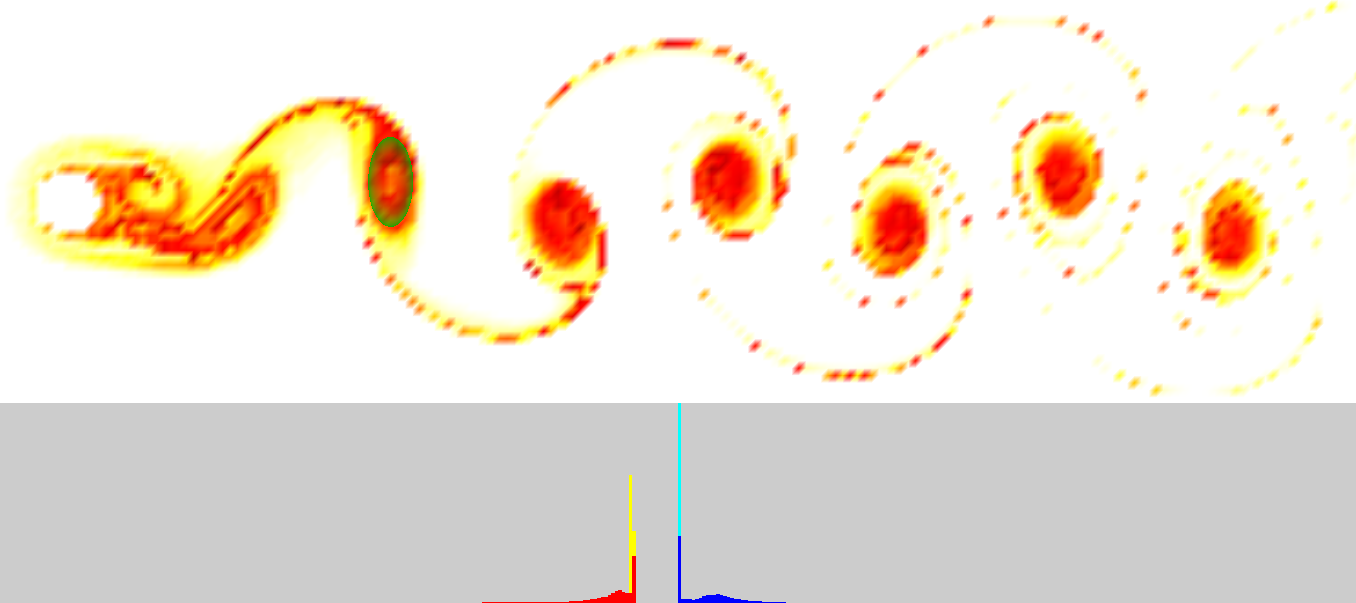
Note that this only holds if $\|\Delta_{t}\nabla_{0}\|\ll 1$. This construction is analogous to the construction of more consecutive transformations. This results in $\sum_{i=0}^{N-1}\mathbf{\epsilon}_{i}(\mathbf{x}_{0},t_{0};\Delta_{t})$, which can be interpreted as a strain progression. This progression is the basis for our deformation dynamics. Note that the approximation error can accumulate for many terms. Here, we study the error introduced by our approach visually. Figure 1 shows the resulting FTLE field (far left) and the calculation of the principal stretch using the sum of the infinitesimal strain to approximate the finite stain. It is clear that an error is introduced, yet we found it to be tolerable for our approach, as the figure suggests a strong correlation between the FTLE values and the approximation sum.

In addition to the infinitesimal strain $\epsilon$, we also consider the infinitesimal rotation tensor: $\mathbf{\omega}=\frac{1}{2}[\Delta_{t}\nabla_{0}-\Delta_{t}\nabla_{0}^{T}]$.

We found that the invariant of the infinitesimal strain tensor $\epsilon$ and the rotation tensor $\omega$ are viable for the construction of the transformation distribution. Note that $\mbox{tr}(\omega)=0$ and for incompressible fluids $\mbox{tr}(\epsilon)=0$ apply. Here, we chose $\alpha=\mbox{det}(\epsilon)\in\mathbb{R}$ and $\beta=\mbox{det}(\omega)\in\mathbb{R}$. $\alpha$ can be interpreted as the infinitesimal squared principal stretch of the fluid parcel, which is an objective measure. $\beta$ can be interpreted as the infinitesimal vorticity magnitude. As vorticity is not objective, we assume the resulting distribution to be not objective.

We now construct the progression set by first computing $\{\alpha_{0},\alpha_{1},\ldots,\alpha_{N-1}\}$ and $\{\beta_{0},\beta_{1},\ldots,\beta_{N-1}\}$ along a pathline using the defined sample distance $\Delta_{t}$. $N=\tau/\Delta_{t}$ applies, where $\tau$ is the integration time. We then compute a histogram $\xi_{p}$ by first constructing a histogram for the set $\alpha$ and the set $\beta$, respectively. The two one-dimensional histograms with $n$ bins are then concatenated to form a one-dimensional histogram with $2n$ bins. Note that constructing a two-dimensional histogram would imply that the sets of invariants are independent, which is not the case, as they both depend on $\nabla_{0}\Delta_{t}$. We normalize $\xi_{p}$ so that the sum of all bins equals one.

Our method is based on the visualization of the similarity of pathline dynamics using a reference deformation distribution and the deformation distribution computed earlier. For visualization, we first compute the reference deformation distribution $\xi_{R}$. The user defines an area $R\subseteq\mathbb{R}^{2}$ for the reference distribution. Here, we use circular regions, but any region is applicable. Now, we construct a distribution for every pathline, where $\mathbf{x}_{0}\in R$ by adding the bins of the corresponding pathlines. After normalizing by the number of elements, we obtain the reference distribution $\xi_{R}$.

We can now calculate the similarity by computing the Jensen-Shannon divergence $JSD(\xi_{p},\xi_{R})$. Small divergence values indicate strong similarity, where a value of zero implies that $\xi_{R}$ and $\xi_{p}$ are the same distribution. Here, we normalize the resulting field by the upper bound, which is $\ln(2)$, when using the natural logarithm. The divergence is then displayed by color mapping.

Amount of Bins: The amount of bins determines the quality of the dynamics distribution. Choosing a value too low leads to a greater variance of the values $\alpha$ and $\beta$ within a bin. As a result, the algorithm can overestimate the similarity between distributions, leading to overall low divergence values. High values increase the computation time and produce a large amount of empty bins, especially if the number of samples is low. We found that the common rule of thumb $n=\sqrt{N}$ produces viable results and a solid starting point for exploration. $N$ can be directly computed from the chosen integration time and sample distance (cf. Figure 2).

Sample Distance $\Delta_{t}$: The sampling distance determines the resolution of our pathline approximation and the quality of the infinitesimal strain tensor. It is straightforward to assume that the parameter should be chosen as small as possible. Increasing the resolution and thus decreasing $\Delta_{t}$ leads to a longer computation time for the dynamics distribution. A high value of $\Delta_{t}$ can lead to artifacts due to the omission of higher-order terms that have a greater impact for higher values of $\Delta_{t}$ (cf. Figure 3e,f).

Integration Time $\tau$: From the construction of the dynamics distribution, it is apparent that a decrease in integration times leads to a decrease in variance. This may lead to a more pronounced divergence. It is desirable to study long pathlines as it reveals more details in the visualized flow structures associated with dissimilarity (cf. Figure 3c,d).

We explore two data sets that describe a time-dependent 2D flow. They are provided by the Computer Graphics Laboratory of ETH Zürich and were used in the work of Günther et al. [8]. The data sets were generated using the Gerris flow solver [23]. The first data set represents the common flow pattern of a von Karman Vortex Street, where the flow is disturbed by a cylinder. The second data set describes a flow that develops due to buoyancy effects caused by a heated cylinder. The vortex street spans $[-0.5,7.5]\times[-0.5,0.5]$ with a grid resolution of $640\times 80$. It consists of $1501$ time steps in the range of $[0,15]$. The heated cylinder data set spans the domain $[-0.5,0.5]\times[-0.5,2.5]$ with a grid resolution of $150\times 450$. It consists of $2001$ time steps in the range of $[0,20]$.

The following computation times were obtained on a Linux system with Ubuntu 20.04 LTS, 32GB of RAM, and an Intel(R) Xeon(R) CPU E5-2630 v3 @ 2.40GHz chip (2 physical processors and 32 threads). This construction of the dynamics distribution is the most costly, as it requires numeric integration for every point. This is only required once for a specified timestep, integration time, and sample distance. Note that we store the dynamics sets $\alpha$ and $\beta$ for a fast recalculation of the reference distribution. In a grid with $M$ vertices and input parameters $\tau$ and $\Delta_{t}$, this results in values $M\tau/\Delta_{t}$ that must be stored in memory. This results in a large but manageable memory footprint for 2D flows on modern workstations. Using the rule of thumb mentioned above, the distributions have a memory footprint of $M\sqrt{\tau\Delta_{t}}$. For the buoyancy data set with the parameters specified in section 4, we measured a computation time for the construction of the dynamic distribution of approximately 13 seconds. The computation of the similarity visualization takes approximately 1 second for this case and does not require additional memory. As the integration and computation of $\alpha$ and $\beta$ are independent of each other, we parallelized these computations using OpenMP.

The resulting visualization is shown in Visualizing Similarity of Pathline Dynamics in 2D Flow Fields and Figure 4. The reference region in Visualizing Similarity of Pathline Dynamics in 2D Flow Fields (top) and Figure 4(left) corresponds to the use case in which the user investigates the dissimilarity (high divergence) from a known base line. This reveals abnormal behavior, which is in this case associated with vortex shedding or, in the case of the heated cylinder, turbulent motion. Visualizing Similarity of Pathline Dynamics in 2D Flow Fields(bottom) corresponds to the use case in which the user is aware of the location of a specific feature. By choosing the reference region to be completely within the feature, focusing on similarity (low divergence) reveals the other similar features. Figure 4(right) is a case in which the user expects turbulence and aims to declutter the visualization. When the reference region is chosen in such a way that turbulence is captured within the reference region, abnormal behavior is more easily identifiable. Note that Visualizing Similarity of Pathline Dynamics in 2D Flow Fields, reveals structures akin to LCS. We assume this to be the result of choosing a reference region with a low (or high) $\alpha$, since dissimilarity to a low (or high) alpha is equivalent to a high magnitude of stretching.