Vision-Based Target Localization
for a Flapping-Wing Aerial Vehicle

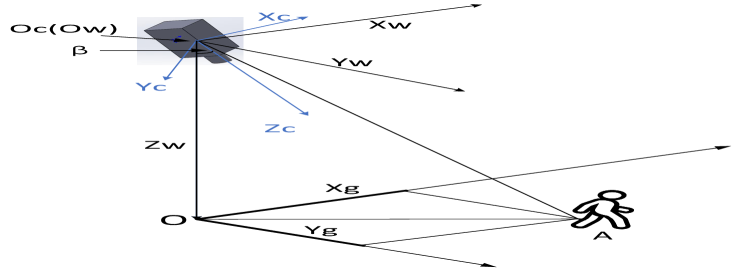
As shown in Fig.1, there are three coordinate systems. First, assuming a man (point A) as the target, we define that the ground coordinate system is $X_{\mathrm{g}}$$O$$Y_{\mathrm{g}}$, and the $O$$X_{\mathrm{g}}$ and $O$$Y_{\mathrm{g}}$ axes point to the east and north respectively. Moreover, supposing point $O_{\mathrm{c}}$ ($O_{\mathrm{w}}$) is the centroid of the camera, the world coordinate system is $O_{\mathrm{w}}$-$X_{\mathrm{w}}$$Y_{\mathrm{w}}$$Z_{\mathrm{w}}$. The point $O$ is the perpendicularly vertical point of $O_{\mathrm{c}}$ on the ground coordinate system, and the $O$$X_{\mathrm{g}}$ and $O$$Y_{\mathrm{g}}$ axes are parallel to the $O_{\mathrm{w}}$$X_{\mathrm{w}}$ and $O_{\mathrm{w}}$$Y_{\mathrm{w}}$ axes respectively. Additionally, the camera coordinate system $O_{\mathrm{c}}$-$X_{\mathrm{c}}$$Y_{\mathrm{c}}$$Z_{\mathrm{c}}$ is formed as follows: take the camera centroid $O_{\mathrm{c}}$ as origin, take the camera optical axis as the $O_{\mathrm{c}}Z_{\mathrm{c}}$ axis, and the $X_{\mathrm{c}}$, $Y_{\mathrm{c}}$, $Z_{\mathrm{c}}$ axes are perpendicular to each other as shown in Fig.1. The angle between $Z_{\mathrm{w}}$ and $Z_{\mathrm{c}}$ is $\beta$.

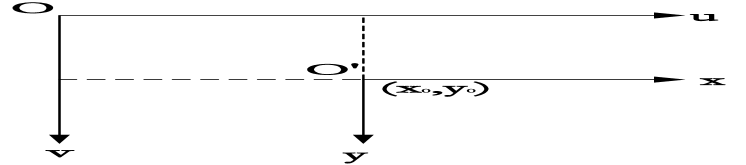
Besides, as shown in Fig.2, there are two image coordinate systems called image coordinate system I (${xO^{\prime}y}$) and image coordinate system II (${uOv}$). Both of them are on the imaging plane, but their origin and measurement unit are different. The origin ($O^{\prime}$) of the image coordinate system I is the midpoint of the imaging plane, while the origin ($O$) of the image coordinate system II is on the top left corner. Moreover, the unit of image coordinate system I is mm, which belongs to its physical unit, while the unit of image coordinate system II is pixel. In addition, the conversion formula that from image coordinate system I to image coordinate system II is

where $(x_{\mathrm{0}},y_{\mathrm{0}})^{T}$ is the principal point and $m_{\mathrm{x}}$, $m_{\mathrm{y}}$ give the number of pixels per unit distance (mm) in horizontal and vertical directions respectively [18].

In order to increase the field of view of aerial photography based on FWAVs, a wide-angle lenses camera is usually chosen to be used [19]. However, the traditional pinhole image model is not suitable for wide-angle cameras, so we adopted a generic fish-eye lenses camera model as shown in Fig.3.

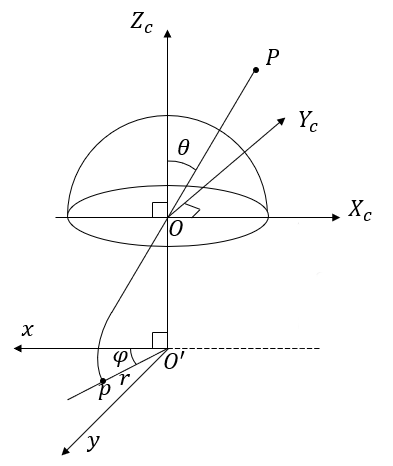
Point $O$ is the center of the camera lenses, $O^{\prime}$ is the image center, $\theta$ is the angle of incidence of projection, and $r$ is the distance from the projection point $p$ to the image center $O^{\prime}$. The plane $xOy$ is the image surface, point $p$ is the image point of the space point $P$, and $\varphi$ is the angle between $O^{\prime}p$ and $x$ axis. The approximate projection model is as follows

In the above equation, $k_{\mathrm{1}}$, $k_{\mathrm{2}}$, $k_{\mathrm{3}}$, $k_{\mathrm{4}}$, $k_{\mathrm{5}}$ represent 5 parameters which can be determined by the calibration procedure.

Based on the formula (2), the coordinate system transformation process is shown in Fig.4. And the projection process is to calculate the coordinate of the target in image coordinate system II for giving its ground coordinate.

Suppose that the coordinate of the ground target in the ground coordinate system is ${A_{g}}={(x_{\mathrm{A}},y_{\mathrm{A}})^{T}}$, the height of the camera is $h$, and the angle between $Z_{\mathrm{w}}$ and $Z_{\mathrm{c}}$ is $\beta$. Then the point A in the world coordinate system is ${A_{w}}=({{x_{\mathrm{A}}},{y_{\mathrm{A}}},{h}})^{T}$. The point in the world coordinate system is transformed into the camera coordinate system by rigid transformation matrix $R$

Then the coordinate of the ground target point in the camera coordinate system is $A_{\mathrm{c}}=\left(X_{\mathrm{c}},Y_{\mathrm{c}},Z_{\mathrm{c}}\right)^{T}$

Then we can get the incidence angle $\theta$, and the angle $\varphi$ (as shown in Fig.3) as follows

By combining (2), we can get the distance $r$. And then we can get the coordinate $(x,y)^{T}$ in the image coordinate system I

And then we can get the coordinate $(u,v)^{T}$ in the image coordinate system II

In order to verify the feasibility and accuracy of the localization algorithm, we designed a set of comparative simulation experiments. The simulation code is written and run by python 3.7, and the experimental platform is a laptop with a 2.9 GHz CPU and 16 G memory, and the operating system is windows 10.

Moreover, according to our real cameras, we set parameters of the generic camera model with $u_{\mathrm{0}}=320$, $v_{\mathrm{0}}=240$, $m_{\mathrm{u}}=188$, $m_{\mathrm{v}}=188$, and the maximum camera angle is 150°. After calibration, we set the parameters in the projection model with $k_{\mathrm{1}}=3.55$, $k_{\mathrm{2}}=0.03$, $k_{\mathrm{3}}=k_{\mathrm{4}}=k_{\mathrm{5}}=0$.

The errors are caused by the measurement of sensors and signal transmission, which include the angle error approximately 0.1°, the height error introduced by the barometer is 0.5 m, and the image detection error is almost 4 pixels.

Moreover, the flight mode of flapping-wing aerial vehicles will cause periodic jitter in the fuselage during flight, leading to jitter and motion blur to the camera. So we then introduced Gaussian noises in the simulation experiment.

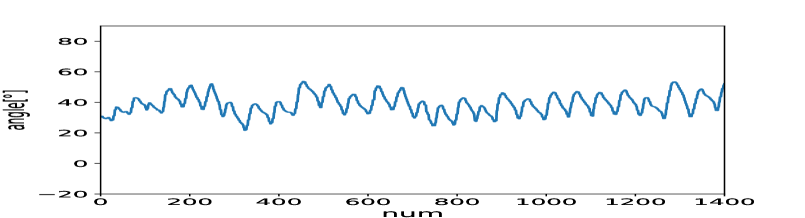
Fig.6 shows the attitude pitch angle of USTBird during the flight. The pitch of USTBird fluctuates periodically around 37° showing that the attack angle of USTBird is about 37°. So we then introduced the Gaussian noise in angle part with the mean value of 37° and with the standard deviation of 0.1° (the respective error level of the sensor as mentioned before). While in the height part, the Gaussian noise is introduced with the mean value of 0 and the standard deviation of 0.5 m (the respective error level of the sensor as mentioned before).

In doing the simulation experiment, we set a fixed point $(x,y,height)^{T}$=$(4,3,10)^{T}$ as our target coordinate in the world coordinate system, and then calculate the coordinate by our localization algorithm many times.

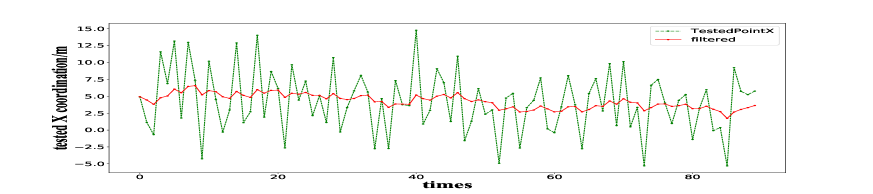
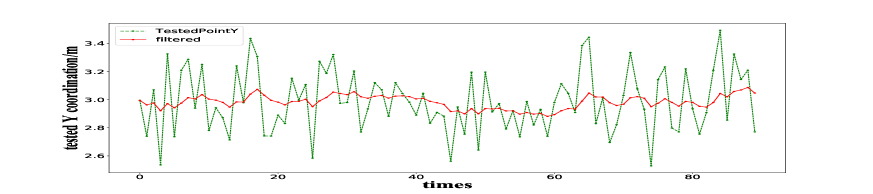
Specifically, the X and Y coordinates are calculated 90 times respectively, and the simulation results are shown in Fig.7 and Fig.8 with the dotted green lines.

As the noise existed in both part of measurement and motion jitter, both of the X and Y coordinate lines are not very smooth even with some shaking points in a very large attitude. So we should then introduce a filter to stabilize the localization values.

The first-order low-pass filtering algorithm originated from the first-order low-pass filter circuit, which is used to eliminate superimposed high-frequency interference components [20]. We could use a first-order low-pass filter to stabilize the localization values influenced by high-frequency noise of the measurement error and motion jitter.

The algorithm formula of the first-order low-pass filter is

where $x_{k-1}$ is the $(k-1)$th value of sampling, $u_{k-1}$ is the $(k-1)$th value of filter output, $u_{k}$ is the $k$th output value of the filter, and $\alpha$ is the filtering coefficient [21].

After testifying the filtering coefficient $\alpha$ many times, we finally chose the filtering coefficient $\alpha$=0.125, which can receive a better filtering effect. The filtered result is shown in Fig.7 and Fig.8 with the red line, and the data analysis results are shown in Table I.

As shown in Table I, the mean value is closer to the set point, and the variance is greatly reduced after filtering. The simulation results show that the filter can eliminate the high-frequency interference and stabilize the localization value to our set real position value. In short, from the simulation results, the localization algorithm and the filter we used have a good effect.