Vertex operator superalgebra/sigma model correspondences:
The four-torus case

The relation between sporadic finite simple groups and symmetries of K3 surfaces and K3 sigma models has attracted a lot of attention since the pioneering work of [1] and [2]. For some instances of this see [3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]. Apart from the Mathieu groups featured in [1, 2], symmetries of ${\cal N}=(4,4)$ supersymmetric non-linear sigma models on K3 surfaces have also been related to other groups, including the sporadic simple Conway groups [17, 18, 19], and the groups of umbral moonshine [20, 21].

The so-called twined elliptic genera play a critical role in quantifying this relation since they are sensitive to the way that symmetries act on quantum states. Of special interest is the fact that many of the twined elliptic genera of sigma models on K3 surfaces can be reproduced by the vertex operator superalgebra (VOSA) $V^{s\natural}$, which has played a prominent role in Conway moonshine [22, 23, 19]. (Here and in the remainder of this work we use sigma model as a shorthand for ${\cal N}=(4,4)$ supersymmetric non-linear sigma model.)

The analysis of [21] indicates that not all the twined K3 elliptic genera can be reproduced by Conway group symmetries of $V^{s\natural}$. It is nonetheless interesting that the single VOSA $V^{s\natural}$ can capture the symmetry properties of a large family of sigma models in the K3 moduli space, especially given that $V^{s\natural}$ is, in physical terms, a chiral theory, with central charge $c=12$, while the K3 sigma models are non-chiral theories, with $c=\bar{c}=6$. Moreover, in §C we explain how all but one of the twined K3 elliptic genera may be recovered from $V^{s\natural}$ if we allow non-Conway group symmetries (which is to say symmetries that do not preserve supersymmetry), or Conway group symmetries that are not of the expected order.

This novel chiral/non-chiral connection between $V^{s\natural}$ and K3 sigma models has been made precise at a special (orbifold) point in the moduli space, where $V^{s\natural}$ can be retrieved as the image of the corresponding K3 theory under reflection: a procedure explored in [19] for the specific case of $V^{s\natural}$ and later formerly investigated in more generality by Taormina–Wendland in [24]. (See also [25] for a complementary approach).

To put this connection in a more structured context let us consider sigma models with target space $X$ within one connected component of the full moduli space ${\cal M}={\cal M}(X)$ of sigma models on $X$, and denote the corresponding sigma models by $\Sigma(X;\mu)$, for $\mu$ a point in $\cal M$. For instance, for $X=T^{4}$ or $X=K3$ the moduli space consists of a single component, and takes the form

Here $\Gamma^{a,b}$ denotes an even unimodular lattice of signature $(a,b)$.

The chiral/non-chiral connection between $V^{s\natural}$ and K3 sigma models discussed above now motivates the following question:

Are there pairs of VOSA/sigma model family pairs $(V,{\cal M}(X))$ such that the following properties hold?

1. 1.

   The symmetry group of $V=V(X)$ contains the symmetry groups of all of the $\Sigma(X;\mu)$ for $\mu\subset{\cal M}(X)$.

2. 2.

   The twined elliptic genera of ${V}$ capture the twined elliptic genera arising from the $\Sigma(X;\mu)$ for all $\mu\in{\cal M}$.

3. 3.

   There exists a particular point $\mu^{*}\in{\cal M}$ such that the reflection procedure maps $\Sigma(X;\mu^{*})$ to ${V}$.

We will refer to pairs $(V,{\cal M})$ satisfying these 3 properties as VOSA/sigma model correspondences.

As we have explained, $(V^{s\natural},{\cal M}(K3))$ comes tantalisingly close to being an example of such a VOSA/sigma model correspondence. However, there are (conjecturally) a handful of twined elliptic genera of $\Sigma(X;\mu)$, with $\mu$ lying in certain high codimensional subspaces of ${\cal M}(X)$, that do not arise from $V^{s\natural}$. See Conjectures 5 and 6, and Table 4 of [21]. As a result, Property 2 above fails to hold for the $(V^{s\natural},{\cal M}(K3))$ pair. Our main objective in this work is to illustrate a complete example of the correspondence, where K3 surfaces are replaced by (complex) four-dimensional tori. The counterpart to $V^{s\natural}$ in this case is the VOSA naturally associated to the $E_{8}$ lattice, which we here denote $V^{f}_{E_{8}}$ (as in [22, 26]). With the $K3$ case in mind this is perhaps unsurprising, given that $V^{s\natural}$ can be written as a suitable $\mathbb{Z}_{2}$ orbifold of $V^{f}_{E_{8}}$ (see [22, 26]), while on the orbifold locus of ${\cal M}(K3)$, the corresponding sigma models can also be obtained as $\mathbb{Z}_{2}$ orbifolds of four-torus sigma models (see Figure 3.2).

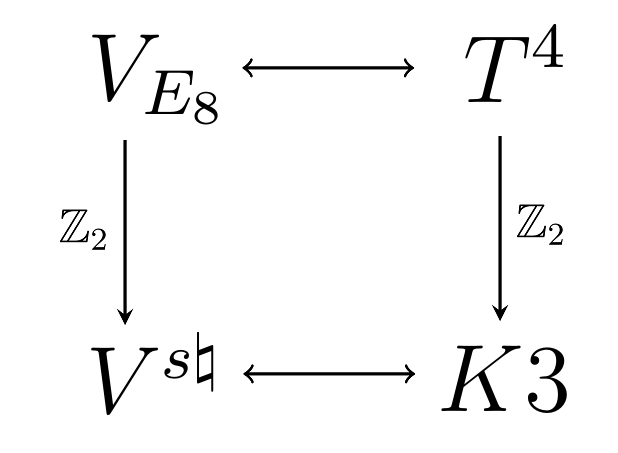
In fact, as we will see, the VOSA/sigma model correspondence works better in the four-torus case since it holds for all points in ${\cal M}(T^{4})$: The twined elliptic genera of any $\Sigma(T^{4};\mu)$ can be reproduced by the supersymmetry preserving twined elliptic genera of $V^{f}_{E_{8}}$. (See Theorem 2.) So all three properties of our proposed VOSA/sigma model correspondence, including the one which failed for the $(V^{s\natural},{\cal M}(K3))$ example, indeed hold in this case. It would be very interesting to understand whether a complete realization of the VOSA/sigma model correspondence might exist even for K3 surfaces. Our results can be regarded as encouraging evidence in this direction.

The rest of the paper is organized as follows. In §2 we discuss the supersymmetry-preserving symmetries of $\Sigma(T^{4};\mu)$ across the moduli space, as well as the corresponding twined elliptic genera. In §3 we summarise important results on the groups arising in §2. In §4 we discuss the VOSA $V^{f}_{E_{8}}$, naturally associated to the $E_{8}$ lattice, and show that its supersymmetry-preserving symmetry group contains all the symmetry groups discussed in §2. Hence we obtain that Property 1 of VOSA/sigma model correspondences holds for $(V^{f}_{E_{8}},{\cal M}(T^{4}))$. We then prove in Theorem 2 that the VOSA $V^{f}_{E_{8}}$ recovers all the twined elliptic general of the $\Sigma(T^{4};\mu)$, thereby proving Property 2.

In §5 we elaborate on the relation between the VOSA/sigma model correspondences for $T^{4}$ and the near example for $K3$ via orbifolding. In particular, we prove in Proposition 3 that the diagram in Figure 1 commutes, for all orbifolding procedures of the theory. Then in §6 we demonstrate that $V^{f}_{E_{8}}$ can be obtained as the image of $\Sigma(T^{4};\mu^{\ast})$ at a particular special point $\mu^{\ast}\in{\cal M}(T^{4})$ under reflection, thus establishing the final VOSA/sigma model correspondence property (Property 3) for $(V^{f}_{E_{8}},{\cal M}(T^{4}))$. This is the content of Theorem 4.

We conclude the paper with three appendices. In the first of these, §A, we provide further information on the supersymmetry-preserving symmetries of four-torus sigma models. In §B we recall, for the convenience of the reader, how automorphisms of a lattice lift to automorphisms of a corresponding lattice VOSA, and detail the workings of this in the specific case of $V^{f}_{E_{8}}$. Finally, in §C we explain how more general twinings of $V^{s\natural}$ may be used to recover the twined K3 elliptic genera that were not computed in [19]. We also review the relationship between $V^{f\natural}$ [22] and $V^{s\natural}$ [23, 19], explain a sense in which the Conway group arises naturally as a group of automorphisms of $V^{s\natural}$, and explain why they are the same as far as twinings of the K3 elliptic genus are concerned.

In this section we setup our notations and collect important background on four-torus sigma models and their symmetries. The exposition follows closely that in [27].

In this section we establish notation and summarise important results on the groups that we will make use of later. In particular, we will show that the $G_{0}$, related to the total symmetry groups of the four-torus sigma models via (2.9), are all subgroups of $W^{+}(E_{8})$, the group of even-determinant Weyl transformations of $E_{8}$. This fact will be crucial in §4, as it makes it possible to equate the twined elliptic genera of the four-torus sigma models and the twined traces of the $E_{8}$ lattice VOSA.

By definition, $W^{+}(E_{8})$ has a natural action on the $E_{8}$ lattice via its unique eight-dimensional irreducible representation and is a subgroup of $SO(8)$. Under the inclusion map $W^{+}(E_{8})\xhookrightarrow{}SO(8)$, the center of $W^{+}(E_{8})$ is mapped to the central $\mathbb{Z}_{2}$ subgroup of $SO(8)$, acting as $-id$ in the eight-dimensional vector representation of $SO(8)$ in the former case and in the eight-dimensional non-trivial representation of $W^{+}(E_{8})$ in the latter case. We denote by $\iota_{v}$ the generator of this latter central subgroup $\langle\iota_{v}\rangle\cong\mathbb{Z}_{2}<W^{+}(E_{8})$. The corresponding central quotient is isomorphic to the finite simple group $O^{+}_{8}(2)$, the group of linear transformations of the vector space $\mathbb{F}_{2}^{8}$ preserving a certain quadratic form. (See e.g. [28] for a discussion of this.) In other words, we have

Recall that $G_{1}$, related to $G_{0}$ as in (2.11), can be identified with subgroups of $W^{+}(E_{8})$ that fix an $E_{8}$ sublattice of rank at least $4$ [27]. Since $\iota_{v}$ does not preserve any subspace in the eight-dimensional vector representation of $W^{+}(E_{8})$, we conclude that $\iota_{v}\not\in G_{1}$, and by combining the inclusion $G_{1}\xhookrightarrow{}W^{+}(E_{8})$ and the projection $W^{+}(E_{8})\xrightarrow[]{\pi^{\prime}}O^{+}_{8}(2)$ we obtain an injective homomorphism $G_{1}\to O^{+}_{8}(2)$. As a consequence, the group $G_{1}$ is always isomorphic to a subgroup of $O^{+}_{8}(2)$.

To show that the discrete part of the sigma model symmetry group $G_{0}$ is always a subgroup of $W^{+}(E_{8})$, it will be useful to consider the group $\textrm{Spin}(8)$. The kernel of the spin covering map $\textrm{Spin}(8)\xrightarrow[]{\pi}SO(8)$ is an involution $\langle\iota_{s}\rangle\cong\mathbb{Z}_{2}$. Considering $W^{+}(E_{8})<SO(8)$, the preimage of the spin covering map is $\langle\iota_{s}\rangle.W^{+}(E_{8})<\textrm{Spin}(8)$. Its center can be identified with the center of $\textrm{Spin}(8)$, given by $\langle\iota_{s},\iota_{v}\rangle\cong\mathbb{Z}_{2}\times\mathbb{Z}_{2}$. We thus have that

The kernel of the spin covering map $\textrm{Spin}(8)\xrightarrow[]{\pi}SO(8)$ is naturally identified with the kernel of the quotient map $G_{0}\to G_{1}$ (cf. (2.11), Table 3.2). Indeed, the preimage of $G_{1}<W^{+}(E_{8})<SO(8)$ in $\langle\iota_{s}\rangle.W^{+}(E_{8})<\textrm{Spin}(8)$ is precisely the group $G_{0}\cong\langle\iota_{s}\rangle.G_{1}$. As we have seen in §2.2, in the sigma models $\iota_{s}$ acts by flipping the sign of all the fermions in the representation $\rho_{\psi}$ (cf. (2.19)).

At this point it is crucial to recall that $\textrm{Spin}(8)$ has a triality symmetry, i.e. an $S_{3}$ outer automorphism group. Also, it has one vector and the two spinor eight-dimensional irreducible representations, which we will denote by $\rho^{s}_{\psi}$, $\rho^{s}_{\rm e}$ and $\rho^{s}_{\rm o}$ respectively, and the action of triality on the group $\textrm{Spin}(8)$ extends to an $S_{3}$ permutation action on the three representations $\rho^{s}_{\psi}$, $\rho^{s}_{\rm e}$ and $\rho^{s}_{\rm o}$. This $S_{3}$ group also permutes the three non-trivial generators $\iota_{v}$, $\iota_{s}$, $\iota_{v}\iota_{s}$ of the center of $\textrm{Spin}(8)$, and in each of the three aforementioned eight-dimensional representations one of these generators acts trivially. Triality for $\textrm{Spin}(8)$ induces an $S_{3}$ group of outer automorphisms of $\langle\iota_{s}\rangle.W^{+}(E_{8})\cong\langle\iota_{s},\iota_{v}\rangle.O^{+}_{8}(2)$.

As a result, the $G_{0}$ subgroup of $\langle\iota_{s}\rangle.W^{+}(E_{8})$ has three representations, which we denote $\rho_{\psi}$, $\rho_{\rm e}$ and $\rho_{\rm o}$, corresponding to three eight-dimensional representations of $\textrm{Spin}(8)$, that are permuted by the outer automorphisms of $\langle\iota_{s}\rangle.W^{+}(E_{8})$. As we have seen in (2.19), in the sigma model the representation $\rho_{\psi}$ captures the action of the symmetry group $G_{0}$ on the eight (left- and right-moving) NS-NS fermions $\chi^{i},\chi^{i^{*}}\tilde{\chi}^{i},\tilde{\chi}^{i^{*}}$. The other two representations, $\rho_{\rm e}$ resp. $\rho_{\rm o}$, capture the action of $G_{0}$ on the Ramond-Ramond sector quantum states with even resp. odd fermion numbers. As mentioned before, in the representation $\rho_{\psi}$ the central involution $\iota_{s}$ acts by flipping the signs of all fermions as well as all bosons (which has to be the case since $G_{0}$ preserves the superconformal algebra). On the other hand, in the representation $\rho_{\rm e}$ the central element of $G_{0}$ acts trivially, so that only the quotient $G_{1}$ acts faithfully on the RR ground states of even fermion numbers. This is also the representation where $G_{1}$ fixes a $4$-dimensional subspace (cf. Table 2).

Now the $S_{3}$ outer automorphisms of $\langle\iota_{s},\iota_{v}\rangle.O^{+}_{8}(2)$ guarantee that the quotient by any of the three generators of the central subgroup $\langle\iota_{s},\iota_{v}\rangle$ is a group isomorphic to $W^{+}(E_{8})$. In particular, since $\iota_{v}\not\in G_{1}$ and hence $G_{0}\cong\langle\iota_{s}\rangle.G_{1}<\langle\iota_{s}\rangle.W^{+}(E_{8})$ does not contain the central involution $\iota_{v}$, the homomorphism $G_{0}\to W^{+}(E_{8})$ induced by the projection

is injective. Thus we have proved the following result.

The discussion of this section is summarized in the following diagram.

In this section we discuss the VOSA side of the VOSA/sigma model correspondence in this case: the $E_{8}$ lattice VOSA $V^{f}_{E_{8}}$. In §4.1 we introduce the theory and set up our notation, and in §4.2 we outline the computation of the twined traces of this VOSA, and prove the main theorm (Theorem 2) of the paper.