Vector meson’s spin alignments in high energy reactions
Abstract
The global spin alignment of vector mesons has been observed by the STAR collaboration at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory (BNL).
It provides a unique opportunity to probe the correlation between the polarized quark and antiquark in the strongly coupled quark-gluon plasma (sQGP) produced in relativistic heavy ion collisions, opening a new window to explore the properties of sQGP.
In addition, spin alignments of vector mesons have also been observed in other high-energy particle collisions such as annihilations at high energies where hadron production is dominated by quark fragmentation mechanism. The results obtained are quite different from those obtained in heavy ion collisions where quark coalescence/combination mechanism dominates suggesting strong dependence on hadronization mechanisms. So comprehensive studies in different hadronization processes are needed.
In this article, we present a brief review of theoretical and experimental advances in the study of vector meson’s spin alignments
in a variety of high-energy particle collisions, with emphasis on hadronization mechanisms.
Keywords: Vector meson, spin alignment, global polarization, relativistic heavy ion collisions, fragmentation
PACS: 12.38.Mh,12.38.–t, 13.88.+e, 13.66.Bc, 25.75.–q, 25.75.Nq
I Introduction
Quantum Chromodynamics (QCD) is the fundamental theory for strong interaction that is responsible for binding quarks and gluons together to form protons, neutrons, and other hadrons. Relativistic Heavy Ion Collisions (RHIC) are a powerful tool for studying QCD and properties of strongly interacting matter under extreme conditions Braun-Munzinger:2015hba ; Florkowski:2018fap ; Ko ; Rapp ; Zhang1 ; ZhaoJ . In these collisions, heavy nuclei are accelerated to nearly light speed and then collide to achieve immense energy density that recreates conditions similar to those just microseconds after the Big Bang, allowing scientists to study quark-gluon plasma (QGP) - a state of matter in which quarks and gluons are decoupled from hadrons Pandav:2022xxx ; HeWB ; Chen:2023mel ; MaYG ; PangLG ; Sun1 ; Chen1 .
Spin is an intrinsic form of angular momentum carried by elementary particles, and it is a (pseudo-)vector quantity that can point to different directions. As elementary particles of strong interaction, quarks and gluons carry spins. As composite particles of strong interaction, many hadrons also carry spins. The spin polarization refers to the alignment of the spin along a specific direction (called spin quantization direction). Spin degrees of freedom have been playing an important role in the development of modern physics since its discovery in 1925. The global polarization effect (GPE) of the quark gluon plasma (QGP) produced in high energy heavy-ion collisions is a new spin effect in particle and nuclear physics. The theoretical prediction Liang:2004ph ; Liang:2004xn ; Gao:2007bc was made almost two decades ago and attracted immediate attention Voloshin:2004ha ; Betz:2007kg ; Ipp:2007ng ; Becattini:2007sr ; Liang:2007ma ; Chen:2007zzq ; Selyuzhenkov:2007ab ; STAR:2008lcm ; STAR:2007ccu . However the enthusiasm was soon dampened by STAR’s earlier attempts Chen:2007zzq ; Selyuzhenkov:2007ab ; STAR:2008lcm ; STAR:2007ccu that gave null results for global -hyperon polarization as well as global spin alignments of vector mesons due to limited statistics in data at that time. The earlier results show that the GPE, even if it exists, could be very small, so it is unclear if it is within the scope and resolution of current experiments. The enthusiasm was aroused by non-vanishing results for the GPE for hyperons in STAR’s beam-energy-scan experiments STAR:2017ckg , which showed that the GPE decreases monotonically with collision energies. Now the GPE has grown to be a sub-field in heavy-ion collisions, see Refs. Wang:2017jpl ; Liang:2019clf ; Gao:2020lxh ; Huang:2020dtn ; Gao:2020vbh ; Becattini:2020ngo ; Becattini:2022zvf ; Becattini:2024uha for recent reviews.
Another surprise came five years later from STAR’s measurements on the global spin alignment of mesons with high statistics STAR:2022fan . The STAR’s results STAR:2022fan seem to conflict with hyperon’s polarization as predicted in Ref. Liang:2004xn that the vector meson’s spin alignment is proportional to quark polarization squared and thus should be much smaller than that observed in STAR’s experiment STAR:2022fan . So STAR’s results are definitely non-trivial and may have deep implication for hadronization mechanism and properties of QCD Yang:2017sdk ; Sheng:2019kmk ; Sheng:2022ffb ; Sheng:2022wsy . When a system of particles exhibits spin polarization, it means that the spins of these particles are aligned more often in a particular direction than randomly oriented. Now the global spin alignment of vector mesons has attracted a broad interest in experimental and theoretical communities Wang:2023fvy ; Chen:2023hnb ; Xin-Li:2023gwh ; Jian-Hua:2023cna ; Li-Juan:2023bws ; Chen:2024bik . Spin polarization in the context of QCD is a critical aspect of understanding the internal structure and dynamics of hadrons. Through both theoretical and experimental approaches, physicists aim to unravel the complexities of how quarks and gluons contribute to the spin and other properties of hadrons. Several theoretical interpretations have been proposed and new measurements are underway.
In addition to relativistic heavy-ion collisions, the vector meson’s spin alignment has also been studied in other high energy processes such as , and collisions DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs ; ZEUS:1999wqh ; NOMAD:2006kuc ; STAR:2008lcm . The results show quite different features and theoretical efforts have also been made to describe them Anselmino:1997ui ; Anselmino:1998jv ; Anselmino:1999cg ; Xu:2001hz ; Xu:2003fq ; Chen:2016moq ; Chen:2016iey ; Chen:2020pty . It is therefore desirable to summarize these experimental and theoretical results and make comparison among different high energy reactions as guidance for future studies.
Firstly, we briefly review spin density matrices for vector mesons as well as measurement methods for the spin alignment, and then review experimental results in different high energy collisions. Secondly, we summarize theoretical approaches in two different hadronization mechanisms as well as the linear response theory for the spin alignment of vector mesons in thermalized QGP. Finally, we present a short summary and outlook.
II Spin density matrices and measurement methods for spin alignment
II.1 Spin density matrices
The spin polarization of particles produced in high energy reaction can be described by the spin density matrix . For particles with spin- such as quarks and anti-quarks, is a Hermitian matrix which can be expanded as
| (1) |
where are Pauli matrices, and is the mean spin polarization vector in the quark’s rest frame.
For spin-1 particles, the spin density matrix is a Hermitian matrix. With the spin quantization axis specified, the spin states are denoted as and the spin density matrix can be put into the form Bacchetta:2000jk
| (5) | ||||
| (6) |
where =1,2,3, and and are 33 traceless matrices defined as Xin-Li:2023gwh ; Becattini:2024uha
| (10) | ||||
| (14) | ||||
| (18) | ||||
| (19) |
The polarization vector in the rest frame of the spin-1 particle in the spin state can be defined as
| (20) | |||
| (21) |
where the spin quantization direction is assumed to be direction. For the measurement of global spin alignment, the spin quantization direction is taken as the direction of global orbital angular momentum, i.e., , while other polarization vectors are determined by conditions and . Another widely used choice is the direction of meson’s three-momentum in the laboratory frame, , corresponding to the helicity polarization. The spin density matrix for different choices of spin quantization directions are related by the following transformation in the spin space,
| (22) |
where and are two spin density matrices corresponding to two set of polarization vectors and , respectively. The transformation matrix is a matrix in the spin space with elements given by the inner product of polarization vectors, .
The spin vector is related to the polarization vector by . If the vector meson is in the pure spin state with , the spin vector is vanishing, . If the vector meson is in the pure spin state with we have , which is parallel or anti-parallel to the spin quantization direction.
II.2 Measurement of spin density matrix through angular distribution of decay product
In high energy reactions, the spin polarization of a particle is mainly measured through the angular distribution of its decay product in two-body decay in the rest frame of . The corresponding formulae are derived using symmetry properties and conservation laws in the decay process.
In the rest frame of , the momenta of the particle and are denoted as , and their spin states are labeled by their helicities and respectively. The decay amplitude is given by,
| (23) |
where stands for the transition operator, denotes the spin state of , and is the helicity state of decay daughters.
We can insert the completeness identity for the helicity states of the two-particle system with fixed (the energy of the system), (total angular momentum quantum number) and (the eigenvalue of ). From energy and angular momentum conservation laws in the decay process in ’s rest frame, we have (the mass of ), and . So we obtain,
| (24) |
The space rotation invariance demands that the helicity amplitude
| (25) |
is independent of . So we obtain,
| (26) |
We see that the angular dependence is solely given by the inner product , which we calculate as follows. First, we calculate it for in -direction, i.e., , which gives a constant independent of . We then transform to in the direction of by a spatial rotation. The rotation can be achieved by three successive rotations in Euler angles that rotate to with the rotation operator Jacob:1959at
| (27) |
Hence, we obtain the inner product as
| (28) |
where is the element of the Wigner rotation matrix and . We note that the definition of the rotation operator in (27) introduces an additional rotation relative to that in Ref. Chung:1971ri .
The spin density matrix of the system of particles 1 and 2 can be defined as
| (29) |
where is the spin density matrix of A. Then the angular distribution is given by
| (30) |
where denotes elements of and is the normalization constant.
Since the helicity amplitude is generally unknown, only in some special cases one can use to determine elements of . Here are three such cases.
(1) , , , as in a spin-1/2 hyperon’s decay into a spin-1/2 baryon and a pion, , where denotes a hyperon. In this case, we have two independent helicity amplitudes and is given by
| (31) |
where is the polarization vector of , is the momentum direction and
| (32) |
is the decay parameter for . We also see that if parity is conserved in the decay process so that , we then have and the isotropic distribution . So Eq. (31) can be used to determine only in weak decays.
(2) , , such as in the vector meson’s decay into two pions, . In this case, the helicity amplitude is a trivial constant that can be absorbed into the normalization constant, so that
| (33) |
If we integrate over , we obtain,
| (34) |
We see that by measuring the distribution in one can extract the value of .
(3) , , such as in the vector meson’s decay into a dilepton pair, . Here, we have four combinations of and . In this case, only if parity and helicity conservation are valid so that and only for , only one non-vanishing helicity amplitude is left and can be absorbed into the normalization constant. We then obtain the angular distribution as
| (35) |
where the coefficients are related to elements of by
| (36) | |||
| (37) | |||
| (38) | |||
| (39) | |||
| (40) |
In principle, one can extract elements of from through these coefficients.
Measurements on hyperon polarization and vector meson’s spin alignment have been carried out in different high energy reactions using Eqs. (31-35) (see e.g. Refs. Lesnik:1975my ; Bunce:1976yb ; Bensinger:1983vc ; Gourlay:1986mf ; TASSO:1984nda ; ALEPH:1996oew ; OPAL:1997oem , DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs ; NOMAD:2006kuc and Chen:2007zzq ; Selyuzhenkov:2007ab ; STAR:2008lcm ; STAR:2007ccu ). In this brief review, we concentrate on spin alignment of vector mesons with light flavors in comparison with hyperon polarization, thus only Eqs. (31) and (33) are involved.
III Experimental results
III.1 Vector meson’s spin alignments in -annihilations
The earliest measurements of vector meson’s spin alignments in high energy reactions might be made at the Large Electron-Position collider (LEP) at European Organization for Nuclear Research (CERN) in the 1990s DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs , where one of the popular polarization axis was the helicity axis defined by the individual particle’s momentum direction. Measurements have been carried out by DELPHI and OPAL Collaborations for and mesons and even for heavy flavor meson such as and DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs . They also measured the off-diagonal element such as . As an example, we show the results from Ref. OPAL:1997vmw in Fig. 1.
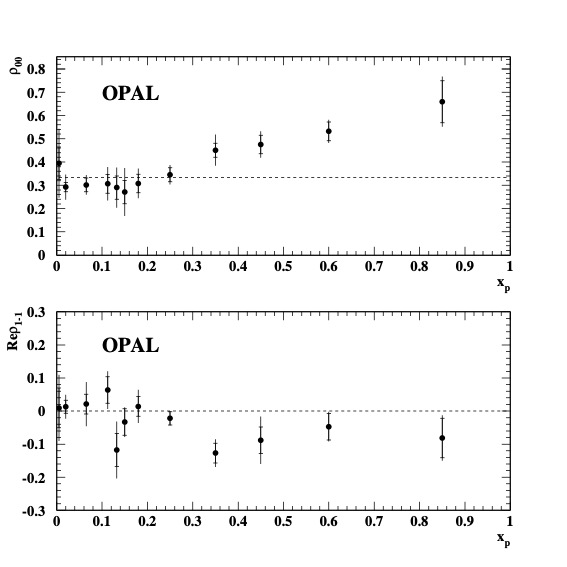
From these measurements DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs in collisions, we see clearly that is significantly larger than 1/3 in the fragmentation region () which show that the spin of vector mesons is significantly aligned in that region. However, at small fractional momenta , null results for and mesons were reported in collisions DELPHI:1997ruo ; OPAL:1997vmw .
The data have attaracted much theoretical attention Anselmino:1997ui ; Anselmino:1998jv ; Anselmino:1999cg ; Xu:2001hz ; Xu:2003fq ; Chen:2016moq ; Chen:2016iey ; Chen:2020pty and we will come back to this later in Sec. VI.
III.2 Global spin alignments of vector mesons in heavy-ion collisions
New measurements of the vector meson’s spin alignment in heavy-ion collisions are different from conventional studies, where a new polarization axis along the nucleus-nucleus system’s orbital angular momentum is defined Liang:2004ph ; Liang:2004xn , and this is the so-called global spin alignment. In experiment, the quantization axis is determined by the normal of the reaction plane, which can be reconstructed by using the charge particle momentum distribution collected in the detector STAR:2022fan . Particles of interest, for example, the vector-meson and are observed by paring of their decay daughters (, ) with subtraction of the combinatorial background. Then the polar angle distribution of Eq. (34) is analyzed, and the is extracted after correction for detection efficiency and acceptance STAR:2022fan .

In 2008 the STAR Collaboration performed a measurement of the vector meson’s global spin alignment in Au+Au collisions at = 200 GeV. Due to limited statistics and only covered top RHIC collision energies, no significant results were reported STAR:2008lcm . Since 2010, the collaboration has been collecting and analyzing data of higher statistics and at lower collision energies, including data in the Beam Energy Scan Phase I (BES-I) runs and high statistics Au+Au runs at = 200 GeV. The analysis was focused on mid-central collisions (20-60%) where larger system angular momenta are expected in comparison with the values in central or peripheral collisions. Fig. 2 presents the transverse momentum dependence of for and in 20-60% central Au+Au collisions at = 11.5, 19.6, 27, 39, 62.4 (54.4), 200 GeV. The results show a non-trivial dependence. For mesons at = 54.4 and 200 GeV, they are larger than 1/3 with about significance at intermediate . At low beam energies the statistics is not sufficient to observe any significant deviation from 1/3. From the calculation in Ref. Liang:2004xn , one naively expect to be smaller than 1/3 due to hadronization of the polarized quark and antiquark via quark combination, and larger than 1/3 due to fragmentation of the quark and antiquark. On the other hand, for mesons for all energies considered, we see that the departure of from 1/3 mainly occurs at 1.0 - 2.4 GeV/c, while at higher the result can be regarded as being consistent with 1/3 within or less significance.
The STAR collaboration also studied the collision energy dependence by integrating with the weight 1/(stat. error)2. Fig. 3 presents for and mesons in 20-60% central Au+Au collisions at collision energies ranging from = 11.5 to 200 GeV STAR:2022fan . We see that for mesons increases with decreasing the collision energy, while for mesons fluctuates around 1/3 with the collision energy. To quantify the effect, the average of is taken over lower collision energies for and . The for mesons, averaged over beam energies between 11.5 and 62.4 GeV, is 0.3512 0.0017 (stat.) 0.0017 (syst.). Taking the total uncertainties as the sum in quadrature of statistical and systematic uncertainties, the result indicates that for mesons is above 1/3 with a significance of , representing the first observation of the global spin alignment. The for mesons, averaged over beam energies between 11.5 and 54.4 GeV, is 0.3356 0.0034 (stat.) 0.0043 (syst.) and is consistent with 1/3. The measurements of the ALICE collaboration in Pb+Pb collisions at 2.76 TeV ALICE:2019aid , taken from the closest data points to the mean for the range used in STAR’s measurements, are also shown for comparison in Fig. 3. The data point for and mesons from ALICE collaboration is more or less consistent with 1/3 with large uncertainties.

According to various studies, there are many sources that contribute to the global spin alignment of mesons including vortical flows Yang:2017sdk , electromagnetic fields Yang:2017sdk generated by the electric currents carried by the colliding nuclei, local spin alignment Xia:2020tyd , quark polarization along the direction of its momentum (helicity polarization) Gao:2021rom , the spin alignment by fragmentation Liang:2004xn of polarized quarks, and the shear stress tensor Li:2022vmb ; Wagner:2022gza ; Dong:2023cng . However, these conventional mechanisms are not sufficient to account for the observed for mesons. It was also proposed that local correlations or fluctuations in turbulent color fields Muller:2021hpe and glasma fields Kumar:2023ghs can also generate a significant contribution to . A recent theoretical development based on local correlations or fluctuations of vector fields can describe the experimental data. The vector field is the ’33’ component of the SU(3) vector multiplet induced by currents of pseudo-Goldstone bosons Manohar:1983md , and it can polarize and quarks in the same way as the electromagnetic field does. The solid curve of Fig. 3 is such a fit to the data. We see that the calculation describes the data reasonably well. The correlation of the vector field can be quantified by and and can be extracted by fitting data, where and are electric and magnetic components of the vector field respectively. We will discuss more details about the theoretical model in Sec. IV.2.
IV Vector meson’s spin alignments in quark combination models
It was well-known that huge angular momenta are generated in non-central high energy heavy-ion collisions Liang:2004ph ; Gao:2007bc . Due to spin-orbit couplings in QCD interaction, such huge angular momenta lead to the global polarization in quark scatterings in the form of the hyperon polarization Liang:2004ph ; Gao:2007bc and vector meson’s spin alignment Liang:2004xn , the so-called GPE.
The GPE depends not only on the global quark polarization but also on the hadronization mechanism. In relativistic heavy-ion collisions, it is envisaged that a system of decomfined quarks and anti-quarks is created in the central rapidity and moderate transverse momentum region. Various aspects of experimental data suggest that hadronization of the system proceeds via combination of quarks and anti-quarks, a mechanism phrased as “quark recombination”, “quark coalescence” or simply as “quark combination”. We simply refer to it as “quark combination model” or “quark coalescence model” in this paper. We will summarize the results of vector meson’s spin alignments by the quark combination model in this section.
IV.1 Vector meson’s spin alignments in non-relativistic quark combination models
In a non-relativistic quark combination model, the physics in the process that (quark) and (antiquark) combine to (meson) can be demonstrated in a clear way. Here, it is envisaged that in the combination process the vector meson’s spin is just the sum over the quark’s and anti-quark’s spins. Hence the spin density matrix and the spin alignment of the vector meson can be calculated from that of the quark and anti-quark. Such a calculation is straightforward and was carried out in Ref. Liang:2004xn , which we will summarize in this subsection.
The global quark polarization was taken as a constant so that the spin density matrix for the quark and antiquark takes the diagonal form Liang:2004xn
| (43) |
The spin density matrix of the system was taken as a direct product of the quark’s and anti-quark’s,
| (44) |
The elements of the spin density matrix for the vector meson is obtained from as
| (45) |
which leads to
| (46) |
where is the vector meson’s spin state in the constituent quark model with and , and are Clebsch-Gordan coefficients. After a straightforward calculation, we obtain the normalized spin alignment as Liang:2004xn ,
| (47) |
If we take (flavor blind for quarks and antiquarks), we simply obtain
| (48) |
In exact the same way, we obtain the global hyperon polarization for , , and Liang:2004ph .
From Eqs. (47) and (48), we see that, in contrast to , is quadratic in and should be less than . We emphasize that the case considered in Ref. Liang:2004xn is over simplified in the fact that only the spin degree of freedom for the quark and antiquark is considered, neglecting other degree(s) of freedom and the correlation among the quark’s and antiquark’s polarization. So it might not be a surprise that the STAR data STAR:2017ckg ; STAR:2022fan for the global spin alignment of mesons show a large deviation from 1/3, far beyond the value estimated from ’s data by its square. In fact, if we make a step forward by considering the dependence of on other degree of freedom Sheng:2019kmk ; Sheng:2020ghv ; Sheng:2022ffb ; Sheng:2022wsy , in Eq. (47) should be replaced by , so we have
| (49) |
The STAR data STAR:2017ckg ; STAR:2022fan indicate
| (50) |
This means that there should be a strong correlation between the polarization of the quark and antiquark. Hence, the study of the global spin alignment for the vector meson in heavy-ion collisions provides a unique opportunity for exploring the local correlation in the quark’s and antiquark’s polarization, a new window for the study of properties of QGP.
It is also emphasized in Ref. Liang:2023talk that the average in Eq. (49) is two-folded: the first average is taken inside the vector meson’s wave function (local correlation) and the second average is taken in the range outside the vector meson’s wave function (long-range correlation). More measurements are needed to tell the difference between two types of correlation Liang:2023talk . A systematic formulation has been presented in Lv:2024uev . It has bee extended to spin 3/2 baryons in Zhang:2024hyq .
IV.2 Vector meson’s spin alignments in quark combination models with phase space dependence
IV.2.1 Non-relativistic model
In this subsection, we consider the non-relativistic quark combination model with phase space dependence Sheng:2020ghv ; Xin-Li:2023gwh . We extend the density operator (1) to the phase space as
| (51) |
where denote spin states, denotes the spin-momentum state, and the momentum measure is defined as . The weight function is the Wigner function in the spin-phase space and can be obtained as
| (52) |
It is a Hermitian matrix in the spin space and can be parameterized as
| (53) |
Here is the un-polarized distribution function, and is the spin polarization in phase space. The density operator for the anti-quark can be defined in the same way. The density operator for a quark-antiquark pair is defined from the direct product of quark’s and anti-quark’s one as . The Wigner function can be normalized as
| (54) |
The quark’s spin quantization direction can be any direction, e.g., the -direction, without loss of generality.
The elements of the vector meson’s density matrix are obtained as
| (55) | |||||
where and are positions and momenta for the quark and the antiquark respectively, and is the normalization factor that ensures . Since we work in the non-relativistic limit, the spin and momentum can be decoupled. Therefore Clebsch-Gordan coefficients and as well as the meson’s wave function appear in Eq. (55). By further neglecting the phase-space dependence of unpolarized distribution functions and choosing as a Gaussian distribution with the width in the momentum space, we derive the spin alignment and other parameters in the angular distribution (33),
where the correlation between quark and antiquark’s polarizations is defined as
| (57) |
We note that in Eq. (LABEL:eq:tensor-polar) the spin quantization direction is set to the -direction.
IV.2.2 Relativistic model in quantum kinetic approach
For a relativistic quark or antiquark, its polarization four-vector is always perpendicular to its four-momentum, implying that the spin with momentum cannot be decoupled as in the non-relativistic case. Consequently, the vector meson’s spin cannot be obtained by the constituent quark’s and anti-quark’s spins through the angular momentum coupling in non-relativistic quantum mechanics. Based on the Kadanoff-Baym equation in the closed-time-path formalism, a relativistic spin kinetic theory for vector mesons has been constructed Sheng:2022ffb to explain experimental data on the spin alignment STAR:2017ckg .
In order to describe spin transport phenomena, we use the matrix-valued spin-dependent distribution (MVSD) for the vector meson. The spin Boltzmann equation with coalescence and dissociation collision terms reads,
| (58) | |||||
where denotes the meson’s normalized polarization vector perpendicular to , and , , , and label the vector meson’s spin states along the spin quantization direction with three values 0 and . Here we have assumed that the vector meson is on its mass-shell . The gain and loss terms in correspond to the coalescence and dissociation processes for the quark and antiquark, respectively. In the dilute limit when distribution functions of the meson, the constituent quark and antiquark are much less than unity, Eq. (58) is simplified as
| (59) |
where the contribution from the dissociation is proportional to the MVSD with the coefficient being independent of the MVSD. The coalescence kernel can be obtained from the Kadanoff-Baym equation,
| (60) | |||||
where and are quark and antiquark masses respectively, , , and are energies for the vector meson, the constituent quark and antiquark respectively, and is the effective vertex of quark-antiquark-meson. Here and are the unpolarized and spin polarization distributions for the quark/antiquark respectively. By neglecting the space dependence (the distributions are homogeneous in space) and setting before the hadronization stage in heavy-ion collisions, one can obtain a formal solution to Eq. (59). Spin density matrix elements can be derived as Sheng:2022wsy ,
| (61) |
This is a relativistic formula for the vector meson’s spin density matrix built from the coalescence kernel (60) encoding the polarization distributions of the constituent quark and antiquark. Clearly the vector meson’s spin density matrix has non-trivial dependence on the spin polarization and momenta of the quark and antiquark.
We consider that and are polarized in a thermal medium by an effective vector field called the field Sheng:2019kmk ; Sheng:2022wsy ; Sheng:2022ffb induced by currents of pseudo-Goldstone bosons Manohar:1983md . The spin polarization of and is then given by
| (62) |
where denotes the velocity of the thermal background at the effective hadronization temperature , is the effective coupling constant of the vertex, and is the field’s strength tensor. Substituting (62) into Eq. (60) and assuming in the meson’s rest frame, we obtain the spin alignment of the meson
| (63) |
where is the mass of the meson, and and are electric and magnetic components of the field in the meson’s rest frame respectively. Here denotes the spin quantization direction. The coefficients and depend only on quark’s and meson’s masses,
| (64) |
We note that the momentum dependence can be obtained by expressing and in Eq. (63) in terms of laboratory frame fields through Lorentz transformation.
| (65) |
where is the Lorentz factor and is the velocity of the meson. Then can be rewritten as
| (66) | |||||
where and are momentum functions. These functions are derived by substituting transformations (IV.2.2) into Eq. (63) and then separating different field components. For the global spin alignment, the explicit expression of reads Sheng:2022ffb
| (67) | |||||
where in the last line is the rank-3 antisymmetric tensor. The explicit expression of can be obtained from by exchanging with . One can further take the space and momentum average of
| (68) |
where the momentum average is defined as
| (69) |
if we want to obtain momentum-integrated data for . Here is its momentum distribution which may contain information about collective flows such as and . If we want to obtain the transverse momentum spectra of , we have to integrate over the azimuthal angle and rapidity and keep , i.e. to replace in (69) by . We see in Eq. (69) that the average depends on the space average field squared which quantifies the field fluctuation. The theoretical results for as functions of transverse momenta, collision energies and centralities are presented in Ref. Sheng:2022wsy , which are in a good agreement with recent STAR data STAR:2022fan .
V Linear response theory for spin alignment of vector mesons in thermal media
In this section, we will show how to calculate the spin alignment of the vector meson from the Kubo formula in linear response theory zubarev1996statistical ; zubarev1997statistical ; Zubarev_1979 ; Kapusta:2006pm in thermalized QGP. The detailed discussion of this topic is in Ref. Dong:2023cng .
The Closed-Time-Path (CTP) formalism is a field-theory based method for many-particle systems in off-equilibrium as well in equilibrium Chou:1984es ; Blaizot:2001nr ; Wang:2001dm ; Berges:2004yj ; Cassing:2008nn ; Crossley:2015evo . When it is used for systems in equilibrium, it is actually the real time formalism of the thermal field theory Kapusta:2006pm ; Kapusta:2023eix . Wigner functions can be obtained from two-point Green’s functions on the CTP Sheng:2021kfc ; Sheng:2022ffb ; Hidaka:2022dmn ; Dong:2023cng ; Becattini:2024uha . The on-shell Wigner function for the vector meson is related to its MVSD (proportional to the spin density matrix) and defined as
| (70) |
where is the “” component of two-point Green’s functions on the CTP, and with being the short-hand notation for the MVSD, being the trace of the MVSD, and being the spin density matrix in Eq. (6). One can check that is always transverse to the on-shell momentum, . The on-shell Wigner function can be decomposed into the scalar (), polarization () and tensor polarization () parts as Sheng:2023chinphyb ; Becattini:2024uha
| (71) |
where each part is defined as
| (72) |
With Eq. (71) one can show that both and are traceless, . Using Eqs. (6) and (70), we obtain
| (73) |
We see that is related to while is related to .
We can extract by projecting
| (74) |
onto in Eq. (70) as
| (75) |
In (74), is the polarization vector along the spin quantization direction. With the first line of Eq. (73) and Eq. (75), we obtain
| (76) |
The above formula relates the Wigner function to .
The medium effects can be described by retarded and advanced two-point Green’s functions through spectral functions. For vector mesons interacting with thermal quarks, the spectral function can be defined through the imaginary part of the retarded two-point Green’s function (propagator in momentum space) as
| (77) |
The definition of two-point Green’s functions and differs by a factor from the usual one in quantum field theory, which are related by and . In Eq. (77), we defined
| (78) |
as the transverse and longitudinal projector respectively with , and are spectral functions in the transverse and longitudinal directions given by Dong:2023cng
| (79) |
where and are from : and , is the sign of , and is an infinitesimal positive number. One can check in Eq. (78) that . In Eq. (79), one can verify that the real parts of and contribute to the mass correction while the imaginary parts of and determines the width or life-time of the quasi-particle mode.
The two-point function is related to and through fetter2003quantum ; zubarev1997statistical
| (80) | |||||
where is the Bose-Einstein distribution with the inverse temperature and the vector meson’s chemical potential . Inserting Eq. (80) into (70) we obtain the on-shell Wigner function from which the spin alignment can be extracted through Eq. (76).
For free vector mesons, the spectral functions are , which give and for the free vector meson following Eqs. (77) and (80).
The non-equilibrium correction to can be calculated through the Kubo formula in linear response theory. The Kubo formula has been derived in Zubarev’s approach to non-equilibrium density operator Zubarev_1979 ; Hosoya:1983id ; Becattini:2019dxo . Detailed derivation is given in Ref. Becattini:2019dxo . Considering the thermal shear tensor as a perturbation from local equilibrium, the next-to-leading order correction of can be written as Dong:2023cng
| (81) |
where . The tensor is expressed as Dong:2023cng
| (82) |
where and are given by Eq. (78). Then the spin alignment of vector mesons can be obtained from Eq. (76) through Eqs. (70) and (81).
Under the quasi-particle approximation (QPA), the self-energies and spectral functions can be calculated analytically by expanding in powers of . This expansion requires , where and are the mass shift and width of the vector meson respectively. Then the spin alignment can be expressed as
| (83) |
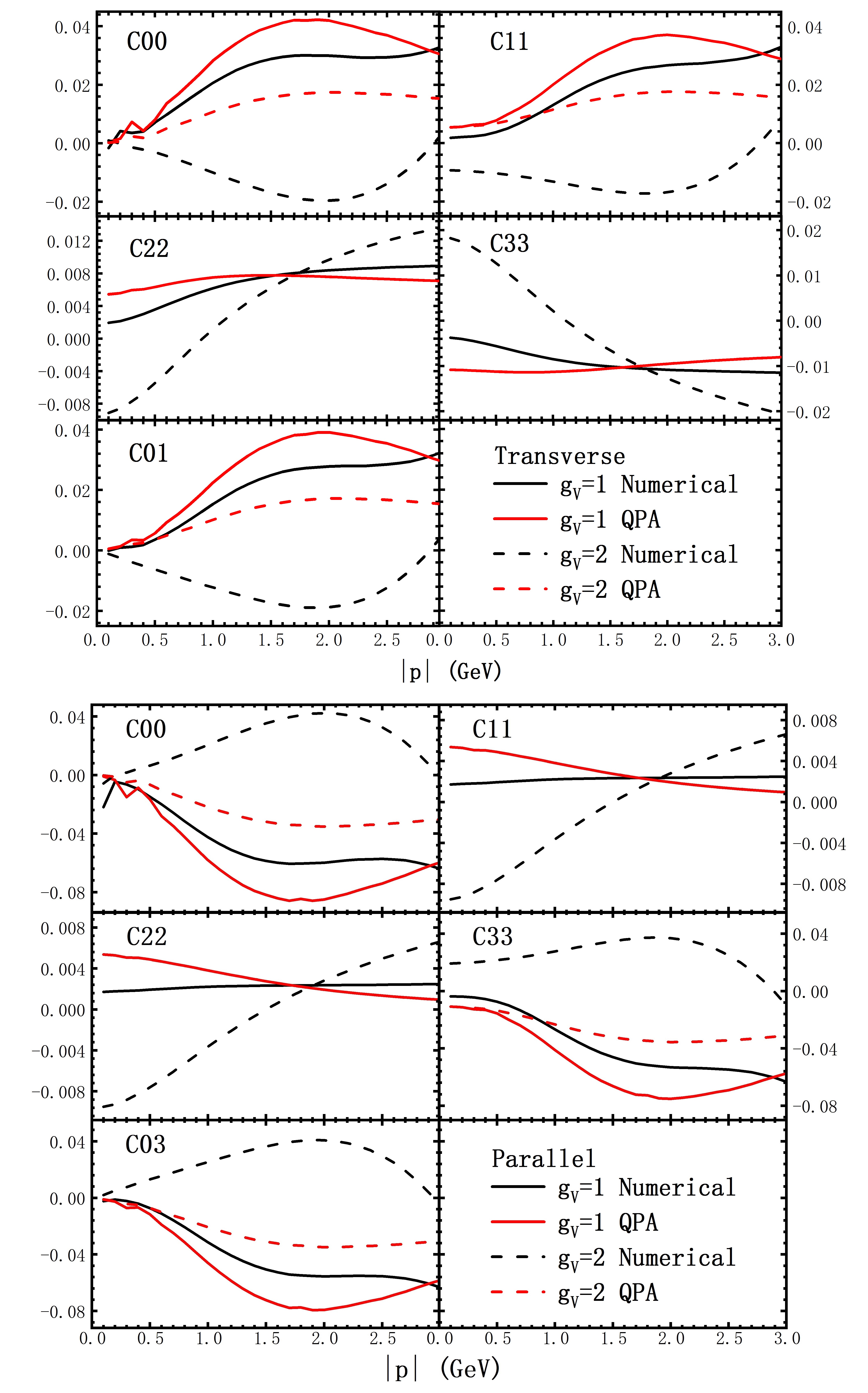
where is the spin alignment independent of the shear stress tensor and is the dimensionless tensor coefficient in the shear stress term. The results under the QPA are compared with full numerical results are shown in Fig. (4). For the values of parameters we choose, the magnitudes of and are and , respectively. As a consequence, if the thermal shear tensor is , the contribution from the thermal shear tensor to the meson’s spin alignment is , which is much smaller than the contribution from the strong force fields Sheng:2022wsy .
VI Vector meson’s spin alignments in quark fragmentation
In high energy reactions, hadron production is normally described by fragmentation functions (FFs). The hadron‘s Polarization can be realized in terms of polarized FFs Chen:2016moq ; Chen:2016iey ; Chen:2020pty . These FFs are defined via quark-quark correlators. Among different high energy reactions, the clean and ideal place to study FFs is in high energy collisions. In Ref. Chen:2016moq , the complete decomposition of quark-quark correlators for spin-1 hadrons with systematic results for hadron polarization in terms of FFs up to twist-3 in have been presented. Experimental measurements have been carried out many years ago for the longitudinal polarization of hyperons ALEPH:1996oew ; OPAL:1997oem and for the spin alignments of vector mesons DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs in the inclusive production process at LEP. Significant effects have been observed. These experimental data have attracted many phenomenological studies Anselmino:1997ui ; Anselmino:1998jv ; Anselmino:1999cg ; Xu:2001hz ; Xu:2003fq ; Chen:2016moq ; Chen:2016iey ; Chen:2020pty and parameterization of corresponding FFs has been obtained Chen:2016moq ; Chen:2016iey ; Chen:2020pty . In this section we will summarize these results.
VI.1 FFs from quark-quark correlator
For the fragmentation of the quark (or anti-quark), the quark-quark correlator as a matrix in Dirac indices is defined by
| (84) |
where and are four-momenta of the quark and hadron respectively, denotes the hadron’s spin, and is the gauge link defined as
| (85) |
which guarantees the gauge invariance of FFs. In the rest part of the paper, for notational simplicity, we suppress the gauge link in forthcoming equations. In this case, the field operator just stands for .
The FFs are obtained from in the following way. First, we expand in terms of matrices as
| (86) |
where coefficients are all real functions and are Lorentz scalar, pseudo-scalar, vector, axial-vector and tensor respectively. Then we expand these coefficient functions according to their respective Lorentz transformation properties in terms of basic Lorentz covariants multiplied by scalar functions which are constructed from available variables. These scalar functions are the FFs.
Clearly, basic Lorentz covariants to be constructed depend strongly on what variables that we have at hand. Besides and , we have variables for spin states which are different for spin-0, 1/2 or 1 hadrons. For this purpose, we need to decompose the spin density matrix in terms of known operators multiplied by Lorentz covariants. For spin-1/2 hadrons, the spin density matrix is decomposed as in Eq. (1), but in the rest frame of the hadron should be generalized to a covariant form . For spin-1 hadrons, the density matrix is usually decomposed as in Eq. (6). The tensor polarization can be parameterized as
| (90) |
We see that, for spin-1 hadrons, besides the polarization vector , there is also a tensor polarization part. The polarization vector is similar to that for spin-1/2 hadrons. The tensor polarization part has five components, namely a Lorentz scalar , a Lorentz vector and a Lorentz tensor that has two components and . The vector meson’s spin alignment is only related to through .
The quark-quark correlator given by Eq. (84) is un-integrated, i.e. it depends on the four-momentum . If we consider three- or one-dimensional FFs, we need to integrate it over and . We take one-dimensional FFs as an example. In this case, after integrating over and , we obtain,
| (91) |
where . After Lorentz decomposition, we obtain terms related to as,
| (92) |
We can obtain the expression for by reversely solving Eqs. (91) and (92),
| (93) |
For comparison, we present the corresponding equations for that describes the longitudinal spin transfer in the fragmentation process
| (94) |
The difference between in Eq. (93) and in Eq. (94) is that is involved in the former while is involved in the latter.
VI.2 Vector meson’s spin alignments from FFs
From Eqs. (93), we see clearly that, similar to the well-known unpolarized FF , is independent of the quark’s polarization because it is a sum over the quark’s spin states
| (95) |
where denotes the quark’s helicity (or chirality), and . In contrast, the result for gives
| (96) |
which depends on the quark’s spin explicitly.
We can draw an important conclusion from Eq. (95) for the spin alignment for the vector meson produced in the fragmentation process : it is determined by and independent of the initial polarization of the quark. The conclusion is rather unexpected because the vector meson’s spin alignment in high energy reactions was first observed in at LEP DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs where initial quarks and anti-quarks are longitudinally polarized. However, this is consistent with space reflection in fragmentation processes where is space reflection invariant while the helicity of the initial quark changes the sign. This conclusion is rather solid since it follows from the general principle of QCD. It can also be tested easily in experiments. In the following we present numerical results for and as examples.
VI.3 Vector meson’s spin alignments in
Suppose that the quark fragmentation mechanism dominates hadron production in annihilation at high energies, we obtain the vector meson’s alignment in as
| (97) | |||
| (98) |
where we also show the result of hyperon polarization for comparison. In Eqs. (97) and (98), and are the quark polarization and production weight at the vertex of annihilation respectively which are determined by the quark’s electric charge, and in the weak interaction current, and so on (see e.g. Chen:2016iey for the detailed expressions), , where and are the four-momenta of the incident and respectively, and is the four-momentum of the produced quark.
The FFs are extracted from data available at a given scale and their scale dependence is determined by the QCD evolution equation, the DGLAP equation Dokshitzer:1977sg ; Gribov:1972ri ; Altarelli:1977zs ; Owens:1978qz ; Georgi:1977mg ; Uematsu:1978yw ; Ravindran:1996ri ; Ravindran:1996jd . In Ref. Chen:2016iey ; Chen:2020pty , such parameterizations of for vector mesons have been obtained for the first time by fitting available data DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj . As comparison, parameterizations of for are also given therein Chen:2016iey ; Chen:2020pty by fitting the LEP data ALEPH:1996oew ; OPAL:1997oem . Here, we show the fitted results obtained there Chen:2016iey ; Chen:2020pty in Figs. 5 and 6.


From Figs. 5 and 6, we see a distinct feature that there is a strong energy dependence for , while the energy dependence for is weak. The former comes mainly from the energy dependence of while the latter comes mainly from the QCD evolution of FFs. The relatively rapid change in the energy region around the mass of boson comes from the influence of . This feature can be tested in future experiments.
VI.4 Vector meson’s spin alignments in
Assuming the universality of FFs, one can calculate vector meson’s spin alignments in other high energy reactions where the fragmentation mechanism dominates. This applies to hadron production at high transverse momentum in collisions and deeply inelastic scatterings. In Ref. Chen:2020pty , such calculations have been carried out in collisions. As examples, we show in Fig. 7 the results obtained there for and in two rapidity regions as functions of .

We see that for vector mesons deviate from significantly showing large spin alignments. Such results can be tested in experiments at RHIC and LHC.
VII Summary and outlook
Spin alignments for vector mesons have been observed in high energy reactions STAR:2022fan ; DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs ; NOMAD:2006kuc . There are two types of spin alignments: global spin alignments in heavy-ion collisions STAR:2022fan and helicity-basis spin alignments in collisions DELPHI:1997ruo ; OPAL:1997vmw ; OPAL:1997nwj ; OPAL:1999hxs . These measurements show different features of spin alignments arising from different hadronization mechanisms in collisions of heavy-ion and .
In high energy heavy-ion collisions in the region of central rapidity and small transverse momentum, hadron production is mainly through quark combination or coalescence. The global spin alignment in this case not only depends on the polarization of quarks and anti-quarks but is also sensitive to the local correlation between the polarization of quarks and that of anti-quarks. Measurements of the global spin alignment in this case provide a good opportunity to study the polarization correlation in the sQGP produced in heavy-ion collisions. The STAR’s measurements of meson’s spin alignments STAR:2022fan is consistent with the theoretical description based on vector fields that lead to a strong local correlation between and Yang:2017sdk ; Sheng:2020ghv ; Sheng:2022ffb ; Sheng:2022wsy . The data were used to extract the strength of the local fluctuation in vector fields Sheng:2022ffb ; Sheng:2022wsy .
In and collisions at high energies, hadron production is dominated by fragmentation with fragmentation functions. It has been shown that the spin alignment of vector mesons in the helicity basis is independent of the polarization of the initial quark in the quark fragmentation process. With the parameterization of corresponding fragmentation functions the prediction on spin alignments of vector mesons in high energy and collisions has been made Chen:2016moq ; Chen:2016iey ; Chen:2020pty .
It is impressive and interesting to see the distinction between the global spin alignments in high energy heavy-ion collisions and in or collisions which are dominated by different hadronization mechanisms.
It is important to extend the measurements to different high energy reactions at different energies to test the universality of these properties.
Further measurements on global spin alignments of different vector mesons in relativistic heavy ion collisions are expected to be carried out in the near future by the STAR Collaboration at RHIC and ALICE Collaboration at LHC.
More studies are also planned at GSI, HIAF and NICA in the lower energy regions.
Also studies in collisions are expected by STAR at RHIC, and in by BESIII at BEPC and Belle II at KEK.
They can also be measured in lepton-nucleon scatterings at future EIC.
Obviously such studies provide new insights into properties of sQGP and hadronization mechanisms.
Acknowledgements
This work was supported in part by the National Key Research and Development Program of China under Contract No. 2022YFA1604900, by the National Natural Science Foundation of China (NSFC) under Contract Nos. 12025501, 11890710, 11890713, 11890714, 12147101 and 12135011, by the Strategic Priority Research Program of the Chinese Academy of Sciences (CAS) under Grant No. XDB34030102 and by the Natural Science Foundation of Shandong Province.
References
- (1) P. Braun-Munzinger, V. Koch, T. Schäfer, and J. Stachel, Phys. Rept. 621, 76 (2016), 1510.00442.
- (2) W. Florkowski, A. Kumar, and R. Ryblewski, Prog. Part. Nucl. Phys. 108, 103709 (2019), 1811.04409.
- (3) C. M. Ko, Nucl. Sci. Tech. 34, 80 (2023).
- (4) R. Rapp, Nucl. Sci. Tech. 34, 63 (2023).
- (5) Y. Zhang, D. W. Zhang, and X. F. Luo, Nucl. Tech. 46, 040001 (2023).
- (6) J. Zhao, J.-H. Chen, X.-G. Huang, and Y.-G. Ma, Nucl. Sci. Tech. 35, 20 (2024).
- (7) A. Pandav, D. Mallick, and B. Mohanty, Prog. Part. Nucl. Phys. 125, 103960 (2022), 2203.07817.
- (8) W.-B. He, Y.-G. Ma, L.-G. Pang, H.-C. Song, and K. Zhou, Nucl. Sci. Tech. 34, 88 (2023).
- (9) J. Chen, X. Dong, Y.-G. Ma, and Z. Xu, Sci. Bull. 68, 3252 (2023), 2311.09877.
- (10) Y. G. Ma, Nucl. Sci. Tech. 34, 97 (2023).
- (11) L. G. Pang and X. N. Wang, Nucl. Sci. Tech. 34, 194 (2023).
- (12) K. J. Sun et al., Nucl. Tech. 46, 040012 (2023).
- (13) Q. Chen, G. L. Ma, and J. H. Chen, Nucl. Tech. 46, 040013 (2023).
- (14) Z.-T. Liang and X.-N. Wang, Phys. Rev. Lett. 94, 102301 (2005), nucl-th/0410079, [Erratum: Phys.Rev.Lett. 96, 039901 (2006)].
- (15) Z.-T. Liang and X.-N. Wang, Phys. Lett. B 629, 20 (2005), nucl-th/0411101.
- (16) J.-H. Gao et al., Phys. Rev. C 77, 044902 (2008), 0710.2943.
- (17) S. A. Voloshin, (2004), nucl-th/0410089.
- (18) B. Betz, M. Gyulassy, and G. Torrieri, Phys. Rev. C 76, 044901 (2007), 0708.0035.
- (19) A. Ipp, A. Di Piazza, J. Evers, and C. H. Keitel, Phys. Lett. B 666, 315 (2008), 0710.5700.
- (20) F. Becattini, F. Piccinini, and J. Rizzo, Phys. Rev. C 77, 024906 (2008), 0711.1253.
- (21) Z.-t. Liang, J. Phys. G 34, S323 (2007), 0705.2852.
- (22) STAR, J. H. Chen, J. Phys. G 34, S331 (2007).
- (23) STAR, I. Selyuzhenkov, J. Phys. G 34, S1099 (2007), nucl-ex/0701034.
- (24) STAR, B. I. Abelev et al., Phys. Rev. C 77, 061902 (2008), 0801.1729.
- (25) STAR, B. I. Abelev et al., Phys. Rev. C 76, 024915 (2007), 0705.1691, [Erratum: Phys.Rev.C 95, 039906 (2017)].
- (26) STAR, L. Adamczyk et al., Nature 548, 62 (2017), 1701.06657.
- (27) Q. Wang, Nucl. Phys. A 967, 225 (2017), 1704.04022.
- (28) Z.-T. Liang, M. A. Lisa, and X.-N. Wang, Nucl. Phys. News 30, 10 (2020), 1912.07822.
- (29) J.-H. Gao, Z.-T. Liang, Q. Wang, and X.-N. Wang, Lect. Notes Phys. 987, 195 (2021), 2009.04803.
- (30) X.-G. Huang, J. Liao, Q. Wang, and X.-L. Xia, Lect. Notes Phys. 987, 281 (2021), 2010.08937.
- (31) J.-H. Gao, G.-L. Ma, S. Pu, and Q. Wang, Nucl. Sci. Tech. 31, 90 (2020), 2005.10432.
- (32) F. Becattini and M. A. Lisa, Ann. Rev. Nucl. Part. Sci. 70, 395 (2020), 2003.03640.
- (33) F. Becattini, Rept. Prog. Phys. 85, 122301 (2022), 2204.01144.
- (34) F. Becattini et al., (2024), 2402.04540.
- (35) STAR, M. S. Abdallah et al., Nature 614, 244 (2023), 2204.02302.
- (36) Y.-G. Yang, R.-H. Fang, Q. Wang, and X.-N. Wang, Phys. Rev. C 97, 034917 (2018), 1711.06008.
- (37) X.-L. Sheng, L. Oliva, and Q. Wang, Phys. Rev. D 101, 096005 (2020), 1910.13684, [Erratum: Phys.Rev.D 105, 099903 (2022)].
- (38) X.-L. Sheng, L. Oliva, Z.-T. Liang, Q. Wang, and X.-N. Wang, Phys. Rev. D 109, 036004 (2024), 2206.05868.
- (39) X.-L. Sheng, L. Oliva, Z.-T. Liang, Q. Wang, and X.-N. Wang, Phys. Rev. Lett. 131, 042304 (2023), 2205.15689.
- (40) X.-N. Wang, Nucl. Sci. Tech. 34, 15 (2023), 2302.00701.
- (41) J. Chen, Z.-T. Liang, Y.-G. Ma, and Q. Wang, Sci. Bull. 68, 874 (2023), 2305.09114.
- (42) X.-L. Sheng, Z.-T. Liang, and Q. Wang, Acta Phys. Sin. 72, 072502 (2023).
- (43) J.-H. Gao, X.-G. Huang, Z.-T. Liang, Q. Wang, and X.-N. Wang, Acta Phys. Sin. 72, 072501 (2023).
- (44) L.-J. Ruan, Z.-B. Xu, and C. Yang, Acta Phys. Sin. 72, 112401 (2023).
- (45) J. Chen et al., Nucl. Phys. News 34, 17 (2024).
- (46) DELPHI, P. Abreu et al., Phys. Lett. B 406, 271 (1997).
- (47) OPAL, K. Ackerstaff et al., Phys. Lett. B 412, 210 (1997), hep-ex/9708022.
- (48) OPAL, K. Ackerstaff et al., Z. Phys. C 74, 437 (1997).
- (49) OPAL, G. Abbiendi et al., Eur. Phys. J. C 16, 61 (2000), hep-ex/9906043.
- (50) ZEUS, J. Breitweg et al., Eur. Phys. J. C 12, 393 (2000), hep-ex/9908026.
- (51) NOMAD, A. Chukanov et al., Eur. Phys. J. C 46, 69 (2006), hep-ex/0604050.
- (52) M. Anselmino, M. Bertini, F. Murgia, and P. Quintairos, Eur. Phys. J. C 2, 539 (1998), hep-ph/9704420.
- (53) M. Anselmino, M. Bertini, F. Murgia, and B. Pire, Phys. Lett. B 438, 347 (1998), hep-ph/9805234.
- (54) M. Anselmino, M. Bertini, F. Caruso, F. Murgia, and P. Quintairos, Eur. Phys. J. C 11, 529 (1999), hep-ph/9904205.
- (55) Q.-h. Xu, C.-x. Liu, and Z.-t. Liang, Phys. Rev. D 63, 111301 (2001), hep-ph/0103267.
- (56) Q.-h. Xu and Z.-t. Liang, Phys. Rev. D 67, 114013 (2003), hep-ph/0304125.
- (57) K.-b. Chen, W.-h. Yang, S.-y. Wei, and Z.-t. Liang, Phys. Rev. D 94, 034003 (2016), 1605.07790.
- (58) K.-b. Chen, W.-h. Yang, Y.-j. Zhou, and Z.-t. Liang, Phys. Rev. D 95, 034009 (2017), 1609.07001.
- (59) K.-b. Chen, Z.-t. Liang, Y.-k. Song, and S.-y. Wei, Phys. Rev. D 102, 034001 (2020), 2002.09890.
- (60) A. Bacchetta and P. J. Mulders, Phys. Rev. D 62, 114004 (2000), hep-ph/0007120.
- (61) M. Jacob and G. C. Wick, Annals Phys. 7, 404 (1959).
- (62) S. U. Chung, (1971).
- (63) A. Lesnik et al., Phys. Rev. Lett. 35, 770 (1975).
- (64) G. Bunce et al., Phys. Rev. Lett. 36, 1113 (1976).
- (65) J. Bensinger et al., Phys. Rev. Lett. 50, 313 (1983).
- (66) S. A. Gourlay et al., Phys. Rev. Lett. 56, 2244 (1986).
- (67) TASSO, M. Althoff et al., Z. Phys. C 27, 27 (1985).
- (68) ALEPH, D. Buskulic et al., Phys. Lett. B 374, 319 (1996).
- (69) OPAL, K. Ackerstaff et al., Eur. Phys. J. C 2, 49 (1998), hep-ex/9708027.
- (70) ALICE, S. Acharya et al., Phys. Rev. Lett. 125, 012301 (2020), 1910.14408.
- (71) X.-L. Sheng, S. Pu, and Q. Wang, Phys. Rev. C 108, 054902 (2023), 2308.14038.
- (72) X.-L. Xia, H. Li, X.-G. Huang, and H. Zhong Huang, Phys. Lett. B 817, 136325 (2021), 2010.01474.
- (73) J.-H. Gao, Phys. Rev. D 104, 076016 (2021), 2105.08293.
- (74) F. Li and S. Y. F. Liu, (2022), 2206.11890.
- (75) D. Wagner, N. Weickgenannt, and E. Speranza, Phys. Rev. Res. 5, 013187 (2023), 2207.01111.
- (76) W.-B. Dong, Y.-L. Yin, X.-L. Sheng, S.-Z. Yang, and Q. Wang, Phys. Rev. D 109, 056025 (2024), 2311.18400.
- (77) B. Müller and D.-L. Yang, Phys. Rev. D 105, L011901 (2022), 2110.15630, [Erratum: Phys.Rev.D 106, 039904 (2022)].
- (78) A. Kumar, B. Müller, and D.-L. Yang, Phys. Rev. D 108, 016020 (2023), 2304.04181.
- (79) A. Manohar and H. Georgi, Nucl. Phys. B 234, 189 (1984).
- (80) X.-L. Sheng, Q. Wang, and X.-N. Wang, Phys. Rev. D 102, 056013 (2020), 2007.05106.
- (81) Z.-t. Liang, Off diagonal elements of the spin density matrix of vector mesons in heavy ion collisions, in The 7th International Conference on Chirality, Vorticity and magnetic field in heavy ion collisions, July 2023, Beijing, China, 2023, https://indico.ihep.ac.cn/event/16043/.
- (82) J.-p. Lv, Z.-h. Yu, Z.-t. Liang, Q. Wang, and X.-N. Wang, Phys. Rev. D 109, 114003 (2024), 2402.13721.
- (83) Z. Zhang, J.-p. Lv, Z.-h. Yu, and Z.-t. Liang, (2024), 2406.03840.
- (84) D. Zubarev, V. Morozov, and G. Röpke, Statistical Mechanics of Nonequilibrium Processes, Basic Concepts, Kinetic TheoryStatistical Mechanics of Nonequilibrium Processes (Wiley-VCH Berlin, 1996).
- (85) D. Zubarev, V. Morozov, and G. Röpke, Statistical Mechanics of Nonequilibrium Processes, Statistical Mechanics of Nonequilibrium Processes. Volume 2: Relaxation and Hydrodynamic ProcessesStatistical Mechanics of Nonequilibrium Processes (Wiley-VCH Berlin, 1997).
- (86) D. N. Zubarev, A. V. Prozorkevich, and S. A. Smolyanskii, Theoretical and Mathematical Physics 40, 821 (1979).
- (87) J. I. Kapusta and C. Gale, Finite-temperature field theory: Principles and applicationsCambridge Monographs on Mathematical Physics (Cambridge University Press, Cambridge, 2011).
- (88) K.-c. Chou, Z.-b. Su, B.-l. Hao, and L. Yu, Phys. Rept. 118, 1 (1985).
- (89) J.-P. Blaizot and E. Iancu, Phys. Rept. 359, 355 (2002), hep-ph/0101103.
- (90) Q. Wang, K. Redlich, H. Stoecker, and W. Greiner, Phys. Rev. Lett. 88, 132303 (2002), nucl-th/0111040.
- (91) J. Berges, AIP Conf. Proc. 739, 3 (2004), hep-ph/0409233.
- (92) W. Cassing, Eur. Phys. J. ST 168, 3 (2009), 0808.0715.
- (93) M. Crossley, P. Glorioso, and H. Liu, JHEP 09, 095 (2017), 1511.03646.
- (94) J. I. Kapusta and C. Gale, Finite-Temperature Field TheoryCambridge Monographs on Mathematical Physics (Cambridge University Press, 2023).
- (95) X.-L. Sheng, N. Weickgenannt, E. Speranza, D. H. Rischke, and Q. Wang, Phys. Rev. D 104, 016029 (2021), 2103.10636.
- (96) Y. Hidaka, S. Pu, Q. Wang, and D.-L. Yang, Prog. Part. Nucl. Phys. 127, 103989 (2022), 2201.07644.
- (97) X.-L. Sheng, Z.-T. Liang, and Q. Wang, Acta Phys. Sin. (in Chinese) 72, 072502 (2023).
- (98) A. Fetter and J. Walecka, Quantum Theory of Many-particle SystemsDover Books on Physics (Dover Publications, New York, 2003).
- (99) A. Hosoya, M.-a. Sakagami, and M. Takao, Annals Phys. 154, 229 (1984).
- (100) F. Becattini, M. Buzzegoli, and E. Grossi, Particles 2, 197 (2019), 1902.01089.
- (101) Y. L. Dokshitzer, Sov. Phys. JETP 46, 641 (1977).
- (102) V. N. Gribov and L. N. Lipatov, Sov. J. Nucl. Phys. 15, 438 (1972).
- (103) G. Altarelli and G. Parisi, Nucl. Phys. B 126, 298 (1977).
- (104) J. F. Owens, Phys. Lett. B 76, 85 (1978).
- (105) H. Georgi and H. D. Politzer, Nucl. Phys. B 136, 445 (1978).
- (106) T. Uematsu, Phys. Lett. B 79, 97 (1978).
- (107) V. Ravindran, Nucl. Phys. B 490, 272 (1997), hep-ph/9607384.
- (108) V. Ravindran, Phys. Lett. B 398, 169 (1997), hep-ph/9606273.