Varying the medium surrounding an optical resonator: An efficient and rigorous way to calculate its spectral changes

Sensing the material surrounding an optical resonator by looking at its eigenmodes, such as localized surface plasmon (SP) modes in metallic nanoparticles [1] or whispering gallery (WG) modes in dielectric micro-spheres [2], has recently become an important application of nanophotonics. However, modelling and optimization of optical resonators for sensing applications, as well as interpreting the sensing information present complicated ‘inverse’ problems which require extensive and repetitive calculations. On the other hand, theoretical approaches, in which the eigenmodes of the system are calculated only once and then used as a fixed basis for treating any changes of the environment, could reduce the computational time dramatically, by orders of magnitude.

The exponential growth with distance of the electromagnetic field of the eigenmodes of an open optical system not only causes the well known issue with the mode normalization [3] but also results in a limited completeness of the eigenmodes. While the former has been recently solved by introducing an exact analytical normalization [4, 5] or by regularizing the exponentially growing fields [6, 7], the latter remains a fundamental obstacle for treating any perturbations in the medium surrounding an open system. At the same time, for a number of technologically crucial applications, such as the refractive index or chirality sensing with optical resonators, it is very important to develop a theory which would accurately and efficiently treat any changes of the medium, not necessarily limited to lowest-order perturbations [8].

The resonant states (RSs) of an optical system, also known as quasi-normal modes [7], are the eigen solutions to Maxwell’s equations with outgoing wave boundary conditions. They fully describe the spectral properties of an optical system, providing direct access to its scattering matrix [9, 10]. Their exact normalization consists of a sum of a volume integral of the square of the RS field with a material-dependent weight function, performed over any finite volume containing the system, and an integral of the fields over the volume surface [4, 3, 5]. Applying any valid regularization to the RS field, such as a Gaussian regularization introduced by Zel’dovich [6], or the one imposed by a perfectly matched layer [7] results in the volume term extended to the surrounding medium and the surface term dropped. Both the RS normalization and orthogonality then take the form of a scalar product, similar to those of a Hermitian system [11]. However, a completeness of such regularized RSs in the full space is still not achievable [12, 13].

Owing to the well-defined boundaries of an optical system, the RSs are complete at least within the minimal convex volume surrounding the system [5]. Such a completeness is at the heart of the resonant-state expansion (RSE), a rigorous method recently developed for treating perturbations of arbitrary shape and strength [4, 14]. The RSE has been generalized to include the frequency dispersion [15] as well as magnetic, chiral, and bi-anisotropic materials [5] and was proven to be orders of magnitude more efficient than popular computational methods [14, 16]. However, a significant limitation of the RSE is that all perturbations must be contained within the basis system.

Recently, a single-mode first-order perturbation theory capable of including homogeneous and isotropic perturbations of the surrounding medium has been developed [8]. This theory uses the analytic normalization of the RSs but treats perturbations in a way entirely different from the RSE. Crucially, it is limited to small perturbations and predicts only linear changes of the RS frequencies with the medium parameters, such as the permittivity. However, the optical modes can be extremely sensitive to even small changes of the environment. In plasmonic resonators, for example, this can be due to strong near fields and hot spots. Also, the single-mode theory obviously fails when two or more RSs affected by perturbations are spectrally close to each other, such as in the examples considered in [17, 18].

In this Letter, we present a rigorous RSE-based approach to treating any changes of the homogeneous isotropic or bi-isotropic medium surrounding the optical system. By making a linear transformation of Maxwell’s equations we map the changes of the surrounding medium onto effective perturbations of the system itself, which is then rigorously treated by the RSE. We also develop a single-mode approximation based on the RS regularization and compare it with the full and diagonal RSE, as well as with the first-order perturbation theory [8].

Let us start assuming that a sufficient number of the RSs of a basis system has been calculated by any means. This basis system is an optical resonator described by generally dispersive permittivity and permeability tensors, $\hat{{\boldsymbol{\varepsilon}}}(k,\textbf{r})$ and $\hat{{\boldsymbol{\mu}}}(k,\textbf{r})$, where $k=\omega/c$ is the light wave number. The RSs are solutions to Maxwell’s equations [5],

$$\left[k_{n}\hat{\mathbb{P}}_{0}(k_{n},\textbf{r})-\hat{\mathbb{D}}(\textbf{r})\right]\vec{\mathbb{F}}_{n}(\textbf{r})=0\,,$$

(1)

satisfying outgoing boundary conditions. Here,

$$\hat{\mathbb{P}}_{0}(k,\textbf{r})=\begin{pmatrix}\hat{{\boldsymbol{\varepsilon}}}(k,\textbf{r})&\hat{\mathbf{0}}\\ \hat{\mathbf{0}}&\hat{{\boldsymbol{\mu}}}(k,\textbf{r})\end{pmatrix},\quad\hat{\mathbb{D}}(\textbf{r})=\begin{pmatrix}\hat{\mathbf{0}}&\nabla\times\\ \nabla\times&\hat{\mathbf{0}}\end{pmatrix},$$

(2)

are, respectively, the $6\times 6$ generalized permittivity and curl operators, $\vec{\mathbb{F}}_{n}(\textbf{r})$ is a $6\times 1$ column vector with components $\textbf{E}_{n}(\textbf{r})$ and $i\textbf{H}_{n}(\textbf{r})$ of the electric and magnetic fields, respectively, $\hat{\mathbf{0}}$ is the $3\times 3$ zero matrix, and $n$ is an index labelling the RSs. Let us use ${\cal V}_{\rm in}$ and ${\cal V}_{\rm out}$ to denote, respectively, the system volume and rest of space. Let us also assume for clarity that the basis system is surrounded by vacuum, i.e. $\hat{{\boldsymbol{\varepsilon}}}(k,\textbf{r})=\hat{{\boldsymbol{\mu}}}(k,\textbf{r})=\hat{\mathbf{1}}$ for $\textbf{r}\in{\cal V}_{\rm out}$, where $\hat{\mathbf{1}}$ is the $3\times 3$ identity matrix — the general case of bi-isotropic system and surrounding medium is treated in Sec. S.I of [12].

Let us also consider a perturbed system which is the same optical resonator placed in a different environment, with modified RSs labelled with index $\nu$ which satisfy Maxwell’s equations

$$\left[k_{\nu}\hat{\mathbb{P}}(k_{\nu},\textbf{r})-\hat{\mathbb{D}}(\textbf{r})\right]\vec{\mathbb{F}}_{\nu}(\textbf{r})=0$$

(3)

with $\hat{\mathbb{P}}(k,\textbf{r})=\hat{\mathbb{P}}_{0}(k,\textbf{r})=\left[\hat{{\boldsymbol{\varepsilon}}}(k,\textbf{r});\hat{{\boldsymbol{\mu}}}(k,\textbf{r})\right]$ for $\textbf{r}\in{\cal V}_{\rm in}$, but $\hat{\mathbb{P}}(k,\textbf{r})=\left[\varepsilon_{b}(k)\hat{\mathbf{1}};\mu_{b}(k)\hat{\mathbf{1}}\right]$ for $\textbf{r}\in{\cal V}_{\rm out}$, where we use brackets for writing block-diagonal tensors like $\hat{\mathbb{P}}_{0}(k,\textbf{r})$ in Eq. (2). The surrounding medium is described by homogeneous isotropic permittivity $\varepsilon_{b}$ and permeability $\mu_{b}$, which in what follows are assumed for clarity of derivation to be frequency independent – the case of dispersive $\varepsilon_{b}(k)$ and $\mu_{b}(k)$ is discussed in Sec. S.I.B of [12].

Now, we perform a linear transformation of Eq. (3), introducing fields E and H and a wave number $k$:

$$\textbf{E}(\textbf{r})=\sqrt{\varepsilon_{b}}\textbf{E}_{\nu}(\textbf{r})\,,\quad\textbf{H}(\textbf{r})=\sqrt{\mu_{b}}\textbf{H}_{\nu}(\textbf{r})\,,\quad k=n_{b}k_{\nu}\,,$$

(4)

where $n_{b}=\sqrt{\varepsilon_{b}\mu_{b}}$ is the refractive index of the surrounding medium. Equation (3) then becomes

$$\left[k\tilde{\mathbb{P}}(k,\textbf{r})-\hat{\mathbb{D}}(\textbf{r})\right]\vec{\mathbb{F}}(\textbf{r})=0\,,$$

(5)

where $\tilde{\mathbb{P}}(k,\textbf{r})=\left[\tilde{{\boldsymbol{\varepsilon}}}(k,\textbf{r});\tilde{{\boldsymbol{\mu}}}(k,\textbf{r})\right]$ with $\tilde{{\boldsymbol{\varepsilon}}}(k,\textbf{r})={\hat{{\boldsymbol{\varepsilon}}}(k/n_{b},\textbf{r})}/{\varepsilon_{b}}$ and $\tilde{{\boldsymbol{\mu}}}(k,\textbf{r})={\hat{{\boldsymbol{\mu}}}(k/n_{b},\textbf{r})}/{\mu_{b}}$, for $\textbf{r}\in{\cal V}_{\rm in}$ and $\tilde{\mathbb{P}}(k,\textbf{r})=\left[\hat{\mathbf{1}};\hat{\mathbf{1}}\right]$ for $\textbf{r}\in{\cal V}_{\rm out}$. In other words, the transformed equation Eq. (5) describes a modified, effective optical system which is again surrounded by vacuum. This implies that the effective perturbation is concentrated within the system volume, and we can therefore solve Eq. (5) with the help of the dispersive RSE, treating Eq. (1) as unperturbed system and $k_{n}$ and $\vec{\mathbb{F}}_{n}$ as basis RSs. To do so, we introduce a perturbation $\Delta\hat{\mathbb{P}}(k,\textbf{r})=\tilde{\mathbb{P}}(k,\textbf{r})-\hat{\mathbb{P}}_{0}(k,\textbf{r})$ for $\textbf{r}\in{\cal V}_{\rm in}$ and $\Delta\hat{\mathbb{P}}(k,\textbf{r})=0$ for $\textbf{r}\in{\cal V}_{\rm out}$, so that Eq. (5) becomes

$$\left[k\hat{\mathbb{P}}_{0}(k,\textbf{r})+k\Delta\hat{\mathbb{P}}(k,\textbf{r})-\hat{\mathbb{D}}(\textbf{r})\right]\vec{\mathbb{F}}(\textbf{r})=0\,.$$

(6)

We solve Eq. (6) by expanding the perturbed RS into the unperturbed ones,

$$\vec{\mathbb{F}}(\textbf{r})=\sum_{n}c_{n}\vec{\mathbb{F}}_{n}\,.$$

Then, according to the dispersive RSE [15, 5], the perturbed RS wave number $k$ and the expansion coefficients $c_{n}$ satisfy a linear matrix eigenvalue equation

	$\displaystyle(k-k_{n})c_{n}$	$\displaystyle=$	$\displaystyle-k\sum\limits_{m}V_{nm}(\infty)c_{m}$
			$\displaystyle+k_{n}\sum\limits_{m}\left[V_{nm}(\infty)-V_{nm}(k_{n})\right]c_{m}\,,$

where

$$V_{nm}(k)=\int\vec{\mathbb{F}}_{n}(\textbf{r})\cdot\Delta\hat{\mathbb{P}}(k,\textbf{r})\vec{\mathbb{F}}_{m}(\textbf{r})d\textbf{r}\,.$$

(8)

This is valid for an arbitrary generalized Drude-Lorentz dispersion of the generalized permittivity,

$$\hat{\mathbb{P}}_{0}(k,\textbf{r})=\hat{\mathbb{P}}_{\infty}(\textbf{r})+\sum\limits_{j}\frac{\hat{\mathbb{Q}}_{j}(\textbf{r})}{k-\Omega_{j}}\,,$$

(9)

where the generalized conductivity $\hat{\mathbb{Q}}_{j}(\textbf{r})$ is the residue of $\hat{\mathbb{P}}_{0}(k,\textbf{r})$ at the pole $k=\Omega_{j}$ in the complex frequency plane [19]. Note that the poles of $\tilde{\mathbb{P}}(k,\textbf{r})$ and $\hat{\mathbb{P}}_{0}(k,\textbf{r})$ are generally different as $n_{b}\neq 1$, so that $\Delta\hat{\mathbb{P}}(k,\textbf{r})$ replaces one group of poles with the other. Both groups have to be taken into account in the basis RSs, e.g. by using the infinitesimal-dispersive RSE (idRSE) [20]. Equation (Varying the medium surrounding an optical resonator: An efficient and rigorous way to calculate its spectral changes ) is an exact result provided that a sufficient number of the RSs are included in the basis to guarantee a required accuracy.

Let us now develop some approximations and simplifications. First of all, consider a single-mode, or diagonal version of Eq. (Varying the medium surrounding an optical resonator: An efficient and rigorous way to calculate its spectral changes ). In this case, the perturbed RS wave number is given by

$$k_{\nu}=\frac{k}{n_{b}}\approx\frac{k_{n}}{n_{b}}\frac{1+V_{nn}(\infty)-V_{nn}(k_{n})}{1+V_{nn}(\infty)}\,.$$

(10)

This can be simplified further, by extracting the first-order contribution of the surrounding medium, assuming $|\varepsilon_{b}-1|\ll 1$ and $|\mu_{b}-1|\ll 1$. In this case, the refractive index is approximated as $n_{b}=\sqrt{\varepsilon_{b}\mu_{b}}\approx(\varepsilon_{b}+\mu_{b})/2$, and

$$k_{\nu}\approx k_{n}\left(1-\frac{\varepsilon_{b}-1}{2}-\frac{\mu_{b}-1}{2}-V_{nn}(k_{n})\right)\,.$$

(11)

Keeping in $V_{nn}(k_{n})$ only the terms linear in $\varepsilon_{b}-1$ and $\mu_{b}-1$, Eq. (11) becomes equivalent to the first-order result presented in [8], see Secs. S.I.C and S.II.D of [12].

Another approximation, very similar to Eq. (10), can be obtained by using the idea of regularization of the RSs. To regularize them, Zel’dovich proposed [6] to multiply all RS wave functions with a Gaussian factor $e^{-\alpha r^{2}}$ and take the limit $\alpha\rightarrow+0$ after integration. This allows one to extend the volume of integration in the normalization integral to the entire space, which gives exactly the same result as the analytic rigorous normalization, as has been recently demonstrated in [21] for the RSs of a homogeneous dielectric sphere. Alternative to this regularization are the complex coordinate transformation [22] and use of perfectly matched layers [23, 7], ideally leading to the same result for the RS norm. Now, with a single-mode approximation, $\vec{\mathbb{F}}_{\nu}(\textbf{r})\approx\vec{\mathbb{F}}_{n}(\textbf{r})$, as in the diagonal RSE considered above, we solve Eq. (3) for the perturbed wave number $k_{\nu}$ as

$$\left\{k_{\nu}\left[\hat{\mathbb{P}}_{0}(\textbf{r})+\delta\hat{\mathbb{P}}(\textbf{r})\right]-\hat{\mathbb{D}}(\textbf{r})\right\}\vec{\mathbb{F}}_{n}(\textbf{r})\approx 0\,,$$

(12)

where the perturbation $\delta\hat{\mathbb{P}}(\textbf{r})=0$ for $\textbf{r}\in{\cal V}_{\rm in}$ and $\delta\hat{\mathbb{P}}(\textbf{r})=\left[\left(\varepsilon_{b}-1\right)\hat{\mathbf{1}};\left(\mu_{b}-1\right)\hat{\mathbf{1}}\right]$ for $\textbf{r}\in{\cal V}_{\rm out}$ – opposite to what we have used in the RSE. Note that for clarity of presentation, dispersion is neglected in Eq. (12). However, we provide illustrations for dispersive systems below and a full derivation with dispersion in Sec. S.II of [12].

Multiplying Eq. (12) with $\vec{\mathbb{F}}_{n}(\textbf{r})$ and integrating over the entire space, assuming regularization, we obtain from Eqs. (1) and (12)

$$k_{\nu}-k_{n}+k_{\nu}\int_{V_{\rm out}}\vec{\mathbb{F}}_{n}(\textbf{r})\cdot\delta\hat{\mathbb{P}}(\textbf{r})\vec{\mathbb{F}}_{n}(\textbf{r})d\textbf{r}\approx 0\,,$$

(13)

where we have used the fact that $\vec{\mathbb{F}}_{n}(\textbf{r})$ is normalized as

$$\int_{{\cal V}_{\rm in}}\vec{\mathbb{F}}_{n}(\textbf{r})\cdot\hat{\mathbb{P}}_{0}(\textbf{r})\vec{\mathbb{F}}_{n}(\textbf{r})d\textbf{r}+\int_{{\cal V}_{\rm out}}\vec{\mathbb{F}}_{n}^{2}(\textbf{r})d\textbf{r}=1\,,$$

(14)

which is equivalent to the exact analytical normalization without regularization [5]. Using the Poynting theorem for the regularized fields,

$$I_{nn}^{E}+W_{nn}^{E}+I_{nn}^{H}+W_{nn}^{H}=0\,,$$

(15)

where

	$\displaystyle\!\!\!\!\!\!I_{nm}^{E}\!=\!\!\int_{{\cal V}_{\rm in}}\!\!\!\textbf{E}_{n}\cdot\hat{{\boldsymbol{\varepsilon}}}(\textbf{r})\textbf{E}_{m}d\textbf{r},\quad W_{nm}^{E}\!=\!\!\int_{{\cal V}_{\rm out}}\!\!\!\!\!\!\textbf{E}_{n}\cdot\textbf{E}_{m}d\textbf{r},$		(16)
	$\displaystyle\!\!\!\!\!\!I_{nm}^{H}\!=\!\!\int_{{\cal V}_{\rm in}}\!\!\!\textbf{H}_{n}\cdot\hat{{\boldsymbol{\mu}}}(\textbf{r})\textbf{H}_{m}d\textbf{r},\quad\!\!\!W_{nm}^{H}\!=\!\!\int_{{\cal V}_{\rm out}}\!\!\!\!\!\!\textbf{H}_{n}\cdot\textbf{H}_{m}d\textbf{r},$		(17)

Eq. (13) then takes the form

$$\frac{k_{n}}{k_{\nu}}\approx 1+\left(\varepsilon_{b}-1\right)\left(\frac{1}{2}-I_{nn}^{E}\right)+\left(\mu_{b}-1\right)\left(\frac{1}{2}+I_{nn}^{H}\right),$$

(18)

where the integral of the perturbation over the surrounding medium, $\int_{V_{\rm out}}\vec{\mathbb{F}}_{n}\cdot\delta\hat{\mathbb{P}}\vec{\mathbb{F}}_{n}d\textbf{r}$, is converted into integrals over the system volume, $I_{nn}^{E}$ and $I_{nn}^{H}$. Let us finally note that keeping in Eq. (18) only terms linear in $\varepsilon_{b}-1$ and $\mu_{b}-1$ makes it identical to the first-order approximation [8]. At the same time, extending the regularized approach to all RSs results in a matrix equation that is similar to the Eq. (Varying the medium surrounding an optical resonator: An efficient and rigorous way to calculate its spectral changes ) but converging to a wrong result, which confirms that the regularized RSs are not complete in the exterior, see Sec. S.II.E of [12].

We illustrate in Figs. 1–4 the full rigorous RSE-based Eq. (Varying the medium surrounding an optical resonator: An efficient and rigorous way to calculate its spectral changes ), its diagonal version Eq. (10), the first-order approximation Eq. (11), and the regularized result Eq. (18) or rather its dispersive analog [12], focusing on two experimentally relevant examples: (i) the dipolar ($l$=1) SP mode of a gold nanosphere of radius $R$ varying between 10 nm and 200 nm [24] and (ii) high-angular momentum ($l=450$) WG modes of a silica micro-sphere of radius $R=39.5\,\mu$m [25, 26]. Both systems are assumed to be nonmagnetic ($\mu=1$), described by an isotropic permittivity, and surrounded by an isotropic dielectric with varying refractive index. For gold, the permittivity is taken in the Drude model, $\varepsilon(k)=\varepsilon_{\infty}-\sigma\gamma/[k(k+i\gamma)]$, with $\varepsilon_{\infty}=4$, $\hbar c\sigma=957$ eV, and $\hbar c\gamma=0.084$ eV fitted to the Johnson and Christy data [27] with the help of the fit program provided in [19]. For silica, the permittivity is calculated using Sellmeier formula [26] at wavelength $\lambda=780$ nm, giving $\varepsilon=2.114$. In the full RSE calculation via Eq. (Varying the medium surrounding an optical resonator: An efficient and rigorous way to calculate its spectral changes ), the only numerical parameter is the number $N$ of the basis RSs which is determined (unless otherwise stated) by the cut-off frequency $k_{c}$, such that all RSs with $k_{n}$ within the circle $|k_{n}\sqrt{\varepsilon(k_{n})}|<k_{c}$ in the complex wave number plane are kept in the basis.

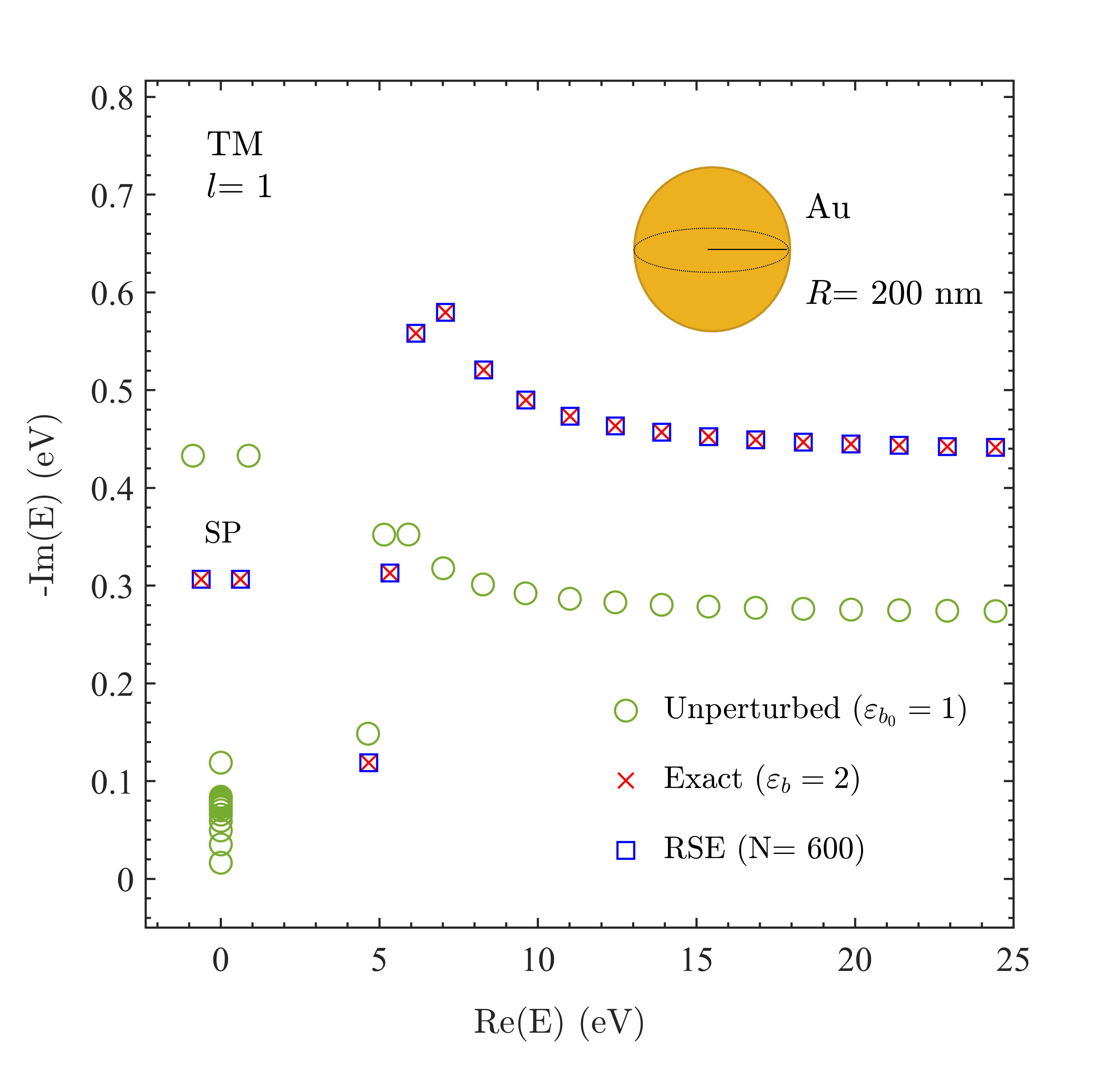
Figure 1 shows in the complex energy plane ($E=\hbar ck$) the spectrum of the RSs of a gold nanosphere of radius $R=200$ nm surrounded by a dielectric with $\varepsilon_{b}=2$, calculated analytically and via the RSE, using as basis system the same sphere in vacuum. The dipolar SP mode is further displayed in Figs. 2 and 3, for varying background permittivity $\varepsilon_{b}$ and sphere radius $R$.

Since the perturbation shifts the unperturbed Drude pole of the permittivity at $k=-i\gamma$ to a new position at $k=-i\gamma n_{b}$, we apply the idRSE which requires including in the basis both the old and the new pole RSs (pRSs) [20], crucial for the RSE to converge to the exact solution, as it is clear from Fig. S4 of [12]. In fact, with pRSs included in the basis, the relative error shown in Fig. 2(c) scales with the basis size as $1/N^{3}$, as usually guaranteed by the RSE [4, 14]. At the same time, the pRSs of the new pole in the idRSE are perturbation-dependent which makes the whole calculation rather inefficient. To avoid this problem, we have replaced the new pRSs with the old ones adapted for the perturbation, as detailed in Sec. S.IV of [12], so that all the basis RSs are calculated only once for all perturbations of the environment.

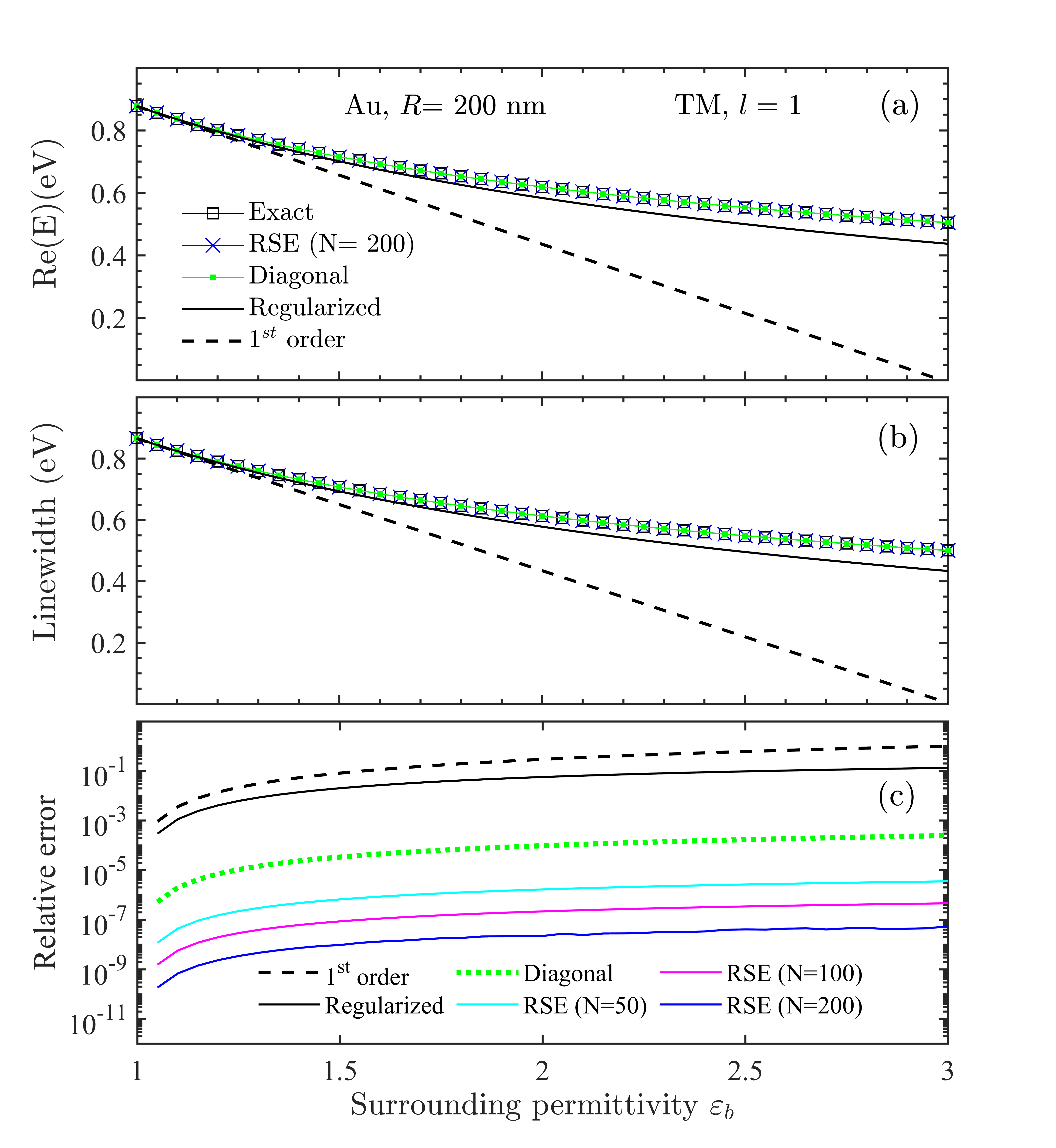
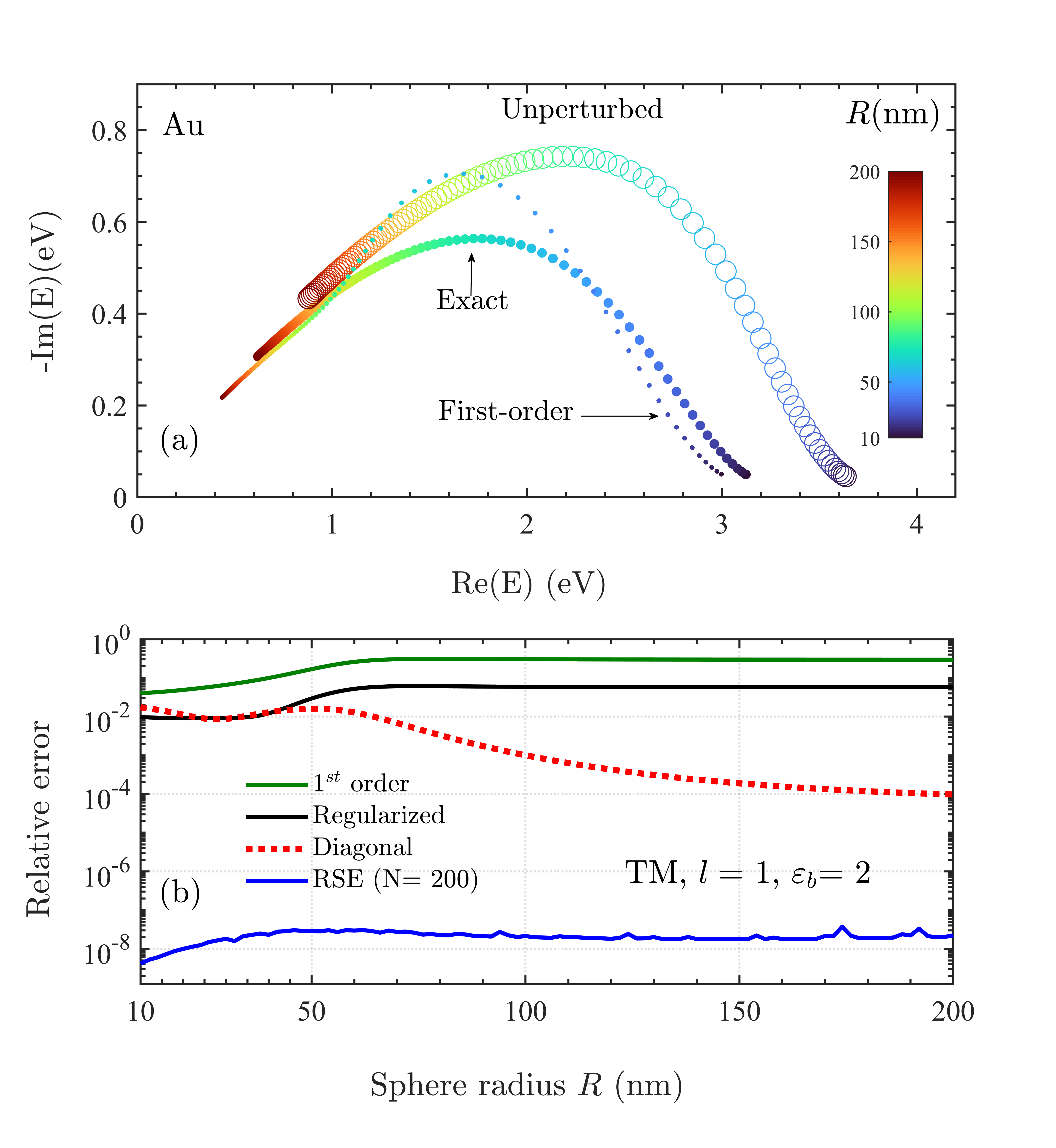
The diagonal approximation is amazingly accurate in this system as it is clear from Fig. 2, also showing that the first-order approximation fails quickly as $\varepsilon_{b}$ deviates from 1. Interestingly, the single-mode regularized version gives a reasonable agreement with the exact solution for the whole range of permittivities and radii considered in Figs. 2 and 3, respectively.

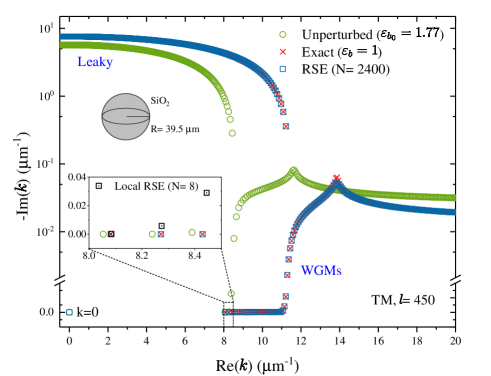
Figure 4 shows the spectra of the RSs of the silica sphere in water ($\varepsilon_{b_{0}}=1.77$) and in vacuum ($\varepsilon_{b}=1$) playing the role of, respectively, the basis and perturbed systems. Since $\varepsilon_{b_{0}}\neq 1$, one has to replace $\varepsilon_{b}$ with a ratio $\varepsilon_{b}/\varepsilon_{b_{0}}$ in all the above equations, see [12] for derivation. To reach in the full RSE the relative error of $10^{-5}$ or below, one needs to keep $N=2400$ states in the basis, see Fig. S8 of [12]. This is because of the very low permittivity contrast in this basis system. The perturbed system has a large number of WG modes which are all well reproduced by the RSE even though the basis system has only four pairs of them. All single mode approximations fail in this case, see [12] for details. However, keeping only the WG modes in basis ($N=8$) provides a very good approximation for the fundamental mode, as it is clear from the inset of Fig. 4 and Fig. S9 of [12].

In conclusion, we have developed a rigorous and efficient RSE-based approach to treating arbitrarily strong homogeneous perturbations of the medium surrounding an optical system, which is crucial for sensing applications. The idea of the approach is to map the changes in the surrounding medium onto the interior of the system, where the resonant states are complete, in this way effectively modifying the resonator while keeping the medium unchanged. Such a modified system is then treated by the RSE which requires a basis of resonant states fixed for all perturbations, with the basis size $N$ determining the accuracy and the error scaling as $1/N^{3}$. Single- and few-mode approximations are shown to be very accurate for the examples provided, going significantly beyond the first-order theory [8].

S.F.A acknowledges scholarship by King Saud University.