Vacancy-Engineered Flat-Band Superconductivity in Holey Graphene

We first revisit Lieb’s theorem that is based on the rank-nullity theoremLieb (1989), with a special emphasis on the nonspatial symmetries, localization of the wave functions, and applications to periodic vacancies. We consider any two- (2D) or three-dimensional (3D) bipartite-lattices described by single-particle Hamiltonian $H({\bf k})$ in momentum space that preserves time-reversal (TR), particle-hole (PH) chiral symmetries

	$\displaystyle TH({\bf k})T^{-1}=H(-{\bf k}).$
	$\displaystyle CH({\bf k})C^{-1}=-H(-{\bf k}).$
	$\displaystyle SH({\bf k})S^{-1}=-H({\bf k})$		(1)

which are nonspatial symmetries particularly relevant to topological orderSchnyder et al. (2008); Ryu et al. (2010); Chiu et al. (2016); von Gersdorff et al. (2021) and topological phase transitionsChen and Schnyder (2019). In these bipartite lattices, the Hamiltonian matrix arranged in the basis of the electron operators of the two sublattices $(c_{B{\bf k}},c_{A{\bf k}})$ is a block-off-diagonal $2\times 2$ matrix, and the symmetry operators are implemented by $T=K$, $C=\sigma_{3}K$ and $S=\sigma_{3}$, where $K$ is the complex conjugation operator.

Now suppose we enlarge the unit cell to contain not 2 but $N=$ even number of sites with the same amount of two sublattices, then the Hamiltonian matrix arranged in the basis $(c_{B_{1}{\bf k}},...,c_{B_{N/2}{\bf k}},c_{A_{1}{\bf k}},...,c_{A_{N/2}{\bf k}})$ remains block-off-diagonal

$\displaystyle H({\bf k})=\left(\begin{array}[]{cc}&Q({\bf k})\\ Q^{{\dagger}}({\bf k})&\\ \end{array}\right),$

(4)

where $Q({\bf k})$ is an $(N/2)\times(N/2)$ square matrix. The symmetry operators are implemented by $C=\sigma_{3}\otimes I_{N/2}K$ and $S=\sigma_{3}\otimes I_{N/2}$ in this case, with $I_{N/2}$ the $(N/2)\times(N/2)$ identity matrix. If we now introduce periodic vacancies into the lattice, the columns and rows in the $H({\bf k})$ in Eq. (4) that correspond to the vacancy sites will be removed. It is then obvious that if the number of vacancies on the $A$ and $B$ sublattices are different, then the unit cell will contain different number of sublattices $N_{A}\neq N_{B}$. As a result, the $Q({\bf k})$ in Eq. (4) as an $N_{A}\times N_{B}$ matrix is not a square matrix anymore, as elaborated in Fig. 1. Nevertheless, the PH and chiral symmetries of the systems still hold since removing the columns and rows in $C=\sigma_{3}\otimes I_{N/2}K$ and $S=\sigma_{3}\otimes I_{N/2}$ that correspond to the vacancy sites preserve Eq. (1). As a result, the band structure at any vacancy configuration is PH symmetric, and the ZEFB wave functions must be localized on one of the two sublattices since they are eigenstates of the chiral operator $S$. In fact, we will prove below that the ZEFB wave functions must localize in the majority sublattices.

Denoting $r(M)$ as the rank and $\eta(M)$ as the nullity of a matrix $M$, our interest is how the nullity of the Hamiltonian $\eta(H)$, which counts the number of ZEFBs, can be nonzero. Without loss of generality, we assume that the vacancy configuration is such that the $B$ sublattices are the majority $N_{B}>N_{A}$. In this case, the rank-nullity theorem states that

$\displaystyle r(Q)+\eta(Q)=N_{A},\;\;\;r(H)+\eta(H)=N_{A}+N_{B}.$

(5)

For $H$ of the form of Eq. (4), the rank satisfies

	$\displaystyle r(Q)=r(Q^{{\dagger}})=r(QQ^{{\dagger}})=r(Q^{{\dagger}}Q),$
	$\displaystyle r(H)=r(Q)+r(Q^{{\dagger}})=2r(Q).$		(6)

Using these simple identities in linear algebra, we now prove the following propositions.

Proposition 1: $\eta(H)>0$ if $Q$ is not square. This can be proved easily from Eqs. (5) and (6)

$\displaystyle\eta(H)=N_{A}+N_{B}-2r(Q)=N_{B}-N_{A}+2\eta(Q).$

(7)

Hence $\eta(H)>0$ if $N_{B}>N_{A}$, meaning that ZEFB must emerge if we remove the two sublattices in different quantities.

Proposition 2: $\eta(H)=N_{B}-N_{A}$ if $\eta(Q)=0$. To prove this, we start from

$\displaystyle r(QQ^{{\dagger}})+\eta(QQ^{{\dagger}})=N_{B},\;\;\;r(Q^{{\dagger}}Q)+\eta(Q^{{\dagger}}Q)=N_{A},\;\;\;\;\;$

(8)

which implies

$\displaystyle r(QQ^{{\dagger}})-r(Q^{{\dagger}}Q)=N_{B}-N_{A}.$

(9)

If $Q$ itself is not singular $\eta(Q)=0$, which is true in many practical examples, then Eq. (5) implies $r(Q)=N_{A}=r(QQ^{{\dagger}})=r(Q^{{\dagger}}Q)$. Then from Eq. (8) one sees that $\eta(QQ^{{\dagger}})=N_{B}-N_{A}$ and $\eta(Q^{{\dagger}}Q)=0$. Because the square of the Hamiltonian $H^{2}={\rm diag}(QQ^{{\dagger}},Q^{{\dagger}}Q)$ has the same nullity and ZEFBs wave functions as $H$, we immediately see that $\eta(H)=\eta(H^{2})=\eta(QQ^{{\dagger}})=N_{B}-N_{A}$. The propositions 1 and 2 constitute the original version of Lieb’s theorem.

Proposition 3: ZEFB wave functions are localized in the majority sublattices if $\eta(Q)=0$. This is simply because the proof for proposition 2 shows that the ZEFB wave functions are given by diagonalizing the first block $QQ^{{\dagger}}$ in $H^{2}$ that belongs to the majority $B$ sublattices, whereas wave functions in $A$ sublattices are zero.

We aim to examine these propositions in the spinless honeycomb lattice with nearest-neighbor hopping

$\displaystyle H=\sum_{\langle ij\rangle}t\,c_{i}^{{\dagger}}c_{j}+U\sum_{i\in v}c_{i}^{{\dagger}}c_{i}$

(10)

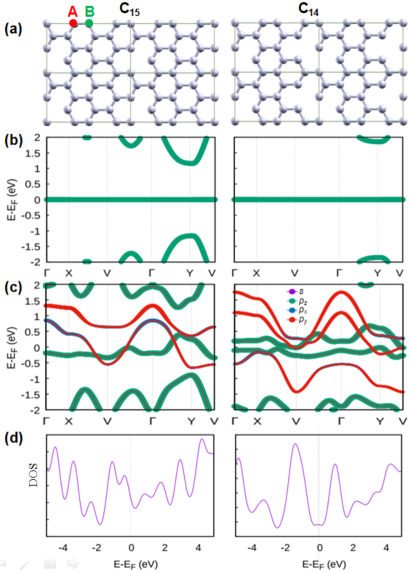
owing to its relevance to the $p_{z}$ orbital of single-layer graphene that will be addressed later, where $c_{i}$ denotes the electron annihilation operator at site $i$, and $U$ is the large on-site potential that can be used to conveniently project out the vacancy sites $i\in v$. Increasing from $U=0$ to $U>100t$ can continuously change the band structure from Dirac points to ZEFBs, similar to that proposed recently in the Lieb-kagome latticesLim et al. (2020), but we will focus on the large on-site potential regime $U>100t$ that completely removes the vacancy sites. We denote these vacancy configurations by C${}_{N_{A}+N_{B}}$. In the left panel of Fig. 2 (a), we show a C₁₅ example of removing a single $A$ sublattice from a $N=16$ rectangular unit cell such that $N_{A}=7$ and $N_{B}=8$. In this case, the BZ is rectangular, and the PH symmetric tight-binding band structure plotted along a high-symmetry line (HSL) clearly indicates a single ZEFB throughout the BZ, as shown in the left panel of Fig. 2 (b). In contrast, the C₁₄ configuration shown in the right panel of Fig. 2 (a) and (b) that removes two $A$ sublattices on the same 16-site unit cell, such that $N_{A}=6$ and $N_{B}=8$, has doubly degenerate ZEFBs $\eta(H)=N_{B}-N_{A}=2$, consistent with proposition 2. In Appendix A, we also elaborate proposition 3 by presenting the wave functions of the ZEFBs for C₁₅ and C₁₄ and show that indeed both are localized on the majority $B$ sublattices. Finally, we remark that although we focus on periodic vacancies on an infinite graphene, the propositions 1 to 3 also explain the number of zero eigenenergies and their wave functions of a finite size graphene with random vacanciesBouzerar and Mayou (2021).

To examine the proposed mechanism on the realistic single-layer graphene, it should be first noted that graphene in reality does not exactly preserve the PH and chiral symmetries in Eq. (1) owing to the complications such as longer range hopping and hybridization between different orbitals, although magnitudes of these factors are much smaller than the nearest-neighbor hoppingCastro Neto et al. (2009). To investigate the effect of these symmetry breaking factors, we turn to density functional theory (DFT) to obtain the band structure of graphene with periodic vacancies. In Fig. 2 (c), we show the DFT band structures and DOS for C₁₅ and C₁₄, which indicate that very narrow bands do occur near the Fermi surface. Although not perfectly flat, these bands are as narrow as $\sim 0.5$eV, reminisce the ZEFBs. Moreover, the DOS at the Fermi surface is dramatically enhanced by these narrow bands compared to the pristine graphene, as indicated by Fig. 2 (d).

We proceed to demonstrate that the proposed mechanism can coexist with another vacancy engineering principle proposed recently, namely the nodal-line semimetals caused by 2D nonsymmorphic vacancy configurationsLiu et al. (2021, ); de Sousa et al. . In these nonsymmorphic configurations, every two carbon atoms map to each other under glide plane operation, resulting in nodal lines at the BZ boundary regardless the details of the Hamiltonian, which serves as a vacancy-engineering principle to obtain symmetry-enforced nodal linesYoung and Kane (2015); Yamakage et al. (2016); Zhao and Schnyder (2016); Wieder et al. (2018). As an example, in Fig. 3 we show a C₂₂ configuration that contains two vacancies on the $A$ sublattice, and additionally a glide plane along ${\hat{\bf x}}$ direction. The resulting DFT band structure indicates that both mechanisms prevail in this situation, yielding a band structure that contains two low energy narrow bands that reminisce doubly degenerate ZEFBs, and in addition every two pairs of bands (each pair is spin degenerate) stick together at the BZ boundary $k_{x}=0$ (the $X-V$ section of Fig. 3 (b)) to form symmetry-enforced nodal lines as predicted. This example indicates that vacancy engineering can combine different crystalline and nonspatial symmetries to produce very exotic band structures that may not be easily found in nature.

The enlarged DOS near the Fermi surface due to the narrow bands is expected to dramatically change the electronic and magnetic properties of the holey graphene compared to the pristine graphene. However, these narrow bands are neither perfectly flat nor entirely located at zero energy, and hence it is unclear at present whether strong correlations will play an important role on the electronic properties in the same way as in TBLGCao et al. (2018a). On the other hand, the phonon band width in graphene is about $\omega_{D}\approx 0.25$eVSaito et al. (2001); Maultzsch et al. (2004); Mohr et al. (2007); Jorio et al. (2011), which means that the narrow bands with band width $\sim 0.5$eV in a large area of the BZ are within the Debye frequency, suggesting a large phase space for phonon-mediated Cooper pairingKopnin et al. (2011); Heikkilä and Volovik (2016). These features motivate us to examine whether a conventional phonon-mediated $s$-wave SC phase emerges in the holey graphene with low energy narrow bands. For this purpose, we resort to the following spinful mean-field model of $s$-wave SC

	$\displaystyle H$	$\displaystyle=$	$\displaystyle\sum_{\langle ij\rangle\sigma}t\,c_{i\sigma}^{{\dagger}}c_{j\sigma}+\sum_{\langle\langle ij\rangle\rangle\sigma}t^{\prime}\,c_{i\sigma}^{{\dagger}}c_{j\sigma}-\sum_{i\sigma}\mu\,c_{i\sigma}^{{\dagger}}c_{i\sigma}$		(11)
			$\displaystyle+\sum_{i}\left(\Delta_{i}c_{i\uparrow}^{{\dagger}}c_{i\downarrow}^{{\dagger}}+\Delta_{i}^{\ast}c_{i\downarrow}c_{i\uparrow}\right)+U\sum_{i\in v}c_{i\sigma}^{{\dagger}}c_{i\sigma},$

where $t=2.8$eV is the nearest-neighbor hopping on the honeycomb lattice, and the on-site potential $U>100t$ is used to project out the vacancy sites $i\in v$. We use the next-nearest-neighbor hopping $t^{\prime}$ and chemical potential $\mu$ to simulate the breaking of chiral symmetry in realistic graphene, and find that the values $t^{\prime}=-0.2$eV and $\mu=0.2$eV can give a reasonable fit to the narrow bands obtained by DFT in both C₁₅ and C₁₄, as demonstrated in the Appendix A. The mean field Hamiltonian is diagonalized into $H={\rm const.}+\sum_{\bf k\alpha}E_{\bf k}\gamma_{\bf k\alpha}^{{\dagger}}\gamma_{\bf k\alpha}$ by a Bogoliubov transformation

	$\displaystyle c_{i\uparrow}=\sum_{\bf k}\gamma_{\bf k\uparrow}u_{\bf k}(i)-\gamma_{\bf k\downarrow}^{{\dagger}}v_{\bf k}^{\ast}(i),$
	$\displaystyle c_{i\downarrow}=\sum_{\bf k}\gamma_{\bf k\downarrow}u_{\bf k}(i)+\gamma_{\bf k\uparrow}^{{\dagger}}v_{\bf k}^{\ast}(i),$		(12)

where $i=1,2...N_{A}+N_{B}$ denotes the site inside a unit cell, and $\gamma_{\bf k\sigma}$ is the annihilation operator of the Bogoliubov quasiparticles. The wave functions $\left\{u_{\bf k}(i),v_{\bf k}(i)\right\}$ and eigenenergy $E_{\bf k}$ satisfy

	$\displaystyle E_{\bf k}u_{\bf k}(i)$	$\displaystyle=$	$\displaystyle\sum_{\langle ij\rangle}t\,u_{\bf k}(j)+\sum_{\langle\langle ij\rangle\rangle}t^{\prime}\,u_{\bf k}(j)$
			$\displaystyle+U\delta_{i\in v}u_{\bf k}(i)+\Delta_{i}v_{\bf k}(i),$
	$\displaystyle E_{\bf k}v_{\bf k}(i)$	$\displaystyle=$	$\displaystyle-\sum_{\langle ij\rangle}t\,v_{\bf k}(j)-\sum_{\langle\langle ij\rangle\rangle}t^{\prime}\,v_{\bf k}(j)$		(13)
			$\displaystyle-U\delta_{i\in v}v_{\bf k}(i)+\Delta_{i}^{\ast}u_{\bf k}(i).$

After the Hamiltonian is diagonalized, the pairing amplitude at site $i$ is calculated by

$\displaystyle\Delta_{i}=\sum_{\bf k}V\theta(\omega_{D}-E_{\bf k})\left[2f(E_{\bf k})-1\right]u_{\bf k}(i)v_{\bf k}^{\ast}(i),$

(14)

where $f(E_{\bf k})=(e^{E_{\bf k}/k_{B}T}+1)^{-1}$ is the Fermi distribution and $V<0$ is the pairing interaction acting within Debye frequency $\omega_{D}=0.25$eV, as ensured by the step function $\theta(\omega_{D}-E_{\bf k})$. Equations (13) and (14) are solved self-consistently until the local pairing amplitude $\Delta_{i}$ converges at a given pairing interaction and temperature $\left\{V,T\right\}$.

Numerical calculation of our mean-field theory applied to the pristine graphene yields $\Delta_{i}=0$ everywhere, consistent with the experimental observation that the single-layer pristine graphene has no SC. In contrast, Fig. 4 (a) and (b) show the local gap $\Delta_{i}$ at zero temperature for the two vacancy configurations C₁₅ and C₁₄ illustrated in Fig. 2. Our result indicates a finite $\Delta_{i}$ in the holey graphene, and moreover $\Delta_{i}$ on the $B$ sublattices is about two orders of magnitude larger than that on the $A$ sublattices. This feature stems from the fact that the chiral symmetry breaking terms are relatively small $\left\{t^{\prime},\mu\right\}\ll t$, so the narrow band wave functions still roughly satisfy the proposition 3 in Sec. II.1 and hence are mainly localized on the $B$ sublattices, as discussed in Appendix A. For C₁₅, the spatially averaged gap $\Delta(T)=\sum_{i}\Delta_{i}/(N_{A}+N_{B})$ at zero temperature $\Delta(0)$ is vanishingly small at small pairing potential $V$. Only when the pairing potential has the same order of magnitude as the hopping $|V|\sim t$ does a sizable gap emerge, implying that a sufficiently strong electron-phonon interaction is needed to support SC in C₁₅. On the other hand, C₁₄ requires much smaller $|V|$ to trigger SC in comparison with C₁₅, suggesting that increasing the number of narrow bands does help to create the SC phase. Concerning the temperature dependence, the spatially averaged gap shows a trend similar to the usual weak coupling superconductors, which vanishes at a critical temperature $T_{c}$ that is higher at larger pairing potential $V$. In addition, $T_{c}$ is generally raised in the configurations with more narrow bands, consistent with that expected from an enlarged DOS. Since the proposed engineering mechanism in principle has no restriction on the number of narrow bands $N_{B}-N_{A}$ (times $2$ if including spin), we anticipate that the vacancy configurations with very different numbers of the two sublattices may yield a very high $T_{c}$, which is presumably more likely to engineer in configurations with a larger unit cell.