Ziwei [email protected]
\addauthorLinlin Yang1, [email protected]
\addauthorYou [email protected]
\addauthorPing [email protected]
\addauthorAngela [email protected]
\addinstitution
National University of Singapore,
Singapore
\addinstitution
University of Bonn,
Germany
\addinstitution
Technical University of Munich,
Germany
\addinstitution
Shanghai Subsidiary of Great Wall Motor Co., Ltd.,
China
UV-Based 3D Hand-Object Reconstruction
UV-Based 3D Hand-Object Reconstruction with Grasp Optimization
Abstract
We propose a novel framework for 3D hand shape reconstruction and hand-object grasp optimization from a single RGB image. The representation of hand-object contact regions is critical for accurate reconstructions. Instead of approximating the contact regions with sparse points, as in previous works, we propose a dense representation in the form of a UV coordinate map. Furthermore, we introduce inference-time optimization to fine-tune the grasp and improve interactions between the hand and the object. Our pipeline increases hand shape reconstruction accuracy and produces a vibrant hand texture. Experiments on datasets such as Ho3D, FreiHAND, and DexYCB reveal that our proposed method outperforms the state-of-the-art.
1 Introduction
3D reconstruction of hand-object interactions is critical for object grasping in augmented and virtual reality (AR/VR) applications [Huang et al.(2020)Huang, Tan, Liu, and Yuan, Yang and Yao(2019), Wan et al.(2020)Wan, Probst, Van Gool, and Yao] We consider the problem of estimating a 3D hand shape when the hand interacts with a known object with a given 6D pose. This set-up lends itself well to AR/VR settings where the hand interacts with a predefined object, perhaps with markers to facilitate the object pose estimation. Such a setting is common, although the majority of previous works [Jiang et al.(2021)Jiang, Liu, Wang, and Wang, Karunratanakul et al.(2020)Karunratanakul, Yang, Zhang, Black, Muandet, and Tang, Karunratanakul et al.(2021)Karunratanakul, Spurr, Fan, Hilliges, and Tang] consider 3D point clouds as input, while we handle the more difficult case of monocular RGB inputs. Additionally, the previous works [Jiang et al.(2021)Jiang, Liu, Wang, and Wang, Christen et al.(2021)Christen, Kocabas, Aksan, Hwangbo, Song, and Hilliges, Christen et al.(2022)Christen, Kocabas, Aksan, Hwangbo, Song, and Hilliges, Karunratanakul et al.(2020)Karunratanakul, Yang, Zhang, Black, Muandet, and Tang, Karunratanakul et al.(2021)Karunratanakul, Spurr, Fan, Hilliges, and Tang, Taheri et al.(2020)Taheri, Ghorbani, Black, and Tzionas] are singularly focused on reconstructing feasible hand-object interactions. They aim to produce hand meshes with minimal penetration to the 3D object without regard for the accuracy of the 3D hand pose. We take on the additional challenge of balancing realistic hand-object interactions with accurate 3D hand poses.
Representation-wise, previous hand-object 3D reconstruction works [Boukhayma et al.(2019)Boukhayma, Bem, and Torr, Khamis et al.(2015)Khamis, Taylor, Shotton, Keskin, Izadi, and Fitzgibbon, Tzionas et al.(2016)Tzionas, Ballan, Srikantha, Aponte, Pollefeys, and Gall, Zimmermann et al.(2019)Zimmermann, Ceylan, Yang, Russell, Argus, and Brox] predominantly with the MANO model [Romero et al.(2017b)Romero, Tzionas, and Black]. MANO is convenient to use, but its accuracy is limited because it cannot represent direct correspondences between the RGB input and the hand surface. This work considers dense representations and, in particular, focuses on UV coordinate maps. UV maps are ideal as they establish dense correspondences between 3D surfaces and 2D images and work well in representing the 3D human body and face [Feng et al.(2018)Feng, Wu, Shao, Wang, and Zhou, Yao et al.(2019)Yao, Fang, Wu, Feng, and Li].
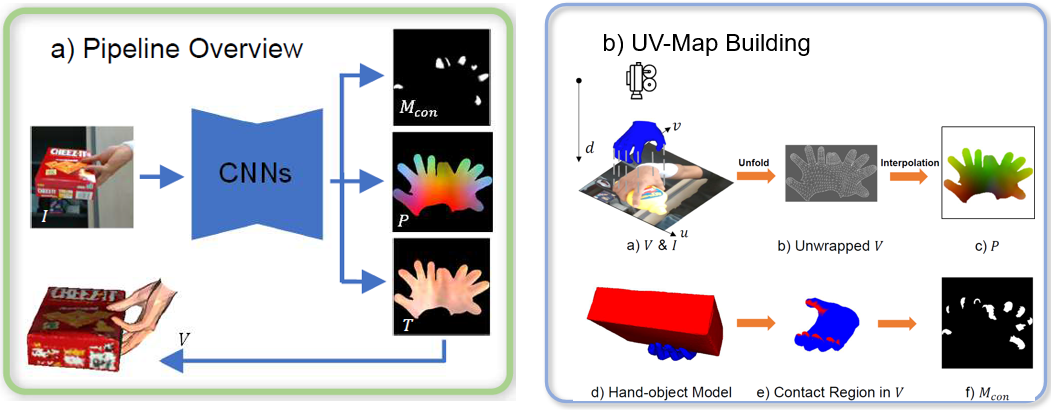
Working with a UV coordinate map has a natural advantage in that we can adopt standard image-based CNN architectures. The CNN captures the pixels’ spatial relationships to aid the 3D modelling while remaining fully convolutional. UV coordinate maps can be easily augmented with additional corresponding information, such as surface texture and regions of object contact. This creates a seamless connection between the 3D hand shape, its appearance, and its interactions with objects in a single representation space (see Fig. 1a). To that end, we propose an RGB2UV network that simultaneously estimates the hand UV coordinates, hand texture map, and hand contact mask.
The hand contact mask is a key novelty of our work. We propose a binary UV contact mask (see Fig. 1b-f) that marks contact regions between the hand surface and the interacting object surfaces. To our knowledge, the contact mask is the first dense representation of hand-object contact. Previous methods [Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid, Yang et al.(2021)Yang, Zhan, Li, Xu, Li, and Lu] work sparsely on a per-vertex or per-point basis and have an obvious efficiency-accuracy trade-off. The more vertices or points considered, the more accurate the contact modelling and the higher the computational price. Working in the UV space allows dense contact modelling and improves reconstruction accuracy while remaining efficient.
Normally, accurate hand surface reconstructions in isolation cannot guarantee realistic hand-object interactions; ensuring realistic interactions in vice-versa may result in inaccurate hand reconstructions [Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid, Li et al.(2021)Li, Yang, Zhan, Lv, Xu, Li, and Lu, Hasson et al.(2020)Hasson, Tekin, Bogo, Laptev, Pollefeys, and Schmid]. The main reason is that the hand and object models (MANO [Romero et al.(2017b)Romero, Tzionas, and Black], YCB [Calli et al.(2015)Calli, Singh, Walsman, Srinivasa, Abbeel, and Dollar]) are all rigid. The rigid assumption is too strong at the contact points, and leads to one mesh penetrating the other [Yang et al.(2021)Yang, Zhan, Li, Xu, Li, and Lu, Jiang et al.(2021)Jiang, Liu, Wang, and Wang], even for ground truth poses. To mitigate these errors, we propose an additional optimization-based refinement procedure to improve the overall grasp. The optimization is performed only during inference and reduces the distances from a hand surface that either penetrates or does not make contact with the object surface. This grasp optimization step significantly improves the feasibility of the hand-object interaction while ensuring accurate hand poses.
Our contributions are summarized as follows: (1) We propose a UV-map-based pipeline for 3D hand reconstruction that simultaneously estimates UV coordinates, hand texture, and contact maps in UV space. (2) Our model is the first to explore dense representations to capture contact regions for hand-object interaction. (3) Our grasp optimization refinement procedure yields more realistic and accurate 3D reconstructions of hand-object interactions. (4) Our model achieves state-of-the-art performance on FreiHAND, Ho3D and DexYCB hand-object reconstruction benchmarks.
2 Related Works
Face, Body and Hand Surface Reconstruction. A popular way to represent human 3D surfaces is via a 3D mesh. Previous works estimate mesh vertices either directly [Ge et al.(2019)Ge, Ren, Li, Xue, Wang, Cai, and Yuan, Choi et al.(2020)Choi, Moon, and Lee, Wan et al.(2020)Wan, Probst, Van Gool, and Yao, Moon and Lee(2020), Ranjan et al.(2018)Ranjan, Bolkart, Sanyal, and Black, Lee and Lee(2020)], or indirectly [Boukhayma et al.(2019)Boukhayma, Bem, and Torr, Zimmermann et al.(2019)Zimmermann, Ceylan, Yang, Russell, Argus, and Brox, Kolotouros et al.(2019)Kolotouros, Pavlakos, Black, and Daniilidis] through a parametric model like SMPL [Loper et al.(2015)Loper, Mahmood, Romero, Pons-Moll, and Black] for the body, 3DMM [Blanz and Vetter(1999)] for the face, and MANO [Romero et al.(2017b)Romero, Tzionas, and Black] for the hand. Parametric models are convenient but cannot provide direct correspondences between the input images and the 3D surface. As such, we learn a dense surface as a UV coordinate map. We are inspired by the success of recent UV works for the human body [Güler et al.(2018)Güler, Neverova, and Kokkinos, Zeng et al.(2020)Zeng, Ouyang, Luo, Liu, and Wang], face [Deng et al.(2018)Deng, Cheng, Xue, Zhou, and Zafeiriou, Lee et al.(2020)Lee, Cho, Kim, Inouye, and Kwak, Kang et al.(2021)Kang, Lee, and Lee], and hand [Chen et al.(2021a)Chen, Chen, Yang, Wu, Li, Xia, and Tan, Wan et al.(2020)Wan, Probst, Van Gool, and Yao]. To the best of our knowledge, our work is the first to explore the use of UV coordinate maps in modelling hand-object interactions and capturing the contact regions.
Texture Learning on Hand Surfaces. Shading and texture cues are often leveraged to solve the self-occlusion problem for hand tracking [de La Gorce et al.(2011)de La Gorce, Fleet, and Paragios, de La Gorce et al.(2008)de La Gorce, Paragios, and Fleet]. Recently, [Chen et al.(2021b)Chen, Tu, Kang, Bao, Zhang, Zhe, Chen, and Yuan] verified that texture modelling helps with the self-supervised learning of shape models. Instead of relying on a parametric texture model [Qian et al.(2020)Qian, Wang, Mueller, Bernard, Golyanik, and Theobalt], we apply a UV texture map. UV texture maps are commonly used to model the surface texture of the face [Deng et al.(2018)Deng, Cheng, Xue, Zhou, and Zafeiriou, Lee et al.(2020)Lee, Cho, Kim, Inouye, and Kwak, Kang et al.(2021)Kang, Lee, and Lee] and, more recently, the human body [Zeng et al.(2020)Zeng, Ouyang, Luo, Liu, and Wang]. We naturally extend UV texture maps for hand-object interactions.
Hand-Object Interactions. Various contact losses have been proposed [Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid, Yang et al.(2021)Yang, Zhan, Li, Xu, Li, and Lu, Hasson et al.(2021)Hasson, Varol, Schmid, and Laptev] to ensure feasible hand-object interactions. Examples such as repulsion loss and attraction loss ensure that the hand makes contact with the object but avoids actual surface penetration. Contact regions, however, are modeled sparsely. Contact points are sparse and selected either statistically [Hasson et al.(2020)Hasson, Tekin, Bogo, Laptev, Pollefeys, and Schmid], or based on hand vertices closest to the object [Li et al.(2021)Li, Yang, Zhan, Lv, Xu, Li, and Lu]. These methods have an accuracy-efficiency trade-off hinging on the number of considered vertices. In contrast, our UV contact mask establishes a dense correspondence between the contact regions and the local image features. It is both accurate and efficient. Our work is the first to explore a joint position, texture and contact-region UV representation for hand-object interactions.
3 Method
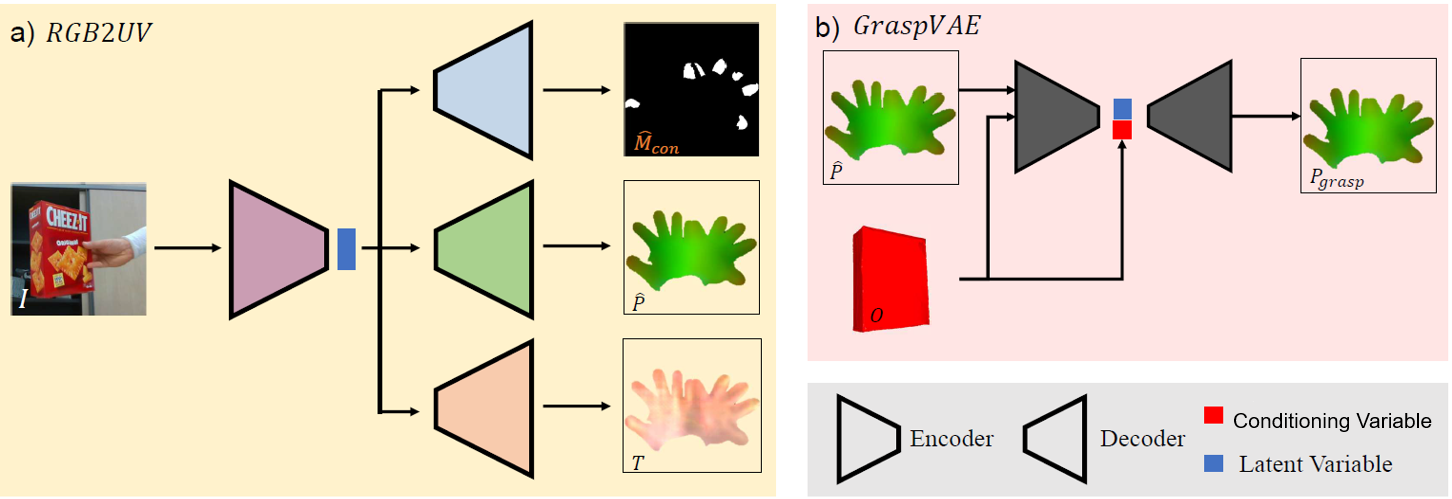
Our method has two components: the RGB2UV network and grasp optimization (see Fig. 2). The RGB2UV network (Sec. 3.1 and 3.2) takes as input an RGB image of a hand-object interaction and outputs a hand UV mask and contact mask. The grasp optimization (Sec. 3.3) adjusts the mesh vertices to refine the hand grasp and reduces penetrations.
3.1 Ground Truth UV, Contact Mask & Texture
UV Coordinate Map. Suppose we are given a 3D hand surface in the form of a 3D mesh and an accompanying RGB image (see Fig. 1 a). The hand mesh stores the 3D position of the 778 vertices in the camera coordinate space. The image records the RGB values of each pixel in the image plane. can be considered a projection of into 2D space, with the mapping
| (1) |
where is a transformation that can project a vertex at into in the image plane with camera parameters . Here, denotes the distance from the camera to the image plane. Because is on the image plane, it only reveals the vertices closest to the camera; we thus consider the vertical distance from the camera to the vertex (see Fig. 1 b-a), and represent each vertex uniquely with .
To represent all the hand vertices, even those not seen in , in one 2D plane, we unwrap the MANO mesh with MANO’s provided UV unfolding template (see Fig. 1 b-b) [Romero et al.(2017b)Romero, Tzionas, and Black]) to arrive at a UV coordinate map with UV coordinates , where
| (2) |
Mapping only the vertices onto the UV map results in a sparse coordinate map. To generate a dense UV representation (Fig. 1 b-c), we interpolate values on each triangular mesh face from neighbouring vertices. Given , the corresponding 3D coordinate is given by the is the inverse transformation of from Eq. 2:
| (3) |
Contact Mask. Based on , we propose a binary contact mask to indicate the contact region in hand-object interactions. Like [Hampali et al.(2020)Hampali, Rad, Oberweger, and Lepetit], contact vertices are defined as the vertices within 4 mm to the grasped object. We first locate contact vertices (Fig. 1 b-e) and their corresponding points in with Eq. 1 and Eq. 2. The contact mask is defined as:
| (4) |
Similar to , direct mapping from to generates a sparse representation. For every triangular plane in , we interpolate all points inside the plane as a contact region if the three vertices are contact vertices to achieve a dense representation of (see Fig. 1 b-f).
Texture. The UV coordinates also conveniently establish a correspondence between the mesh vertices and texture information. The texture map gives information on hand appearance. For every point in , similar to Eq. 2, we obtain the texture map: . With Eq. 3, the texture of the vertices in the hand mesh can be tracked in .
3.2 UV Estimation from an RGB Image
The RGB2UV network, , estimates the UV coordinate map , contact mask , and texture map from an input image . With prepared data tuples , as described in Sec. 3.1, the network can be trained in a supervised way. Similar to previous works [Chen et al.(2021a)Chen, Chen, Yang, Wu, Li, Xia, and Tan, Zeng et al.(2020)Zeng, Ouyang, Luo, Liu, and Wang, Yao et al.(2019)Yao, Fang, Wu, Feng, and Li], we use a U-Net style encoder-decoder with a symmetric ResNet50 and skip connections between the corresponding encoder and decoder layers.
Our network features three decoders: a hand UV coordinate map decoder, a contact mask decoder, and a UV texture decoder (see Fig 2 a). The encoder and three decoders are trained jointly with five losses:
| (5) |
UV Coordinate Map Decoder. This decoder is learned with the hand UV coordinate map loss , hand UV gradient loss . These losses are L1 terms between the ground truth and the predicted UV coordinate maps and , and their respective gradients and :
| (6) |
where is a mask in the UV space indicating the entire hand region. is applied to constrain the consideration of the UV coordinate map and their gradients to only valid regions on the hand’s surface in and .
Contact Mask Decoder. This decoder is learned with the L1 contact mask loss between the ground truth and predicted contact mask and respectively: . To ensure correctness in the hand pose represented by the coordinate map and contact mask decoders, we add an additional mesh vertex loss . The hand mesh implicitly represents the pose of the hand, so a loss between ground truth and estimated improves the accuracy of the estimated pose. The pose loss is defined as: where represents ground truth hand mesh vertices and is sampled from .
Texture Decoder. As there is no ground truth for UV texture, we apply self-supervised training to estimate the UV texture map. With given camera parameters , the ground truth mesh vertices can be projected into the plane to obtain a view-specific hand silhouette via a differentiable renderer111We use the built-in renderer from the pytorch3D library [Ravi et al.(2020)Ravi, Reizenstein, Novotny, Gordon, Lo, Johnson, and Gkioxari].. The hand region in RGB image can be isolated with by applying as a mask. On the other hand, we also render the hand image with the estimated UV coordinate and texture map, i.e\bmvaOneDot and . The texture decoder can then be trained by minimizing the distance between and . We apply a photometric consistency loss [Chen et al.(2021b)Chen, Tu, Kang, Bao, Zhang, Zhe, Chen, and Yuan] for training, which consists of an RGB pixel loss term and a structure similarity loss based on the structural similarity index [Brunet et al.(2011)Brunet, Vrscay, and Wang] SSIM:
| (7) |
3.3 Grasp Optimization
The RGB2UV network is standalone and does not take any object information into consideration. Even though the ground truth 6D object pose is provided in our setup, this does not ensure feasible hand grasps or naturalistic hand-object interactions. Therefore, we introduce a grasp optimization step for further refinement. Instead of refining the 3D hand mesh directly, which is very high-dimensional with 778 vertices, we work in a latent variable space to reduce the dimensionality of the optimization. Specifically, we learn a conditional VAE with an encoder and a decoder , which we name GraspVAE.
During inference, the estimated UV coordinate map is encoded into a latent variable with GraspVAE’s . The latent is refined to through optimization to minimize the penetrations between the object mesh and the estimated hand mesh. Finally, is decoded with into a UV coordinate map and converted into a hand mesh. Note the optimization happens during inference only, whereas and are learned during training.
GraspVAE is a conditional VAE with a ResNet18 encoder and three transposed convolution layers as the decoder. It is conditioned on the object vertices (see Fig. 2 b) to estimate a refined UV coordinate map from the estimated from the RGB2UV network, i.e\bmvaOneDot . GraspVAE is trained with the combined loss
| (8) |
Here, is the standard Kullback-Leibler divergence loss used in VAE models, where represents the latent variables encoded from input . The term denotes a Gaussian prior where is an identity matrix. The term is the distribution of , while the function estimates the closest distance between a hand vertex and object vertices . The penetration loss is applied to penalize hand vertices , where represents the set of hand vertices inside the object. Existing works [Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid] identify from the entire hand mesh, which is computationally inefficient. Our contact mask restricts the search area and decreases the processing time. For more details on training a conditional VAE, we refer the reader to [Sohn et al.(2015)Sohn, Lee, and Yan].
Latent-Space Optimization. During inference, the learned GraspVAE model is used to estimate a refined UV map. Specifically, we encode the given object vertices and estimated , i.e\bmvaOneDot and solve for an optimized , with as initialization:
| (9) |
The hand UV map is generated with , where denotes a concatenation operation. The refined hand mesh can then be generated from with Eqs. 2 and 3. More details are given in the Supplementary.
Hand Only VAE. To further highlight the strengths of our grasp optimization, we introduce a variant of GraspVAE named Hand Only VAE to refine the hand shape accuracy with. Similar to GraspVAE, the encoder of Hand Only VAE is a ResNet18 network and the decoder contains three transposed convolution layers. Hand Only VAE is trained with in Eq. 8, but without . Thus, the role of in grasp optimization can be visualized from differences between results of Hand Only VAE and GraspVAE.
4 Experiments
Implementation Details. The Adam optimizer is applied to train all networks over 80 epochs with a batch size of 64. We start with an initial learning rate of for all training and lower it by a factor of 10 at the 20th, 40th and 60th epochs. After GraspVAE is trained, we use the learning rate of to update the latent variables until the loss difference is lower than for grasp optimization. The parameters are set empirically all to 1, except for , . The VAE latent space is 128 dimensions.
Datasets. We evaluate on RGB-based hand-object benchmarks HO3D [Hampali et al.(2020)Hampali, Rad, Oberweger, and Lepetit, Hampali et al.(2021)Hampali, Sarkar, and Lepetit], DexYCB [Chao et al.(2021)Chao, Yang, Xiang, Molchanov, Handa, Tremblay, Narang, Van Wyk, Iqbal, Birchfield, et al.], and FreiHAND [Zimmermann et al.(2019)Zimmermann, Ceylan, Yang, Russell, Argus, and Brox]. We compare HO3D with state-of-the-art for both v2 and v3 and report our results through their leaderboard (v2222https://competitions.codalab.org/competitions/22485#results , v3333https://competitions.codalab.org/competitions/33267#results ). For DexYCB dataset, we use the official “S0” split. Since FreiHAND does not provide object models and object annotations, we only evaluate the hand shape reconstruction on our RGB2UV network and our Hand Only pipeline. Results are reported through their leaderboard444https://competitions.codalab.org/competitions/21238#results.
Metrics. For evaluating the hand pose and shape accuracy, we use the mean-per-joint-position-error (MPJPE) (cm) for 3D joints and mean-per-vertex-position-error (MPVPE) (cm) for mesh vertices. For evaluating the hand-object interaction, we measure the penetration depth (PD) (mm), solid intersection volume (SIV) () [Yang et al.(2021)Yang, Zhan, Li, Xu, Li, and Lu] and Simulation Displacement (SD) (cm) [Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid]. PD is based on the maximum distance of all hand vertices inside the object with respect to their closet object vertices. SIV is defined as the total voxel volume of hand vertices inside the object after converting the object model into voxels. SD measures grasp stability in a simulation space that the hand is fixed and the grasped object is subjected to gravity.
| Dataset | FreiHand | Ho3D V2 | Ho3D V3 | DexYCB | |||||||||||||
| Method | MPJPE | MPVPE | MPJPE | MPVPE | PD | SIV | SD | MPJPE | MPVPE | PD | SIV | SD | MPJPE | MPVPE | PD | SIV | SD |
| Hampali[Hampali et al.(2020)Hampali, Rad, Oberweger, and Lepetit] | - | - | 1.07 | 1.06 | 12.34 | 17.28 | 4.02 | - | - | - | - | - | - | - | - | - | - |
| Hasson[Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid] | 1.33 | 1.33 | 1.10 | 1.12 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| Hasson[Hasson et al.(2020)Hasson, Tekin, Bogo, Laptev, Pollefeys, and Schmid] | 1.33 | 1.33 | 1.14 | 1.09 | 18.44 | 14.35 | 4.10 | - | - | - | - | - | - | - | - | - | - |
| GraspField [Karunratanakul et al.(2020)Karunratanakul, Yang, Zhang, Black, Muandet, and Tang] | - | - | 1.38 | 1.36 | 14.61 | 14.92 | 3.29 | - | - | - | - | - | - | - | - | - | - |
| Li [Li et al.(2021)Li, Yang, Zhan, Lv, Xu, Li, and Lu] | - | - | 1.13 | 1.10 | 11.32 | 14.67 | 3.94 | 1.08 | 1.09 | 16.78 | 10.87 | 3.90 | 1.28 | 1.33 | 9.47 | 11.02 | 3.64 |
| Chen [Chen et al.(2021a)Chen, Chen, Yang, Wu, Li, Xia, and Tan] | 0.72 | 0.74 | 0.99 | 1.01 | 10.25 | 15.38 | 4.05 | 1.25 | 1.24 | 17.87 | 12.56 | 4.02 | 1.23 | 1.13 | 8.64 | 12.38 | 3.36 |
| Dataset GT | - | - | - | - | - | - | - | - | - | - | - | - | 0 | 0 | 4.58 | 7.16 | 1.48 |
| MANO CNN | 1.10 | 1.09 | 1.30 | 1.30 | 17.42 | 14.2 | 4.33 | 1.38 | 1.37 | 18.65 | 14.78 | 4.36 | 1.39 | 1.40 | 16.24 | 15.38 | 4.08 |
| MANO Fit | 1.37 | 1.37 | 1.58 | 1.61 | 21.37 | 18.0 | 4.82 | 1.66 | 1.65 | 22.04 | 15.60 | 4.65 | 1.49 | 1.43 | 18.56 | 17.60 | 4.86 |
| RGB2UV | 0.75 | 0.78 | 1.08 | 1.07 | 11.33 | 17.24 | 4.24 | 1.22 | 1.23 | 16.72 | 13.50 | 4.27 | 1.20 | 1.19 | 7.03 | 11.02 | 3.28 |
| Hand Only | 0.71 | 0.73 | 1.04 | 1.04 | 9.68 | 14.1 | 3.92 | 1.08 | 1.04 | 13.07 | 11.77 | 3.88 | 1.09 | 1.02 | 6.44 | 9.32 | 2.98 |
| Hand+Object | - | - | 1.25 | 1.33 | 7.66 | 10.4 | 3.22 | 1.28 | 1.26 | 9.67 | 8.66 | 3.01 | 1.29 | 1.27 | 5.05 | 7.11 | 2.64 |
4.1 Comparison with the State-of-the-Art
Quantitative Results.
Comparison with state-of-the-art results of [Chen et al.(2021a)Chen, Chen, Yang, Wu, Li, Xia, and Tan, Li et al.(2021)Li, Yang, Zhan, Lv, Xu, Li, and Lu, Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid, Hasson et al.(2020)Hasson, Tekin, Bogo, Laptev, Pollefeys, and Schmid, Hampali et al.(2020)Hampali, Rad, Oberweger, and Lepetit] in Table 1 are based on their released source code and default parameters. Considering only the hand pose and shape accuracy, our Hand Only pipeline obtains the lowest MPJPE and MPVPE on Ho3D V3 and DexYCB. Especially on the DexYCB dataset, compared with the latest works, our method reduces the pose error MPJPE by 10%. For hand-object interaction, our Hand-Object pipeline also achieves the lowest PD, SIV and SD for Ho3D V2 and DexYCB. Comparing the results for the DexYCB dataset, our grasp results verify the effectiveness of our pipeline.
Qualitative Results. Visualizations of our hand surfaces in Fig. 3 verify our texture learning and grasp optimization effectiveness.Additionally, Fig. 4 compares our method to state-of-the-art, demonstrating our improved grasp feasibility. More qualitative results can be found in the supplementary material.
Texture Map Results. Visualizations of our results are all rendered with textures from our texture decoder. Fig. 3 also reports appearance similarity between the projected hand and its ground truth via SSIM (higher is better). Our model can even estimate the texture for unobserved vertices, i.e\bmvaOneDotthe results of view 2, highlighting our model’s ability to generalize appearance. We further compare our hand texture reconstruction results with [Chen et al.(2021b)Chen, Tu, Kang, Bao, Zhang, Zhe, Chen, and Yuan] in the supplementary material and show that our reconstruction results are better.

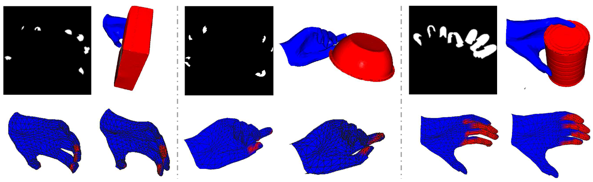
Contact Mask Results. Fig. 6 shows predicted contact masks for DexYCB. Estimated contact regions are similar to the ground truth. Our generated contact masks has an average Intersection over Union (IoU) of . Efficiency-wise, our contact mask is times faster than point-based methods [Yang et al.(2021)Yang, Zhan, Li, Xu, Li, and Lu, Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid]. Detailed experimental results are given in the supplementary material.
4.2 Ablation Study
MANO Baselines. We also compare with two simple MANO baselines in Table 1. MANO CNN is a pipeline that regresses the MANO parameters through the differentiable MANO layer [Zimmermann et al.(2019)Zimmermann, Ceylan, Yang, Russell, Argus, and Brox, Taheri et al.(2020)Taheri, Ghorbani, Black, and Tzionas]. MANO Fit uses inverse-kinematics method to fit MANO parameters from our estimated hand vertices. We outperform these baselines; especially on FreiHAND, our method achieves significant improvements (40% over MANO CNN and MANO Fit).


GraspVAE. The impact of GraspVAE is shown in Table 1 (Hand-Only vs Hand-Object). Grasp optimization worsens MPJPE and MPVPE but improves PD, SIV and SD because the optimization limits penetration between the hand and object at the expense of less accurate hand pose and shape. Fig. 5 shows examples before and after optimization. Optimization reduces the penetration and this is verified with lower PD, SIV and SD. Furthermore, compared with RGB2UV pipeline, using the Hand Only VAE refinement reduces pose errors by nearly 10%. This reveals the efficiency of our proposed Hand Only VAE and emphasizes the importance of refinement for predicting UV coordinate maps.
4.3 Limitations
In our RGB2UV pipeline, we used a silhouette of the hand projection to isolate the hand in the RGB image . If directly use provided object information, the object can be removed by using an object silhouette but it would break the spatial correlation of hand-object interaction. Therefore, without removing hand object may result in spilling over into the hand texture results; this is especially the case when the area of the hand in the image is very small, or there is significant occlusion from the object (see Fig. 7). These limitations can be improved by considering multi-view information, which would exclude the extreme viewpoints and enable a feasible hand reconstruction to be obtained.

5 Conclusion
This work proposes a hand surface framework for estimating hand-object interaction from RGB images. We explored UV coordinate maps for hand-object surface modelling and designed the first dense representation to model contact regions. Additionally, we introduce grasp optimization to improve the feasibility of the hand UV coordinate map. Experimental results show that our proposed method outperforms existing 3D hand-object interaction methods.
6 Acknowledgments
This research is supported by the Ministry of Education, Singapore, under its MOE Academic Research Fund Tier 2 (STEM RIE2025 MOE-T2EP20220-0015).
References
- [Blanz and Vetter(1999)] Volker Blanz and Thomas Vetter. A morphable model for the synthesis of 3d faces. In Proceedings of the 26th annual conference on Computer graphics and interactive techniques, pages 187–194, 1999.
- [Boukhayma et al.(2019)Boukhayma, Bem, and Torr] Adnane Boukhayma, Rodrigo de Bem, and Philip HS Torr. 3d hand shape and pose from images in the wild. In CVPR, 2019.
- [Brahmbhatt et al.(2020)Brahmbhatt, Tang, Twigg, Kemp, and Hays] Samarth Brahmbhatt, Chengcheng Tang, Christopher D Twigg, Charles C Kemp, and James Hays. Contactpose: A dataset of grasps with object contact and hand pose. In ECCV, 2020.
- [Brunet et al.(2011)Brunet, Vrscay, and Wang] Dominique Brunet, Edward R Vrscay, and Zhou Wang. On the mathematical properties of the structural similarity index. TIP, 21(4):1488–1499, 2011.
- [Cai et al.(2018)Cai, Ge, Cai, and Yuan] Yujun Cai, Liuhao Ge, Jianfei Cai, and Junsong Yuan. Weakly-supervised 3d hand pose estimation from monocular rgb images. In ECCV, 2018.
- [Calli et al.(2015)Calli, Singh, Walsman, Srinivasa, Abbeel, and Dollar] Berk Calli, Arjun Singh, Aaron Walsman, Siddhartha Srinivasa, Pieter Abbeel, and Aaron M Dollar. The ycb object and model set: Towards common benchmarks for manipulation research. In ICAR, 2015.
- [Cao et al.(2021)Cao, Radosavovic, Kanazawa, and Malik] Zhe Cao, Ilija Radosavovic, Angjoo Kanazawa, and Jitendra Malik. Reconstructing hand-object interactions in the wild. In ICCV, pages 12417–12426, 2021.
- [Chao et al.(2021)Chao, Yang, Xiang, Molchanov, Handa, Tremblay, Narang, Van Wyk, Iqbal, Birchfield, et al.] Yu-Wei Chao, Wei Yang, Yu Xiang, Pavlo Molchanov, Ankur Handa, Jonathan Tremblay, Yashraj S Narang, Karl Van Wyk, Umar Iqbal, Stan Birchfield, et al. Dexycb: A benchmark for capturing hand grasping of objects. In CVPR, 2021.
- [Chen et al.(2021a)Chen, Chen, Yang, Wu, Li, Xia, and Tan] Ping Chen, Yujin Chen, Dong Yang, Fangyin Wu, Qin Li, Qingpei Xia, and Yong Tan. I2uv-handnet: Image-to-uv prediction network for accurate and high-fidelity 3d hand mesh modeling. In ICCV, 2021a.
- [Chen et al.(2021b)Chen, Tu, Kang, Bao, Zhang, Zhe, Chen, and Yuan] Yujin Chen, Zhigang Tu, Di Kang, Linchao Bao, Ying Zhang, Xuefei Zhe, Ruizhi Chen, and Junsong Yuan. Model-based 3d hand reconstruction via self-supervised learning. In CVPR, 2021b.
- [Choi et al.(2020)Choi, Moon, and Lee] Hongsuk Choi, Gyeongsik Moon, and Kyoung Mu Lee. Pose2mesh: Graph convolutional network for 3d human pose and mesh recovery from a 2d human pose. In ECCV, 2020.
- [Christen et al.(2021)Christen, Kocabas, Aksan, Hwangbo, Song, and Hilliges] Sammy Christen, Muhammed Kocabas, Emre Aksan, Jemin Hwangbo, Jie Song, and Otmar Hilliges. D-grasp: Physically plausible dynamic grasp synthesis for hand-object interactions. arXiv preprint arXiv:2112.03028, 2021.
- [Christen et al.(2022)Christen, Kocabas, Aksan, Hwangbo, Song, and Hilliges] Sammy Christen, Muhammed Kocabas, Emre Aksan, Jemin Hwangbo, Jie Song, and Otmar Hilliges. D-grasp: Physically plausible dynamic grasp synthesis for hand-object interactions. In CVPR, 2022.
- [de La Gorce et al.(2008)de La Gorce, Paragios, and Fleet] Martin de La Gorce, Nikos Paragios, and David J Fleet. Model-based hand tracking with texture, shading and self-occlusions. In CVPR, 2008.
- [de La Gorce et al.(2011)de La Gorce, Fleet, and Paragios] Martin de La Gorce, David J Fleet, and Nikos Paragios. Model-based 3d hand pose estimation from monocular video. TPAMI, 33(9):1793–1805, 2011.
- [Deng et al.(2018)Deng, Cheng, Xue, Zhou, and Zafeiriou] Jiankang Deng, Shiyang Cheng, Niannan Xue, Yuxiang Zhou, and Stefanos Zafeiriou. Uv-gan: Adversarial facial uv map completion for pose-invariant face recognition. In CVPR, 2018.
- [Engelmann et al.(2017)Engelmann, Kontogianni, Hermans, and Leibe] Francis Engelmann, Theodora Kontogianni, Alexander Hermans, and Bastian Leibe. Exploring spatial context for 3d semantic segmentation of point clouds. In ICCVW, 2017.
- [Fan et al.(2017)Fan, Su, and Guibas] Haoqiang Fan, Hao Su, and Leonidas J Guibas. A point set generation network for 3d object reconstruction from a single image. In CVPR, 2017.
- [Feng et al.(2018)Feng, Wu, Shao, Wang, and Zhou] Yao Feng, Fan Wu, Xiaohu Shao, Yanfeng Wang, and Xi Zhou. Joint 3d face reconstruction and dense alignment with position map regression network. In ECCV, 2018.
- [Ge et al.(2019)Ge, Ren, Li, Xue, Wang, Cai, and Yuan] Liuhao Ge, Zhou Ren, Yuncheng Li, Zehao Xue, Yingying Wang, Jianfei Cai, and Junsong Yuan. 3d hand shape and pose estimation from a single rgb image. In CVPR, 2019.
- [Groueix et al.(2018)Groueix, Fisher, Kim, Russell, and Aubry] Thibault Groueix, Matthew Fisher, Vladimir G Kim, Bryan C Russell, and Mathieu Aubry. A papier-mâché approach to learning 3d surface generation. In CVPR, 2018.
- [Güler et al.(2018)Güler, Neverova, and Kokkinos] Rıza Alp Güler, Natalia Neverova, and Iasonas Kokkinos. Densepose: Dense human pose estimation in the wild. In CVPR, 2018.
- [Hampali et al.(2020)Hampali, Rad, Oberweger, and Lepetit] Shreyas Hampali, Mahdi Rad, Markus Oberweger, and Vincent Lepetit. Honnotate: A method for 3d annotation of hand and object poses. In CVPR, 2020.
- [Hampali et al.(2021)Hampali, Sarkar, and Lepetit] Shreyas Hampali, Sayan Deb Sarkar, and Vincent Lepetit. Ho-3d_v3: Improving the accuracy of hand-object annotations of the ho-3d dataset. arXiv preprint arXiv:2107.00887, 2021.
- [Hasson et al.(2019)Hasson, Varol, Tzionas, Kalevatykh, Black, Laptev, and Schmid] Yana Hasson, Gul Varol, Dimitrios Tzionas, Igor Kalevatykh, Michael J Black, Ivan Laptev, and Cordelia Schmid. Learning joint reconstruction of hands and manipulated objects. In CVPR, 2019.
- [Hasson et al.(2020)Hasson, Tekin, Bogo, Laptev, Pollefeys, and Schmid] Yana Hasson, Bugra Tekin, Federica Bogo, Ivan Laptev, Marc Pollefeys, and Cordelia Schmid. Leveraging photometric consistency over time for sparsely supervised hand-object reconstruction. In CVPR, 2020.
- [Hasson et al.(2021)Hasson, Varol, Schmid, and Laptev] Yana Hasson, Gül Varol, Cordelia Schmid, and Ivan Laptev. Towards unconstrained joint hand-object reconstruction from rgb videos. In 3DV, 2021.
- [He et al.(2016)He, Zhang, Ren, and Sun] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In CVPR, 2016.
- [Huang et al.(2020)Huang, Tan, Liu, and Yuan] Lin Huang, Jianchao Tan, Ji Liu, and Junsong Yuan. Hand-transformer: non-autoregressive structured modeling for 3d hand pose estimation. In ECCV, 2020.
- [Jain and Learned-Miller(2011)] Vidit Jain and Erik Learned-Miller. Online domain adaptation of a pre-trained cascade of classifiers. In CVPR, pages 577–584. IEEE, 2011.
- [Jiang et al.(2021)Jiang, Liu, Wang, and Wang] Hanwen Jiang, Shaowei Liu, Jiashun Wang, and Xiaolong Wang. Hand-object contact consistency reasoning for human grasps generation. arXiv preprint arXiv:2104.03304, 2021.
- [Kang et al.(2021)Kang, Lee, and Lee] Jiwoo Kang, Seongmin Lee, and Sanghoon Lee. Competitive learning of facial fitting and synthesis using uv energy. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021.
- [Karunratanakul et al.(2020)Karunratanakul, Yang, Zhang, Black, Muandet, and Tang] Korrawe Karunratanakul, Jinlong Yang, Yan Zhang, Michael J Black, Krikamol Muandet, and Siyu Tang. Grasping field: Learning implicit representations for human grasps. In 3DV, 2020.
- [Karunratanakul et al.(2021)Karunratanakul, Spurr, Fan, Hilliges, and Tang] Korrawe Karunratanakul, Adrian Spurr, Zicong Fan, Otmar Hilliges, and Siyu Tang. A skeleton-driven neural occupancy representation for articulated hands. In 3DV, 2021.
- [Khamis et al.(2015)Khamis, Taylor, Shotton, Keskin, Izadi, and Fitzgibbon] Sameh Khamis, Jonathan Taylor, Jamie Shotton, Cem Keskin, Shahram Izadi, and Andrew Fitzgibbon. Learning an efficient model of hand shape variation from depth images. In CVPR, 2015.
- [Kolotouros et al.(2019)Kolotouros, Pavlakos, Black, and Daniilidis] Nikos Kolotouros, Georgios Pavlakos, Michael J Black, and Kostas Daniilidis. Learning to reconstruct 3d human pose and shape via model-fitting in the loop. In ICCV, 2019.
- [Kulon et al.(2020)Kulon, Guler, Kokkinos, Bronstein, and Zafeiriou] Dominik Kulon, Riza Alp Guler, Iasonas Kokkinos, Michael M Bronstein, and Stefanos Zafeiriou. Weakly-supervised mesh-convolutional hand reconstruction in the wild. In CVPR, 2020.
- [Lee and Lee(2020)] Gun-Hee Lee and Seong-Whan Lee. Uncertainty-aware mesh decoder for high fidelity 3d face reconstruction. In CVPR, 2020.
- [Lee et al.(2020)Lee, Cho, Kim, Inouye, and Kwak] Myunggi Lee, Wonwoong Cho, Moonheum Kim, David Inouye, and Nojun Kwak. Styleuv: Diverse and high-fidelity uv map generative model. arXiv preprint arXiv:2011.12893, 2020.
- [Li et al.(2021)Li, Yang, Zhan, Lv, Xu, Li, and Lu] Kailin Li, Lixin Yang, Xinyu Zhan, Jun Lv, Wenqiang Xu, Jiefeng Li, and Cewu Lu. Artiboost: Boosting articulated 3d hand-object pose estimation via online exploration and synthesis. arXiv preprint arXiv:2109.05488, 2021.
- [Lin et al.(2021a)Lin, Wang, and Liu] Kevin Lin, Lijuan Wang, and Zicheng Liu. End-to-end human pose and mesh reconstruction with transformers. In CVPR, 2021a.
- [Lin et al.(2021b)Lin, Wang, and Liu] Kevin Lin, Lijuan Wang, and Zicheng Liu. Mesh graphormer. In ICCV, 2021b.
- [Liu et al.(2017)Liu, Li, Zhang, Zhou, Ye, Wang, and Lu] Fangyu Liu, Shuaipeng Li, Liqiang Zhang, Chenghu Zhou, Rongtian Ye, Yuebin Wang, and Jiwen Lu. 3dcnn-dqn-rnn: A deep reinforcement learning framework for semantic parsing of large-scale 3d point clouds. In ICCV, 2017.
- [Loper et al.(2015)Loper, Mahmood, Romero, Pons-Moll, and Black] Matthew Loper, Naureen Mahmood, Javier Romero, Gerard Pons-Moll, and Michael J Black. Smpl: A skinned multi-person linear model. ACM transactions on graphics (TOG), 34(6):1–16, 2015.
- [Melax et al.(2013)Melax, Keselman, and Orsten] Stan Melax, Leonid Keselman, and Sterling Orsten. Dynamics based 3d skeletal hand tracking. In Proceedings of the ACM SIGGRAPH Symposium on Interactive 3D Graphics and Games, pages 184–184, 2013.
- [Moon and Lee(2020)] Gyeongsik Moon and Kyoung Mu Lee. I2l-meshnet: Image-to-lixel prediction network for accurate 3d human pose and mesh estimation from a single rgb image. In ECCV, 2020.
- [Mullapudi et al.(2019)Mullapudi, Chen, Zhang, Ramanan, and Fatahalian] Ravi Teja Mullapudi, Steven Chen, Keyi Zhang, Deva Ramanan, and Kayvon Fatahalian. Online model distillation for efficient video inference. In ICCV, 2019.
- [Oikonomidis et al.(2011)Oikonomidis, Kyriazis, and Argyros] Iason Oikonomidis, Nikolaos Kyriazis, and Antonis A Argyros. Efficient model-based 3d tracking of hand articulations using kinect. In BmVC, 2011.
- [Qi et al.(2017a)Qi, Su, Mo, and Guibas] Charles R Qi, Hao Su, Kaichun Mo, and Leonidas J Guibas. Pointnet: Deep learning on point sets for 3d classification and segmentation. In CVPR, 2017a.
- [Qi et al.(2017b)Qi, Yi, Su, and Guibas] Charles Ruizhongtai Qi, Li Yi, Hao Su, and Leonidas J Guibas. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. NeurIPS, 2017b.
- [Qian et al.(2020)Qian, Wang, Mueller, Bernard, Golyanik, and Theobalt] Neng Qian, Jiayi Wang, Franziska Mueller, Florian Bernard, Vladislav Golyanik, and Christian Theobalt. Parametric hand texture model for 3d hand reconstruction and personalization. In ECCV, 2020.
- [Ranjan et al.(2018)Ranjan, Bolkart, Sanyal, and Black] Anurag Ranjan, Timo Bolkart, Soubhik Sanyal, and Michael J Black. Generating 3d faces using convolutional mesh autoencoders. In ECCV, 2018.
- [Ravi et al.(2020)Ravi, Reizenstein, Novotny, Gordon, Lo, Johnson, and Gkioxari] Nikhila Ravi, Jeremy Reizenstein, David Novotny, Taylor Gordon, Wan-Yen Lo, Justin Johnson, and Georgia Gkioxari. Accelerating 3d deep learning with pytorch3d. arXiv:2007.08501, 2020.
- [Romero et al.(2017a)Romero, Tzionas, and Black] Javier Romero, Dimitrios Tzionas, and Michael J. Black. Embodied hands: Modeling and capturing hands and bodies together. ACM Transactions on Graphics, (Proc. SIGGRAPH Asia), 36(6), November 2017a.
- [Romero et al.(2017b)Romero, Tzionas, and Black] Javier Romero, Dimitrios Tzionas, and Michael J Black. Embodied hands: Modeling and capturing hands and bodies together. ACM Transactions on Graphics (ToG), 2017b.
- [Ronneberger et al.(2015)Ronneberger, Fischer, and Brox] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, 2015.
- [Sohn et al.(2015)Sohn, Lee, and Yan] Kihyuk Sohn, Honglak Lee, and Xinchen Yan. Learning structured output representation using deep conditional generative models. NeurIPS, 2015.
- [Spurr et al.(2020)Spurr, Iqbal, Molchanov, Hilliges, and Kautz] Adrian Spurr, Umar Iqbal, Pavlo Molchanov, Otmar Hilliges, and Jan Kautz. Weakly supervised 3d hand pose estimation via biomechanical constraints. In ECCV, 2020.
- [Sun et al.(2020)Sun, Wang, Liu, Miller, Efros, and Hardt] Yu Sun, Xiaolong Wang, Zhuang Liu, John Miller, Alexei Efros, and Moritz Hardt. Test-time training with self-supervision for generalization under distribution shifts. In ICML, pages 9229–9248, 2020.
- [Taheri et al.(2020)Taheri, Ghorbani, Black, and Tzionas] Omid Taheri, Nima Ghorbani, Michael J Black, and Dimitrios Tzionas. Grab: A dataset of whole-body human grasping of objects. In ECCV, pages 581–600. Springer, 2020.
- [Tzionas et al.(2016)Tzionas, Ballan, Srikantha, Aponte, Pollefeys, and Gall] Dimitrios Tzionas, Luca Ballan, Abhilash Srikantha, Pablo Aponte, Marc Pollefeys, and Juergen Gall. Capturing hands in action using discriminative salient points and physics simulation. IJCV, 118(2):172–193, 2016.
- [Wan et al.(2020)Wan, Probst, Van Gool, and Yao] Chengde Wan, Thomas Probst, Luc Van Gool, and Angela Yao. Dual grid net: Hand mesh vertex regression from single depth maps. In ECCV, 2020.
- [Xiang et al.(2017)Xiang, Schmidt, Narayanan, and Fox] Yu Xiang, Tanner Schmidt, Venkatraman Narayanan, and Dieter Fox. Posecnn: A convolutional neural network for 6d object pose estimation in cluttered scenes. arXiv preprint arXiv:1711.00199, 2017.
- [Yang and Yao(2019)] Linlin Yang and Angela Yao. Disentangling latent hands for image synthesis and pose estimation. In CVPR, 2019.
- [Yang et al.(2021)Yang, Zhan, Li, Xu, Li, and Lu] Lixin Yang, Xinyu Zhan, Kailin Li, Wenqiang Xu, Jiefeng Li, and Cewu Lu. Cpf: Learning a contact potential field to model the hand-object interaction. In ICCV, 2021.
- [Yang et al.(2018)Yang, Feng, Shen, and Tian] Yaoqing Yang, Chen Feng, Yiru Shen, and Dong Tian. Foldingnet: Point cloud auto-encoder via deep grid deformation. In CVPR, pages 206–215, 2018.
- [Yao et al.(2019)Yao, Fang, Wu, Feng, and Li] Pengfei Yao, Zheng Fang, Fan Wu, Yao Feng, and Jiwei Li. Densebody: Directly regressing dense 3d human pose and shape from a single color image. arXiv preprint arXiv:1903.10153, 2019.
- [Zeng et al.(2020)Zeng, Ouyang, Luo, Liu, and Wang] Wang Zeng, Wanli Ouyang, Ping Luo, Wentao Liu, and Xiaogang Wang. 3d human mesh regression with dense correspondence. In CVPR, 2020.
- [Zhang et al.(2020)Zhang, Fang, Wah, and Torr] Feihu Zhang, Jin Fang, Benjamin Wah, and Philip Torr. Deep fusionnet for point cloud semantic segmentation. In ECCV, 2020.
- [Zhu et al.(2019)Zhu, Zuo, Wang, Cao, and Yang] Hao Zhu, Xinxin Zuo, Sen Wang, Xun Cao, and Ruigang Yang. Detailed human shape estimation from a single image by hierarchical mesh deformation. In CVPR, 2019.
- [Zimmermann and Brox(2017)] Christian Zimmermann and Thomas Brox. Learning to estimate 3d hand pose from single rgb images. In ICCV, 2017.
- [Zimmermann et al.(2019)Zimmermann, Ceylan, Yang, Russell, Argus, and Brox] Christian Zimmermann, Duygu Ceylan, Jimei Yang, Bryan Russell, Max Argus, and Thomas Brox. Freihand: A dataset for markerless capture of hand pose and shape from single rgb images. In ICCV, 2019.