Unveiling the Hybridization Process in a Quantum Critical Ferromagnet by Ultrafast Optical Spectroscopy
Abstract
We report the ultrafast optical pump-probe spectroscopy measurements on the recently discovered quantum critical ferromagnet CeRh6Ge4. Our experimental results reveal the two-stage development of the hybridization between localized moments and conduction electrons with lowering temperature, as evidenced by (1) the presence of hybridization fluctuation for temperatures from 85 K () to 140 K (), and (2) the emergence of collective hybridization below the coherence temperature, , marked by the opening of an indirect gap of 2 12 meV. We also observe three coherent phonon modes being softened anomalously below , reflecting directly their coupling with the emergent coherent heavy electrons. Our findings establish the universal nature of the hybridization process in different heavy fermion systems.
The ferromagnetic (FM) quantum critical point (QCP) is generally believed to be prohibited in a pure FM system as it is often interrupted by other competing phases or first-order phase transitions M. Brando2016 . The recent discovery of a FM QCP in the stoichiometric Kondo lattice compound CeRh6Ge4 under pressure has stimulated great interest on its origin and the nature of its associated strange metal phase B. Shen2020 . One proposal for the existence of a FM QCP is that the local moments may form a triplet resonating valence bound state in the FM state and cause a singular transformation in the patterns of their entanglement with conduction electrons as the Kondo singlets develop at the QCP Piers Coleman2020 , which leads to an abrupt jump of the Fermi surface volume. This is similar to the scenario of a local QCP in the antiferromagnetic Kondo lattice compounds Si_Science_2010 . One may naturally ask if and how different types of inter-site magnetic correlations among localized moments (even outside the quantum critical regime) might have an effect on their hybridization process with conduction electrons and the resulting Fermi surface change. It is thus important to explore the band evolution of CeRh6Ge4 near the Fermi energy () and compare it with the antiferromagnetic analogues.
In this respect, the quantum oscillations and angle-resolved photoemission spectroscopy (ARPES) are the most direct experimental approaches to probe the band structure and its evolution. However, ARPES is highly limited by its energy resolution when applied on the heavy fermion materials Q. Y. Chen2017 ; A. Koitzsch2008 ; A. Koitzsch2013 . So far, it has not been able to reveal the formation of the indirect hybridization gap with an order of meV near . Fortunately, the ultrafast optical pump-probe spectroscopy has recently been demonstrated to provide an alternative route to detect the hybridization dynamics over a wide temperature range Y. P. Liu2020 . It can reveal not only the “band bending” probed by the ARPES far above the coherence temperature but also the opening of the indirect hybridization gap below the coherence temperature, thus proposing a unified picture for spectroscopic and transport measurements. Although the measurements can only be performed at ambient pressure away from the quantum critical point, one may still expect some useful information on the microscopic dynamics of the hybridization physics. Indeed, this optical technique provides a unique way to investigate the dynamics of excited quasiparticles coupled to collective bosonic excitations in quantum systems J. Demsar2003 ; E. E. Chia2010 ; J. Qi2013 ; R. Y. Chen2016 , and thus can help us to detect simultaneously the exotic fermionic and bosonic responses near and far from the coherent temperature , below which the heavy electron state is developed.
In this work, we report the optical pump-probe measurements on CeRh6Ge4 for the first time. Hybridization processes between the localized moments and conduction electrons are unraveled via the photoexcited quasiparticle dynamics in this material. Specifically, we have observed that the quasiparticle relaxation rate () in the short timescale shows a clear reduction as the temperature decreases across 140 K. Remarkably, exhibits an apparent fluence-dependence for (=855 K), in comparison with the fluence-independent behaviour for . Such findings enable us to predict in CeRh6Ge4 (1) the occurrence of a narrow indirect hybridization gap of about 12 meV in the density of states (DOS) associated with the formation of coherent heavy electrons below , and (2) the existence of precursor hybridization fluctuations between and . These results are in resemblance of that reported previously for CeCoIn5 Y. P. Liu2020 and independent of the low-temperature magnetic properties. By contrast, recent measurements of quantum oscillations and calculations of band structure suggest a localized nature of 4 electrons in CeRh6Ge4 in the ground state A. Wang2021 , suggesting the necessity of a better theoretical understanding.
The ultrafast time-resolved differential reflectivity measurements were performed on the single crystal CeRh6Ge4 from 5 K to room temperature using a Ti:sapphire femtosecond laser producing a pulse width of 35 fs at centre wavelength of 800 nm (1.55 eV). Typical results are shown in Fig. 1(a). More experimental details and data can be found in the Supplemental Material. After photoexcitation, strong instantaneous rise can be clearly seen at all investigated temperatures. The lateral dynamics show obvious damped oscillations superimposed on the non-oscillating background (see Fig. 1(b)). Generally, the time evolution of within the first tens of picoseconds can be attributed to the electron-electron (e-e) and electron-boson scattering processes in strongly correlated and metallic-like systems D. N. Basov2011 ; C. Gadermaier2010 . The bosons may involve phonon or other bosonic excitations C. Giannetti2016 ; M. C. Wang2018 .
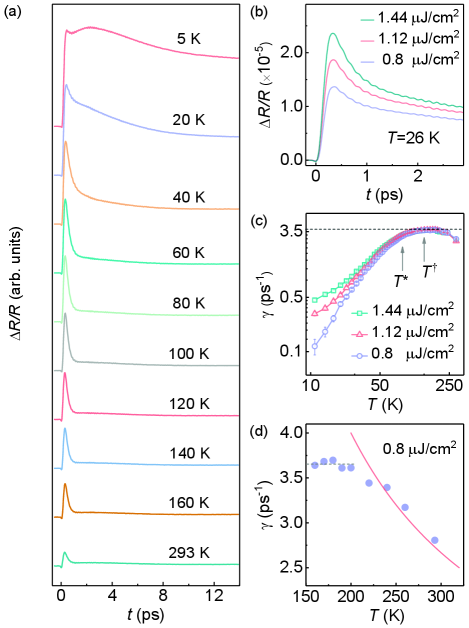
We first focus on the non-oscillatory part of the signal. As shown in Fig. 1(b), the initial decay below ps demonstrates a strong fluence-dependent behaviour. A bump-like behaviour consisting of a second rise clearly appears when the temperature is below 20 K, and leads to the initial decay hidden inside a tiny peak at very low temperatures. Similar signals with a second rise have also been obtained in many heavy fermion materials and other strongly correlated systems, and could originate from the excitations of electronic origins entangled with the electron-phonon (e-ph) and nonthermal e-e scatterings Y. P. Liu2020 ; J. Demsar2003 ; P. Kusar2005 . We can fit the data within 1.5 ps after the max of signal using a single exponential formula, , to investigate the quasiparticle relaxation quantitatively. Here, and are the amplitude and decay rate, respectively. Figure 1(c) shows the derived as a function of temperature under various pump fluence. An evident fluence-dependent trend is observed below a critical temperature of K, defined as , which is very close to the temperature where the magnetic resistivity exhibits a coherence peak (see the Supplemental Material) B. Shen2020 . This concurrence indicates that the quasiparticle relaxation is influenced by the coherent heavy electron state emerging below , the same as that have been observed in CeCoIn5.
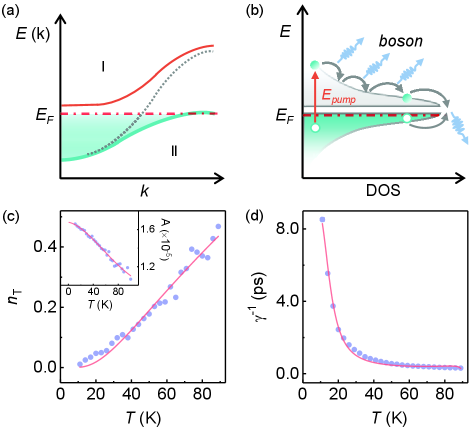
The fluence-dependent phenomena of the decay rate below can be explained by the widely used Rothwarf-Taylor (RT) model A. Rothwarf1967 ; V. V. Kabanov2005 , where the dynamics of quasiparticles () and bosons () are well described by the presence of a narrow energy gap in DOS. Specifically, the relaxation of the excited quasiparticles with an energy larger than the gap () is accomplished by the emission of high frequency bosons that can subsequently re-excite electron-hole pairs, as formulated by A. Rothwarf1967 ; V. V. Kabanov2005
| (1) |
where is the external excitation, is the total number of quasiparticles, is the recombination rate of electron-hole pairs, is the density of high frequency bosons with the energy larger than 2, is the probability per unit time for generating the nonequilibrium quasiparticles by such bosons, is the escaping rate of the high frequency bosons, and is the thermal-equilibrium boson density. As long as or is large enough V. V. Kabanov2005 , the quasiparticle relaxation dynamics is dominated by the so-called bimolecular recombination process, which contributes the nonlinear term and is fluence-dependent. This type of process is schematically shown in Figs. 2(a)-(b), and can exactly elucidate the physics behind the fluence-dependent in Fig. 1(c).
The gap formation in the DOS can be studied by fitting the and using the RT model J. Demsar_JPCM2006 ; V. V. Kabanov1999 ; E. E. M. Chia2007 ,
| (2) |
where , and are fitting parameters, respectively. is the density of quasiparticles thermally excited across the gap and () is a constant determined by the shape of the gapped DOS J. Demsar2006 . For a typical DOS of the Bardeen-Cooper-Schrieffer (BCS) form, we may fix and obtain a good fit as shown Figs. 2(c) and (d). This yields a gap of the magnitude of meV, reflecting the formation of an indirect hybridization gap below due to collective hybridization associated with the emergence of coherent heavy electron states near .
For temperatures above , the fluence-independency clearly indicates the closing of the indirect hybridization gap. However, we notice that the behaviour of can be further separated into two regimes. For (140 K) , firstly shows a saturation behavior and then decreases slightly as the temperature increases. Such -dependence cannot be explained by the conventional two-temperature model Allen_PRL_1987 . Rather, it indicates a nonthermal process, i.e., the relaxation time due to the e-e collisions can be longer than the e-ph relaxation time () C. Gadermaier2010 , or the thermal distribution by e-e scatterings cannot be instantaneously attained, even though the excited fermionic quasiparticles may relax close to . Such process may be described by a nonequilibrium model C. Gadermaier2010 : , where represents the e-ph coupling and is the lattice temperature. If we assume in the high temperature regime, i.e. 230 K, this model can well explain why the measured becomes smaller as increases (see Fig. 1(d)), which strongly supports the existence of the nonthermal process within the initial several picoseconds. We further obtain 94 meV2. Assuming the Debye frequency to be 7 THz (or 28 meV) based on our measurements discussed below, we can estimate that takes a value of 0.23.
Between and , decreases with lowering temperature. Similar -dependence has been observed in CeCoIn5 Y. P. Liu2020 , where, in the absence of the indirect hybridization gap, precursor hybridization fluctuations in a short correlation time- or length-scale were proposed to explain the reduction of decay rate below D. Hu2019 . In specific, both the e-e and electron-boson scatterings of the excited quasiparticles are expected to be suppressed as the fluctuating moments start to participate in the hybridization with the conduction electrons. The development of hybridization fluctuations can further cause the renormalization (bending) of the conduction bands even in the high temperature regime (e.g. 100 K) Q. Y. Chen2017 , a prediction based on our experimental observation to be examined using ARPES in CeRh6Ge4. This suggests that the moments are not decoupled from conduction electrons in the paramagnetic state as one may naively think for a small Fermi surface at ambient pressure. Note that how the hybridization process evolves below 5 K remains to be investigated.
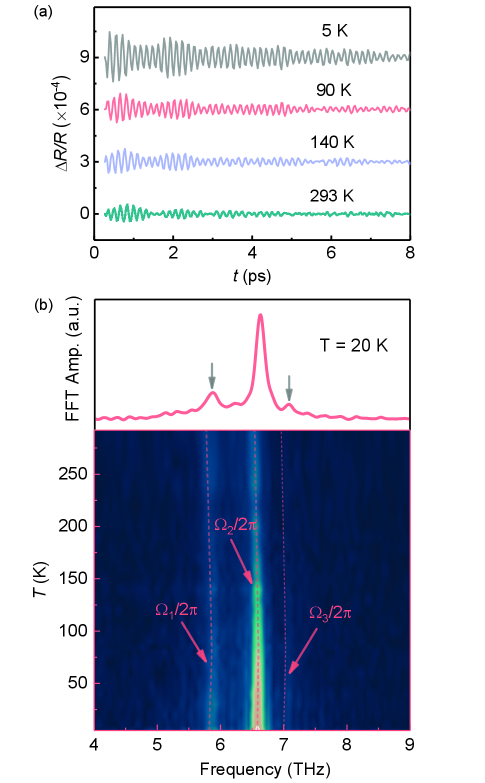
The above results demonstrate that the hybridization dynamics in CeRh6Ge4 also exhibits a two-stage process, with the onset of precursor hybridization fluctuations below and the opening of an indirect hybridization gap below , in resemblance of that in CeCoIn5. The separation of the two stages is also manifested by the oscillatory component superimposed on the signals. The oscillations with terahertz (THz) frequency generally originate from the coherent optical phonons triggered by displacive excitations or photoexcited Raman process H. J. Zeiger1992 ; R. Merlin1997 .
Figures 3(a) and (b) plot the oscillatory components extracted from the decay process after subtracting the nonoscillatory background. Three obvious terahertz modes were observed at all investigated temperatures including 5.8 THz, 6.6 THz, 7 THz. The oscillation components can be fitted quantitatively using the following formula,
| (3) |
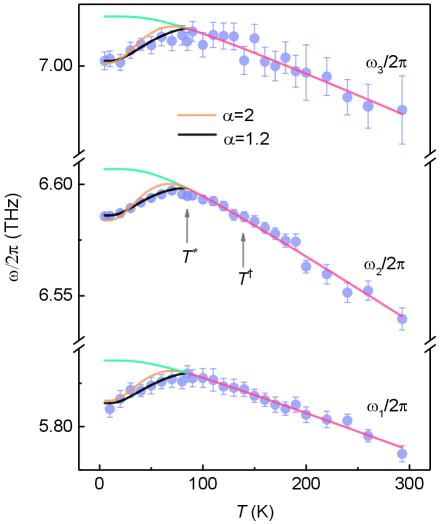
where , , , and () are the amplitude, damping rate, frequency, and phase, respectively. and are related to an underdamped harmonic oscillator. , where is the natural frequency. The temperature-dependent evolution of is shown in Fig. 4. We see a sharp downturn below for all three phonon modes, instead of a gradual flattening expected by the anharmonic decay model M. Balkanski1983 ; J. Menendez1984 (see also the Supplemental Material), as indicated by the green lines in Fig. 4. By contrast, the -dependent for can be well explained by the anharmonic phonon-phonon coupling (red lines).
The anomaly around cannot arise from the phonon-magnon coupling effect because the long-range FM ordering in CeRh6Ge4 appears below a Curie temperature of 2.5 K. To understand quantitatively the peculiar behavior of for , we calculated the values of that represent the deviation between the expected values from anharmonic phonon model and the experimental . Such deviation must be associated with the appearance of collective hybridization and the consequent gap opening in the DOS. In fact, can be connected to the quasiparticle density () via the density of Kondo singlets Y. P. Liu2020 , which is proportional to . Our best fit using , where is a fitting parameter, yields , as shown in Fig. 4. Surprisingly, this value of is nearly the same as that obtained in CeCoIn5 within the experimental errors, while the mean-field theory predicted . This indicates that a new and generic theory is required in order to explain the anomalous phonon softening below in two quite different systems. In essence, this theory should take into account variation of the electron-phonon coupling induced by the DOS change near in the presence of collective hybridization. Clearly, the observed frequency softening further proves that the phonon renormalization can be a useful probe of the coherent heavy electron states.
Altogether, our results reveal the detailed hybridization process in the FM Kondo lattice compound CeRh6Ge4 over a wide temperature range. The reduction of the relaxation rate below 140 K suggests the possibility of “band bending” already in this high temperature region, which could be detected in future ARPES experiments. Below the coherence temperature 85 K, we unveil an indirect band gap of 12 meV, which plays the role of a protector of the coherent heavy electron state. The associated anomalous softenning in the frequencies of coherent optical phonons provides a benchmark for further theories. The observed two-stage hybridization process is in close resemblance of that in CeCoIn5. The distinction in the magnetic correlations appear to have no significant influence at least in the measured temperature range (above 5 K) and at ambient pressure. This seems to suggest a universal mechanism for the onset of heavy electron coherence independent of the details of the inter-site coupling among localized moments. We should also note that our results in the normal state are in contrast with the observation of a small Fermi surface in the ferromagnetic ground state A. Wang2021 . This distinction was not anticipated in previous theories. It remains open how the hybridization process changes upon entering the magnetic state. More elaborated studies are needed to clarify this point, and particularly its influence on the properties of quantum criticality Wang_arXiv_2020 .
Note: During the submission of our manuscript, we realize an ARPES work on CeRh6Ge4 by Y. Wu et al. Wu_submitted , providing evidence for anisotropic hybridization between - and conduction electrons in the high temperature regime.
This work was supported by the National Natural Science Foundation of China (Grants No. 11974070, No. 11974306, No. 12034017, No. 11734006, No. 11774401, and No. 11974306), the Frontier Science Project of Dongguan (2019622101004), the National Key RD Program of China (Grants No. 2017YFA0303100, No. 2018YFA0307400, and No. 2016YFA0300202), the Science Challenge Project of China (No. TZ2016004), the Chinese Academy of Sciences Interdisciplinary Innovation Team, the Strategic Priority Research Program of CAS (XDB33010100), and the Key R&D Program of Zhejiang Province, China (2021C01002).
References
- (1) M. Brando, D. Belitz, F. M. Grosche, and T. R. Kirkpatrick, Rev. Mod. Phys. 88, 039901 (2016).
- (2) B. Shen et al., Nature 579, 51 (2020).
- (3) Piers Coleman, Yashar Komijani, and Elio J. König, Phys. Rev. Lett. 125, 077001 (2020)
- (4) Q. Si and F. Steglich, Science 329, 1161 (2010).
- (5) Q. Y. Chen et al., Phys. Rev. B 96 045107 (2017).
- (6) A. Koitzsch et al., Phys. Rev. B 77, 155128 (2008).
- (7) A. Koitzsch, T. K. Kim, U. Treske, M. Knupfer, B. Büchner, M. Richter, I. Opahle, R. Follath, E. D. Bauer, and J. L. Sarrao, Phys. Rev. B 88, 035124 (2013).
- (8) Y. P. Liu et al., Phys. Rev. Lett. 124, 057404 (2020).
- (9) J. Demsar, R. D. Averitt, K. H. Ahn, M. J. Graf, S. A. Trugman, V. V. Kabanov, J. L. Sarrao, and A. J. Taylor, Phys. Rev. Lett. 91, 027401 (2003).
- (10) E. E. Chia et al., Phys. Rev. Lett. 104, 027003 (2010).
- (11) J. Qi et al., Phys. Rev. Lett. 111, 057402 (2013).
- (12) R. Y. Chen, S. J. Zhang, E. D. Bauer, J. D. Thompson, and N. L. Wang, Phys. Rev. B 94, 035161 (2016)
- (13) A. Wang et al., arXiv:2101.08972 (2021).
- (14) C. Gadermaier et al., Phys. Rev. Lett. 105, 257001 (2010).
- (15) D. N. Basov, R. D. Averitt, Dirk van der Marel, M. Dressel, and K. Haule, Rev. Mod. Phys. 83, 471 (2011)
- (16) C. Giannetti, M. Capone, D. Fausti, M. Fabrizio, F. Parmigiani, and D. Mihailovic, Advances in Physics 65, 58 (2016).
- (17) M. C. Wang, H. S. Yu, J. Xiong, Y. F. Yang, S. N. Luo, K. Jin, and J. Qi, Phys. Rev. B 97, 155157 (2018).
- (18) P. Kusar, J. Demsar, D. Mihailovic, and S. Sugai, Phys. Rev. B 72, 014544 (2005).
- (19) A. Rothwarf and B. N. Taylor, Phys. Rev. Lett. 19, 27 (1967).
- (20) V. V. Kabanov, J. Demsar, and D. Mihailovic, Phys. Rev. Lett. 95, 147002 (2005).
- (21) J. Demsar, J. L. Sarrao, and A. J. Taylor, J. Phys. Condens. Matter 18, R281 (2006).
- (22) V. V. Kabanov, J. Demsar, B. Podobnik, and D. Mihailovic, Phys. Rev. B 59, 1497 (1999).
- (23) Elbert E. M. Chia, Jian-Xin Zhu, D. Talbayev, R. D. Averitt, A. J. Taylor, Kyu-Hwan Oh, In-Sun Jo, and S.-I. Lee, Phys. Rev. Lett. 99, 147008 (2007).
- (24) J. Demsar, V. K. Thorsmolle, J. L. Sarrao, and A. J. Taylor, Phys. Rev. Lett. 96, 037401 (2006).
- (25) P. B. Allen, Phys. Rev. Lett. 59, 1460 (1987).
- (26) D. Hu, J.-J. Dong, and Y.-F. Yang, Phys. Rev. B 100, 195133 (2019).
- (27) H. J. Zeiger, J. Vidal, T. K. Cheng, E. P. Ippen, G. Dresselhaus, and M. S. Dresselhaus, Phys. Rev. B 45, 768 (1992).
- (28) R. Merlin, Solid State Commun. 102, 207 (1997).
- (29) M. Balkanski, R. F. Wallis, and E. Haro, Phys. Rev. B 28, 1928 (1983).
- (30) J. Menendez and M. Cardona, Phys. Rev. B 29, 2051 (1984).
- (31) J. Wang and Y.-F. Yang, arXiv:2009.00543 (2020).
- (32) Y. Wu, Y. Zhang, F. Du, B. Shen,H. Zheng, Y. Fang, M. Smidman, C. Cao, F. Steglich, H. Q. Yuan, J. D. Denlinger, and Y. Liu, Submitted.