11email: {jayeon.yoo,jis3613,nojunk}@snu.ac.kr
Unsupervised Domain Adaptation for One-stage Object Detector using Offsets to Bounding Box
Abstract
Most existing domain adaptive object detection methods exploit adversarial feature alignment to adapt the model to a new domain. Recent advances in adversarial feature alignment strives to reduce the negative effect of alignment, or negative transfer, that occurs because the distribution of features varies depending on the category of objects. However, by analyzing the features of the anchor-free one-stage detector, in this paper, we find that negative transfer may occur because the feature distribution varies depending on the regression value for the offset to the bounding box as well as the category. To obtain domain invariance by addressing this issue, we align the feature conditioned on the offset value, considering the modality of the feature distribution. With a very simple and effective conditioning method, we propose OADA (Offset-Aware Domain Adaptive object detector) that achieves state-of-the-art performances in various experimental settings. In addition, by analyzing through singular value decomposition, we find that our model enhances both discriminability and transferability.
Keywords:
Unsupervised Domain Adaptation, Object Detection, Offset-Aware1 Introduction
Deep-learning-based object detection has shown successful results by learning from a large amount of labeled data. However, if the distribution of test data is significantly different from that of training data, the model performance is severely impaired. In practice, this performance degradation can be very fatal because the domains in which the object detection model should operate can be very diverse. To address this problem, the most effective way is to re-train the model with a lot of data from the new environment whenever the environment changes. However, obtaining a large amount of labeled data is a very expensive process, especially in object detection task which requires annotating the bounding boxes and the classes of objects in an image. Unsupervised Domain Adaptation (UDA) provides an efficient solution to this domain-shift problem in a way that it adapts the model to a new environment by training with unlabeled datasets from the new environment (target domain) as well as rich datasets from the original environment (source domain). Based on the theoretical analysis of [11], aligning the feature distribution of the source and the target domain in an adversarial manner is one of the most effective ways in various tasks such as classification [11, 41, 1, 26] and segmentation [27, 43, 7, 6]. A seminal work [5] is the first to deal with Domain Adaptive Object Detection (DAOD) aligning backbone features via an adversarial method, and many follow-up studies have continued in this line of research. Unlike classification and segmentation tasks classifying an image and each pixel as one category, object detection is a task of classifying the categories and regressing the bounding box of each foreground object. Focusing on this difference, many studies further align local features [32] or instance-level features corresponding to the foreground rather than the background [14, 38].
While one-stage detectors such as FCOS [36] and YOLO [28] are more advantageous for real-world environments because of its efficient structures and high inference speed, most DAOD studies [5, 32, 15, 9, 2, 37, 44] have been conducted on two-stage detectors, such as Faster R-CNN [29]. They use proposals generated by Region Proposal Network (RPN) to obtain instance-level features corresponding to the objects, making it difficult to extend straightforwardly to one-stage detectors that do not rely on RPN. Recently, several DAOD methods specialized in one-stage detector have been proposed [14, 25]. They prevent negative transfer that can occur when a feature is indiscriminately aligned by focusing on a foreground object or further aligning a feature according to the category of the object. However, for FCOS, an one-stage detector that estimates offsets from each point of the feature map to the four sides of a bounding box, the features differ in distribution not only by categories but also by offsets. Accordingly, existing feature alignment may not be sufficient to prevent negative transfer.



Fig. 1 shows the TSNE of features corresponding to foreground objects obtained from the backbone of FCOS trained on the Cityscape dataset [8] consisting of 8 classes. In Fig. 1(a), different colors refer to different classes. Since instances of Car (orange) and Person (blue) are dominant, the difference in feature distribution between the Car and the Person is clearly visible. This phenomenon fits well with the intention of [3, 37, 45, 40, 46] which align the feature distribution of the source and the target domain in a class-wise manner. Fig. 1(b) and 1(c) show the feature distribution in another perspective, the distance to the boundary of the GT bounding box. In Fig. 1(b), color codes are used to measure the offset, the distance from the feature point to the top side of the bounding box, in the log scale: the redder, the larger the offset is, while the bluer, the smaller. It shows that the distribution of the backbone features varies markedly with offsets. Comparing Fig. 1(a) and 1(b), even features in the same category have varying distribution depending on their offset. Since object detection requires bounding box regression as well as classification, especially in case of FCOS which predicts the offsets of (left, top, right, bottom) to the four sides of bounding boxes, the backbone features are not only clustered by categories but also distributed according to the offsets. Paying attention to this analysis, we conditionally align features of the source and the target domains according to their offsets.
Therefore, in this paper, we propose an Offset-Aware Domain Adaptive object detection method (OADA) that aligns the features of the source and the target domain conditional to the offset values to suppress the negative transfer in an anchor-free one-stage detector such as FCOS. Specifically, to align instance-level features and obtain reliable offset values, we use label information for the source domain and classification confidence for the target domain. And then, we convert continuous offsets into categorical probability vectors and get offset-aware features by outer-producting that probability vectors and backbone features. We prevent negative transfer that may occur while aligning the features to have the same marginal distribution by making the offset-aware features domain-invariant using a domain discriminator. Essentially, this is equivalent to intentionally forming a discriminator embedding space that is roughly partitioned by the offset. As a result, we can efficiently align features with a single strong discriminator, opening up new possibilities for offset-aware feature alignment in a very simple yet effective manner. Our contributions can be summarized as follows:
-
•
We present a domain adaptation method which is specialized for anchor-free one-stage detector by analyzing the characteristics of it.
-
•
We prevent negative transfer when aligning instance-level features in domain adaptive object detection by making domain-invariant offset-aware features in a highly efficient manner.
-
•
We find that our proposed method enhances both discriminability and transferability by analyzing through singular value decomposition.
-
•
We show the effectiveness of our proposed method (OADA) through extensive experiments on three widely used domain adaptation benchmarks, Cityscapes Foggy Cityscapes and Sim10k, KITTI Cityscapes and it achieves state-of-the-art performance in all benchmarks.
2 Related Works
2.1 Object Detection
Deep-learning-based object detection can be categorized into anchor-based and anchor-free methods. Anchor-based detectors define various sizes and ratios of anchors in advance and utilize them to match the output of the detector with the ground-truth. On the other hand, anchor-free detectors do not utilize any anchors but rather directly localize objects employing fully convolutional layers. Moreover, depending on whether region proposal network (RPN) is used or not, object detectors can also be classified into two-stage and one-stage detectors. Faster R-CNN [29] is a representative anchor-based two-stage detector while SSD [22] and YOLO [28] are anchor-based one-stage detectors. There are some renowned anchor-free one-stage detectors as well. Cornernet [20] and Centernet [10] localize objects by predicting the keypoints or the center of an object while FCOS [36] directly computes the offset from each location on the feature map to the ground-truth bounding box. Most works of DAOD have been conducted on Faster R-CNN, a two-stage detector and relatively few works have been done using an anchor-free one-stage detector. There are several works [3, 30, 18] that have been conducted on SSD, a representative one-stage anchor-based detector and only [14, 25] carried out domain adaptation using FCOS, an anchor-free one-stage detector. Our work focuses on boosting the domain adaptation performance on FCOS [36] leveraging its anchor-free architecture and fast speed.
2.2 UDA for Object Detection
There are three main approaches of UDA for object detection tasks: adversarial alignment, image translation, and self-training. Image-translation-based methods translate the source domain images into another domain using a generative model [19, 9, 34, 2, 30, 15] to adapt to the target domain. Self-training-based methods [31, 17, 9, 18, 25] generate pseudo-labels for the target domain images with the model pre-trained on the source domain and re-train the model with the pseudo labels. For adversarial alignment methods, [5] is a seminal work that aligns the feature distribution of the source and the target domain using a domain discriminator based on the Faster R-CNN [29]. Since then, there have been studies to align feature distribution at multiple levels [32, 13], studies focusing on the importance of local features in detection, and studies to align instance-level features that may correspond to objects [39, 44, 14]. Recently, there have been attempts [3, 37, 45, 40, 46] to align the instance-level features in a class-wise manner, focusing on the fact that the distribution of instance-level features is clustered by class. Based on our observation that the feature distribution varies depending on the offset values in FCOS [36] and the detection task requires not only classification but also regression, we propose an adversarial alignment scheme with state-of-the-art performances in various experimental settings by aligning the features in an offset-aware manner.
3 Method
In this section, we describe our method shown in Fig. 2, which aligns instance-level features between the two domains in an offset-aware manner in detail. Since our method investigates domain adaptation of a representative anchor-free one-stage detector, FCOS [36], a brief introduction about it is given in Sec. 3.1.

3.1 Preliminary: FCOS


FCOS [36] is a representative one-stage detector that predicts object categories and bounding boxes densely in feature maps without a RPN. FCOS uses five levels of feature maps () produced from the backbone network following FPN [21] to detect various sizes of objects. At each location of the feature map, it predicts the corresponding object category, the centerness indicating how central the current location is to the object, and the distances from the current location to the left, top, right, and bottom of the nearest ground-truth bounding box as shown in Fig. 3. With a design that five levels of feature maps have different resolutions decreasing by a factor of , the maximum distance responsible for each feature level is set to ().
FCOS differs from conventional anchor-based or RPN-based object detectors which regress four values to correct anchors or proposals. We observe that the features are distributed according not only to object categories but also to offsets, the distances to the nearest bounding boxes, and it is more pronounced in FCOS due to its characteristics of predicting directly using the features. Focusing on this observation, our proposed method tries to align the features of the source and the target domains by conditioning the features with the offsets.
3.2 Problem Formulation
Consider the setting where we adapt the object detector to the target domain using labeled source domain data and unlabeled target domain data which share the same label space consisting of classes. When training a detector, we only have access to and , where is the input image, and and are the object categories and the bounding box coordinates of all the objects existing in . and are the numbers of samples in and .
3.3 Global Alignment
To ensure that the object detector works well on the target domain, we align the features of both the source and the target domain to have a marginally similar distribution through an adversarial aligning method using a global domain discriminator . Let and be the feature maps obtained by feeding the source domain image and the target domain image to the backbone, respectively. When the spatial size of a feature map is , is trained to classify the domain of the feature map pixel-wisely by the binary cross entropy loss as in (1). The label of the source domain is 1, while that of the target is 0.
| (1) |
Using the gradient reversal layer (GRL) proposed in [11], the backbone is adversarially trained to prevent the domain discriminator from correctly distinguishing the source and the target domains, thereby generating domain-invariant features.
3.4 Generating Conditional Features to Offset Values
In order to align features in an offset-aware manner, the features and the corresponding offsets can be concatenated and inputted to the domain discriminator. However, simply concatenating them is not enough to fully utilize the correlation between features and offset values. Inspired by [24], which considers the correlation between features and categorical predictions, our method does not simply concatenate but outer-product features and offset values. Unlike classification which uses a categorical vector, an offset value is a continuous real value. Hence, the product of the feature and the offset value only has the effect of scaling the feature. To effectively condition the feature according to the corresponding offset values, each offset value of is converted into a probability vector corresponding to bins using (2). In the equation, refers to the offset value for at the location in the feature map. To convert the offset to an -dimensional probability vector, we calculate the probability using the distance of the log of the offset value to a predefined value for the -th bin. Note that we have bins and . Assuming that the probability of belonging to the -th bin is proportional to a normal distribution with its mean and a shared variance , it becomes as follows:
| (2) |
Here, is a temperature value to make the distribution smooth, and in all of our experiments, both and are set to 0.1. In all of our main experiments, is set to 3 for each feature level, and for each bin is set to for -th level () to satisfy and because each feature level is responsible for a different object scale. Fig. 4 shows the probability of belonging to each bin when there are three bins. The obtained probability vector still maintains the relative distance relationship of the real offset value as .
However, the probability vector is uniformly initialized for all bins since the regressed offsets may not be accurate at the beginning of training. During the first warm-up iterations, we gradually increase the rate of using the probability vector as iteration () progresses utilizing the alpha-blending as follows:
| (3) |
Here, is the constant value between 0 and 1 that smoothes the probability vector , and the closer it is to 1, the more uniform becomes. We show the effects of in Sec.4.5. In all the experiments, is set to 6k, the half of the first learning rate decay point. is a vector consisting of only ones.
Using , we can obtain the features which are conditional to the offset values by outer-producting them as follows:
| (4) |
Here, is a feature vector located at location in the feature map and is the probability vector of the corresponding offset value obtained from (3). By outer-producting and , we can get a new feature, conditioned on the offsets. By flattening , the conditioned feature map with the same spatial resolution as is obtained, which is fed into the domain discriminator .
Outer product is effective in conditioning because it considers the correlation between features and offsets without loss of information, hence it enables features to have different characteristics depending on offset values. Consider a case where and for , and conditionally align to , the top offsets. Suppose that feature vector located at have a small top offset prediction, i.e. and , resulting in the probability vector via (2). Conditioned feature obtained by outer-producting and is a matrix. The first row of would be similar to the original feature , but the elements in the other rows would be almost zero. On the other hand, obtained by e.g. with a large top offset would have the original feature in the third row but have almost zero elements in another rows. Therefore, a domain discriminator is trained to classify the domain of the features in different subspaces according to the offsets. As a result, the backbone will generate features that are domain invariant conditioned on offsets to fool the discriminator.
3.5 How to get a confident offset value?

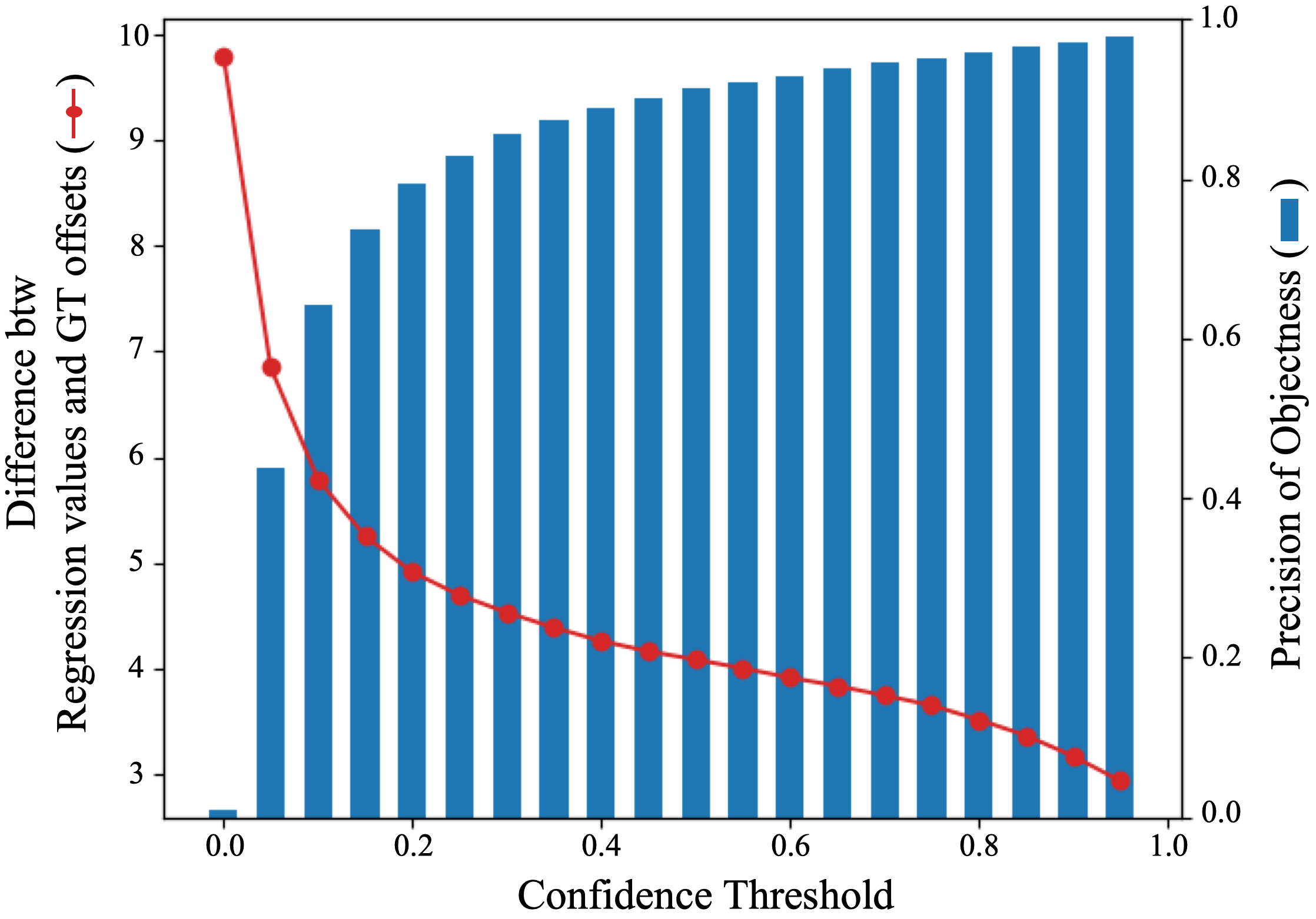
To generate a feature conditioned on the offsets, we need to know which location in the feature map corresponds to the object and the accurate offset value at that location. For the labeled source domain, we can easily obtain the ground-truth value of which location corresponds to the object in each feature map and the offsets. Since FCOS calculates the object mask corresponding to each category in the feature map and the distance from each location to the GT bounding box, we can utilize this mask and the ground-truth offset values, . On the other hand, in the unlabeled target domain, we should inevitably use predicted values. Although classification confidence is the probability of predicting the category of an object rather than a regression, by using it, we can simply and effectively select instance-level features with high objectness and obtain reliable regression values for those features. Fig. 5 is the analysis of features obtained by feeding a target domain image into the globally aligned model of Sec. 3.3. The blue bar represents the ratio corresponding to the actual objects among the features having a confidence value higher than the threshold value of the x-axis, and the red line represents the average of the difference between the regression values and the GT offsets of the features. The higher the confidence threshold, the higher the probability of the feature’s location belonging to an actual object, and the closer the regression value is to the GT offset value. In , which is the category classification probability at the -th location of the feature map, (the maximum probability among all classes) can be viewed as objectness which is the probability that the location corresponds to an object. Therefore, we generate a mask where is higher than a threshold , and we weight the activated part with that max probability value as follows:
| (5) |
Finally, we align the distribution of features of the source and the target which is conditioned on the offset by minimizing the following adversarial loss:
| (6) |
Here, is the adversarial loss conditional to the offset value using the discriminator . Since the correlation between the regression values for the left and the right and between the top and the bottom are strong, conditioning is performed only for the left and the top. represents whether the domain is the source or the target. is the indicator function and is the elementwise multiplication. Through this, the instance-level features of both domains can be aligned to have the same distribution conditional to the offset.
3.6 Overall Loss
Using labeled source domain data, the backbone and heads of FCOS are trained by minimizing object detection loss consisting of object classification loss and bounding box regression loss , as in [36]:
| (7) |
In addition, we introduce in (1) to ensure that the overall features of both domains have the similar marginal distribution and in (6) to allow the instance-level features to have the same conditional distribution to offsets, as follows:
| (8) |
where and are parameters balancing the loss components.
4 Experiments
4.1 Datasets
We conduct experiments on three scenarios: adaptation to adverse weather driving (Cityscapes to Foggy Cityscapes, i.e. CS FoggyCS), adaptation from synthetic data to real data (Sim10k to Cityscapes, i.e. Sim10k CS), and adaptation to a different camera modality (KITTI to Cityscapes, i.e. KITTI CS).
-
•
Cityscapes [8] consists of clear city images under driving scenarios, summing to 2,975 and 500 images for training and validation, respectively. There are 8 categories, i.e., person, rider, car, truck, bus, train, motorcycle and bicycle.
-
•
Foggy Cityscapes [33] is a synthetic dataset that is rendered by adding fog to the Cityscapes images. We use Cityscapes as the source, and Foggy Cityscapes as the target to simulate domain shift caused by the weather condition.
-
•
Sim10k [16] consists of 10,000 synthesized city images. For the adaptation scenario from synthetic data to real data, we set Sim10k as the source domain and Cityscapes as the target domain. Only car class is considered.
-
•
KITTI [12] consisting of 7,481 images is a driving scenario dataset similar to Cityscapes, but there is a difference in camera modality. For adaptive scenarios to other camera modalities, we use KITTI as the source and Cityscapes as the target. Similar to Sim10k to Cityscapes, only car category is used.
| Method | Detector | person | rider | car | truck | bus | train | mbike | bicycle | |
| Source Only | Faster-RCNN | 17.8 | 23.6 | 27.1 | 11.9 | 23.8 | 9.1 | 14.4 | 22.8 | 18.8 |
| DAFaster [5] | 25.0 | 31.0 | 40.5 | 22.1 | 35.3 | 20.2 | 20.0 | 27.1 | 27.6 | |
| Selective DA [47] | 33.5 | 38.0 | 48.5 | 26.5 | 39.0 | 23.3 | 28.0 | 33.6 | 33.8 | |
| MAF [13] | 28.2 | 39.5 | 43.9 | 23.8 | 39.9 | 33.3 | 29.2 | 33.9 | 34.0 | |
| SWDA[32] | 29.9 | 42.3 | 43.5 | 24.5 | 36.2 | 32.6 | 30.0 | 35.3 | 34.3 | |
| HTCN [2] | 33.2 | 47.5 | 47.9 | 31.6 | 47.4 | 40.9 | 32.3 | 37.1 | 39.8 | |
| UMT [9] | 34.2 | 48.8 | 51.1 | 30.8 | 51.9 | 42.5 | 33.9 | 38.2 | 41.2 | |
| MeGA-CDA [37] | 37.7 | 49.0 | 52.4 | 25.4 | 49.2 | 46.9 | 34.5 | 39.0 | 41.8 | |
| Oracle | 37.2 | 48.2 | 52.7 | 35.2 | 52.2 | 48.5 | 35.3 | 38.8 | 43.5 | |
| Source Only | FCOS | 30.2 | 27.4 | 34.2 | 6.8 | 18.0 | 2.7 | 14.4 | 29.3 | 20.4 |
| EPM [14] | 41.9 | 38.7 | 56.7 | 22.6 | 41.5 | 26.8 | 24.6 | 35.5 | 36.0 | |
| EPM∗ [14] | 44.9 | 44.4 | 60.6 | 26.5 | 45.5 | 28.9 | 30.6 | 37.5 | 39.9 | |
| SSAL [25] | 45.1 | 47.4 | 59.4 | 24.5 | 50.0 | 25.7 | 26.0 | 38.7 | 39.6 | |
| GA† | 43.2 | 40.5 | 58.2 | 28.2 | 43.6 | 24.2 | 27.1 | 35.3 | 37.5 | |
| OADA (Offset-Left) | 46.2 | 45.0 | 62.2 | 26.8 | 49.0 | 39.2 | 33.1 | 39.1 | 42.6 | |
| OADA (Offset-Top) | 45.9 | 46.3 | 61.8 | 30.0 | 48.2 | 36.0 | 34.2 | 39.0 | 42.7 | |
| OADA (Offset-Left & Top) | 47.3 | 45.6 | 62.8 | 30.7 | 48.0 | 49.4 | 34.6 | 39.5 | 44.8 | |
| OADA (Offset-Left & Top + Self-Training) | 47.8 | 46.5 | 62.9 | 32.1 | 48.5 | 50.9 | 34.3 | 39.8 | 45.4 | |
| Oracle | 49.6 | 47.5 | 67.2 | 31.3 | 52.2 | 42.1 | 32.9 | 41.7 | 45.6 |
| Sim10k | KITTI | ||
| Method | Detector | ||
| Source Only | Faster-RCNN | 34.3 | 30.2 |
| DAFaster [47] | 38.9 | 38.5 | |
| SWDA [32] | 40.1 | 37.9 | |
| MAF [13] | 41.1 | 41.0 | |
| HTCN [2] | 42.5 | - | |
| Selective DA [47] | 43.0 | 42.5 | |
| UMT [9] | 43.1 | - | |
| MeGA-CDA [37] | 44.8 | 43.0 | |
| Oracle | 69.7 | 69.7 | |
| Source Only | FCOS | 40.4 | 44.2 |
| EPM [14] | 49.0 | 45.0 | |
| EPM∗ [14] | 51.1 | 43.7 | |
| SSAL[25] | 51.8 | 45.6 | |
| GA† | 49.7 | 43.1 | |
| OADA (Offset-Left) | 55.4 | 45.6 | |
| OADA (Offset-Top) | 55.7 | 45.8 | |
| OADA (Offset-Left & Top) | 56.6 | 46.3 | |
| OADA (Offset-Left & Top + Self-Training) | 59.2 | 47.8 | |
| Oracle | 72.7 | 72.7 |
4.2 Implementation Details
We use VGG-16 [35] backbone and fully-convolutional head consisting of three branches of classification, regression and centerness following [36]. For the domain discriminators, and , fully-convolutional layers with the same structure as the head are used. We initialize the backbone with the Image-Net pretrained model and reduce the overall domain gap using only object detection loss and global alignment at the beginning of training. Then, we train the model for 20k iterations with weight decay of 1e-4, initial learning rate of 0.02 for CS FoggyCS, 0.01 for Sim10k CS and 0.005 for KITTI CS, respectively. We decay the learning rate at 12k and 18k iteration by the rate of one-tenth. During training, and are fixed as 0.01 and 0.1, respectively. We set the weight for the Gradient Reversal Layer (GRL) to 0.02 for global alignment and 0.2 for our conditional alignment. Also, we set the confidence threshold in (5) as for CS FoggyCS and for Sim10k, KITTI Cityscapes to reduce the effects of incorrect predictions. We set to 6k which is the half of the first learning rate decay point and in (3) to 0.2. Input image is resized to 800 for shorter side, and 1333 or less for longer side following [14, 25, 36].
4.3 Overall Performance
In Table 1, we compare the performance of our method (OADA) with other existing methods in CS FoggyCS setting. When EPM [14] based on FCOS is trained in the exact same setting as ours, the performance is 3.9%p higher than what was reported. Conditional alignment on the offsets to the left and the top side of the bounding box improves performance by 22.2%p and 22.3%p respectively compared to Source Only, by 5.7%p and 6.0%p compared to GA† which is only globally aligned and by 2.7%p and 2.8%p compared to EPM* that we reimplemented. Since Foggy Cityscapes has 8 categories of objects and has various aspect ratios, when conditioning is performed on both the left and the top offsets, the additional performance gain is very larger by 2.1%p or more, achieving the state-of-the-art regardless of the detector architecture. By initializing with the OADA (Offset-Left & Top) pre-trained model and training once more with self-training [23], we get a model almost similar to Oracle lagging only by 0.2%p. Detailed implementation of self-training is explained in the supplementary.
Table 2 shows the adaptation results of Sim10k and KITTI CS. In Sim10k CS, conditional alignment using left and top offsets improves mAP by 15.0%p and 15.3%p, respectively, compared to Source-Only and 4.3%p and 4.6%p over re-implemented EPM*. Likewise, in KITTI CS, our methods using left and top offsets improve the performance by 1.4%p and 1.6%p, respectively, over Source-Only and 1.9%p and 2.1%p over EPM*. In these two benchmarks, only the car class is considered, so the gain of OADA (Offset-Left & Top) is not as large as the multi-category setting, but there are still additional gain of 0.9%p and 0.5%p for Sim10k and KITTI. Our conditional aligning alone already achieves the state-of-the-art performance but greater performance can be obtained by employing the self-training as in OADA (Offset-Left & Top + Self-Training).
4.4 Analysis on Discriminability and Transferability
Chen et. al [4] argued that aligning the feature distribution through adversarial alignment increases the transferability of features, but they did not take the discriminability into account, the ability to perform tasks well. They measure the discriminability via singular value decomposition (SVD) of the target domain feature maps and measure the transferability by estimating the corresponding angle between the feature spaces of the source and the target domain. Using their proposed metrics [4, 42], we compare the discriminability and transferability of Ours (OADA) with Source Only, GA of Sec. 3.3, EPM [14] and Oracle models in CSFoggy CS. When and are feature matrix of the source and the target domain respectively, we apply SVD as follows:
| (9) |



Discriminability: Fig. 7a plots the top-20 greatest singular values of obtained from the five models. The singular values are sorted in descending order from left to right on the x-axis. These values are normalized so that the maximum singular value is 1. It can be seen that Ours (red) has a similar decreasing ratio to the Oracle model (black), while GA and EPM models have significantly larger one singular value and relatively much smaller other singular values than the largest one. This means that informative signals corresponding to small singular values are greatly compromised in GA and EPM, where the entire features (GA) or the features close to the center of an object (EPM) are being aligned. On the other hand, Ours has a more gentle decreasing ratio, which shows that it maintains discriminability compared to other adversarial alignment methods.
Transferability: Transferability between the source and the target domain is measured through the similarity of each principal component of the two feature spaces [4]. Fig. 7b shows the cosine similarity of eigenvectors corresponding to the top 20 singular values in and obtained in descending order. While SourceOnly and Oracle, which do not perform feature alignment, have low corresponding angles of principal components between and , overall correspondences increase in models that align feature spaces in an adversarial manner. Particularly, Ours shows higher similarity between the source and the target domain feature space than GA and EPM. From this observation, it can be seen that aligning the features in an offset-aware manner is effective in increasing the transferability without harming the discriminability for object detection.
4.5 Ablation Studies
| Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.1 | 0.2 | 0.5 | 1.0 | 1 | 2 | 3 | 4 | 5 | |
| OADA(Offset-Left & Top) | 42.6 | 43.4 | 44.8 | 43.3 | 42.6 | 42.4 | 44.2 | 44.8 | 44.3 | 41.4 |
in (3): Table 3 shows the effect of that smoothes used for feature conditioning. When , conditioning is done using only , which is the probability vector of an offset, without smoothing after the warm-up period. Since the softmax in (2) makes almost one-hot vector in most cases, the values of certain rows of conditioned feature are almost zero. This strongly constrains the dimension of the conditioned features. On the other hand, when , we outer-product the feature with an uniform vector without offeset-aware conditioning throughout training. In this case, the feature dimension given to the discriminator is the same, but performance is greatly degraded because there is no conditioning according to the offset. , in which relatively strongly constrained features are used in the discriminator, is most appropriate.
Number of bins: Table 3 also shows ablations results of the number of bins, . The reference value for the -th bin is set according to the size of objects for which the feature of each level is responsible. The detailed values are in the supplementary. When , there is no conditioning on offsets and only the mask is used, nevertheless it is more effective than GA and EPM. is sufficiently effective in offset conditioning, improving by 2.4%p. When the number of bins is increased excessively, the constraint on the subspace of the conditioned feature becomes too strong, resulting in performance deterioration.
Conditioning strategies: We compare various conditioning strategies in Fig. 7. When the feature and offset values are simply concatenated (Concatenate) and the feature is multiplied by offset values (Multiply), there is a very slight performance improvement of 0.1%p or performance degradation of -0.8%p compared to the case when only the unconditioned feature is used (Base). In order to compare the method of conditioning while increasing the dimension of features to the same as OADA, we also experiment with the case, Multiply&Stack, where original features, features multiplied by top (left) offsets and features multiplied by bottom (right) offsets are stacked. In this case, there is a significant performance improvement, but it is still far behind our OADA, which means that it is much more effective to convert the offset value into a probability vector and outer-product it with the feature for conditioning.
| Model | Datasets | Confidence Threshold () | |||
|---|---|---|---|---|---|
| 0.0 | 0.3 | 0.5 | 0.7 | ||
| OADA(Offset-Top) | Cityscapes Foggy Cityscapes | 37.0 | 42.7 | 41.7 | 37.3 |
| Sim10k Cityscapes | 48.5 | 53.6 | 55.7 | 53.6 | |
| KITTI Cityscapes | 43.8 | 44.8 | 45.8 | 44.0 | |
Confidence thresholds: In (5), the confidence threshold, , is used to generate a mask which activates spatial locations with high objectness and accurate regression values for the target domain. Table 4 shows ablation results for when conditioning is performed only on the top offsets. In CS Foggy CS, the performance is best when and in Sim10k, KITTI CS when . We conjecture that it is due to the difference of the domain gap between the source and the target domain in each scenario. Referring to Fig. 5(a), in the case of CS Foggy CS, when the confidence is more than 0.3, the precision is already more than 0.9 and the difference between GT and regression value is less than 5. However, in the case of Sim10k CS, the confidence must be at least 0.5 to obtain a similar level of precision and difference as shown in Fig. 5(b). This shows that must be adjusted with respect to the domain gap.
5 Conclusions
In this paper, we propose an Offset-Aware Domain Adaptive object detection method which conditionally aligns the feature distribution according to the offsets. Our method improves both discriminability and transferability by addressing negative transfer considering the modality of the feature distribution of an anchor-free one-stage detector. On various benchmarks, ours also achieves the state-of-the-art performance by significantly outperforming existing methods.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant (2021R1A2C3006659) and IITP grant (NO.2021-0-01343, Artificial Intelligence Graduate School Program - Seoul National University), both funded by the Korea government (MSIT). It was also supported by SNUAILAB.
References
- [1] Caron, M., Bojanowski, P., Joulin, A., Douze, M.: Deep clustering for unsupervised learning of visual features. In: European Conference on Computer Vision (ECCV). Springer (2018)
- [2] Chen, C., Zheng, Z., Ding, X., Huang, Y., Dou, Q.: Harmonizing transferability and discriminability for adapting object detectors (2020)
- [3] Chen, C., Zheng, Z., Huang, Y., Ding, X., Yu, Y.: I3net: Implicit instance-invariant network for adapting one-stage object detectors. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2021)
- [4] Chen, X., Wang, S., Long, M., Wang, J.: Transferability vs. discriminability: Batch spectral penalization for adversarial domain adaptation. In: Proceedings of the 36th International Conference on Machine Learning (ICML) (2019)
- [5] Chen, Y., Li, W., Sakaridis, C., Dai, D., Gool, L.V.: Domain adaptive faster r-cnn for object detection in the wild. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2018)
- [6] Chung, I., Kim, D., Kwak, N.: Maximizing cosine similarity between spatial features for unsupervised domain adaptation in semantic segmentation. In: Proceedings of the Winter Conference on Applications of Computer Vision (WACV) (2022)
- [7] Chung, I., Yoo, J., Kwak, N.: Exploiting inter-pixel correlations in unsupervised domain adaptation for semantic segmentation (2022)
- [8] Cordts, M., Omran, M., Ramos, S., Rehfeld, T., Enzweiler, M., Benenson, R., Franke, U., Roth, S., Schiele, B.: The cityscapes dataset for semantic urban scene understanding. In: Proceedings of the IEEE conference on computer vision and pattern recognition (2016)
- [9] Deng, J., Li, W., Chen, Y., Duan, L.: Unbiased mean teacher for cross-domain object detection (2021)
- [10] Duan, K., Bai, S., Xie, L., Qi, H., Huang, Q., Tian, Q.: Centernet: Keypoint triplets for object detection. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) (2019)
- [11] Ganin, Y., Lempitsky, V.: Unsupervised domain adaptation by backpropagation. In: Proceedings of the 32 nd International Conference on Machine Learning (2015)
- [12] Geiger, A., Lenz, P., Urtasun, R.: Are we ready for autonomous driving? the kitti vision benchmark suite. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2012)
- [13] He, Z., Zhang, L.: Multi-adversarial faster-rcnn for unrestricted object detection. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (2019)
- [14] Hsu, C.C., Tsai, Y.H., Lin, Y.Y., Yang, M.H.: Every pixel matters: Center-aware feature alignment for domain adaptive object detector. In: European Conference on Computer Vision (ECCV). Springer (2020)
- [15] Hsu, H.K., Yao, C.H., Tsai, Y.H., Hung, W.C., Tseng, H.Y., Singh, M., Yang, M.H.: Progressive domain adaptation for object detection. In: Proceedings of the Winter Conference on Applications of Computer Vision (WACV) (2020)
- [16] Johnson-Roberson, M., Barto, C., Mehta, R., Sridhar, S.N., Rosaen, K., Vasudevan, R.: Driving in the matrix: Can virtual worlds replace human-generated annotations for real world tasks? arXiv preprint arXiv:1610.01983 (2016)
- [17] Khodabandeh, M., Vahdat, A., Ranjbar, M., Macready, W.G.: A robust learning approach to domain adaptive object detection. In: Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) (2019)
- [18] Kim, S., Choi, J., Kim, T., Kim, C.: Self-training and adversarial background regularization for unsupervised domain adaptive one-stage object detection (2019)
- [19] Kim, T., Jeong, M., Kim, S., Choi, S., Kim, C.: Diversify and match: A domain adaptive representation learning paradigm for object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019)
- [20] Law, H., Deng, J.: Cornernet: Detecting objects as paired keypoints. In: European Conference on Computer Vision (ECCV) (2018)
- [21] Lin, T.Y., Dollár, P., Girshick, R., He, K., Hariharan, B., Belongie, S.: Feature pyramid networks for object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2017)
- [22] Liu, W., Anguelov, D., Erhan, D., Szegedy, C., Reed, S., Fu, C.Y., Berg, A.C.: Ssd: Single shot multibox detector. In: European Conference on Computer Vision (ECCV) (2016)
- [23] Liu, Y.C., Ma, C.Y., He, Z., Kuo, C.W., Chen, K., Zhang, P., Wu, B., Kira, Z., Vajda, P.: Unbiased teacher for semi-supervised object detection. In: Proceedings of the International Conference on Learning Representations (ICLR) (2021)
- [24] Long, M., Cao, Z., Wang, J., Jordan, M.I.: Conditional adversarial domain adaptation (2018)
- [25] Munir, M.A., Khan, M.H., Sarfraz, M.S., Ali, M.: Synergizing between self-training and adversarial learning for domain adaptive object detection. In: Conference on Neural Information Processing Systems (NIPS) (2021)
- [26] Na, J., Jung, H., Chang, H.J., Hwang, W.: Fixbi: Bridging domain spaces for unsupervised domain adaptation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2021)
- [27] Pan, F., Shin, I., Rameau, F., Lee, Seokju annd Kweon, I.S.: Unsupervised intra-domain adaptation for semantic segmentation through self-supervision. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [28] Redmon, J., Divvala, S., Girshick, R., Farhadi, A.: You only look once: Unified, real-time object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2016)
- [29] Ren, S., He, K., Girshick, R., Sun, J.: Faster r-cnn: Towards real-time object detection with region proposal networks (2016)
- [30] Rodriguez, A.L., Mikolajczyk, K.: Domain adaptation for object detection via style consistency. In: Proceedings of the British Machine Vision Conference (BMVC) (2019)
- [31] RoyChowdhury, A., Chakrabarty, P., Singh, A., Jin, S., Jiang, H., Cao, L., Learned-Miller, E.: Automatic adaptation of object detectors to new domains using self-training. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019)
- [32] Saito, K., Ushiku, Y., Harada, T., Saenko, K.: Strong-weak distribution alignment for adaptive object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (2019)
- [33] Sakaridis, C., Dai, D., Van Gool, L.: Semantic foggy scene understanding with synthetic data. International Journal of Computer Vision (IJCV) (2018)
- [34] Shan, Y., Lu, W.F., Chew, C.M.: Pixel and feature level based domain adaption for object detection in autonomous driving (2018)
- [35] Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition. In: Proceedings of the International Conference on Learning Representations (ICLR) (2015)
- [36] Tian, Z., Shen, C., Chen, H., He, T.: Fcos: Fully convolutional one-stage object detection. In: Proceedings of the IEEE/CVF international conference on computer vision (2019)
- [37] VS, V., Gupta, V., Oza, P., Sindagi, V.A., Patel, V.M.: Mega-cda: Memory guided attention for category-aware unsupervised domain adaptive object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (2021)
- [38] Xu, C.D., Zhao, X.R., Jin, X., Wei, X.S.: Exploring categorical regularization for domain adaptive object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [39] Xu, C.D., Zhao, X.R., Jin, X., Wei, X.S.: Exploring categorical regularization for domain adaptive object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [40] Xu, M., Wang, H., Ni, B., Tian, Q., Zhang, W.: Cross-domain detection via graph-induced prototype alignment. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [41] Xu, M., Zhang, J., Ni, B., Li, T., Wang, C., Tian, Q., Zhang, W.: Adversarial domain adaptation with domain mixup. In: Thirty-Fourth AAAI Conference on Artificial Intelligence (AAAI) (2020)
- [42] Yang, J., Zou, H., Zhou, Y., Zeng, Z., Xie, L.: Mind the discriminability: Asymmetric adversarial domain adaptation. In: European Conference on Computer Vision (ECCV). Springer (2020)
- [43] Yang, Y., Soatto, S.: Fda: Fourier domain adaptation for semantic segmentation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [44] Zhao, Z., Guo, Y., Shen, H., Ye, J.: Adaptive object detection with dual multi-label prediction (2020)
- [45] Zhao, Z., Guo, Y., Shen, H., Ye, J.: Adaptive object detection with dual multi-label prediction. In: European Conference on Computer Vision (ECCV). Springer (2020)
- [46] Zheng, Y., Huang, D., Liu, S., Wang, Y.: Cross-domain object detection through coarse-to-fine feature adaptation. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2020)
- [47] Zhu, X., Pang, J., Yang, C., Shi, J., Lin, D.: Adapting object detectors via selective cross-domain alignment. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019)