Unruh-DeWitt Detector Differentiation of Black Holes and Exotic Compact Objects

The discovery of gravitational waves from compact binary mergers have inspired many recent studies on exotic compact objects (ECOs), whose defining feature is their compactness: their radius is very close to that of a black hole with the same mass whilst lacking an event horizon. Explicit examples of such compact horizonless objects include gravastars Mazur:2001fv , boson stars Schunck:2003kk , wormholes, and 2-2 holes Holdom:2016nek . While some investigations are concerned with the consistency of semi-classical physics near horizons Baccetti:2018otf ; Terno:2020tsq , most studies are concerned with finding distinctive signatures from postmerger gravitational wave echoes Abedi:2016hgu ; Mark:2017dnq ; Conklin:2017lwb ; Cardoso:2019rvt ; Holdom:2019bdv , in which a wave that falls inside the gravitational potential barrier reflects off the ECO boundary and returns to the barrier after some time delay $t_{d}$.

In this paper, we study the response of an Unruh-DeWitt (UDW) detector unruh ; deWitt in this context. Assuming no angular momentum exchange, the light-matter interaction is well described as a local interaction between a scalar quantum field $\phi(x)$ and a local detector comprising two states: $\left|0\right\rangle$, with vanishing state energy, and $\left|\Omega\right\rangle$ of energy $\Omega$, where $\Omega$ may be a positive or negative real number Funai:2018wqq . If $\Omega>0$ then $\left|0\right\rangle$ is the ground state. Known as a UDW detector, the interaction Hamiltonian is

where $\chi(\tau)$ is the switching function encoding the time dependence of the interaction, whose coupling constant is $\lambda$, and $\mathsf{x}(\tau)$ is the detector’s trajectory with $\tau$ its proper time. The quantity $\mu({\tau})$ is the monopole operator of the detector $\mu=e^{i\Omega\tau}\sigma^{+}+e^{-i\Omega\tau}\sigma^{-}$ with $\sigma^{+}=\left|\Omega\right\rangle\left\langle 0\right|$ and $\sigma^{-}=\left|0\right\rangle\left\langle\Omega\right|$ the respective raising and lowering operators.

Perturbing to first-order in $\lambda$, the transition probability is byd

where $\mathcal{F}(\Omega)$ is the response function

$W(\tau^{\prime},\tau^{\prime\prime})=\langle 0|\phi(\mathsf{x}(\tau^{\prime}))\phi(\mathsf{x}(\tau^{\prime\prime}))|0\rangle$ is the pull-back of the Wightman distribution on the detector’s worldline. When the switching function is a Heaviside step function whose switch-on time is taken to be in the asymptotic past, we can drop the external $\tau^{\prime}$-integral of (3) by a change of variables and obtain the transition rate byd ; Louko:2007mu

representing the number of particles detected per unit proper time.

The spacetime of a Schwarzschild black hole in $3+1$ spacetime dimensions has the metric form (in geometric units where $c=G=1$)

where $M$ is the black hole mass, with the event horizon at $r_{H}=2M$. Mode solutions of the Klein-Gordon equation for the massless scalar field $\phi$ in this background have the form

where $Y_{\ell m}$ is the spherical harmonic function. The radial function $\rho_{\omega\ell}$ satisfies

where the tortoise coordinate $r^{*}$ satisfies $dr^{*}/dr=(1-2M/r)^{-1}$. The gravitational potential is

for the scalar field perturbation of angular momentum $l$. $V(r)$ has a peak at $r_{\rm peak}$, which is close to $r=3M$. Note that we can rescale $\bar{r}=r/(2M),\,\bar{\omega}=2M\omega$ so that the dependence on $M$ in all equations is removed.

We model the ECO as an exterior Schwarzschild spacetime patched to a spherically symmetric interior metric at radius $r=r_{0}$, with $r_{0}/r_{H}-1\ll 1$, with a boundary condition at $r_{0}$ parameterized by the reflection coefficient $R^{W}$. Typical quantum gravity arguments suggest that $r_{0}-r_{H}$ is related to the Planck length, as for the brick wall model tHooft:1984kcu . The space between $r_{0}$ and $r_{\rm peak}$ acts as a cavity, and has an associated time delay¹¹1LIGO data favors the time delay $t_{d}\approx 600\,M$ Holdom:2019bdv , which sets a preferred value for $r^{*}_{0}\approx-149.2$.

expressed in tortoise coordinates. An ECO boundary closer to the would-be horizon (i.e., smaller $r^{*}_{0}$) maps to a larger time delay $t_{d}$. The tortoise coordinate can be chosen such that $r^{*}_{\rm peak}\approx 0$.

In this section, we review the formalism for the calculation of the detector’s response rate in the black hole context Hodgkinson:2014iua , which we will then extend to the ECO scenario.

The most distinctive feature in the comparison of an ECO to a black hole is the resonance spectrum of $T^{\text{in}}_{\omega\ell}$ (i.e., the transfer function). In Figure 1, we show the $T^{\text{in}}_{\omega\ell}$ spectrum of two benchmark models with small $(t_{d}=66.5\,M)$ and large $(t_{d}=160M)$ time delays.

The position and width of these resonances are determined from the real and imaginary parts of the complex poles of $T^{\text{in}}_{\omega\ell}$, which are affected by both the ECO boundary condition and the gravitational potential. The spacings of the resonance spikes is related to the time delay such that⁴⁴4Note that the actual $\Delta\omega$ has a small frequency dependence resulting from the finite width of the gravitational potential around $r^{*}_{\rm peak}$.

Therefore, the resonance spacing is smaller for a larger time delay (i.e., when $r_{0}$ is closer to the would-be horizon). For a zero $R^{W}$, $T^{\text{in}}_{\omega\ell}$ has no resonances at all since the boundary is perfectly absorbing, and thus is equivalent to the $T^{\text{in}}_{\omega\ell}$ of a black hole. Differing time delays in this case do not affect the result since different locations of a perfect-absorbing boundary are equivalent for the wave modes. As we will demonstrate, these resonance structures will also show up in the UDW detector’s response rate, yielding distinct structures in contrast to the black hole.

Using (32), the response rate can be calculated with the $l$ sum truncated to $l_{\rm max}$ such that the contribution with $l=l_{\rm max}+1$ is negligible. It turns out that $l_{\rm max}$ increases for a larger radial distance $R$ and a larger $|\Omega/T_{\rm loc}|$, and is insensitive to the boundary condition and time delay changes. For example, when $|\Omega/T_{\rm loc}|$ goes to 20, $l_{\rm max}\approx 5$ for $R=4M$, and $l_{\rm max}\approx 15$ for $R=15M$. We give an analytic approximation of $l_{\rm max}$ in Appendix B. To illustrate some general features, we present in Figures 2 the response rate for the previous two benchmark examples with different ($t_{d}$,$R$).

Note that the first row of Figure 2 is for the case where the static detector is inside the cavity ($R=2.5M$), in contrast to the second and third rows where the detector is placed outside ($R=4M$ and $R=15M$).

We easily see the striking resonance patterns of the response rate in the first row of Figure 2, which match those of $|T^{\text{in}}_{\omega\ell}|$ shown in Figure 1 that are independent of $R$; cases with the smaller time delay have resonances more sparse in distribution, and vice versa. Comparing to those of the second and third rows, we see as the distance gets larger, the resonances become more suppressed in size. We give a detailed analysis in the next section.

In the second and thirds rows of Figure 2, we see a general trend for the detector’s response rate to grow roughly linearly with $|\Omega/T_{\rm loc}|$. But in the second row, we see that an ECO with $R^{W}=0$ has a response rate that is relatively lower than that of the black hole, even though the boundaries of both objects are perfectly absorbing. Comparing Eq. (18) and Eq. (26), we see that this is because the ECO case has no up-mode contribution for any $R^{W}$. By comparison to the second row, the third row then shows that the extra up-mode contribution in the black hole response becomes relatively smaller for increasing $R$. In the large $R$ limit all the response rates approach the Minkowski vacuum state result, which is proportional to $-\Theta(-\Omega)\Omega$.

From Eq. (28), we see the behaviour of $\operatorname{\Phi^{\text{in}}_{\omega\ell}}$ and the resulting $\mathcal{\dot{F}_{\rm ECO}}$ is dominated by $T^{\text{in}}_{\omega\ell}$ at small $r$ and by $R^{\text{in}}_{\omega\ell}$ at large $r$ up to some complex phase factors. To see this more explicitly, we can take absolute value of $\Phi_{\omega l}^{\textrm{in}}$, obtaining

from Eq. (28), where $\theta=\arccos(\Re(R^{\text{in}}_{\omega\ell})/|R^{\text{in}}_{\omega\ell}|)$. The value of $\theta$ can also have large fluctuations at the location of the $T^{\text{in}}_{\omega\ell}$ resonances, as the benchmark model in Figure 3a shows. We see that $|\operatorname{\Phi^{\text{in}}_{\omega\ell}}|r$ goes to $|T_{\omega l}^{\textrm{in}}|(1+R^{W})$ when approaching the ECO boundary, and at large $r$ to some value between $(1-|R^{\text{in}}_{\omega\ell}|)$ and $(1+|R^{\text{in}}_{\omega\ell}|)$, as the example in Figure 3b illustrates. From Eq. (30), we see that $|R^{\text{in}}_{\omega\ell}|\leq 1$ for $R^{W}\leq 1$, but $|T^{\text{in}}_{\omega\ell}|$ can display relatively large resonance peaks. This, in conjunction with (34) and (35), partially explains why $|\operatorname{\Phi^{\text{in}}_{\omega\ell}}|r$ and the corresponding contribution in $\mathcal{\dot{F}}$ at given $l$ exhibit smaller resonances at a larger distance.

Note that Eqs. (34) and (35) give a good match to the exact result (25) for $|r^{*}-r^{*}_{\rm peak}|$ sufficiently large, that is provided $\omega^{2}$ is larger than $V(r)$, thus mapping to the parameter space of large $\omega$ and small $l$. These features can also be seen in the example shown in Fig (3)b, where the exact result of $|\operatorname{\Phi^{\text{in}}_{\omega\ell}}|r$ at $l=0$ matches the approximate form well, with resonances fluctuating between 0 and +2, while all larger $l\geq 1$ show notable deviation at small $|\Omega/T_{\rm loc}|$ $(=8\pi M\,|\omega|)$.

As Figure 1 shows, the resonance structures of $T^{\text{in}}_{\omega\ell}$ (and thus the similar structure of $R^{\text{in}}_{\omega\ell}$) shift to a larger $|\Omega/T_{\rm loc}|$ for a larger $l$. As $r$ increases, $l_{\rm max}$ also becomes large (Appendix B), so that the $l$-summed results have more dependence on large $l$ yielding a milder resonance structure at a given frequency. This also illustrates why the $\mathcal{\dot{F}}$ results in Figures 2 show milder resonances at a larger distance for a given $\Omega/T_{\rm loc}$. This further implies that we can identify a clear resonance structure at very large $R$ provided the time delay is large so that the resonances are located at small frequencies where $l_{\rm max}$ is small. For illustration, we give a benchmark example of a very large time delay $(t_{d}=600M)$ with the detector at a very large distance $R=150M$ in Figure 4. We can see that the resonances of $|T^{\text{in}}_{\omega\ell}|$ at small $l$ in Figure 4a are clearly reflected in the response rate result shown in Figure 4b, even at this large $R$.

For physical realizations of the ECO model, $|R^{W}|$ can be taken to be slightly less than one to account for a small amount of damping. Damping may be needed in the case of spinning ECOs to avoid an instability. In the case of a static 2-2-hole the damping may be explicitly calculated, and the resulting frequency dependent damping is largest for small frequencies Holdom:2020onl . For our static ECO study we shall illustrate the effect of damping by choosing a constant value $R^{W}=-0.98$. We show in Figure 5a the $T^{\text{in}}_{\omega\ell}$ function with large time delay $t_{d}=160M$, with the related response rate at small distance ($R=4M$) depicted in Figure 5b. Comparing to the $R^{W}=-1$ case shown in Figure 1b and the right figure in the second row of Figure 2, we observe that the response rate for $R^{W}=-0.98$ is close to the $R^{W}=-1$ case, except that the resonance heights of $T^{\text{in}}_{\omega\ell}$ and $\mathcal{\dot{F}_{\rm ECO}}$ are both noticeably milder than those for $R^{W}=-1$. It turns out that this feature is also present in all other examples we have examined, including the large-$R$ cases.

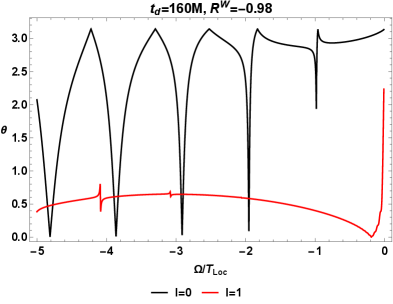
For the $R^{W}=-0.98$ examples at large $R$, the exact result of $|\Phi_{\omega l}^{\textrm{in}}|r$ can be approximated by Eq. (35). From (30), when $|R^{W}|$ is close but not equal to unity, the resonances of $T^{\text{in}}_{\omega\ell}$ can show up as dips in $|R^{\text{in}}_{\omega\ell}|$, as shown in Figure 6 for a benchmark example with a time delay $t_{d}=160M$. These dips can potentially translate to large dips in $M\dot{\mathcal{F}}$ at large $R$, considering Eq. (35).

However, our numerical results indicate that the resonance heights of $\mathcal{\dot{F}_{\rm ECO}}$ for $R^{W}=-0.98$ are noticeably milder than those for $R^{W}=-1$ even at large $R$. This relates to the fact that, despite the large dips in $|R^{\text{in}}_{\omega\ell}|$ for $R^{W}=-0.98$, it has either the same or smaller fluctuations in $\theta$ than for $R^{W}=-1$, as a comparison of Figure 7a with Figure 3a shows.

We have calculated the response rate of an Unruh-DeWitt detector placed away from a general exotic compact object (ECO) having an exterior spacetime identical to that of a Schwarzschild black hole. Due to the absence of an event horizon and the corresponding up-modes in the vacuum fields, a perfectly absorbing ECO ($R^{W}=0$) spacetime has a smaller detector response rate than that of the same-mass black hole, with a smaller ratio for a larger detector gap and a smaller distance. The cavity between an ECO’s reflective boundary ($R^{W}\neq 0$) and the gravitational potential peak determines the time delay $t_{d}$ and results in distinct resonance structures, connected to the poles of the transfer function $T^{\text{in}}_{\omega\ell}$. Thus, the observed spacing of the resonance structures tells us about the fundamental length scale at which the ECO deviates from a black hole.

Finally, we presented a detailed analysis on the large-distance behaviour of the resonance structures and the damping effect in the response rate, and showed how a large cavity size can increase the chances of observing resonance structure at large distances.

Our study provides a new alternative way to differentiate a static black hole from an ECO with a static UDW detector. The obvious next generalization is to study what happens to a spinning ECO. Likewise, it will be interesting to see how the results change if we consider detectors in motion, such as in geodesic orbits. We leave these investigations for future work.