Universal sieve-based strategies for efficient estimation
using machine learning tools

A common statistical problem consists of using available data in order to learn about a summary of the underlying data-generating mechanism. In many cases, this summary involves function-valued features of the distribution that cannot be estimated at a parametric rate under a nonparametric model — for example, a regression function or the density function of the distribution. Examples of useful summaries involving such features include average treatment effects [26], average derivatives [13], moments of the conditional mean function [28], variable importance measures [35] and treatment effect heterogeneity measures [14]. For ease of implementation and interpretation, in traditional approaches to estimation, these features have typically been restricted to have simple forms encoded by parametric or restrictive semiparametric models. However, when these models are misspecified, both the interpretation and validity of subsequent inferences can be compromised. To circumvent this difficulty, investigators have increasingly relied on machine learning (ML) methods to flexibly estimate these function-valued features.

Once estimates of the function-valued features are obtained, it is natural to consider plug-in estimators of the summary of interest. However, in general, such estimators are not root-$n$-consistent and asymptotically normal, and hence not asymptotically efficient (referred to as efficient henceforth). Lacking this property is problematic since it often forms the basis for constructing valid confidence intervals and hypothesis tests [3, 23]. When the function-valued features are estimated by ML methods, in order for the plug-in estimator to be CAN, the ML methods must not only estimate the involved function-valued features well, but must also satisfy a small-bias property with respect to the summary of interest [23, 33]. Unfortunately, because ML methods generally seek to optimize out-of-sample performance, they seldom satisfy the latter property.

The targeted minimum loss-based estimation (TMLE) framework provides a means of constructing efficient plug-in estimators [30, 33]. Given an (almost arbitrary) initial ML fit that provides a good estimate of the function-valued features involved, TMLE produces an adjusted fit such that the resulting plug-in estimator has reduced bias and is efficient. This adjustment process is referred to as targeting since a generic estimate of the function-valued features is modified to better suit the goal of estimating the summary of interest. Though TMLE provides a general template for constructing efficient estimators, its implementation requires specialized expertise, namely knowledge of the analytic expression for an influence function of the summary of interest. Influence functions arise in semiparametric efficiency theory and are key to establishing efficiency, but can be difficult to derive. Furthermore, even when an influence function is known analytically, additional expertise is needed to construct a TMLE for a given problem.

Alternative approaches for constructing efficient plug-in estimators have been proposed in the literature, including the use of undersmoothing [21], twicing kernels [23], and sieves [4, 22, 28]. These methods neither require knowing an influence function nor performing any targeting of the function-valued feature estimates. Hence, the same fits can be used to simultaneously estimate different summaries of the data-generating distribution, even if these summaries were not pre-specified when obtaining the fit. These approaches also circumvent the difficulties in obtaining an influence function. However, these methods all rely on smoothness conditions on derivatives of the functional features that may be overly stringent. In addition, undersmoothing provides limited guidance on the choice of the tuning parameter; the twicing kernel method requires the use of a higher-order kernel, which may lead to poor performance in small to moderate samples [17].

In contrast, under some conditions, sieve estimation can produce a flexible fit with the optimal out-of-sample performance while also yielding an efficient — and therefore root-$n$-consistent and asymptotically normal — plug-in estimator [28]. In this paper, we focus on extensions of this approach. In sieve estimation, we first assume that the unknown function falls in a rich function space, and construct a sequence of approximating subspaces indexed by sample size that increase in complexity as sample size grows. We require that, in the limit, the functions in the subspaces can approximate any function in the rich function space arbitrarily well. These approximating subspaces are referred to as sieves. By using an ordinary fitting procedure that optimizes the estimation of the function-valued feature within the sieve, the bias of the plug-in estimator can decrease sufficiently fast as the sieve grows in order for that estimator to be efficient. Thus sieve estimation requires no explicit targeting for the summary of interest.

The series estimator is one of the best known and most widely used sieve techniques. These sieves are taken as the span of the first finitely many terms in a basis that is chosen by the user to approximate the true function well. Common choices of the basis include polynomials, splines, trigonometric series and wavelets, among others. However, series estimators usually require strong smoothness assumptions on derivative of the unknown function in order for the flexible fit to converge at a sufficient rate to ensure the resulting plug-in estimator is efficient. As the dimension of the problem increases, the smoothness requirement may become prohibitive. Moreover, even if the smoothness assumption is satisfied, a prohibitively large sample size may be needed for some series estimators to produce a good fit. For example, if the unknown function is smooth but is a constant over a region, estimation based on a polynomial series can perform poorly in small to moderate samples.

Series estimators may also require the user to choose the number of terms in the series in such a way that results in a sufficient convergence rate. The rates at which the number of terms should grow with sample size have been thoroughly studied (e.g. [4, 22, 28]). However, these results only provide minimal guidance for applications because there is no indication on how to select the actual number of terms for a given sample size. In practice, the number of terms is the series is often chosen by CV. Upper bounds on the convergence rate of the series estimator as a function of sample size and the number of terms have been derived, and it has been shown that the optimal number of terms that minimizes the bound can also lead to an efficient plug-in estimator [28]. However, CV tends to select the number of terms that optimizes the actual convergence rate [31], which may differ from the number of terms minimizing the derived bound on the convergence rate. Even though the use of CV-tuned sieve estimators has achieved good numerical performance, to the best of our knowledge, there is no theoretical guarantee that they lead to an efficient plug-in estimator.

Two variants of traditional series estimators were proposed in [3]. These methods can use two bases to approximate the unknown function-valued features and the corresponding gradient separately, whereas in traditional series estimators, only one basis is used for both approximations. Consequently, these variants may be applied to more general cases than traditional series estimators. However, like traditional series estimators, they also suffer from the inflexibility of the pre-specified bases.

In this paper we present two approaches that can partially overcome these shortcomings.

1. 1.

   Estimating the unknown function with Highly Adaptive Lasso (HAL) [1, 29].
   If we are willing to assume the unknown functions have a finite variation norm, then they may be estimated via HAL. If the tuning parameter is chosen carefully, then we may obtain an efficient plug-in estimator. This method can help overcome the stringent smoothness assumptions on derivatives that are required by existing series estimators, as we discussed earlier.

2. 2.

   Using data-adaptive series based on an initial ML fit.
   As long as the initial ML algorithm converges to the unknown function at a sufficient rate, we show that, for certain types of summaries, it is possible to obtain an efficient plug-in estimator with a particular data-adaptive series. The smoothness assumption on the unknown function can be greatly relaxed due to the introduction of the ML algorithm into the procedure. Moreover, for summaries that are highly smooth, we show that the number of terms in the series can be selected by CV.

Although the first approach is not an example of sieve estimation, both approaches are motivated by the sieve literature and can be shown to lead to asymptotically efficient plug-in estimators using the sieve estimation theory derived in [28]. The flexible fits of the functional features from both approaches can be plugged in for a rich class of estimands.

We remark that, although we do not have to restrict ourselves to the plug-in approach in order to construct an asymptotically efficient estimator, other estimators do not overcome the shortcomings described in Section 1.2 and can have other undesirable properties. For example, the popular one-step correction approach (also called debiasing in the recent literature on high-dimensional statistics) [25] constructs efficient estimators by adding a bias reduction term to the plug-in estimator. Thus, it is not a plug-in estimator itself, and as a consequence, one-step estimators may not respect known constraints on the estimand — for example, bounds on a scalar-valued estimand (e.g., the estimand is a probability and must lie in $[0,1]$) or shape constraints on a vector-valued estimand (e.g., monotonicity constraints). This drawback is also typical for other non-plug-in estimators, such as those derived via estimating equations [32] and double machine learning [5, 6]. Additionally, as with the other procedures described above, the one-step correction approach requires the analytic expression of an influence function.

Our paper is organized as follows. We introduce the problem setup and notation in Section 2. We consider plug-in estimators based on HAL in Section 3, data-adaptive series in Section 4, and its generalized version that is applicable to more general summaries in Section 5. Section 6 concludes with a discussion. Technical proofs of lemmas and theorems (Appendix D), simulation details (Appendix E) and other additional details are provided in the Appendix.

Recently, the Highly Adaptive Lasso (HAL) was proposed as a flexible ML algorithm that only requires a mild smoothness condition on the unknown function and has a well-described implementation [1, 29]. In this subsection, we briefly review HAL. We first heuristically introduce its definition and desirable properties, and then introduce the definition and implementation more formally. For ease of presentation, for the moment, we assume that $\theta_{0}$ is real-valued.

In HAL, $\theta_{0}$ is assumed to fall in the class of càdlàg functions (right-continuous with left limits) defined on $\mathcal{X}\subseteq\mathbb{R}^{d}$ with variation norm bounded by a finite constant $M$. In this section, we denote this function class by $\Theta_{{\mathrm{v}},M}$. The variation norm of a càdlàg function $\theta$, denoted by $\|\theta\|_{{\mathrm{v}}}$, characterizes the total variability of $\theta$ as its argument ranges over the domain, so $\|\cdot\|_{{\mathrm{v}}}$ is a global smoothness measure and $\Theta_{{\mathrm{v}},M}$ is a large function class that even contains functions with discontinuities. Fig. 1 presents some examples of univariate càdlàg functions with finite variation norms for illustration. Because $\Theta_{{\mathrm{v}},M}$ is a rich class, it can be plausible that $\theta_{0}\in\Theta_{{\mathrm{v}},M}$ for some $M<\infty$. The HAL estimator of $\theta_{0}$ is then $\hat{\theta}_{n}=\hat{\theta}_{n,M}\in\operatorname*{argmin}_{\theta\in\Theta_{{\mathrm{v}},M}}n^{-1}\sum_{i=1}^{n}\ell(\theta)(V_{i})$. Under this assumption, it has been shown that $\|\hat{\theta}_{n}-\theta_{0}\|=o_{p}(n^{-1/4})$ regardless of the dimension of $X$ under additional mild conditions [29]. Thus, estimation with HAL replaces the usual smoothness requirement on derivatives of traditional series estimators by a requirement on global smoothness, namely $\theta_{0}\in\Theta_{{\mathrm{v}},M}$ for some $M$.

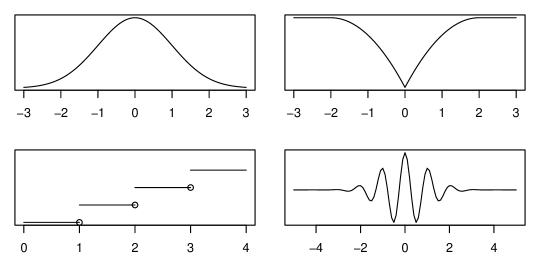
We next formally present the definition of variation norm of a càdlàg function $\theta:[x^{(\ell)},x^{(u)}]\subseteq\mathbb{R}^{d}\rightarrow\mathbb{R}$. Here, $x^{(\ell)}$ and $x^{(u)}$ are vectors in $\mathbb{R}^{d}$; with $\leq$ being entrywise, $[x^{(\ell)},x^{(u)}]:=\{x\in\mathbb{R}^{d}:x^{(\ell)}\leq x\leq x^{(u)}\}$.

For any nonempty index set $s\subseteq\{1,2,\ldots,d\}$ and any $x=(x_{1},x_{2},\ldots,x_{d})\in[x^{(\ell)},x^{(u)}]$, we define $x_{s}:=\{x_{j}:j\in s\}$ and $x_{-s}:=\{x_{j}:j\in\{1,2,\ldots,d\}\setminus s\}$ to be entries of $x$ with indices in and not in $s$ respectively. We defined the $s$-section of $\theta$ as $\theta_{s}:=\theta(x_{1}\mathbbm{1}(1\in s),x_{2}\mathbbm{1}(2\in s),\ldots,x_{d}\mathbbm{1}(d\in s))$. We can subsequently obtain the following representation of $\theta$ at any $x\in[x^{(\ell)},x^{(u)}]$ in terms of sums and integrals of the variation of $s$-sections of $\theta$ [10]:

$$\theta(x)=\theta(x^{(\ell)})+\sum_{s\in\{1,\ldots,d\},s\neq\emptyset}\int_{(x^{(\ell)},x]}\theta_{s}(d\tilde{x}).$$

The variation norm is then subsequently defined as

$$\|\theta\|_{\mathrm{v}}:=|\theta(x^{(\ell)})|+\sum_{s\in\{1,\ldots,d\},s\neq\emptyset}\int_{(x^{(\ell)},x^{(u)}]}|\theta_{s}(d\tilde{x})|.$$

We refer to [1] and [29] for more details on variation norm. Notably, this notion of variation norm coincides with that of Hardy and Krause [24].

We finally briefly introduce the algorithm to compute a HAL estimator. It can be shown that an empirical risk minimizer in $\Theta_{{\mathrm{v}},M}$ is a step function that only jumps at sample points, namely

$$x\mapsto\beta_{0}+\sum_{s\subseteq\{1,\ldots,d\},s\neq\emptyset}\sum_{j=1}^{n}\mathbbm{1}(X_{j,s}\leq x_{s})\beta_{s,j}.$$

Here, $\beta_{0}$ and all $\beta_{s,j}$ are real numbers. To find an empirical risk minimizer in $\Theta_{{\mathrm{v}},M}$ in the above form, we may solve the following optimization problem:

		$\displaystyle\min_{\theta}\sum_{i=1}^{n}\ell(\theta)(V_{i})$
	subject to	$\displaystyle\theta:x\mapsto\beta_{0}+\sum_{s\subseteq\{1,\ldots,d\},s\neq\emptyset}\sum_{j=1}^{n}\mathbbm{1}(X_{j,s}\leq x_{s})\beta_{s,j}$
		$\displaystyle|\beta_{0}|+\sum_{s\subseteq\{1,\ldots,d\},s\neq\emptyset}\sum_{j=1}^{n}|\beta_{s,j}|\leq M.$

The constraint imposes an upper bound on the $\ell_{1}$ norm of a vector. Therefore, for common loss functions, we may use software for LASSO regression [Tibshirani1996]. For example, if the loss function is the squared-error loss, then we may run a LASSO linear regression to obtain a HAL estimate.

In this section, we consider plug-in estimators based on HAL. For ease of illustration, for the rest of this section, we consider scalar-valued $\Psi$, and will discuss vector-valued $\Psi$ only at the end of this subsection. We further introduce the following conditions needed to establish that the HAL-based plug-in estimator is efficient.

Condition B2 ensures that certain perturbations of $\theta_{0}$ still lie in $\Theta_{{\mathrm{v}},M}$, a crucial requirement for proving the asymptotic linearity of our proposed plug-in estimator. In addition, since $\dot{\Psi}$ may depend on components of $P_{0}$ other than $\theta_{0}$ as in Examples 2–4, Conditions B1–B2 may also impose conditions on these components.

In this section, we fix an $M$ that satisfies Condition B2. Additional technical conditions can be found in Appendix B.1. Let $\hat{\theta}_{n}=\hat{\theta}_{n,M}\in\operatorname*{argmin}_{\theta\in\Theta_{{\mathrm{v}},M}}n^{-1}\sum_{i=1}^{n}\ell(\theta)(V_{i})$ denote the HAL fit obtained using the bound $M$ in Condition B2.

We note that $\hat{\theta}_{n}$ is not a typical sieve estimator because $M$ is fixed and there is no explicit sequence of growing approximating spaces $\Theta_{n}$. Nevertheless, we may view this method as a special case of sieve estimation with degenerate sieves $\Theta_{n}=\Theta_{{\mathrm{v}},M}$ for all $n$. This allows us to utilize existing results [28] to show the asymptotic linearity and efficiency of the plug-in estimator based on $\hat{\theta}_{n}$. We next formally present this result.

We note that, for HAL to achieve the optimal convergence rate, we only need that $M\geq\|\theta_{0}\|_{{\mathrm{v}}}$ [1, 29]. The requirement of a larger $M$ imposed by Condition B2 resembles undersmoothing [21], as using a larger $M$ would result in a fit that is less smooth than that based on the CV-selected bound. The $L^{2}(P_{0})$-convergence rate of the flexible fit using the larger bound remains the same, but the leading constant may be larger. This is in contrast to traditional undersmoothing, which leads to a fit with a suboptimal rate of convergence.

Under some conditions, the following lemma provides a loose bound on $\|\dot{\Psi}\|_{{\mathrm{v}}}$ in the case that $\dot{\Psi}$ has a particular structure. Such a bound can be used to select an appropriate bound on variation norm that satisfies Condition B2.

As we discussed at the end of Section 2, such structures as $\dot{\Psi}=\dot{\psi}\circ\theta_{0}$ are common, especially if we augment $\theta_{0}$ to include other implicitly relevant components of $P_{0}$. For example, in Example 2, we may augment $\theta_{0}$ with $p_{0}$ and $p_{0}^{\prime}$; in Examples 3 and 4, we may augment $\theta_{0}$ with the propensity score function.

When $\theta_{0}$ is $\mathbb{R}^{q}$-valued, $\theta_{0}$ can often be viewed as a collection of $q$ real-valued variation-independent functions $\eta_{10},\ldots,\eta_{q0}$. In this case, we can define $\Theta_{{\mathrm{v}},M}=\{(\eta_{1},\ldots,\eta_{q}):\eta_{j}\text{ is c\`{a}dl\`{a}g},\|\eta_{j}\|_{{\mathrm{v}}}\leq M_{j},j=1,\ldots,q\}$ for a positive vector $M=(M_{1},\ldots,M_{q})$. The subsequent arguments follow analogously, where now each $\eta_{j}$ is treated as a separate function.

We remark that an undersmoothing condition such as B2 appears to be necessary for a HAL-based plug-in estimator to be efficient. We illustrate this numerically in Section 3.3. The choice of a sufficiently large bound $M$ required by Theorem 1 is by no means trivial, since this choice requires knowledge that the user may not have. Nevertheless, this result forms the basis of the data-driven method that we propose in Section 3.3 for choosing $M$. We also remark that, if we wish to plug in the same $\hat{\theta}_{n}$ based on HAL for a rich estimands, the chosen bound $M$ needs to be sufficiently large for all estimands of interest.

Another method to construct efficient plug-in estimators based on HAL has been independently developed [VanderLaan2019]. Unlike our approach based on sieve theory, in this work, the authors directly analyzed the first-order bias of the plug-in estimator using influence functions. In terms of ease of implementation, their method requires specifying a constant involved in a threshold of the empirical mean of the basis functions, which may be difficult to specify in applications. Our approach in Section 3.3 may also require specifying an unknown constant to obtain a valid upper bound on $\|\dot{\Psi}\|_{{\mathrm{v}}}$, but in some cases the constant may be set to zero, and our simulation suggests that the performance is not sensitive to the choice of the constant.

Since it is hard to prespecify a bound $M$ on the variation norm that is sufficiently large to satisfy Condition B2 but also sufficiently small to avoid overfitting for a given data set, it is desirable to select $M$ in a data-adaptive manner. A seemingly natural approach makes use of $k$-fold CV. In particular, for each candidate bound $M$, partition the data into $k$ folds of approximately equal size ($k$ is fixed and does not depend on $n$), in each fold evaluate the performance of the HAL estimator fitted on all other folds based on this candidate $M$, and use the candidate bound $M_{n}$ with the best average performance across all folds to obtain the final fit. It has been shown that $\hat{\theta}_{n,M_{n}}$ can achieve the optimal convergence rate under mild conditions [31], but $M_{n}$ appears not to satisfy Condition B2 in general. In particular, the derived bound on $\|\hat{\theta}_{n}-\theta_{0}\|$ relies on an empirical process term, namely $\sup_{\theta\in\Theta_{{\mathrm{v}},M}}|(P_{n}-P_{0})\{\ell(\theta)-\ell(\theta_{0})\}|$, and a larger $M$ implies a larger space $\Theta_{{\mathrm{v}},M}$. Therefore, the bound on $\|\hat{\theta}_{n}-\theta_{0}\|$ grows with $M$. Because $k$-fold CV seeks to optimize out-of-sample performance, $M_{n}$ generally appears to be close to $\|\theta_{0}\|_{{\mathrm{v}}}$ and not sufficiently large to obtain an efficient plug-in estimator.

To avoid this issue with the CV-selected bound, we propose a method that takes inspiration from $k$-fold CV, but modifies the bound so that it is guaranteed to yield an efficient plug-in estimator for $\Psi(\theta_{0})$. This method may require the analytic expression for $\dot{\Psi}$. In Sections 4 and 5, we present methods that do not require this knowledge.

1. 1.

   Derive an upper bound on $\|\dot{\Psi}\|_{{\mathrm{v}}}$. This bound is a non-decreasing function of the variation norms of functions that can be learned from data (e.g., using Lemma 1). In other words, find a non-decreasing function $F$ such that $\|\dot{\Psi}\|_{{\mathrm{v}}}\leq F(\|\eta_{10}\|_{{\mathrm{v}}},\ldots,\|\eta_{q0}\|_{{\mathrm{v}}})$ for unknown functions $\eta_{10},\ldots,\eta_{q0}$ that can be assumed to be càdlàg with finite variation norm and can be estimated with HAL.

2. 2.

   Estimate $\theta_{0},\eta_{10},\ldots,\eta_{q0}$ by HAL with $k$-fold CV, and denote the CV-selected bounds for these functions by $M_{n},M_{1n},\ldots,M_{qn}$.

3. 3.

   For a small $\epsilon>0$, use the bound $M_{n}+\epsilon+F(M_{1n}+\epsilon,\ldots,M_{qn}+\epsilon)$ to estimate $\theta_{0}$ with HAL and plug in the fit. We refer to this step of slightly increasing the bounds as $\epsilon$-relaxation.

It follows from Lemma 2 in the Appendix that this method would yield a sufficiently large bound with probability tending to one. In practice, it is desirable for the bound derived on $\|\dot{\Psi}\|_{{\mathrm{v}}}$ to be relatively tight to avoid choosing an overly large bound that leads to overfitting in small to moderate samples. We remark that multiplying by $1+\epsilon$ rater than adding $\epsilon$ to each argument also leads to a valid choice for the bound; that is, the bound $M_{n}(1+\epsilon)+F(M_{1n}(1+\epsilon),\ldots,M_{qn}(1+\epsilon))$ is also sufficiently large with probability tending to one. In practice, the user may increase each CV-selected bound by, for example, 5% or 10%. Although it is more natural and convenient to directly use $M_{n}+F(M_{1n},\ldots,M_{qn})$ as the bound, we have only been able to prove the result with a small $\epsilon$-relaxation. However, if the bound is loose and $F$ is continuous, we can show that $\epsilon$-relaxation is unnecessary. The formal argument can be found after Lemma 2 in the Appendix.

As for methods based on knowledge of an influence function, deriving $\dot{\Psi}$ and a bound for its variation norm requires some expertise, but in some cases this task can be straightforward. The derivation of an influence function is typically based on a fluctuation in the space of distributions, but in many cases, the relation between such fluctuations and the summary of interest is implicit and difficult to handle. In contrast, the derivation of $\dot{\Psi}$ is based on a fluctuation of $\theta_{0}$, and the summary of interest explicitly depends on $\theta_{0}$. As a consequence, it can be simpler to derive $\dot{\Psi}$ than to derive an influence function. For example, for the summary $\Psi_{\kappa}(\theta_{0})=P_{0}\theta_{0}^{\kappa}$ in Example 1, we find that $\dot{\Psi}_{\kappa}=\kappa\theta_{0}^{\kappa-1}$ by straightforward calculation, whereas the influence function given in Theorem 1 is more difficult to directly derive analytically.

We illustrate the fact that $M_{n}$ may not be sufficiently large and show that our proposed method resolves this issue via a simulation study in which $\theta_{0}:x\mapsto\mathbb{E}_{P_{0}}[Y|X=x]$ and $\Psi:\theta_{0}\mapsto P_{0}\theta_{0}^{2}$. We compare the performance of the plug-in estimators based on the 10-fold CV-selected bound on variation norm (M.cv), the bound derived from the analytic expression of $\dot{\Psi}$ with and without $\epsilon$-relaxation (M.gcv+ and M.gcv respectively), and a sufficiently large oracle choice satisfying Condition B2 (M.oracle). We According to Lemma 1, M.oracle is $3\|\theta_{0}\|_{{\mathrm{v}}}$ and M.gcv is 3$\times$M.cv. We also investigate the performance of 95% Wald CIs based on the influence function. For each resulting plug-in estimator, we investigate the following quantities: $n\cdot\text{MSE}$, $\sqrt{n}\cdot|\text{bias}|$ and CI coverage. More details of this simulation are provided in Appendix E. In theory, for an efficient estimator, we should find that $n\cdot\text{MSE}$ tends to a constant (the variance of the influence function $\xi^{2}:=P_{0}\text{IF}^{2}$), $\sqrt{n}\cdot|\text{bias}|$ tends to $0$, and 95% Wald CIs have approximately 95% coverage.

We report performance summaries in Fig 2 and Table 1 with this criterion, from which it appears that the plug-in estimators with M.oracle and M.gcv+ achieve efficiency, while the plug-in estimator based on M.cv does not. The desirable performance of M.oracle and M.gcv+ agrees with the available theory, whereas the poor performance of M.cv suggests that cross-validation may not yield a valid choice of variation norm in general. Interestingly, M.gcv performs similarly to M.oracle and M.gcv+. We conjecture that using an $\epsilon$-relaxation is unnecessary in this setting. In Fig 3, we can also see that M.cv tends to $\|\theta_{0}\|_{{\mathrm{v}}}$ and has a high probability of being less than M.oracle. Therefore, this simulation suggests that using a sufficiently large bound — in particular, a bound larger than the CV-selected bound — may be necessary and sufficient for the plug-in estimator to achieve efficiency.

For ease of illustration, we consider the case that $\Psi$ is scalar-valued in this section. As we will describe next, our proposed estimation procedure for function-valued features does not rely on $\Psi$ and hence can be used for a class of summaries.

Suppose that $\Theta$ is a vector space of $\mathbb{R}^{q}$-valued functions equipped with the $L^{2}(P_{0})$-inner product. Further, suppose that $\dot{\Psi}=\dot{\psi}\circ\theta_{0}$ for some function $\dot{\psi}:\mathbb{R}^{q}\rightarrow\mathbb{R}^{q}$. This holds, for example, when $\Psi:\theta\mapsto P_{0}(f\circ\theta)$ for a fixed differentiable function $f$ in Example 1. In this case, $\dot{\Psi}=f^{\prime}\circ\theta_{0}$ and hence $\dot{\psi}=f^{\prime}$. Particularly useful examples include Examples 1 and 4. For now we assume that the marginal distribution of $X$ is known so that we only need to estimate $\theta_{0}$ for this summary. We will address the more difficult case in which the marginal distribution of $X$ is unknown in Section 4.3.

Let $\theta_{n}^{0}$ be a given initial flexible ML fit of $\theta_{0}$ and consider the data-adaptive sieve-like subspaces based on $\theta_{n}^{0}$, $\Theta_{n}:=\Theta_{n,\theta_{n}^{0}}:=\text{Span}\{\phi_{1},\phi_{2},\ldots,\phi_{K}\}\circ\theta_{n}^{0}$, where $\phi_{1},\phi_{2},\ldots$ are $\mathbb{R}^{q}$-valued basis functions in a series defined on $\mathbb{R}^{q}$ and $K=K(n)$ is a deterministic number of terms in the series — we will consider selecting $K$ via CV in Section 4.4. Let $\theta_{n}^{*}=\theta_{n}^{*}(\theta_{n}^{0})\in\operatorname*{argmin}_{\theta\in\Theta_{n}}n^{-1}\sum_{i=1}^{n}\ell(\theta)(V_{i})$ denote the series estimator within this data-adaptive sieve-like subspace that minimizes the empirical risk. We propose to use $\Psi(\theta_{n}^{*})$ to estimate $\Psi(\theta_{0})$.

Following [4, 28], our proofs of the validity of our data-adaptive series approach make heavy use of projection operators. We use $\pi_{n}:=\pi_{n,\theta_{n}^{0}}$ to denote the projection operator for functions in $\Theta$ onto $\Theta_{n}=\Theta_{n,\theta_{n}^{0}}$ with respect to $\langle\cdot,\cdot\rangle$. For any function $\theta\in\Theta$, let $\Pi_{n,\theta}$ denote the operator that takes as input a function $g:\mathbb{R}^{q}\rightarrow\mathbb{R}^{q}$ for which $g\circ\theta\in L^{2}(P_{0})$ and outputs a function $\Pi_{n,\theta}(g):\mathbb{R}^{q}\rightarrow\mathbb{R}^{q}$ such that $\Pi_{n,\theta}(g)\circ\theta=\pi_{n,\theta}(g\circ\theta)$. In other words, letting $\beta_{j}$ be the quantity that depends on $g$ and $\theta$ such that $\pi_{n,\theta}(g\circ\theta)=(\sum_{j=1}^{K}\beta_{j}\phi_{j})\circ\theta$, we define $\Pi_{n,\theta}(g):=\sum_{j=1}^{K}\beta_{j}\phi_{j}$. The operator $\Pi_{n,\theta}$ may also be interpreted as follows: letting $P_{\theta}$ be the distribution of $\theta(X)$ with $V=(X,Z)\sim P_{0}$, then $\Pi_{n,\theta}$ is the projection operator of functions $\mathbb{R}^{q}\rightarrow\mathbb{R}^{q}$ with respect to the $L^{2}(P_{\theta})$-inner product. We use $\mathcal{I}$ to denote the identity function in $\mathbb{R}^{q}$.

We now present additional conditions we will require to ensure that $\Psi(\theta_{n}^{*})$ is an efficient estimator of $\Psi(\theta_{0})$.

Appendix B.2 contains further technical conditions and Appendix C discusses their plausibility. As discussed in Appendix C, Conditions C2–C4 typically imply restrictions on the growth rate of $K$: if $K$ grows too fast with $n$, then Condition C2 may be violated; if $K$ instead grows too slow, then Conditions C3 and C4 may be violated. For the generalized moment $\Psi:\theta\mapsto P_{0}(f\circ\theta)$ with a fixed known function $f$ in Example 1, Condition C4 typically also imposes a smoothness condition $f$ so that $f^{\prime}$ can be approximated by the series well. Our conditions are closely related to the conditions in Theorem 1 of [28]. Conditions C1–C3 and C6 serve as sufficient conditions for the condition on the smoothness of $\Psi$ and the convergence rate of $\theta^{*}_{n}$ in Theorem 1 of [28]. Together with Conditions C4 and C7, we can derive Lemma 4, which is similar to the first part of Condition C of [28]. The empirical process condition C8 is sufficient for Conditions A, D and the second part of C in Theorem 1 in [28].

We now present a theorem ensuring the asymptotic linearity and efficiency of the plug-in estimator based on $\theta_{n}^{*}$.

We now generalize the setting considered thus far by allowing the parameter to depend both on $\theta_{0}$ and on $P_{0}$, i.e., estimating $\Psi(\theta_{0},P_{0})$. The example given at the beginning of Section 4.1, namely that of estimating $\Psi(\theta_{0})=P_{0}(f\circ\theta_{0})$, is a special case of this more general setting. In what follows, we will make use of the following conditions:

By the functional delta method, it follows that $\Psi(\theta_{0},P_{n})=\Psi(\theta_{0},P_{0})+P_{n}\text{IF}_{0}+o_{p}(n^{-1/2})$ for a function $\text{IF}_{0}$ satisfying $P_{0}\text{IF}_{0}=0$ and $P_{0}\text{IF}_{0}^{2}<\infty$.

This condition usually holds, for example, when $\Psi(\theta_{0},P_{0})=P_{0}(f\circ\theta_{0})$, as in this case the left-hand side is equal to $(P_{n}-P_{0})(f\circ\theta_{n}^{*}-f\circ\theta_{0})$, which is $o_{p}(n^{-1/2})$ under empirical process conditions.