Universal scaling of nanoparticle deposition by colloidal droplet drying
Abstract
We present a comprehensive study of nanoparticle deposition from drying of colloidal droplets. By means of lattice Boltzmann modeling and theoretical analysis, various deposition patterns, including mountain-like, uniform and coffee ring, as well as un-/symmetrical multiring/mountain-like patterns are achieved. The ratio of nanoparticles deposited at droplet peripheries and center is proposed to quantify different patterns. Its value is controlled by the competition between the capillary flow and nanoparticle diffusion, leading to a linear dependence on an effective Péclet number, across over three orders of magnitude. Remarkably, the final deposition pattern can be predicted based on material properties only.
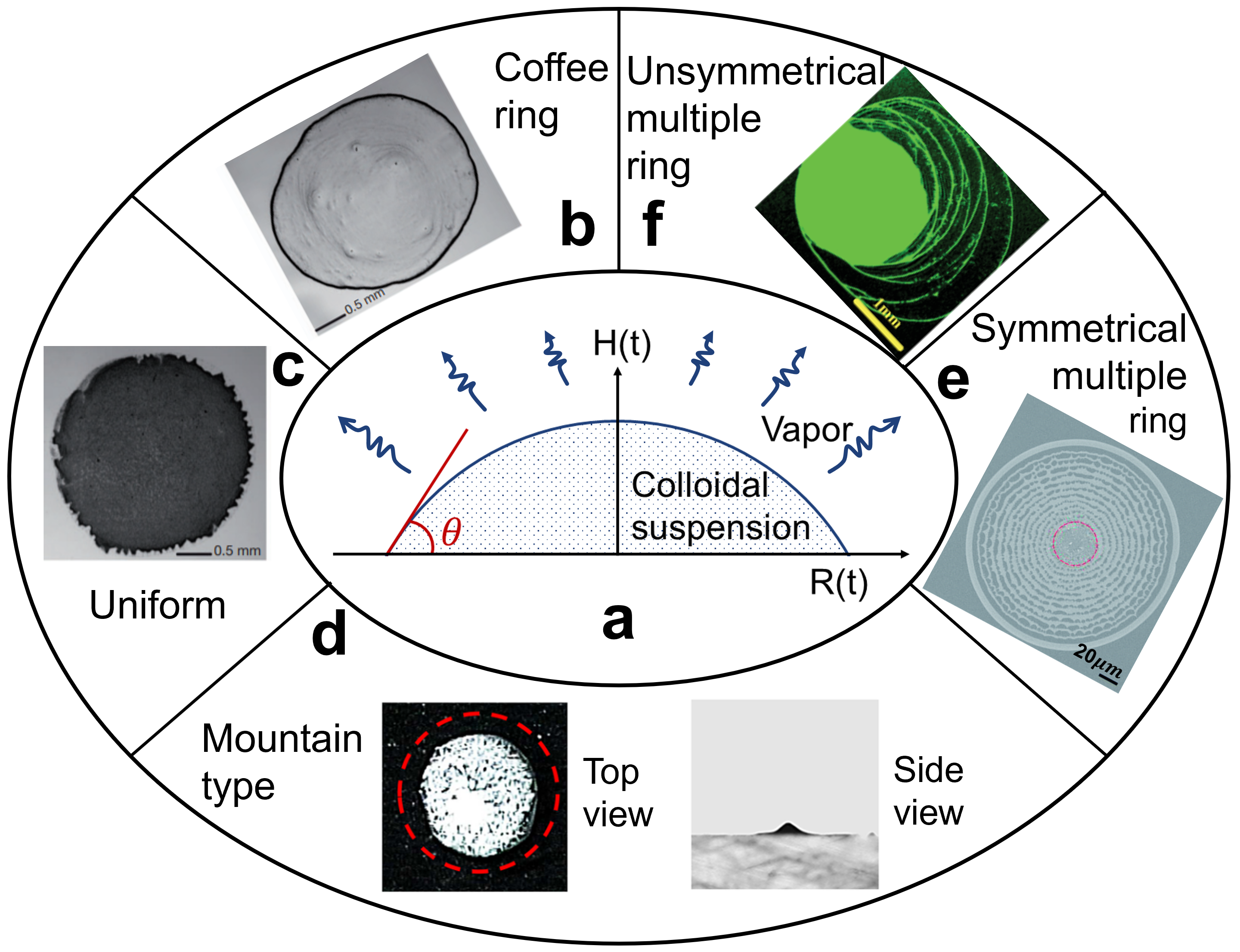
Evaporation of colloidal suspension with induced nanoparticle deposition (Fig. 1) is ubiquitously observed in nature and widely applied in the industry [1, 2]. The best-known example is the coffee ring formation (Fig. 1b), where most of particles are swept to the pinned contact line of the droplet. The physical mechanism first explained by Deegan et al. [3] is that, an internal capillary flow induced by different evaporation rates over the droplet surface drives the nanoparticles from the apex to the periphery of the droplet. Multiring patterns (Fig. 1e-f) are reported when stick-slip behavior occurs caused by sufficient contact angle hysteresis [4, 5, 6, 7]. Opposite to ring depositions, a mountain-like deposition (Fig. 1d) is observed when a droplet evaporates with a receding contact line [8, 9]. Uniform depositions (Fig. 1c) can be achieved by using non-spherical nanoparticles [10] or adjusting the pH value of the liquid [11]. Other deposition patterns, such as volcano-like and hexagonal cells type have also been reported when drying a polymer solution [12] or surfactant-laden aqueous drop [13].
To understand the underlying mechanisms of diverse depositions, Deegan et al. [14] first applied a theoretical model to predict liquid flow and particle distribution in evaporating droplets. Hu & Larson [15, 16] proposed a simple approximation of the evaporation rate and also investigated the microfluid flow based on theoretical and finite element analyses. The effects of Marangoni stress on microfluid flow, evaporation rate and deposition pattern were further elaborated in [17, 18]. Frastia et al. [19] proposed a dynamic model to predict the multiring deposition considering varying particle concentration and evaporation rate. Man & Doi [20] predicted a ring to mountain-like transition based on the modeling of fluid flow and contact line motion, which is further extended to multiple ring deposition [21]. Kaplan & Mahadevan [22] developed a multiphase model by coupling the inhomogeneous evaporation rate, droplet internal flow, and local nanoparticle concentration. They also proposed a dimensionless number to characterize the transition from ring to uniform deposition. The deposition dynamics is found to depend on many parameters, such as surface heterogeneity, contact angle, surface tension, liquid viscosity and nanoparticle diffusivity.
Despite the extensive efforts of previous studies, a comprehensive analysis of the effects of various surface/liquid properties is lacking, as well as the construction of a universal governing law quantitatively characterizing the different deposition patterns. In this Letter we accomplish precisely this task; by combining colloidal particle modeling [23, 24, 25, 26] with a lattice Boltzmann treatment [27, 28, 29, 30, 31, 32, 33] of the fluid droplet, we unveil a universal relation linking the characteristic features of the deposition pattern to a single dimensionless parameter.
The proposed double-distribution multiple-relaxation-time lattice Boltzmann model (MRT LBM) for two-phase flow and nanoparticle modeling is introduced in Supplementary Material with two validation cases, i.e., a 1D colloidal liquid drying (Fig. S1, S2) and a 2D colloidal droplet drying on flat surface with single stick-slip process (Fig. S3-S6) [10, 34]. Besides the methodological aspects, we elaborate on the physical mechanisms of various drying and deposition patterns and transition criteria among each, as summarized in Fig. 1. Fig. 1a illustrates the colloidal droplet drying on a flat surface, while Fig. 1b-f show the potential deposition patterns ranging from coffee ring, uniform, mountain type to symmetrical and unsymmetrical multiple rings.
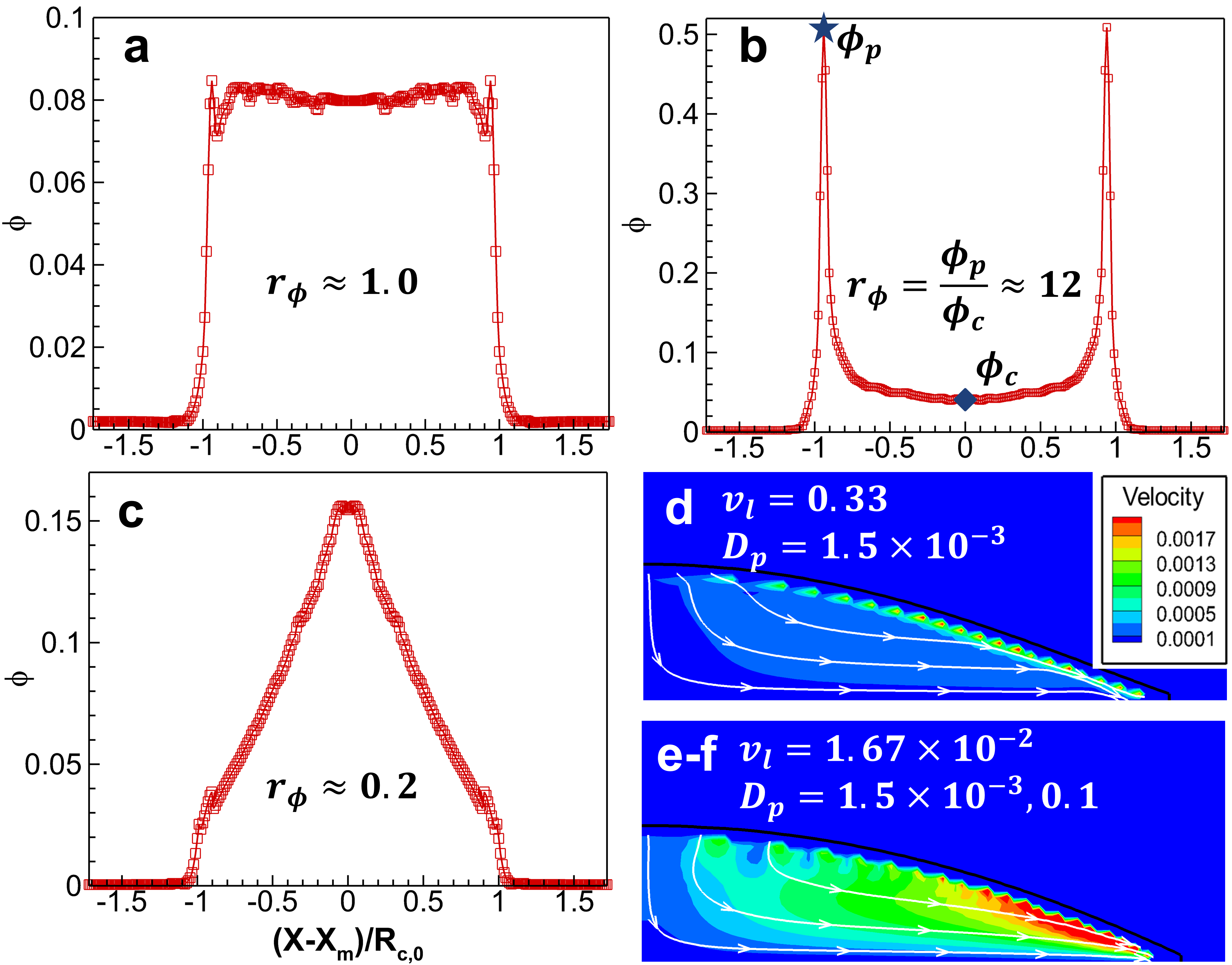
We first focus on the simple deposition patterns corresponding to Fig. 1b-d with the initial colloidal nanoparticle concentration , surface tension , the equilibrium and receding contact angles and . To quantify the various deposition, we propose to use the deposition ratio [10], where and are the depositions at the droplet periphery and center, respectively. The horizontal axis of deposition is normalized by droplet initial contact radius respect to the center location , i.e., . As shown in Fig. 2a-c, corresponds to a uniform deposition (Supplementary movie SM01), while and represent coffee ring (SM02) and mountain-like (SM03) deposition patterns, respectively. In the isothermal evaporation, two major nanoparticle transport processes take place during droplet drying, i.e., capillary transport and diffusion. The former is induced by an unequal drying rate at the droplet surface (Fig. S6) and depends on liquid properties and drying conditions, while the latter is induced by concentration differences and depends on the diffusion coefficient determined by Stokes–Einstein equation [35, 29]. The internal capillary flow for different liquid/nanoparticle parameters corresponding to deposition patterns in Fig. 2a-c is shown in Fig. 2d-f. Comparison between Fig. 2d and e indicates that strong capillary flow at low liquid viscosity leads to more deposition at the contact line. Fig. 2e and f show an identical capillary flow owing to the same fluid properties. At a higher diffusion coefficient (Fig. 2f), the diffusion transport is more significant so that nanoparticles are effectively redistributed to be uniform in the stick period before their deposition, and mountain-like deposition (Fig. 2c) finally forms due to the receding of the contact line during the slip phase, bringing nanoparticles to the center (SM03).
Further, to achieve the complex un-/concentric multiple ring depositions as shown in Fig. 1e-f, we model the drying process of a colloidal droplet with consecutive stick-processes. The local nanoparticle deposition is assumed to have negligible influence on the receding contact angle. Compared with the single stick-slip motion discussed above, the governing rules of contact angle for the multiple stick-slip processes are [20]:
| (1) |
where is the measured local contact angle at the liquid-gas interface. We first consider “case a” where the hysteresis range (, ) is uniform over the entire simulation domain. As shown in Fig. 3a, the droplet follows the stick-slip cycles and the location of two contact points and at both sides of the droplet remain symmetric during drying. Fig. 3c shows the contact radius stays unchanged when the contact angle is decreasing from to during stick phase, while it drops during the contact line slip with increasing contact angle. The pinning time gradually decreases within each stick-slip process due to decreasing droplet volume. The final deposition is shown in Fig. 3e with solid red lines (SM04).
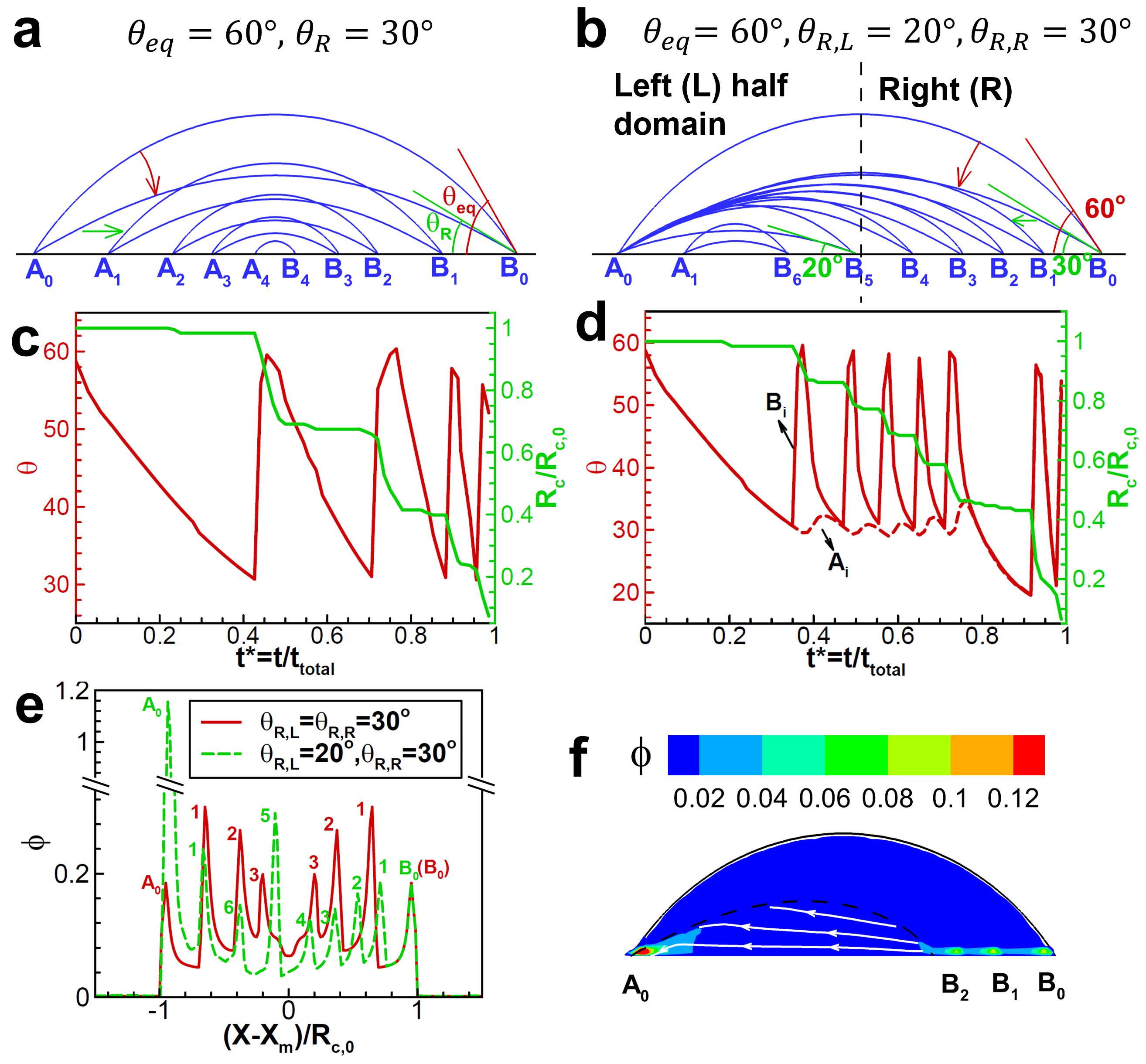
When the surface roughness is non-uniform, a variation of the contact angle hysteresis range occurs in space [5, 6]. As an example, we consider “case b” where the left- and right-half domains show the same initial contact angle but with different receding contact angles and . Fig. 3b shows the drying process is asymmetric initially. After contact point B crosses the dashed hysteresis border reaching the left-half domain (at ), the drying becomes and remains symmetrical until drying completion (SM05). As shown in Fig. 3d, the contact angle at contact point B changes repetitively between and before , while the contact angle at contact point A only fluctuates within a small range (). The reason of the latter is attributed to the fast receding of contact point B, providing insufficient time for contact point A to recover to initial contact angle . After , the contact angle curves of contact point A and B coincide indicating symmetric drying afterwards. For nanoparticles, Fig. 3e shows a very high deposition at initial contact point in case b, caused by the long duration of capillary flow towards this point before it depins, as shown in Fig. 3f. Besides, the deposition peak of case b is about 4 times of case a, indicating the unsymmetrical stick-slip processes promote the nanoparticle accumulation, compared to symmetrical ones.
Furthermore, we show that liquid/nanoparticle properties can alter the final deposition pattern obtained after consecutive stick-slip processes. Similar to Fig. 2, we change the liquid viscosity , surface tension and nanoparticle diffusion coefficient . The contact angle hysteresis conditions are set the same as in Fig. 3a-b. We use the average deposition ratio to quantify various deposition patterns, where represents the stick point. Fig. 4 shows 3 different deposition patterns ranging from the multiple ring depositions (Fig. 4a with ) to approximately-uniform (Fig. 4b with ) and mountain-like depositions (Fig. 4c with ), regardless of the contact angle hysteresis uniformity. The mechanisms of various depositions in Fig. 4 are similar to those in Fig. 2.
As we explained in Fig. 2, the two mechanisms account for the nanoparticle transport during isothermal evaporation are droplet internal capillary flow and nanoparticle diffusion, which determine the deposition ratio. In the following, we investigate and quantify the competition of the two processes considering all patterns studied above, by using the dimensionless Péclet number representing their strength ratio. is the characteristic fluid velocity due to internal capillary transport and is the initial contact radius. The estimation of is based on lubrication theory [22, 36]. We define the droplet aspect ratio , where and are the droplet height and contact radius during the drying process, respectively. Under a thin film assumption , the balance between radial pressure gradient and viscous force can be written as . However, when the droplet contact angle is high leading to a high aspect ratio (), the viscous force in vertical direction has also to be considered, i.e., . Using Laplace’s law, we obtain the pressure . The two corresponding scaling relations are and , and their combination makes the scaled characteristic velocity . Using as a simplification the initial aspect ratio , we obtain the effective Péclet number as
| (2) |
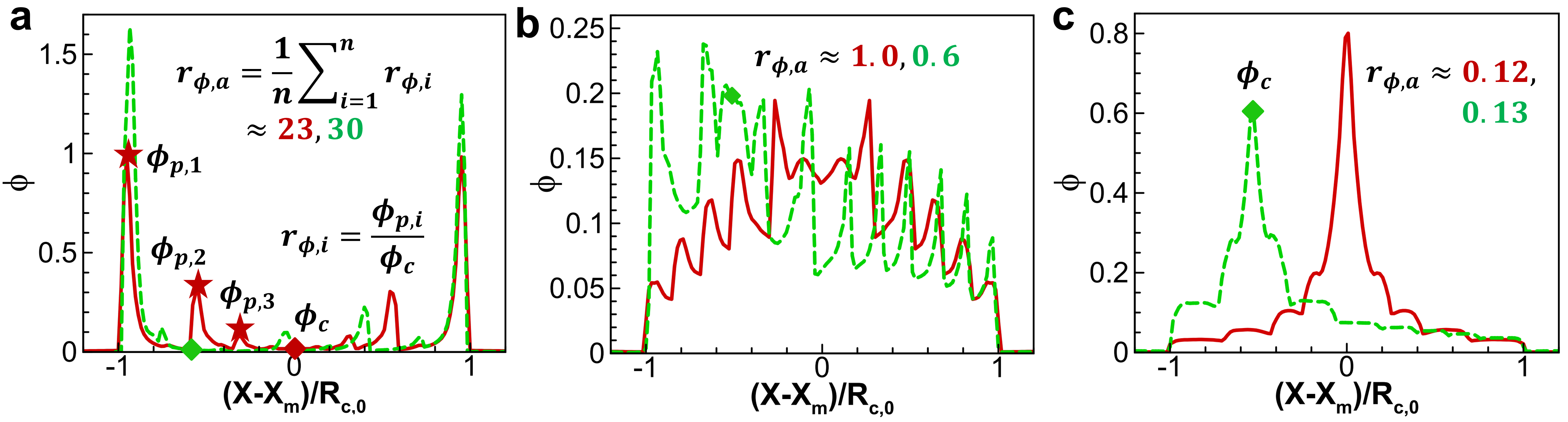
Eq.(2) shows that high liquid-vapor surface tension , high initial aspect ratio , low liquid viscosity , low nanoparticle diffusion coefficient lead to high . We performed an extensive parametric analysis spanning , , , and [corresponding to ]. The deposition curves for the different parameters are shown in Fig. S7. The coffee ring is preferably formed at high , low and small , while mountain-like depositions are observed at opposite parameter limits. Uniform deposition occurs at intermediate conditions. To investigate the relation between and the final nanoparticle deposition pattern quantitatively, we plot the deposition ratio against . Fig. 5 shows a very neat linear relation (the slope is 1 for the log-log axes):
| (3) |
within a large range of values covering over 3 orders of magnitude. The prefactor indicates that very intense capillary flow is required to transport the nanoparticles at the pinned contact point. The scaling relation is further extended to depositions after consecutive stick-slip processes as shown in Fig. 3 and Fig. 4. For each stick-slip process ( for instance), we first calculate two Péclet numbers at the beginning of stick phase () and slip phase () with Eq.(2). Then we use their subtraction () to quantify the nanoparticle motion in the stick-slip phase. To consider all stick-slip processes during drying, we simply use the average value of as the effective Peclect number, i.e., . More explanations are given in Fig. S8 in Supplementary Files. Note that unsymmetrical drying and deposition processes can be similarly treated. Extensive simulations spanning , , , and are conducted, with the modeled deposition profiles shown in Fig. S9-10. The comparison between the average deposition ratio and average effective Péclet number after symmetrical/ unsymmetrical multiple stick-slip processes is also given in Fig. 5. Note that, for expression simplicity and uniformity, we still use and instead of and in the figure. Generally, a good agreement is achieved. Some deviations are observed, mainly because droplet profiles are not exactly circular when experiencing consecutive stick-slip, affecting the estimation of pressure and further the . For all the studied cases from simple mountain-like, uniform, single ring to un-/symmetrical multiple rings, the overall coefficient of determination is up to , indicating very good reliability to estimate by Eq.(3) through the effective Péclet number in Eq.(2).
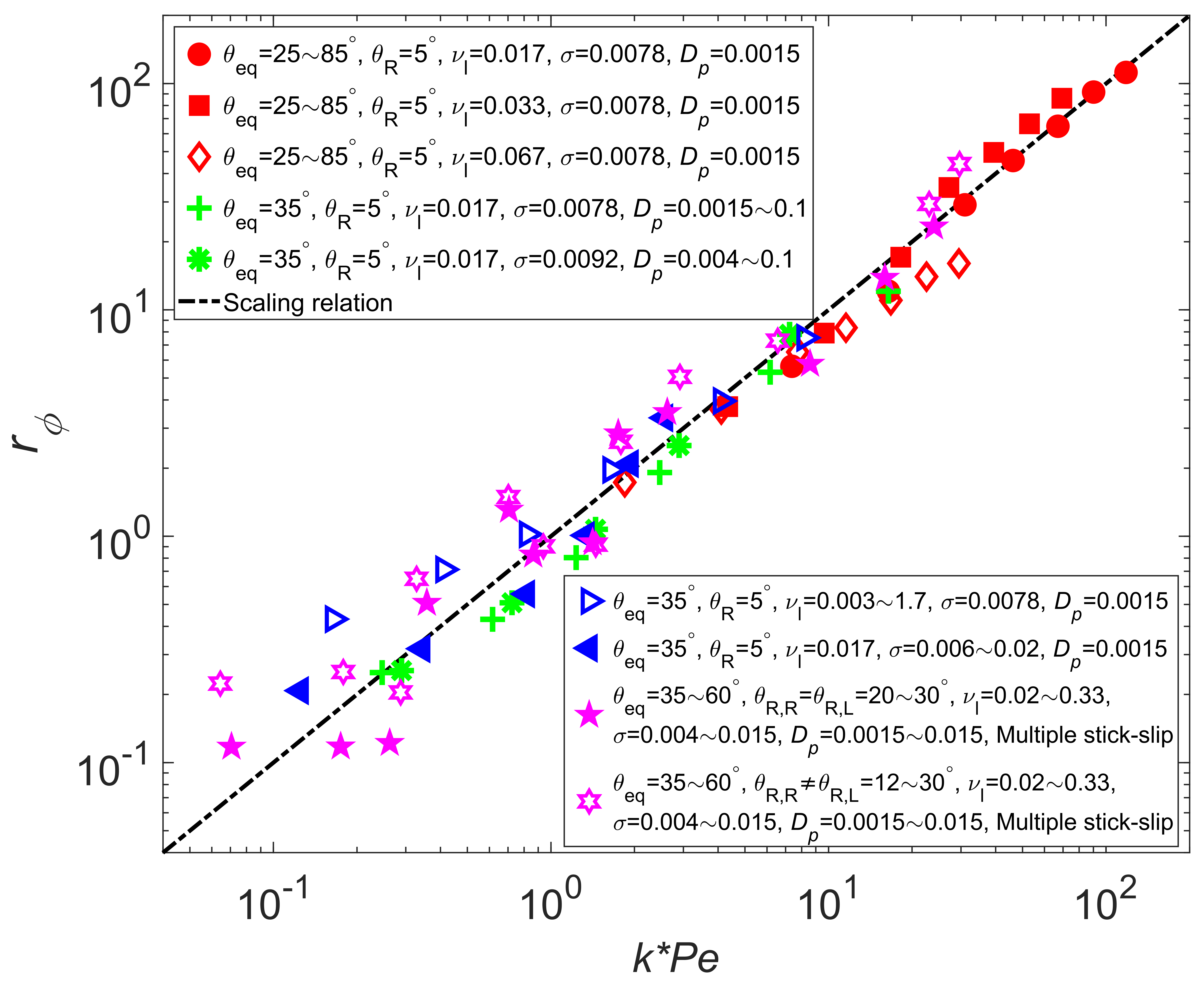
To conclude, based on extensive numerical simulations and theoretical analysis, we proposed a scaling relation for the colloidal droplet evaporation which can quantitatively describe the final nanoparticle deposition ratio for various patterns, from ring, uniform to mountain-like depositions, experiencing single or multiple symmetrical/unsymmetrical stick-slip processes. It confirms that complex nanoparticle deposition behaviors are elegantly controlled by the balance of capillary convection and diffusion of nanoparticles through an effective Péclet number. The effective Péclet number is a priori and concisely defined on the solvent/nanoparticle/substrate properties, which therefore can be potentially applied in real applications to guide nanoparticle depositions like ink-jet printing and nanomaterial fabrication, to name but a few. What remains to be studied, among others, is the Marangoni effects on nanoparticle transport caused by temperature variation or surfactant gradient.
I Acknowledgements
This work is supported by Swiss National Science Foundation (SNF, project No. 175793) and the Fundamental Research Funds for the Central Universities (G2022KY05105). Computational support is provided by Swiss National Super Computing Center (Project No. s1081). Q. K. acknowledges LANL’s LDRD Program. S. S. is funded by the European Research Council under the European Unions Horizon 2020 Framework Programme (No. FP/2014-2020)/ERC Grant Agreement No. 739964 (COPMAT).
References
- Bonn et al. [2009] D. Bonn, J. Eggers, J. Indekeu, and J. Meunier, Wetting and spreading, Reviews of Modern Physics 81, 739 (2009).
- Mampallil and Eral [2018] D. Mampallil and H. B. Eral, A review on suppression and utilization of the coffee-ring effect, Advances in Colloid and Interface Science 252, 38 (2018).
- Deegan et al. [1997] R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel, and T. A. Witten, Capillary flow as the cause of ring stains from dried liquid drops, Nature 389, 827 (1997).
- Shmuylovich et al. [2002] L. Shmuylovich, A. Q. Shen, and H. A. Stone, Surface morphology of drying latex films: Multiple ring formation, Langmuir 18, 3441 (2002).
- Maheshwari et al. [2008] S. Maheshwari, L. Zhang, Y. Zhu, and H. C. Chang, Coupling between precipitation and contact-line dynamics: Multiring stains and stick-slip motion, Physical Review Letters 100, 1 (2008).
- Moffat et al. [2009] J. R. Moffat, K. Sefiane, and M. E. Shanahan, Effect of TiO2 nanoparticles on contact line stick-slip behavior of volatile drops, Journal of Physical Chemistry B 113, 8860 (2009).
- Yang et al. [2014] X. Yang, C. Y. Li, and Y. Sun, From multi-ring to spider web and radial spoke: Competition between the receding contact line and particle deposition in a drying colloidal drop, Soft Matter 10, 4458 (2014).
- Willmer et al. [2010] D. Willmer, K. A. Baldwin, C. Kwartnik, and D. J. Fairhurst, Growth of solid conical structures during multistage drying of sessile poly(ethylene oxide) droplets, Physical Chemistry Chemical Physics 12, 3998 (2010).
- Li et al. [2014] Y. F. Li, Y. J. Sheng, and H. K. Tsao, Solute concentration-dependent contact angle hysteresis and evaporation stains, Langmuir 30, 7716 (2014).
- Yunker et al. [2011] P. J. Yunker, T. Still, M. A. Lohr, and A. G. Yodh, Suppression of the coffee-ring effect by shape-dependent capillary interactions, Nature 476, 308 (2011).
- Bhardwaj et al. [2010] R. Bhardwaj, X. Fang, P. Somasundaran, and D. Attinger, Self-assembly of colloidal particles from evaporating droplets: Role of DLVO interactions and proposition of a phase diagram, Langmuir 26, 7833 (2010), arXiv:1010.2564 .
- Kajiya et al. [2009] T. Kajiya, C. Monteux, T. Narita, F. Lequeux, and M. Doi, Contact-line recession leaving a macroscopic polymer film in the drying droplets of water-poly(N, N-dimethylacrylamide) (PDMA) solution, Langmuir 25, 6934 (2009).
- Truskett and Stebe [2003] V. N. Truskett and K. J. Stebe, Influence of surfactants on an evaporating drop: Fluorescence images and particle deposition patterns, Langmuir 19, 8271 (2003).
- Deegan et al. [2000] R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel, and T. A. Witten, Contact line deposits in an evaporating drop, Physical Review E - Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics 62, 756 (2000).
- Hu and Larson [2002] H. Hu and R. G. Larson, Evaporation of a sessile droplet on a substrate, Journal of Physical Chemistry B 106, 1334 (2002).
- Hu and Larson [2005a] H. Hu and R. G. Larson, Analysis of the microfluid flow in an evaporating sessile droplet, Langmuir 21, 3963 (2005a).
- Hu and Larson [2005b] H. Hu and R. G. Larson, Analysis of the effects of marangoni stresses on the microflow in an evaporating sessile droplet, Langmuir 21, 3972 (2005b).
- Bhardwaj et al. [2009] R. Bhardwaj, X. Fang, and D. Attinger, Pattern formation during the evaporation of a colloidal nanoliter drop: A numerical and experimental study, New Journal of Physics 11, 10.1088/1367-2630/11/7/075020 (2009).
- Frastia et al. [2011] L. Frastia, A. J. Archer, and U. Thiele, Dynamical model for the formation of patterned deposits at receding contact lines, Physical Review Letters 106, 1 (2011).
- Man and Doi [2016] X. Man and M. Doi, Ring to Mountain Transition in Deposition Pattern of Drying Droplets, Physical Review Letters 116, 066101 (2016).
- Wu et al. [2018] M. Wu, X. Man, and M. Doi, Multi-ring Deposition Pattern of Drying Droplets, Langmuir 34, 9572 (2018), arXiv:1807.09673 .
- Kaplan and Mahadevan [2015] C. N. Kaplan and L. Mahadevan, Evaporation-driven ring and film deposition from colloidal droplets, Journal of Fluid Mechanics 781, R2 (2015), arXiv:1411.4748 .
- Zhang et al. [2021] C. Zhang, H. Zhang, Y. Zhao, and C. Yang, An immersed boundary-lattice Boltzmann model for simulation of deposited particle patterns in an evaporating sessile droplet with dispersed particles, International Journal of Heat and Mass Transfer 181, 121905 (2021).
- Zhao and Yong [2018] M. Zhao and X. Yong, Nanoparticle motion on the surface of drying droplets, Physical Review Fluids 3, 1 (2018).
- Qin et al. [2019a] F. Qin, A. Mazloomi Moqaddam, L. Del Carro, Q. Kang, T. Brunschwiler, D. Derome, and J. Carmeliet, Tricoupled hybrid lattice Boltzmann model for nonisothermal drying of colloidal suspensions in micropore structures, Physical Review E 99, 10.1103/PhysRevE.99.053306 (2019a).
- Nath and Ray [2021] G. Nath and B. Ray, Manipulating the three-phase contact line of an evaporating particle-laden droplet to get desirable microstructures: A lattice Boltzmann study, Physics of Fluids 33, 083304 (2021).
- Li et al. [2016] Q. Li, K. H. Luo, Q. J. Kang, Y. L. He, Q. Chen, and Q. Liu, Lattice Boltzmann methods for multiphase flow and phase-change heat transfer, Progress in Energy and Combustion Science 52, 62 (2016), arXiv:1508.00940 .
- Huang et al. [2021] R. Huang, H. Wu, and N. A. Adams, Mesoscopic Lattice Boltzmann Modeling of the Liquid-Vapor Phase Transition, Physical Review Letters 126, 244501 (2021), arXiv:2106.01557 .
- Qin et al. [2019b] F. Qin, L. Del Carro, A. Mazloomi Moqaddam, Q. Kang, T. Brunschwiler, D. Derome, and J. Carmeliet, Study of non-isothermal liquid evaporation in synthetic micro-pore structures with hybrid lattice Boltzmann model, Journal of Fluid Mechanics 866, 33 (2019b).
- Wöhrwag et al. [2018] M. Wöhrwag, C. Semprebon, A. M. Moqaddam, I. Karlin, and H. Kusumaatmaja, Ternary Free-Energy Entropic Lattice Boltzmann Model with a High Density Ratio, Physical Review Letters 120, 234501 (2018).
- Succi [2018] S. Succi, The Lattice Boltzmann Equation: For Complex States of Flowing Matter (2018).
- Benzi et al. [2009] R. Benzi, S. Chibbaro, and S. Succi, Mesoscopic lattice Boltzmann modeling of flowing soft systems, Physical Review Letters 102, 2 (2009).
- Higuera and Succi [1989] F. J. Higuera and S. Succi, Simulating the flow around a circular cylinder with a lattice boltzmann equation, Epl 8, 517 (1989).
- Stauber et al. [2015] J. M. Stauber, S. K. Wilson, B. R. Duffy, and K. Sefiane, On the lifetimes of evaporating droplets with related initial and receding contact angles, Physics of Fluids 27, 10.1063/1.4935232 (2015).
- Costigliola et al. [2019] L. Costigliola, D. M. Heyes, T. B. Schrøder, and J. C. Dyre, Revisiting the Stokes-Einstein relation without a hydrodynamic diameter, Journal of Chemical Physics 150, 10.1063/1.5080662 (2019).
- Oron et al. [1997] A. Oron, S. H. Davis, and S. G. Bankoff, Long-scale evolution of thin liquid films, Reviews of Modern Physics 69, 931 (1997).