Unitary Scattering Protected by Pseudo-Hermiticity
Abstract
The Hermitian systems possess unitary scattering; however, the Hermiticity is unnecessary for a unitary scattering although the scattering under the influence of non-Hermiticity is mostly non-unitary. Here we prove that the unitary scattering is protected by certain type of pseudo-Hermiticity and unaffected by the degree of non-Hermiticity. The energy conservation is violated in the scattering process and recovers after scattering. The subsystem of the pseudo-Hermitian scattering center including only the connection sites is Hermitian. These findings provide fundamental insights on the unitary scattering, pseudo-Hermiticity, and energy conservation; and are promising for the light propagation, mesoscopic electron transport, and quantum interference in the non-Hermitian systems.
Pseudo-Hermiticity is important in non-Hermitian physics. The pseudo-Hermiticity ensures the spectrum of the non-Hermitian system to be entirely real or partly complex in conjugate pairs Ali02 . A non-Hermitian system is pseudo-Hermitian if its Hamiltonian under a unitary transformation equals to the Hermitian conjugation of the Hamiltonian Jones05 . The parity-time () symmetric non-Hermitian systems are the mostly investigated pseudo-Hermitian systems Bender98 ; Dorey01 ; Muga05 ; LJin09 ; Joglekar11 ; Suchkov16 ; Chong17 ; Lai21 ; Chen20 ; Lv21 ; Zi21 , which possess non-unitary dynamics even their spectra are entirely real. The state involving nonorthogonal eigenmodes exhibits non-unitary intensity oscillation as observed in the coupled optical waveguides Ganainy07 ; Makris08 ; CERuter ; nevertheless, the eigenstates are orthogonal and the time-evolution is unitary under the biorthogonal norm Ali04 ; Brody13 . Interestingly, the state only involving real-valued orthogonal eigenmodes in the pseudo-Hermitian systems exhibits an intensity-preserving dynamics LJinPRA11 . Otherwise, the intensity exponentially increases/decreases in the broken -symmetric phase Kottos10 ; Zheng10 or polynomially increases at the exceptional point where the -symmetric phase transition occurs PWang16 ; LGe18 ; Xue19 . The exceptional point in the -symmetric systems is experimentally realized in optical/acoustic cavity resonators LYang14 ; CTChanPRX16 , in the single-photon interferometric quantum simulation Xue20 , in the single nitrogen-vacancy center JDu21 and so on Ueda20 .
Non-Hermitian systems provide unprecedented opportunities in recent decades Moiseyev . The rapid developments in non-Hermitian physics greatly stimulate novel applications in optics, condensed matter physics, quantum physics, and material science Konotop16 ; Kivshar ; LFeng ; Longhi ; Ganainy ; Alu ; LYang ; YFChen ; for example, the exceptional point enhanced optical sensing Wiersig14 ; Hodaei17 ; Clerk18 ; Lai19 ; Cai20 , robust energy transfer Harris16 ; Fan17 , lasing Feng14 ; Harari18 , and many other intriguing phenomena including the coherence perfect absorption YDChong10 ; Longhi10 ; HCao11 ; HChen14 ; TKottos17 ; Jeffers19 , unidirectional reflectionless/invisibility ZLin2011 ; Regensburger12 ; LFeng2013 ; Zhu14 ; JHWu14 ; Sounas15 ; Makris20 , absorption LonghiOL15 ; Sweeney19 , amplification CLi17 ; Fleury18 , and lasing were discovered Ali09 ; Ramezani14 ; LJinPRL . These reveal the non-unitary feature and the asymmetric feature of scattering affected by the non-Hermiticity Muga17 . In addition, the conservation is an important topic in non-Hermitian physics Alexandre17 ; Xue20 ; LGe20 . The energy conservation from the unitary scattering was reported in several non-Hermitian scattering centers LJinPRA12 ; LGe12 ; Ahmed13 ; Mostafazadeh14 ; LJinPRA18 . Thus, the Hermiticity is unnecessary for a unitary scattering; however, the non-unitary scattering more commonly appears in the non-Hermitian systems because of the lack of energy conservation Muga04 ; Cannata07 ; JonesPRD07 ; ZnojilPRD08 ; SRotter13 ; Schomerus13 ; Kottos15 ; LGe15 ; LJin16 ; Pagneux17 ; ZZhao19 ; Droulias19 ; Novitsky20 ; Haque20 ; Schomerus21 ; Economou21 ; Krasnok19 . Then, what is essential for a unitary scattering and the energy conservation in non-Hermitian physics? This is a fundamental and important problem. Here we thoroughly solve this problem and unveil that the pseudo-Hermiticity plays a vital role.
In this Letter, we report that the unitary scattering in the non-Hermitian systems is protected by certain type of pseudo-Hermiticity. Under the pseudo-Hermiticity protection, the total probability of wave injection remains unity after scattering; whereas the energy conservation is violated in the scattering process as affected by the non-Hermiticity. We report that the unitary scattering and energy conservation are independent of the degree of non-Hermiticity, but strongly depend on the structure of the scattering center. We provide novel understandings of pseudo-Hermiticity from the perspective of scattering; and present fundamental insights on the unitary and non-unitary scattering. Furthermore, the consequences of symmetry protections on the scattering matrix under the time-reversal symmetry and reciprocity generalized for the non-Hermitian systems are presented.
A lattice model is schematically illustrated in Fig. 1 and characterizes the discrete systems modeled under the tight-binding approximation in contrast to the continuous models Muga19 ; Muga20 ; for example, the coupled resonators/waveguides LFeng2013 ; Schomerus14 , acoustic crystals Zhu14 ; Fleury15 ; BZhang20 , cold atoms in optical lattice Gou20 , and electronic circuits Kottos11 ; Joglekar21 . These experimental platforms are intensively used for studying the non-Hermitian Hamiltonians. In general, the scattering center has sites; and all the ports are connected to different sites of the scattering center ().
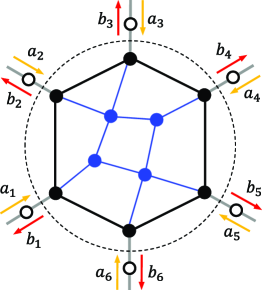
The properties of the scattering center are fully characterized by the scattering matrix . Acting the scattering matrix on the incoming wave amplitudes yields the outgoing wave amplitudes
| (1) |
where represents the incoming wave amplitudes of all the ports before scattering, and represents the outgoing wave amplitudes of all the ports after scattering. The scattering matrix element describes the output in the -th port for the wave injection in the -th port.
The wavefunction at the steady-state is the superposition of the plane waves with the opposite momenta propagating in the opposite directions. The incoming wave is and the outgoing wave is for the momentum , where the integer indexes the sites of the ports and represents the connection site of the scattering center. To reflect the properties of the scattering center , all the ports are chosen identical and uniform until the scattering center. For the wave injection in the -th port, the wavefunction in the -th port is and the wavefunction in the -th port is .
Symmetries are extremely important in physics. The pseudo-Hermitian scattering center satisfies
| (2) |
In the superscripts, is the complex conjugation operation, is the transpose operation, and is the unitary matrix defined in the real space representation of the scattering center with KawabataPRX19 ; HZhouPRB19 . The progresses on the symmetry classification have greatly advanced our knowledge on the symmetric scattering in non-Hermitian physics LJinCPL . In general case, the pseudo-Hermiticity cannot ensure the unitary scattering; however, the scattering matrix is unitary if the unitary matrix satisfies
| (3) |
where identical matrix is for the subsystem including only the connection sites and the unitary matrix is for the subsystem including only the bulk sites. For all the basis of the scattering center, the connection sites are exactly mapped to themselves under the unitary transformation . In Fig. 1, the black part is Hermitian and the blue part is pseudo-Hermitian; otherwise, the unitary scattering is not ensured.
Applying the unitary transformation to the pseudo-Hermitian scattering system, the bulk sites (the blue circles in Fig. 1) and the couplings between the bulk and connection sites (the blue lines in Fig. 1) are altered, but the subsystem including all the connection sites (the black circles and lines in Fig. 1) is unchanged. Consequently, the wavefunctions of the connection sites and all the ports are invariant under the unitary transformation . Thus, the scattering matrix for the scattering center is identical with the scattering matrix for the scattering center .
From Eq. (1), we obtain . After applying the complex conjugation operation to the wavefunctions of the scattering system, the vector indicates the incoming wave amplitudes, and the vector indicates the outgoing wave amplitudes. Thus, stands for the scattering matrix of the scattering center .
Then, the scattering matrix is also the scattering matrix of . Notably, the scattering matrix for is STProof . From the pseudo-Hermiticity of , we obtain the relation . Therefore, the scattering matrix is unitary
| (4) |
The unity element in the -th row and -th column of is for the input in the -th port. The unity diagonal elements of yield the unity total probability and energy conservation after scattering for the input in any port. However, the dynamics is non-unitary and the energy conservation is invalid as affected by the non-Hermiticity in the scattering process. Notably, the pseudo-Hermiticity-protected unitary scattering is independent of the degree of non-Hermiticity. Under the pseudo-Hermiticity protection, the unitary scattering is unaffected by the strengths of non-Hermitian couplings and the rates of gains/losses; however, these non-Hermitian elements affect the reflections, the transmissions, and the dynamics in the scattering process.
The pseudo-Hermitian scattering centers holding unitary scattering have featured structures. denotes the subsystem that only contains the connection sites; denotes the subsystem that only contains the bulk sites; and denote the couplings between the connection sites and the bulk sites. The scattering center is
| (5) |
The pseudo-Hermiticity and the block diagonal in Eq. (3) yield
| (6) |
From , we have , ; and . Therefore, yields .
The unitary scattering requires three constrains
| (7) |
The pseudo-Hermitian scattering center may have all kinds of non-Hermitian elements including the gain/loss, the imaginary/complex coupling, the asymmetric coupling, and etc. These non-Hermitian elements may simultaneously present in the pseudo-Hermitian scattering center that possessing the unitary scattering. The constrain (i) requires that the subsystem including only the connection sites is Hermitian. The constrain (ii) requires that the subsystem including only the bulk sites is pseudo-Hermitian. The constrain (iii) is the requirement on the couplings and between the connection sites and the bulk sites. Thus, the gain and loss cannot appear at the connection sites, but can appear on the bulk sites in the balanced pairs; whereas the non-Hermitian couplings including both the imaginary/complex coupling and the asymmetric coupling cannot appear between the connection sites, but can appear among the bulk sites or as the connection couplings in and . Otherwise, the scattering is non-unitary.
The pseudo-Hermiticity-protected two-port scattering centers possess symmetric transmission and reflection for the wave injections from the opposite directions ( and ). This is obtained from the unitary scattering with SSI , where and ( and ) are the transmission and reflection coefficients for the input in the left (right) port. These explain the unitary and symmetric scattering in the two-port non-Hermitian scattering centers LGe12 ; Ahmed13 ; Mostafazadeh14 ; LJinPRA18 ; LJinPRA12 . However, the symmetric scattering is not promised in the multi-port scattering centers although the scattering is unitary. In a circulator, the wave injected in the port resonantly outgoes from the port , respectively Fleury14 . The scattering is asymmetric when considering the wave input and output in any two of the three ports.
We have rigorously proved that the unitary scattering and the energy conservation in the non-Hermitian systems are protected by certain pseudo-Hermiticity if the unitary matrix that defined the pseudo-Hermiticity satisfies Eq. (3). Furthermore, we elaborate a two-port scattering center to emphasize the importance of the scattering center configuration and a three-port scattering center to emphasize the importance of the port configuration for the unitary scattering. In the schematics, each site stands for a resonator with frequency . The ports until the scattering center are uniform at the coupling . The light propagation in the coupled resonator optical waveguides is govern by the discrete lattice model Kippenberg02 , and the dispersion relation supported by the ports is Ali09 ; Ramezani14 .
The two-port pseudo-Hermitian scattering center in Fig. 2(a) includes two resonators with balanced gain and loss ( and ) and two connection resonators ( and ). If each connection resonator is equally coupled to the gain and loss resonators, the equations of motion for the scattering center are
| (8) |
where is the wavefunction for the resonator of the scattering center and is the wavefunction for the first resonator of the port . The transmission and reflection coefficients , as functions of the input wave vector are obtained from the steady-state solution; the scattering matrix is unitary .
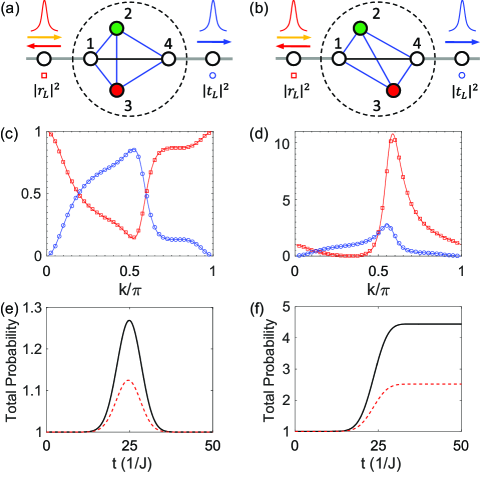
The four-site scattering center is pseudo-Hermitian with the Hamiltonian and the unitary matrix
| (9) |
where and are the gain and loss; all the couplings , , , are real numbers. In the subspaces of connection sites and bulk sites, satisfies Eq. (3). Thus, the scattering matrix is unitary and symmetric. Notably, the scattering is still unitary if the real couplings and are simultaneously imaginary.
The transmission and reflection for the unitary scattering in Fig. 2(a) are depicted in Fig. 2(c). The energy conservation holds after scattering and the total transmitted and reflected wave probability is unity; however, the dynamics is non-unitary and the energy conservation is invalid in the scattering process as numerically simulated in Fig. 2(e) using a Gaussian profile initial excitation of the momentum centered at the site , where controls the width, is the normalization factor, and is the basis of port site . The scattering process begins when the wave packet reaching the scattering center and the total probability of the excitation starts to change as time because of the influence of non-Hermiticity. The velocity of the Gaussian wave packet obtained from the dispersion relation is . The scattering process ends when the wave packet leaving the scattering center and the total probability no longer changes as time. The dynamics after scattering reflects the steady-state solution. The reflected backward going wave packet indicates the reflection and the transmitted forward going wave packet indicates the transmission Kim06 .
Alternatively, if each connection resonator is unequally coupled to the gain and loss resonators as shown in Fig. 2(b), the four-site scattering center is still pseudo-Hermitian with and
| (10) |
where is the Pauli matrix. Notably, the unitary transformation is not block diagonalized in the subspaces of connection sites and bulk sites. In this situation, the scattering matrix is non-unitary although the non-Hermitian scattering center is pseudo-Hermitian. The transmission and reflection for the non-unitary scattering in Fig. 2(b) are depicted in Fig. 2(d). The scattering is non-unitary in the entire scattering process and the total probability after scattering is non-unity as demonstrated in Fig. 2(f).
The unitary scattering is still possible if the couplings between the ports and the scattering center are properly redesigned. If both two ports in Fig. 2(b) are simultaneously coupled to sites and through the first sites of the ports at the same strength , the scattering becomes unitary. The first sites of two ports effectively become the connection sites of a six-site scattering center and satisfies Eq. (3) with .
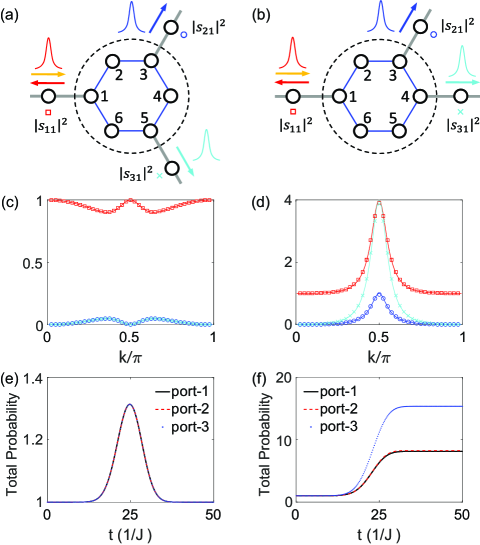
The unitary scattering is also subtle to the port configuration. We consider a multi-port pseudo-Hermitian scattering center with six sites and three ports. The Hamiltonian of the scattering center reads
| (11) |
where () is the annihilation (creation) operator for the mode of resonator and satisfies (). The resonator detuning is real. The coupling is non-Hermitian and can be realized through the gain Fleury18 ; HCWu20 . The scattering center is pseudo-Hermitian for the unitary matrix . In the couple mode theory, the equation of motion for the light field of the scattering center resonator is
| (12) |
If the three ports are respectively connected to the odd-site (or the even-site ) in Fig. 3(a), the additional term presents in the right side of the equations of motion for the sites (or ). This pseudo-Hermiticity ensures a unitary scattering . The scattering coefficients are obtained from the steady-state solution. The transmission and reflection in the three ports are depicted in Fig. 3(c). The unity total probability after scattering reflects the energy conservation as demonstrated in Fig. 3(e), where the initial excitation is that used in the two-port scattering center. Notably, additional Hermitian couplings presented among three connections sites will not affect the unitary scattering.
If the three ports are simultaneously connected to the odd-site and even-site of the scattering center; for example, the three ports are connected to the sites in Fig. 3(b). The scattering is non-unitary. The transmission and reflection in the three ports are depicted in Fig. 3(d), the non-unity total probability indicates the non-unitary scattering and the absence of energy conservation as observed in Fig. 3(f). The scattering coefficients diverge and lasing occurs at the spectral singularity and for all the six sites Ali09 ; LJinPRL .
All the three constrains in Eq. (7) are satisfied for the unitary scattering, but at least one of the three constrains is not satisfied for the non-unitary scattering in the exemplified pseudo-Hermitian scattering centers. Nevertheless, any pseudo-Hermitian scattering center can exhibit a unitary scattering if the couplings between the scattering center and the ports are properly redesigned according to its structure information, which is completely encoded in the unitary operator . In this situation, the scattering center is effectively enlarged to include the first sites of the ports. The original pseudo-Hermitian scattering center plays the role as the subsystem of the enlarged scattering center . The couplings between the scattering center and the first sites of the ports should be reconstructed to satisfy , where the unitary operator defines the pseudo-Hermiticity of the original scattering center with . The unitary operator defines the pseudo-Hermiticity of the enlarged scattering center
| (13) |
After the reconstruction, the effective scattering center has the unitary scattering and ensures the energy conservation.
In addition, the operations of Hermitian conjugation (), complex conjugation (), transpose (), and the unit element constitute a (also called ) Abelian group. Three operations define the pseudo-Hermiticity , the time-reversal symmetry , and the reciprocity for the non-Hermitian systems, respectively. The pseudo-Hermiticity ensures , the time-reversal symmetry ensures , and the reciprocity ensures if the unitary operator satisfies Eq. (3).
In conclusion, the unitary scattering and the energy conservation are ensured by certain pseudo-Hermiticity, where the scattering center structure plays an important role. The pseudo-Hermiticity protected unitary scattering is independent of the degree of non-Hermiticity. The energy conservation holds after scattering although it is invalid in the scattering process under the influence of the non-Hermiticity. We also demonstrate how to create a unitary scattering in the pseudo-Hermitian system with a non-unitary scattering through reconstructing the connection couplings. We unveil the physics of unitary scattering, present novel understanding of pseudo-Hermiticity, and provide fundamental insight on the energy conservation in non-Hermitian physics. Our findings are also important guiding principles promising for the non-unitary scattering. These findings shed light on the fundamental research and potential applications of non-Hermitian scattering including the light propagation, mesoscopic electron transport, and quantum interference Jiang21 .
Acknowledgements.
We acknowledge the support of National Natural Science Foundation of China (Grant No. 11975128).References
- (1) A. Mostafazadeh, Pseudo-Hermiticity versus PT symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian, J. Math. Phys. 43, 205 (2002).
- (2) H. F. Jones, On pseudo-Hermitian Hamiltonians and their Hermitian counterparts, J. Phys. A: Math. Gen. 38, 1741 (2005).
- (3) C. M. Bender and S. Boettcher, Real Spectra in Non-Hermitian Hamiltonians Having Symmetry, Phys. Rev. Lett. 80, 5243 (1998).
- (4) P. Dorey, C. Dunning, and R. Tateo, Spectral equivalences, Bethe Ansatz equations, and reality properties in -symmetric quantum mechanics. J. Phys. A 34, 5679 (2001).
- (5) A. Ruschhaupt, F. Delgado, and J. G. Muga, Physical realization of -symmetric potential scattering in a planar slab waveguide, J. Phys. A: Math. Gen. 38, L171 (2005).
- (6) L. Jin and Z. Song, Solutions of -symmetric tight-binding chain and its equivalent Hermitian counterpart, Phys. Rev. A 80, 052107 (2009).
- (7) Y. N. Joglekar and A. Saxena, Robust -symmetric chain and properties of its Hermitian counterpart, Phys. Rev. A 83, 050101(R) (2011).
- (8) S. V. Suchkov, F. Fotsa-Ngaffo, A. Kenfack-Jiotsa, A. D. Tikeng, T. C. Kofane, Y. S. Kivshar, and A. A. Sukhorukov, Non-Hermitian trimers: -symmetry versus pseudo-Hermiticity, New J. Phys. 18, 065005 (2016).
- (9) P. Chen and Y. D. Chong, Pseudo-Hermitian Hamiltonians generating waveguide mode evolution, Phys. Rev. A 95, 062113 (2017).
- (10) L. Luo, J. Luo, H. Chu, and Y. Lai, Pseudo-Hermitian Systems Constructed by Transformation Optics with Robustly Balanced Loss and Gain, Adv. Photonics Res. 2, 2000081 (2021).
- (11) L. Duan, Y.-Z. Wang, and Q.-H. Chen, Symmetry of a Square-Wave Modulated Two-Level System, Chin. Phys. Lett. 37, 081101 (2020).
- (12) S. Lei, D. Bai, Z. Ren, and M. Lyu, Finding Short-Range Parity-Time Phase-Transition Points with a Neural Network, Chin. Phys. Lett. 38, 051101 (2021).
- (13) Q. Song, S. Dai, D. Han, Z. Q. Zhang, C. T. Chan, and J. Zi, PT Symmetry Induced Rings of Lasing Threshold Modes Embedded with Discrete Bound States in the Continuum, Chin. Phys. Lett. 38, 084203 (2021).
- (14) R. El-Ganainy, K. G. Makris, D. N. Christodoulides, and Z. H. Musslimani, Theory of coupled optical -symmetric structures, Opt. Lett. 32, 2632 (2007).
- (15) K. G. Makris, R. El-Ganainy, D. N. Christodoulides, and Z. H. Musslimani, Beam Dynamics in Symmetric Optical Lattices, Phys. Rev. Lett. 100, 103904 (2008).
- (16) C. E. Rüter, K. G. Makris, R. El-Ganainy, D. N. Christodoulides, M. Segev, and D. Kip, Observation of parity–time symmetry in optics, Nat. Phys. 6, 192 (2010).
- (17) A. Mostafazadeh and A. Batal, Physical aspects of pseudo-Hermitian and -symmetric quantum mechanics, J. Phys. A: Math. Gen. 37, 11645 (2004).
- (18) D. C. Brody, Biorthogonal quantum mechanics. J. Phys. A 47, 035305 (2013).
- (19) L. Jin and Z. Song, Hermitian dynamics in a class of pseudo-Hermitian networks, Phys. Rev. A 84, 042116 (2011).
- (20) T. Kottos, Broken symmetry makes light work, Nat. Phys. 6, 166 (2010).
- (21) M. C. Zheng, D. N. Christodoulides, R. Fleischmann, and T. Kottos, optical lattices and universality in beam dynamics, Phys. Rev. A 82, 010103(R) (2010).
- (22) P. Wang, L. Jin, G. Zhang, and Z. Song, Wave emission and absorption at spectral singularities, Phys. Rev. A 94, 053834 (2016).
- (23) L. Ge, Non-Hermitian lattices with a flat band and polynomial power increase, Photon. Res. 6, A10 (2018).
- (24) L. Xiao, K. Wang, X. Zhan, Z. Bian, K. Kawabata, M. Ueda, W. Yi, and P. Xue, Observation of Critical Phenomena in Parity-Time-Symmetric Quantum Dynamics, Phys. Rev. Lett. 123, 230401 (2019).
- (25) B. Peng, S. K. Özdemir, F. Lei, F. Monifi1, M. Gianfreda, G. L. Long, S. Fan, F. Nori, C. M. Bender, and L. Yang, Parity–time-symmetric whispering-gallery microcavities, Nat. Phys. 10, 394 (2014).
- (26) K. Ding, G. Ma, M. Xiao, Z. Q. Zhang, and C. T. Chan, Emergence, Coalescence, and Topological Properties of Multiple Exceptional Points and Their Experimental Realization, Phys. Rev. X 6, 021007 (2016).
- (27) Z. Bian, L. Xiao, K. Wang, X. Zhan, F. A. Onanga, F. Ruzicka, W. Yi, Y. N. Joglekar, and P. Xue, Conserved quantities in parity-time symmetric systems, Phys. Rev. Research 2, 022039(R) (2020).
- (28) W. Liu, Y. Wu, C.-K. Duan, X. Rong, and J. Du, Dynamically Encircling an Exceptional Point in a Real Quantum System, Phys. Rev. Lett. 126, 170506 (2021).
- (29) Y. Ashida, Z. Gong, and M. Ueda, Non-Hermitian physics, Adv. Phys. 69, 249 (2020).
- (30) N. Moiseyev, Non-Hermitian Quantum Mechanics (Cambridge University Press, Cambridge, England, 2011).
- (31) V. V. Konotop, J. Yang, and D. A. Zezyulin, Nonlinear waves in -symmetric systems, Rev. Mod. Phys. 88, 035002 (2016).
- (32) S. V. Suchkov, A. A. Sukhorukov, J. Huang, S. V. Dmitriev, C. Lee, and Y. S. Kivshar, Nonlinear switching and solitons in -symmetric photonic systems, Laser Photon. Rev. 10, 177 (2016).
- (33) L. Feng, R. El-Ganainy, and L. Ge, Non-Hermitian photonics based on parity-time symmetry, Nat. Photon. 11, 752 (2017).
- (34) S. Longhi, Parity-time symmetry meets photonics: A new twist in non-Hermitian optics, Europhys. Lett. 120, 64001 (2017).
- (35) R. El-Ganainy, K. G. Makris, M. Khajavikhan, Z. H. Musslimani, S. Rotter, and D. N. Christodoulides, Non-Hermitian physics and symmetry, Nat. Phys. 14, 11 (2018).
- (36) M.-A. Miri and A. Alù, Exceptional points in optics and photonics, Science 363, eaar7709 (2019).
- (37) S. K. Özdemir, S. Rotter, F. Nori, and L. Yang, Parity-time symmetry and exceptional points in photonics, Nat. Mater. 18, 783 (2019).
- (38) S. K. Gupta, Y. Zou, X.-Y. Zhu, M.-H. Lu, L.-J. Zhang, X.-P. Liu, and Y.-F. Chen, Parity-Time Symmetry in Non-Hermitian Complex Optical Media, Adv. Mater. 32, 1903639 (2019).
- (39) J. Wiersig, Enhancing the Sensitivity of Frequency and Energy Splitting Detection by Using Exceptional Points: Application to Microcavity Sensors for Single-Particle Detection, Phys. Rev. Lett. 112, 203901 (2014).
- (40) H. Hodaei, A. U. Hassan, S. Wittek, H. Garcia-Gracia, R. El-Ganainy, D. N. Christodoulides, and M. Khajavikhan, Enhanced sensitivity at higher-order exceptional points, Nature (London) 548, 187 (2017); W. Chen, S. K. Ozdemir, G. Zhao, J. Wiersig, and L. Yang, Exceptional points enhance sensing in an optical microcavity, Nature (London) 548, 192 (2017).
- (41) H.-K. Lau and A. A. Clerk, Fundamental limits and non-reciprocal approaches in non-Hermitian quantum sensing, Nat. Commun. 9, 4320 (2018).
- (42) Y.-H. Lai, Y.-K. Lu, M.-G. Suh, Z. Yuan, and K. Vahala, Observation of the exceptional-point enhanced Sagnac effect, Nature (London) 576, 65 (2019); M. P. Hokmabadi, A. Schumer, D. N. Christodoulides, and M. Khajavikhan, Non-Hermitian ring laser gyroscopes with enhanced Sagnac sensitivity, Nature (London) 576, 70 (2019).
- (43) Y. Chu, Y. Liu, H. Liu, and J. Cai, Quantum Sensing with a Single-Qubit Pseudo-Hermitian System, Phys. Rev. Lett. 124, 020501 (2020).
- (44) H. Xu, D. Mason, L. Jiang, and J. G. E. Harris, Topological energy transfer in an optomechanical system with exceptional points, Nature (London) 537, 80 (2016).
- (45) S. Assawaworrarit, X. Yu, and S. Fan, Robust wireless power transfer using a nonlinear parity-time-symmetric circuit, Nature (London) 546, 387 (2017).
- (46) L. Feng, Z. J. Wong, R. M. Ma, Y. Wang, and X. Zhang, Single-mode laser by parity–time symmetry breaking, Science 346, 972 (2014); H. Hodaei, M.-A. Miri, M. Heinrich, D. N. Christodoulides, and M. Khajavikhan, Parity-time-symmetric microring lasers, Science 346, 975 (2014).
- (47) G. Harari, M. A. Bandres, Y. Lumer, M. C. Rechtsman, Y. D. Chong, M. Khajavikhan, D. N. Christodoulides, and M. Segev, Topological insulator laser: Theory, Science 359, eaar4003 (2018); M. A. Bandres, S. Wittek, G. Harari, M. Parto, J. Ren, M. Segev, D. Christodoulides, and M. Khajavikhan, Topological insulator laser: Experiments, Science 359, eaar4005 (2018).
- (48) Y. D. Chong, L. Ge, H. Cao, and A. D. Stone, Coherent Perfect Absorbers: Time-Reversed Lasers, Phys. Rev. Lett. 105, 053901 (2010).
- (49) S. Longhi, -symmetric laser absorber, Phys. Rev. A 82, 031801(R) (2010).
- (50) W. Wan, Y. Chong, L. Ge, H. Noh, A. D. Stone, and H. Cao, Time-Reversed Lasing and Interferometric Control of Absorption, Science 331, 889 (2011).
- (51) Y. Sun, W. Tan, H. Q. Li, J. Li, and H. Chen, Experimental Demonstration of a Coherent Perfect Absorber with PT Phase Transition, Phys. Rev. Lett. 112, 143903 (2014).
- (52) H. Li, S. Suwunnarat, R. Fleischmann, H. Schanz, and T. Kottos, Random Matrix Theory Approach to Chaotic Coherent Perfect Absorbers, Phys. Rev. Lett. 118, 044101 (2017).
- (53) J. Jeffers, Nonlocal Coherent Perfect Absorption, Phys. Rev. Letts. 123, 143602 (2019).
- (54) Z. Lin, H. Ramezani, T. Eichelkraut, T. Kottos, H. Cao, and D. N. Christodoulides, Unidirectional Invisibility Induced by -Symmetric Periodic Structures, Phys. Rev. Lett. 106, 213901 (2011).
- (55) A. Regensburger, C. Bersch, M.-A. Miri, G. Onishchukov, D. N. Christodoulides, and U. Peschel, Parity–time synthetic photonic lattices, Nature (London) 488, 167 (2012).
- (56) L. Feng, Y.-L. Xu, W. S. Fegadolli, M.-H. Lu, J. E. B. Oliveira, V. R. Almeida, Y.-F. Chen, and A. Scherer, Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies, Nat. Mater. 12, 108 (2013).
- (57) X. Zhu, H. Ramezani, C. Shi, J. Zhu, and X. Zhang, -Symmetric Acoustics, Phys. Rev. X 4, 031042 (2014).
- (58) J.-H. Wu, M. Artoni, and G. C. La Rocca, Non-Hermitian Degeneracies and Unidirectional Reflectionless Atomic Lattices, Phys. Rev. Lett. 113, 123004 (2014).
- (59) D. L. Sounas, R. Fleury, and A. Alù, Unidirectional Cloaking Based on Metasurfaces with Balanced Loss and Gain, Phys. Rev. Appl. 4, 014005 (2015).
- (60) K. G. Makris, I. Kresic, A. Brandstötter, and S. Rotter, Scattering-free channels of invisibility across non-Hermitian media, Optica 7, 619 (2020).
- (61) S. Longhi, Non-reciprocal transmission in photonic lattices based on unidirectional coherent perfect absorption, Opt. Letts. 40, 1278 (2015).
- (62) W. R. Sweeney, C. W. Hsu, S. Rotter, and A. D. Stone, Perfectly Absorbing Exceptional Points and Chiral Absorbers, Phys. Rev. Letts. 122, 093901 (2019).
- (63) C. Li, L. Jin, and Z. Song, Non-Hermitian interferometer: Unidirectional amplification without distortion, Phys. Rev. A 95, 022125 (2017).
- (64) T. T. Koutserimpas and R. Fleury, Nonreciprocal Gain in Non-Hermitian Time-Floquet Systems, Phys. Rev. Lett. 120, 087401 (2018).
- (65) A. Mostafazadeh, Spectral Singularities of Complex Scattering Potentials and Infinite Reflection and Transmission Coefficients at Real Energies, Phys. Rev. Lett. 102, 220402 (2009).
- (66) H. Ramezani, H.-K. Li, Y. Wang, and X. Zhang, Unidirectional Spectral Singularities, Phys. Rev. Lett. 113, 263905 (2014).
- (67) L. Jin and Z. Song, Incident Direction Independent Wave Propagation and Unidirectional Lasing, Phys. Rev. Lett. 121, 073901 (2018).
- (68) A. Ruschhaupt, T. Dowdall, M. A. Simón, and J. G. Muga, Asymmetric scattering by non-Hermitian potentials, Eur. Phys. Lett. 120, 20001 (2017).
- (69) J. Alexandre, P. Millington, and D. Seynaeve, Symmetries and conservation laws in non-Hermitian field theories, Phys. Rev. D 96, 065027 (2017).
- (70) J. D. H. Rivero and L. Ge, Pseudochirality: A Manifestation of Noether’s Theorem in Non-Hermitian Systems, Phys. Rev. Lett. 125, 083902 (2020).
- (71) L. Ge, Y. D. Chong, and A. D. Stone, Conservation relations and anisotropic transmission resonances in one-dimensional -symmetric photonic heterostructures, Phys. Rev. A 85, 023802 (2012).
- (72) Z. Ahmed, Reciprocity and unitarity in scattering from a non-Hermitian complex -symmetric potential, Phys. Lett. A 377, 957 (2013).
- (73) A. Mostafazadeh, Generalized unitarity and reciprocity relations for -symmetric scattering potentials, J. Phys. A: Math. Theor. 47, 505303 (2014).
- (74) L. Jin, Scattering properties of a parity-time-antisymmetric non-Hermitian system, Phys. Rev. A 98, 022117 (2018).
- (75) L. Jin and Z. Song, Hermitian scattering behavior for a non-Hermitian scattering center, Phys. Rev. A 85, 012111 (2012).
- (76) J. G. Muga, J. P. Palao, B. Navarro, and I. L. Egusquiza, Complex absorbing potentials, Phys. Rep. 395, 357 (2004).
- (77) F. Cannata, J.-P. Dedonder, and A. Ventura, Scattering in -symmetric quantum mechanics, Ann. Phys. 322, 397 (2007).
- (78) H. F. Jones, Scattering from localized non-Hermitian potentials, Phys. Rev. D 76, 125003 (2007).
- (79) M. Znojil, Scattering theory with localized non-Hermiticities, Phys. Rev. D 78, 025026 (2008).
- (80) P. Ambichl, K. G. Makris, L. Ge, Y. Chong, A. D. Stone, and S. Rotter, Breaking of Symmetry in Bounded and Unbounded Scattering Systems, Phys. Rev. X 3, 041030 (2013).
- (81) H. Schomerus, From scattering theory to complex wave dynamics in non-Hermitian -symmetric resonators, Phil. Trans. R. Soc. A 371, 20120194 (2013).
- (82) A. Basiri, I. Vitebskiy, and T. Kottos, Light scattering in pseudopassive media with uniformly balanced gain and loss, Phys. Rev. A 91, 063843 (2015).
- (83) L. Ge, K. G. Makris, D. N. Christodoulides, and L. Feng, Scattering in - and -symmetric multimode waveguides: Generalized conservation laws and spontaneous symmetry breaking beyond one dimension, Phys. Rev. A 92, 062135 (2015).
- (84) L. Jin, X. Z. Zhang, G. Zhang, and Z. Song, Reciprocal and unidirectional scattering of parity-time symmetric structures, Sci. Rep. 6, 20976 (2016).
- (85) Y. Aurégan and V. Pagneux, -symmetric scattering in flow duct acoustics, Phys. Rev. Lett. 118, 174301 (2017).
- (86) Z. Zhao, C. Guo, and S. Fan, Connection of temporal coupled-mode-theory formalisms for a resonant optical system and its time-reversal conjugate, Phys. Rev. A 99, 033839 (2019).
- (87) S. Droulias, I. Katsantonis, M. Kafesaki, C. M. Soukoulis, and E. N. Economou, Chiral Metamaterials with Symmetry and Beyond, Phys. Rev. Lett. 122, 213201 (2019).
- (88) A. Novitsky, D. Lyakhov, D. Michels, A. A. Pavlov, A. S. Shalin, and D. V. Novitsky, Unambiguous scattering matrix for non-Hermitian systems, Phys. Rev. A 101, 043834 (2020).
- (89) P. C. Burke, J. Wiersig, and M. Haque, Non-Hermitian scattering on a tight-binding lattice, Phys. Rev. A 102, 012212 (2020).
- (90) H. Ghaemi-Dizicheh and H. Schomerus, Compatibility of transport effects in non-Hermitian nonreciprocal systems, Phys. Rev. A 104, 023515 (2021).
- (91) A. F. Tzortzakakis, K. G. Makris, A. Szameit, and E. N. Economou, Transport and spectral features in non-Hermitian open systems, Phys. Rev. Research 3, 013208 (2021).
- (92) A. Krasnok, D. Baranov, H. Li, M.-A. Miri, F. Monticone, and A. Alù, Anomalies in light scattering, Adv. Opt. Photon. 11, 892 (2019).
- (93) M. A. Simón, A. Buendía, A. Kiely, A. Mostafazadeh, and J. G. Muga, -matrix pole symmetries for non-Hermitian scattering Hamiltonians, Phys. Rev. A 99, 052110 (2019).
- (94) A. Ruschhaupt, A. Kiely, M. A. Simón, and J. G. Muga, Quantum-optical implementation of non-Hermitian potentials for asymmetric scattering, Phys. Rev. A 102, 053705 (2020).
- (95) H. Schomerus and J. Wiersig, Non-Hermitian-transport effects in coupled-resonator optical waveguides, Phys. Rev. A 90, 053819 (2014).
- (96) R. Fleury, D. Sounas, and A. Alù, An invisible acoustic sensor based on parity-time symmetry, Nat. Commun. 6, 5905 (2015).
- (97) H. Gao, H. Xue, Q. Wang, Z. Gu, T. Liu, J. Zhu, and B. Zhang, Observation of topological edge states induced solely by non-Hermiticity in an acoustic crystal, Phys. Rev. B 101, 180303(R) (2020).
- (98) W. Gou, T. Chen, D. Xie, T. Xiao, T.-S. Deng, B. Gadway, W. Yi, and B. Yan, Tunable Nonreciprocal Quantum Transport through a Dissipative Aharonov-Bohm Ring in Ultracold Atoms, Phys. Rev. Lett. 124, 070402 (2020).
- (99) J. Schindler, A. Li, M. C. Zheng, F. M. Ellis, and T. Kottos, Experimental study of active LRC circuits with symmetries, Phys. Rev. A 84, 040101(R) (2011).
- (100) Z. A. Cochran, A. Saxena, and Y. N. Joglekar, Parity-time symmetric systems with memory, Phys. Rev. Research 3, 013135 (2021).
- (101) K. Kawabata, K. Shiozaki, M. Ueda, and M. Sato, Symmetry and Topology in Non-Hermitian Physics, Phys. Rev. X 9, 041015 (2019).
- (102) H. Zhou and J. Y. Lee, Periodic table for topological bands with non-Hermitian symmetries, Phys. Rev. B 99, 235112 (2019).
- (103) L. Jin and Z. Song, Symmetry-Protected Scattering in Non-Hermitian Linear Systems, Chin. Phys. Lett. 38, 024202 (2021).
- (104) For a rigorous proof, please see Eq. (12) in Ref. LJinCPL and compare the scattering coefficients of the scattering centers and . Notice that the symbols , , , and in Ref. LJinCPL are , , , and of the scattering matrix with our current notations for any pair of ports and . The fact is also used in the proof for any square matrix .
- (105) From the off-diagonal term of , we obtain . From the diagonal terms of , we obtain .
- (106) R. Fleury, D. L. Sounas, C. F. Sieck, M. R. Haberman, and A. Alù, Sound Isolation and Giant Linear Nonreciprocity in a Compact Acoustic Circulator, Science 343, 516 (2014).
- (107) T. J. Kippenberg, S. M. Spillane, and K. J. Vahala, Modal coupling in traveling-wave resonators, Opt. Lett. 27, 1669 (2002).
- (108) W. Kim, L. Covaci, and F. Marsiglio, Impurity scattering of wave packets on a lattice, Phys. Rev. B 74, 205120 (2006).
- (109) H. C. Wu, X. M. Yang, L. Jin, and Z. Song, Untying links through anti-parity-time-symmetric coupling, Phys. Rev. B 102, 161101(R) (2020).
- (110) M. Xi, R. Wang, J. Lu, and J.-H. Jiang, Coulomb Thermoelectric Drag in Four-Terminal Mesoscopic Quantum Transport, Chin. Phys. Lett. 38, 088801 (2021).