Uniqueness of 4-manifolds described as sequences of 3-d handlebodies

Throughout this paper, we let $\Sigma_{g}$ be a fixed closed orientable surface of genus $g$. We denote by $S_{g,b}$ some surface homeomorphic to a surface of genus $g$ with $b$ boundary components. Many of the constructions in this paper take in an object associated to $\Sigma_{g}$ and extract a sequence of handlebodies bounded by $\Sigma_{g}$. Adjacent handlebodies in these sequences are closely related, in a way made precise by the following definition.

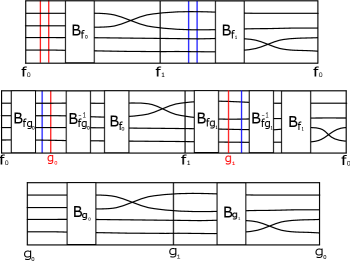
By theorems of Waldhausen [28] and Haken [9], cut systems for a pair of minimally dual handlebodies can be made to look exactly like those in Figure 1, after some handle slides and a homeomorphism of $\Sigma_{g}$. Following Gay and Kirby in [7], a sequence of dual handlebodies gives rise to a unique smooth 4-manifold as described in the definition below, and illustrated in Figure 2.

Given a loop of dual handlebodies $L$, we will see that the 4-manifold $X^{4}(L)$ comes naturally equipped with the structure of a multisection. These generalizations of trisections were defined and studied in [13], and we reproduce the definition here.

There are various equivalence relations one could consider on a multisection, but in this paper, we will primarily be using the following.

Given a loop $L=(H_{1},...,H_{n})$ of dual handlebodies, the multisection structure on $X^{4}(L)$ is given by $X^{4}(L)=X_{1}\cup X_{2}\cup\cdots\cup X_{n}$ where $X_{i}$ is the union of $H_{i}$, $H_{i+1}$ and the copy of $\natural^{k_{i}}S^{1}\times B^{3}$ filling them in. If $L$ is a sequence of minimally dual handlebodies, then the induced multisection is thin. We call this multisection structure T(L), and we will show that it is well defined up to diffeomorphisms of multisection in Section 3.2.

We also note that the 4-manifold, together with the multisection structure, can be reconstructed from an ordered sequence of cut systems for the handlebodies $H_{i}$ drawn on $\Sigma_{g}$. This is called a multisection diagram and we refer the reader to the top and bottom of Figure 17 for some basic examples and to [13] for more involved examples.

In this paper, we require that Morse functions be stable so that, in particular, each critical value has at most one critical point in its preimage. In this section, following [8], we will show how to extract a sequence of dual handlebodies from a generic path of Morse functions on $\Sigma_{g}$. We begin by associating a handlebody to a Morse function.

In addition to the data of the handlebody $H(f)$, a Morse function also gives rise to a family of cut systems for the handlebody $H(f)$. In fact, a Morse function most naturally gives rise to a pants decomposition, which is a collection of $3g-3$ disjoint, non-isotopic, essential, simple closed curves.

Any two Morse functions $f_{0}$ and $f_{1}$ on $\Sigma_{g}$ are connected by a 1-parameter family of functions, $f_{t}$ which is Morse except for at a finite number of critical times where the function is “near Morse” [6]. In these paths, at any critical time, $c$, $f_{c}$ has either two critical points mapping to the same critical value, which we call a critical value exchange, or has a single birth or death singularity. We call a path containing only such critical times a generic path of Morse functions.

Let $f_{t}$ be a generic path of Morse functions and let $c$ be a critical time. Since critical times are isolated, we can take $\epsilon$ be sufficiently small so that there are no other critical times in $[c-\epsilon,c+\epsilon]$. We seek to understand how the handlebodies associated to the functions change as we pass a critical time. Note that since a handlebody is completely determined by a cut system, $H(f_{t})$ is determined by $C(f_{t})$. Since birth and death singularities only introduce or remove null-homotopic level sets, if $c$ is a birth or death time, $H(f_{c-\epsilon})=H(f_{c+\epsilon}).$ If $c$ is a critical value exchange, then, by Euler characteristic considerations, $f^{-1}([c-\epsilon,c+\epsilon])$ contains some number of annuli, which can be ignored, together with either two disjoint copies of $S_{0,3}$, a copy of $S_{0,4}$, or a copy of $S_{1,2}$.

In the case that the two critical points lie two disjoint copies of $S_{0,3}$, $P(f_{c-\epsilon})=P(f_{c+\epsilon})$ so that the handlebodies do not change. Since we can select a cut system disjoint from a $S_{0,4}$ subsurface, if the saddles at $c$ occur in $S_{0,4}$ then again $H(f_{c-\epsilon})=H(f_{c+\epsilon}).$ On the other hand, if the saddles at $c$ occur in $S_{1,2}$, then up to homeomorphism, the level sets of $f_{c-\epsilon}$ and $f_{c+\epsilon}$ are the curves at the left and the right of Figure 6. Since in this case we can choose $C(f_{c-\epsilon})$ and $C(f_{c+\epsilon})$ to be identical, aside from two curves which intersect once, $H(f_{c-\epsilon})$ and $H(f_{c+\epsilon})$ are minimally dual handlebodies. We summarize this discussion in the following lemma, first observed in [10] and explicitly proven in Lemma 10 of [8].

We next define an equivalence relation among paths of Morse functions which still captures the information of the handlebodies determined by the functions. Since only critical value exchanges in $S_{1,2}$ affected the handlebody, we are free to modify paths to include other types of singularities without changing the handlebodies defined. In addition, the particular path of Morse functions realizing a single crossing exchange in $S_{1,2}$ is immaterial in the handlebodies defined on each side, and we will also account for this.

Having defined our first object of interest, we next turn our attention to graphs associated to curves on a surface. In this section, we will show that loops in appropriate quotients of these complexes are in bijection with $\mathfrak{M}_{h}(\Sigma).$ We begin with the pants decompositions. The collection of all of the pants decompositions of a surface can be arranged into a graph described below, and whose edges can be seen in Figure 3.

The other complex of interest in this paper will organize the cut systems of a surface into a complex. Following work of Wajnryb [27] and Johnson [14], Kirby and Thompson [16] arranged the cut systems of a given surface into a graph, whose edges can be seen in Figure 4, and which is defined below.

In the definition of the pants complex we excluded genus 1 surfaces. Here, following [11], we define $P(\Sigma_{1})$ to be $C(\Sigma_{1})$. This complex only contains type 1 edges and is isomorphic to the Farey graph.

Slightly abusing notation, we will often refer to vertices in these complexes and the set of curves they correspond to on a surface using the same symbol. It is well known that a cut system determines a handlebody uniquely determined by the fact that all of the curves in the cut system bound a disk. Similarly, there is a unique handlebody corresponding to a pants decomposition, where all of the curves in the pants decomposition bound disks. Given a vertex $c\in C(\Sigma)$ or $p\in P(\Sigma)$ we denote this unique handlebody by H(c) or H(p), respectively.

We define an equivalence relation on vertices in $C(\Sigma)$, $\sim_{0}$, to be $c\sim_{0}c^{\prime}$ if $c$ and $c^{\prime}$ are connected by a sequence of only type-0 edges. Similarly, if $p,p^{\prime}\in P(\Sigma),$ then we say $p\sim_{A}p^{\prime}$ if $p$ and $p^{\prime}$ are connected by a sequence of only A-edges. After taking the initial quotients by these relations, two vertices may have multiple edges between them. We will further quotient any two edges relating the same vertex to obtain the complexes $\mathbf{C(\Sigma)/\sim_{0}}$ and $\mathbf{P(\Sigma)/\sim_{A}}$. We refer to the images of vertices $c\in C(\Sigma)$ and $p\in P(\Sigma)$ in the quotient complexes $C(\Sigma)/\sim_{0}$ and $P(\Sigma)/\sim_{A}$ by $[c]_{0}$ and $[p]_{A}$ respectively.

In the proof above we saw that $\sim_{0}$ and $\sim_{A}$ simply relate vertices corresponding to the same handlebody, so that $H([c]_{0})$ and $H([p]_{A})$ are well defined handlebodies. Moreover, two handlebodies corresponding to adjacent handlebodies in these complexes form a Heegaard splitting for $\#^{g-1}S^{1}\times S^{2}$ so that they are, in particular, dual handlebodies. We therefore call the quotient graph $C(\Sigma)/\sim_{0}\,\cong P(\Sigma)/\sim_{A}$ the dual handlebody graph and denote it $\mathbf{D(\Sigma)}$. Given the preceding discussion, the following is immediate.

In this subsection we seek to produce a bijection, $D$, between $\mathfrak{M}_{h}(\Sigma)$ and loops in $D(\Sigma)$. We define the map below, noting that we will later prove well definedness.

Much of the work in proving $D$ is a surjection is carried out in [11] where the authors assign a loop in $P(\Sigma)$ to a generic loop of Morse functions on $\Sigma$. In that work, there is not a canonical choice of loop in $P(\Sigma)$ corresponding to a loop of generic Morse functions, however by attaching 2-cells to $P(\Sigma)$, the choice can be made unique up to homotopy in the resulting 2-complex. In this paper, the quotients defined deal with the ambiguity.

We next seek to show that the map $D$ defined above is an injection. The following theorem, which the author of [18] attributes to Matveev will be useful in our proof.

Recall that in Definition 7, we defined a relation on paths of Morse functions which we called a torus crossing replacement. This relation involved paths of Morse functions which involve at most one critical value crossing in a copy of $S_{1,2}$. The following proposition will give us a useful path of Morse functions involving no critical value crossings in $S_{1,2}$ between Morse functions on $\Sigma_{g}$ yielding the same handlebody.

Given a generic path of Morse functions $f_{t}$, we may draw the critical value set in $\mathbb{R}\times I$ as a Cerf graphic [6]. To add clarity to this picture, we will place all of singularities of $f_{t}$ which are not critical value crossings in a torus into a Cerf box and draw all of the tori crossings to highlight these critical times. Examples of such graphics with two critical value crossings in tori are given in Figure 9. Proposition 2 showed that given two Morse functions $f_{0}$ and $g_{0}$ with $H(f_{0})=H(g_{0})$ we can find a path with no critical value crossings in tori. We represent this homotopy by the Cerf box $B_{fg_{0}}$ and it is the main input into the main proposition of this section. The proof is also illustrated in Figure 9.

In Section 2.1 we described how to take a sequence of dual handlebodies and produce a multisection. We also noted that if the handlebodies were minimally dual, then the induced multisection was thin. By factoring through this construction, we get a map, $T$, from loops in $D(\Sigma)$ to the set of thin multisections with multisection surface $\Sigma_{g}$ up to diffeomorphism, which we denoted $T(\Sigma_{g})$. We seek to show that $T:\text{loops in }D(\Sigma_{g})\to T(\Sigma_{g})$ is a bijection.

We compile the results of this section into the following summary theorem.

We will be concerned with how to import information of the singular sets of our maps onto a reference surface. This will be facilitated by the following definition.

In the definition above, the point $c$ may be a Lefschetz singularity, so long as no interior points of the arc pass through Lefschetz singularities or cusps. Given a directed reference path $p$, starting at $b$, we can draw the vanishing cycle of a Lefschetz singularity or an index-2 fold singularity of $c$ on $f^{-1}(b):=\Sigma$ by parallel transport. We call the resulting curve $c_{p}$. Intuitively, $c_{p}$ is the curve which contracts as we approach $c$ via the path $p$. See [4] for details on this construction.

We next seek to understand how vanishing cycles change as we modify a Morse 2-function. Following [2], we say a local modification of critical images which takes a critical image $C_{0}$ and produces a critical image $C_{1}$ is always realizable if there is a smooth 1-parameter family of smooth maps $F_{t}:X^{4}\to D^{2}$ such that the critical image of $F_{0}$ is $C_{0}$ and the critical image of $F_{1}$ is $C_{1}$. We will need three particular always realizable moves in this paper.

The first is the unsink move of [20], which takes folds of index 1 and index 2 meeting at a cusp, and transforms them into a fold with no cusp, together with a Lefschetz singularity. The modification of critical images, together with the resulting vanishing cycles along the reference paths drawn is given in Figure 10. In particular if the vanishing cycle associated to first indefinite fold (ordered by increasing counterclockwise angle) is $\alpha$ and the second is $\beta$, then the resulting Lefschetz singularity has vanishing cycle $\tau_{\alpha}(\beta)$, where $\tau$ denotes a right handed Dehn twist.

The second is the push move, which moves a Lefschetz singularity over an indefinite fold towards the side with the higher genus fiber. This modifies the critical image in a straightforward way and the vanishing cycle associated to the Lefschetz singularity is unchanged. This move was introduced by Baykur in [3].

The third is the wrinkle move of [20], which transforms a Lefschetz singularity into a fold with three cusps. The modification of critical images, together with the resulting vanishing cycles along the reference paths drawn is given in Figure 11. The three resulting vanishing cycles of the indefinite folds are characterized by the property that they each intersect transversely once positively and that any arc from one boundary component of the surface to the other must intersect one of the curves. We note that the effect of wrinkling on relative trisection diagrams is studied in [5].

Given a basepoint $b$, a critical point $c$, and two directed paths $p$ and $p^{\prime}$ between $b$ and $c$, a homotopy from $p$ to $p^{\prime}$ may cross over some cusps or Lefschetz singularities. Given some data about the Lefschetz singularities and the cusp singularities, one can deduce the relations between $c_{p}$ and $c_{p^{\prime}}$. These changes in the vanishing cycles were explored in depth in [1] where this change is called a $\Delta_{1}$ move and [12] where this move was first analyzed.

We note that this lemma is obtained by applying an unsink to the cusp to obtain a Lefschetz singularity with vanishing cycle $\tau_{c_{1}}(c_{2})$ and using the well known monodromy of this Lefschetz singularity.

In [13] we define a composition of the unsink, push, and wrinkle moves which we call a UPW move, pictured in Figure 16. In this paper, we will additionally track reference paths in order to obtain a new multisection diagram. This will allow us to extract information about how the 3-dimensional handlebodies change under this operation in order to give corresponding moves in the dual handlebody complex.

We next seek to describe the genus $g+1$ multisection diagram obtained after performing a UPW move on a genus $g$ multisection. This move begins by locating a cusp in the Morse 2-function, which corresponds to two curves $c_{i}$ and $c_{i+1}$ which intersect once on the corresponding multisection diagram. These two curves, together with the Lefschetz singularity obtained by unsinking the cusp lie in the punctured torus neighbourhood of $c_{i}\cup c_{i+1}$ as shown on the right of Figure 10. We will only modify the diagram in this neighbourhood, as described in the following proposition.