Uniform fluctuation and wandering bounds in first passage percolation
Abstract.
We consider first passage percolation on certain isotropic random graphs in . We assume exponential concentration of passage times , on some scale whenever is of order , with “growning like ” for some . Heuristically this means transverse wandering of geodesics should be at most of order . We show that in fact uniform versions of exponential concentration and wandering bounds hold: except with probability exponentially small in , there are no in a natural cylinder of length and radius for which either (i) , or (ii) the geodesic from to wanders more than distance from the cylinder axis. We also establish that for the time constant , the “nonrandom error” is at most a constant multiple of .
Key words and phrases:
first passage percolation, geodesic, exponential concentration2010 Mathematics Subject Classification:
60K35 Primary 82B43 Secondary1. Introduction.
In i.i.d. first passage percolation (FPP) on a graph , i.i.d. (edge) passage times are attached to the edges , and for a path in , the (path) passage time is the sum of the times over . For , the passage time from to is
| (1.1) |
The geodesic from to is the path, denoted , which minimizes the path passage time; when is a continuous random variable (as we always assume), a unique geodesic exists a.s. [17].
There are two exponents of primary interest in the study of FPP. First, the fluctuations (i.e. standard deviation) of passage times for of scale in are believed to be of order for some , with . Second, the typical transverse wandering of a geodesic, meaning the maximum distance from any point on to the straight line (denoted ) from to , is believed to be of order for some . For of order , if contains a vertex at distance of order from (not too near or ), then the associated extra distance traveled by the geodesic in order to pass through is of order . For such wandering to have non-negligible probability, the passage time fluctuations should be at least as large as the extra distance; heuristically this leads to the relation . There are various ways to formally define the exponents ; these must allow for the fact that the true scales of fluctuations and wandering are not known to be pure powers of . Chatterjee [9] gave a rigorous version of the relationship , under the assumption that multiple possible definitions of each exponent actually agree.
Looking more finely than just at the level of exponents, the heuristic for says that if the fluctuation scale is for of order , then the scale of transverse wandering should be
In [2] and (for ) in [14] it was shown that under natural assumptions, the transverse wandering with high probability does not exceed . One of our main results here is an upper bound on wandering: under somewhat weaker assumptions, for all , the probability of wandering greater than decays as or faster, for . Previously such a result has only been known for integrable cases of last passage percolation (LPP) in , from [8] (with in place of ) and [7]. The bound is optimal in the sense of being on the scale , though the second power of in the exponent may not be optimal, as suggested by LPP results in in [15].
In fact we have this bound uniformly over many geodesics simultaneously, in the following sense: Consider a cylinder of length and radius , and let and . Then under the assumptions we will make, the probability that there exists any geodesic , with in the cylinder and , which wanders farther than from the cylinder axis decays as or faster, for . The scale here is optimal, though the decay may not be, based on LPP results for in [15].
By comparison, in [2] it was shown roughly that if there is exponential concentration on some scale which “grows like a power of ,” uniformly for passage times over distance , then the probability of a transverse fluctuation of size for a single geodesic is bounded by for all . This tells us nothing, though, about transverse fluctuations of size with , which should also be subject to exponential concentration, as in our present result.
It should be emphasized that in our transverse wandering (and other) results, is not necessarily the actual scale of the standard deviation—it need only be an upper bound in the sense that exponential concentration holds for passage times on scale . Then the corresponding value is the scale that appears in the upper bound for transverse wandering.
Our uniform wandering bound will be a byproduct of another uniform–bound result for passage times; to describe it we first discuss exponential bounds. For the lattice , Kesten [18] proved that, assuming
| (1.2) |
(where is the bond percolation threshold for ), there is exponential concentration of on scale for :
Talagrand [26] improved this: assuming just an exponential moment for ,
Damron, Hanson, and Sosoe [11] improved the bound to a subgaussian scale: under (1.2),
None of these bounds are near–optimal, though—an optimal bound would be on the scale of the standard deviation of . What we will prove here is roughly as follows. Suppose passage times satisfy exponential concentration on a scale , uniformly:
| (1.3) |
for some which “grows like ” for some , in a sense we will make precise. Then for a cylinder of length and radius for some fixed , we have concentration on the same scale, uniformly over :
| (1.4) |
for all large and . This has previously been proved for integrable models of LPP in ([8], [6]), but even the non-integrable part of the proof there does not carry over to FPP—see Remark 1.8.
For there is no generally-agreed-upon value of in the physics literature. Heuristics and simulations suggest that should decrease with dimension; simulations in [25] for a model believed to be in the same (KPZ) universality class as FPP show a decrease from to as increases from 2 to 7. Some have predicted the existence of a finite upper critical dimension, possibly as low as 3.5, above which ([13],[20]); others predict that is positive for all ([3],[24]), with simulations in [19] showing all the way to , decaying approximately as . Our results here require so they only have content below the upper critical dimension, should it be finite.
In the preceding and throughout the paper, and , and represent unspecified constants which depend only on the graph (or its distribution, if it is random) and the distribution of the passage times (or speeds , to be given below.) We use for constants which occur outside of proofs and may be referenced later; any given has the same value at all occurrences. We use for those which do not recur and are only needed inside one proof. For the ’s we restart the numbering with in each proof, and the values are different in different proofs.
As is standard, since passage times are subadditive, assumptions much weaker than (1.2) guarantee the a.s. existence (positive and finite for ) of the limit
| (1.5) |
for ; extends to with rational coordinates by considering only with , and then to a norm on by uniform continuity. We write for the unit ball of this norm. To obtain the optimal uniform results for wandering and (1.4) for fluctuations, we need to understand both parts of the discrepancy
| (1.6) |
Here in the parentheses on the right are the random part and nonrandom part of the discrepancy. In [1] it was shown that under (1.2),
| (1.7) |
In [27] the error term was improved to , and in [14] to for all . For the Euclidean first passage percolation of [16], the analog of (1.7) was proved in [12] with an error term of for arbitrary , where is a scale on which an exponential bound is known (analogous to in (1.3)) and is the –times–iterated logarithm. Here we will obtain an essentially optimal bound for the nonrandom part: if satisfies certain regularly and (1.3) holds, then a log factor as in the earlier bounds is unnecessary in our context: we have
| (1.8) |
There is a strong interdependence among this result, our uniform wandering bounds, and (1.4), as discussed in Remark 1.7.
Analogs of (1.8), of (1.4), and of of our uniform wandering result, with optimal scale , are known for certain integrable models of directed last passage percolation (LPP). We note that an exponential bound like (1.3), but with centering at the analog of instead of at , shows that (i) (1.8) must hold, and (ii) an exponential bound like (1.3) must also hold with centering at . Such a recentered bound appears in [8] (extracted from [4]) and in [21] for LPP on with exponential passage times, in [22], [23] for LPP based on a Poisson process in the unit square, and in [10] for LPP on with geometric passage times. An analog of our transverse wandering bound for LPP on with exponential passage times appears in [7]. All of these require integral probability methods, which are not available for FPP.
Rather than work on the lattice , we will consider isotropic models, built on a random graph embedded in . The dilation of such an embedded graph is the least such that, for every there is a path from to in for which the total (Euclidean) length of the edges is at most . We say that such a graph has bounded dilation if there exists such that with probability one the dilation of is at most . For , the restriction of to is the graph with vertex set for some and edge set .
We require that the graph satisfy the assumptions A1 below, which are somewhat stringent and include bounded dilation, but we will construct an example that works. (We see no need to make the graph as general as possible; we simply need one to know we can work with one that has certain desirable properties.) That example is built roughly as follows. We first construct a point process to serve as vertices, with satisfying those parts of A1 which involve only the vertices. To make a graph from we use the Voronoi diagram, which divides into closed polyhedrons (called Voronoi cells), the interior of the polygon consisting of those points which are strictly closer to than to any other point of . We refer to as the center point of , and define by for . To produce the Delaunay graph (or Delaunay triangulation in ) one places an edge between each pair for which and have a face of positive –volume in common. For , it is known that the dilation of the Delaunay graph of any locally finite subset of is at most 1.998 [28], ensuring A1 is fully satisfied, but such bounded dilation for is not known. We therefore modify the Delaunay graph by adding certain non-nearest-neighbor edges of uniformly bounded length, by a deterministic local rule, and show that bounded dilation then holds. Here and in what follows, by the length of an edge we mean the Euclidean distance , which we denote .
Our FPP proofs for isotropic random graphs should adapt to , but (we expect) only by assuming two unproven properties of FPP on : first, uniform curvature of , and second, a kind of smoothness of the mean as the direction changes:
Results in [1] show that for lattice FPP, the left side is . This is (implicitly) improved to in [27] and to for all , in [14].
Here then are the assumptions must satisfy.
A1. Acceptability of random graphs.
-
(i)
is isotropic, stationary, and ergodic;
-
(ii)
Bounded hole size: every open ball in of radius 1 contains at least one vertex of ;
-
(iii)
Finite range of dependence: there exists such that if are Lebesgue–measurable subsets of separated by distance , then the restrictions of to and to are independent;
-
(iv)
Bounded dilation: the dilation of is bounded a.s. (and hence equal to some nonrandom a.s., by (i));
-
(v)
Exponential bound for the local density: given there exist such that for all and , ;
We say a random graph with these properties is acceptable. We will show that acceptable random graphs exist. By rescaling, we may replace radius 1 in (ii) by any other positive value. Condition (v) can be weakened from exponential to stretched exponential; we use exponential to simplify the exposition.
Conditionally on we define a collection of i.i.d. nonnegative continuous random variables . Formally the pair is defined on a probability space , with determined by .
In contrast to the usual FPP on a true lattice, here we view not as a time but as a speed. We thus define the passage time of a bond to be , and proceed “as usual”: for , a path from to is a finite sequence of alternating vertices and edges of , of the form . We may designate a path by specifying only the vertices. The (path) passage time of is
and the passage time from to is
| (1.9) |
More generally, for we define
For technical convenience we do not require that paths be self-avoiding, but for the moment this is irrelevant because geodesics are always self-avoiding.
For general not necessarily in , we take “a geodesic from to ” to mean a geodesic from the center point to . Let . We assume the following.
A2. properties.
-
(i)
is a continuous random variable.
-
(ii)
There exists such that .
Here (i) guarantees that there is at most one geodesic from to a.s., for each .
We do not assume that in (1.3) is a power of , but we do require that it “grows like ” for some in a sense similar to [2], as follows. We call a nonnegative function powerlike (with exponent ) if there exist and constants such that
| (1.10) |
If (1.10) holds with we say is sublinearly powerlike.
The requirement that be sublinearly powerlike is perhaps not as stringent as it first appears, due to Lemma 1.2 below. It implies that if one is only interested in fluctuations at the level of exponents , and one knows uniform the exponential tightness (1.3) but not necessarily the powerlike property for , then there is a sublinearly powerlike function with the same for which (1.3) holds.
Remark 1.1.
If is powerlike, then so is the increasing function ; by further increasing (though by at most a constant factor) we may make it strictly increasing and continuous while preserving the powerlike property. Therefore we may and do without loss of generality always assume is strictly increasing and continuous. The inverse function is well-defined, and for we have and in the sense that
The following is proved in section 8.
Lemma 1.2.
Let satisfy
Then there exist which is sublinearly powerlike with the same exponent , and given we may take to satisfy (1.10) with .
For general not necessarily in , we write for . In general we view as an undirected path, but at times we will refer to, for example, the first point of with some property. Hence when appropriate, and clear from the context, we view as a path from to .
Our final standard assumption is the following.
A3. Uniform exponential tightness.
For some which is sublinearly powerlike with exponent ,
| (1.11) |
The isotropic property assumed for in A1 means that for all , where , and depends only on , so we define
Let be the Euclidean unit ball of and define the cylinders
Here is our first main result.
Theorem 1.3.
Suppose and satisfy A1, A2, and A3. Then given there exist constants such that for all ,
| (1.12) |
and
| (1.13) |
Equation (1.13) is weaker than (1.12) in the sense that is (up to a constant) smaller than (see Lemma 3.6), but stronger in that it isn’t limited to .
We can split (1.12) into upward and downward deviations:
Then the downward–deviations part of (1.12) is a consequence of (1.13) and Proposition 3.3 below, because
for some . In general, if we think of to as an increment a path might make within in going from the one end to the other in the direction, then measures progress made by that increment in the direction, so it is a natural normalization of in the context of such paths. It is also sufficient for application to the next two theorems.
Remark 1.4.
For (1.12) in Theorem 1.3 we can replace the conditions with . This is because there exists such that is contained in “thin cylinders” (not necessarily oriented parallel to ) of length between and and radius such that every pair as in (1.12) is contained in one of these cylinders. Here does not depend on or . We can apply the theorem to each thin cylinder, since , then sum over the thin cylinders.
We will use Theorem 1.3 together with a coarse-graining scheme in establishing the following.
Theorem 1.5.
Suppose and satisfy A1, A2, and A3. There exists such that
| (1.14) |
As we have noted, for of order , if contains a vertex at distance of order from (not too near or ), then the associated extra distance traveled by the geodesic is of order , and by Theorem 1.5 the same is true for in place of . Since the corresponding passage times satisfy , this means that either
The assumption (1.11) says the first of these is unlikely, and Theorems 1.3 and 1.5 can be used to show it is unlikely that there exists a for which the second or third occurs. (Not without complications, though, as we cannot assume .) This is the idea behind the following. For define intervals enlarging :
| (1.15) |
where “sufficiently large” will be specified later, and
For we have ; in this case we may view as being the cylinder fattened transversally to width , and lengthened by an amount which varies with the size of relative to , chosen to be “enough to make wandering of geodesics out the cylinder end at least as unlikely as out the sides.”
For we write for so .
Theorem 1.6.
Suppose and satisfy A1, A2, and A3. There exist such that for all ,
| (1.16) |
We include the condition because we are primarily interested in transverse fluctuations of geodesics out the side of , so we wish to avoid oriented in a too–transverse direction.
Remark 1.7.
Remark 1.8.
In [8] and [6], an alternate strategy was used to prove LPP analogs (in integrable cases) of Theorems 1.3 and 1.6 in . Theorem 1.5 was already known for that context—see the comments following (1.8). Essentially the strategy for the Theorem 1.3 analog in [8] is this, when translated to FPP: first the easier upward–deviations half of Theorem 1.3 is proved. For downward deviations, consider the points 0 and , and a cylinder of radius with axis from to . Suppose there are (random) vertices with for which the passage time is fast: for some large . From the upward–deviations half of Theorem 1.3, with high probability we have also and . From this, using that is proportional to and , assuming is large enough,
| (1.17) |
This has probability exponentially small in , by (1.11), hence so does the probability of such existing. This strategy does not work for FPP, however, as it requires one to already know Theorem 1.5 to obtain the second inequality in (1.17).
2. Existence of acceptable random graphs
We construct a random graph satisfying A1. We begin by constructing the point process of vertices. We start with a “space–time” Poisson process (which we view as a random countable set) of density 1 with respect to Lebesgue measure in . We say a point appears at time in if , and we say is empty at time if no point in appears in during . We then define
| for some and with , appears at time in and | |||
In other words, we keep in the coordinate of a point of if is the first point to appear in some ball of radius . Then almost surely, for each there is a unique point , and we view as the time at which appeared in . With probability one, every unit ball in contains a point of . We call the available–space point process.
For the set recall that denotes the corresponding Voronoi cells. More generally we write for the Voronoi cell containing any (with some arbitrary convention if is on the boundary of multiple cells), and for the unique point of in . When convenient we view as the line segment joining and . Let denote the open Euclidean ball of radius about . For , the Delaunay graph of is our graph . For we fix and use
We call the augmented Delaunay graph of . The edges in which are not in the Delaunay graph are called augmentation edges. We write to denote that are adjacent vertices in , and to denote adjacency in the Delaunay graph of . If , then for all . Hence by A1(ii),
| (2.1) |
Similarly if then contains no point of , so ; thus
| (2.2) |
Remark 2.1.
The purpose of augmentation is roughly the following. Consider the line segment between . It passes through a sequence of Voronoi cells , and there is a corresponding path in the Delaunay graph. If too many of the cells are “thin,” then the Delaunay path length may be much greater than , making it difficult to bound the dilation. The augmentation effectively allows paths in that skip over such problematic sequences of cells, at least for a small distance, enabling us to prove bounded dilation while preserving other properties of the Delaunay triangulation. We can reduce the occurrence of augmentation to involve an arbitrarily small proportion of vertices by using a small enough . We will not give details here.
For and let .
Proposition 2.2.
The augmented Delaunay graph of the available–space point process satisfies A1.
Proof.
A1(i) for follows from the same properties for ; since is constructed from via isotropic and translation-invariant local rules, A1(i) also holds for . A1(ii) follows from the fact that the first point of to appear in any radius-1 ball is always a point of .
To prove A1(iii), observe first that by (2.1), given the cell and all Delaunay edges are determined by . Therefore the collection of Voronoi cells intersecting is determined by , and hence so are all augmentation edges . , in turn, is determined by , so for , the restriction is determined by . Since is independent in disjoint regions, A1(iii) follows with .
Turning to A1(v), let and , and let . For let denote the cube and . This means the cubes in form a shell around , with a smaller shell of cubes in between, and the diameter of is less than . Then any radius- ball intersecting must contain a cube in . Letting it follows that at time , for some , at least points of have appeared in but none in . Letting be the number of points of appearing in before the first point of appears in , this says that . Since it follows that
| (2.3) |
and hence for ,
| (2.4) |
Let , so and . Now is a lattice of cubes, and we divide it into sublattices, each consisting of a cube together with all its translates by vectors in which intersect . We label these sublattices of cubes as , and the cardinality satisfies
| (2.5) |
for each . We denote the corresponding union of cubes as . The spacing of the cubes in means that that the shells are disjoint, so the variables are i.i.d.
For , taking in (2.4) we obtain and hence using (2.5), provided is large (depending on ),
| (2.6) |
proving A1(v).
Finally we consider A1(iv). Let . As in Remark 2.1, passes through a sequence of Voronoi cells , and there is a corresponding path in the Delaunay graph. (There is probability 0 that intersects some in just a single point, so we will ignore this possibility, meaning that “passes through” here is unambiguous.) For let be the first point of in and let , so by convexity of cells, for all . We select indices iteratively, taking as the least index for which either or . Then is always a Delaunay or augmentation edge, so we consider the path in ; in particular we want to bound relative to for .
3. Straightness of geodesics and and regularity of means
For and , let
| (3.1) |
the latter being a cube (ignoring the boundary.) More generally for we define to be the cube containing , with some arbitrary rule for cube–boundary points.
The bound (1.3) applies to deterministic ; we cannot for example take . Instead for random we can apply (1.3) to nearby points of for some , and use the following. It is the only place the assumption A2(iv) of bounded dilation is used.
Lemma 3.1.
Suppose and satisfy A1, A2, and A3. There exist constants as follows.
(i) Let and . Then
(ii) For all ,
Proof.
To prove (i) we condition on . Given , by A1(iv) there exists a path in with
Writing for , for we have
| (3.2) |
so using A2(ii) it follows that for some ,
| (3.3) |
where is the large-deviations rate function of the variables . From this, using A1(v),
| (3.4) |
proving (i).
To prove (ii) we apply (3.3) to and , and use the fact that for all . ∎
Building on Lemma 3.1 we obtain the following.
Lemma 3.2.
Suppose and satisfy A1, A2, and A3. There exist constants as follows. For all and with and ,
| (3.5) |
We write
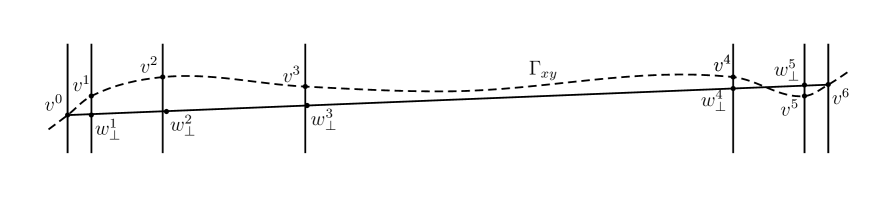
to denote that the vertices appear in the order in traversing from to . For preceding in we write for the segment of from to . (Here we do not require .) For in a geodesic and , let be the first vertex in before satisfying . We then call the trailing s-segment of in . Note that by (2.1), . Define the hyperplanes, slabs, and halfspaces
We turn next to a weaker version of Theorem 1.5 similar to (1.7); we will need it on the way to the proof of Theorem 1.5. The proof of (1.7) in [1] does not carry over immediately to the present situation, as it uses translation invariance of the lattice. But we can use radial symmetry here to give a distinctly shorter proof than that of (1.7) in [1].
Recall is nonnegative by subadditivity of . For technical convenience we assume in A1(ii).
Proposition 3.3.
Suppose and satisfy A1, A2, and A3. There exists such that for all ,
| (3.7) |
Proof.
It is sufficient to prove the bound for all sufficiently large , so we will tacitly assume is large, as needed.
We consider the geodesic for a fixed large . Let be as in A1(iii). For let be the first vertex in with the property that the trailing -segment of in is contained in , and let be the starting point of this trailing segment. From (2.1) it is easy to see that we must have . It follows that ; we denote this last region by . Note that any two sets are separated by distance at least .
We need to control the entropy of the collection of pairs . To do this, we enlarge this collection in such a way that we can put a natural tree structure on it. To that end, let be the first vertex in , if one exists, which is at distance at least from . Then let be such that is the trailing -segment of in , and let , which contains . We repeat this to obtain , stopping when no exists. Note this preserves the property of separation by distance at least . Also, each new is within distance of some already-existing .
We define the discrete approximations , and then let
which contains ; the sets are separated from each other by distance at least . We call primary pairs, and secondary pairs. Since , we have
| (3.8) |
We now make a graph with vertices by placing an edge between the ith and jth pairs if . The construction ensures that the resulting graph is connected, and it is easy to see that the disjointness of the sets means the number of neighbors of any pair is bounded by some . We label as the root, and by some arbitrary algorithm, we take a spanning tree of the graph, which we denote . For counting purposes, we view two such trees as the same if they have the same pairs , and the same set of primary pairs. We define parents and offspring in this rooted tree in the usual way: for a given pair , its parent is the first pair after in the unique path from to the root, and its offspring are those pairs having as parent.
The tree determines what we will call an abstract tree, in which all that is specified is the number of offspring of the root, then the number of offspring of each of these offspring, etc. The number of possible abstract trees here with vertices is at most , and, provided is large, for each such abstract tree the number of corresponding actual trees is at most , so the number of trees consisting of pairs is at most .
We now consider all possible trees , with vertices , and with primary. Let denote the number of vertices in the tree . We have
| (3.9) |
We proceed by contradiction: we want to show that for some , if then the right side of (3) approaches 0 as , which means a.s. , contradicting the definition of .
Thus suppose
| (3.10) |
with to be specified, and fix with vertices with . For let
taking the value when there is no such path. is determined by the configuration in
There must exist satisfying and
It follows that, letting
the ’s are independent (since the sets are separated from each other by distance more than ) and satisfy
| (3.11) |
Each is stochastically larger than
From (1.10) and (3.8) we have for some that From (3.8), (3.10), and subadditivity we also have
Hence from Lemma 3.2 we obtain that provided is large, for all ,
| (3.12) |
By increasing we may make this valid for all . We then have for and ,
| (3.13) |
Recalling (3) and (3.11) we then have
| (3.14) |
so by (3), provided (and hence ) and (in (3.10)) are large,
| (3.15) |
As we have noted, since this approaches 0 as , it contradicts the fact that a.s. Thus (3.10) must be false. ∎
We need to use a result from [2] to the effect that “geodesics are very straight.” It is proved there for FPP on a lattice, but the proof goes through essentially unchanged for the present context. The heuristics are as follows: suppose the geodesic passes through a vertex at distance from ; by symmetry we may suppose . The geodesic then travels a corresponding extra distance . If the angle between and is small, this extra distance is of order , and from (1.11), the cost of this (meaning log of the probability) is of order . If instead the angle between and is not small, the extra distance is of order and the cost is of order . We can combine these into a single statement by saying the cost for general should be whichever of these two costs is smaller, at least for .
The exact formulation of the straightness result contains extra log factors relative to the preceding heuristic, due to the need to bound the probability for all simultaneously. It is as follows, using the constants of (1.10). Define and by
Here factoring out a power of on the right, and the use of the sup, ensure that is strictly increasing. Note that by (1.10) we have
| (3.16) |
Then define
| (3.17) |
Note that by (1.10) and (3.16), for large ,
| (3.18) |
The “min” in the definition of is in accordance with our heuristic: from [2], we have for large that for from (1.10),
| (3.19) |
Finally, define the symmetric version of :
| (3.20) |
This makes the right half of the region the mirror image of the left half; this region is a “tube” (narrower near the ends) surrounding the line from 0 to bounded by the shell , augmented by a cylinder of radius and length around each endpoint, so we will call it a tube–and–cylinders region.
We will also consider tube–and–cylinders regions around general pairs in place of . To that end, let be translation by followed by some unitary transformation which takes to the positive horizontal axis, so that . (The particular choice of unitary transformation does not matter.) Then is a tube–and–cylinders region containing .
The proof of the acceptable–random–graphs version of the straightness bound is little changed from the lattice-FPP version in [2]; we can readily use Lemma 3.1(i) to change the result from “point–to–point” (say, 0 to ) to “ball–to–ball,” with a sup over and . We omit the details.
Proposition 3.4.
Suppose and satisfy A1, A2, and A3. There exist constants as follows. For all ,
| (3.21) |
We next bound transverse increments of passage times from 0, that is, increments which are (approximately) along the boundary of a ball of large radius , over distances . The following lattice-FPP result from [2] carries over straightforwardly to the present context with the help of Lemma 3.1(i), and again we omit details. Recalling the cubes of side define
Proposition 3.5.
Suppose and satisfy A1, A2, and A3. There exist constants as follows. For all with
| (3.22) |
and all , we have
| (3.23) |
We next prove a seemingly obvious fact: is approximately increasing in .
Lemma 3.6.
Suppose and satisfy A1, A2, and A3. Given there exist constants as follows.
(i) Let . Let satisfying . Then
| (3.24) |
Here .
(ii) For all ,
| (3.25) |
Remark 3.7.
Proof of Lemma 3.6..
We prove (i), then obtain (ii) as a straightforward consequence. The idea is to show that must with high probability approach approximately horizontally, which forces to be near with high probability; a non-horizontal approach would force the sup in (3.21) to be large.
Suppose (3.24) holds under the added condition . Then for we can take with and see that the hypotheses are satisfied with in place of . (This may require increasing , but without dependence on .) Applying (3.24) times then yields
Therefore it is sufficient to prove the lemma for . It is also sufficient to consider for any fixed .
With to be specified, define
| (3.26) |
Note that provided (and hence and ) is large, which we henceforth tacitly assume, and provided is small, we have and . Suppose . We have (meaning lies to the left of the cylinder around in the tube-and-cylinders region ) and so by (3.18),
| (3.27) |
Thus . We let , so for . See Figure 1. Then for such , recalling , we have
so assuming is large and is small,
| (3.28) |
Also for , and hence by (1.10), . It follows that provided we choose large enough in (3.26),
With (3.28) and Proposition 3.3, this yields that provided is large,
| (3.29) |
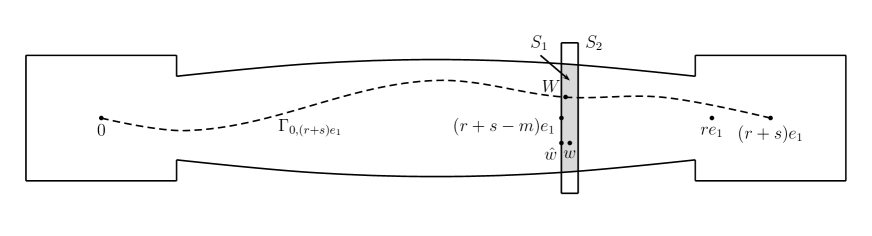
We need a lower bound for . Since , we can choose small enough so . Provided is large enough (in the lemma statement, and depending on ), since we have
| (3.30) |
Observe that for every vertex we have
| (3.31) |
Let
and let be the first vertex in satisfying . If then by (3.31) and subadditivity we have
Hence
| (3.32) |
It follows from (1.3) that for some
Assuming is small, by Proposition 3.4 and (3.30) we have
| (3.33) |
Combining these yields
| (3.34) |
To use (3) we also need a lower bound for . For , using (3),
| (3.35) |
We consider the first probability on the right in (3); the second probability is similar. For we have using (3.27) that
and then from (1.10),
From these and Lemma 3.2 (see there) we obtain that if is large enough, then for ,
| (3.36) |
The same bound holds for the second probability on the right in (3). With (3) and the definition of in (3.26) this shows that
We now prove (ii). From (i), there exists such that whenever ; there then exists such that whenever . We therefore have
which proves (3.25). ∎
4. Proof of Theorem 1.3—downward deviations
We use a multiscale argument which is related to chaining. But first we dispense with simpler cases that only require Lemma 3.2 and Proposition 3.4. The first such case is pairs which are close together. For technical convenience later, we prove the following also for geodesics with endpoints in the set , satisfying for fixed and large, given by
| (4.1) |
with to be specified.
Lemma 4.1.
Suppose and satisfy A1, A2, and A3. There exist constants for all and ,
| (4.2) |
Proof.
Lemma 4.1 means we need only consider satisfying
| (4.5) |
Writing for the angle between nonzero vectors , this means that for large ,
| (4.6) |
A second simple case is small . For fixed and , from Lemma 3.1 for all we have , so for we have , and hence the probability in (1.13) is 0. Therefore there exist such that (1.13) is valid for all and .
A third simple case is , with large enough. As in (4) and (4), for from Lemma 3.2 we then have
| (4.7) |
It follows that, for from Theorem 1.3, we need only consider , and therefore also , which means .
A fourth simple case is pairs for which goes well outside , when is large and . Assuming is large, , from the third simple case, is the choice of interest in the following.
Lemma 4.2.
Suppose and satisfy A1, A2, and A3. Then given there exist constants such that for as above, for all we have
Proof.
Note the assumptions guarantee . Let with , and let satisfy (4.5), with . Recall the transformation which takes to . Suppose and let ; we may take with . We claim that, for from (3.20), we have , with from the definition of . We consider several cases.
Case 1. , that is, is to the side of . See Figure 2. From symmetry we may assume . Note that in the definition (3.17) of , the case is the relevant one here if and only if . We have
| (4.8) |
and , so
Also as in (4.8),
so
Therefore under Case 1,
| (4.9) |
and symmetrically the same holds for .
Case 2. with , or with , that is, is past the end of but is to the side of . See Figure 2. The two ends are symmetric so we need only consider with . Let be the hyperplane through perpendicular to , and let be the orthogonal projection of into , so and . Since , by (4.6) the angle is small enough that we have and hence, for from (4.6),
| (4.10) |
therefore
Further, similarly to (4.10), since the small angle ensures , we have
| (4.11) |
and therefore using (1.10),
This proves the right side of (4.9) under Case 2.
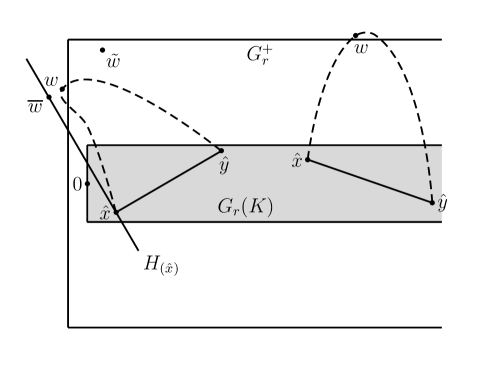
Case 3. with , or with , that is, is past the end of and is past the end of . The two ends are again symmetric so we need only consider with . Then so
4.1. Step 1. Setting up the coarse-graining.
For purposes of coarse–graining and multiscale analysis of paths, we build grids inside on various scales, using small parameters satsfying
| (4.13) |
in the sense that the ratio of each term to the one following must be taken sufficiently large, in a manner to be specified. We choose these so and are integers. There is also a fourth parameter , and we further require
| (4.14) |
all of (4.14) can be satisfied by taking small enough after choosing . For , a jth–scale hyperplane is one of form , and the jth–scale grid in is
where is to be specified. Note that larger values correspond to smaller scales, and since is an integer, a th–scale hyperplane for some is also a th–scale hyperplane for . A hyperplane is maximally jth–scale if it is th–scale but not th–scale.
The th–scale grid divides a th–scale hyperplane into cubes which we call jth–scale blocks. For concreteness we take these blocks to be products of left–open–right–closed intervals. Each point of the hyperplane then lies in a unique such block. For a point in a th–scale hyperplane, the jth–scale coarse–grain approximation of is the point which is the unique corner point in the block containing . We abbreviate coarse–grain as CG. The definition ensures that two points with the same th–scale CG approximation also have the same th–scale CG approximation for all larger scales .
A transverse step in the th–scale grid is a step from some to some satisfying ; a longitudinal step is from to satisfying . Define
so from (1.10),
| (4.15) |
Here is chosen so that the typical transverse fluctuation for a geodesic making one longitudinal step is transverse steps.
On short enough length scales, coarse–graining is unnecessary because we can use Proposition 3.5 and Lemma 4.1. More precisely, we will need only consider where is the least for which
| (4.16) |
Provided is large, this means the spacings and of the th–scale grid are large, and therefore we can choose so that is an integer multiple of , and then choose such that is an integer multiple of . Then (since and are integers) for all , the th–scale grid in every th–scale hyperplane is contained in , which we call the basic grid.
We say an interval in has th–scale length if its length is between and .
Given with , satisfying (4.12), we define a hyperplane collection , which depends on the geodesic , constructed inductively as follows. All hyperplanes have , and we view the hyperplanes as ordered by their indices. Let be the least such that there are at least 4 th–scale hyperplanes between and . Subject always to the constraint , at scale we put in the th scale hyperplanes second closest to and to ; we call these –terminal hyperplanes. The gap between the –terminal hyperplanes is at least and at most . In general, when we have chosen the th–scale hyperplanes in for some , each gap between consecutive ones is called a th–scale interval, and the hyperplanes bounding it are the endpoint hyperplanes of the interval. For any interval we also call an interval; which meaning should be clear from the context. A th–scale interval is short if it has th–scale length, and long otherwise. We then add th–scale hyperplanes to , of 3 types.
-
(i)
The first type consists of two hyperplanes, which are the th–scale hyperplanes second closest to and to , which we call –terminal hyperplanes. A –terminal hyperplane may also be a th–scale hyperplane on some larger scale , in which case we call it an incidental kth–scale hyperplane.
-
(ii)
As a second type, for each non-incidental th–scale hyperplane we put in the closest th–scale hyperplanes on either side of , that is, and , which we call sandwiching hyperplanes.
-
(iii)
The third type is th–scale joining hyperplanes; we place between 1 and 4 of these in each long th–scale interval, depending on the behavior of in the interval in a manner to be specified below. Joining hyperplanes are always placed in the “extremal 10ths” of the long interval; more precisely, if the th–scale interval has th–scale length then they are placed at distance from one of the endpoints for some , with at most 2 such hyperplanes at either end.
We use superscripts and for quantities associated with left–end and right–end joining hyperplanes, respectively. We continue adding hyperplanes through all scales from to ; after adding th–scale hyperplanes, is complete and we stop.
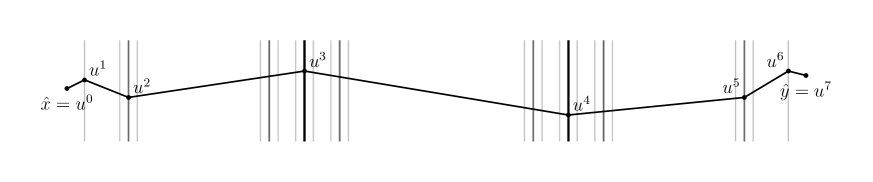
A terminal jth–scale interval in is an interval between a terminal th–scale hyperplane and the terminal th–scale hyperplane closest to it; the length of such an interval is necessarily between and , so it is short. In Figure 3, the interval between the hyperplanes containing and is a terminal th–scale interval.
At most 6 th–scale hyperplanes are added inside each th–scale interval, and only 1 if the interval is terminal. Therefore if contains th–scale hyperplanes, then the number of th–scale hyperplanes is at most . It follows that
| (4.17) |
In keeping with (iii) above, we will designate up to four random values in for each long th–scale interval , for each , depending on . These will satisfy
We call the values outer joining points, and inner joining points; the inner ones will represent locations where a certain other path traversing can be guided to coalesce with , and we call the (potential) joining hyperplanes of the interval . We say “potential” because not all are necessarily actually included in ; which are included, and with what values of , depend on rules to be described.
Recall that denotes the closest point to in the basic grid, and . We need only consider the case in which each share a Voronoi cell with a basic grid point, that is,
| (4.18) |
we readily obtain the general case from this via Lemma 3.1, since for every the point satisfies (4.18) and . Since , (4.18) ensures that . For and a path in from to , for vertices in , write for the segment of from to and let denote the entry point of into , that is, the first vertex of in , necessarily next to (in the sense that its Voronoi cell intersects .) Our aim is to approximate a general geodesic (subject to (4.12)) by a CG one via certain marked (basic) grid points which we will designate, lying in hyperplanes . In the geodesic , the first and last marked grid points are and (see (4.18).) Initially, the ones in between are the discrete approximations of the entry points corresponding to each of the hyperplanes . Here since and , we always have . Later we will remove some of these initial marked grid points, and replace others with their th–scale CG approximations for various . This means not every necessarily contains a marked grid point, in all our CG approximations. When a path has a marked grid point in some , we denote that marked grid point as . For all our CG approximations, the first and last marked grid points are and , and for some the ones in between each lie in the th–scale grid in some th–scale hyperplane . If such a CG path has marked grid points in consecutive th–scale hyperplanes of , we say makes a jth–scale transition from to . Such a transition involves one longitudinal step and some number of transverse steps in direction for each , going from to . We say a th–scale transition is normal if for all , and sidestepping otherwise. Even on the smallest scale , every th–scale transition with is nearly in the direction, in that its angle satisfies (similarly to (4.6))
| (4.19) |
provided is large, with from the definition of .
We refer to a path from to , together with its marked grid points, as a marked path; the path alone, without the marked grid points, is called the underlying path. We may write a marked path as ; here the are grid points. The pairs are called links of the path. If is the concatenation of the geodesics , we call it a marked piecewise–geodesic path; we abbreviate piecewise–geodesic as PG. (Recall that when , denotes .) Unless otherwise specified, when we give a marked path by writing its marked points in this way, we assume the path is the (unique) marked PG path given by those marked points.
Recall that
with being cubes of side . Suppose we have a marked PG path
contained in . We associate four quantities to this path:
Using the standard fact that for some ,
| (4.20) |
we see that provided is large and all , represents added length in relative to the lower bound , in that
| (4.21) |
Informally we refer to as the extra length of the path . From (4.20), subadditivity of , and Lemma 3.6 we obtain, after reducing if necessary,
| (4.22) |
In our applications of (4.22), the last condition will always be satisfied due to (4.19). In general, provided is large and all lie in , with much larger than the width of , we have
| (4.23) |
We can now define the joining points in a long th–scale interval of th–scale length, where . We begin with , which lie in the left part of . We first define modified values of which will appear in Lemmas 4.5 and 4.6:
| (4.24) |
We consider a marked PG path with marked points in the th–scale grid: let
and for each let
and let
| (4.25) |
We may view as an approximation of the “extra distance at scale ,” that is, of ; is this extra distance normalized by the fluctuation size. For let , and let
| (4.26) |
see Figure 4. Then
| (4.27) |
so in view of (4.19), there is an “extra distance”
| (4.28) |
Suppose that for some we have
| (4.29) |
as happens if is maximized at . From (1.10), the second inequality ensures that
| (4.30) |
and the first inequality in (4.29) tells us that
| (4.31) |
It then follows from (4.28), (4.30), and (4.31) that the path from to is bowed in the sense that
| (4.32) |
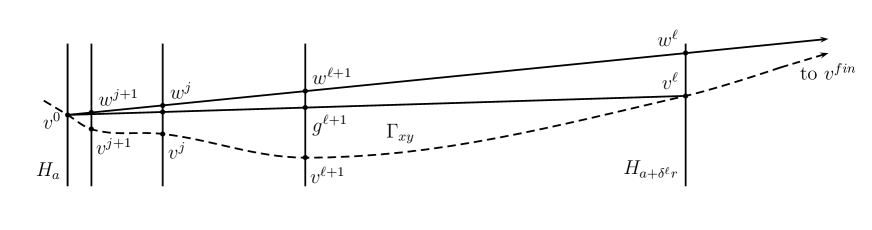
Motivated by this we let
| (4.33) |
We refer to the 3 options in (4.33) as the forward, bowed, and totally unbowed cases, respectively. They may be interpreted as follows. In the forward case the initial steps have little sidestepping, and we will see that this eliminates the need to exploit bowedness; this should be viewed as the “baseline” or “most likely” case. Otherwise we look for a scale , with , on which is bowed as in (4.32), by seeking a scale (the arg max) satisfying (4.29). In the bowed case such a scale exists; see Figure 4. In the totally unbowed case there is no such scale, meaning is maximized for essentially the full length scale of the interval . By (4.31) this forces the extra distance to be very large. We define the inner and outer joining points as
We define in a mirror image manner to in , going backwards from to instead of forward from to . That is, we use the points in place of the ’s and in place of ; otherwise the definition is the same, and the analogs of (4.28), (4.30), and (4.31) are valid for the analog of .
We now describe the rules for which of the four th–scale joining hyperplanes with , in a long th–scale interval , are included in . We note again that the endpoint and sandwiching hyperplanes at both ends of are always included; in some instances the sandwiching hyperplanes coincide with outer joining hyperplanes, so these criteria never rule out the inclusion of such hyperplanes.
-
(i)
If both ends of have the forward case, then we include the inner joining hyperplanes in ; these are at distance from the interval ends. The outer ones coincide with the sandwiching hyperplanes at distance from the interval ends, so they are included as well.
-
(ii)
If both ends have the bowed case, then we include both the inner and outer joining hyperplanes in . We note that when either of , the corresponding outer joining hyperplane coincides with the sandwiching hyperplane as in (i), so it is already in on that basis.
-
(iii)
If both ends have the totally unbowed case, then we include only the inner joining hyperplanes.
-
(iv)
If the two ends have different cases, we determine which end of the interval is dominant according to the criterion described next. We then include the joining hyperplane(s) only at the dominant end, 1 or 2 hyperplanes in accordance with (i)—(iii) above. We call this the mixed case.
To determine the dominant end of a long th–scale interval , necessarily having th–scale length for some , in the mixed case, we first select those non–sandwiching hyperplanes which are candidates for inclusion in , in accordance with (i)—(iii) above. (For example, if the path has the bowed case with at the left end and the forward case at the right, we select the inner and outer joining hyperplanes on the left, and only the inner on the right.) For these candidate hyperplanes, along with the 4 endpoint and sandwiching hyperplanes in , we consider the corresponding “tentative” marked PG path (part of ) with a marked point in each of the hyperplanes: with or 6, where and are th and th–scale CG approximations. The inner joining hyperplanes contain , with 2 or 3; we call this the central index; the gap from to is the longest in , at least . Let be the orthogonal projection of into the line ; see Figure 5. We use the fact that the excess length can be approximately split into components associated with the two ends, as follows. When the central index is we have
| (4.34) |
For the first difference on the right we have from (4.20)
and similarly for the third difference, while for the middle one,
so the middle difference in (4.1) is only a small fraction of the whole:
| (4.36) |
We designate the left end of as dominant if the first of the 3 differences on the right in (4.1) is larger than the third difference, and the right end in the reverse case. As given in (iv) above, we include in only the candidate joining hyperplanes from the dominant end; the non-dominant end has its endpoint and sandwiching hyperplanes but no joining ones.
We note that if (for illustration) the left end is dominant, then, after excluding the right-end joining hyperplanes, we are left with the marked PG path , for which the contribution of the right end to the extra length can be bounded: we have
| (4.37) |
where the last inequality follows from dominance of the left end, so similarly to (4.36),
| (4.38) |
The same bound with in place of holds symmetrically when the right end is dominant.
Remark 4.3.
In the bowed case at the left end of a th–scale interval , with , define
and symmetrically at the right end. See Figure 4; there is here. We have from (4.31) and (4.33)
| (4.39) |
and as in (4.30) it follows from these that
| (4.40) |
The advantage of (4.40) is that it depends only on and not on , whereas in (4.3) the points do depend on . What we have shown is that if there exists with for which (4.3) holds, then (4.40) holds, not involving . We further have , while by the first half of (4.30) we have and , so
| (4.41) |
Again the left and right expressions in (4.3) depend only on , not on .
In (1.13) we may interpret as a reduction in the time allotted to go from to , relative to . In place of the reduction relative to , we can consider a modified reduction, call it , which is relative to :
The modified reduction is larger: using (4.23) we see that
We will need to (roughly speaking) allocate pieces of to the various transitions made by and certain related paths. Motivated by this, we define the jth–scale allocation of a transition to be
| (4.42) |
In (4.42) the factor is used due to (4.17). For a marked PG path as above, with marks in the th–scale grid, we have from (4.21)
| (4.43) |
Also, since , all are large provided is large and .
Remark 4.4.
We now present an outline of the strategy of the proof. Each geodesic can be viewed as a marked PG path with marks in the basic grid in each of the hyperplanes of . The goal is to gradually coarsen this approximation on successively larger length scales until we obtain a final path . The number of possible final paths (outside of a collection of “bad” paths having negligible probability) is small enough so that a version of (1.13) can be proved for final paths.
To perform the coarsening we iterate a two-stage process, with the exception that the first iteration has only one stage. The first iteration is on the th scale, the second on the larger th scale, and so on. For the th–scale iteration, we perform a set of operations on the original marked PG path (essentially ) called shifting to the th–scale grid, replacing each marked grid point (located in the basic grid) in each hyperplane in with a nearby point in the th–scale grid. Each further iteration has two stages. For the th scale (second) iteration, in the first stage we shift those marked points lying in th–scale hyperplanes in to the th–scale grid. In the second stage of the iteration, we remove from the marked PG path those marked points not lying in th–scale hyperplanes, with exceptions for points in terminal hyperplanes. See Figure 6. In general, for the th–scale iteration (), at the start of the iteration all the marked points in non-terminal hyperplanes are th–scale grid points in th–scale hyperplanes; in the first stage we shift the ones in th–scale hyperplanes to the th–scale grid, and in the second stage we remove the ones not in th–scale hyperplanes, again with exceptions in terminal hyperplanes.

The difficulty is that as we alter the marked PG path, the length and corresponding –sum change, with marked–point deletions always reducing these sums, and we need to ensure that, with high probability, the corresponding sum of passage times “tracks” these changes at least partly, to within a certain allocated error related to the above–mentioned . For shifting to a grid the tracking is not too difficult to achieve, as the allowed error turns out to be larger than the change in –sum being tracked. But for removal of marked points the tracking requires multiple different strategies, depending on the options in (4.33) for the marked grid point locations in the gap between each two successive th–scale hyperplanes in . The particular tracking needed is that, with high probability to within the allocated errors, when marked points are removed from a gap, the decrease in total passage time is at least a positive fraction of the decrease in –sum. The primary difficulty in achieving this is that if the gap has a large length , then the relevant passage time fluctuation size may overwhelm both the reduction in –sum and the allocated errors; here the remedy involves the “joining hyperplanes.” We also make use of what we call intermediate paths, which (in most cases) have total passage time and –sum in between the values that exist before and after the marked–point removal, and are chosen so that they are relatively easy to compare to the pre–removal path.
In (1.13) the passage time reduction for the full path is , which a priori suggests that the total of the allocated errors associated to a path should not exceed this amount. There is no natural way to work with such a small total error yet achieve bounds uniformly over all . However, we will see that the tracking enables us to increase the total of the allocated errors by an amount proportional to the extra Euclidean length of the original marked PG path relative to the “horizontal” distance , which gives the second term in parentheses in the formula (4.42). With this the necessary uniformity can be achieved, both for the tracking and for the fluctuation bounds on passage times of final paths .
4.2. Step 2. Performing the th–scale (first) iteration of coarse–graining.
As described in Remark 4.4, for the th–scale iteration we perform a sequence of operations on marked PG paths called shifting to the jth–scale grid, in the hyperplanes of . The th–scale iteration is different from those that follow, in that there is no second stage of removing marked points, and no need for the “tracking” of Remark 4.4. In general we will refer to the marked PG path existing before a shift or removal operation as the current (marked) path, and the modified one resulting from the operation as the updated (marked) path. The allocations of (4.42) are used only for the th–scale iteration; we will define other allocations later.
For the th scale, every is a th–scale hyperplane. Suppose with . Let , and define by . At the start, the current path is with marks at the grid points :
Note that is a marked path, but not necessarily a marked PG path, since need only pass near , not necessarily through it. By near we mean that both and lie in the same cube of the basic grid.
Recall that the blocks of have side . The first shift to the th–scale grid happens in , replacing with to produce the updated marked path
with the underlying path being the concatenation of the geodesics . Next we repeat this in , replacing with . We continue this way performing shifts to the th–scale grid in , producing the updated path
with the underlying path now (in view of (4.18)) being the marked PG path given by these points.
Let us analyze the effect of these shifts on . Consider the th shift, replacing with . From (4.6) and basic geometry we have
| (4.44) |
Consider first the “sidestepping” case: . Since , we have from (4.14), (4.15), and (4.44) that provided is large, for ,
| (4.45) |
Now consider the “normal” case: . From (4.14), (4.15), and (4.44) we have
| (4.46) |
We can interchange the roles of and and/or replace with , so it follows from (4.2) and (4.2) that
| (4.47) |
and
| (4.48) |
and then also
| (4.49) |
and
| (4.50) |
We claim that
| (4.51) |
It is enough to show
| (4.52) |
To that end, we have
so
| (4.53) |
From (4.14), the last term satisfies
| (4.54) |
If the th transition has very small sidestep, that is,
| (4.55) |
then provided is large, since , using (4.14) the first term on the right in (4.53) satisfies
| (4.56) |
If instead the th transition has larger sidestep, meaning
| (4.57) |
then the first term on the right in (4.53) satisfies
| (4.58) |
Together, (4.53)—(4.58) prove (4.52), and thus also (4.51). This same proof shows that
| (4.59) |
and similarly for .
From (4.1), (4.47), (4.48), and (4.59) we bound the total change in length from all shifts to the th–scale grid:
| (4.60) |
and similarly, using (4.49)–(4.50) instead of (4.47)–(4.48),
| (4.61) |
In view of (4.59), the derivation of (4.60) and (4.61) is also valid if we replace with , which gives the alternate bound
| (4.62) |
For basic grid points define
We have
| (4.63) |
and a form of approximate subadditivity holds: for basic grid points ,
| (4.64) |
From Lemma 3.1 we have for sufficiently large that the event
satisfies
| (4.65) |
Before proceeding we stress that , and should always be viewed at functions of . From (4.1) we have
| (4.66) |
Therefore
| (4.67) |
The key inclusion here is the second one, as it takes us from an event involving the passage time of the original path to an event involving the th–scale CG approximation , up to the “tracking error event” given in the last line. The name is only partly suitable here—bounding the last probability in (4.2) is related to the tracking of Remark 4.4, in that we are ensuring that changing the path from to doesn’t change too much, but the change in -sum here is too small to require being tracked.
4.3. Step 3. Bounding the tracking–error event for the th–scale–iteration.
Consider next the tracking–error event
from the right side of (4.2). Recalling Remark 4.4, this reflects the failure of the passage time to track well when the path changes from to its th–scale CG approximation . We have
| (4.68) |
and therefore using (4.59),
| (4.69) |
Let us consider any one of the events in the first union on the right in (4.3); we prepare to apply Proposition 3.5. We assume as the opposite case is similar. Define by
and let
We observe that in (4.2) and (4.2), one can replace with any given positive constant, if is large enough. Consequently we have
| (4.70) |
We split into two corresponding increments, using (4.64):
| (4.71) |
and define the corresponding unions
so that (4.3) says the first union in (4.3) is contained in . Define the set of corresponding to (4.12)
with from (4.12), and define the events
For configurations , all lie in , so the number of possible tuples arising from some is at most . Define by
so that . By (1.10),
From this, (4.14), and (4.16),
| (4.72) |
Now
so for we have for some that
In view of (4.70) and (4.72) we then get from Proposition 3.5 and Lemma 4.2 that
| (4.73) |
Next, recalling (4.70), we observe that and provided is large,
so using (4.70) and the bound on in (4.12) we have from Lemmas 3.1 and 3.2 that
| (4.74) |
4.4. Step 4. Further iterations of coarse–graining: preparation.
For the th–scale and later iterations of coarse–graining we use allocations associated not to a particular transition, but to the shifting of the marked grid point in some th–scale current marked PG path to the th–scale grid. Specifically, in such a shift the marked grid point in the th–scale grid is replaced by the th–scale CG approximation , and the other marked grid points are left unchanged. Consider an initial marked PG path when an iteration of shifts to the th–scale grid begins:
with . Suppose that for some not containing two consecutive integers, the marked grid points are the ones shifted, one at a time, in the iteration, updating the path from via a sequence of intermediate paths to a final . Note that since does not contain two consecutive integers, the shifts of different ’s do not “interact,” as shifting only affects the path between and and only affects among the marks; we will refer to this aspect as noninteraction of shifts.
Recall from (4.24). The allocation we use most widely, in both stages of each iteration, is which appears in the next lemma. is a variant of
Lemma 4.5.
Let . Consider a marked PG path
in with , and , and let , not containing two consecutive integers. Define
and for with , let
| (4.76) |
Then provided is sufficiently large,
| (4.77) |
and
| (4.78) |
The bound (4.77) would be trivial if we used instead of the definition of . The point of Lemma 4.5 is that when the transitions affected by the shifting start or end at points which are at distance a large multiple of from , it increases the usable value of by a multiple of , manifested in the definition of . Here by “usable” we mean “not so big that (4.77) or (4.78) fails.”
Proof of Lemma 4.5..
If for some then so we have from (4.20)
| (4.79) |
so
| (4.80) |
while if , since is large,
| (4.81) |
| (4.82) |
From (4.20) we also get
which with (4.82) yields (4.77). The proof of (4.78) is similar, the only (inconsequential) difference being that when we sum the terms over all , most terms get counted twice, for and , whereas each was counted at most once when we summed over in (4.77). ∎
Lemma 4.6.
There exist constants such that, provided (4.14) holds and is sufficiently large, we have for all
| (4.83) |
Proof.
Let
for from the definition (4.1) of . We decompose the pairs appearing in (4.6) into subclasses according to the size of and the degree of sidestepping , as follows. Fix . Let
First, for we have
and from (4.15)
Hence and Lemma 3.2, provided is large,
| (4.84) |
Second, for we can drop the second term in brackets in (4.76):
and from (4.15)
Hence again using Lemma 3.2, provided is large,
| (4.85) |
Third, for we have
and from (4.15)
so similarly to (4.4)
| (4.86) |
Finally, for we can again drop the second term in brackets in (4.76), and we have analogously
and
so
| (4.87) |
Since is large, (4.6) follows from (4.14) and (4.4)—(4.4). ∎
For and , a th–scale joining 4–path is a marked PG path with , such that for some th–scale hyperplane ,
| (4.88) |
In a th–scale interval with left endpoint , these four hyperplanes represent the hyperplane at , a sandwiching th–scale hyperplane, and two possible joining hyperplanes. The pairs , are the links of the joining 4–path. Let be the point where intersects the hyperplane containing . The intermediate path corresponding to is ; note these points are collinear. Recalling Remark 4.3, we say the th–scale joining 4–path is internally bowed if
| (4.89) |
(compare to (4.40)) and
| (4.90) |
(compare to (4.3)) or equivalently
| (4.91) |
We define special allocations to deal with internally bowed paths. For each th–scale joining 4–path let
Note that by (4.88), here is a function of . We will need an analog of Lemma 4.6 which enables us to deal with joining 4-paths as single units. Normally for th–scale links (length of order ), where the fluctuations of the passage time are of order , we need th–scale allocations (proportional to ) to get a good bound from Lemma 3.2, but in the next lemma we are able to use th–scale allocations even for much longer th–scale lengths, by taking advantage of bowedness.
Lemma 4.7.
There exist constants as follows. Let and .
(i) For every th–scale joining 4–path in , and from (3.25),
| (4.92) |
(ii)
| in , and , for which | ||||
| (4.93) |
(iii)
| corresponding intermediate path , | ||||
| and , for which | ||||
| (4.94) |
Proof.
(ii) and (iii). The proof of (iii) is a slightly simplified version of the proof of (ii), so we only prove (ii). We proceed as in Lemma 4.6. We decompose the set of joining 4–paths according to the sizes of and , and the degree of bowedness, measured by the left side of (4.89). From Remark 4.3, every internally bowed th–scale joining 4–path in satisfies
| (4.96) |
Thus define for
| (4.97) |
is defined similarly with the first condition in (4.4) replaced by . is defined similarly with the last condition in (4.4) replaced by
Every internally bowed joining 4–path in is in one of these classes, since by (4.96) we don’t need classes with .
Suppose is in . We have
| (4.98) |
Hence for each , by Lemma 3.2,
| (4.99) |
Regarding the size of , the number of possible (necessarily in ) in a given th–scale hyperplane is at most
The upper bound for in (4.4) gives , which with the last upper bound in (4.4) yields
so for a given the number of possible is at most
The upper bound for in (4.4) implies
and for given , the point is determined, and then the number of possible is at most
Combining these, we see that
4.5. Step 5. First stage of the th–scale (second) iteration of coarse–graining: shifting to the th–scale grid.
The current marked PG path at the start of the th–scale iteration step is . We rename it now as
We shift certain points to the th grid; the procedure is somewhat different from the th–scale iteration step, as we are starting from a th–scale marked PG path . Fix and, recalling , let
then relabel as , so and are the terminal th–scale hyperplanes, and define indices by , so the are the marked points in non-incidental th–scale hyperplanes. Observe that every th–scale interval, including terminal ones, has at least one th–scale hyperplane in its interior; hence for all .
For each non-incidental th–scale hyperplane in let . Also let , and . We shift to the th scale grid in each non-incidental th–scale hyperplane , replacing with for , to create the updated path which we denote . Letting (so if if ) , we may equivalently write this as
The black path from to in Figure 6 illustrates a segment of such a path, with for some there; the vertices between and are points with . In the second stage of the iteration we will remove marked points in non-terminal th–scale hyperplanes to create the path
By Lemma 4.5 we have
| (4.100) |
while similarly to (4.60) and (4.62),
| (4.101) |
and
| (4.102) |
(The only notable change from the derivation of (4.60) and (4.62) is that now, since we are shifting to the th scale, we have the bound
larger only by a constant compared to the analogous bound in (4.2)–(4.2).) Then (4.100) and (4.102) give
| (4.103) |
From (4.101) and (4.103), analogously to (4.2), we have for the event on the right in (4.3) that
| (4.104) |
Remark 4.8.
In view of Remark 4.4, in the context of shifting to the grid, we can think of “tracking” as corresponding showing that a probability of form
| (4.105) |
is small, or similarly with replaced by its approximation . In (4.5) the particular allocations chosen are . The event in (4.8) says that, as the shifting–to–the–grid process changes the –length of the path, the change in –sum fails to track even a small fraction of the change in –length, to within the error given by the allocations. Further, in (4.3) and on the left in (4.5),
| (4.106) |
represents roughly the accumulated error allocations used in the completed th–scale iteration. Thus what (4.101) and (4.102) say is that for the current shift to the grid, the change in –length (or in its approximation ) is negligible in the sense of being small relative to the accumulated allocations, making tracking only a minor issue here. This negligible–ness will not be valid for the marked–point–removal stage of the iteration, however.
It should also be noted that from the first to second lines in (4.5), the coefficients 2, 4 become 4, 6. The difference, if it is negative, represents a reduction of the original value
Observe that failure to track is a one–sided phenomenon—we only care about failure of the –sum to track decreases in –length created by shifting to the grid, not increases. In the point–removal stage, the –length always decreases, and we care that the –sum decreases at least proportionally.
Using Lemma 4.6 we have for the last event in (4.5)
| (4.107) |
establishing tracking as desired. Combining this with (4.3) and (4.5) yields
| (4.108) |
Analogously to the comment after (4.3), the increase of the coefficients 2, 4 in (4.3) to be 4, 6 in (4.5), together with the introduction of the additional term with coefficient , represent a further reduction taken from the original bound in (1.13), allocated to bound errors in the first stage of the th–scale iteration, just completed.
4.6. Step 6. Second stage of the th–scale (second) coarse–graining iteration: removing marked points.
For the next update of the current marked PG path , we remove all the marked points in non-terminal th–scale hyperplanes to create the updated marked PG path
Here we recall that and lie in terminal th–scale hyperplanes, and lie in th–scale hyperplanes. As with , etc., and should be viewed as functions of .
In this second stage, the removal of marked points always reduces the Euclidean length of the path (see Figure 5), meaning , and on average the reduction in passage time, , should be about times the reduction in length. Here a tracking failure means the actual reduction in passage time is at most times the reduction in length, to within an allocated error; see the last probability in (4.6).
From (4.101) we have
and therefore, assuming is small,
From this and (4.5) we obtain the setup to establish tracking:
| (4.109) |
Let us consider the contribution to the difference of sums , appearing in the last probability in (4.6), from a single th–scale interval . Removing the marked points from the hyperplanes in the interior of changes the marked PG path from the full path
to the direct path (that is, .) We then have
| (4.110) |
Given and with all in some grid , we define
From Lemma 4.5 we have
| (4.111) |
so the last probability in (4.6) is bounded above by
| (4.112) |
This is the tracking–failure event (see Remark 4.4) for the marked–point–removal stage of the iteration, and our main task is to bound its probability. The last of the 3 terms on the right inside the probability can be viewed as part of the allocation of allowed errors. As noted in Remark 4.8, the quantity
in the second probabilty in (4.6) represents the accumulated error allocations used in the 1.5 iterations completed so far; the allocations for the present stage increase the 4 and 6 to 5 and 7 in the third probability in (4.6). Our ability to bound the tracking–failure event is what allows us to replace the quantity
in that second probability in (4.6) to obtain the third probability. We need each iteration to involve similar such replacement, so that when the iterations are complete this term becomes
which is typically negative and can in part cancel the accumulated error allocations (see (4.162).)
Let be the point ; note does not necessarily lie in any th–scale grid. Let be the orthogonal projection of into , noting that by (4.19), is much smaller than . (Note the indexing of marked points differs here from that used in Step 1 in defining . Our here has index matching that of the point in the hyperplane, whereas in Step 1 has index corresponding to the distance from the left end of the interval.)
We continue considering the contribution to the difference of sums in (4.6) from a single th–scale interval . We split into cases according to the type of interval .
Case 1. is a short non–terminal th–scale interval. Here includes no joining hyperplanes in the interval, so it includes exactly two maximally th–scale (sandwiching) hyperplanes there, at distance from each end; see Figure 7. We introduce the intermediate path
which has the same endpoints and satisfies . To bound (4.6) we use the expression on the right in (4.110). Applying Lemma 3.6 with yields
and therefore
| (4.113) |

This is the essential property of the intermediate path: when we look at the bowedness of the full path relative to the intermediate path (represented by the left side of (4.113)), and relative to the direct path (right side of (4.113), without ), the first is at least fraction of the second, to within a constant. By (4.64), for the intermediate path also satisfies
| (4.114) |
Similarly to (4.111), since in Case 1 , we have
| (4.115) |
From (4.110)—(4.115) it follows that the contribution to the tracking–failure probability (4.6) from short non–terminal intervals is bounded by
| (4.116) |
The terms and are negligible in (4.116) relative to , because the latter is of the order of a power of , due to . All of the increments in the last event have . We can therefore bound the last probability similarly to Lemma 4.6, with the main difference being that in place of pairs in the definitions of we need to consider 4–tuples corresponding to values of . This means the exponents in the bounds on become . The values are determined by so their presence does not increase the necessary size of in the lemma. As with the sets in the lemma proof, we can decompose the possible 4–tuples according to the size of , and and sum over the possible size ranges. Otherwise the proof remains the same, and we get that the last probability in (4.116) is bounded by
| (4.117) |
Case 2. is a terminal th–scale interval (meaning either or ). The proof is similar to Case 1, except that the interval includes only one maximally th–scale (sandwiching) hyperplane between the two terminal hyperplanes that are at the ends of the interval, so the full path in the interval has form . We obtain for the terminal–interval contribution to the tracking–failure probability (4.6) the bound
| (4.118) |
Case 3. is a long non–terminal th–scale interval. Such an interval, and thus also the middle increment of the 3 comprising in Case 1, may be much longer than . Therefore the quantity used on the right side of (4.116) for that increment is no longer large enough to give a useful bound on the probability. To avoid this problem we will sometimes use a different intermediate path in which coincides with the full path between the inner joining hyperplanes, so differs from the full path only near the ends of , while preserving the property (4.113) (this preservation being the purpose of our choice of .) Equation (4.113) represents what we may informally call deterministic tracking, a nonrandom analog of the tracking of Remark 4.4 which facilitates our desired (random) form of tracking.
Fix a long non–terminal th–scale interval , and suppose it has th–scale length for some . The hyperplanes of in are the th–scale ones at each endpoint, two sandwiching th–scale hyperplanes at distance from each end, and between 2 and 4 th–scale joining hyperplanes between these. These hyperplanes are at the joining points , and , with two exceptions. First, if then the first of these 4 joining hyperplanes coincides with the left–end sandwiching one, and similarly for , which reduces the number of th–scale joining hyperplanes to fewer than 4, as discussed in criterion (ii) after (4.33). Second, in the totally unbowed case (third option in (4.33)) at either end of , there is no outer joining hyperplane at that end, as in criterion (iii). We define to be the number of th–scale hyperplanes in the interior of .
Case 3a. The bowed case (second option in (4.33)) for both , with . Since we must have and . Here the full path is
and the direct path again is . Define
see Figure 8. This time the intermediate path is defined as
which coincides with between the inner joining hyperplanes, which is “most” of . We denote the parts of the paths outside the inner joining hyperplanes by
with defined similarly with in place of , so that
| (4.119) |
For the corresponding quantities for means, similarly to (4.113), but using in Lemma 3.6, we have
| (4.120) |

We claim that deterministic tracking holds in the sense that
| (4.121) |
This and (4.6) give the full analog of (4.113) for Case 3a. To prove the claim, suppose for some . Recall and from (4.25) and (4.26), noting that in our present notation, there have become , with different superscript labeling. Using (4.28)—(4.30) with ,
and hence
| (4.122) |
Here the second inequality uses the fact that is nearly perpendicular to , by (4.19). In the other direction, recalling has th–scale length (so ) and supposing , since and we have similarly to (4.1) and (4.36)
| (4.123) |
Now the first ratio on the right is , so it follows from (4.30) and (4.6) that
and similarly
Hence from (4.6) and the second equality in (4.20),
| (4.124) |
which implies
| (4.125) |
proving the claim (4.121) when we take small.
From Lemma 4.7(i) we have
| (4.126) |
and the equivalent “mirror image” of Lemma 4.7 covers symmetrically, incorporating a symmetric definition of joining 4–path.
The analog of (4.114) remains valid, and we now have the ingredients (4.6), (4.121) and (4.126) for the analog of (4.116), bounding the bowed–case contribution to the tracking–failure probability (4.6)—see (4.6) below:
| and long non–terminal th–scale, in the bowed case of (4.33) | |||
| for some with and long non–terminal th–scale, in the | |||
| with , for some with and long non–terminal | |||
| th–scale with and , in the bowed case of | |||
| (4.127) |
Here the first inequality uses that
and that from (4.126), (4.121), and then (4.6),
| (4.128) |
For the in the last event in (4.127), the applies to and the applies to . An application of Lemma 4.7(ii) and (iii) with , followed by summing over , bounds the last (tracking–failure) probability in (4.127) by
| (4.129) |
Case 3b. The bowed case (second option in (4.33)) for both , with . This means we have at least one of . If for example , then what were in Case 3a the two points are now the same point, so effectively there is no separate point . Instead we have only the equivalent of , so joining 4–paths become joining 3–paths. This has no significant effect on the arguments, including Lemma 4.7, other than some simplifications, and the bound in (4.6) still applies for the corresponding contribution to the tracking–failure probability (4.6):
| and long non–terminal th–scale, in the bowed case of (4.33) | ||||
| (4.130) |
Case 3c. The forward case (first option in (4.33)) for both . Here we have as there are only inner joining points, at distance from each end of . As before the direct path is , and the full path is
by (4.64), for we have
| (4.131) |
We claim that in the forward case we have
| (4.132) |
By (4.131), this means that in the forward case there is no tracking failure:
| long non–terminal th–scale, in the forward case of (4.33) | ||||
| (4.133) |
To prove (4.132), we first observe that from the definition (4.76),
| (4.134) |
From (4.20) and (4.33), since ,
| (4.135) |
Since (4.16) ensures the right side of (4.134) is much larger than , the claim (4.132) follows from (4.134) and (4.6).
Case 3d. The totally unbowed case (third option in (4.33)) for both . Here we have as there are the sandwiching hyperplanes at distance from each end of , and inner joining hyperplanes at distance from each end, with such that is of th–scale length; there are no outer joining hyperplanes. See Figure 9. From (4.31) (valid now for in place of ) and (4.33), this means that
| (4.136) |
Here the second term in the max comes from the fact that to come under the third (totally unbowed) option in (4.33), we must have . We note that the definition of the totally unbowed case gives (4.6) for in place of , but by (4.19) this only changes each of the 4 terms in (4.6) by a factor as , so we have accounted for this via the factor 1/2 in front of the max. The bound (4.6) is for the left end of ; a symmetric bound is valid for the right end. As before, the direct path is , and the full path is
but this time the intermediate path is
These points are collinear so .

We use a special allocation for the totally unbowed case, the same for all 10 links of and , defined (when is of th–scale length) as
Now so by Lemma 3.6,
while from(4.20),
| (4.137) |
From these we get deterministic tracking:
| (4.138) |
We now can establish the analog of (4.116) and (4.127) for the totally–unbowed–case contribution to the tracking–failure probability (4.6), using (4.64) and (4.6):
| for some with long non–terminal th–scale, in the totally unbowed case of | ||
| and some with long non–terminal th–scale, in the totally unbowed case | |||
| (4.139) |
Here we have again used , from (4.16), to ensure . With the second term of the max in (4.6) in mind, suppose that for some and some we have
| (4.140) |
| (4.141) |
and
| (4.142) |
Then using (1.10),
| (4.143) |
and by Lemma 3.2, for every possible value of and every link , we have
| (4.144) |
It is important here that the lower bound (4.143) not depend on the length scale of , except through the factor which is always at least 1. Similarly to the entropy bounds in Lemmas 4.6 and 4.7, and in Case 3c, we see that the number of possible choices of satisfying (4.140)—(4.6) is at most
| (4.145) |
Here the dots separate bounds for the number of choices (up to a constant) of endpoint hyperplanes and then of , and finally of . For , (4.143) and (4.145) remain valid for with replaced by 1. For with
(i.e. too small to satisfy (4.6) for any ) they remain valid with replaced by 1. (Note that from the definition (4.33) of the totally unbowed case, covers all cases.) Hence as in previous cases, inserting the bound (4.143) into (4.144), multiplying by the entropy factor (4.145), and summing over , and we get that the right side of (4.139) is bounded by
| (4.146) |
We have thus bounded the totally–unbowed–case contribution to the tracking–failure probability (4.6).
Case 3e. Mixed cases, which we subdivide as mixed forward case, mixed bowed case, and mixed totally unbowed case, according to the condition at the dominant end (as defined after (4.36)) of . In previous cases we have assumed that the same option in (4.33) occurs at both ends of the interval , but this is strictly for clarity of exposition. As explained in Step 1, in mixed cases we have joining hyperplanes only at the dominant end of . The situation is symmetric so let us assume the left end is dominant. In mixed cases the full path in is always , with or 5. Suppose is a th–scale interval of th–scale length. The intermediate paths are analogous to those in cases 3a—3d, as follows. If the dominant left end has the forward case then there is one joining hyperplane in , containing , at the left end at distance from , and the intermediate path is
If the (dominant) left end has the totally unbowed case then there is one (inner) joining hyperplane in , containing , at the left end at distance from , and the intermediate path follows the line from to :
If the left end has the bowed case with then there are two joining hyperplanes in , containing and , at the left end at distances and from , and the intermediate path is
see Figure 8. If the left end has the bowed case with then there is one (inner) joining hyperplane in , containing , at the left end at distance from , and the intermediate path is
similar to Figure 8 but with the middle two hyperplanes coinciding. In each case, we define the subpaths and between the left end of the interval and the left inner joining hyperplane. In all cases the arguments are essentially the same as in the analogous non-mixed case, with the addition that for the final transition ending at , one uses (4.38) to bound . We will not reiterate the arguments here, but simply state that the result is again the analog of (4.116) and (4.127), bounding the mixed–case contribution to the tracking–failure probability (4.6):
| in the mixed totally unbowed case) for some with long non–terminal | ||||
| (4.147) |
where
As in Cases 3a–3d, the right side of (4.6), and thus the mixed–case contribution to the tracking–failure event (4.6), is bounded above by
| (4.148) |
for some .
We have now bounded all contributions to (4.6), by the sum of (4.117), (4.6), (4.6), (4.6), (4.6), (4.146), and (4.148). From this and (4.6) we have the completion of the th–scale iteration:
| (4.149) |
As in the comments after (4.3) and (4.5), the increase of the coefficients 4, 6 in (4.3) to be 5, 7 in (4.5), together with an increment to the “length–change” term with coefficient , represent a further reduction taken from the original bound in (1.13), and allocated to bound errors in the second stage of the th–scale iteration, just completed. In this second stage, however, the increment of the length–change term, due to replacing with , is negative (removing points reduces path length) and may compensate at least in part for the increases from 4, 6 to 5, 7. This compensation, made possible by control of tracking errors, is what allows the total allocation through all iterations to potentially exceed the entire original bound —see (4.162).
4.7. Step 7. Further iterations of coarse–graining.
The further iterations proceed quite similarly to the th–scale iteration; for the most part, to do the th–scale iteration we simply replace throughout by . We will sketch the th–scale (third) iteration to make the pattern clear.
For the first stage of the th–scale iteration, the current marked PG path at the start is , which we rename . Letting
we shift each , to the th–scale grid, creating the updated marked PG path
Removing those which lie in non-terminal th–scale hyperplanes then creates the marked PG path
in which (recalling (4.18)) , and lie in terminal th–scale hyperplanes, lie in terminal th–scale hyperplanes, and lie in th–scale hyperplanes. Noninteraction of shifts again applies (see Step 4), since if and both lie in th–scale hyperplanes then there are sandwiching hyperplanes, at least, in between, ensuring . For we write for the portion of in the interval (denoted ) from to , and define by , analogous to used in the previous iteration.
Similarly to (4.100)—(4.102) we have
| (4.150) |
| (4.151) |
and
| (4.152) |
These lead to a tracking bound like (4.5) for the first stage (shifting to the th–scale grid) using Lemma 4.6:
| (4.153) |
As with (4.3) and (4.5), with (4.6) this yields
| (4.154) |
Remark 4.9.
The second probability here contains three quantities of the form
with certain additional integer coefficients: 2 and 4 in the first quantity, 3 in the second quantity, and 2 in the third. As noted in Remark 4.8 and after (4.5), (4.6), and (4.6), these represent the accumulated error allocations from the th, th, and (first–stage) th–scale iterations, respectively. We have split these out here for clarity; in (4.6) and (4.6) the first two of the three quantities are combined, giving the terms with coefficients 5 and 7. In general after the first stage of the th–scale iteration (which is the source of the third quantity), the second quantity would represent allocations from all stages through . With this in mind we define the accumulated–allocations upper bounds
| (4.155) |
and
| (4.156) |
with a valid upper bound after the first stage of the th–scale iteration, and valid after the second stage. Comparing (4.9) to (4.5), in this case we have , the sum in (4.9) has no terms, and the other two terms on the right in (4.5) merge into one. Comparing (4.9) to (4.6), in this instance also , and the sum in (4.9) has one term which is merged with the other term in (4.6). Equation (4.9) may also be compared to (4.3), where and the sum in (4.9) has no terms. We can rewrite the second probability in (4.7) as
| (4.157) |
Moving on to the second stage of the th–scale iteration, from (4.7), using the form (4.9), we have similarly to (4.6) and (4.6)
| (4.158) |
the last probability being the tracking–failure probability. We now divide into Cases 1–5 as in the th–scale iteration. In each case (excluding 3c) there is an intermediate path in each th–scale interval , which is slower than the direct path (up to a multiple of log ), satisfying
assuming , and hence
and which satisfies deterministic tracking in a form like (4.113), sometimes with extra terms in the form of error allocations, as in (4.6); this deterministic tracking says that the intermediate path is sufficiently shorter relative to the full path, to within the error given by the allocations. This enables us to bound the last probability in (4.7) by a tracking–failure probability of the form
| (4.159) |
differently for each of the 5 cases; see for example (4.139) for the totally–unbowed case. This is then bounded by summing probabilities of form
over all possible links of paths for all , using Lemmas 4.6 and 4.7. The end result of the th–scale iteration is that
| (4.160) |
After all iterations are completed through the th scale, this becomes
| (4.161) |
We claim that
| (4.162) |
This says that the (typically negative) second term on the left, representing part of the cumulative effects of tracking, is enough to adequately cancel the (positive) cumulative allocations ; see the comments after (4.6) and (4.6). To prove (4.162) we make the subclaim
| (4.163) |
Assuming (4.163) and assuming satisfies we have from the definition (4.9)
| (4.164) |
and (4.162) follows. To prove (4.163) we use (4.101) (which generalizes to all in place of ) and the fact that, since removing points reduces length, we have for all . This yields that for all ,
| (4.165) |
and therefore
| (4.166) |
from which (4.163) follows, and hence also (4.162). The right side of (4.7) is therefore bounded above by
| (4.167) |
4.8. Step 8. Final marked CG paths.
In , only terminal hyperplanes contain marked points (excluding ), one at each end of for each scale . The marked point in the –terminal hyperplane is in the grid for all . As noted in Step 1, the gap between the –terminal hyperplanes is at least and at most . Now is our final CG path, so we rename it
where . We also define a projected path with collinear marked points
where is the projection onto the axis. For , the links and each have one end in a –terminal hyperplane and the other in a –terminal hyperplane; these will be called the jth–scale links of . The links and are called final links, and the link between –terminal hyperplanes is called a macroscopic link. See Figure 3 in Section 4.1, where is the macroscopic link, which (by definition of ) always covers at least 1/5 the length of .
We have so by Lemma 3.6, since ,
Therefore, using (4.64), the probability in (4.7) is bounded above by
| (4.168) |
To bound this we use allocations
for th–scale links, for final links, and for macroscopic links. From (4.80) and (4.81) we have
Therefore using also (4.21) the total of these for all links in a path satisfies
| (4.169) |
Therefore the last probability in (4.8) is bounded above by
| (4.170) |
Considering the probability for final links , the number of possible such links in is at most and for each such link we have from Lemma 3.2 and (4.16)
| (4.171) |
The probabilities for th–scale and macroscopic links can be bounded using minor modifications of Lemma 4.6, showing that (4.8) (and hence also the probability on the right in (4.7)) is bounded above by
| (4.172) |
With (4.7) this completes the proof of (1.13). As noted after Theorem (1.3), the downward–deviations part of (1.12) is a consequence, so the proof of the downward–deviations part of Theorem (1.3) is complete.
5. Proof of Theorem 1.6 for fixed .
We move on to step (2) of the strategy in Remark 1.7. As with the proof of Theorem 1.3 (downward deviations), there are simpler cases which can be proved from Lemma 3.2 and do not require Theorem 1.3. These we can handle uniformly over ; after dealing with these, in Lemma 5.1 we will handle the main case for the moment only for fixed .
Let
| (5.1) |
with to be specified;
we will consider separately short geodesics (meaning ) and longer ones.
When with , taking to be the first vertex in outside , we see that one of the following cases must hold.
Transverse wandering cases (see Figure 10):
-
(i)
(non-transverse wandering) there exist with with , and with
-
(ii)
(wandering by short geodesics) there exist with with , and with
-
(iii)
(large wandering) and there exist with with , and with
(5.2) -
(iv)
(moderate wandering) and there exist with
(5.3)
where is to be specified. In all cases (i)–(iv) we assume .
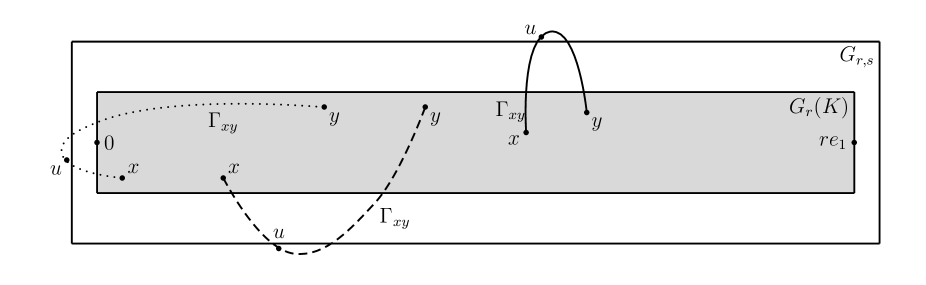
Cases (i)—(iii) are the ones which do not require Theorem 1.3 and can be proved from Lemma 3.2. This is because the exponent obtained from that lemma is at least of order , meaning it dominates the entropy from the number of possible choices of .
It follows from routine geometry that under (i), for from (1.15) we have
so also, using Lemma 3.6,
| (5.4) |
while
Therefore one of the following 6 quantities
exceeds 1/6 of the right side of (5.4). There are at most possible values of under (i), so from Lemmas 3.1 and 3.2, provided is sufficiently large we have
| (5.5) |
Under (ii) we have for some
Further, for we have or equivalently . Hence similarly to (i), provided we take large in (5.1),
| (5.6) |
Under (iii) we have
Hence as in (i) and (ii) we get
| (5.7) |
To deal with (iv) and complete the proof for fixed , we have the following. We note the difference from Lemma 4.2, which covered many simultaneously but considered only larger transverse wandering, of order or more.
Lemma 5.1.
Suppose and satisfy A1, A2, and A3. There exist such that for all and all with ,
| (5.8) |
Proof.
Fix and let . We consider first the case of . Let satisfy , and for from (1.10) let
the latter being a slice of . Define by . Then , and from (1.10) we have , and is a translate of .
In view of (5.5) and (5.6), we need only consider as in (5.3); in particular . Here we have for some
so as in transverse wandering cases (i)–(iii), since one of the quantities
must exceed . It follows from (1.11) and the downward–deviations part of Theorem 1.3 (with there taken as here) that for we have
| (5.9) |
∎
6. Proof of Theorem 1.5.
We move to (3) of Remark 1.7. We begin with an extension of a consequence of Theorem 1.3, removing the requirement that lie in the same tube as , to create a bound on the probability of a fast “hyperplane–block to hyperplane” passage time. Define
Lemma 6.1.
Suppose and satisfy A1, A2, and A3. There exist constants such that for all and ,
| (6.1) |
Proof.
It is enough to consider and . We first deal with large . With to be specified we have
| (6.2) |
For from (4.20), let . For , and for of the last event, we have from (4.20) and Lemma 3.6
| (6.3) |
and the number of allowed is at most . Therefore by Lemma 3.2, provided is large, the sum up to on the right side of (6) is bounded above by
| (6.4) |
For , in place of (6.3) we have
and we obtain similarly that the sum from to on the right side of (6) is bounded above by
| (6.5) |
The last inequality uses .
We now deal with the remaining case . For from Theorem 1.3, we take to be specified and subdivide into blocks
Let denote the center point of and let
Given , there exists a cylinder , with axis containing , radius , and length , which contains and . See Figure 11. Further, is a positive integer multiple of , and for and satisfying for some , we have using (4.20) and Lemma 3.6(i) that

Define the “small box”
We now tile a region of with translates of . Fix to be specified and let be the least for which . Define the “big box”
so the width of is near . For let be translated by , and let ; see Figure 12. Then the number of small boxes comprising is
and we have . Let be the event in (6.1) translated to , that is, we replace with and with . Fix to be specified; when we say is a fast source. Let , so
| (6.8) |
by Proposition 3.3.
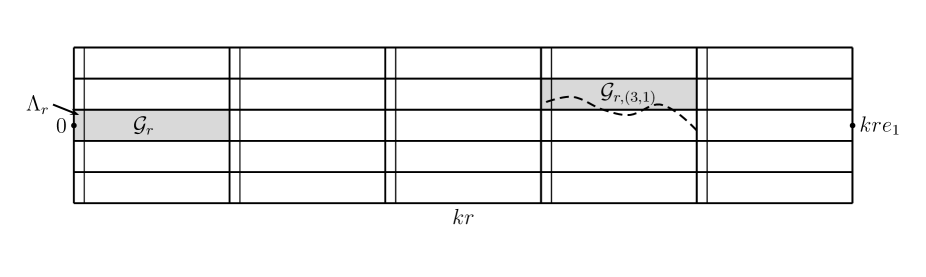
We now consider the passage time between the ends of the big box. If then must intersect at least of the regions , one for each . If there are no fast sources, this means . Provided is large, it then follows from Lemmas 5.1 and 6.1 that
| (6.9) |
By taking large and then large, we can make the right side of (6) less than 1/2 for all . On the other hand, from (1.11) for large we have
From this and (6) it follows that
| (6.10) |
Fix large enough so , with from (1.10), and, to get a contradiction, suppose there exists arbitrarily large with . By (1.10) and (6.10) we then have
Then iteration and (6.8) give that for all , . Since this is false for large , we must have for all large , so is bounded, which completes the proof of Theorem 1.5, and thus (3) of Remark 1.7.
7. Proof of Theorem 1.3—upward deviations.
We move on to (4) of Remark 1.7. The proof is similar to the LPP proof for in ([8] Proposition 10.1). As with downward deviations, we need only consider as in (4.18). Let be as in the downward–deviations proof, and
so for some depending on . Note that does not depend on ; the –terminal hyperplane at each end of is just the second–closest th–scale hyperplane to the endpoint. We form a marked PG path
by taking as the closest point to in the th–scale grid, when is a –terminal hyperplane; this means and (from (4.16).) Thus the CG approximation gets coarser as we move away from the endpoints of the interval. See Figure 3.
We proceed generally as in Step 8 of the proof for downward deviations. Let be the orthogonal projection of into . We use the terminology th–scale link, final link, and macroscopic link from there. For , for a th–scale link we have
| (7.1) |
Further, the angle between and satisfies and therefore
| (7.2) |
and similarly for in place of . We have also so from (4.20) and the bound on we also get
Combining this with (4.13), (7.1), and (7.2) we see that
and therefore by Theorem 1.5, using (4.13) and the assumption ,
| (7.3) |
It follows using Lemma 3.2 that
| (7.4) |
The same is valid for a final link, with . For macroscopic links it is valid with replaced by , giving
| (7.5) |
The numbers of possible links inside are as follows:
-
(i)
th–scale links: at most ,
-
(ii)
final links: at most ,
-
(iii)
macroscopic links: at most .
Since , provided is taken large enough it follows from these bounds and (4.14), (7), (7.5) that
| (7.6) |
If is not in any of the events in (7), and , then for all as in (1.12),
Taking it follows that
which completes the proof of Theorem 1.3 for downward deviations.
8. Proof of Theorem 1.6 and Lemma 1.2.
We finish with (5) of Remark 1.7 by proving Theorem 1.6. In the proof in section 5 for fixed , transverse wandering cases (i)–(iii) were dealt with uniformly over , so we need only consider the case there:
(iv) and there exist with
| (8.1) |
See the dashed line in Figure 10. As in section 5, this means that, for from Lemma 3.6,
while
so by Theorem 1.3 and Remark 1.4,
| (8.2) |
Together with cases (i)–(iii) in section 5, this completes the proof of Theorem 1.6.
Proof of Lemma 1.2.
Fix (large) and , and define
so and hence . Letting
we define as follows. First let on . Then for those with , define on by
For with , define on by
Since it is easily seen that if we take sufficiently large, then the slope of the piecewise–linear function is never more than , and the slope at approaches 0 as . Defining by
it follows that for all ,
and the sublinearly powerlike property follows. ∎
References
- [1] Alexander, K. S. (1997). Approximation of subadditive functions and rates of convergence in limiting shape results. Ann. Probab. 24 30–55.
- [2] Alexander, K. S. (2020). Geodesics, bigeodesics, and coalescence in first passage percolation in general dimension. arXiv:2001.08736 [math.PR]
- [3] Alves, S. G., Oliveira, T. J., and Ferreira, S. C. (2018). Universality of fluctuations in the Kardar-Parisi-Zhang class in high dimensions and its upper critical dimension. Phys. Rev. E 90 020103. arXiv:1405.0974 [cond-mat.stat-mech]
- [4] Baik, J., Ferrari, P. L., and Péché, S. (2014). Convergence of the two-point function of the stationary TASEP. Singular phenomena and scalingin mathematical models, 91–110, Springer, Cham. arXiv:1209.0116 [math-ph]
- [5] Balász, Busani, O., and Seppäläinen, T. (2020). Nonexistence of bi-infinite geodesics in the exponential corner growth model. Forum Math. Sigma 8, Paper No. e46, 1–34. arXiv:1909.06883 [math.PR]
- [6] Basu, R., Hoffman, C., and Sly, A. (2018). Nonexistence of bigeodesics in integrable models of last passage percolation. arXiv:1811.04908 [math.PR]
- [7] Basu, R., Sarkar, S., and Sly, A. (2019). Coalescence of geodesics in exactly solvable models of last passage percolation. J. Math. Phys. 60 093301, 22 pp. arXiv:1704.05219 [math.PR]
- [8] Basu, R., Sidoravicius, V., and Sly, A. (2016). Last passage percolation with a defect line and the solution of the slow bond problem. arXiv:1408.3464 [math.PR]
- [9] Chatterjee, S. (2013). The universal relation between scaling exponents in first-passage percolation.Ann. of Math. (2) 127, no. 2, 663–697. arXiv:1105.4566 [math.PR]
- [10] Corwin, I., Liu, Z., and Wang, D. (2016). Fluctuations of TASEP and LPP with general initial data. Ann. Appl. Probab. 26, 2030–2082. arXiv:1412.5087 [math.PR]
- [11] Damron, M., Hanson, J., and Sosoe, P. (2014). Subdiffusive concentration in first-passage percolation. Electon. J. Probab. 19, Paper No. 109, 27 pp. arXiv:1401.0917 [math.PR]
- [12] Damron, M. and Wang, X. (2016). Entropy reduction in Euclidean first-passage percolation. Electon. J. Probab. 21, Paper No. 65, 23 pp. arXiv:1605.06665 [math.PR]
- [13] Fogedby, H. C. (2006). Kardar-Parisi-Zhang equation in the weak noise limit: Pattern formation and upper critical dimension. Phys. Rev. E 73 031104. arXiv:cond-mat/0510268 [cond-mat.stat-mech]
- [14] Gangopadhyay, U. (2020). Fluctuations of transverse increments in two-dimensional first passage percolation. arXiv:2011:14686 [math.pr]
- [15] Ganguly, S. and Hegde, M. (2020). Optimal tail exponents in general last passage percolation via bootstrapping & geodesic geometry. arXiv:math.PR/2007.03594
- [16] Howard, C. D. and Newman, C. M. (1997). Euclidean models of first-passage percolation. Probab. Th. Rel. Fields 108, 153–170.
- [17] Kesten, H. (1986). H. Kesten. Aspects of first passage percolation. In Ecole d’Eté de probabilité de Saint-Flour XIV - 1984, Lecture Notes in Math. 1180, Springer, Berlin, 125–264.
- [18] Kesten, H. (1993). On the speed of convergence in first-passage percolation. Ann. Appl. Probab. 3 296–338.
- [19] Kim, S.-W. and Kim, J. M. (2014). A restricted solid-on-solid model in higher dimensions. J. Stat. Mech. 2014 P07005.
- [20] Le Doussal, P. and Wiese, K. J. (2005). Two-loop functional renormalization for elastic manifolds pinned by disorder in dimensions. Phys. Rev. E 72 035101. arXiv:cond-mat/0501315 [cond-mat.dis-nn]
- [21] Ledoux, M. and Rider, B. (2010) Small deviations for beta ensembles. Electron. J. Probab. 15, 1319–1343. arXiv:0912.5040 [math.PR]
- [22] Loẅe, M. and Merkl, F. (2001). Moderate deviations for longest increasing subsequences: The upper tail. Comm. Pure Appl. Math. 54, 1488–1519.
- [23] Loẅe, M., Merkl, F., and Rolles, S. (2002). Moderate deviations for longest increasing subsequences: The lower tail. J. Theor. Probab. 15, 1031–1047.
- [24] Marinari, E., Pagnani, A., Parisi, G., Rácz, Z. (2002). Width distributions and the upper critical dimension of Kardar-Parisi-Zhang interfaces. Phys. Rev. E 65 026136. arXiv:cond-mat/0105158 [cond-mat.stat-mech]
- [25] Rodrigues, E. A., Oliveira, F. A., and Mello, B. A. (2015). On the existence of an upper critical dimension for systems within the KPZ universality class. Acta. Phys. Pol. B 46, 1231–1234. arXiv:cond-mat/1502.06121 [cond-mat.stat-mech]
- [26] Talagrand, M. (1995). Concentration of measure and isoperimetric inequalities in product spaces. Publications Mathématiques de l’Institut des hautes Etudes Scientifiques 81(1), 73–205.
- [27] Tessera, R. (2018). Speed of convergence in first passage percolation and geodesicity of the average distance. Ann. Inst. Henri Poincaré Probab. Stat. 54, 569–586. arXiv:1410.1701 [math.PR]
- [28] Xia, G. (2013). The stretch factor of the Delaunay triangulation is less than 1.998. SIAM J. Comput. 42, 1620–1659. arXiv:1103.4361 [cs.CG]