Unified Optimal Transport Framework for Universal Domain Adaptation

Optimal Transport is a constrained optimization problem that seeks an efficient solution of transporting one distribution of mass to another. We now briefly recall the well-known optimal transport formulation.

Let $\Sigma_{r}:=\{\bm{x}\in\mathbb{R}_{+}^{r}|\bm{x}^{\top}\mathbf{1}_{r}=1\}$ denote the probability simplex, where $\mathbf{1}_{d}$ is a $d$-dimensional vector of ones. Given two simplex vectors $\bm{\alpha}\in\Sigma_{r}$ and $\bm{\beta}\in\Sigma_{c}$, we can write the transport polytope of $\bm{\alpha}$ and $\bm{\beta}$ as follows:

$$\mathbf{U}(\bm{\alpha},\bm{\beta})=\left\{\mathbf{Q}\in\mathbb{R}_{+}^{r\times c}|\mathbf{Q}\mathbf{1}_{c}=\bm{\alpha},\mathbf{Q}^{\top}\mathbf{1}_{r}=\bm{\beta}\right\}.$$

(1)

The transport polytope $\mathbf{U}(\bm{\alpha},\bm{\beta})$ can also be interpreted as a set of all possible joint probabilities of $(X,Y)$, where $X$ and $Y$ are two $d$-dimensional random variables with marginal distribution $\bm{\alpha}$ and $\bm{\beta}$, respectively. Following SwAV [6], given a similarity matrix $\mathbf{M}\in\mathbb{R}^{r\times c}$ instead of distance matrix in [11], the coupling matrix (or joint probability) $\mathbf{Q}^{*}$ mapping $\bm{\alpha}$ to $\bm{\beta}$ can be quantified by optimizing the following maximization problem:

$$\text{OT}^{\varepsilon}(\mathbf{M},\bm{\alpha},\bm{\beta})=\operatorname*{argmax}_{\mathbf{Q}\in\mathbf{U}(\bm{\alpha},\bm{\beta})}\text{Tr}(\mathbf{Q}^{\top}\mathbf{M})+\varepsilon\textit{H}(\mathbf{Q}),$$

(2)

where $\varepsilon>0$ and $\textit{H}(\mathbf{Q})=-\sum_{ij}\mathbf{Q}_{ij}\log\mathbf{Q}_{ij}$ is the entropic regularization term. The optimal $\mathbf{Q}^{*}$ has been shown to be unique with the form $\mathbf{Q}^{*}=\text{Diag}(\mathbf{u})\exp\left(\mathbf{M}/\varepsilon\right)\text{Diag}(\mathbf{v})$, where $\mathbf{u}$ and $\mathbf{v}$ can be solved by Sinkhorn’s Algorithm [11].

Since $\mathbf{Q}^{*}$ satisfies the mass constraint (1) $\mathbf{U}(\bm{\alpha},\bm{\beta})$ strictly, the objective $\text{OT}^{\varepsilon}(\mathbf{M},\bm{\alpha},\bm{\beta})$ is not suitable for partial displacement problem. In light of this, Unbalanced OT is proposed to relax the conservation of marginal constraints by allowing the system to use soft penalties [10]. The unbalanced OT is formulated as

$$\text{UOT}^{\varepsilon,\kappa}(\mathbf{M},\bm{\alpha},\bm{\beta})=\operatorname*{argmax}_{\mathbf{Q}\in\mathbb{R}_{+}}\text{Tr}(\mathbf{Q}^{\top}\mathbf{M})+\varepsilon\textit{H}(\mathbf{Q})-\kappa\big{(}D_{\text{KL}}(\mathbf{Q}\mathbf{1}_{c}||\bm{\alpha})+D_{\text{KL}}(\mathbf{Q}^{\top}\mathbf{1}_{r}||\bm{\beta})\big{)},$$

(3)

where $D_{\text{KL}}$ is Kullback-Leibler Divergence. Then the optimization problem (3) can be solved by generalized Sinkhorn’s algorithm [10].

To extract common knowledge, we propose an Unbalanced OT-based Common Class Detection (CCD) method, which considers a partial mapping problem between target samples and source prototypes from the perspective of cross domain. Note that our method uses prototypes to encourage a more global-aware alignment, which discovers intrinsic differences among common and target-private samples by exploiting the statistical information of the assignment matrix obtained from the optimal transport. Since UniDA allows private classes in both source and target domains, partial alignment should be considered to avoid misalignment between target-private samples and source classes. Hence we formulate the problem mapping target features to the source prototypes $\mathbf{C}_{s}=[\mathbf{c}^{s}_{1},\cdots,\mathbf{c}^{s}_{|\mathcal{C}_{s}|}]^{\top}$ with unbalanced OT objective to obtain the optimal assignment matrix $\mathbf{Q}^{st}$, i.e.

$$\mathbf{Q}^{st}=\text{UOT}^{\varepsilon,\kappa}(\mathbf{S}^{st},\frac{1}{B}\mathbf{1}_{B},\frac{1}{|\mathcal{C}_{s}|}\mathbf{1}_{|\mathcal{C}_{s}|}),$$

(4)

where $\mathbf{S}^{st}=\mathbf{Z}^{t}\mathbf{C}_{s}^{\top}$ refers to cosine similarity between target samples and source prototypes, and the mini-batch target $\ell_{2}$-normalized features $\mathbf{Z}^{t}=[\mathbf{z}^{t}_{1},\cdots,\mathbf{z}^{t}_{B}]^{\top}$ with batch-size $B$ are extracted by feature extractor $f$, i.e. $\mathbf{z}^{t}_{i}=f(\mathbf{x}^{t}_{i})/\left\|f(\mathbf{x}^{t}_{i})\right\|_{2}$. Here we use the same prototype-based classifier in [34] to learn source prototypes. Note that the private samples will be assigned with relatively low weights in $\mathbf{Q}^{st}$. Based on this observation, our CCD selects target samples with top confidence as common classes.

Firstly, the assignment matrix is normalized as $\bar{\mathbf{Q}}^{st}=\mathbf{Q}^{st}/\sum\mathbf{Q}^{st}$. Then we discover statistical property from normalized $\bar{\mathbf{Q}}^{st}$ and generate scores from the statistical perspectives of both target samples and source prototypes. For the $i$-th row in $\bar{\mathbf{Q}}^{st}$, it can be seen as a vanilla prediction probability vector and we can get pseudo-label $\hat{y}^{t}_{i}$ by argmax operation. And we assign target samples confidence score $w^{t}_{i}$ with the maximum value of the $i$-th row in $\bar{\mathbf{Q}}^{st}$, i.e.

$$w^{t}_{i}=\max(\{\bar{\mathbf{Q}}_{i,1}^{st},\bar{\mathbf{Q}}_{i,2}^{st},\cdots,\bar{\mathbf{Q}}_{i,|\mathcal{C}_{s}|}^{st}\}).$$

(5)

A higher score $w^{t}_{i}$ means $\mathbf{z}^{t}_{i}$ is relatively closer to a source prototype than any other samples and is more likely from a common class. Meanwhile, to select target common samples with top confidence, we also evaluate source prototypes confidence score $w^{s}_{j}$ with the sum of the $j$-th column, i.e.

$$w^{s}_{j}=\sum_{i=1}^{B}\bar{\mathbf{Q}}_{i,j}^{st}.$$

(6)

Analogously, a higher score $w^{s}_{j}$ means $\mathbf{c}^{s}_{j}$ is more likely a common source prototype, which is assigned to target samples more frequently. Then the common samples are detected by statistics mean, i.e.

$$\delta_{i}=\left\{\begin{aligned} 1,&\quad w^{t}_{i}\geq\frac{1}{B}\;\text{and}\;w^{s}_{\hat{y}^{t}_{i}}\geq\frac{1}{|\mathcal{C}_{s}|}\\ 0,&\quad\text{otherwise}\end{aligned}\right.,$$

(7)

where $\delta_{i}=1$ indicates the sample $\mathbf{x}_{i}^{t}$ is detected as common sample with top confidence, which can be assigned with pseudo label $\hat{y}^{t}_{i}$ by argmax operation. We can use pseudo labels of selected target samples to compute inter-domain common class detection loss by standard cross-entropy loss, i.e.

$$\mathcal{L}_{CCD}=\frac{\sum_{i=1}^{B}\delta_{i}\cdot\mathcal{L}_{CE}(\mathbf{z}^{t}_{i},\hat{y}^{t}_{i})}{\sum_{i=1}^{B}\delta_{i}},$$

(8)

To ensure that statistics mean can discover the intrinsic difference between common and private classes, we need to guarantee that the input features for partial mapping should be sampled from the target domain distribution with enough sampling density. Therefore, we implement a FIFO memory queue [20] to save previous target features for filling mini-batch features, which avoids the limitation led by the lack of statistical property for target samples.

Adaptive filling for unbalanced proportion of positive and negative. Unfortunately, using statistics mean as a threshold in Eq. (7) may misclassify some common samples as private class in some extremely unbalanced cases, such as there are few private samples indeed. Essentially, the assignment weight is determined by the relative distance between samples and prototypes, and private samples with low similarity set negative examples for the others. To automatically detect target samples, we design an adaptive filling mechanism for positive and negative unbalanced proportions. Our strategy is to fill the gap of unbalanced proportion to be balanced like Fig. 2 depicted. Firstly, samples with high similarity larger than a rough boundary $\gamma$ are defined as positive and the others are negative. Then we implement adaptive filling to be balanced when the proportion of positive or negative samples exceeds $50\%$. For negative filling, we synthesize fake private feature $\mathbf{z}^{t}_{i}$ by mixing up target feature $\mathbf{z}^{t}_{i}$ and its farthest source prototypes evenly, i.e. $\hat{\mathbf{z}}^{n}_{i}=\frac{1}{2}\big{(}\mathbf{z}^{t}_{i}+\operatorname*{argmin}_{\mathbf{c}^{s}_{k}}(\mathbf{z}^{t}_{i}{\mathbf{c}^{s}_{k}}^{\top})\big{)}$.

For positive filling, we first do the CCD without adaptive filling by Eq.(7) to obtain confident features and then reuse these filtered confident features for positive filling. Note that the filling samples are randomly sampled from mix-up negatives or CCD positives and the filling size is the gap between unfilled positive and negative. After adaptive filling for balanced proportion, our CCD is adaptive for detecting confident common samples.

Adaptive update for marginal probability vector. The marginal probability vector $\bm{\beta}$ in Objective (4) can be interpreted as a weight budget for source prototypes to be mapped with target samples. However, the source domain may own source private class, which is unreasonable to set the weight budget equally for each source prototype, i.e. $\bm{\beta}=\frac{1}{|\mathcal{C}_{s}|}\mathbf{1}_{|\mathcal{C}_{s}|}$. Therefore, we use the $\bar{\mathbf{Q}}^{st}$ obtained in the last iteration to update $\bm{\beta}$ with the moving average for adapting to the real source distribution , i.e.

$$\bm{\beta}^{(t+1)}=\mu\bm{\beta}^{(t)}+(1-\mu)\widetilde{\bm{\beta}}^{(t)},\quad\text{and}\quad\bm{\beta}^{(0)}=\frac{1}{|\mathcal{C}_{s}|}\mathbf{1}_{|\mathcal{C}_{s}|},$$

(9)

where $\widetilde{\bm{\beta}}^{(t)}$ is the sum of column in $\bar{\mathbf{Q}}^{st}$ solved in the $\bm{\beta}^{(t)}$ case.

To exploit target global and local structure and feature representation, we propose an OT-based Private Class Discovery (PCD) clustering technique that considers a full mapping problem between target sample features and target prototypes. Especially, our PCD avoids reliance on the number of target classes and encourages global discrimination of clusters as well as local consistency of samples.

To solve this, we pre-define $K$ learnable target prototypes $\mathbf{C}_{t}$ and initialize them randomly, where larger $K$ can be determined by the larger number of target samples. Then we assign target features $\bar{\mathbf{Z}}^{t}$ with the prototypes $\mathbf{C}_{t}$ by solving the optimal transport optimization problem:

$$\mathbf{Q}^{tt}=\text{OT}^{\varepsilon}(\mathbf{S}^{tt},\frac{1}{K}\mathbf{1}_{K},\frac{1}{2B}\mathbf{1}_{2B}),$$

(10)

where $\mathbf{S}^{tt}=\bar{\mathbf{Z}}^{t}\mathbf{C}_{t}^{\top}$ refers to cosine similarity between target samples and target prototypes, and $\bar{\mathbf{Z}}^{t}$ is the concatenation of the mini-batch target features $\mathbf{Z}^{t}$ and their nearest neighbor features. The marginal constraint of uniform distribution enforces that on average each prototype is selected at least $2B/K$ times in the batch.

The solution $\mathbf{Q}^{tt}$ satisfies the constraint strictly, i.e. the sum of each row equals to $1/K$. To obtain prototype assignment for each target sample, the soft pseudo-label matrix $\tilde{\mathbf{Q}}^{tt}=\mathbf{Q}^{tt}\times B$ ensures the $i$-th row $\mathbf{q}^{tt}_{i}$ is a probability vector. To encourage global discrimination of clusters, the learnable prototypes $\mathbf{C}_{t}$ and the feature extractor $f$ are optimized by minimizing $\mathcal{L}_{global}$, i.e.

$$\mathcal{L}_{global}=\frac{1}{B}\sum_{i=1}^{B}\ell(\tilde{\mathbf{q}}^{tt}_{i},\mathbf{z}^{t}_{i}),$$

(11)

where the cross-entropy loss $\ell(\mathbf{q}_{i},\mathbf{z}_{i})$ is presented as

$$\ell(\mathbf{q}_{i},\mathbf{z}_{i})=-\sum_{k=1}^{K}q_{i,k}\log p_{i,k},\quad\text{where}\quad p_{i,k}=\frac{\exp{(\mathbf{z}_{i}^{T}\mathbf{c}_{k}/\tau)}}{\sum_{k^{{}^{\prime}}=1}^{K}\exp{(\mathbf{z}_{i}^{T}\mathbf{c}_{k^{{}^{\prime}}}/\tau)}}.$$

(12)

To encourage local consistency of samples, we swap prediction between anchor feature $\mathbf{z}^{t}_{i}$ and its nearest neighbor feature $\tilde{\mathbf{z}}^{t}_{i}$ retrieved from the memory queue. Note that instead of swapped prediction between the different views of anchor image in SwAV [6], our swapped $\mathcal{L}_{local}$ is based on anchor-neighbor swapping, i.e.

$$\mathcal{L}_{local}=\frac{1}{2B}\sum_{i=1}^{B}\bigg{[}\ell(\tilde{\mathbf{q}}^{tt}_{B+i},\mathbf{z}^{t}_{i})+\ell(\tilde{\mathbf{q}}^{tt}_{i},\tilde{\mathbf{z}}^{t}_{i})\bigg{]}.$$

(13)

Eventually, to encourage both global discrimination of clusters and local consistency of samples, our $\mathcal{L}_{PCD}$ is presented as

$$\mathcal{L}_{PCD}=\frac{1}{2}(\mathcal{L}_{global}+\mathcal{L}_{local}).$$

(14)

Similar to Sec.3.2, since OT encourages a more deliberative mapping under marginal constraint, we also need to fill input features with the previous target features in memory queue before solving the optimization problem (10).

In UniDA, the partial alignment for common class detection and representation learning for private class discovery are based on UOT and OT models, respectively. Therefore, we can summarize the above two models in a unified framework, i.e. UniOT. Considering cross-entropy loss $\mathcal{L}_{cls}$ on source samples, Common Class Discovery loss $\mathcal{L}_{CCD}$ and Private Class Discovery loss $\mathcal{L}_{PCD}$, our overall objective can be expressed as

$$\mathcal{L}_{overall}=\mathcal{L}_{cls}+\lambda(\mathcal{L}_{CCD}+\mathcal{L}_{PCD}).$$

(15)

In the testing phase, only feature extractor $f$ and prototype-based classifier $\mathbf{C}_{s}$ are preserved. We solve the optimization problem (4) for all the concatenated target features and adaptive filled features. Then compute $w^{t}_{j}$ in Eq. 5 for each sample. For those samples who satisfy $w^{t}_{j}\geq\frac{1}{n}$ are assigned with the nearest source class, where $n$ is the sum of the total size of target samples $n_{t}$ and adaptive filling size. Otherwise, the samples are marked as unknown.

Our implementation of optimal transport solver is based on POT [16]. We employ pretrained Res-Net-50 [21] on ImageNet [13] as our initial backbone. The feature extractor consists of backbone and projection layers which are the same as [6] but BatchNorm layer is removed. We adopt the same optimizer details as [24]. The batch size is set to 36 for both source and target domains. For all experiments, the initial learning rate is set to $1\times 10^{-2}$ for all new layers and $1\times 10^{-3}$ for pretrained backbone. The total training steps are set to be 10K for all datasets. For the pre-defined number of target prototypes, a larger size of target domain indicates a larger $K$. Therefore, we empirically set $K=50$ for Office, $K=150$ for Office-Home, $K=500$ for VisDA, $K=1000$ for DomainNet. We default $\gamma=0.7$, $\mu=0.7$, $\tau=0.1$, $\varepsilon=0.01$, $\kappa=0.5$ and $\lambda=0.1$ for all datasets. We set the size of memory queue 2K for Office and Office-Home, 10K for VisDA and DomainNet.

All experiments are implemented on a GPU of NVIDIA TITAN V with 12GB. Each experiment takes about 2.5 hours. Our code is available at: https://github.com/changwxx/UniOT-for-UniDA.

Comparison with state-of-the-arts. Tab. 1 and 2 show the H-score results for Office, Office-Home, VisDA and DomainNet. Our UniOT achieves the best performance on all benchmarks. H-score on non-UniDA methods are reported from [18], and UniOT methods are reported from original papers accordingly, except for DANCE [34] since they did not report H-score and we reproduce it with their released code for fair comparison, marked as ‡. In particular, with respect to H³-score in Tab. 3, our UniOT surpasses other methods by $7\%$ and $9\%$ in Office and Office-Home datasets respectively, which demonstrates that our UniOT achieves balanced performance for both common class detection and private class discovery.

Evaluation of the effectiveness of the proposed CCD and PCD. To evaluate the contribution of $\mathcal{L}_{CCD}$, $\mathcal{L}_{global}$ and $\mathcal{L}_{local}$, we train the model with different combination of each component. As shown in Tab.4, the combination of $\mathcal{L}_{global}$ and $\mathcal{L}_{local}$, i.e. $\mathcal{L}_{PCD}$, brings significant contribution since target representation is crucial for distinguishing common and private samples. Especially, $\mathcal{L}_{global}$ contributes more than $\mathcal{L}_{local}$, which demonstrates the benefit of global discrimination of clusters for representation learning. Besides, we also conduct experiments for CCD without adaptive filling and denote the loss as $\mathcal{L}_{CCD}^{{\dagger}}$, which verifies the effectiveness of adaptive filling design.

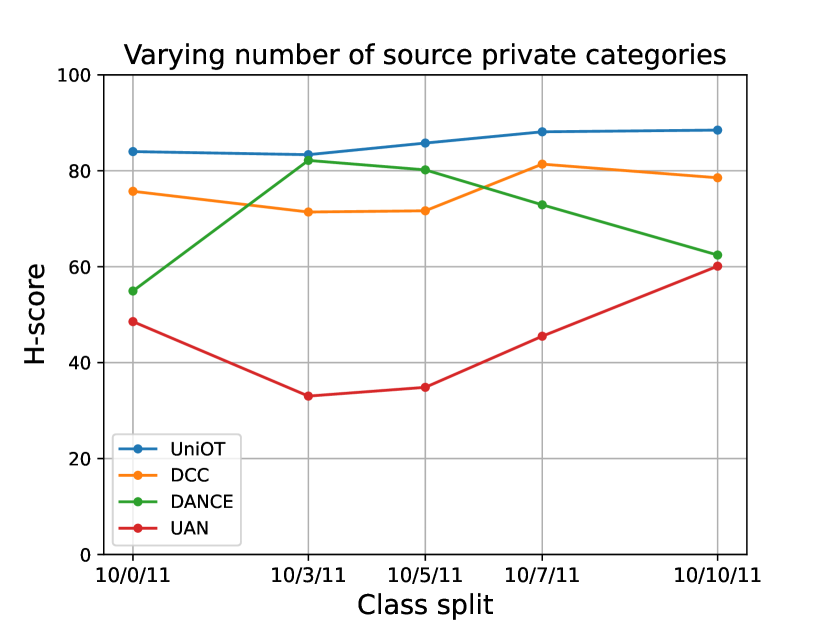
Robustness in realistic UniDA. We compare the performance of our UniOT with DCC, DANCE and UAN under different categories split. In this analysis, we perform on A2W of Office with a fixed common label set $\mathcal{C}$ and target-private label set $\overline{\mathcal{C}}_{t}$, but the different size of source-private label set $\overline{\mathcal{C}}_{s}$. We set 10 categories for $\mathcal{C}$, 11 categories for $\overline{\mathcal{C}}_{t}$ and vary the number of $\overline{\mathcal{C}}_{s}$. Fig. 3(a) shows that our UniOT always outperforms other methods. Besides, UniOT is not sensitive to the variation of source-private classes while other methods are not stable enough. Additionally, we also analyze the behavior of UniOT under the different size of target-private label set $\overline{\mathcal{C}}_{t}$. We also perform on A2W of Office with a fixed common label set $\mathcal{C}$ for 10 categories and source-private label set $\overline{\mathcal{C}}_{s}$ for 10 categories. Fig. 3(b) shows that our UniOT still performs better, while the other methods present sensitivity to the number of target-private classes. Therefore, UniOT is more robust to the variation of target-private classes.

Feature visualization for comparison with existing UniDA methods. We use t-SNE [37] to visualize the learned target features for Rw2Pr of Office-Home. As shown in Fig. 4, the common samples are colored in black and the private samples are colored with other non-black colors by their ground-truth classes. Fig. 4(b) shows that UAN cannot recognize different categories among target-private samples since they treat all target-private samples as a single class. Especially, our UniOT discovers the global and local structure of target-private samples. Fig. 4(d) validates that UniOT learns a better target representation with global discrimination and local consistency of samples compared to DANCE shown in Fig. 4(c).