Unexpectedly enhanced $\bm{\alpha}$-particle preformation in ⁴⁸Ti probed by the $\bm{(p,p\alpha)}$ reaction

—Introduction. Since Gamow explained the $\alpha$ decay as the quantum tunneling of $\alpha$ particle out of an atomic nucleus [1], the formation of $\alpha$ particle in nuclei has been a fundamental subject for understanding the structure and decay of nuclei [2, 3, 4, 5]. It has been considered that $\alpha$ particles are formed at a low-density nuclear surface with a certain probability, which is called the preformation factor or the $\alpha$-particle preformation probability. It determines the lifetime of heavy and superheavy nuclei, and its empirical values have often been estimated from the $\alpha$ decay lifetime. For instance, the very short lifetime of ${}^{108}{\rm Xe}$ and ${}^{104}{\rm Te}$ were recently measured [6, 7], and the enhancement of the $\alpha$-particle preformation probability beyond proton-rich nucleus ${}^{100}{\rm Sn}$ has been discussed [8, 9, 10].

It is also well known that the $\alpha$-particle preformation manifests itself in light nuclei as $\alpha$ clustering [11, 12] and is closely related to the synthesis of elements in stars [13, 14]. Because it exhibits the unique excitation spectra, $\alpha$ clustering has been identified in many light nuclei [15, 16]. Compared to heavy or light mass nuclei, the $\alpha$-particle preformation in medium-mass nuclei has been poorly known. Generally, it is believed that $\alpha$-particle preformation is hindered in medium-mass nuclei because of the largely negative $\alpha$-decay $Q$-values. The deep binding energies of these nuclei also lead to the dominance of the mean-field dynamics over the four nucleon correlation preventing $\alpha$-particle formation. However, such hindrance of $\alpha$-particle preformation has never been quantitatively confirmed by experiment due to the lack of reliable measure for the $\alpha$-particle preformation.

The proton-induced $\alpha$-knockout reaction $(p,p\alpha)$ has been expected as the sensitive probe for the $\alpha$-particle preformation [17, 18, 19, 20, 21]. Due to the strong absorption effect, the $\alpha$ particle kicked by the projectile proton cannot get out from the interior of the target nucleus. Consequently, the reaction is only sensitive to the $\alpha$ particles formed on the surface of the target nucleus. Several experiments have been conducted to measure the $\alpha$-particle preformation probability in light-medium mass nuclei. Carey et al. reported a systematic measurement of the $(p,p\alpha)$ reactions with various target nuclei from ${}^{16}{\rm O}$ to ${}^{66}{\rm Zn}$ [19]. However, due to the lack of quantitative analysis, the absolute value of the $\alpha$-particle preformation probabilities deduced from the cross sections have large uncertainty.

Recently, it has been shown that the distorted wave impulse approximation (DWIA) with reliable optical potentials realizes an accurate description of the $(p,p\alpha)$ reaction [22]. Taking well-known light-mass $\alpha$ clustered nucleus ${}^{20}{\rm Ne}$ as an example, it was demonstrated that the $\alpha$-particle preformation probability is quantitatively evaluated. The new analysis showed that the $\alpha$-particle preformation probability of ${}^{20}{\rm Ne}$ is smaller than that estimated by Carey et al. by a factor of two. Among the nuclei studied by Carey et al., ${}^{48}{\rm Ti}$ is the only one except for ${}^{20}{\rm Ne}$, for which the optical potentials between a proton, $\alpha$ particle, the residue (${}^{44}\mathrm{Ca}$), and the target nucleus (${}^{48}{\rm Ti}$) have already been known accurately [23, 24, 25]. Furthermore, the residue ${}^{44}\mathrm{Ca}$ is a magic stable nucleus as an inert core, and hence, the enhancement of the $\alpha$-particle preformation can be expected. Therefore, the DWIA analysis of the ${}^{48}{\rm Ti}(p,p\alpha)^{44}{\rm Ca}$ reaction must shed new insight into the $\alpha$-particle preformation in medium-mass nuclei.

—DWIA framework. The DWIA framework [26, 27, 28, 22] has been adopted to describe the ${}^{48}{\rm Ti}(p,p\alpha)^{44}{\rm Ca}$ reaction. Within the factorization approximation, the triple differential cross section is given as,

where $T_{p}$, $\Omega_{p}$ and $\Omega_{\alpha}$ are the kinetic energy of the emitted proton, the solid angles of the proton and $\alpha$ particles, respectively. $C_{0}F_{\rm kin}$ is the kinematical factor, and $\mathrm{d}\sigma_{p\alpha}/\mathrm{d}\Omega_{p\alpha}$ is the $p$-$\alpha$ differential cross section at the $p$-$\alpha$ relative momentum of the $(p,p\alpha)$ reaction kinematics. The detail of this approximation is given in Refs. [26, 27], and the validity of this approximation has been tested and confirmed [26]. The reduced transition matrix element $\bar{T}$ is defined as,

where $\bm{k}_{0}$ is the momentum of the incident proton. Equation (2) shows the sensitivity of the cross section to the $\alpha$-particle preformation because it depends on the probability amplitude of the $\alpha$-particle preformation $y(R)$. The other ingredients of the analysis are the optical potentials for the $p$-${}^{48}{\rm Ti}$, $p$-${}^{44}{\rm Ca}$, and $\alpha$-${}^{44}{\rm Ca}$ scattering, which are used to describe the distorted waves $\chi_{p}^{(\pm)}(\bm{R})$ and $\chi_{\alpha}^{(-)}(\bm{R})$; the superscripts $(+)$ and $(-)$ indicate outgoing and incoming boundary conditions, respectively. It was shown that the use of the accurate optical potentials is essential for the precise description of the cross sections and the evaluation of $\alpha$-particle preformation. In the present work, the EDAD1 optical potential  [24, 25] with Dirac phenomenology has been adopted to the $p$-${}^{48}\mathrm{Ti}$ and $p$-${}^{44}\mathrm{Ca}$ distorted waves. This potential reproduces the proton-nucleus elastic scattering with various stable targets from ${}^{12}{\rm C}$ to ${}^{208}{\rm Pb}$ in a wide energy range from 20 MeV to 1 GeV. For the $\alpha$-${}^{44}\mathrm{Ca}$ distorted wave, we applied the optical potential proposed by Delbar et al. [23], which reproduces the elastic differential cross sections from 24.1 to 100 MeV very accurately. All these optical potentials cover the required energy range for the analysis of the ${}^{48}{\rm Ti}(p,p\alpha)^{44}{\rm Ca}$ reaction.

—The $\alpha$-particle preformation probability. The probability amplitude for $\alpha$-particle preformation, called the reduced width amplitude (RWA), is defined as,

where $\Phi_{\alpha}$, $\Phi_{\rm Ca}$, and $\Phi_{\rm Ti}$ denote the ground state wave functions of the $\alpha$ particle, the residue (${}^{44}\mathrm{Ca}$), and the target nucleus (${}^{48}{\rm Ti}$), respectively. In this work, the $\alpha$ is assumed to have a $(0s)^{4}$ configuration, and the wave functions of ${}^{44}{\rm Ca}$ and ${}^{48}{\rm Ti}$ are described by using the antisymmetrized molecular dynamics (AMD) [29, 30, 31]. The parity-projected AMD wave function is given as,

where $P_{x}$ is the parity operator, $\mathcal{A}$ is the antisymmetrizer and $\varphi_{i}$ is the nucleon wave packet. The centroid of a nucleon wave packet is a complex vector $\bm{Z}_{i}$, in which the real (imaginary) part describes the mean position (momentum) of a nucleon. The parameters of the model wave function are the centroids $\bm{Z}_{i}$, the spin directions $\alpha_{i}$ and $\beta_{i}$, and the Gaussian widths $\nu_{x}$, $\nu_{y}$, and $\nu_{z}$. The wave function of ${}^{44}{\rm Ca}$ is calculated within the mean-field approximation, i.e., the parameters are optimized to minimize the intrinsic energy $E=\braket{\Psi}{H}{\Psi}/\braket{\Psi}{\Psi}$. Here, the Hamiltonian consists of the nucleon kinetic energies, the effective nucleon-nucleon interaction, and the Coulomb interaction. As an effective nucleon-nucleon interaction, we have used Gogny D1S density functional [32] that reasonably reproduces the fundamental nuclear properties. After the energy minimization, the ${}^{44}{\rm Ca}$ wave function is projected to $J^{\pi}=0^{+}$ to calculate the RWA [Eq. (4)] using the Laplace expansion method [33].

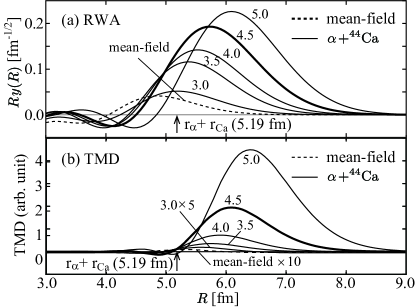
The wave function of ${}^{48}{\rm Ti}$ is also calculated in the same manner. The obtained wave function, i.e., the mean-field solution for ${}^{48}{\rm Ti}$, is shown in Fig. 1 (a). It has an almost spherical shape and does not clearly show the $\alpha$-particle preformation. Indeed, the RWA calculated from this mean-field solution [Fig. 2 (a)] has only a small peak at $R=4.8$ fm, and as discussed later, it is too small to reproduce the observed cross section. Therefore, we artificially generate the test wave functions of ${}^{48}{\rm Ti}$ that exhibit prominent $\alpha$-particle preformation. For this purpose, we introduce an approximate inter-nuclear distance $d$ [34, 35],

where the first and second terms correspond to the center-of-mass of $\alpha$ and ${}^{44}{\rm Ca}$, respectively. We perform the energy variation with the constraint on the value of $d$ and obtain the wave functions which mimic the $\alpha$-particle preformation with various inter-nuclear distance as shown in Fig. 1 (b)–(f). The RWAs calculated from these wave functions shown in Fig. 2 (a) have prominent peaks that become higher and move outward with the increase of $d$. Note that the RWAs are strongly suppressed in the interior of the residual nucleus ($R\lesssim 5$ fm) due to the Pauli principle. Consequently, the peak position is not necessarily the same as the value of $d$.

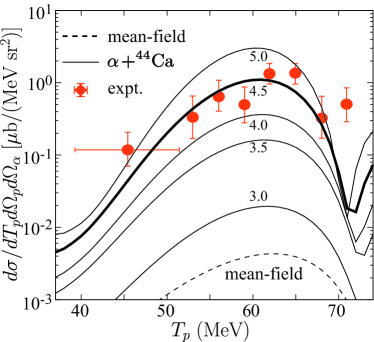
—Results and Discussions. Figure 3 shows the triple differential cross sections of the ${}^{48}\mathrm{Ti}(p,p\alpha){}^{44}\mathrm{Ca}$ reaction obtained by the DWIA calculations using the RWAs shown in Fig. 2 (a). The cross sections are plotted as functions of the outgoing proton energy. The incident proton energy, the emitted angles of the proton and $\alpha$ particle are set to the same values as in the experiment by Carey et al. [19]. Unexpectedly, it is found that the mean-field solution does not reproduce the observed cross section at all. It underestimates the cross section in three orders of magnitude, which cannot be explained by the uncertainty of the optical potentials used in DWIA analysis or the density functional (Gogny D1S) used to calculate the mean-field solution. Consequently, we conclude that the $\alpha$ preformation probability is much larger than that described by the mean-field solution.

To estimate the degree of $\alpha$-particle preformation, we have also tested the RWAs obtained from the $\alpha+{}^{44}\mathrm{Ca}$ wave functions with various inter-nuclear distances. Figure 3 shows that these RWAs yield much larger cross sections than the mean-field solution, and the cross section increases by approximately one order of magnitude for every 1 fm increase of the inter-nuclear distance. It is found that the RWA obtained from the $\alpha+{}^{44}\mathrm{Ca}$ wave function with $d=4.5$ fm gives the most plausible description of the observed cross section. The peripherality of the $(p,p\alpha)$ reaction is confirmed from the real part of the transition matrix density (TMD) [27] that is defined as,

Note that the integral of TMD over the distance is equal to the square of the transition matrix $T$, and hence, $\delta(R)$ gives a hint at which distance $R$ the reaction takes places. As shown in Fig. 2 (b), TMD is negligible in the interior region ($R\lesssim 5$ fm) due to the strong absorption of an $\alpha$ particle and small RWA. It explains why the cross section with the mean-field solution is smaller in order of magnitude than that with the $\alpha+{}^{44}\mathrm{Ca}$ wave functions. We also note that the peak position ($T_{p}\sim 63$ MeV) and width of the cross section are approximately determined by the kinematical condition (recoil-less condition for the residue ${}^{44}{\rm Ca}$) and the momentum distribution of the RWA, respectively.

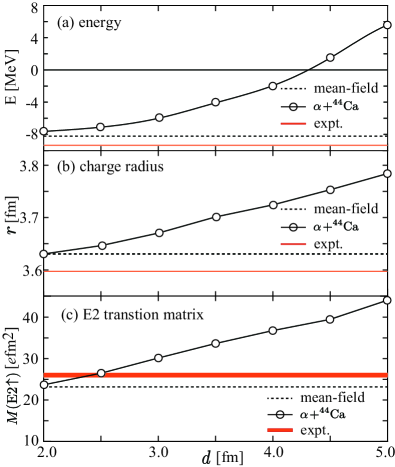
Although the $\alpha+{}^{44}\mathrm{Ca}$ wave function with $d=4.5$ fm gives the best result for the ${}^{48}{\rm Ti}(p,p\alpha)^{44}{\rm Ca}$ reaction, its validity should be verified from different perspectives. Firstly, it must be noted that the binding energies of the $\alpha+{}^{44}\mathrm{Ca}$ wave functions are much smaller than that of the mean-field solution because of the artificial constraint imposed on the inter-nuclear distance [Eq. (7)]. Figure 4 (a) shows that the binding energy of the $\alpha+{}^{44}\mathrm{Ca}$ wave function rapidly decreases as the inter-nuclear distance increases. At $d=$4.5 fm, it underestimates the experimental value [36] by approximately 10 MeV and yields the positive $Q$-value of the $\alpha$ decay, whereas the mean-field solution gives reasonable binding energy and $Q$-value. Panels (b) and (c) show the charge radius and the reduced matrix elements for the E2 transition from the ground state to the $2^{+}_{1}$ state, respectively. As expected, both the charge radius and E2 transition matrix elements increase with the inter-nuclear distance. Although the $\alpha+{}^{44}\mathrm{Ca}$ wave function gives reasonable values at $d=2.0$–2.5 fm, it overestimates the observed values [37, 38] at $d=4.5$ fm. In short, the $\alpha+{}^{44}\mathrm{Ca}$ wave function can describe the ${}^{48}{\rm Ti}(p,p\alpha)^{44}{\rm Ca}$ reaction, but it fails to reproduce the fundamental structural properties. On the contrary, the mean-field solution offers a better description of the energy, radius, and E2 transition but fails in the $\alpha$ knockout reaction. From these results, we can deduce that the ground state wave function should be an admixture of the mean-field solution and the $\alpha+{}^{44}\mathrm{Ca}$ type wave functions. The mean-field solution should be the dominant component of the ground state due to its large binding energy, but the contamination of the $\alpha+{}^{44}\mathrm{Ca}$ wave function is indispensable to explain the observed large $\alpha$ knockout cross section.

—Summary. The ${}^{48}{\rm Ti}(p,p\alpha)^{44}{\rm Ca}$ reaction has been studied to investigate the $\alpha$-particle preformation in a medium-mass nucleus ${}^{48}{\rm Ti}$. The DWIA analysis using accurate optical potentials offers a reliable and quantitative description of the $\alpha$-knockout reaction, and it has revealed that the $\alpha$-particle preformation in ${}^{48}{\rm Ti}$ is unexpectedly enhanced. It has been shown that the mean-field solution underestimates the cross section in orders of magnitude, and one must assume the $\alpha+{}^{44}\mathrm{Ca}$ wave function whose the inter-nuclear distance is as large as $d=4.5$ fm to reproduce the observed cross section. However, the $\alpha+{}^{44}\mathrm{Ca}$ wave function fails to explain other basic properties of ${}^{48}{\rm Ti}$, which are reasonably described by the mean-field approximation. Hence, we conclude that the ground state is an admixture of the mean-field and $\alpha+{}^{44}\mathrm{Ca}$ configurations. This new insight requests the systematic analysis of the $(p,p\alpha)$ reactions to reveal the universality of the $\alpha$-particle preformation and poses a challenge to the microscopic nuclear models for describing $\alpha$-particle preformation in medium-mass nuclei.