Unexpected Information Leakage of Differential Privacy Due to Linear Property of Queries

The differential privacy is state of the art conception for privacy preservation [9]. Since the conception of differential privacy is proposed, there have been some analyses about its information leakage. There are mainly two lines of papers. The first line is related to assumption of data generation. In differential privacy, records in data sets are assumed to be independent. But the assumption is not always true in real application scenarios [17]. For example, Bob or one of his 9 immediate family members may have contracted a highly infectious disease. The whole family is infected together or none of them is infected with high probability [18]. The correlation among family members makes it easier for attackers to infer whether Bob is infected by querying ”how many people are infected by the disease in Bob’s family”. There are some papers aiming at fixing the correlation problem. Lv et al. research the problem in scenarios of big data [13]. Wu et al. research the problem from the perspective of game theory [19]. Zhang et al. research the problem in machine learning [22]. The key of fixing correlation problem is to find an appropriate quantity to quantify correlation among data records. Then added noise of differential privacy mechanisms is calibrated by the quantity. Chen et al. quantify degree of correlation by Gaussian correlation model [4]. Zhu et al. propose conception of correlated sensitivity to quantify degree of correlation [23]. A strength of the line is that the unexpected information leakage is not related to certain differential privacy mechanisms. A weakness is that the unexpected information leakage is only related to correlated records not for all records.

The second line is related to the extensional conception of sensitivity of differential privacy. There is a difficult trade-off in differential privacy mechanisms, namely trade-off between magnitude of noise and data utility [7] [10]. In order to reduce the magnitude of noise, various alternative conceptions for sensitivity are proposed such as elastic sensitivity [11] and record sensitivity [9]. Some of these proposed conceptions are weak and lead to unexpected information leakage. The local sensitivity is an example [14]. The goal of local sensitivity is to release data with database-based additive noise. That is, the noise magnitude is determined not only by the queries which are to be released, but also by the data set itself. However, the noise calibrated by local sensitivity is too small, resulting in information leakage. For example, let $f_{med}(x)=median(x_{1},x_{2},\dots,x_{n})$, where $x_{i}$ are sorted real number from bound interval such as $[0,\Lambda]$. If the $f_{med}(x)$ is released with noise magnitude proportional to local sensitivity, then the probability of receiving a non-zero answer is zero when $x_{1}=\dots=x_{m+1}=0$,$x_{m+2}=\dots=x_{n}=\Lambda$. Whereas the probability of receiving a non-zero answer is non-negligible when $x_{1}=\dots=x_{m}=0$,$x_{m+1}=\dots=x_{n}=\Lambda$. Where $n$ is odd and $m=\frac{n+1}{2}$. The analyses for extensional conceptions of sensitivity are difficult because how big the noise magnitude needs to be is hard to quantify.

The goal of membership inference attacks is to determine that a given data record is in a target data set or not. The attack is firstly demonstrated by Homer [8]. Their paper has so much big influence on privacy community that the USA National Institute of Health (NIH) switches policies in case of membership information leakage in process of releasing statistical data. The membership inference attacks has been valued since then. Shokri et al. quantitatively investigate membership inference attacks against machine learning models [16]. Rahman et al. analyze membership inference attacks against deep learning model which is protected by differential privacy mechanisms [15]. Yeom et al. investigate the relationship between overfitting and membership inference attacks, finding that ”overfitting is sufficient to allow an attacker to perform membership inference attack” [21]. Backes et al. explore the membership inference attacks against miRNA expression data set [3]. Almadhoun et al. discuss membership inference attacks against differential privacy mechanisms [1]. They take advantage of dependence of data records. Almadhoun et al also analyze an application of membership inference against genomic data sets [2].

In brief, the first line is about the special records which are correlated with each other and the second line is about trade-off between noise magnitude and data utility. Different from the mentioned two lines, we will discuss unexpected information leakage from a novel angle. In this paper, from the view of query functions, we show that differential privacy mechanisms do not take liner property of queries into account, resulting in unexpected information leakage.

In the next section, background knowledge will be introduced briefly, including the conception of differential privacy, the linear property and the hypothesis test. In the section 3, how to obtain multiple answers for linear queries is presented. In the section 4, the proposed membership inference attacks method will be presented and an instance of attack will be given. In section 5, experimental results will be showed. At last, the conclusion will be claimed.

The differential privacy is the most popular conception of privacy preservation. It formalizes a strong privacy guarantee: even if attackers know all data records except one, attackers cannot get much information of the record which attackers don’t know [6] [12]. To that end, differential privacy mechanisms guarantee that its outputs are insensitive to any particular data record. That is, presence or absence of any record has limited influence on outputs of differential privacy mechanisms. The presence or absence of one record in a data set is captured by a conception of neighboring databases. Specifically, databases $D$ and $D^{\prime}$ are neighboring databases denoted by $D\sim D^{\prime}$ if there is only one different record between $D$ and $D^{\prime}$ denoted by $d(D,D^{\prime})=1$.

Definition 1(differential privacy) Any random mechanism $M:D^{n}\to R^{d}$ preserves $\epsilon$-DP(differential privacy) if for any neighboring databases $D$ and $D^{\prime}$ such that $d(D,D^{\prime})=1$ and for all sets of possible output $S$:

Here, the $\epsilon$ is the privacy budget. The privacy guarantee is quantified by the privacy budget. The smaller the privacy budget is, the stronger the privacy guarantee is.

The Laplace mechanism is a famous and foundational mechanism in the field of differential privacy. It is to deal with numerical data. The Laplace mechanism is based on a conception of global sensitivity. The global sensitivity quantifies the max difference of query’s answer, which is caused by presence or absence of one record.

Definition 2 (global sensitivity) For a given database $D$ and query $q$, the global sensitivity denoted by $\Delta D$ is

The Laplace mechanism covers the difference by noise drawn from Laplace distribution with location parameter $\mu=0$ and scale parameter $b=\frac{\Delta D}{\epsilon}$.

Definition 3 (Laplace mechanism) For given database $D$, query $q$ and privacy budget $\epsilon$, the output of Laplace mechanism is

Here, the $Lap(0,\frac{\Delta D}{\epsilon})$ represents noise drawn from a Laplace distribution with location parameter 0 and scale parameter $\frac{\Delta D}{\epsilon}$.

Differential privacy mechanisms have many good properties which make it possible to build complex differential privacy mechanisms by basic block algorithms. Two of them are Sequential Composition Theorem and Parallel Composition Theorem.

Sequential Composition Theorem Let $A_{1},A_{2},\cdots,A_{k}$ be $k$ algorithms that satisfy $\epsilon_{1}$-DP,$\epsilon_{2}$-DP, $\cdots$,$\epsilon_{k}$-DP respectively. Publishing $t=<t_{1},t_{2},\cdots,t_{k}>$ satisfies $(\sum_{i=1}^{k}\epsilon_{i})$-DP. Where, $t_{1}=A_{1}(D),t_{2}=A_{2}(t_{1},D),t_{3}=A_{3}(<t_{1},t_{2},D>),\cdots,t_{k}=A_{k}(<t_{1},t_{2},t_{3},\cdots,t_{k-1}>,D)$.

Parallel Composition Theorem Let $A_{1},A_{2},\cdots,A_{k}$ be $k$ algorithms that satisfy $\epsilon_{1}$-DP,$\epsilon_{2}$-DP, $\dots$,$\epsilon_{k}$-DP respectively. Publishing $t=<t_{1},t_{2},\cdots,t_{k}>$ satisfies $(max_{i\in[1,2\cdots k]}\epsilon_{i})$-DP. Where, $t_{1}=A_{1}(D_{1}),t_{2}=A_{2}(t_{1},D_{2}),t_{3}=A_{3}(<t_{1},t_{2},D_{3}>),\cdots,t_{k}=A_{k}(<t_{1},t_{2},t_{3},\cdots,t_{k-1}>,D_{k})$ and $D_{i}\cap D_{j}=\emptyset$ for all $i\neq j$,

The linear query is one kind of fundamental queries. It is used widely. For example, sum and counting query are popular linear queries. The linear query has a very good property, namely linear property.

Definition 4 (linear property) For linear query $q$ and data set $D$ such that $D=D_{1}\cup D_{2}$ and $\varnothing=D_{1}\cap D_{2}$, we have

The counting query is one kind of linear queries so it satisfies the linear property.

The hypothesis test is a statistic tool to determine whether fluctuation of experimental results is only due to randomness. Its main goal is to guarantee the confidence level of experimental conclusions. To that end, there are three steps in hypothesis test logically. Firstly, an assumption about experimental conclusions is made. The assumption needs to be contrary to conclusions which are achieved by experimental results. The assumption is called null hypothesis denoted by $H_{0}$. The opposite hypothesis of null hypothesis is called alternative hypothesis denoted by $H_{1}$. Secondly, a statistics is chosen. The statistics needs to be related to the assumption and its probability distribution function is known. Thirdly, the probability of experimental results is calculated through the known distribution. If the probability is smaller than a predetermined threshold, experimental conclusions are reliable. The procedure can guarantee that when the assumption which is contrary to experimental conclusions is right, the experimental results occur with extremely small probability. That is, the experimental results are not only due to randomness.

The concrete steps of hypothesis test method are clear. Firstly, a predetermined probability threshold needs to be chosen and it is called significance level. Secondly, the experimental results’ probability is calculated and the probability is called $p$ value. At last, a decision is made. In specific, if the $p$ value is greater than the predetermined significance level, alternative hypothesis is accepted. Otherwise, the null hypothesis is accepted.

The one-sample t-test is an useful hypothesis test method. It is used to determine whether samples come from a distribution with a certain mean.

Attackers can issue query $q_{s}(D)$ to the differential privacy mechanism $M$. The $q_{s}(D)$ means computing the query $q$ over the target data set $D$ under the condition $s$ which specifies the range of data records. In other words, the $q_{s}(D)$ is equal to $q(D\cap D_{s})$ where the $D_{s}$ is the set of records which satisfy the condition $s$. For example, ”count the number of students whose age is greater than 10 in a classroom”. The query $q$ is the counting query, the data set $D$ is the set of all students in the classroom and the condition $s$ is that ” the age is greater than 10”.

Suppose that the target record is denoted by $x$ and the background knowledge of attackers is a set of data records denoted by $D_{know}$. The goal is to obtain multiple answers for a linear query $q(\{x\}\cup D_{know})$. The $s$ represents the condition such that $D_{s}=\{x\}\cup D_{know}$. Therefore, the target query can be expressed as $q_{s}$ and its answer can be expressed as $M(q_{s},D,\epsilon)$.

Attackers choose a subset $D_{i}\subset D_{know}$, construct a query condition $s_{i}$ such that $D_{s_{i}}=D_{i}\cup\{x\}$, issue query $q_{s_{i}}(D)$ to the differential privacy mechanism and obtain $a_{i}=M(q_{s_{i}},D,\epsilon)=q_{s_{i}}(D)+Lap(0,\epsilon/\Delta D)$ as return. Let $\hat{a}_{i}=q(D_{know}\setminus D_{i})+a_{i}$.

The data set $D_{i}$ is a subset of $D_{know}$ and the $D_{know}$ is background knowledge of attackers so attackers can compute $q(D_{know}\setminus D_{i})$ locally by themselves. The $\hat{a}_{i}$ is an answer of the target query $q(\{x\}\cup D_{know})$, which will be proved in next subsection.

Through another subset $D_{j}\subset D_{know}$, attackers can get another answer of the target query. Therefore, attackers can get multiple answers of the target query. If $D_{i}\cap D_{j}=\emptyset$ for all $i\neq j$, the totally consumed privacy budget is different from the differential privacy mechanism’s perspective and attackers’ perspective. The claim is proved in next subsection.

The whole idea of this paper is showed in Fig 1, including the method to obtain multiple answers for the target query and the membership inference attacks method which is presented in detail at next section.

In this subsection, the proposed method is analyzed in terms of correctness and privacy respectively. In the theorem 1, we prove that linear queries’ multiple answers can be obtained. In theorem 2, we analyze the amount of background knowledge of attackers. Then, totally consumed privacy budget is analyzed from the two perspectives.

Theorem 1: $\hat{a}_{1},\hat{a}_{2},\dots,\hat{a}_{m}$ are i.i.d. samples of the target linear queries’ answer calculated by differential privacy mechanisms over the target data set $D$.

Proof:

For $\forall i$, we have

We know that $q_{s_{i}}(D)=q((D_{i}\cup\{x\})\cap D)$. And we also know

And

In addition, $q$ is linear query. We have

Here $D_{u}$ is union set of $D_{know}\setminus D_{i}$ and $(D_{i}\cup\{x\})\cap D$.

So, we have

So, we have

According to the equality (1), for all $\hat{a}_{1},\hat{a}_{2},\dots,\hat{a}_{m}$, the noise $Lap(0,\frac{\Delta D}{\epsilon})$ are i.i.d. samples of a Laplace distribution. So, the $\hat{a}_{1},\hat{a}_{2},\dots,\hat{a}_{m}$ are i.i.d. samples of the target query’s answer. $\hfill\Box$

The background knowledge is a foundation of proposed method. The background knowledge is a set of known records in the proposed method, although it is captured by prior probability distribution in some papers such as [20]. It is easier to obtain some records of a target data set than to obtain a prior probability distribution of the target data set. For example, with respect to score of students, it is easier to collect some students’ score than to obtain a prior probability distribution of students’ score.

The number of records in $D_{know}$ is a way to quantify the amount of background knowledge of attackers.

Theorem 2: The number of records in $D_{know}$ needs to be greater than $m$.

Proof:

As known before, a subset of $D_{know}$ can be used to generate an i.i.d. sample for the target query’s answer. The number of i.i.d. samples is $m$. Therefore, the number of records in $D_{know}$ should guarantee that the number of possibly used subsets of $D_{know}$ is equal to or greater than $m$.

In the proposed method, all possibly used subsets are disjoint with each other. Therefore, the number of possibly used subset is equal to the number of records in $D_{know}$ at most. In specific, each possibly used subset has only one record of $D_{know}$.

In a word, the number of records in $D_{know}$ needs to be greater than $m$.

$\hfill\Box$

The privacy budget is the key parameter for privacy guarantee in differential privacy mechanisms. The smaller the privacy budget is, the stronger the privacy guarantee is. One good property of differential privacy is that the totally consumed privacy budget can be calculated in a cumulative way.

Theorem 3: From attackers’ perspective, the totally consumed privacy budget is $\epsilon_{t}$.

Proof

For $\forall i$, the consumed privacy budget of $M(q_{s_{i}},D,\epsilon)$ is $\epsilon=\frac{\epsilon_{t}}{m}$. By the theorem 1, attackers obtain $m$ answers for the target query from the differential privacy mechanism. According to the Sequential Composition Theorem, the totally consumed privacy budget is

$\hfill\Box$

From the attackers’ perspective, the totally consumed privacy budget can be unreasonably large if there are enough records in the set of background knowledge. In specific, if attackers can consume $\epsilon$ privacy budget to obtain one answer of the target query, then attackers can consume $m*\epsilon$ privacy budget to obtain $m$ different answers of the target query using the proposed method. So, if there are enough records in the set of background knowledge, attackers can consume unreasonably large privacy budget for the target query. However, from the differential privacy mechanism’s perspective, the totally consumed privacy budget is different.

Theorem 4: From the differential privacy mechanism’s perspective, when the target record $x$ is not in the target data set the totally consumed privacy budget is $\epsilon$. When the target record $x$ is in the target data set, the differential privacy mechanism responds $m$ different query with $\epsilon$ privacy budget for each response, in resulting $\epsilon_{t}$ in total.

Proof

Firstly, when the target record $x$ is not in the target data set $D$, for $\forall\ i$ we have

The consumed privacy budget of $q_{s_{i}}$ is denoted by $\epsilon_{i}$. For $\forall\ 0<i\neq j<m$, we know $D_{i}\cap D_{j}=\emptyset$. According to the Parallel Composition Theorem, the totally consumed privacy budget is

Secondly, when the target record $x$ is in the target data set $D$, for $\forall\ i$ we have

For $\forall\ 0<i\neq j<m$, we have

According to the Sequential Composition Theorem, the totally consumed privacy budget is

In a word, from the differential privacy mechanism’s perspective, it responds $m$ different query with $\epsilon$ privacy budget for each response, in resulting $\epsilon_{t}$ in total. That is, from the differential privacy mechanism’s perspective, the target query only consume privacy budget $\epsilon$. $\hfill\Box$

In a word, the totally consumed privacy budget is delicately analyzed from attackers’ perspective and differential privacy mechanism’s perspective in the theorem 3 and 4 respectively. The attackers can consume unreasonably large privacy budget while the differential privacy mechanism may not beware. Whether the differential privacy mechanism bewares the unreasonably large consumed privacy budget depends on weather the target record is in the target data set. That is, the presence or absence of the target record has key influence on behavior of the differential privacy mechanism. Thus, it is possible to infer whether the target record is in the target data set by observing outputs of differential privacy mechanism.

The membership inference attacks is to determine whether a data record is in a data set. Specifically, there is a target data set with sensitive information and a differential privacy mechanism is used to protect the target data set. Attackers has black-box access to the differential privacy mechanism. Given a data record, attackers guess: whether the given record is in the target data set. The formal definition of membership inference attacks is as follows:

Definition 5 (membership inference attacks): Given black-box access to a differential privacy mechanism $M$ and a target record $x$, attackers guess whether the target record is in the the target data set $D$.

Here, the $A$ represents membership inference attacks method. If the attacks method asserts that the target record is in the target data set, it outputs 1. Otherwise, it outputs 0.

There are three assumptions about the black-box access of the differential privacy mechanism.

(1) For the same query, the black-box access returns the same answer no matter how many times the query is issued. If attackers can get a new answer for the same query from the black-box access when attackers issue the query every time, then attackers can get multiple i.i.d. samples of the target query’s answer trivially. With multiple i.i.d. samples, it is trivial for attackers to infer sensitive information of records. Thus, this assumption is reasonable.

(2) For every different query, the black-box access returns an answer. The second assumption guarantees the utility of differential privacy mechanisms. If the black-box access refuses to answer queries which are issued first time, the utility of differential privacy mechanisms is damaged, resulting in useless mechanisms.

(3) There is a threshold of the totally consumed privacy budget. When the totally consumed privacy budget is greater than the threshold, the black-box access aborts. The consumed privacy budget is accumulative and when totally consumed privacy budget is greater than a certain limitation, leaking information is trivial.

The ability of attackers is limited. The black-box access means that attackers issue a query to a differential privacy mechanism and gets a result as return. Attackers cannot get any other information from the differential privacy mechanism.

The security of the Laplace mechanism is based on perturbation. The differential privacy requires that presence or absence of one record cannot be identified through mechanisms’ outputs. The Laplace mechanism satisfies the requirement by perturbation. Specifically, queries’ answer are perturbed by noise. The noise is drawn from a Laplace distribution whose variance is related to two factors. The first factor is strength of privacy guarantee. The second factor is maximum difference of query’s answer, which is caused by presence or absence of any one record. The maximum difference is captured by the conception of sensitivity which is denoted by $\Delta D$. The strength of privacy guarantee is captured by the conception of privacy budget which is denoted by $\epsilon$. The variance of noise distribution is related to ratio of the sensitivity to the privacy budget. Specifically, the variance is $2(\Delta D/\epsilon)^{2}$.

The key idea behind the Laplace mechanism is: If the sensitivity is far less than fluctuation of added noise, it is hard to tell that variation of the Laplace mechanism’s outputs happens due to noise distribution’s fluctuation or due to presence or absence of a record. This idea can be described intuitively by formula $\Delta D\ll 2(\Delta D/\epsilon)^{2}$.

The goal of covering the sensitivity can be achieved if the privacy budget is appropriately small. That is, for appropriately small privacy budget, the sensitivity could be much less than variance of noise distribution.

In a word, for the Laplace mechanism, the sensitivity is covered by fluctuation of noise. So, the security foundation of the Laplace mechanism can be described by formula $\Delta D\ll 2(\Delta D/\epsilon)^{2}$ intuitively. However, the formula may not hold for some queries, which we will discuss in next subsection.

The hypothesis test is an appropriate tool to construct membership inference attacks method against the Laplace mechanism. In the Laplace mechanism, the difference caused by presence or absence of one record is covered by the fluctuation of noise. However, the hypothesis test method is designed to determine that variation are just due to random noise or other reasons. In other words, the hypothesis test can be used to determine that variation of the Laplace mechanism’s outputs is just due to randomness of noise or due to presence or absence of a record.

The counting query is an appropriate query to perform membership inference attacks against the Laplace mechanism. In specific, it is acceptable for most cases that value of the privacy budget is from 0 to 1. Let’s check the inequality $\Delta D\ll 2(\Delta D/\epsilon)^{2}$. For counting query, when the privacy budget is 1, the sensitivity is 1 and the variance of noise distribution is 2. The sensitivity is just a half of variance. When privacy budget is 0.5, the sensitivity is 1 and the variance is 8. So the sensitivity is one eighth of variance. In a word, the inequality $\Delta D\ll 2(\Delta D/\epsilon)^{2}$ may not hold for counting query when the privacy budget takes values which are generally considered to be an appropriate value for the privacy budget.

There are other three reasons why the target linear query should be the counting query. Firstly, the counting query makes the attacks method technically right. The counting query satisfies linear property and the sensitivity of counting query is always 1. These two properties make it possible to obtain multiple i.i.d. samples for the counting query’s answer. In addition, the hypothesis test method works on i.i.d. samples. Thus, the proposed membership inference attacks method is technically right due to unique properties of the counting query.

Secondly, the proposed attacks method is based on counting query so that it can work in a wide range. The counting query is very common. On the one hand, it is a common need to confirm the number of records which meet specific requirements, such as $sql$ statement ” select count(*) from table student where student.age $\leq$ 20 ”. On the other hand, there are a lot of complex queries which are based on the counting query.

Thirdly, the difference of query’s answer, which is caused by presence or absence of one record, is most easily detected by hypothesis test method when the target query is the counting query. As mentioned before, the difference is smaller than or equal to the sensitivity and the sensitivity is far smaller than variance of noise distribution. Thus, it is hard to detect whether variation of the Laplace mechanism’s outputs is due to presence or absence of one record. However, when the target query is the counting query, the difference caused by presence or absence of any record is 1, reaching the value of sensitivity. So, the counting query makes it most easy to detect whether the variation of outputs is caused by presence or absence of one record.

This subsection presents how to perform membership inference attacks against the Laplace mechanism.

Attackers aim for determining whether a target record $x$ is in a target data set $D$. The background knowledge of attackers is denoted by $D_{know}$ which is a subset of target data set $D$. The target linear query is the counting query $q(\{x\}\cup D_{know})$. The $s$ represents the condition such that $D_{s}=\{x\}\cup D_{know}$. So, the target query can be expressed as $q_{s}(D)$ and its answer can be expressed as $M(q_{s},D,\epsilon)$.

The membership inference attacks method consists of two subroutines. The first subroutine is to obtain multiple i.i.d. samples for the target query’s answer. The first subroutine is feasible due to the linear property of the counting query, which is proved in previous section. By the first subroutine, attackers can obtain $m$ i.i.d. samples of the target query’s answer and the samples are $\hat{a}_{1},\hat{a}_{2},\dots,\hat{a}_{m}$. When the target record $x$ is in the target data set $D$,

Therefore, the mean of samples is $q(D_{know}\cup\{x\})$. When the target record $x$ is not in data set $D$

Therefore, the mean of samples is $q(D_{know})$.

Attackers can determine whether the target record is in the target data set by comparing $q(D_{know})$ with the mean of samples. The procedure of comparison is implemented by hypotheses test method in the second subroutine.

In the second subroutine, the hypothesis test method is used to determine whether the samples which are obtained in the first subroutine are drawn from a distribution with mean $q(D_{know})$. If the mean of samples is determined to be $q(D_{know})$, the assertion is that the target record is not in the target data set. Otherwise, the assertion is that the target record is in the target data set.

In the second subroutine, the key is to find an appropriate hypothesis test method. That is, it is key to find an appropriate statistics. The one-sample t-test is chosen. The $T$ statistics follows $T$ distribution and the $T$ statistics is as follows

Here, the $\mu$ is distribution mean and the $m$ is the number of samples. The $\bar{X}$ is the sample mean and the $S$ is sample standard variance. When the samples are denoted by $\hat{a}_{1},\hat{a}_{2},\dots,\hat{a}_{m}$ we have

And,

The one-sample t-test is an appropriate hypothesis test method because it is designed to determine whether some samples are drawn from a distribution with a certain mean.

The significance level is 0.05. There are two widely accepted choices for significance level, namely $0.01$ and $0.05$. We desire that as long as difference is statistically significant, the alternative hypothesis could be accepted. So we choose $0.05$ as value of significance level.

There is a table where $p$ value can be searched by the freedom and the value of statistic $T$. The freedom is $m-1$ and the value of statistic $T$ can be calculated as above.

The success rate of proposed attacks method is tightly related to two factors including the amount of background knowledge of attackers and the threshold of privacy budget in black-box access. According to the two factors, there are four cases faced by attackers, as shown in Fig 2.

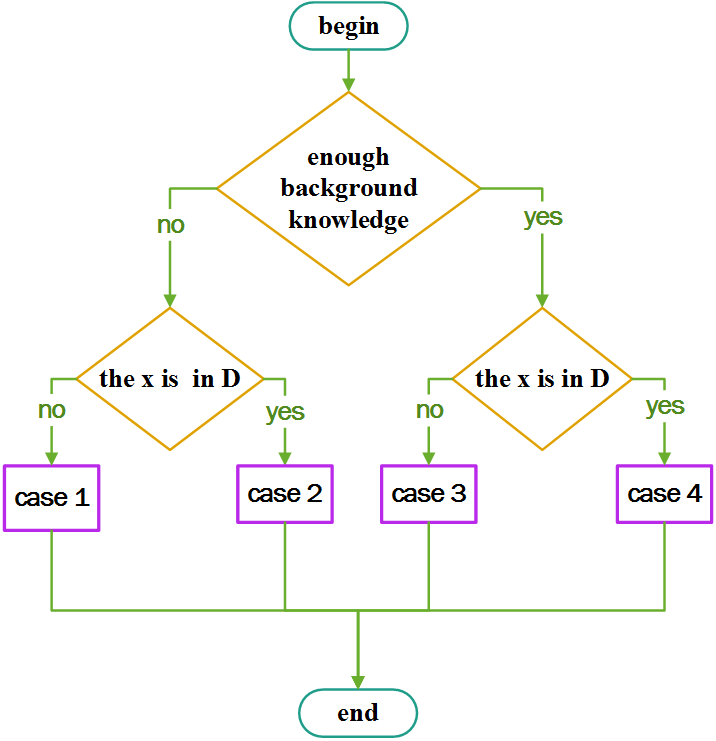
Suppose that the threshold of the privacy budget is $\epsilon_{l}$. When the totally consumed privacy budget is greater than the threshold from the differential privacy mechanism’s perspective, the black-box access of differential privacy mechanisms aborts. The ”enough background knowledge” means that attackers can construct as many as needed number of queries such that the totally consumed privacy budget is greater than the threshold, resulting in abortion of black-box access.

For the case 4, there is enough background knowledge available to attackers. That is, there is enough number of records in $D_{know}$. In addition, the target record $x$ is in the target data set. By the theorem 4, from the differential privacy mechanism’s perspective, the totally consumed privacy budget is $m\epsilon$. Because the background knowledge is enough, attackers can make the $m$ big enough such that $m\epsilon>\epsilon_{l}$, result in abortion of the black-box.

For the case 3, there is enough number of records in $D_{know}$ and the target record $x$ is in not the target data set. By the theorem 4, from the differential privacy mechanism’s perspective, the totally consumed privacy budget is $\epsilon$ no matter how many queries attackers issue. So the black-box access never aborts. By the theorem 3, from attackers’ perspective, the totally consumed privacy budget is $m\epsilon$. Thus, attackers can issue as many as needed queries such that the $m\epsilon$ is unreasonably large, resulting in that attackers can find the absence of the target record trivially by the hypothesis test method.

For the case 2 and the case 1, the background knowledge is not enough. Thus, attackers cannot consume unreasonably large privacy budget or force the black-box access to abort. In these cases, the success rate is tightly related to the exact amount of background knowledge. For these two cases, we will give a delicate analysis about the success rate in theorem 5.

In brief, from attackers’ perspective, they issue as many as possible queries to consume as much as possible privacy budget. In specific, there are three possible results. Firstly, the black-box access aborts, which means that the totally consumed privacy budget is greater than the threshold and the target record is in the target data set. Secondly, the black-box access does not aborts and the totally consumed privacy budget is so big that attackers can find the absence of the target record. Thirdly, all records of attackers’ background knowledge are used and attackers obtain multiple answers of the target query. Attackers determine whether the target record is in the target data set by hypothesis test method. The success rate of using hypothesis test method is analyzed in theorem 5 at next.

The hypothesis test method has two types error shown in Table 1. Based on the Table 1, the success rate of proposed attacks method can be calculated. The proof of theorem 5 is deferred to the appendix.

Theorem 5 The success rate $R$ of the proposed membership inference attacks method is

$\hfill\Box$

Here, the $T_{(m-1,0.975)}$ is the value of $T$ statistic when the freedom of $T$ distribution is $m-1$ and the cumulative probability is 0.975. The $f(t)$ is the probability density function of $T$ distribution with freedom $m-1$. The $\mu_{0}$ is the mean assumed in null hypothesis. The $\mu_{1}$ is the true mean of distribution when the null hypothesis is wrong. We have

In above formula, $\mu_{0}-\mu_{1}$ is equal to $-1$ because the query $q$ is the counting query. The $m$ is the number of obtained samples from the Laplace mechanism by black-box access. The $S$ is the standard deviation of obtained samples.

As mentioned before, the standard deviation of noise distribution is $\sqrt{2}\Delta D/\epsilon$. In addition, for the counting query the sensitivity $\Delta D$ is 1. The standard deviation of sample could be substituted with standard deviation of noise distribution. That is, the $S$ could be substituted with $\sqrt{2}\Delta D/\epsilon$. Then, the $R$ is

The $\epsilon$ is the privacy budget consumed by each query. By the above formula, the $R$ increases when the number of obtained samples increases.

In terms of totally consumed privacy budget, the pattern is different. In specific, the totally consumed privacy budget $\epsilon_{t}$ is equal to $m\epsilon$. So, the $R$ is

According to the above formula, the $R$ decreases when the number of obtained samples increases under the condition that the totally consumed privacy budget is predetermined.

By the theorem 2, the maximum number of samples is equal to the number of records in $D_{know}$ at most. Let $r$ be the number of records in $D_{know}$. The above two formulas become

And

In above analyses, the consumed privacy budget is calculated from attackers’ perspective. However, there are two cases if the consumed privacy budget is calculated from differential privacy mechanisms’ perspective. Firstly, if the target record is in the target data set, the consumed privacy budget is the same with that of attackers’ perspective. Secondly, if the target record is not in the target data set, the consumed privacy budget is $\epsilon$ which is the amount of privacy budget consumed by one query.