Understanding Robust Overfitting from the Feature Generalization Perspective
Abstract
Adversarial training (AT) constructs robust neural networks by incorporating adversarial perturbations into natural data. However, it is plagued by the issue of robust overfitting (RO), which severely damages the model’s robustness. In this paper, we investigate RO from a novel feature generalization perspective. Specifically, we design factor ablation experiments to assess the respective impacts of natural data and adversarial perturbations on RO, identifying that the inducing factor of RO stems from natural data. Given that the only difference between adversarial and natural training lies in the inclusion of adversarial perturbations, we further hypothesize that adversarial perturbations degrade the generalization of features in natural data and verify this hypothesis through extensive experiments. Based on these findings, we provide a holistic view of RO from the feature generalization perspective and explain various empirical behaviors associated with RO. To examine our feature generalization perspective, we devise two representative methods, attack strength and data augmentation, to prevent the feature generalization degradation during AT. Extensive experiments conducted on benchmark datasets demonstrate that the proposed methods can effectively mitigate RO and enhance adversarial robustness.
1 Introduction
Adversarial training (AT) [26] has been proved to be reliable to improve a model’s robustness against adversarial attacks [33, 14]. It constructs robust neural networks by incorporating adversarial perturbations into natural data and training models using adversarial data generated on-the-fly. AT has been established as one of the most effective empirical defenses [4]. Although promising to improve the model’s robustness, AT is plagued by the issue of robust overfitting (RO) [30]. That is, after a certain point during AT, the model’s robust accuracy continues to substantially decrease with further training. This phenomenon has been consistently observed across different datasets, network architectures, and AT variants [30].
In this work, we investigate RO from a novel feature generalization perspective. Firstly, we conduct a series of factor ablation experiments to identify the inducing factors of RO. Specifically, we consider natural data and adversarial perturbations from small-loss training data as distinct factors and employ factor ablation adversarial training to assess their individual impacts on RO. We observe that simultaneously removing adversarial perturbations and natural data from small-loss training data greatly mitigate RO. However, experiments that only remove adversarial perturbations still exhibits a severe degree of RO. Given that these factor ablation experiments strictly adhere to the controlling variables principle, with the sole variation being the inclusion of natural data in the training set, we can infer that the inducing factor of RO stems from natural data.
Given that the only difference between adversarial and natural training lies in the inclusion of adversarial perturbations in the natural data, we further hypothesize that adversarial perturbations may degrade the generalization of features in natural data and lead to the emergence of RO. To validate this hypothesis, we introduce an additional adversarial perturbation into the training natural data during AT. We observe that as the additional adversarial perturbation is incorporated, the model’s test robustness deteriorates. This suggests that the additional adversarial perturbations have a detrimental effect on feature generalization. Furthermore, we are able to simulate the RO phenomenon during AT by linearly increasing the budget of additional adversarial perturbations. These experimental results demonstrate that adversarial perturbations can degrade feature generalization and induce the emergence of RO phenomenon.
Based on these findings, we provide a holistic view of RO from the feature generalization perspective. In standard AT, a robustness gap exists between the training and test data due to factors like the memorization effect of deep networks [3, 12] and the distribution deviation between the finite training and test data. Certain small-loss training data maintain a significant robustness gap when compared to the test data. However, adversarial perturbations are generated on the fly and adaptively adjusted based on the model’s robustness. The robustness gap between training and test data leads to distinct adversarial perturbations for the features in natural data. These distinct adversarial perturbations degrade feature generalization. The degradation of feature generalization, in turn, weakens the model’s test performance and widens the robustness gap between training and test data, thus forming a vicious cycle. Additionally, we provide explanations for various empirical behaviors associated with RO based on our feature generalization perspective.
To examine our feature generalization perspective, we propose two representative methods: attack strength and data augmentation. Specifically, the attack strength method adjusts adversarial perturbations on small-loss training data to verify their impact on feature generalization, and the data augmentation method adjusts model’s robustness on small-loss training data to assess the effect of the robustness gap on feature generalization. Both methods can effectively prevent feature generalization degradation during AT and mitigate RO, thereby validating our feature generalization understanding of RO. Additionally, extensive experiments conducted on benchmark datasets demonstrate the efficacy of these methods in enhancing adversarial robustness. To sum up, our contributions are as follows:
-
•
We conduct factor ablation AT adhering to the principle of controlling variables and identify that the inducing factor of RO stems from natural data.
-
•
We further hypothesize that adversarial perturbations degrade the generalization of features in natural data and validate this hypothesis through extensive experiments.
-
•
Based on these findings, we provide a holistic view of RO from the feature generalization perspective and explain various empirical behaviors associated with RO.
-
•
To examine our feature generalization perspective, we propose two representative methods to prevent the degradation of feature generalization. Extensive experiments demonstrate that the proposed methods effectively mitigate RO and enhance adversarial robustness.
2 Related Work
In this section, we provide a brief overview of related works from two perspectives: AT and RO.
2.1 Adversarial Training
Let , and denote the network with model parameter , the input space, and the loss function, respectively. Given a -class dataset , where and denotes its corresponding label, the objective function of natural training is defined as follows:
| (1) |
where the network learns features in natural data that are correlated with associated labels to minimize the empirical risk of misclassifying natural inputs. However, evidence [33, 36, 17] suggests that naturally trained models tend to learn fragile features that are vulnerable to adversarial attacks. To address this issue, AT [14, 26] introduces adversarial perturbations to each data point by transforming into . The adversarial perturbations are constrained by a pre-specified budget, i.e. , where can be , etc. Therefore, the objective of AT is to solve the following min-max optimization problem:
| (2) |
where the inner maximization process aims to generate adversarial data that maximizes the classification loss, and the outer minimization process optimizes model parameter using the generated adversarial data. This iterative procedure aims to train an adversarially robust classifier. The most commonly employed approach for generating adversarial data is Projected Gradient Descent (PGD) [26], which applies adversarial attack to natural data over multiple steps with a step size of :
| (3) |
where represents the adversarial perturbation at step , and denotes the projection operator.
Besides standard AT, there are also several AT variants [20, 44, 39]. One typical variant is TRADES [44], which trains the network on both natural data and adversarial data:
| (4) |
where CE is the cross-entropy loss that encourages the network to maximize natural accuracy, KL is the Kullback-Leibler divergence that encourages robustness improvement, and the hyperparameter is used to regulate the tradeoff between natural accuracy and adversarial robustness.
2.2 Robust Overfitting
RO was initially observed in standard AT [26]. Subsequent systematic studies by Rice et al. [30] showed that traditional remedies for overfitting in deep learning offer limited help in addressing RO in AT, prompting further efforts to explore RO. Schmidt et al. [31] attributed RO to sample complexity theory and suggested that robust generalization requires more training data, which is supported by empirical results in derivative works [6, 2, 43]. Other works also proposed various strategies to mitigate RO without relying on additional training data, such as sample reweighting [39, 45, 25], label smoothing [18], stochastic weight averaging [7], temporal ensembling [12], knowledge distillation [7], weight regularization [40, 41], and data augmentation [29, 34, 22]. Additionally, RO has been studied from various perspectives, such as label noise [11], input-loss landscape [23] and minimax game [37]. In this work, we provide a novel feature generalization understanding of RO.
3 Method
In this section, we begin with factor ablation experiments to identify the inducing factors of RO (Section 3.1). Furthermore, we propose a hypothesis that adversarial perturbations degrade feature generalization and verify this hypothesis through extensive experiments. Following this, we provide a holistic view of RO from the feature generalization perspective and explain various empirical behaviors associated with RO (Section 3.2). Lastly, we present two representative methods aimed at examining our feature generalization understanding of RO (Section 3.3).




3.1 Factor Ablation Adversarial Training
Drawing inspiration from the data ablation experiments conducted by Yu et al. [41], which investigated the influence of small-loss training data on RO by excluding such data during training, we propose factor ablation adversarial training as a method to pinpoint the inducing factors of RO. Following a similar experimental setup, we also utilize a fixed loss threshold to differentiate small-loss training data. For instance, in the CIFAR10 dataset, data with an adversarial loss below 1.7 is regarded as small-loss training data. Unlike data ablation experiments that treat adversarial data as a single entity, our approach considers natural data and adversarial perturbations from small-loss training data as separate factors. We conduct more granular factor ablation adversarial training to identify the specific factor inducing RO. Specifically, we train a PreAct ResNet-18 model on CIFAR-10 dataset under the threat model and remove designated factors before RO occurs (i.e., at the 100th epoch). These experiments include: i) baseline, which is a baseline group where no factors are removed; ii) data & perturbation, which removes both natural data and adversarial perturbations from small-loss training data; and iii) perturbation, which solely removes adversarial perturbations from small-loss training data.
It’s important to note that these experiments strictly adhere to the principle of controlling variables. They are entirely identical before RO occurred, with the sole distinction among different experimental groups being the removal of designated factors from the training set. The experimental results of factor ablation adversarial training are summarized in Figure 1(a). It is observed that the data & perturbation group demonstrates a significant alleviation of RO, whereas both the baseline and perturbation groups continue to exhibit severe RO. Given that the only difference between the data & perturbation and perturbation groups lies in the inclusion of natural data in the training set, we can infer that the inducing factor of RO stems from natural data. Similar effects can be observed across different datasets, network architectures, and AT variants (see Appendix A), indicating that it is a general finding in adversarial training.
3.2 Analysis of Robust Overfitting from the Feature Generalization Perspective
Based on the factor ablation experiments in Section 3.1, we know that natural data acts as the inducing factor of RO. It’s noteworthy that natural data is also present in natural training. However, in natural training, RO phenomenon is typically absent. For instance, deep learning models trained on natural data often achieve zero training error, effectively memorizing the training data, without observable detrimental effects on generalization performance [30]. In contrast, RO is a dominant phenomenon in AT, which commonly exhibits significantly degraded generalization performance. Given that the only difference between adversarial and natural training lies in the inclusion of adversarial perturbations in the natural data, a natural hypothesis arises: adversarial perturbations may degrade the generalization of features in natural data and lead to the emergence of RO.

Verification. To validate the aforementioned hypothesis, before generating training adversarial data in AT, we introduce an additional adversarial perturbation into the training natural data and observe the model’s robust generalization performance. Specifically, before the onset of RO (i.e., between the 50th and 100th epochs), we incorporate an extra adversarial perturbation in the opposite direction into the training natural data and observe the model’s test robustness. We conduct experiments with varying budgets of additional adversarial perturbations, such as . The model’s test robustness is shown in Figure 1(b). It is important to note that the additional adversarial perturbations are introduced only on the training natural data, while the model and the test data remain unchanged, ensuring that the model’s robustness on the test data remains unaffected. However, we observe that as the additional adversarial perturbation is incorporated, the model’s test robustness deteriorates, indicating that the additional adversarial perturbations exert a detrimental effect on feature generalization. Furthermore, we linearly increase the budget of additional adversarial perturbations between the 50th and 100th epochs, and the model’s test robustness is summarized in Figure 1(c). It is observed that the RO phenomenon can be simulated by adjusting the adversarial perturbations on training data. In Appendix B, we also provide more experimental results conducted at different stages of training. These experimental results support our hypothesis that the adversarial perturbations can degrade feature generalization and induce the emergence of RO.
A holistic view of RO from the feature generalization perspective. In standard AT, there exists a robustness gap between the training and test data before the onset of RO, as shown in Figure 1(d). This robustness gap arises due to factors such as the memorization effect of deep networks [3, 12] and the distribution deviation between the finite training and test data. Certain small-loss training data maintain a significant robustness gap when compared to the test data. However, adversarial perturbations are generated on the fly and adaptively adjusted based on the model’s robustness. For instance, consider a single data point, when the model’s robustness is poor, adversarial perturbations mainly impede the model’s learning of non-robust features. Conversely, when the model’s robustness is strong, adversarial perturbation will hinder the model’s learning of robust features because the process of generating adversarial perturbation aims to maximize the classification loss. The robustness gap between training and test data leads to distinct adversarial perturbations for the features in natural data, degrading feature generalization. As feature generalization deteriorates, the model’s adversarial robustness on the test data progressively declines, and the robustness gap between training and test data continues to widen, forming a vicious cycle, as illustrated in Figure 2.
Based on the analysis above, some small-loss training data maintain a significant robustness gap compared to the test data. This can explain why removing small-loss adversarial data from the training data can effectively prevent RO. Furthermore, AT exhibits some other empirical behaviors associated with RO, for instance, as the perturbation budget increases, the extent of RO initially rises and then decreases. Our feature generalization perspective provides an intuitive explanation: as the perturbation budget increases from 0, the impact of adversarial perturbations on the generalization of features in natural data also grows, leading to a higher probability of RO phenomenon during AT. This can explain why natural training does not exhibit RO, and as the adversarial perturbation budget increases, the extent of RO also rises. However, with a further increase in the perturbation budget, the model’s robustness on the training data is limited, leading to a narrowing robustness gap between training and test data. The narrowing robustness gap reduces the generation of adversarial perturbations that degrade feature generalization. Therefore, the extent of RO gradually decreases.
3.3 The Proposed Methods
In Section 3.2, we analyze RO as a result of the degradation of Feature Generalization (ROFG), which arises from the distinct adversarial perturbations for the features in natural data. In this part, we introduce two approaches to examine our feature generalization understanding of RO.
ROFG through attack strength. In order to verify our analysis that adversarial perturbations on some small-loss training data degrade feature generalization, we conduct AT with varying attack strengths to generate adversarial perturbations on the small-loss training data before RO occurs (i.e., at the 100th epoch). Specifically, we use a fixed loss threshold to distinguish small-loss training data and train PreAct ResNet-18 on CIFAR10 under the threat model with adjusted perturbation budgets on small-loss training data, ranging from to . The pseudocode is provided in Algorithm 1, which utilizes attack strength to adjust the adversarial perturbations on small-loss training data, referred to as ROFGAS.
For ROFGAS with different perturbation budgets , we evaluate the model’s training and test robustness under the standard perturbation budget of , with the learning curves summarized in Figure 3(a). We observe a clear correlation between the applied perturbation budgets and the extent of RO. Specifically, the greater the perturbation budgets , the milder the extent of RO. When the perturbation budget exceeds a certain threshold, such as , the model exhibits almost no RO. It is worth noting that similar patterns are also observed across different datasets, network architectures, and AT variants (as shown in Appendix C). These experimental results demonstrate that adjusting adversarial perturbations on small-loss training data can effectively prevent the degradation of feature generalization, thereby alleviating the RO phenomenon, validating our feature generalization understanding of RO.




ROFG through data augmentation. To further support our analysis that the model’s robustness gap between training and test data promotes the generation of adversarial perturbations that degrades feature generalization, we employ data augmentation techniques to weaken the model’s robustness on small-loss training data before RO occurs (i.e., at the 100th epoch). However, the image transformations in data augmentation techniques are often stochastic and may not yield the desired effect. To address this issue, we iteratively apply random image transformations to the small-loss training data, consistently selecting the transformed data that does not fall within the small-loss scope. Specifically, we use a fixed loss threshold to distinguish small-loss training data, and set a threshold for the proportion of small-loss training data when train PreAct ResNet-18 on CIFAR10 under the threat model. At the beginning of each iteration, we check whether the proportion of small-loss training data meets the specified threshold . If this proportion is below the specified threshold , we apply random image transformations to the small-loss training data until the specified threshold is reached. The pseudocode is provided in Algorithm 2, where the adopted data augmentation technique is AugMix [16]. We refer to this adversarial training pipeline, empowered by the data augmentation technique, as ROFGDA.
The learning curves of ROFGDA with different thresholds are summarized in Figure 3(b). We observe a clear correlation between the threshold and the extent of RO. As the robustness gap between small-loss training data and test data decreases, the extent of RO becomes increasingly mild. Furthermore, the observed effects are consistent across different datasets, network architectures, and AT variants (as shown in Appendix D). These experimental results show that narrowing the model’s robustness gap between training and test data can effectively prevent the degradation of feature generalization, supporting our feature generalization understanding of RO.
4 Experiment
In this section, we validate the effectiveness of the proposed methods. In Section 4.1, we provide the ablation analysis of ROFGAS and ROFGDA. Section 4.2 presents the performance evaluation of ROFGAS and ROFGDA. In Section 4.3, we discuss the limitations of the proposed methods.
Setup. We conducted extensive experiments across different benchmark datasets (CIFAR10 and CIFAR100 [21]), network architectures (PreAct ResNet-18 [15] and Wide ResNet-34-10 [42]), and adversarial training approaches (AT [26], TRADES [44], AWP [40], and MLCAT [41]). For training, we follow the same experimental settings as outlined in Rice et al. [30]. Regarding robustness evaluation, we employ PGD-20 [26] and AutoAttack (AA) [8] as adversarial attack methods. Detailed descriptions of the experimental setup can be found in Appendix E.





4.1 Analysis of the Proposed Methods
We investigate the impacts of algorithmic components in ROFGAS and ROFGDA under the PreAct ResNet-18 architecture on the CIFAR10 dataset.
The impact of attack strength. We empirically verify the effectiveness of attack strength component in ROFGAS by comparing the performances of models trained using different perturbation budgets . Specifically, we conduct ROFGAS with the perturbation budget ranging from 0/255 to 24/255, and the results are summarized in Figure 4(a). It is evident that as increases, the robustness gap between the “Best” and “Last” checkpoints steadily decreases, demonstrating its effectiveness. For adversarial robustness, we observe a trend of initially increasing and then decreasing. This is not surprising since the attack strength component with excessively large perturbation budgets is inherently detrimental to robustness improvement under the standard perturbation budget (). Therefore, in practice, we need to adjust the perturbation budget to balance the mitigation of RO and robustness improvement.
The importance of loss threshold . Identifying exactly which adversarial perturbations degrade feature generalization is generally intractable. To address this, we introduce a fixed loss threshold , which is used to distinguish small-loss training data. We conduct ROFGAS experiments with varying from 1.2 to 2.0, and the model’s robustness performances are summarized in Figure 4(b). We observe a trend of initially increasing and then decreasing robustness, which implies that adversarial perturbations degrading feature generalization are primarily concentrated in the small-loss training data, suggesting the importance of the loss threshold .
The effect of data augmentation. We further investigate the effect of the data augmentation component by conducting ROFGDA with different thresholds . The results are summarized in Figure 4(c). It is observed that as decreases, the robustness gap between the "Best" and "Last" checkpoints steadily shrinks. Additionally, we explore the use of different data augmentation techniques to implement ROFGDA in Appendix F. It is observed that all implementations of ROFGDA can effectively mitigate RO, suggesting that the proposed approach is generally effective regardless of the chosen data augmentation technique. For adversarial robustness, as decreases, the model’s robustness performance initially increases and then decreases. This trend may be due to the data augmentation component weakening the model’s robustness on the training data, thereby degrading the model’s defense against strong attacks.
| Method | Dataset | Natural | PGD-20 | AA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Best | Last | Best | Last | Best | Last | ||||
| AT | CIFAR10 | 82.310.18 | 84.110.40 | 52.280.37 | 44.460.14 | 48.090.11 | 42.010.10 | ||
| ROFGDA | 82.580.25 | 85.450.24 | 53.950.27 | 49.690.10 | 48.480.09 | 44.440.18 | |||
| ROFGAS | 77.680.52 | 78.040.10 | 56.370.33 | 51.960.08 | 49.370.19 | 45.970.16 | |||
| AT | CIFAR100 | 55.140.12 | 55.830.20 | 28.930.36 | 20.870.33 | 24.530.02 | 18.920.20 | ||
| ROFGDA | 55.790.39 | 57.920.50 | 29.400.15 | 25.510.17 | 24.800.12 | 21.590.03 | |||
| ROFGAS | 51.020.27 | 51.060.35 | 30.250.36 | 26.190.31 | 25.630.05 | 22.670.14 | |||
| TRADES | CIFAR10 | 81.500.31 | 82.270.40 | 52.920.19 | 49.950.21 | 48.900.16 | 46.920.09 | ||
| TRADES-ROFGDA | 82.890.25 | 83.280.17 | 53.140.24 | 52.130.36 | 49.120.13 | 48.410.06 | |||
| TRADES-ROFGAS | 80.920.52 | 80.970.52 | 53.490.31 | 52.040.25 | 49.880.15 | 48.910.07 | |||
| AWP | CIFAR10 | 81.010.52 | 81.610.46 | 55.360.36 | 55.050.13 | 50.120.07 | 49.850.20 | ||
| AWP-ROFGDA | 81.120.30 | 81.630.44 | 55.890.22 | 55.320.18 | 50.490.13 | 50.190.13 | |||
| AWP-ROFGAS | 79.390.14 | 79.850.41 | 56.060.11 | 55.670.20 | 50.790.10 | 50.450.08 | |||
| MLCAT | CIFAR10 | 81.700.19 | 82.260.29 | 58.330.26 | 58.250.12 | 50.540.10 | 50.460.11 | ||
| MLCAT-ROFGDA | 82.060.13 | 82.500.20 | 58.760.37 | 58.570.22 | 50.610.16 | 50.520.08 | |||
| MLCAT-ROFGAS | 80.640.37 | 81.410.17 | 58.910.38 | 58.740.17 | 50.880.10 | 50.650.06 | |||
| Method | Dataset | Natural | PGD-20 | AA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Best | Last | Best | Last | Best | Last | ||||
| AT | CIFAR10 | 85.490.23 | 86.500.33 | 55.400.37 | 47.140.29 | 52.310.13 | 45.740.16 | ||
| ROFGAS | 82.640.12 | 82.710.55 | 59.070.21 | 51.180.19 | 53.040.08 | 47.220.19 | |||
| AT | CIFAR100 | 60.900.13 | 59.070.31 | 31.350.25 | 26.030.32 | 27.420.07 | 24.390.07 | ||
| ROFGAS | 55.780.32 | 52.750.40 | 33.480.26 | 28.400.25 | 28.860.02 | 24.580.18 | |||
| TRADES | CIFAR10 | 84.780.51 | 84.700.13 | 56.250.37 | 48.490.21 | 53.120.14 | 46.690.15 | ||
| TRADES-ROFGAS | 83.360.48 | 83.170.42 | 57.070.23 | 49.650.20 | 53.790.10 | 47.710.04 | |||
| AWP | CIFAR10 | 85.300.12 | 85.390.29 | 58.350.36 | 57.160.29 | 53.070.09 | 52.490.04 | ||
| AWP-ROFGAS | 84.400.22 | 84.710.50 | 59.560.09 | 57.650.21 | 54.700.12 | 53.080.17 | |||
| MLCAT | CIFAR10 | 86.720.16 | 87.320.15 | 62.630.27 | 61.910.24 | 54.730.10 | 54.610.13 | ||
| MLCAT-ROFGAS | 86.460.43 | 86.740.18 | 63.590.32 | 62.400.11 | 55.380.12 | 54.850.05 | |||
4.2 Performance Evaluation
The proposed ROFGAS and ROFGDA methods can effectively mitigate RO, as demonstrated in Section 3.3, Appendix C, and Appendix D, validating our feature generalization perspective. Regarding adversarial robustness, we conduct experiments under the PreAct ResNet-18 architecture across different datasets and adversarial training methods. The performance of the “Best” and “Last” checkpoints is provided in Table 1. It is observed that for methods exhibiting RO, such as AT [26] and TRADES [44], the proposed methods significantly improve model robustness. For methods already mitigating RO, such as AWP [40] and MLCAT [41], our methods still can achieve some complementary robustness improvement, demonstrating the significance of our feature generalization perspective. In Table 1, we can see that ROFGAS outperforms ROFGDA under AA in all settings. Thus we further conduct experiments using ROFGAS under the Wide ResNet-34-10 architecture, with the results shown in Table 2. It is observed that under the stronger backbone network, the ROFGAS method significantly enhances model robustness across different datasets and adversarial training methods. Additionally, we conduct additional experiments using ROFGAS on the Tiny-ImageNet dataset [13] and VGG-16 architecture [32], with the results shown in Appendix G. Consistently, the proposed approach mitigates RO and boosts adversarial robustness, demonstrating its effectiveness.
4.3 Limitations
While the proposed methods contribute to validating our feature generalization perspective, they have certain limitations. Firstly, they introduce additional components into the standard AT pipeline, thereby increasing computational complexity. For instance, under a single GeForce RTX 3080 GPU, the average training time per epoch in standard AT is 147.7s, while for ROFGAS and ROFGDA, it extends to 261.6s and 1222.9s, respectively. Moreover, our methods have yet to achieve state-of-the-art adversarial robustness, and they often cannot simultaneously achieve optimal robustness improvement and RO mitigation, as discussed in Section 4.1. However, it is worth noting that the main focus of this work is to provide a novel feature generalization understanding of RO. These methods are specifically tailored to verify our feature generalization perspective, and these limitations essentially do not compromise our understanding of RO.
5 Conclusion
This paper investigate RO from a novel feature generalization perspective. First, we conduct factor ablation adversarial training and identify that the inducing factor of RO stems from natural data. Furthermore, we hypothesize adversarial perturbations degrade the generalization of features in natural data and validate this hypothesis through extensive experiments. Based on these findings, we provide a holistic view of RO from the feature generalization perspective and explain various empirical behaviors associated with RO. We also design two representative methods to examine our feature generalization perspective: attack strength and data augmentation. Extensive experiments demonstrate that the proposed methods effectively mitigate RO and can enhance adversarial robustness across different adversarial training methods, network architectures, and benchmark datasets.
References
- [1] S. Addepalli, S. Jain, G. Sriramanan, and R. Venkatesh Babu. Scaling adversarial training to large perturbation bounds. In European Conference on Computer Vision, pages 301–316. Springer, 2022.
- [2] J.-B. Alayrac, J. Uesato, P.-S. Huang, A. Fawzi, R. Stanforth, and P. Kohli. Are labels required for improving adversarial robustness? Advances in Neural Information Processing Systems, 32, 2019.
- [3] D. Arpit, S. Jastrzębski, N. Ballas, D. Krueger, E. Bengio, M. S. Kanwal, T. Maharaj, A. Fischer, A. Courville, Y. Bengio, et al. A closer look at memorization in deep networks. In International conference on machine learning, pages 233–242. PMLR, 2017.
- [4] A. Athalye, N. Carlini, and D. Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In International conference on machine learning, pages 274–283. PMLR, 2018.
- [5] Q.-Z. Cai, C. Liu, and D. Song. Curriculum adversarial training. In Proceedings of the 27th International Joint Conference on Artificial Intelligence, pages 3740–3747, 2018.
- [6] Y. Carmon, A. Raghunathan, L. Schmidt, J. C. Duchi, and P. S. Liang. Unlabeled data improves adversarial robustness. Advances in Neural Information Processing Systems, 32, 2019.
- [7] T. Chen, Z. Zhang, S. Liu, S. Chang, and Z. Wang. Robust overfitting may be mitigated by properly learned smoothening. In International Conference on Learning Representations, 2020.
- [8] F. Croce and M. Hein. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In International conference on machine learning. PMLR, 2020.
- [9] E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan, and Q. V. Le. Autoaugment: Learning augmentation strategies from data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 113–123, 2019.
- [10] E. D. Cubuk, B. Zoph, J. Shlens, and Q. V. Le. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition workshops, pages 702–703, 2020.
- [11] C. Dong, L. Liu, and J. Shang. Label noise in adversarial training: A novel perspective to study robust overfitting. Advances in Neural Information Processing Systems, 35:17556–17567, 2022.
- [12] Y. Dong, K. Xu, X. Yang, T. Pang, Z. Deng, H. Su, and J. Zhu. Exploring memorization in adversarial training. In International Conference on Learning Representations, 2022.
- [13] L. Fei-Fei, R. Krishna, and A. Karpathy. Tiny imagenet visual recognition challenge. CS231n Convolutional Neural Networks for Visual Recognition, Stanford University.
- [14] I. J. Goodfellow, J. Shlens, and C. Szegedy. Explaining and harnessing adversarial examples. In International Conference on Learning Representations, 2015.
- [15] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
- [16] D. Hendrycks, N. Mu, E. D. Cubuk, B. Zoph, J. Gilmer, and B. Lakshminarayanan. Augmix: A simple data processing method to improve robustness and uncertainty. In International Conference on Learning Representations, 2020.
- [17] A. Ilyas, S. Santurkar, D. Tsipras, L. Engstrom, B. Tran, and A. Madry. Adversarial examples are not bugs, they are features. Advances in neural information processing systems, 32, 2019.
- [18] P. Izmailov, D. Podoprikhin, T. Garipov, D. Vetrov, and A. G. Wilson. Averaging weights leads to wider optima and better generalization. arXiv preprint arXiv:1803.05407, 2018.
- [19] X. Jia, Y. Zhang, B. Wu, K. Ma, J. Wang, and X. Cao. Las-at: adversarial training with learnable attack strategy. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 13398–13408, 2022.
- [20] H. Kannan, A. Kurakin, and I. Goodfellow. Adversarial logit pairing. arXiv preprint arXiv:1803.06373, 2018.
- [21] A. Krizhevsky, G. Hinton, et al. Learning multiple layers of features from tiny images. 2009.
- [22] L. Li and M. Spratling. Data augmentation alone can improve adversarial training. arXiv preprint arXiv:2301.09879, 2023.
- [23] L. Li and M. Spratling. Understanding and combating robust overfitting via input loss landscape analysis and regularization. Pattern Recognition, 136:109229, 2023.
- [24] C. Liu, M. Salzmann, T. Lin, R. Tomioka, and S. Süsstrunk. On the loss landscape of adversarial training: Identifying challenges and how to overcome them. Advances in Neural Information Processing Systems, 33:21476–21487, 2020.
- [25] F. Liu, B. Han, T. Liu, C. Gong, G. Niu, M. Zhou, M. Sugiyama, et al. Probabilistic margins for instance reweighting in adversarial training. Advances in Neural Information Processing Systems, 34:23258–23269, 2021.
- [26] A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu. Towards deep learning models resistant to adversarial attacks. In International Conference on Learning Representations, 2018.
- [27] S. G. Müller and F. Hutter. Trivialaugment: Tuning-free yet state-of-the-art data augmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 774–782, 2021.
- [28] T. Pang, K. Xu, C. Du, N. Chen, and J. Zhu. Improving adversarial robustness via promoting ensemble diversity. In International Conference on Machine Learning, pages 4970–4979. PMLR, 2019.
- [29] S.-A. Rebuffi, S. Gowal, D. A. Calian, F. Stimberg, O. Wiles, and T. A. Mann. Data augmentation can improve robustness. Advances in Neural Information Processing Systems, 34, 2021.
- [30] L. Rice, E. Wong, and Z. Kolter. Overfitting in adversarially robust deep learning. In International Conference on Machine Learning, pages 8093–8104. PMLR, 2020.
- [31] L. Schmidt, S. Santurkar, D. Tsipras, K. Talwar, and A. Madry. Adversarially robust generalization requires more data. Advances in Neural Information Processing Systems, 31, 2018.
- [32] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
- [33] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus. Intriguing properties of neural networks. In International Conference on Learning Representations, 2014.
- [34] J. Tack, S. Yu, J. Jeong, M. Kim, S. J. Hwang, and J. Shin. Consistency regularization for adversarial robustness. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 36, pages 8414–8422, 2022.
- [35] F. Tramèr, A. Kurakin, N. Papernot, I. Goodfellow, D. Boneh, and P. McDaniel. Ensemble adversarial training: Attacks and defenses. In International Conference on Learning Representations, 2018.
- [36] D. Tsipras, S. Santurkar, L. Engstrom, A. Turner, and A. Madry. Robustness may be at odds with accuracy. In International Conference on Learning Representations, 2018.
- [37] Y. Wang, L. Li, J. Yang, Z. Lin, and Y. Wang. Balance, imbalance, and rebalance: Understanding robust overfitting from a minimax game perspective. In Thirty-seventh Conference on Neural Information Processing Systems, 2023.
- [38] Y. Wang, X. Ma, J. Bailey, J. Yi, B. Zhou, and Q. Gu. On the convergence and robustness of adversarial training. In International Conference on Machine Learning, pages 6586–6595. PMLR, 2019.
- [39] Y. Wang, D. Zou, J. Yi, J. Bailey, X. Ma, and Q. Gu. Improving adversarial robustness requires revisiting misclassified examples. In International Conference on Learning Representations, 2019.
- [40] D. Wu, S.-T. Xia, and Y. Wang. Adversarial weight perturbation helps robust generalization. Advances in Neural Information Processing Systems, 33:2958–2969, 2020.
- [41] C. Yu, B. Han, L. Shen, J. Yu, C. Gong, M. Gong, and T. Liu. Understanding robust overfitting of adversarial training and beyond. In International Conference on Machine Learning, pages 25595–25610. PMLR, 2022.
- [42] S. Zagoruyko and N. Komodakis. Wide residual networks. In British Machine Vision Conference 2016. British Machine Vision Association, 2016.
- [43] R. Zhai, T. Cai, D. He, C. Dan, K. He, J. Hopcroft, and L. Wang. Adversarially robust generalization just requires more unlabeled data. arXiv preprint arXiv:1906.00555, 2019.
- [44] H. Zhang, Y. Yu, J. Jiao, E. Xing, L. El Ghaoui, and M. Jordan. Theoretically principled trade-off between robustness and accuracy. In International Conference on Machine Learning, pages 7472–7482. PMLR, 2019.
- [45] J. Zhang, J. Zhu, G. Niu, B. Han, M. Sugiyama, and M. Kankanhalli. Geometry-aware instance-reweighted adversarial training. In International Conference on Learning Representations, 2020.
Appendix A Additional Results for Factor Ablation Adversarial Training
In this section, we present additional results regarding factor ablation adversarial training across different datasets, network architectures, and AT variants. We utilize the same experimental setup as described in Section 3.1, employing a fixed loss threshold of 1.7 for the CIFAR10 dataset and 4.0 for the CIFAR100 dataset to distinguish small-loss training data. In the data & perturbation group, we remove both natural data and adversarial perturbations from small-loss training data. In the perturbation group, we solely remove adversarial perturbations from small-loss training data. The experimental results are summarized in Figure 5. It is observed that the data & perturbation group consistently exhibits significant relief from RO, while the perturbation group shows severe RO. Since the only difference between the data & perturbation and perturbation groups is the inclusion of natural data in the training set, these experimental results suggest that the inducing factor of RO stems from natural data.







Appendix B Additional Results for Verification and Inducing Experiments
In this section, we present additional results from verification and inducing experiments conducted at different stages of training. We utilize the same experimental setup as described in Section 3.2, which involves incorporating an additional adversarial perturbation in the opposite direction into the training natural data and observing the model’s test robustness. Specifically, we conduct experiments with varying budgets of additional adversarial perturbations at the 25th and 75th epochs, such as . The model’s test robustness is shown in Figure 6(a) and (b). It is observed that as the additional adversarial perturbation is incorporated, the model’s test robustness deteriorates at different stages of training, indicating that the additional adversarial perturbations exert a detrimental effect on feature generalization. It is worth noting that if we replace the additional adversarial perturbations with random noise of the same budget, the model does not exhibit the corresponding robust generalization degradation. This indicates that it is not taken for granted that adding extra perturbations to the training natural data will degrade the model’s test robustness. Furthermore, we linearly increase the budget of additional adversarial perturbations at the 25th and 75th epochs, and the model’s test robustness is summarized in Figure 6(c) and (d). We observe that the RO phenomenon can be simulated by adjusting the adversarial perturbations on training data. These experimental results support our hypothesis that the adversarial perturbations can degrade feature generalization and induce the emergence of RO.
Appendix C Additional Results for ROFGAS
In this section, we present additional results for ROFGAS. We utilize a fixed loss threshold of 1.7 for the CIFAR10 dataset and 4.0 for the CIFAR100 dataset to distinguish small-loss training data. We conducted ROFGAS with varying perturbation budgets across different datasets, network architectures, and AT variants. The results are summarized in Figure 7 and 8. Consistently, we observe a clear correlation between the applied perturbation budgets and the extent of RO. As the perturbation budgets increases, the robustness gap between the “Best” and “Last” models decreases. These experimental results suggest that adjusting adversarial perturbations on small-loss training data can effectively prevent the degradation of feature generalization and mitigate RO, validating our feature generalization understanding of RO.


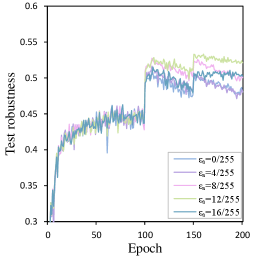



Appendix D Additional Results for ROFGDA
In this section, we provide additional results of ROFGDA to support our feature generalization perspective. We conducted ROFGDA with different thresholds across different datasets, network architectures, and AT variants. The results are summarized in Figure 9 and 10. Consistently, we observe a clear correlation between the threshold and the extent of RO. As the robustness gap between small-loss training data and test data decreases, the extent of RO becomes increasingly mild. These experimental results show that narrowing the model’s robustness gap between training and test data can effectively prevent the degradation of feature generalization and mitigate RO, supporting our feature generalization understanding of RO.






Appendix E Experimental Setup
Our project is implemented using the PyTorch framework on servers equipped with four GeForce RTX 3080 and one Tesla V100 GPUs. The code and related models will be publicly released for verification and use. We conducted extensive experiments across different benchmark datasets (CIFAR10 and CIFAR100 [21]), network architectures (PreAct ResNet-18 [15] and Wide ResNet-34-10 [42]), and adversarial training approaches (AT [26], TRADES [44], AWP [40], and MLCAT [41]). Throughout our experiments, we utilize the infinity norm as the adversarial perturbation constraint.
For training, we follow the experimental settings outlined in Rice et al.[30]. The network undergoes 200 epochs of training using stochastic gradient descent (SGD) with a momentum of 0.9, weight decay of , and an initial learning rate of 0.1. The learning rate is reduced by a factor of 10 at the 100th and 150th epochs. Standard data augmentation techniques, including random cropping with 4 pixels of padding and random horizontal flips, are applied.
For the adversarial setting, we use the 10-step PGD with a perturbation budget of and a step size of , following the standard setting of PGD-AT [26]. In ROFGAS, the number of PGD steps linearly increases with the adjusted perturbation budget . For instance, a 10-step PGD is utilized for , while a 20-step PGD is applied for .
For performance evaluation, we present the model’s learning curves to demonstrate their effectiveness in mitigating RO. The model’s robustness is assessed using multiple attack methods, including 20-step PGD (PGD-20) [26] and AutoAttack (AA) [8]. We report the results for both the “Best” and “Last” checkpoints, along with the standard deviations from 5 runs. The configurations for ROFGAS and ROFGDA are detailed in Table 3, and other hyperparameters for the baseline methods are set as per their original papers.
| Network | Dataset | Method | Hyperparameter | Training time per epoch | ||||
| GeForce RTX 3080 | Tesla V100 | |||||||
| PreAct ResNet-18 | CIFAR10 | ROFGDA | 1.7 | - | 0.6 | 1222.9s | - | |
| ROFGAS | 1.7 | 14/255 | - | 261.6s | - | |||
| CIFAR100 | ROFGDA | 3.5 | - | 0.6 | 1264.3s | - | ||
| ROFGAS | 3.5 | 15/255 | - | 274.0s | - | |||
| CIFAR10 | TRADES-ROFGDA | 1.9 | - | 0.8 | - | - | ||
| TRADES-ROFGAS | 1.9 | 10/255 | - | - | - | |||
| CIFAR10 | AWP-ROFGDA | 0.8 | - | 0.8 | 219.7s | - | ||
| AWP-ROFGAS | 0.8 | 12/255 | - | 247.0s | - | |||
| CIFAR10 | MLCAT-ROFGDA | 0.7 | - | 0.8 | 354.4s | - | ||
| MLCAT-ROFGAS | 0.7 | 11/255 | - | 387.4s | - | |||
| Wide ResNet-34-10 | CIFAR10 | ROFGAS | 1.4 | 13/255 | - | - | 1872.1s | |
| CIFAR100 | ROFGAS | 4.2 | 16/255 | - | - | 2053.9s | ||
| CIFAR10 | TRADES-ROFGAS | 1.9 | 10/255 | - | - | - | ||
| CIFAR10 | AWP-ROFGAS | 1.1 | 10/255 | - | - | 1794.0s | ||
| CIFAR10 | MLCAT-ROFGAS | 0.8 | 9/255 | - | - | 2650.9s | ||



Appendix F The Impact of Data Augmentation Techniques in ROFGDA
In this section, we explore the use of different data augmentation techniques to implement ROFGDA. Specifically, we conduct experiments with ROFGDA using three popular data augmentation techniques: AutoAugment [9], RandAugment [10], and TrivialAugment [27]. The results are summarized in Figure 11. We observe that the model’s test robustness exhibits considerable oscillation, likely due to the significant changes in input images caused by these data augmentation techniques. Nevertheless, all implementations of ROFGDA effectively mitigate RO by narrowing the robustness gap between small-loss training data and test data. These experimental results suggest that the proposed ROFGDA is generally effective regardless of the chosen data augmentation techniques.
Appendix G Experimental Results on More Dataset and Network Architecture
In this section, we conduct experiments with ROFGAS on additional dataset and network architecture, such as VGG-16 [32] and Tiny-ImageNet [13]. For the VGG-16 architecture, we set the hyperparameters of ROFGAS to and . For the Tiny-ImageNet dataset, the hyperparameters of ROFGAS are set to and . As demonstrated by the results in Table 4, the proposed approach consistently mitigates RO and enhances adversarial robustness, demonstrating its effectiveness.
| Method | Dataset | Network | Natural | PGD-20 | AA | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Last | Best | Last | Best | Last | |||||
| AT | CIFAR10 | VGG-16 | 78.840.36 | 81.890.13 | 49.630.21 | 43.940.34 | 43.700.13 | 39.950.08 | ||
| ROFGAS | 75.710.14 | 76.930.38 | 53.060.11 | 50.620.09 | 46.090.18 | 43.870.15 | ||||
| AT | Tiny-ImageNet | PreAct ResNet-18 | 45.510.54 | 45.940.11 | 21.340.25 | 15.640.13 | 17.100.10 | 13.210.13 | ||
| ROFGAS | 39.030.18 | 39.060.23 | 22.200.24 | 20.480.21 | 17.910.02 | 16.450.07 | ||||