Understanding photoluminescence of coupled metallic nanostructures based on a coupling classic harmonic oscillator model

Photoluminescence (PL) phenomena from noble metals have been widely studied since the first report over 50 years ago Mooradian (1969). PL can be excited not only from bulk materials, but also from thin films and nanostructures Boyd, Yu, and Shen (1986); Mohamed et al. (2000); Cai et al. (2018); Balykin and Melentiev (2018); Cai et al. (2019). Particularly, the localized surface plasmon resonance (LSPR) effect enhances the emissions in the case of metallic nanostructures, thus resulting in numerous applications such as optical recording Zijlstra, Chon, and Gu (2009); Taylor, Kim, and Chon (2012), biosensing Lu et al. (2012); Zhang et al. (2018), orientation probes Zhang et al. (2013); Lu et al. (2015), local temperature detection Carattino, Caldarola, and Orrit (2018); Zhang et al. (2019); Hastman et al. (2020).

The origin of PL has been discussed in plenty of studies, with different explanations such as interband transitions enhanced by LSPR Shahbazyan (2013), microscopic explanation for enhanced PL from gold nanoparticles Dulkeith et al. (2004), classic oscillator model assisted with electron distributions for single mode emission Cheng et al. (2018), and non-equilibrium electron dynamics affecting PL of metallic nanostructures Zhang et al. (2020). Nevertheless, the coupling PL phenomena are seldom investigated in theory. For example, Prodan E. et al. present a molecular orbital theory to describe the coupling plasmon modes introduced by the metallic nanostructures of arbitrary shape Prodan et al. (2003). Jain P. K. et al. provide a semiempirical “plasmon ruler equation” based on discrete dipole approximation (DDA) simulation method to estimate the plasmon shifts as a function of the separation between the nanoparticles Jain, Huang, and El-Sayed (2007). However, the developed models based on quantum theories are neither lack of details on the emission spectra, especially for PL, nor lack of intrinsic physical pictures. Hence, a clear picture for coupling PL spectra is required to be built up.

In this study, we present a practical model to give a deep understanding on PL from coupled metallic nanostructures, e.g., gold nanorods or nanospheres. This model is based on the classic harmonic oscillator model, considering two oscillators that interact with each other. We treat the interaction part, i.e., coupling coefficients, between the two in a non-phenomenological way. That is, the coupling coefficients are obtained from the intrinsic physics rather than just assuming as several parameters. The model show reasonable results to explain PL and white light scattering spectra of coupled metallic nanostructures for different situations. This work would help to understand coupling PL phenomena in a classical way.

Consider that two metallic nanostructures treated as two oscillators are close to each other and are driven by the electric field of the excitation light. The schematic is shown in Fig. 1. In order to obtain the emission electric field from them, we need to find out the differential equations of them. Define $x_{1}(t)$ and $x_{2}(t)$ as the displacements relative to equilibrium positions of each oscillator, thus $\dot{x}_{1}(t)$ and $\dot{x}_{2}(t)$ the velocities, and $\ddot{x}_{1}(t)$ and $\ddot{x}_{2}(t)$ the accelerations. The equations should be in this form:

	$\displaystyle\ddot{x}_{1}+2\beta_{01}\dot{x}_{1}+\omega_{01}^{2}x_{1}-\frac{F_{21}}{m_{e}}=C_{1}\mathrm{exp}(-\mathrm{i}\omega_{ex}t),$		(1a)
	$\displaystyle\ddot{x}_{2}+2\beta_{02}\dot{x}_{2}+\omega_{02}^{2}x_{2}-\frac{F_{12}}{m_{e}}=C_{2}\mathrm{exp}(-\mathrm{i}\omega_{ex}t).$		(1b)

Here, $F_{21}$ and $F_{12}$ are the interaction forces between Oscillator 1 and Oscillator 2, $C_{1}=E_{1}/m_{e}$, $C_{2}=E_{2}/m_{e}$, and $m_{e}$ is the mass of electron. $E_{1}$ and $E_{2}$ are the amplitudes of the excitation electric field at the positions of the two oscillators, and usually $E_{1}=E_{2}=E_{0}$ is a good approximation. $\beta_{01}$ and $\beta_{02}$ represent the damping coefficients, and $\omega_{01}$ and $\omega_{02}$ represent the inherent circular frequencies. The next step is to find out the interaction parts of the equations.

The electric field introduced by a moving charged particle is given by:Griffiths (2013)

$$\mathbf{E}=\frac{q}{4\pi\varepsilon_{0}}\frac{r}{(\mathbf{r}\cdot\mathbf{u})^{3}}\left[(c^{2}-v^{2})\mathbf{u}+\mathbf{r}\times(\mathbf{u}\times\mathbf{a})\right],$$

(2)

where $q$ is the charge of the particle, $\varepsilon_{0}$ is the permittivity of vacuum, and $\mathbf{u}\equiv c\mathbf{r}/r-\mathbf{v}$. Here, $c$ is the velocity of light in vacuum, $\mathbf{v}$ and $\mathbf{a}$ are the velocity and the acceleration of the particle, respectively, and $\mathbf{r}$ is the displacement vector from the particle to field point. In our one-dimension case, when considering the electric field introduced by one oscillator acting on the other oscillator, the second part of Eq. 2 is zero due to the fact that $\mathbf{u}$ and $\mathbf{a}$ are parallel. Besides, we notice that the charged particle that moves is the electron while the positive ion is assumed to be at rest. Hence, the interacted electric field at one oscillator should be contributed to both positive charged ion and negative charged electron of the other oscillator. Therefore, the electric field can be written as:

	$\displaystyle E_{21}$	$\displaystyle=-\frac{+e}{4\pi\varepsilon_{0}}\frac{1}{(r_{0}-x_{1})^{2}}+\frac{-e}{4\pi\varepsilon_{0}}\frac{1}{r^{2}}(-\frac{c-\dot{x}_{2}}{c+\dot{x}_{2}})$
		$\displaystyle\cong-\frac{e}{2\pi\varepsilon_{0}r_{0}^{2}}(\frac{\dot{x}_{2}}{c}+\frac{x_{2}}{r_{0}}),$		(3a)
	$\displaystyle E_{12}$	$\displaystyle=+\frac{+e}{4\pi\varepsilon_{0}}\frac{1}{(r_{0}+x_{2})^{2}}+\frac{-e}{4\pi\varepsilon_{0}}\frac{1}{r^{2}}(\frac{c+\dot{x}_{2}}{c-\dot{x}_{2}})$
		$\displaystyle\cong-\frac{e}{2\pi\varepsilon_{0}r_{0}^{2}}(\frac{\dot{x}_{1}}{c}+\frac{x_{1}}{r_{0}}).$		(3b)

Here, we use the conditions $v/c\ll 1$ and $x/r_{0}\ll 1$ for approximation. Notice that $E_{21}$ is the electric field in Oscillator 1 introduced by one pair of the electrons and ions in Oscillator 2, and $E_{12}$ is the electric field in Oscillator 2 introduced by one pair of the electrons and ions in Oscillator 1. Hence, the interaction forces should be written as $F_{21}=-N_{2}eE_{21}$ and $F_{12}=-N_{1}eE_{12}$, where $N_{1}$ and $N_{2}$ are the effective numbers of free electrons in Oscillator 1 and Oscillator 2, respectively. We define the coupling coefficients as:

	$\displaystyle\gamma_{21}=\frac{N_{2}e^{2}}{2\pi\varepsilon_{0}m_{e}r_{0}^{2}c},\ \gamma_{12}=\frac{N_{1}e^{2}}{2\pi\varepsilon_{0}m_{e}r_{0}^{2}c},$		(4)
	$\displaystyle g_{21}^{2}=\frac{N_{2}e^{2}}{2\pi\varepsilon_{0}m_{e}r_{0}^{3}},\ g_{12}^{2}=\frac{N_{1}e^{2}}{2\pi\varepsilon_{0}m_{e}r_{0}^{3}},$

thus Eq. (1) can be written as:

	$\displaystyle\ddot{x}_{1}+2\beta_{01}\dot{x}_{1}+\omega_{01}^{2}x_{1}-\gamma_{21}\dot{x}_{2}-g_{21}^{2}x_{2}=C_{1}\mathrm{exp}(-\mathrm{i}\omega_{ex}t),$		(5a)
	$\displaystyle\ddot{x}_{2}+2\beta_{02}\dot{x}_{2}+\omega_{02}^{2}x_{2}-\gamma_{12}\dot{x}_{1}-g_{12}^{2}x_{1}=C_{2}\mathrm{exp}(-\mathrm{i}\omega_{ex}t).$		(5b)

For simplicity, we assume $N_{1}=N_{2}=N$, thus $\gamma_{21}=\gamma_{12}=\gamma$, $g_{21}=g_{12}=g$, and if we define $\frac{1}{\kappa}=\frac{\gamma^{3}}{g^{4}}=\frac{Ne^{2}}{2\pi\varepsilon_{0}m_{e}c^{3}}$, it results in a simple form for $\gamma$ and $g$:

$$\gamma=\frac{1}{\kappa}(\frac{c}{r_{0}})^{2},\ g^{2}=\frac{1}{\kappa}(\frac{c}{r_{0}})^{3}.$$

(6)

Firstly, we consider the situation without coupling, i.e., $\gamma=g=0$. In such conditions, Eq. 5 is degenerated into the simple form:

	$\displaystyle\ddot{x}_{1}+2\beta_{01}\dot{x}_{1}+\omega_{01}^{2}x_{1}=C_{1}\mathrm{exp}(-\mathrm{i}\omega_{ex}t),$		(7a)
	$\displaystyle\ddot{x}_{2}+2\beta_{02}\dot{x}_{2}+\omega_{02}^{2}x_{2}=C_{2}\mathrm{exp}(-\mathrm{i}\omega_{ex}t).$		(7b)

The general solutions are:

	$\displaystyle x_{1}(t)=\mathrm{exp}(-\beta_{01}t\pm\mathrm{i}\omega_{c1}t),\ \mathrm{exp}(-\mathrm{i}\omega_{ex}t),$		(8a)
	$\displaystyle x_{2}(t)=\mathrm{exp}(-\beta_{02}t\pm\mathrm{i}\omega_{c2}t),\ \mathrm{exp}(-\mathrm{i}\omega_{ex}t).$		(8b)

Here, $\omega_{c1}=\sqrt{\omega_{01}^{2}-\beta_{01}^{2}}$ and $\omega_{c2}=\sqrt{\omega_{02}^{2}-\beta_{02}^{2}}$ represent the resonant circular frequencies, respectively, which are different from the inherent ones ($\omega_{01},\ \omega_{02}$). The coefficients that represent amplitudes are omitted for the moment, which can be obtained with the initial conditions. The details of this kind of individual oscillator has been discussed carefully in our previous work. Cheng et al. (2018)

Secondly, we start to consider the coupling situation without excitation light, i.e., $C_{1}=C_{2}=0$. The equations are:

	$\displaystyle\ddot{x}_{1}+2\beta_{01}\dot{x}_{1}+\omega_{01}^{2}x_{1}-\gamma\dot{x}_{2}-g^{2}x_{2}=0,$		(9a)
	$\displaystyle\ddot{x}_{2}+2\beta_{02}\dot{x}_{2}+\omega_{02}^{2}x_{2}-\gamma\dot{x}_{1}-g^{2}x_{1}=0.$		(9b)

To solve Eq. (9), we can assume that $x_{1}(t)=A\mathrm{exp}(\alpha t)$ and $x_{2}(t)=B\mathrm{exp}(\alpha t)$, and substitute them back into Eq. (9), thus obtaining:

	$\displaystyle A(\alpha^{2}+2\beta_{01}\alpha+w_{01}^{2})-B(\gamma\alpha+g^{2})=0,$		(10a)
	$\displaystyle B(\alpha^{2}+2\beta_{02}\alpha+w_{02}^{2})-A(\gamma\alpha+g^{2})=0.$		(10b)

Obviously, to obtain non-zero solutions, $\alpha$ should satisfy:

$$(\alpha^{2}+2\beta_{01}\alpha+w_{01}^{2})(\alpha^{2}+2\beta_{02}\alpha+w_{02}^{2})=(\gamma\alpha+g^{2})^{2}.$$

(11)

Notice that Eq. (11) has analytic solutions for $\alpha$, marked as $\alpha_{1}$, $\alpha_{2}$, $\alpha_{3}$ and $\alpha_{4}$. However, the expressions are so complex that we would not write in the text. Instead, to illustrate the physical significance of $\alpha$, we rewrite it in this form:

	$\displaystyle\alpha_{1}=-\beta_{1}+\mathrm{i}\omega_{1},\ \alpha_{2}=-\beta_{1}-\mathrm{i}\omega_{1},$		(12)
	$\displaystyle\alpha_{3}=-\beta_{2}+\mathrm{i}\omega_{2},\ \alpha_{4}=-\beta_{2}-\mathrm{i}\omega_{2}.$

Here, $\omega_{1}$ and $\omega_{2}$ are the new generated resonant circular frequencies when the two oscillators couple. We can call them Mode 1 and Mode 2, respectively. In a more special case, i.e., $\beta_{01}=\beta_{02}=\beta_{0}$, $\omega_{01}=\omega_{02}=\omega_{0}$, the solutions of Eq. (11) are expressed easily:

	$\displaystyle\omega_{1}=\sqrt{w_{0}^{2}+g^{2}-(\beta_{0}+\gamma/2)^{2}},\ \beta_{1}=\beta_{0}+\gamma/2,$		(13)
	$\displaystyle\omega_{2}=\sqrt{w_{0}^{2}-g^{2}-(\beta_{0}-\gamma/2)^{2}},\ \beta_{2}=\beta_{0}-\gamma/2.$

Thirdly, notice that the particular solutions for Eq. (5) are $x_{1}(t)=\mathrm{exp}(-\mathrm{i}\omega_{ex}t)$ and $x_{2}(t)=\mathrm{exp}(-\mathrm{i}\omega_{ex}t)$ (amplitudes are omitted). Therefore, combining these particular solutions and the general ones [Eq. (8)], we obtain the total solutions of Eq. (5) in a symmetric form:

	$\displaystyle x_{1}(t)$	$\displaystyle=A_{1}\mathrm{exp}(\Omega_{1}t)+A_{2}\mathrm{exp}(\Omega_{2}t)+A_{3}\mathrm{exp}(\Omega_{3}t),$		(14a)
	$\displaystyle x_{2}(t)$	$\displaystyle=B_{1}\mathrm{exp}(\Omega_{1}t)+B_{2}\mathrm{exp}(\Omega_{2}t)+B_{3}\mathrm{exp}(\Omega_{3}t),$		(14b)

where $\Omega_{1}=-\beta_{1}-\mathrm{i}\omega_{1}$, $\Omega_{2}=-\beta_{2}-\mathrm{i}\omega_{2}$, and $\Omega_{3}=-\mathrm{i}\omega_{ex}$. We emphasize here that Eq. (13) is just a special case for $\omega_{1}$ and $\omega_{2}$, and the general case for them should satisfy Eq. (12). The initial conditions are $x_{1}(0)=x_{2}(0)=0,\ \dot{x}_{1}(0)=\dot{x}_{2}(0)=0,\ \ddot{x}_{1}(0)=\ddot{x}_{2}(0)=C_{0}$, where we assume that $C_{1}=C_{2}=C_{0}$ due to the subwavelength scale of the system. Hence, these coefficients are obtained as:

	$\displaystyle A_{1}=B_{1}=\frac{C_{0}}{(\Omega_{1}-\Omega_{2})(\Omega_{1}-\Omega_{3})},$		(15a)
	$\displaystyle A_{2}=B_{2}=\frac{C_{0}}{(\Omega_{2}-\Omega_{3})(\Omega_{2}-\Omega_{1})},$		(15b)
	$\displaystyle A_{3}=B_{3}=\frac{C_{0}}{(\Omega_{3}-\Omega_{1})(\Omega_{3}-\Omega_{2})}.$		(15c)

This results in the fact that $x_{1}(t)=x_{2}(t)=x(t)$.

At last, we deal with the far field radiation. For simplicity, we consider the electric field at the position $\mathbf{d}$, where $\mathbf{d}$ is perpendicular to $x$-axis, and $d=|\mathbf{d}|$ is the distance between field point and the center of the two oscillators. The assumption of $d\gg r_{0}$ is reasonable for far field radiation. Hence, the first part of Eq. (2) is ignored compared with the second part, thus giving the electric field introduced by Oscillator 1 and Oscillator 2 as:

$$E_{far}(t)\cong\frac{Ne}{4\pi\varepsilon_{0}c^{2}d}(\ddot{x}_{1}(t)+\ddot{x}_{2}(t))=D\ddot{x}(t),$$

(16)

where $D=\frac{Ne}{2\pi\varepsilon_{0}c^{2}d}$, and $E_{far}$ is $x$-polarized. The emission intensity in the frequency domain, i.e., emission spectrum, can be evaluated by Cheng et al. (2018):

$$I(\omega)=Re\left<\int_{0}^{\infty}E_{far}^{*}(t)E_{far}(t+\tau)\ \mathrm{exp}(\mathrm{i}\omega\tau)\ \mathrm{d}\tau\right>,$$

(17)

where $Re\left<Q\right>$ is the real part of $\left<Q\right>$, and $\left<Q\right>=\frac{1}{t_{0}}\int_{0}^{t_{0}}Q\mathrm{d}t$ is the time average of quantity $Q$. The calculated result is:

	$\displaystyle I(\omega)$	$\displaystyle=|A_{1}^{\prime}|^{2}\frac{1-\mathrm{exp}(-2\beta_{1}t_{0})}{2\beta_{1}t_{0}}\frac{\beta_{1}}{(\omega-\omega_{1})^{2}+\beta_{1}^{2}}$		(18)
		$\displaystyle+|A_{2}^{\prime}|^{2}\frac{1-\mathrm{exp}(-2\beta_{2}t_{0})}{2\beta_{2}t_{0}}\frac{\beta_{2}}{(\omega-\omega_{2})^{2}+\beta_{2}^{2}}$
		$\displaystyle+|A_{3}^{\prime}|^{2}\sqrt{2\pi}\delta(\omega-\omega_{ex}),$

where $A_{j}^{\prime}=A_{j}\Omega_{j}^{2}D$ for $j=1,2,3$. Here, we ignore the cross terms in the calculation because the time average is zero when $\omega_{1}\neq\omega_{2}$.

As our previous work explains Cheng et al. (2018), the emission spectrum is separated into two parts, one is the inelastic part ($I_{inela}$) which corresponds to PL spectrum, and the other is the elastic part ($I_{ela}$) which corresponds to white light scattering spectrum. Rewrite Eq. (18) as:

	$\displaystyle I_{inela}(\omega)$	$\displaystyle=|A_{1}^{\prime}|^{2}\frac{1-\mathrm{exp}(-2\beta_{1}t_{0})}{2\beta_{1}t_{0}}\frac{\beta_{1}}{(\omega-\omega_{1})^{2}+\beta_{1}^{2}}$
		$\displaystyle+|A_{2}^{\prime}|^{2}\frac{1-\mathrm{exp}(-2\beta_{2}t_{0})}{2\beta_{2}t_{0}}\frac{\beta_{2}}{(\omega-\omega_{2})^{2}+\beta_{2}^{2}},$		(19a)
	$\displaystyle I_{ela}(\omega)$	$\displaystyle=|A_{3}^{\prime}|^{2}\sqrt{2\pi}\delta(\omega-\omega_{ex}).$		(19b)

Therefore, the PL spectrum is given by Eq. (19a), i.e.,

$$I_{PL}(\omega)=I_{inela}(\omega),$$

(20)

while the white light scattering spectrum is given from Eq. (19b) as long as $\omega_{ex}$ is substitute by $\omega$:

$$I_{sca}(\omega)=I_{ela}(\omega_{ex}\to\omega)=\sqrt{2\pi}|A_{3}^{\prime}(\omega_{ex}\to\omega)|^{2}.$$

(21)

To show the coupling modes for PL more clearly and to understand PL phenomenon more easily, we do not consider the electron distributions here as before Cheng et al. (2018), which contributes mostly to the anti-Stokes part of PL spectra, though this model would be more accuracy for PL when assisted with the electron distributions.

Start from the coupling coefficients, $g$ and $\gamma$. Fig. 2a shows $g$ and $\gamma$ varying with the distance $r_{0}$, calculated from Eq. (6). It implicates that the coupling coefficients decrease with the increase of $r_{0}$, and $\gamma$ is smaller than $g$. When $r_{0}$ is small enough, the coupling coefficients get large. Since these two coefficients are both related to $r_{0}$, we take one of them, i.e., $g$, as the coupling strength in the rest of this work.

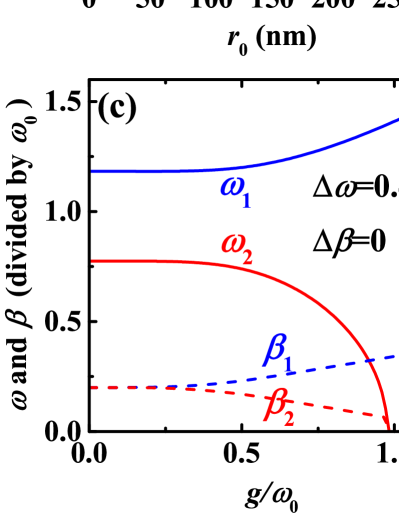
Fig. 2b-d show the new generated resonant circular frequencies ($\omega_{1},\ \omega_{2}$) and damping coefficients ($\beta_{1},\ \beta_{2}$) in different cases of the coupled oscillators as a function of the coupling strength $g$, calculated from Eq. (11) and (12). The simplest one (Fig. 2b) is that the two oscillators are the same. The two new modes split when coupling, and the splitting increases with the increase of $g$. Here, we generally call the increasing $\omega$ “blue branch”, and the decreasing $\omega$ “red branch”. On the other hand, the two damping coefficients also splits, and one increases (corresponding blue branch), the other decreases (red branch). Notice that there is a cut-off coupling strength for the red branch at around $g_{cut}\approx\omega_{0}$. In Fig. 2c, the situation is almost the same, i.e., the difference of $\omega$ and $\beta$ between the two branches increase with the increase of $g$, and there also exists $g_{cut}$. The difference between Fig. 2b and 2c is that, to obtain the same level of splitting, the former needs a smaller $g$ than the latter does. That is, the former gets a better coupling efficient than the latter does. In Fig. 2d, due to the fact that $\omega_{c1}=\sqrt{\omega_{01}^{2}-\beta_{01}^{2}}=0.954\omega_{0}$ and $\omega_{c2}=\sqrt{\omega_{02}^{2}-\beta_{02}^{2}}=0.995\omega_{0}$, it results in $\omega_{c1}<\omega_{c2}$ with a small difference. The difference of $\omega$ between the two branches ($\omega_{1}-\omega_{2}$) increases from negative value to zero and then increase to positive value as the increase of $g$. On the other hand, the difference of $\beta$ between the two branches ($\beta_{1}-\beta_{2}$) decreases and then increases as the increase of $g$. Also, $g_{cut}$ exists in this case. The coupling efficient in Fig. 2 follows the relation: $\mathrm{(b)}>\mathrm{(d)}>\mathrm{(c)}$.

Furthermore, the effective free electrons number affects the splitting as shown in Fig. 3, giving three values of $N$ as examples. Firstly, we find out the behaviors of $\omega_{1}$ and $\omega_{2}$ as $g$ increases for each figure. In Fig. 3a, $\omega_{1}$ increases and then decreases, while $\omega_{2}$ decreases, indicating that $\omega_{1}$ has a maximal value. In Fig. 3b, $\omega_{1}$ decreases and then increases and finally decreases, while $\omega_{2}$ increases and then decreases, indicating that both $\omega_{1}$ and $\omega_{2}$ have maximal values. In Fig. 3c, $\omega_{1}$ decreases, while $\omega_{2}$ increases slightly and then decreases. In Fig. 3d, $\omega_{1}$ decreases, while $\omega_{2}$ increases and then decreases, the curves of which almost coincide with each other at the range around $g=0.3\omega_{0}$ to $g=0.5\omega_{0}$. In Fig. 3e, the behaviors are similar to the ones in Fig. 3c. In Fig. 3f, the behaviors are similar to the ones in Fig. 3d, but the two curves cross rather than coincide. Secondly, we find out the similar behaviors for these parameters in a general view. In all cases, there are cut-off coupling strengths for both modes, writing as $g_{cut1}$ and $g_{cut2}$, at which $\omega_{1}=0$ and $\omega_{2}=0$, respectively. The differences are, for smaller $N$ ($10^{8}$ or $10^{9}$), $g_{cut1}>g_{cut2}$, while for larger $N$ ($10^{10}$), $g_{cut1}<g_{cut2}$. As $g$ increases, the splitting of damping coefficients $\beta_{1}$ and $\beta_{2}$ gets larger. Furthermore, another interesting result is that there is a point $g_{0}$ (shown with black cross circle) at which $\beta_{2}(g_{0})=0$ for each case, and $g_{0}<g_{cut2}$. This is different from the one in Fig. 2 where $g_{0}>g_{cut2}$. When $g<g_{0}$, Mode 2 behaves normally. However, when $g>g_{0}$, $\beta_{2}<0$ indicates that this is an exponentially increasing mode, which should be removed from the total solutions [Eq. (14)], resulting in the absence of Mode 2. The most special case is when $g=g_{0}$ (or $g\to g_{0}^{+}$), which corresponds to a lossless (or low loss) mode. In frequency domain this mode would results in a narrow spectrum. However, the effective free electrons number that satisfy this condition is so large that it is almost impossible for a metallic nanostructure. Therefore, in the rest of this work, we only consider the number at the order of magnitudes of $N=10^{6}$.

In Eq. (14), $A_{1}$, $A_{2}$ and $A_{3}$ represent the amplitudes of the three corresponding modes of $x(t)$. When considering the far field, one should use the amplitudes of $\ddot{x}(t)$, i.e., $A_{1}^{\prime}$, $A_{2}^{\prime}$ and $A_{3}^{\prime}$. Obviously, the frequency of the excitation light plays a significant role in the amplitudes.

Fig. 4 shows these amplitudes as a function of $\omega_{ex}$. In the first case (Fig. 4a), i.e., two same oscillators, the coupled resonant circular frequencies (relative to $\omega_{0}$) are calculated as $(\omega_{1}-\omega_{0})/\omega_{0}=0.11$ and $(\omega_{2}-\omega_{0})/\omega_{0}=-0.13$. We find that to obtain the maximum intensities of Mode 1 and Mode 2 of the emission field, the circular frequency of the excitation light $\omega_{ex}$ should be close the corresponding circular resonant frequencies. For Mode 3, there are two peaks when varying $\omega_{ex}$, which correspond to around $\omega_{1}$ and $\omega_{2}$, respectively. In the second case (Fig. 4b), i.e., two different oscillators ($\omega_{1}>\omega_{2}$), the coupled resonant circular frequencies (relative to $\omega_{0}$) are calculated as 0.22 and -0.24, respectively, which, however, corresponds to a weak coupling due to the frequency splitting is small. This result has been identified in Fig. 2. Also, the intensities of Mode 1 and Mode 2 for far field reach their maximums when $\omega_{ex}$ is close to the resonant circular frequencies for each of them, and the two corresponding peaks appear for Mode 3.

For practical purpose, we consider two metallic nanostructures, e.g., gold nanorods or nanospheres, as the two oscillators, each of which has an individual resonant mode. Fig. 5 shows the coupling PL spectra for different coupling strengths at two different excitation wavelengths, calculated from Eq. (20). With the increase of $g$, the splitting of the two modes of PL increases, and the total emission intensities decrease. The decrease of the intensities origin from Eq. (15a) and (15b). Take Eq. (15a) as an example to explain. The amplitudes depend not only on $|\omega_{1}-\omega_{ex}|$ (this has been discussed in Fig. 4), but also on $|\omega_{1}-\omega_{2}|$. When $g$ increases, $|\omega_{1}-\omega_{2}|$ increases, resulting in the decrease of the amplitude of Mode 1. So does Mode 2. Therefore, the PL intensities decrease as $g$ increases.

Besides, when excited by 532 nm laser, Mode 1 is close to it, resulting in a larger intensity than the one of Mode 2. While excited by 633 nm laser, Mode 2 is close to it, resulting in a larger intensity than the one of Mode 1. This is consistent with the results in Fig. 4. Here, unit “eV” and unit “Hz” for $g$ satisfy the following relationship:

$$g[\mathrm{eV}]=\frac{\hbar}{e}g[\mathrm{Hz}],$$

(22)

where $\hbar$ is the reduced Planck constant. So does the damping coefficient $\beta$.

Fig. 6 shows the coupling white light scattering spectra for different coupling strengths in different cases, calculated from Eq. (21). In Fig. 6a, i.e., two oscillators with different resonant wavelengths, with the increase of $g$, the splitting of the two modes increases, which behaves the same as PL does. However, the scattering intensities stay in the same level which is different from PL spectra. In Fig. 6b, i.e., two same oscillators, with the increase of $g$, Mode 2 red-shifts, while Mode 1 is hardly to be obtained. Also, the intensities stay in the same level. This behavior agrees well with the experiments Su et al. (2003); Sönnichsen et al. (2005); Hu et al. (2012).

The authors declare no conflicts of interest.

The data that support the findings of this study are available from the corresponding author upon reasonable request.