Understanding of different types of rolling motion of on aluminium surface.
Abstract
Can a molecule chemisorbed on an aluminium surface, exhibit rolling motion and even move on the surface? Here we presents the results of our calculation which shows that can move on that surface utilizing its own rolling motion. This rolling motion involves breaking and making of several bonds. We have analyzed three possible mechanisms, in one, only carbon atoms of hexagonal rings are involved in the process, in another case only carbon atoms of pentagonal rings are involved in the process and in the last case carbon atoms of both the hexagonal and pentagonal rings are involved in the process. We found that the activation energy for rolling motion involving, only hexagonal rings is kcal mol-1, only pentagonal rings is kcal mol-1 and both hexagonal and pentagonal rings is kcal mol-1. Rate constants are estimated using classical version of transition state theory for rolling motion involving, only hexagonal rings is , only pentagonal rings is and both hexagonal and pentagonal rings is .
1 Introduction
In the recent past, design and synthesis of molecular machines has got considerable attention from the research community [1]. Those molecules, which can perform any type of unusual motion, e.g., rotation, shuttling, harpooning are being investigated [2]. In this letter we report the results of one such investigation. We put one molecule on the aluminium surface and explore the possibilities of rolling motion of the molecule on that aluminium surface [7].
2 Computational Details
The molecular mechanics calculations were carried out using the MM+ force field Incorporated in Hyperchem version 7.0, with Polak-Ribiere gradient algorithm and a root mean square gradient of 0.001 kcal/(Åmol). 2
3 Absorption of Fullerene molecule on aluminium surface
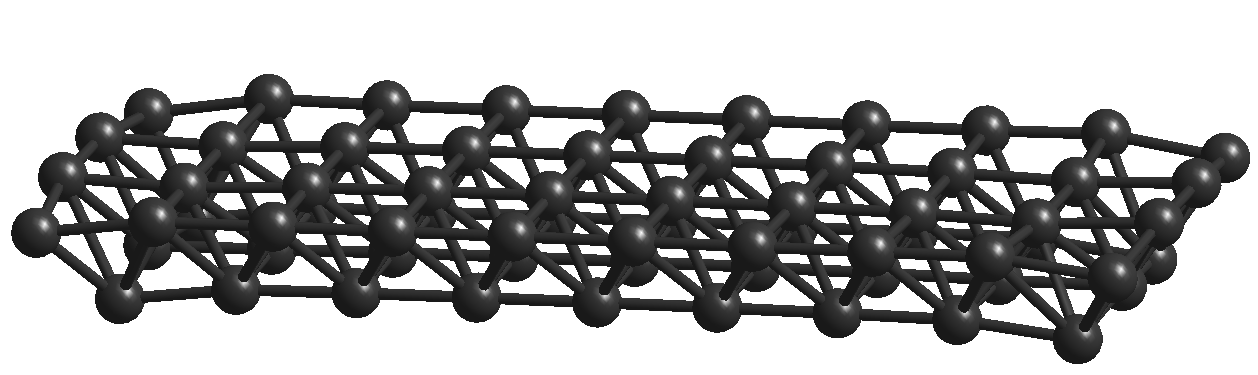
We start with a fcc (face centered cubic) lattice made by using atoms. Surface of this lattice in general provides cubic absorption sites. Molecular mechanics method is used to optimize the structure of this Al lattice and the energy this optimized lattice is found to be kcal mol-1. The average distance between two aluminium atoms in this optimized lattice is found to be Å. Then we place one molecule on the surface of this optimized Al lattice and we optimize the geometry of the whole system i.e., molecule seating on the surface of the Al lattice. Due to absorption of molecule on this surface, covalent bonds are formed between the carbon atoms of the molecule and the aluminium atoms of the Al lattice. As a result of these four new bonds, the shape of this molecule sitting on the Al surface, gets distorted as shown in Fig.2. In Fig.2 only two new C-Al bonds in the front side can be seen but there are two more C-Al bonds which are not visible.

Therefore four carbon atoms of the molecule are participating in bond formation with the surface of the Aluminium lattice - these four carbon atoms are present either in pentagonal ring or in hexagonal ring. Some hexagonal rings (case: A) surrounded only by hexagonal rings while some other hexagonal rings (case: B) are surrounded by both pentagonal and hexagonal rings and all pentagonal rings are always surrounded by hexagonal rings only (case: C). In Table. 1, a summary of optimized energy value for all three cases are given. The average value of the Al-C bond length is found to be 1.98Å.



| Adsorbed | Optimized Energy |
|---|---|
| (kcal mol-1) | |
| Case A | 1109.55 |
| Case B | 1109.60 |
| Case C | 1090.18 |



4 Rolling motion of fullerene on aluminium-surface:
In this section we consider the possibility of rolling motion of on the surface of Aluminium lattice. We do not consider the sliding motion because, in general the activation energy for sliding motion is quite larger than the rolling motion [4]. We use an interesting approach to estimate the activation energy for rolling motion of molecule on the surface of Al-lattice. We first optimize the geometry of the whole system ( plus Al- lattice) with molecule in the initial state and then we calculate energy by increasing the length of those two C-Al bonds which are going to be broken as a result of rolling motion of . Then we repeat the same calculation by optimizing the geometry of the whole system ( plus Al- lattice) with molecule in the final state and then we calculate energy by decreasing the length of those two C-Al bonds which are going to be formed as a result of rolling motion of . Then we find when (value of four C-Al bond distances which are effected by rolling motion) the energy of initial state is equal or more than the energy of the final state - that geometry corresponds to the Transition state. For checking the accuracy of our method, we use the same procedure for estimating activation energy for several systems and find that the our results are in good agreement with those available in literature [4]. As we have four carbon atoms of involved in the formation of bonds with the Al-surface, we denote length of those four carbon-aluminium bonds by , , , . Rolling motion of on the Al-surface changes bond lengths of two of these four carbon-aluminium bonds and we denote length of those two carbon-aluminium bonds by and . Rolling motion of on the Al-surface does not change bond lengths of other two carbon-aluminium bonds and we denote length of those two carbon-aluminium bonds by and . First we consider the rolling motion of molecule on the aluminium surface, where both in the initial and final states, all four carbon atoms forming bonds with the aluminium surface belongs to the pentagonal ring. The energy of the whole system increases for the initial state with the increase in bond length of first two C-Al bonds i.e., as given in Table 2. We fix the bond lengths of middle two C-Al bonds i.e., . Now we look at the decrease in energy of the whole system as a result of formation of two new C-Al bonds i.e., for the final state. As we decrease the value of C3, C3’ energy of the final state is decreases. We find when (values of C1,C1’;,C3,C3’) the energy of the initial state is equal to the energy of the final state i.e., the transition state, these value of C1,C1’;,C3,C3’ is used to calculate the energy of transition state. We find the activation energy for this event by subtracting the energy of the initial state from the energy of the Transition State.






| I. S. (kcal mol-1) | T.S. (kcal mol-1) | F.S. (kcal mol-1) |
|---|---|---|
| 1112.78 | 1196.12 | 2514.72 |
| 1133.71 | 1188.99 | 2196.44 |
| 1200.85 | 1179.14 | 1755.09 |
| 1284.57 | 1191.62 | 1547.54 |
| 1363.84 | 1200.33 | 1434.56 |
| 1431.59 | 1211.56 | 1349.85 |
| 1507.58 | 1210.31 | 1312.83 |
In Table 2, we have data for rolling motion of molecule on the aluminium surface, where both in the initial and final states, all four carbon atoms forming bonds with the aluminium surface belongs to the pentagonal ring. In the first column of Table 2, we have data for the energy of the initial state for different values of , , and , in the second column of Table 2, we have data for the energy of the Transition state for different values of , , and and in the third column of Table 2, we have data for the energy of the Final state for different values of , , and . We use those values of , , and which are appropriate for rolling motion of on the surface of Al lattice. As the the values of and increases (bond breaking process), the energy of initial state increases and as the values of and decreases (bond making process), the energy of the final state decreases. The value of , , and at which energy of the initial state increase to a value which is more than that of the final state - that geometry is called transition state geometry. Using this value of , , and one finds the energy of the transition state to be 1211.56 kcal mol-1 (from Table 2). Therefore activation energy is estimated by subtracting the energy of the initial state from the energy of the transition state i.e., kcal mol-1. Using a similar method we calculate the energy of the transitions state for rolling motion of molecule on the aluminium surface where (i) in the initial state, all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring - in the final state all four carbon atoms forming bonds with the aluminium surface belongs to the pentagonal ring and (ii) both in the initial and final states, all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring. The energy of the transition states for case (i) is 1115.57 kcal mol-1 and for case (ii) is 1111.24 kcal mol-1.
| I.S. (kcal mol-1) | T.S. (kcal mol-1) | F.S. (kcal mol-1) |
|---|---|---|
| 1125.72 | 1183.07 | 1961.14 |
| 1157.63 | 1148.83 | 1815.12 |
| 1281.38 | 1126.19 | 1636.90 |
| 1379.78 | 1126.19 | 1579.39 |
| 1487.17 | 1116.17 | 1497.74 |
| 1546.70 | 1115.57 | 1459.75 |
| I.S.(kcal mol-1) | T.S. (kcal mol-1) | F.S. (kcal mol-1) |
|---|---|---|
| 1123.17 | 1187.96 | 3185.12 |
| 1162.20 | 1144.45 | 2792.91 |
| 1196.29 | 1134.22 | 2652.47 |
| 1270.46 | 1123.97 | 2473.89 |
| 1393.44 | 1115.30 | 2299.81 |
| 1467.28 | 1111.69 | 2188.70 |
| 1561.15 | 1109.44 | 2041.19 |
| 1690.67 | 1109.83 | 1868.37 |
| 1734.57 | 1110.41 | 1822.25 |
| 1823.023 | 1111.24 | 1760.85 |
We find the activation energy for the rolling motion of molecule on the aluminium surface, where (a) both in the initial and final states, all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring (with imaginary frequency 3.16 ), (b) in the initial state, all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring and in the final state all four carbon atoms forming bonds with the aluminium surface belongs to the pentagonal ring (with imaginary frequency 25.62 ) and (c) both in the initial and final states, all four carbon atoms forming bonds with the aluminium surface belongs to the pentagonal ring (with imaginary frequency 57.73 ) and we report activation energy values for all three cases in Table 8. Normal model analysis is performed and the rate constants are estimated using classical version of Transition state theory and we report rate constant values at room temperature for all three cases in Table 8.
5 Conclusions
It is easy for the molecule to roll on the surface of Al lattice when both in the initial and final states, all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring and the rate constant of this process is very fast with rate constant . Therefore rolling motion of molecule on the surface of Al lattice continues through all states where all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring. It is also possible for the molecule to roll with a slower speed on the surface of Al lattice when in the initial state, all four carbon atoms forming bonds with the aluminium surface belongs to the hexagonal ring and in the final state all four carbon atoms forming bonds with the aluminium surface belongs to the pentagonal ring.
| Rolling with bonds | (kcal mol-1) | Rate const. |
|---|---|---|
| Hexagon and Hexagon | 1.69 | |
| Hexagon and Pentagon | 5.97 | |
| Pentagon and Pentagon | 121.38 |
6 Acknowledgements
One of the authors (S.K.) thanks Dr. Bidisa Das for several interesting discussions and another author (A.C.) thanks IIT Mandi for providing PDA. This work is a part of S.K.’s M.Sc. (chemistry) thesis.
References
- [1] Acc. Chem. Res., 34, 2001.
- [2] V. Balzani, A. Credi, F. M. Ramyo and J. F. Stoddart, Angew. Chem. (Int. Edn. Engl.) 39 (2000) 3348.
- [3] H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F Curl and R. Smalley Nature, 318 (1985) 152.
- [4] B. Das and K. L. Sebastian, Chem. Phys. Lett., 330 (2000) 433.
- [5] E. R. Kay, D. A. Leigh, and F. Zerbetto, Angew. Chem. (Int. Edn. Engl.), 46 (2007) 72.
- [6] R. P. Feynman, in Handbook of Nanoscience, Engineering, and Technology 3rd edn. edited by W. A. Goddard, D. Brenner, S. E. Lyshevski and G. F. Iafrate, CRC press (2012).
- [7] Y. Shirai, A. J. Osgood, Y. Zhao, K. F. Kelly and J. M. Tour, Nano Lett., 5 (2005) 2330.
- [8] H. D. Beckhaus, C. Rüchardt, M. Kao, F. Diederich and C. S. Foote, Angew. Chem. (Int. Edn. Engl.), 31 (1992) 63.
- [9] X. Lu, and Z. Chen, Chem. Rev., 105 (2005) 3643.