Understanding glass-like Vogel-Fulcher-Tammann equilibration times:
microcanonical effective temperatures in quenched 3D martensites

Glassy freezing or structural arrest of a rapidly cooled liquid or colloidal system R1 ; R2 ; R3 ; R4 ; R5 that pre-empts crystallisation, has been investigated for more than a century. Supercooled liquid models can yield heterogeneous domains of competing crystal structuresR3 ; R5 . Equilibration time divergences at a glassy freezing temperature $T_{G}$, have been fitted to Vogel-Fulcher-Tammann (VFT) $\sim e^{1/T-T_{G}}$, or other forms R2 ; R4 . It is natural to study generic equilibration scenarios R6 ; R7 ; R8 ; R9 in specific structural-domain systems that have long relaxation times R1 ; R2 ; R3 ; R4 ; R5 ; R10 ; R11 ; R12 ; R13 ; R14 ; R15 ; R16 .

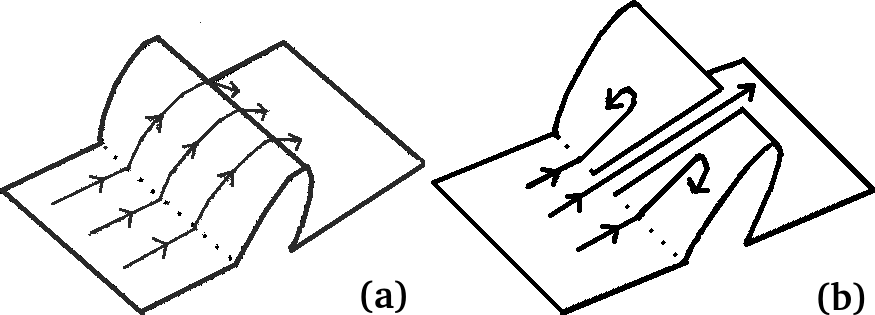
After a sudden quench, a system on a free energy landscape, has competing pathways to the new global minimum, delayed by free energy barriers $\{\Delta F=\Delta U-T\Delta S\}$. The delay rates $e^{-\Delta F/T}$ will be from energy barriers ($\sim e^{-\Delta U/T})$ and entropy barriers ($\sim e^{-|\Delta S|}$), schematically depicted in Fig 1. Ritort and colleagues R6 ; R7 ; R8 ; R9 have proposed a Partial Equilibration Scenario (PES) for re-equilibrations delayed by entropy barriers. Over a waiting time $t_{w}$, a post-quench ageing system rapidly explores configuration shells of energy $E(t_{w})$, entropy $S(E)$, and (inverse) micro-canonical effective temperature $1/T_{eff}(t_{w})\equiv dS(E)/dE$. Passages to a lower shell of $E(t_{w}+1)\equiv E^{\prime}=E(t_{w})+\delta E$ are driven by spontaneous heat releases ($\delta E=\delta Q<0$) to the bath at $T$. The PES says that an iteration of these cooling steps ratchets the system down to the new canonical equilibrium. The non-equilibrium probability distribution for energy changes R6 ; R8 $P_{0}(\delta E;t_{w})$ is peaked at positive energies, with an exponential tail for $\delta E<0$, whose fall-off $\sim e^{\delta E/2T_{eff}(t_{w})}$ determines the effective temperature. The PES distribution has been studied by analytic Monte Carlo (MC) methods for harmonic oscillators R8 , and by numerical MC simulations of spin glasses and Lennard-Jones liquids R7 ; R9 . We note that if the effective temperature of the heat-release probability vanishes at some $T=T_{d}$, then there is an arrest of the PES cooling process.

We consider solid-solid structural transitions of martensites R10 ; R11 ; R12 ; R13 ; R14 ; R15 ; R16 , quenched below a thermodynamic $T_{0}$, with competing domains and slow relaxations R11 ; R17 . Martensites undergo first-order, diffusionless transitions R5 ; R10 from the higher-symmetry austenite, with atomic shifts locked to their unit-cell distortions (‘military transformations’). The order-parameter strains have degenerate lower-symmetry ‘variants’ separated by crystallographically oriented Domain Walls (DW), that can form complex microstructures R10 ; R14 ; R15 . A long-standing puzzle R11 ; R12 is that while quenches of austenite to below an (athermal) ‘martensite start’ temperature $T_{1}>T$ results in avalanche martensitic conversions, quenches above it $T_{1}<T$, show delayed conversions instead of no conversions. Resistivity, as a transition diagnostic, is flat during post-quench ‘incubations’, that end in sudden drops at a delayed avalancheR11 . Delays rise sharply, for shallower quenches approaching a third temperature $T_{d}$ that is in between, $T_{1}<T_{d}<T_{0}$. When a bath quench $T$ goes a few percent closer to $T_{d}$, the resistivity-drops go from a few seconds after, to ten thousand seconds after, the temperature quench R12 .

In this Letter we do MC simulations in three dimensions, with vector order parameter strains, for four structural transitions R18 . We present here the cubic-tetragonal (CT) transitionR15 , with a strain order parameter of components $N_{OP}=2$, with three competing unit-cell ‘variants’ $N_{V}=3$. We confirm for all four transitions, that the PES energy change distribution has the predicted generic behaviour: an exponential tail, with an effective temperature that regulates heat releasesR6 ; R7 ; R8 ; R9 .

For our specific case of quenches across a first order transition, the Order Parameter (OP) rises from zero, enabling the waiting time $t_{w}$ to be defined by rising-OP marker events at $t_{m}$, that depend on $T$. This choice $t_{w}=t_{m}(T)$ induces quench-temperature dependences: $T_{eff}(t_{w})\rightarrow T_{eff}(T)$ and $P_{0}(\delta E;t_{w})\rightarrow P_{0}(\delta E,T)$. For passages to lower energy shells, the OP evolution must satisfy $T$-controlled entropy-barrier constraints, postulated as of two types: a) A constraint that OP configurations must find and enter a Fourier space bottleneck that is like a Golf Hole (GH) that funnels into fast passage, as suggested for protein folding R19 ; or b) A constraint that the OP states need transient catalysts to enable fast passages, as inspired by facilitation modelsR20 ; R21 ; R22 . Our case is a), and we find a linear vanishing $T_{eff}(T)\sim(T_{d}-T)$. The ‘search freezing’ temperature $T_{d}$ occurs at a pinch-off on warming, of the $\vec{k}$-space inner radius of an angularly modulated bottleneck. Equilibration times are exponential in entropy barriers R11 ; R12 ; R23 , and for quenches $T_{d}>T>T_{1}$, diverge as ${\bar{t}}_{m}(T)\sim e^{1/T_{eff}(T)}\sim e^{1/(T_{d}-T)}$. Thus VFT -like behaviour is not restricted to the glass transition. Conversely, entropy barriers vanish and delay times collapse for $T<T_{1}$, when the bottleneck expands on cooling to span the Brillouin zone.

We derive a discretized-strain Hamiltonian R15 in 3D, from a crystal-symmetry invariant strain free energy $F$, that has Compatibility R14 , Ginzburg, and Landau terms in $F/E_{0}=\sum_{\vec{r},\vec{r}^{\prime}}f_{C}+\sum_{\vec{r}}[f_{G}+f_{L}]$, with $E_{0}$ an energy scale. There are six independent physical strainsR15 in 3D, that are linear combinations of Cartesian tensor strains: compressional $e_{1}$; deviatoric or rectangular $e_{2},e_{3}$ , and shear $e_{4},e_{5},e_{6}$. The OP of the cubic-tetragonal (CT) transition are two deviatoric strains ${\vec{e}}=(e_{3},e_{2})=(\frac{1}{\sqrt{6}}\{e_{xx}+e_{yy}-2e_{zz}\},\frac{1}{\sqrt{2}}\{e_{xx}-e_{yy}\})$. Austenite is $\vec{e}=\vec{0}$.

The remaining $6-N_{OP}$ non-OP strains (one compressional and three shears) enter the Hamiltonian as harmonic springs. These are minimized subject to a linear St Venant Compatibility constraintR14 that says no dislocations are generated: the double-curl of the strain tensor must vanish. There are three independent algebraic equations in $\vec{k}$ space, connecting OP and non-OP strains R15 . The harmonic non-OP strains then analytically yield an OP-OP interaction, whose transition-specific, anisotropic Compatibility kernel R15 is a $2\times 2$matrix, $U_{\ell\ell^{\prime}}({\hat{k}})$ where $\ell,\ell^{\prime}=2,3$. There is a prefactor of $(1-\delta_{\vec{k},0})$, and dependence on direction $\hat{k}={\vec{k}}/|\vec{k}|$.

The Landau free energy for CT is $f_{L}(\vec{e})=[(\tau-1){\vec{e}}^{2}-2(e_{3}^{3}-3e_{3}e_{2}^{2})+{\vec{e}}^{~{}4}]$ and has 4 minima, at $N_{V}=3$ variants plus at zero strain. Here $\tau(T)\equiv(T-T_{c})/(T_{0}-T_{c})$, and $\tau(T_{c})=0$ at the spinodal $T_{c}$, while $\tau(T_{0})=1$ at the first-order transition temperature, scaled to be unity $T_{0}=1$.

In ‘polar’ coordinates, $\vec{e}\equiv|\vec{e}|\vec{S}$. Here the unit-magnitude ‘variant vectors’ $\vec{S}(\vec{r})$ specify the unit-cell variants on either side of a Domain Wall (DW), that can be martensite-martensite or martensite-austenite. The nonzero $N_{V}=3$ martensite-variants have spins R15 $\vec{S}=(S_{3},S_{2})=(1,0),(-1/2,{\sqrt{3}}/2),(-1/2,-{\sqrt{3}}/2)$, pointing to corners of an equilateral triangle in a unit circle, while the centroid $\vec{S}=(0,0)$ is austenite. Thus ${\vec{S}}^{2}=0$ or $1$.

The degenerate Landau minima are at mean-OP magnitudes $\bar{\varepsilon}(T)=(3/4)[1+\sqrt{1-(8\tau/9)}]$. The variant domains have mostly-flat strain magnitudes, approximated by $\bar{\varepsilon}(T)$. Substituting ${\vec{e}}(\vec{r})\rightarrow\bar{\varepsilon}(T){\vec{S}}(\vec{r})$, the Landau term becomes $f_{L}(\vec{e})\rightarrow f_{L}(T){\vec{S}}(\vec{r})^{2}$. Here $f_{L}(T)\equiv{{\bar{\varepsilon}}(T)}^{2}g_{L}(T)\leq 0$, where $g_{L}=(\tau-1)+({\bar{\varepsilon}}(T)-1)^{2}\leq 0$. At $T={T_{0}}^{-}$, the OP is unity $\bar{\varepsilon}=1$ and $g_{L}=0$.

Notice a separation of time scale responses to $T$ quenches: the OP magnitude $\bar{\varepsilon}(T)$ responds immediately, at $t=1$, while Domain Walls can take thousands of time steps $t$, to evolve successively from DW Vapour to DW Liquid to a DW Crystal of twins. For our case of shallow quenches $T_{d}>T>T_{1}$, it is the DW Vapour-to-Liquid conversion has the long (bottleneck type) delays studied here. See VideosR21 A,B. The DW moves by correlated flips of spins that bracket it, while domain spins remain locked: a dynamical heterogeneity in space and time R3 ; R5 .  [For deeper quenches $T<<T_{1}$ not studied here, it is the DW Liquid-to-Crystal twin orientation that has long (facilitation type) delays. See VideoR21 C.]

The total hamiltonian is $\beta H=\beta H_{L}+\beta H_{G}+\beta H_{C}$, without extrinsic disorder. It is diagonal in Fourier space,

$$\begin{array}[]{rr}\beta H=\dfrac{D_{0}}{2}[\sum_{\ell,\ell^{\prime}}\sum_{\vec{k}}[\epsilon_{\ell,\ell^{\prime}}(\vec{k},T){\vec{S}}_{\ell}(\vec{k}){\vec{S}}^{*}_{\ell^{\prime}}(\vec{k})],\end{array}$$

(1)

with $D_{0}\equiv 2{\bar{\varepsilon}}(T)^{2}E_{0}/T$. The spectrum, with $K_{\mu}(\vec{k})\equiv 2\sin(k_{\mu}/2)$ and $\mu=x,y,z$, is

$$\epsilon_{\ell,\ell^{\prime}}(\vec{k},T)\equiv\{g_{L}(T)+\xi_{0}^{2}{\vec{K}}^{2}\}\delta_{\ell,\ell^{\prime}}+\frac{A_{1}}{2}U_{\ell\ell^{\prime}}(\hat{k}).$$

(2)

The anisotropic Compatibility kernel in the energy spectrum can induce preferred DW orientations R14 ; R15 ; R16 ; R21 . For example the $\ell=\ell^{\prime}$ kernel $U_{\ell,\ell}(\hat{k})$ is smallest $U_{\ell,\ell}(min)=0$ at the most favoured orientation, and largest $U_{\ell,\ell}(max)>0$ for most disfavoured. The negative sign of the Landau term $H_{L}\sim g_{L}<0$ and the positive signs of the Ginzburg term $H_{G}\sim\vec{k}^{2}>0$ and the Compatibility term $H_{C}>0$ imply the spectrum $\epsilon_{\ell,\ell}(\vec{k},T)$ could vanish along some Fourier contour. This contour will be angularly modulated, through the anisotropy of the Compatibility kernel R15 ; R16 .

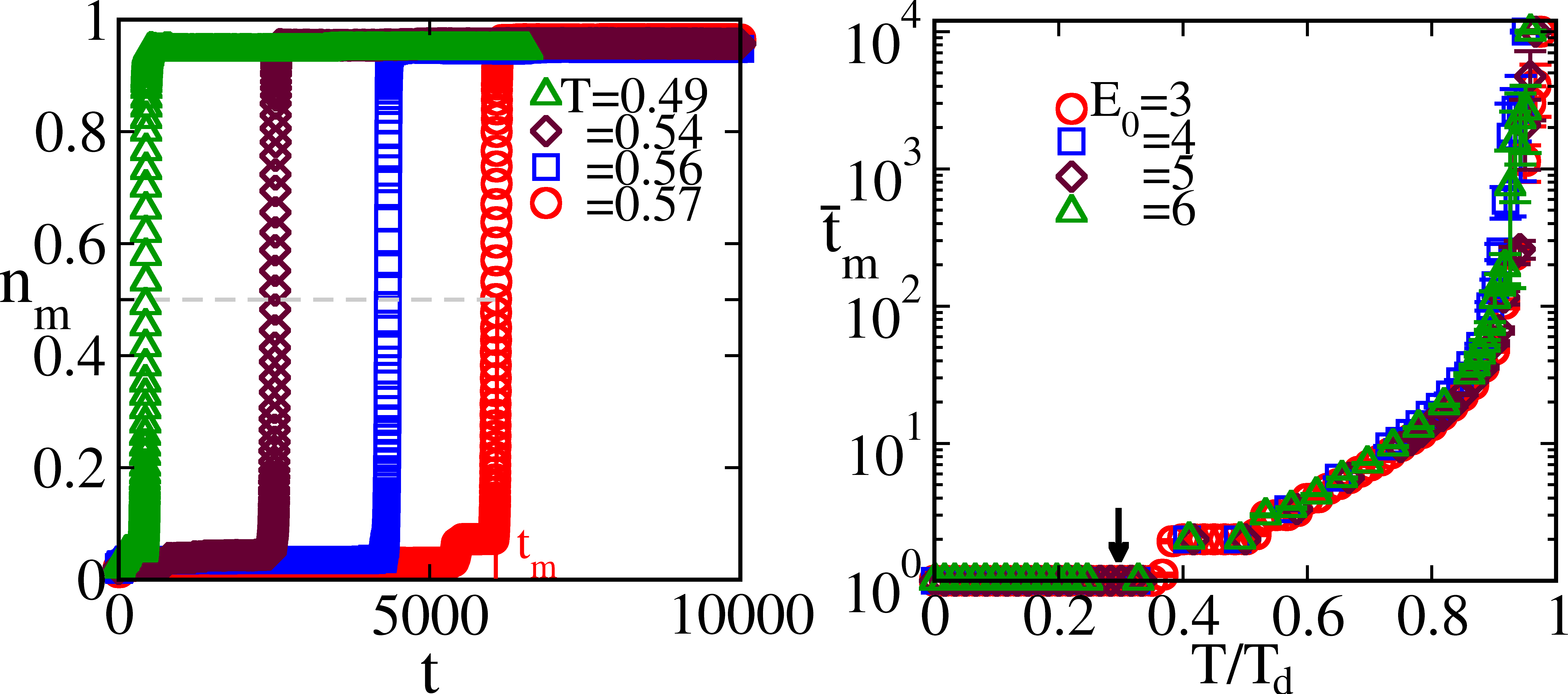
In MC simulations, the initial state $t=0$ is high-temperature austenite that is randomly and dilutely ($2\%$) seeded with martensite unit-cells. Typical parameters are $T_{0}=1$; $\xi_{0}^{2}=1$; $T_{c}=0.95$; $E_{0}=3$; system volume $N=L^{3}=16^{3}$; $N_{runs}=100$; and holding times $t_{h}=10^{4}$ MC sweeps.The martensite fraction is $n_{m}(t)\equiv\frac{1}{N}\sum_{\vec{r}}{S}^{2}(\vec{r},t)\leq 1$, with $n_{m}=0$ or $1$ for uniform austenite or martensite. The conversion time $t_{m}$ is defined as when R16 $n_{m}(t_{m})=1/2$. An athermal martensite droplet or embryo can rapidly form anywhere, and after waiting till $t_{w}=t_{m}$, can propagate rapidly to the rest of the system R13 . Hence it is mean rates ${\bar{r}}_{m}$ (or inverse times), that are averaged over runs, analogous to total resistors in parallel determined by the smallest resistance. Mean times ${\bar{t}}_{m}$ are inverse mean rates: ${\bar{t}}_{m}(T)\equiv 1/{{\bar{r}}_{m}(T)}$.

The MC procedure is standard, but with a crucial extra data retention R6 ; R7 ; R8 ; R9 of energy changes.
0. Take $N$ sites, each with a vector spin of $N_{OP}$ components, in one of $N_{V}+1$ possible values (including zero) at MC time $t$. Each $\{{\vec{S}}(\vec{r})\}$ set is a ‘configuration’.
1. Randomly pick one of $N$ sites, and randomly flip the spin on it to a new direction/value, and find the (positive/negative) $\delta E$ changes for the new configuration.
2. If the energy change $\delta E\leq 0$, then accept the flip. If $\delta E>0$, then accept flip with probability $e^{-\delta E/T}$. Record this $\delta E$, that is not usually retained after use.
3. Repeat steps 1 and 2. Stop after $N$ such spin-flips. This configuration has the conversion fraction $n_{m}(t+1)$.
4. We collect R24 all $\{\delta E\}$ from each spin-flip (configuration change) within each MC sweep of every run, up to the conversion time for that run, $t\leq t_{m}(T)\leq t_{h}$. The set size $N\times{t}_{m}\times N_{run}$ has up to $16^{3}\times 10^{4}\times 100$ data points. We take six quenches, from $T=T_{1}$ up to $T_{d}$.

Figure 2a shows $n_{m}(t)$, the martensite conversion-fraction in a single run, versus MC time $t$ for different temperatures $T$. For quenches $T\leq T_{1}$, avalanche conversions, characteristic of athermal martensite, occur in the very first sweep over all spins ($t=1$). We identify $T_{1}$ with the martensite start temperature R11 ; R12 $M_{s}=T_{1}$. For higher temperatures $T>T_{1}$, there is a curious ‘incubation’ period, when nothing happens macroscopically, until a postponed avalanche at $t_{w}=t_{m}$. These modelsR16 ; R24 display the delayed transitions and burst-like growth of order, characteristic of martensites and manganites R11 ; R12 ; R17 . Fig 2b shows that for $T$ above $T_{1}$ (downward arrow), and approaching $T_{d}$, the mean incubation delays rise steeply, due to entropic bottlenecks.

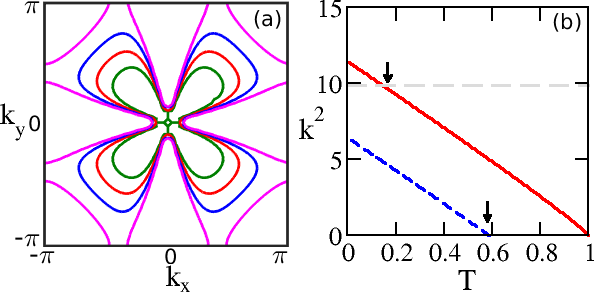
For our model, the boundary of a 3D bottleneck is from the spectrum set equal to zero $\epsilon_{\ell,\ell}(\vec{k})=0$, defining an anisotropic surface in $\vec{k}$-space. For the CT case, a [1,1,1] slice can intersect the bottleneck surface as an open, butterfly-shaped locus with an inner and outer radius, inside the Brillouin Zone (BZ). See Fig 3. For $T\leq T_{1}$, the radius $k_{out}(T)$ is larger than a BZ scale $\sim\pi$, and martensitic passages are immediate. For $T_{1}<T<T_{d}<T_{0},$ the butterfly bottleneck shrinks on warming. At $T=T_{d}$, the inner squared-radius $k_{in}(T)^{2}=|g_{L}(T)|-(A_{1}/2)U_{\ell,\ell}(max)$ vanishes, and the topology of the connected butterfly changes to that of a segmented four-petaled flower: entropy barriers diverge, and PES heat releases are arrested. For the ‘precursor’ region R14 $T_{d}<T<T_{0}$, PES passages are energetically available, but entropically inaccessisible. Repeated bottleneck entry attempts could induce vibrations. See VideoR21 D. Finally, at $T=T_{0}=1$, the outer squared-radius $k_{out}(T)^{2}=|g_{L}(T)|$ also vanishes: the bottleneck becomes a point, and only austenite exists.

We collect the $O(1)$ changes $\{\delta E\}$ to the $O(N)$ energy $E$. The probability $P_{0}(\delta E,T)$ to access $E^{\prime}$ from $E$, is proportional to the number of target states $\Omega(E^{\prime})$. With $S(E^{\prime})=\ln\Omega(E^{\prime})$, the probability ratio $R_{0}(\delta E)$ of energy changes is related to the entropy change $\Delta S(\delta E)\equiv S(E^{\prime})-S(E)<0$ by a fluctuation relation for aging R1 ; R2 ; R3 ; R4 :

$$R_{0}\equiv\frac{P_{0}(\delta E,T)}{P_{0}(-\delta E,T)}=\frac{\Omega(E^{\prime})}{\Omega(E)}=e^{\Delta S(\delta E)}.$$

(3)

Entropy barriers $S_{B}\equiv-\Delta S>0$ rise, when the searched-for states become rarer. Since $R_{0}(\delta E)R_{0}(-\delta E)\equiv 1$, the entropy change is odd, $\Delta S(\delta E)+\Delta S(-\delta E)=0$, and a solution for the PES distribution is

$$P_{0}(\delta E,T)={P_{0}}^{(+)}(\delta E)~{}e^{\frac{1}{2}\Delta S(\delta E)},$$

(4)

with an even ${P_{0}}^{(+)}(\delta E)\equiv\sqrt{P_{0}(\delta E,T)~{}P_{0}(-\delta E,T)}$. The leading entropy-change term for small heat releases is $\Delta S\simeq\beta_{eff}\delta E$ where $\beta_{eff}\equiv 1/T_{eff}$. For $\delta E=-|\delta E|<0$, the Boltzmann-like form $P_{0}\simeq e^{-\frac{1}{2}\beta_{eff}(T)|\delta E|}$ gives a physical meaning to the effective temperature, as a search range denoting accessible energy shells. If $\beta_{eff}\rightarrow 0$, entropy barriers collapse, and passages are immediate. If $T_{eff}\rightarrow 0$, then entropy barriers diverge, and passages cease. Glass-like freezing is a shutdown of PES searches.

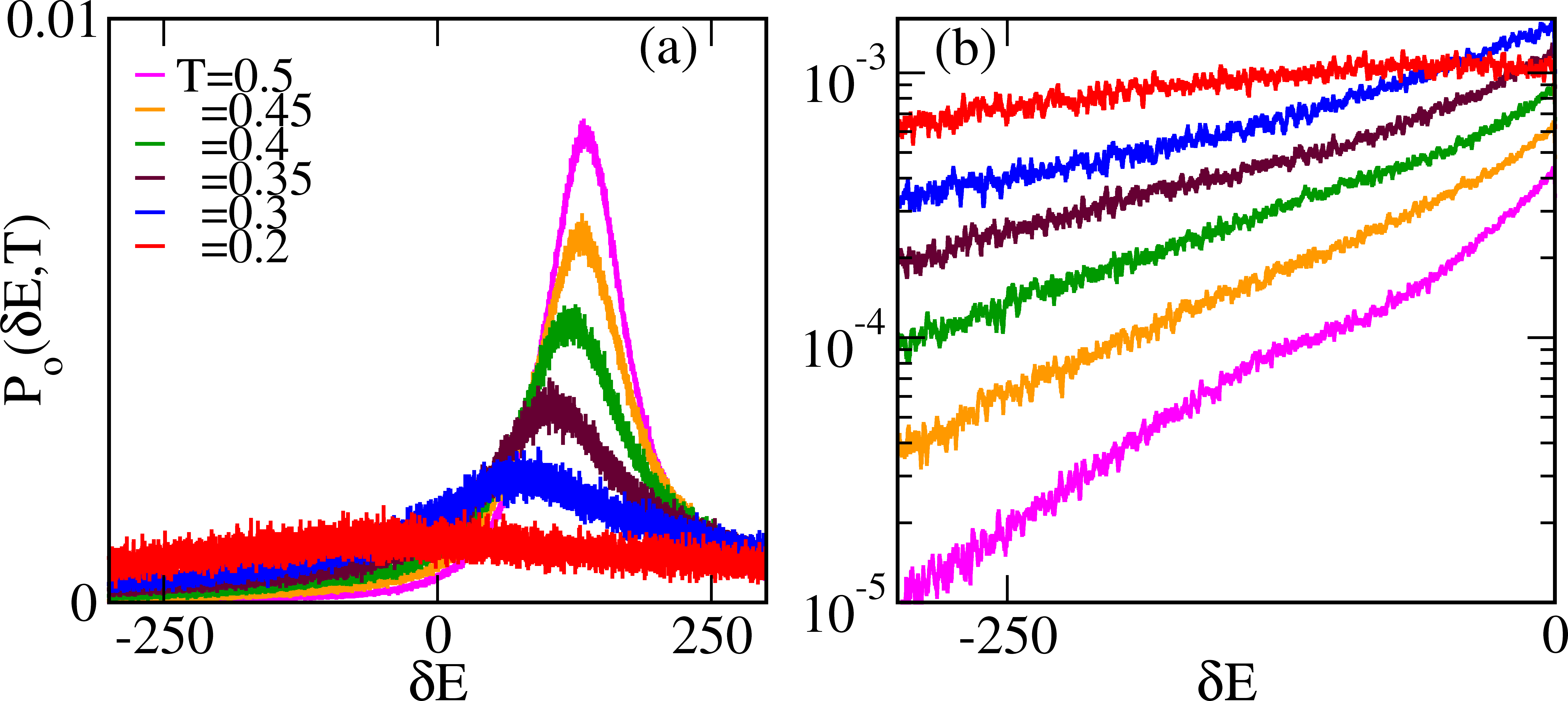
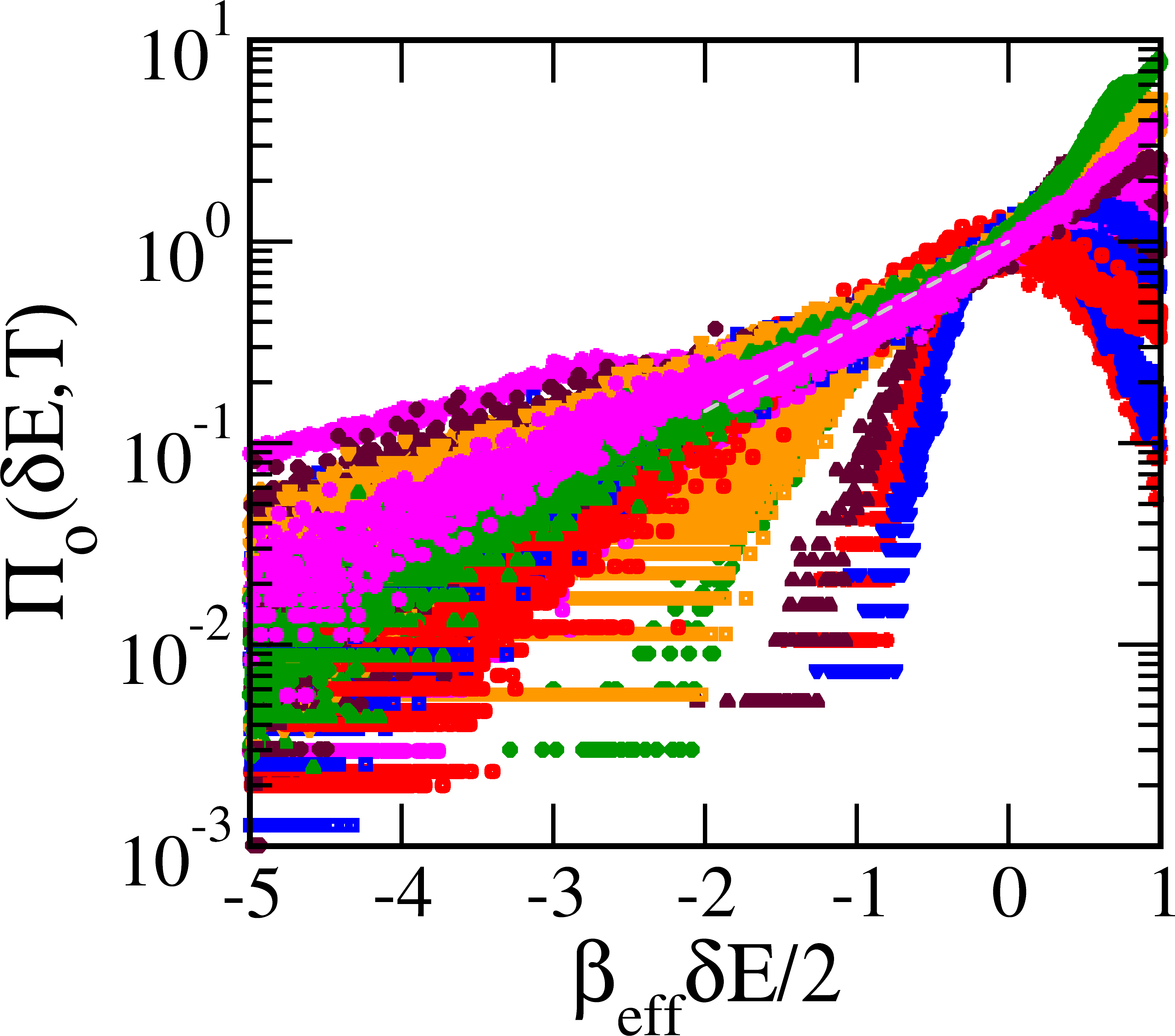
Fig 4a shows that, as in PES models R6 ; R7 ; R8 ; R9 , the $P_{0}(\delta E,T)$ peaks are at positive $\delta E$, understood as a completion-of-square between a gaussian peaked at the origin and an exponential tail for $\delta E<0$. Fig 4b shows a zoom-in near the origin, where the slopes define $\frac{1}{2}\beta_{eff}(T)$.

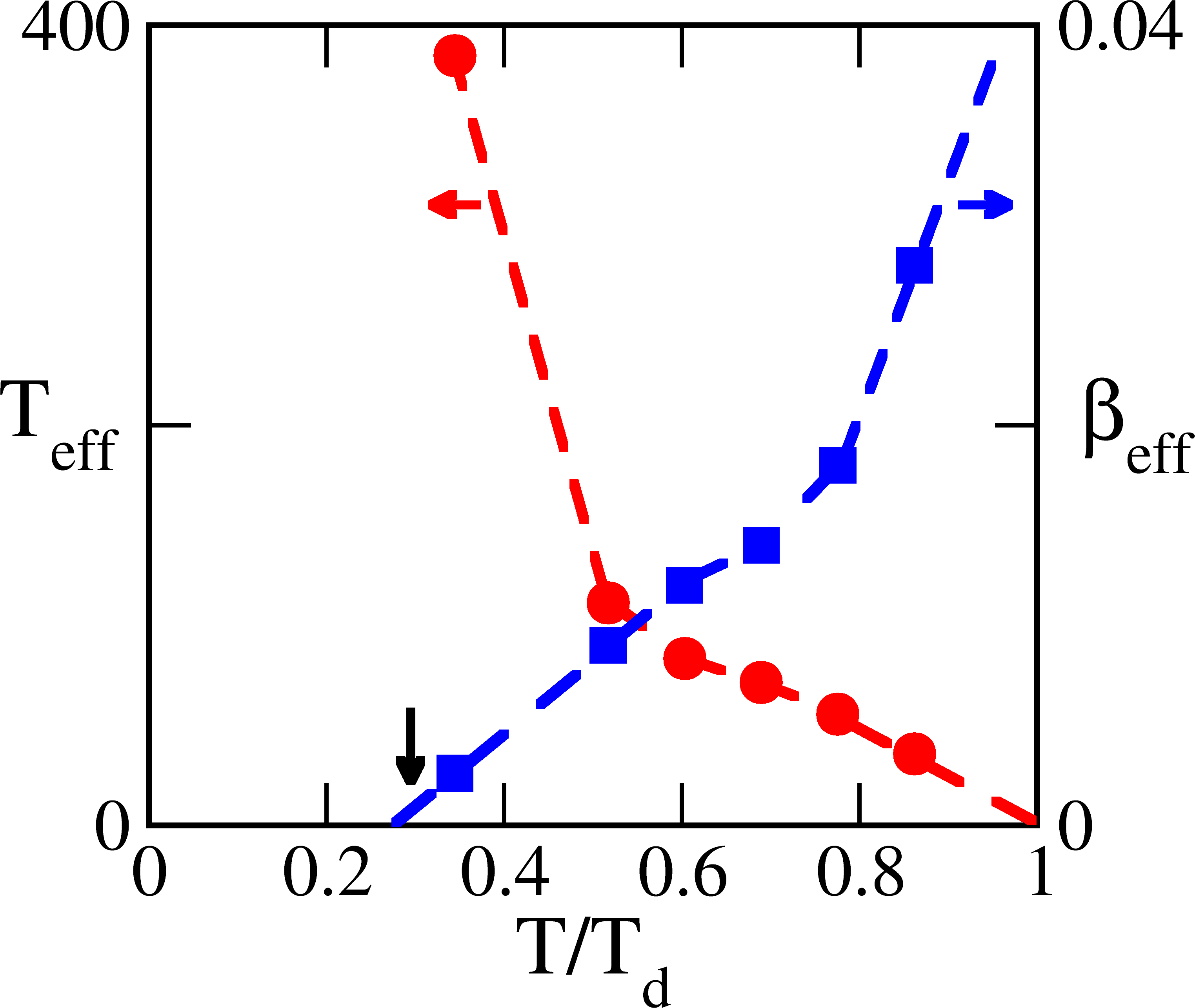
Fig 5 shows the dependence of $\beta_{eff}(T)$ and $T_{eff}(T)$ on the quench temperature $T$. The data suggest a linear vanishing of $T_{eff}\simeq(T_{d}-T)/(B_{0}T_{d})$ near $T_{d}$, at a search freezing and a suppression of the heat releases to the bath. There is also a linear vanishing of $\beta_{eff}\sim T-T_{1}$ near $T_{1}$, at a search avalanche and prompt equilibration.

Fig 6 shows log-linear plots for a scaled $\Pi_{0}(\delta E,T)\equiv P_{0}(\delta E,T)/P_{0}(0,T)$ versus the entropy-barrier related variable $\frac{1}{2}\beta_{eff}\delta E$. Data are for four 3D structural transitions R18 ; R23 , and six $T$ between the collapse ($T_{1}$) and divergence ($T_{d}$) of entropy barriers.

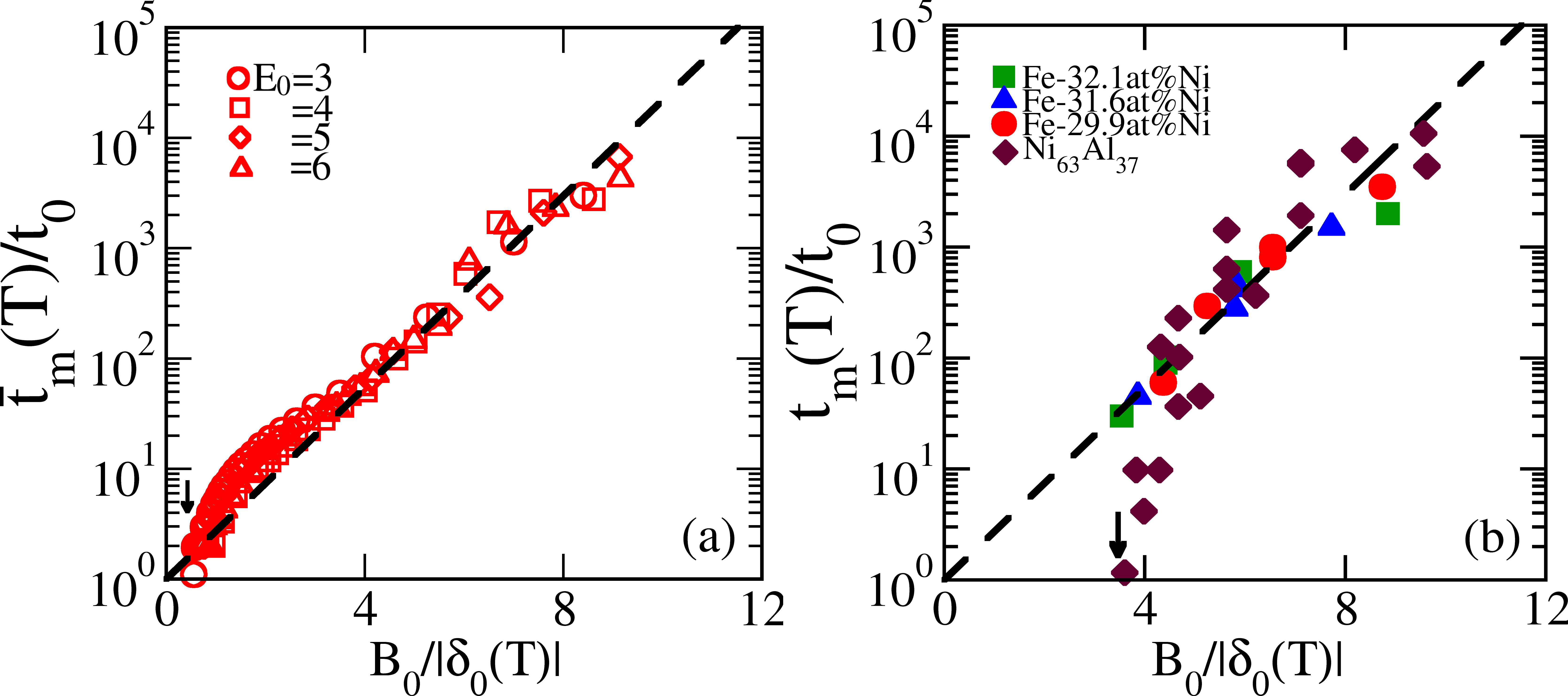
The mean conversion time is exponential in the entropy barrier R23 ${\bar{t}}\sim e^{1/T_{eff}(T)}$, so near $T_{d}$ we have ${\bar{t}}_{m}(T)\simeq t_{0}e^{B_{0}/|\delta_{0}(T)|}$, where the constants $B_{0},t_{0}$ can be fixed by simulational and experimental data R24 . The initial slope in $|\delta_{0}|$ of $1/\ln{{\bar{t}}_{m}(T)}$ gives $1/B_{0}$; and the extrapolated intercept of $\ln{{\bar{t}}_{m}(T)}$ versus $B_{0}/|\delta_{0}(T_{0})|$ gives $t_{0}$. For Ni-Al data R11 the ‘fragility’ parameter R2 $B_{0}T_{d}\simeq 1.23$ Kelvin, and the austenite-martensite DW hop time is $t_{0}\simeq 1$ sec.

Fig 7a shows that CT times show VFT behaviour near $T_{d}$ and fall-off behaviour near $T_{1}$. Fig 7b shows data extracted from Ni-Al and Fe-Al alloysR11 ; R12 are similar.

Signatures of PES could be sought, in previous simulations or experimentsR3 ; R5 under systematic temperature quenches, with a recording of energy releases. Further experimental work on martensitic alloys R11 ; R12 could record signal and noise under systematic quench steps of $1/|\delta_{0}|$, over the delay region $T_{d}>T>T_{1}$; as well as the precursor R14 ; R21 region $T_{0}>T>T_{d}$ above it. Non-stationary distributions of energy releases might be determined through concurrent resistive, photonic, acoustic, and elastic signalsR25 . Finally, one might speculate that complex oxides quenched near their structural/ functional transitions, could show PES ageing behaviour in their (strain-coupled) functional variablesR17 ; R18 .

In summary, post-quench ageing in athermal martensites shows characteristic signatures of the Partial Equilibration Scenario. The conversion arrest and delay-divergence found in 3D simulations and alloy experiments, are understood as arising from a vanishing of the search temperature that governs the PES cooling process.

Acknowledgement: It is a pleasure to thank Smarajit Karmakar for valuable discussions on the glass transition.