This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

Unconditionally optimal error estimate of a linearized variable-time-step BDF2 scheme for nonlinear parabolic equations

Chengchao Zhao Beijing Computational Science Research Center, Beijing, 100193, P.R. China ([email protected]).    Nan Liu School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China ([email protected])    Yuheng Ma School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China ([email protected])    Jiwei Zhang School of Mathematics and Statistics, and Hubei Key Laboratory of Computational Science, Wuhan University, Wuhan 430072, China ([email protected]). He is supported partially by NSFC under grant 11771035.
(September 1, 2021)
Abstract

In this paper we consider a linearized variable-time-step two-step backward differentiation formula (BDF2) scheme for solving nonlinear parabolic equations. The scheme is constructed by using the variable time-step BDF2 for the linear term and a Newton linearized method for the nonlinear term in time combining with a Galerkin finite element method (FEM) in space. We prove the unconditionally optimal error estimate of the proposed scheme under mild restrictions on the ratio of adjacent time-steps, i.e. 0<rk<rmax≈4.86450<r_{k}<r_{\max}\approx 4.8645 and on the maximum time step. The proof involves the discrete orthogonal convolution (DOC) and discrete complementary convolution (DCC) kernels, and the error splitting approach. In addition, our analysis also shows that the first level solution u1u^{1} obtained by BDF1 (i.e. backward Euler scheme) does not cause the loss of global accuracy of second order. Numerical examples are provided to demonstrate our theoretical results.

keywords: two-step backward differentiation formula; the discrete orthogonal convolution kernels; the discrete complementary convolution kernels; error estimates; variable time-step; Unconditional error estimate; error splitting approach

1 Introduction

In this paper, we focus on the unconditionally optimal error estimate of a linearized second-order two-step backward differentiation formula (BDF2) scheme with variable time steps for solving the following general nonlinear parabolic equation [4, 21]:

∂tu=Δ​u+f​(u),\displaystyle\partial_{t}u=\Delta u+f(u), 𝒙∈Ω,t∈(0,T],\displaystyle\bm{x}\in\Omega,t\in(0,T], (1.1)
u​(𝒙,0)=u0​(𝒙),\displaystyle u(\bm{x},0)=u_{0}(\bm{x}), 𝒙∈Ω,\displaystyle\bm{x}\in\Omega,
u​(𝒙,t)=0,\displaystyle u(\bm{x},t)=0, 𝒙∈∂Ω,t∈[0,T],\displaystyle\bm{x}\in\partial\Omega,t\in[0,T],

where Ω⊂ℝd​(d=1,2,3)\Omega\subset\mathbb{R}^{d}(d=1,2,3) is a bounded convex domain. To construct variable time-step schemes, we first set the variable time levels 0=t0<t1<⋯<tN=T0=t_{0}<t_{1}<\cdots<t_{N}=T, the kkth time-step size τk:=tk−tk−1\tau_{k}:=t_{k}-t_{k-1}, the maximum step size τ:=max1≤k≤N⁡τk\tau:=\max_{1\leq k\leq N}\tau_{k}, and the adjacent time-step ratios rk=τk/τk−1, 2≤k≤N.r_{k}=\tau_{k}/\tau_{k-1},\;2\leq k\leq N. Set uk=u​(tk),∇τuk:=uk−uk−1,r1≡0u^{k}=u(t_{k}),\nabla_{\tau}u^{k}:=u^{k}-u^{k-1},\;r_{1}\equiv 0, and denote UnU^{n} by the approximation of the exact solution u​(tn)u(t_{n}). The first step value U1U^{1} is calculated by one-step backward difference formula (BDF1), and the other Un​(n>1)U^{n}\;(n>1) is calculated by BDF2 formula with variable time steps, which are respectively given as

𝒟1​U1=1τ1​∇τU1,𝒟2​Un=1+2​rnτn​(1+rn)​∇τUn−rn2τn​(1+rn)​∇τUn−1.\mathcal{D}_{1}U^{1}=\frac{1}{\tau_{1}}\nabla_{\tau}U^{1},\quad\mathcal{D}_{2}U^{n}=\frac{1+2r_{n}}{\tau_{n}(1+r_{n})}\nabla_{\tau}U^{n}-\frac{r_{n}^{2}}{\tau_{n}(1+r_{n})}\nabla_{\tau}U^{n-1}. (1.2)

The nonlinear term is approximated by a linearized method, i.e., the Newton linearized method given as

f​(un)≈f​(Un−1)+f′​(Un−1)​∇τUn.\displaystyle f({u^{n}})\approx f(U^{n-1})+f^{\prime}(U^{n-1})\nabla_{\tau}U^{n}. (1.3)

Thus the semi-discrete BDF2 scheme with variable time steps to problem (1.1) is given as

𝒟2​Un=Δ​Un+f​(Un−1)+f′​(Un−1)​∇τUn,\displaystyle\mathcal{D}_{2}U^{n}=\Delta U^{n}+f(U^{n-1})+f^{\prime}(U^{n-1})\nabla_{\tau}U^{n}, for1≤n≤N,\displaystyle\text{for}\quad 1\leq n\leq N, (1.4)
U0​(𝒙)=u0​(𝒙),\displaystyle U^{0}(\bm{x})=u_{0}(\bm{x}), 𝒙∈Ω,\displaystyle\bm{x}\in\Omega, (1.5)
Un​(𝒙)=0,\displaystyle U^{n}(\bm{x})=0, 𝒙∈∂Ω,n=0,1,⋯,N.\displaystyle\bm{x}\in\partial\Omega,\quad n=0,1,\cdots,N. (1.6)

Here the BDF1 and BDF2 formulas have been written as a unified convolution form of

𝒟2​Un=∑k=1nbn−k(n)​∇τUk,n≥1\mathcal{D}_{2}U^{n}=\sum_{k=1}^{n}b_{n-k}^{(n)}\nabla_{\tau}U^{k},\quad\quad n\geq 1 (1.7)

by taking b0(n)=(1+2​rn)/(τn​(1+rn)),b1(n)=−rn2/(τn​(1+rn))​and​bj(n)=0​ for ​2≤j≤n−1.b_{0}^{(n)}=(1+2r_{n})/(\tau_{n}(1+r_{n})),\;b_{1}^{(n)}=-r_{n}^{2}/(\tau_{n}(1+r_{n}))\;\text{and}\;b_{j}^{(n)}=0\;\text{ for }2\leq j\leq n-1.

For the spatial discretization, let ℐh\mathcal{I}_{h} be the quasiuniform partition of Ω\Omega with triangles in ℝ2\mathbb{R}^{2} or tetrahedra Ti​(i=1,⋯,M)T_{i}\;(i=1,\cdots,M) in ℝ3\mathbb{R}^{3}, see [11, 19]. Denote the spatial mesh size by h=max1≤i≤M⁡{diam​Ti}h=\max_{1\leq i\leq M}\{\text{diam}\ T_{i}\} and the finite-dimensional subspace of H01​(Ω)H^{1}_{0}(\Omega) by VhV_{h} which consists of piecewise polynomials of degree r​(r≥1)r\;(r\geq 1) on ℐh\mathcal{I}_{h}. Then, the Newton linearized Galerkin FEM BDF2 scheme with variable time steps is to find Uhn∈VhU^{n}_{h}\in V_{h} such that

(𝒟2​Uhn,vh)=−(∇Uhn,∇vh)+(f​(Uhn−1)+f′​(Uhn−1)​∇τUhn,vh),∀vh∈Vh.\displaystyle(\mathcal{D}_{2}U_{h}^{n},v_{h})=-(\nabla U_{h}^{n},\nabla v_{h})+(f(U_{h}^{n-1})+f^{\prime}(U_{h}^{n-1})\nabla_{\tau}U_{h}^{n},v_{h}),\quad\forall v_{h}\in V_{h}. (1.8)

Efficiency, accuracy and reliability are of key considerations in numerical analysis and scientific computing. For the time-dependent models appeared in science and engineering, a heuristic and promising method to improve efficiency without sacrificing accuracy is the time adaptive method. For instance, one may employ the coarse-grained or refined time steps based on the solutions changing slowly or rapidly to capture the dynamics of the solutions. Another alternative approach is to employ high-order methods in time to have the same accuracy with a relatively large time-step. In this paper, we consider the second order BDF2 scheme with variable time steps.

Due to its nice property (AA-stable), the BDF2 method with variable time steps has been widely used in various models to obtain computationally efficient, accurate results [2, 23, 20, 16, 15, 13]. Much works have been carried out on its stability and error estimates [22, 17, 5, 3, 2, 1], but the analysis even for linear parabolic problems (i.e., problem (1.1) with f​(u)=0f(u)=0) is already highly nontrivial and challenging as documented in the classic book [19, Chapter 10]. One also refers to the details in [6, 7, 5, 8, 18]. In particular, with the energy method and under a ratio condition 0<rk≤1.8680<r_{k}\leq 1.868, Becker [1] presents that the variable time-step BDF2 scheme for a linear parabolic problems is zero-stable. After that, Emmrich [3] gives the similar result with 0<rk≤1.910<r_{k}\leq 1.91. Recently, a promising work in [2] introduce a novel generalized discrete Grönwall-type inequality for the Cahn-Hilliard equation to obtain an energy stability with 0<rk≤3.5610<r_{k}\leq 3.561. The works in [17, 22] consider linear parabolic equations based on DOC kernels under 0≤rk≤3.5610\leq r_{k}\leq 3.561 [17] and 0<rk≤4.86450<r_{k}\leq 4.8645 [22], respectively. In addition, the robust second-order convergence is further analyzed in [22]. The robustness here means the optimal second-order accuracy holds valid only requiring the time-step sizes 0<rk≤4.86450<r_{k}\leq 4.8645.

For the variable-time-step BDF2 method applied to nonlinear parabolic equations, there has a great progress on the error estimates for the Cahn-Hilliard equation [2], molecular beam epitaxial model without slope selection [23, 15], phase field crystal model [13], and references therein. Among all the numerical methods in [2, 23, 15, 13], the implicit schemes are utlized to deal with the nonlinear terms. Although the implicit schemes are unconditionally stable, they need to solve a nonlinear algebraic system in each time level. To circumvent the extra computational cost for iteratively solving the nonlinear algebraic system, a popular approach is to employ the linearized methods to approximate the nonlinear terms. Combining the variable-time-step BDF2 for linear terms with a linearized method for nonlinear terms, it is natural to ask if the proposed implicit-explicit schemes still remain unconditionally stable. In addition, the focus of this paper is on the general nonlinearity ff, which also brings the extra analysis difficulty comparing with the phase-fields models studied in [2, 23, 15, 13], since the good property of the energy dissipation for the phase-fields models does not hold any more for general nonlinearity.

In this paper, we aim to address the unconditionally optimal error estimate 𝒪​(τ2+hr+1)\mathcal{O}(\tau^{2}+h^{r+1}) of the linearized scheme (1.8) in the sense of L2L^{2}-norm under the following two conditions:

  • A1 :

    0<rk≤rmax−δ0<r_{k}\leq r_{\max}-\delta for any small constant 0<δ<rmax≈4.86450<\delta<r_{\max}\approx 4.8645 and 2≤k≤N2\leq k\leq N, where rmax=16​(1196−12​1773+1196+12​1773)+43r_{\max}=\frac{1}{6}\left(\sqrt[3]{1196\!-\!12\sqrt{177}}+\sqrt[3]{1196\!+\!12\sqrt{177}}\right)+\frac{4}{3} is the root of equation x3=(1+2​x)2x^{3}=(1+2x)^{2};

  • A2 :

    there exists a constant C^\hat{C} independent of τ\tau and NN such that the maximum time step size τ\tau satisfies τ≤C^​1N\tau\leq\hat{C}\frac{1}{\sqrt{N}}.

The proof of the error estimate is established by the introduction of the temporal-spatial error splitting approach and the concepts of DOC and DCC kernels. The error splitting approach, developed in [9], is used to overcome the unnecessary restrictions of the temporal and spacial mesh sizes. The main idea of the error splitting approach is to first consider the boundedness of ‖Un‖H2\|U^{n}\|_{H^{2}} for the solution to semi-discrete equation (1.4), and then to obtain the estimate of ‖Uhn‖L∞\|U_{h}^{n}\|_{L^{\infty}} for the fully discrete equation (1.8) by using the following strategy

‖Uhn‖L∞\displaystyle\|U_{h}^{n}\|_{L^{\infty}} ≤‖Rh​Un‖L∞+‖Rh​Un−Uhn‖L∞\displaystyle\leq\|R_{h}U^{n}\|_{L^{\infty}}+\|R_{h}U^{n}-U_{h}^{n}\|_{L^{\infty}}
≤C​‖Un‖H2+C​h−d/2​‖Rh​Un−Uhn‖L2\displaystyle\leq C\|U^{n}\|_{H^{2}}+Ch^{-d/2}\|R_{h}U^{n}-U_{h}^{n}\|_{L^{2}} (1.9)
≤C+C​h−d/2​h2,\displaystyle\leq C+Ch^{-d/2}h^{2},

where RhR_{h} is the projection operator.

The concepts of DOC and DCC kernels, developed in [17, 22], are used to present the stability and convergence analysis under a mild restriction on the ratio of adjacent time-steps, i.e., A1. The condition A1 is the mildest restriction in the current literatures, as far as we know, for the variable time-step BDF2 method. On the other hand, due to the usage of a linearized scheme to approximate the general nonlinearity, our optimal error estimate in time suffers from another restriction on the maximum time step, i.e., A2. Noting that the condition A2 only involves the maximum time step, hence it is mild and acceptable/reasonable for the practical simulations to have the convergence order.

For general nonlinearity, our improvements are twofold: (i) comparing with the fully implicit schemes developed [2, 23, 15, 13], a linearized scheme is considered in this paper, and its first rigorous proof of unconditionally optimal convergence is presented under mild restrictions on A1 and A2; (ii) the linearized BDF2 scheme (1.8) still has the second-order accuracy in time as the first order BDF1 method is used only once to compute the first step value.

The remainder of this paper is organized as follows. In section 2, we present several important properties of the DOC kernels and DCC kernels which play a key role in our stability and convergence analysis. The unconditional L∞L^{\infty} boundedness of numerical solutions of the fully discrete scheme is derived in section 3 and then the unconditionally optimal L2L^{2}-norm error estimate is obtained in section 4. In section 5, numerical examples are provided to confirm our theoretical analysis.

2 Setting

In this paper, we assume there exists a constant ℳ\mathcal{M} such that the solution of problem (1.1) satisfies

‖u0‖Hr+1\displaystyle\|u_{0}\|_{H^{r+1}} +‖u‖L∞​((0,T);Hr+1)+‖∂tu‖L∞​((0,T);Hr+1)\displaystyle+\|u\|_{L^{\infty}((0,T);H^{r+1})}+\|\partial_{t}u\|_{L^{\infty}((0,T);H^{r+1})}
+‖∂t​tu‖L∞​((0,T);L2)+‖∂t​t​tu‖L∞​((0,T);L2)≤ℳ,r≥1.\displaystyle+{\|\partial_{tt}u\|_{L^{\infty}((0,T);L^{2})}+\|\partial_{ttt}u\|_{L^{\infty}((0,T);L^{2})}\leq\mathcal{M}},\ r\geq 1. (2.1)

2.1 The properties of DOC and DCC kernels

We here present the definitions and properties of DCC and DOC kernels, which play crucial roles in our analysis to overcome the difficulties resulted from the variable time steps. The DCC kernels introduced in [10, 14] are defined by

∑j=knpn−j(n)​bj−k(j)≡1,∀1≤k≤n, 1≤n≤N,\sum_{j=k}^{n}p_{n-j}^{(n)}b_{j-k}^{(j)}\equiv 1,\quad\forall 1\leq k\leq n,\;1\leq n\leq N, (2.2)

which satisfy

∑j=1npn−j(n)​𝒟2​uj=∑j=1npn−j(n)​∑l=1jbj−l(j)​∇τul=∑l=1n∇τul​∑j=lnpn−j(n)​bj−l(j)=un−u0,∀n≥1.\sum_{j=1}^{n}p_{n-j}^{(n)}\mathcal{D}_{2}u^{j}=\sum_{j=1}^{n}p_{n-j}^{(n)}\sum_{l=1}^{j}b_{j-l}^{(j)}\nabla_{\tau}u^{l}=\sum_{l=1}^{n}\nabla_{\tau}u^{l}\sum_{j=l}^{n}p_{n-j}^{(n)}b_{j-l}^{(j)}=u^{n}-u^{0},\quad\forall n\geq 1. (2.3)

The DOC kernels in [17] is defined by

∑j=knθn−j(n)​bj−k(j)=δn​k,∀1≤k≤n, 1≤n≤N,\displaystyle\sum_{j=k}^{n}\theta_{n-j}^{(n)}b_{j-k}^{(j)}=\delta_{nk},\quad\forall 1\leq k\leq n,\;1\leq n\leq N, (2.4)

where the Kronecker delta symbol δn​k\delta_{nk} holds δn​k=1\delta_{nk}=1 if n=kn=k and δn​k=0\delta_{nk}=0 if n≠kn\neq k. By exchanging the summation order, it is straightforward to verify that the DOC kernels satisfy

∑j=1nθn−j(n)​𝒟2​uj=∑l=1n∇τul​∑j=lnθn−j(n)​bj−l(j)=un−un−1,1≤n≤N.\sum_{j=1}^{n}\theta_{n-j}^{(n)}\mathcal{D}_{2}u^{j}=\sum_{l=1}^{n}\nabla_{\tau}u^{l}\sum_{j=l}^{n}\theta_{n-j}^{(n)}b_{j-l}^{(j)}=u^{n}-u^{n-1},\quad 1\leq n\leq N. (2.5)

Set p−1(n):=0,∀n≥0p^{(n)}_{-1}:=0,\forall n\geq 0. The DCC and DOC kernels have the following relations (see [22, Proposition 2.1])

pn−j(n)=∑l=jnθl−j(l),θn−j(n)=pn−j(n)−pn−1−j(n−1),∀1≤j≤n.\displaystyle p^{(n)}_{n-j}=\sum_{l=j}^{n}\theta^{(l)}_{l-j},\quad\theta^{(n)}_{n-j}=p^{(n)}_{n-j}-p^{(n-1)}_{n-1-j},\quad\forall 1\leq j\leq n. (2.6)

We now present several useful lemmas with details in [17, 22, 23].

Lemma 2.1 (​​[23]).

Assume the time step ratio rkr_{k} satisfies A1. For any real sequence {wk}k=1n\{w_{k}\}_{k=1}^{n} and any given small constant 0<δ<rmax≈4.86450<\delta<r_{\max}\approx 4.8645, it holds

2​wk​∑j=1kbk−j(k)​wj≥rk+1​rmax(1+rk+1)​wk2τk−rk​rmax(1+rk)​wk−12τk−1+δ​wk220​τk,k≥2,\displaystyle 2w_{k}\sum_{j=1}^{k}b^{(k)}_{k-j}w_{j}\geq\frac{r_{k+1}\sqrt{r_{\max}}}{(1+r_{k+1})}\frac{w_{k}^{2}}{\tau_{k}}-\frac{r_{k}\sqrt{r_{\max}}}{(1+r_{k})}\frac{w_{k-1}^{2}}{\tau_{k-1}}+\frac{\delta w_{k}^{2}}{20\tau_{k}},\quad k\geq 2, (2.7)
2​∑k=1nwk​∑j=1kbk−j(k)​wj≥δ20​∑k=1nwk2τk≥0,for ​n≥1.\displaystyle 2\sum_{k=1}^{n}w_{k}\sum_{j=1}^{k}b^{(k)}_{k-j}w_{j}\geq\frac{\delta}{20}\sum_{k=1}^{n}\frac{w_{k}^{2}}{\tau_{k}}\geq 0,\quad\text{for }n\geq 1. (2.8)
Corollary 2.1 (​​[22]).

If the condition in lemma 2.1 are satisfied, then we have the following inequality

∑k=1nwk​∑j=1kθk−j(k)​wj≥0,for ​n≥1.\displaystyle\sum_{k=1}^{n}w_{k}\sum_{j=1}^{k}\theta^{(k)}_{k-j}w_{j}\geq 0,\quad\text{for }n\geq 1. (2.9)
Lemma 2.2 (​​[17]).

The DOC kernels θn−j(n)\theta_{n-j}^{(n)} satisfy

θn−j(n)\displaystyle\theta_{n-j}^{(n)} >0​ for ​ 1≤j≤n, and ∑j=1nθn−j(n)=τn​ for ​n≥1.\displaystyle>0\;\text{ for }\;1\leq j\leq n,\qquad\text{ and }\qquad\sum_{j=1}^{n}\theta_{n-j}^{(n)}=\tau_{n}\;\text{ for }\;n\geq 1. (2.10)
Proposition 2.1.

(​​​[22, Proposition 2.2]). The DCC kernels pn−k(n)p^{(n)}_{n-k} defined in (2.2) satisfy

∑j=1npn−j(n)=∑k=1n∑j=1kθk−j(k)=tn,pn−j(n)≤2​τ.\displaystyle\sum_{j=1}^{n}p^{(n)}_{n-j}=\sum_{k=1}^{n}\sum_{j=1}^{k}\theta^{(k)}_{k-j}=t_{n},\qquad p^{(n)}_{n-j}\leq 2\tau. (2.11)

3 The L∞L^{\infty} boundedness of the fully discrete solution UhnU^{n}_{h}

The key point in this paper, to deal with the nonlinear term in (1.8), is the L∞L^{\infty} boundedness of the numerical solution UhnU^{n}_{h}. To this end, we present several useful lemmas as follows, including the discrete Grönwall inequality and the temporal consistency errors. For convenience, here and after we denote ∥⋅∥:=∥⋅∥L2\|\cdot\|:=\|\cdot\|_{L^{2}}.

Lemma 3.1 (Discrete Grönwall inequality).

Assume λ>0\lambda>0 and the sequences {vj}j=1N\{v_{j}\}_{j=1}^{N} and {ηj}j=0N\{\eta_{j}\}_{j=0}^{N} are nonnegative. If

vn≤λ​∑j=1n−1τj​vj+∑j=0nηj,for1≤n≤N,v_{n}\leq\lambda\sum_{j=1}^{n-1}\tau_{j}v_{j}+\sum_{j=0}^{n}\eta_{j},\quad\text{for}\quad 1\leq n\leq N,

then it holds

vn≤exp⁡(λ​tn−1)​∑j=0nηj,for1≤n≤N.v_{n}\leq\exp\big{(}\lambda t_{n-1}\big{)}\sum_{j=0}^{n}\eta^{j},\quad\text{for}\quad 1\leq n\leq N.

Lemma 3.1 can be proved by the standard induction hypothesis and we omit it here.

Lemma 3.2 (​​[12]).

Assume the regularity condition (2.1) holds and the nonlinear function f=f​(u)∈C2​(ℝ)f=f(u)\in C^{2}(\mathbb{R}). Denote the local truncation error by

Rfj=f​(uj)−f​(uj−1)−f′​(uj−1)​∇τuj,1≤j≤N.\displaystyle R_{f}^{j}=f(u^{j})-f(u^{j-1})-f^{\prime}(u^{j-1})\nabla_{\tau}u^{j},\quad 1\leq j\leq N. (3.1)

Then we have the following estimates of the truncation error

‖Rfj‖≤Cf​τj2,1≤j≤N,\displaystyle\|R_{f}^{j}\|\leq C_{f}\tau_{j}^{2},\quad 1\leq j\leq N, (3.2)

where Cf:=12​CΩ​sup|u|≤CΩ​ℳ|f′′​(u)|​ℳ2C_{f}:=\frac{1}{2}C_{\Omega}\sup_{|u|\leq C_{\Omega}\mathcal{M}}|f^{\prime\prime}(u)|\mathcal{M}^{2}.

Lemma 3.3.

Assume the regularity condition (2.1) holds, the truncation error RtjR_{t}^{j} has the properties:

‖Rt1‖≤ℳ2​τ1,‖Rtj‖≤32​ℳ​τj​τ,2≤j≤N.\displaystyle\|R_{t}^{1}\|\leq\frac{\mathcal{M}}{2}\tau_{1},\quad\|R_{t}^{j}\|\leq\frac{3}{2}\mathcal{M}\tau_{j}\tau,\quad 2\leq j\leq N. (3.3)

The proofs of Lemmas 3.2 and 3.3 mainly use the Taylor expansion, and are left to Appendix 7.1 and 7.2 for brevity.

3.1 Analysis of a semi-discrete scheme

As indicated in (1.9), we first consider the boundedness of the solution to semi-discrete scheme (1.4) in this subsection, and leave the boundedness of the error ‖Un−Uhn‖L∞\|U^{n}-U_{h}^{n}\|_{L^{\infty}} in next subsection.

Let en=un−Un​(n=0,1,…,N)e^{n}=u^{n}-U^{n}\;(n=0,1,\ldots,N). Subtracting (1.4) from (1.1), one has

𝒟2​en=Δ​en+Rtn+Rfn+E1n,\displaystyle\mathcal{D}_{2}e^{n}=\Delta e^{n}+R_{t}^{n}+R_{f}^{n}+E_{1}^{n}, (3.4)

where E1n=f​(un−1)+f′​(un−1)​∇τun−f​(Un−1)−f′​(Un−1)​∇τUn.E_{1}^{n}=f(u^{n-1})+f^{\prime}(u^{n-1})\nabla_{\tau}u^{n}-f(U^{n-1})-f^{\prime}(U^{n-1})\nabla_{\tau}U^{n}.

Theorem 3.1.

Assume the conditions A1 and A2 and the regularity condition (2.1) hold, and the nonlinear function f∈C2​(ℝ)f\in C^{2}(\mathbb{R}). Then the semi-discrete system (1.4) has a unique solution UnU^{n}. Moreover, there exists an τ∗∗>0\tau^{**}>0 such that the following estimates hold for all τ≤τ∗∗\tau\leq\tau^{**}

‖en‖H1≤C1​τ32,\displaystyle\|e^{n}\|_{H^{1}}\leq C_{1}\tau^{\frac{3}{2}}, (3.5)
‖Un‖L∞≤CΩ​‖Uk‖H2≤CΩ​(ℳ+1),\displaystyle\|U^{n}\|_{L^{\infty}}\leq C_{\Omega}\|U^{k}\|_{H^{2}}\leq C_{\Omega}(\mathcal{M}+1), (3.6)
∑j=1n‖∇τej‖H2≤C2.\displaystyle\sum_{j=1}^{n}\|\nabla_{\tau}e^{j}\|_{H^{2}}\leq C_{2}. (3.7)

More precisely, in (3.5), we have ‖en‖≤C3​τ2\|e^{n}\|\leq C_{3}\tau^{2} and ‖∇en‖≤C4​τ32\|\nabla e^{n}\|\leq C_{4}\tau^{\frac{3}{2}}, where Ci​(i=1,2,3,4)C_{i}\;(i=1,2,3,4) are positive constants independent of τ\tau.

Proof. Set

τ∗∗=min⁡{1,1/(8​C5),1/C8},\displaystyle\tau^{**}=\min\{1,1/(8C_{5}),1/C_{8}\}, (3.8)

where C5,C8C_{5},C_{8} will be determined later. Noting that, at each time level, (1.4) is a linear elliptic problem, it is easy to obtain the existence and uniqueness of solution UnU^{n}. We here use the mathematical induction to prove (3.5) and (3.6), which obviously hold for the initial level n=0n=0. Assume (3.5) and (3.6) hold for 0≤n≤k−1​(k≤N)0\leq n\leq k-1\;(k\leq N). Based on the boundedness of ‖Un−1‖L∞\|U^{n-1}\|_{L^{\infty}} and ‖un−1‖L∞\|u^{n-1}\|_{L^{\infty}} for 1≤n≤k1\leq n\leq k, we have

‖E1n‖\displaystyle\|E_{1}^{n}\| =‖f​(un−1)+f′​(un−1)​∇τun−(f​(Un−1)+f′​(Un−1)​∇τUn)‖\displaystyle=\|f(u^{n-1})+f^{\prime}(u^{n-1})\nabla_{\tau}u^{n}-(f(U^{n-1})+f^{\prime}(U^{n-1})\nabla_{\tau}U^{n})\|
≤‖f​(un−1)−f​(Un−1)‖+‖(f′​(un−1)−f′​(Un−1))​un‖+‖f′​(Un−1)​(un−Un)‖\displaystyle\leq\|f(u^{n-1})-f(U^{n-1})\|+\|(f^{\prime}(u^{n-1})-f^{\prime}(U^{n-1}))u^{n}\|+\|f^{\prime}(U^{n-1})(u^{n}-U^{n})\|
+‖(f′​(un−1)−f′​(Un−1))​un−1‖+‖f′​(Un−1)​(un−1−Un−1)‖\displaystyle\quad+\|(f^{\prime}(u^{n-1})-f^{\prime}(U^{n-1}))u^{n-1}\|+\|f^{\prime}(U^{n-1})(u^{n-1}-U^{n-1})\|
≤C5​(‖en−1‖+‖en‖),\displaystyle\leq C_{5}(\|e^{n-1}\|+\|e^{n}\|), (3.9)

where C5=2​sup|v|≤CΩ​(ℳ+1)|f′​(v)|+2​CΩ​ℳ​sup|v|≤CΩ​(ℳ+1)|f′′​(v)|.C_{5}=2\sup_{\lvert v\rvert\leq C_{\Omega}(\mathcal{M}+1)}\lvert f^{\prime}(v)\rvert+2C_{\Omega}\mathcal{M}\sup_{\lvert v\rvert\leq C_{\Omega}(\mathcal{M}+1)}\lvert f^{\prime\prime}(v)\rvert.

We now prove that (3.5) and (3.6) hold at n=kn=k. Set n=jn=j in (3.4). Multiplying θl−j(l)\theta_{l-j}^{(l)} to both sides of (3.4), and summing the resulting from 1 to ll, we have

∇τel=∑j=1lθl−j(l)​(Δ​ej+E1j)+∑j=1lθl−j(l)​(Rtj+Rfj),\displaystyle\nabla_{\tau}e^{l}=\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\Delta e^{j}+E_{1}^{j})+\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j}), (3.10)

where the property of DOC kernels (2.5) is used. Then taking the inner product with ele^{l} on both sides of (3.10), and summing the resulting equality from 1 to kk, one has

∑l=1k(∇τel,el)=∑l=1k∑j=1lθl−j(l)​(Δ​ej+E1j,el)+∑l=1k∑j=1lθl−j(l)​(Rtj+Rfj,el).\begin{split}\sum_{l=1}^{k}(\nabla_{\tau}e^{l},e^{l})&=\sum_{l=1}^{k}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\Delta e^{j}+E_{1}^{j},e^{l})+\sum_{l=1}^{k}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j},e^{l}).\\ \end{split} (3.11)

Applying (2.8), integration by parts and the inequality 2​(a−b)​a≥a2−b22(a-b)a\geq a^{2}-b^{2} to (3.11), we have

‖ek‖2−‖e0‖2\displaystyle\|e^{k}\|^{2}-\|e^{0}\|^{2} ≤2​∑l=1k∑j=1lθl−j(l)​(E1j,el)+2​∑l=1k∑j=1lθl−j(l)​(Rtj+Rfj,el)\displaystyle\leq 2\sum_{l=1}^{k}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(E_{1}^{j},e^{l})+2\sum_{l=1}^{k}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j},e^{l})
≤2​∑l=1k‖el‖​∑j=1lθl−j(l)​‖E1j‖+2​∑l=1k‖el‖​‖∑j=1lθl−j(l)​(Rtj+Rfj)‖,\displaystyle\leq 2\sum_{l=1}^{k}\|e^{l}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}\|E_{1}^{j}\|+2\sum_{l=1}^{k}\|e^{l}\|\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|,

which together with the inequality (3.9) and ‖e0‖=0\|e^{0}\|=0 produces

‖ek‖2≤2​C5​∑l=1k‖el‖​∑j=1lθl−j(l)​(‖ej‖+‖ej−1‖)+2​∑l=1k‖el‖​‖∑j=1lθl−j(l)​(Rtj+Rfj)‖.\|e^{k}\|^{2}\leq 2C_{5}\sum_{l=1}^{k}\|e^{l}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|e^{j}\|+\|e^{j-1}\|)+2\sum_{l=1}^{k}\|e^{l}\|\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|. (3.12)

Choosing an integer k∗​(0≤k∗≤k)k^{*}(0\leq k^{*}\leq k) such that ‖ek∗‖=max0≤i≤k⁡‖ei‖\|e^{k^{*}}\|=\max_{0\leq i\leq k}\|e^{i}\|, then the inequality (3.12) yields

‖ek‖​‖ek∗‖≤‖ek∗‖2\displaystyle\|e^{k}\|\|e^{k^{*}}\|\leq\|e^{k^{*}}\|^{2} ≤4​C5​‖ek∗‖​∑l=1k∗τl​‖el‖+2​‖ek∗‖​∑l=1k∗‖∑j=1lθl−j(l)​(Rtj+Rfj)‖\displaystyle\leq 4C_{5}\|e^{k^{*}}\|\sum_{l=1}^{k^{*}}\tau_{l}\|e^{l}\|+2\|e^{k^{*}}\|\sum_{l=1}^{k^{*}}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|
≤4​C5​‖ek∗‖​∑l=1kτl​‖el‖+2​‖ek∗‖​∑l=1k‖∑j=1lθl−j(l)​(Rtj+Rfj)‖.\displaystyle\leq 4C_{5}\|e^{k^{*}}\|\sum_{l=1}^{k}\tau_{l}\|e^{l}\|+2\|e^{k^{*}}\|\sum_{l=1}^{k}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|. (3.13)

where (2.10) is used. Thus, we arrive at

‖ek‖≤4​C5​∑l=1kτl​‖el‖+2​∑l=1k‖∑j=1lθl−j(l)​(Rtj+Rfj)‖.\begin{split}\|e^{k}\|&\leq 4C_{5}\sum_{l=1}^{k}\tau_{l}\|e^{l}\|+2\sum_{l=1}^{k}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|.\end{split} (3.14)

It follows from (3.8) that

‖ek‖≤8​C5​∑l=1k−1τl​‖el‖+4​∑l=1k‖∑j=1lθl−j(l)​(Rtj+Rfj)‖.\begin{split}\|e^{k}\|&\leq 8C_{5}\sum_{l=1}^{k-1}\tau_{l}\|e^{l}\|+4\sum_{l=1}^{k}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|.\end{split} (3.15)

According to Proposition 2.1 and Lemmas 2.2, 3.1, 3.2 and 3.3, it holds

‖ek‖\displaystyle\|e^{k}\| ≤4​exp⁡(8​C5​tk−1)​(∑l=1k‖∑j=1lθl−j(l)​(Rtj+Rfj)‖)\displaystyle\leq 4\exp(8C_{5}t_{k-1})\big{(}\sum_{l=1}^{k}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j})\|\big{)}
≤4​exp⁡(8​C5​tk−1)​(∑j=1kpk−j(k)​‖Rfj‖+∑j=2kpk−j(k)​‖Rtj‖+pk−1(k)​‖Rt1‖)\displaystyle\leq 4\exp(8C_{5}t_{k-1})\Big{(}\sum_{j=1}^{k}p^{(k)}_{k-j}\|R_{f}^{j}\|+\sum_{j=2}^{k}p^{(k)}_{k-j}\|R_{t}^{j}\|+p^{(k)}_{k-1}\|R_{t}^{1}\|\Big{)}
≤4​ℳ​exp⁡(8​C5​T)​(Cf​T+32​ℳ​T+ℳ)​τ2:=C3​τ2.\displaystyle\leq 4\mathcal{M}\exp(8C_{5}T)\Big{(}C_{f}T+\frac{3}{2}\mathcal{M}T+\mathcal{M}\Big{)}\tau^{2}:=C_{3}\tau^{2}. (3.16)

Similarly, set n=ln=l in (3.4) and taking inner product with ∇τel\nabla_{\tau}e^{l} on both sides of (3.4), one has

(𝒟2​el,∇τel)\displaystyle(\mathcal{D}_{2}e^{l},\nabla_{\tau}e^{l}) =(Δ​el,∇τel)+(Rtl+Rfl+E1l,∇τel)\displaystyle=(\Delta e^{l},\nabla_{\tau}e^{l})+(R_{t}^{l}+R_{f}^{l}+E_{1}^{l},\nabla_{\tau}e^{l})
=−(∇el,∇τ∇⁡el)+(Rtl+Rfl+E1l,∇τel).\displaystyle=-(\nabla e^{l},\nabla_{\tau}\nabla e^{l})+(R_{t}^{l}+R_{f}^{l}+E_{1}^{l},\nabla_{\tau}e^{l}). (3.17)

Summing ll from 1 to kk on (3.17), using (2.8) and the identity 2​a​(a−b)=a2−b2+(a−b)22a(a-b)=a^{2}-b^{2}+(a-b)^{2}, we have

δ20​∑l=1k‖∇τel‖τl+‖∇ek‖2−‖∇e0‖2+∑l=1k‖∇τ∇⁡el‖2≤2​∑l=1k(Rtl+Rfl+E1l,∇τel).\displaystyle\frac{\delta}{20}\sum_{l=1}^{k}\frac{\|\nabla_{\tau}e^{l}\|}{\tau_{l}}+\|\nabla e^{k}\|^{2}-\|\nabla e^{0}\|^{2}+\sum_{l=1}^{k}\|\nabla_{\tau}\nabla e^{l}\|^{2}\leq 2\sum_{l=1}^{k}(R_{t}^{l}+R_{f}^{l}+E_{1}^{l},\nabla_{\tau}e^{l}). (3.18)

It follows from the Young’s inequality that

2​∑l=1k(Rtl+Rfl+E1l,∇τel)≤∑l=1k(δ20​‖∇τel‖2τl+20​τlδ​‖Rtl+Rfl+E1l‖2).\displaystyle 2\sum_{l=1}^{k}(R_{t}^{l}+R_{f}^{l}+E_{1}^{l},\nabla_{\tau}e^{l})\leq\sum_{l=1}^{k}\Big{(}\frac{\delta}{20}\frac{\|\nabla_{\tau}e^{l}\|^{2}}{\tau_{l}}+\frac{20\tau_{l}}{\delta}\|R_{t}^{l}+R_{f}^{l}+E_{1}^{l}\|^{2}\Big{)}. (3.19)

Applying (3.19) and ∇e0=0\nabla e^{0}=0 to (3.18), we arrive at

‖∇ek‖2+∑l=1k‖∇τ∇⁡el‖2\displaystyle\|\nabla e^{k}\|^{2}+\sum_{l=1}^{k}\|\nabla_{\tau}\nabla e^{l}\|^{2} ≤20δ​∑l=1kτl​‖Rtl+Rfl+E1l‖2\displaystyle\leq\frac{20}{\delta}\sum_{l=1}^{k}\tau_{l}\|R_{t}^{l}+R_{f}^{l}+E_{1}^{l}\|^{2}
≤60δ​(τ1​‖Rt1‖2+∑l=2kτl​‖Rtl‖2+∑l=1kτl​(‖Rfl‖2+‖E1l‖2)).\displaystyle\leq\frac{60}{\delta}\Big{(}\tau_{1}\|R_{t}^{1}\|^{2}+\sum_{l=2}^{k}\tau_{l}\|R_{t}^{l}\|^{2}+\sum_{l=1}^{k}\tau_{l}(\|R_{f}^{l}\|^{2}+\|E_{1}^{l}\|^{2})\Big{)}. (3.20)

Applying the estimates (3.9) and (3.16), Lemmas 3.2 and 3.3 to the inequality (3.20), one yields

‖∇ek‖2+∑l=1k‖∇τ∇⁡el‖2\displaystyle\|\nabla e^{k}\|^{2}+\sum_{l=1}^{k}\|\nabla_{\tau}\nabla e^{l}\|^{2} ≤60δ​τ3​(ℳ24+94​ℳ2​T​τ+T​Cf2​τ+2​T​C52​C32​τ)\displaystyle\leq\frac{60}{\delta}\tau^{3}\Big{(}\frac{\mathcal{M}^{2}}{4}+\frac{9}{4}\mathcal{M}^{2}T\tau+TC_{f}^{2}\tau+2TC_{5}^{2}C_{3}^{2}\tau\Big{)}
≤60δ​τ3​(ℳ24+94​ℳ2​T+T​Cf2+2​T​C52​C32):=C42​τ3,\displaystyle\leq\frac{60}{\delta}\tau^{3}\Big{(}\frac{\mathcal{M}^{2}}{4}+\frac{9}{4}\mathcal{M}^{2}T+TC_{f}^{2}+2TC_{5}^{2}C_{3}^{2}\Big{)}:=C_{4}^{2}\tau^{3}, (3.21)

where τ≤1\tau\leq 1 in (3.8) is used. Thus, the estimates (3.1) and (3.16) yield the following H1H^{1} norm estimate

‖ek‖H1≤C32+C42​τ32:=C1​τ32.\displaystyle\|e^{k}\|_{H^{1}}\leq\sqrt{C_{3}^{2}+C_{4}^{2}}\tau^{\frac{3}{2}}:=C_{1}\tau^{\frac{3}{2}}. (3.22)

In the remainder, we will prove ‖Uk‖L∞≤CΩ​(ℳ+1)\|U^{k}\|_{L^{\infty}}\leq C_{\Omega}(\mathcal{M}+1). To do so, we need to estimate ‖Δ​ek‖\|\Delta e^{k}\| due to the facts that |ek|2≤C~​‖Δ​ek‖|e^{k}|_{2}\leq\tilde{C}\|\Delta e^{k}\| (here |⋅|2|\cdot|_{2} denote the semi-norm of H2H^{2}-norm) and

‖Uk‖L∞≤‖uk‖L∞+‖ek‖L∞≤CΩ​ℳ+CΩ​‖ek‖H2,\displaystyle\|U^{k}\|_{L^{\infty}}\leq\|u^{k}\|_{L^{\infty}}+\|e^{k}\|_{L^{\infty}}\leq C_{\Omega}\mathcal{M}+C_{\Omega}\|e^{k}\|_{H^{2}}, (3.23)

where the embedding theorem is used in the last inequality. We now consider the estimate of ‖Δ​ek‖\|\Delta e^{k}\| by taking inner product with −∇τΔ​el-\nabla_{\tau}\Delta e^{l} on both sides of (3.4) (set n=ln=l), and have

(𝒟2​∇el,∇τ∇⁡el)+(Δ​el,∇τΔ​el)=(Rtl+Rfl+E1l,−∇τΔ​el).\displaystyle(\mathcal{D}_{2}\nabla e^{l},\nabla_{\tau}\nabla e^{l})+(\Delta e^{l},\nabla_{\tau}\Delta e^{l})=(R_{t}^{l}+R_{f}^{l}+E_{1}^{l},-\nabla_{\tau}\Delta e^{l}). (3.24)

Summing ll from 1 to kk on (3.24), using 2​(a−b)​a=a2−b2+(a−b)22(a-b)a=a^{2}-b^{2}+(a-b)^{2}, the positiveness (2.8) and Δ​e0=0\Delta e^{0}=0, we have

∑l=1k‖∇τΔ​el‖2+‖Δ​ek‖2≤2​∑l=1k‖Rtl+Rfl+E1l‖​‖∇τΔ​el‖,{\sum_{l=1}^{k}\|\nabla_{\tau}\Delta e^{l}\|^{2}+}\|\Delta e^{k}\|^{2}\leq 2\sum_{l=1}^{k}\|R_{t}^{l}+R_{f}^{l}+E_{1}^{l}\|\|\nabla_{\tau}\Delta e^{l}\|, (3.25)

Applying the Young’s inequality to (3.25), one has

‖Δ​ek‖2\displaystyle\|\Delta e^{k}\|^{2} ≤∑l=1k‖Rtl+Rfl+E1l‖2.\displaystyle\leq\sum_{l=1}^{k}\|R_{t}^{l}+R_{f}^{l}+E_{1}^{l}\|^{2}. (3.26)

According to (3.9) and (3.16) and Lemmas 3.2 and 3.3, one has

∑l=1k‖Rtl+Rfl+E1l‖2\displaystyle\sum_{l=1}^{k}\|R_{t}^{l}+R_{f}^{l}+E_{1}^{l}\|^{2} ≤3​(‖Rt1‖2+∑l=2k‖Rtl‖2+∑l=1k(‖Rfl‖2+‖E1l‖2))\displaystyle\leq 3\big{(}\|R_{t}^{1}\|^{2}+\sum_{l=2}^{k}\|R_{t}^{l}\|^{2}+\sum_{l=1}^{k}(\|R_{f}^{l}\|^{2}+\|E_{1}^{l}\|^{2})\big{)}
≤(34​ℳ2+274​ℳ2​tk​τ+3​Cf2​tk​τ+3​C52​C32​k​τ2)​τ2\displaystyle\leq\big{(}\frac{3}{4}\mathcal{M}^{2}+\frac{27}{4}\mathcal{M}^{2}t_{k}\tau+3C_{f}^{2}t_{k}\tau+3C_{5}^{2}C_{3}^{2}k\tau^{2}\big{)}\tau^{2}
≤(34​ℳ2+274​ℳ​T+3​Cf2​T+3​C52​C32​C^)​τ2:=C72​τ2,\displaystyle\leq\big{(}\frac{3}{4}\mathcal{M}^{2}+\frac{27}{4}\mathcal{M}T+3C_{f}^{2}T+3C_{5}^{2}C_{3}^{2}\hat{C}\big{)}\tau^{2}:=C_{7}^{2}\tau^{2}, (3.27)

where one uses the maximum time-step assumption A2 and (3.8) in the last inequality. Inserting (3.27) into (3.26), we derive

‖Δ​ek‖≤C7​τ.\displaystyle\|\Delta e^{k}\|\leq C_{7}\tau. (3.28)

Thus, from the estimates (3.28) and (3.22), the condition (3.8) and the facts that |ek|2≤C~​‖Δ​ek‖|e^{k}|_{2}\leq\tilde{C}\|\Delta e^{k}\|, we arrive at

‖ek‖H2≤C8​τ,\displaystyle\|e^{k}\|_{H^{2}}\leq C_{8}\tau, (3.29)

where C8=C12+C~2​C72C_{8}=\sqrt{C_{1}^{2}+\tilde{C}^{2}C_{7}^{2}}. Thus, combining (3.29), (3.23) and (3.8), one has

‖Uk‖L∞≤‖uk‖L∞+‖ek‖L∞≤CΩ​(ℳ+C8​τ)≤CΩ​(ℳ+1).\|U^{k}\|_{L^{\infty}}\leq\|u^{k}\|_{L^{\infty}}+\|e^{k}\|_{L^{\infty}}\leq C_{\Omega}\Big{(}\mathcal{M}+C_{8}\tau\Big{)}\leq C_{\Omega}(\mathcal{M}+1). (3.30)

Therefore, (3.5) and (3.6) hold for n=kn=k, i.e., the estimates (3.5) and (3.6) are proved.

The last claim (3.7) can be proved based on the result (3.30). With the help of Cauchy inequality, from (3.16) and (3.1) and the fact |∇τel|2≤C~​‖∇τΔ​el‖|\nabla_{\tau}e^{l}|_{2}\leq\tilde{C}\|\nabla_{\tau}\Delta e^{l}\|, we have

(∑l=1n‖∇τel‖H2)2\displaystyle\big{(}\sum_{l=1}^{n}\|\nabla_{\tau}e^{l}\|_{H^{2}}\big{)}^{2} ≤n​∑l=1n‖∇τel‖H22≤n​∑l=1n‖∇τel‖2+n​∑l=1n‖∇τ∇⁡el‖2+n​C~2​∑l=1n‖∇τΔ​el‖2\displaystyle\leq n\sum_{l=1}^{n}\|\nabla_{\tau}e^{l}\|_{H^{2}}^{2}\leq n\sum_{l=1}^{n}\|\nabla_{\tau}e^{l}\|^{2}+n\sum_{l=1}^{n}\|\nabla_{\tau}\nabla e^{l}\|^{2}+n\tilde{C}^{2}\sum_{l=1}^{n}{\|\nabla_{\tau}\Delta e^{l}\|^{2}}
≤4​C32​N2​τ4+N​C42​τ3+N​C~2​∑l=1n‖∇τΔ​el‖2.\displaystyle\leq 4C_{3}^{2}N^{2}\tau^{4}+NC_{4}^{2}\tau^{3}+N\tilde{C}^{2}\sum_{l=1}^{n}{\|\nabla_{\tau}\Delta e^{l}\|^{2}}\;. (3.31)

We now estimate ∑l=1n‖∇τΔ​el‖2\sum_{l=1}^{n}\|\nabla_{\tau}\Delta e^{l}\|^{2}. Applying the Young’s inequality 2​a​b≤8​a2+12​b22ab\leq 8a^{2}+\frac{1}{2}b^{2} and inequality (3.27) to (3.25), one has

∑l=1k‖∇τΔ​ek‖2≤16​∑l=1k‖Rtl+Rfl+E1l‖2≤C72​τ2.\displaystyle\sum_{l=1}^{k}\|\nabla_{\tau}\Delta e^{k}\|^{2}\leq 16\sum_{l=1}^{k}\|R_{t}^{l}+R_{f}^{l}+E_{1}^{l}\|^{2}\leq C_{7}^{2}\tau^{2}. (3.32)

Inserting (3.32) into (3.1), then it follows from the condition A2 and (3.8) that

(∑l=1n‖∇τel‖H2)2≤4​C32​C^2+C42​C^+C72​C~2​C^:=C22.\displaystyle\big{(}\sum_{l=1}^{n}\|\nabla_{\tau}e^{l}\|_{H^{2}}\big{)}^{2}\leq 4C_{3}^{2}\hat{C}^{2}+C_{4}^{2}\hat{C}+C_{7}^{2}\tilde{C}^{2}\hat{C}:=C_{2}^{2}.

The proof is completed.  

3.2 Analysis of the fully discrete scheme

We now consider the boundedness of the fully discrete solution UhnU_{h}^{n}, which plays the key role of the proof of Theorem 4.1. Define the Ritz projection operator Rh:H01​(Ω)→Vh⊆H01​(Ω)R_{h}:H^{1}_{0}(\Omega)\rightarrow V_{h}\subseteq H^{1}_{0}(\Omega) by

(∇(v−Rh​v),∇ω)=0,∀ω∈Vh.\displaystyle(\nabla(v-R_{h}v),\nabla\omega)=0,\quad\forall\omega\in V_{h}. (3.33)

The Ritz projection RhR_{h} has the following estimate (for example, see [19, Lemma 1.1])

‖v−Rh​v‖+h​‖∇(v−Rh​v)‖≤CΩ​hs​‖v‖Hs,∀v∈Hs​(Ω)∩H01​(Ω),1≤s≤r+1.\displaystyle\|v-R_{h}v\|+h\|\nabla(v-R_{h}v)\|\leq C_{\Omega}h^{s}\|v\|_{H^{s}},\quad\forall v\in H^{s}(\Omega)\cap H^{1}_{0}(\Omega),1\leq s\leq r+1. (3.34)

Thanks to the boundedness of the semi-discrete solutions and (1.9), we only need to estimate ‖Un−Uhn‖L∞\|U^{n}-U_{h}^{n}\|_{L^{\infty}}, which can be split by the Ritz projection into the following two parts

Un−Uhn=Un−Rh​Un+Rh​Un−Uhn:=ηn+ξn,n=0,1,…,N.\displaystyle U^{n}-U_{h}^{n}=U^{n}-R_{h}U^{n}+R_{h}U^{n}-U_{h}^{n}:=\eta^{n}+\xi^{n},\quad n=0,1,\ldots,N. (3.35)

For the projection error ηn\eta^{n}, it follows from (3.34) that

‖ηn‖≤CΩ​hs​‖Un‖Hs,0≤s≤r+1.\displaystyle\|\eta^{n}\|\leq C_{\Omega}h^{s}\|U^{n}\|_{H^{s}},\quad 0\leq s\leq r+1. (3.36)

Thus, in remainder of this subsection, the focus is on the estimate of the second term ξn\xi^{n}. To do so, we now consider the weak form of the semi-discrete equation (1.4) given as

(𝒟2​Un,vh)=−(∇Un,∇vh)+(f​(Un−1)+f′​(Un−1)​∇τUn,vh),∀vh∈H01​(Ω).\displaystyle(\mathcal{D}_{2}U^{n},v_{h})=-(\nabla U^{n},\nabla v_{h})+(f(U^{n-1})+f^{\prime}(U^{n-1})\nabla_{\tau}U^{n},v_{h}),\quad\forall v_{h}\in H^{1}_{0}(\Omega). (3.37)

Subtracting (1.8) from (3.37), one can use the orthogonality (3.33) to obtain

(𝒟2​ξn,vh)=−(∇ξn,∇vh)−(𝒟2​ηn,vh)+(E2n,vh),∀vh∈Vh,\displaystyle(\mathcal{D}_{2}\xi^{n},v_{h})=-(\nabla\xi^{n},\nabla v_{h})-(\mathcal{D}_{2}\eta^{n},v_{h})+(E_{2}^{n},v_{h}),\quad\forall v_{h}\in V_{h}\,, (3.38)

where

E2n=f​(Un−1)+f′​(Un−1)​∇τUn−(f​(Uhn−1)+f′​(Uhn−1)​∇τUhn).\displaystyle E_{2}^{n}=f(U^{n-1})+f^{\prime}(U^{n-1})\nabla_{\tau}U^{n}-\Big{(}f(U_{h}^{n-1})+f^{\prime}(U_{h}^{n-1})\nabla_{\tau}U_{h}^{n}\Big{)}. (3.39)

Let n=jn=j in (3.38). Then, multiplying θl−j(l)\theta_{l-j}^{(l)} by (3.38), summing jj from 1 to ll, and using the property (2.5), one has

(∇τξl,vh)=−(∑j=1lθl−j(l)​∇ξj,∇vh)−(∇τηl,vh)+(∑j=1lθl−j(l)​E2j,vh).\displaystyle(\nabla_{\tau}\xi^{l},v_{h})=-(\sum_{j=1}^{l}\theta_{l-j}^{(l)}\nabla\xi^{j},\nabla v_{h})-(\nabla_{\tau}\eta^{l},v_{h})+(\sum_{j=1}^{l}\theta_{l-j}^{(l)}E_{2}^{j},v_{h}). (3.40)
Theorem 3.2.

Assume the semi-discrete scheme (1.4) has a unique solution Un​(n=1,…,N)U^{n}\;(n=1,\dots,N). Then the finite element system defined in (1.8) has a unique solution Uhn​(n=1,…,N)U_{h}^{n}\;(n=1,\dots,N), and there exist τ∗⁣∗∗=min⁡{τ∗∗,1/(8​C11)}\tau^{***}=\min\{\tau^{**},1/(8C_{11})\} and h∗∗=(C10​CΩ)−24−dh^{**}=(C_{10}C_{\Omega})^{-\frac{2}{4-d}} such that when τ<τ∗⁣∗∗\tau<\tau^{***} and h<h∗∗h<h^{**}, it holds

‖ξn‖≤C10​h2,\displaystyle\|\xi^{n}\|\leq C_{10}h^{2}, (3.41)
‖Uhn‖L∞≤Q,\displaystyle\|U_{h}^{n}\|_{L^{\infty}}\leq Q, (3.42)

where Q=C¯​(ℳ+1)+1Q=\bar{C}(\mathcal{M}+1)+1, C10,C11,CΩC_{10},C_{11},C_{\Omega} are constants independent of τ\tau.

Proof. It is obvious that the solution UhnU_{h}^{n} of (1.8) uniquely exists since the coefficients matrice of (1.8) is diagonally dominant. Similar to the proof of Theorem 3.1, the mathematical induction is also used to prove (3.41) and (3.42). At the beginning, it is easy to check ξ0+η0=U0−Uh0=0\xi^{0}+\eta^{0}=U^{0}-U^{0}_{h}=0 by (3.39), and the inequality (3.41) also holds for n=0n=0 according to (3.34). Assume (3.41) holds for all n≤k−1n\leq k-1. It is known that ‖Rh​v‖L∞≤C¯​‖v‖H2\|R_{h}v\|_{L^{\infty}}\leq\bar{C}\|v\|_{H^{2}} for any v∈H2​(Ω)v\in H^{2}(\Omega). Thus, from Theorem 3.1, the projection Rh​UnR_{h}U^{n} is bounded in the sense of L∞L^{\infty}-norm, namely

‖Rh​Un‖L∞≤C¯​(ℳ+1).\displaystyle\|R_{h}U^{n}\|_{L^{\infty}}\leq\bar{C}(\mathcal{M}+1).

Together with (3.36), it holds for n≤k−1n\leq k-1 and h≤h∗∗=(C10​CΩ)−24−dh\leq h^{**}=(C_{10}C_{\Omega})^{-\frac{2}{4-d}} that

‖Uhn‖L∞≤‖Rh​Un‖L∞+‖ξn‖L∞≤‖Rh​Un‖L∞+CΩ​h−d2​‖ξn‖≤‖Rh​Un‖L∞+CΩ​C10​h−d2​h2≤‖Rh​Un‖L∞+1≤Q.\begin{split}\|U_{h}^{n}\|_{L^{\infty}}&\leq\;\|R_{h}U^{n}\|_{L^{\infty}}+\|\xi^{n}\|_{L^{\infty}}\;\leq\;\|R_{h}U^{n}\|_{L^{\infty}}+C_{\Omega}h^{-\frac{d}{2}}\|\xi^{n}\|\\ &\leq\;\|R_{h}U^{n}\|_{L^{\infty}}+C_{\Omega}C_{10}h^{-\frac{d}{2}}h^{2}\;\leq\;\|R_{h}U^{n}\|_{L^{\infty}}+1\;\leq Q.\end{split} (3.43)

Due to the boundedness of ‖Uk−1‖L∞||U^{k-1}||_{L^{\infty}} and ‖Uhk−1‖L∞||U_{h}^{k-1}||_{L^{\infty}}, one has

‖E2k‖\displaystyle\|E_{2}^{k}\| ≤‖f​(Uk−1)+f′​(Uk−1)​∇τUk−(f​(Uhk−1)+f′​(Uhk−1)​∇τUhk)‖\displaystyle\leq\|f(U^{k-1})+f^{\prime}(U^{k-1})\nabla_{\tau}U^{k}-(f(U_{h}^{k-1})+f^{\prime}(U_{h}^{k-1})\nabla_{\tau}U_{h}^{k})\|
≤‖f​(Uk−1)−f​(Uhk−1)‖+‖(f′​(Uk−1)−f′​(Uhk−1))​Uk‖+‖f′​(Uhk−1)​(Uk−Uhk)‖\displaystyle\leq\|f(U^{k-1})-f(U_{h}^{k-1})\|+\|(f^{\prime}(U^{k-1})-f^{\prime}(U_{h}^{k-1}))U^{k}\|+\|f^{\prime}(U_{h}^{k-1})(U^{k}-U_{h}^{k})\|
+‖(f′​(Uk−1)−f′​(Uhk−1))​Uk−1‖+‖f′​(Uhk−1)​(Uk−1−Uhk−1)‖\displaystyle\quad+\|(f^{\prime}(U^{k-1})-f^{\prime}(U_{h}^{k-1}))U^{k-1}\|+\|f^{\prime}(U_{h}^{k-1})(U^{k-1}-U_{h}^{k-1})\|
≤C11​(‖Uk−1−Uhk−1‖+‖Uk−Uhk‖)\displaystyle\leq C_{11}(\|U^{k-1}-U_{h}^{k-1}\|+\|U^{k}-U_{h}^{k}\|)
≤C11​(‖ξk−1‖+‖ξk‖+‖ηk−1‖+‖ηk‖)\displaystyle\leq C_{11}(\|\xi^{k-1}\|+\|\xi^{k}\|+\|\eta^{k-1}\|+\|\eta^{k}\|)
≤C11​(‖ξk−1‖+‖ξk‖+2​CΩ​(ℳ+1)​h2),\displaystyle\leq C_{11}\Big{(}\|\xi^{k-1}\|+\|\xi^{k}\|+2C_{\Omega}(\mathcal{M}+1)h^{2}\Big{)}, (3.44)

where one uses (3.36) in the last inequality above, and

C11:=3​sup|v|≤max⁡(CΩ​(ℳ+1),Q)|f′​(v)|+2​CΩ​(ℳ+1)​sup|v|≤max⁡(CΩ​(ℳ+1),Q)|f′′​(v)|.C_{11}:=3\sup_{\lvert v\rvert\leq\max{(C_{\Omega}(\mathcal{M}+1),Q)}}\lvert f^{\prime}(v)\rvert+2C_{\Omega}(\mathcal{M}+1)\sup_{\lvert v\rvert\leq\max{(C_{\Omega}(\mathcal{M}+1),Q)}}\lvert f^{\prime\prime}(v)\rvert.

Taking vh=ξlv_{h}=\xi^{l} in (3.40) and summing ll from 11 to kk, one has

∑l=1k(∇τξl,ξl)\displaystyle\sum_{l=1}^{k}(\nabla_{\tau}\xi^{l},\xi^{l}) =−∑l=1k(∑j=1lθl−j(l)​∇ξj,∇ξl)−∑l=1k(∇τηj,ξl)+∑l=1k(∑j=1lθl−j(l)​E2j,ξl)\displaystyle=-\sum_{l=1}^{k}(\sum_{j=1}^{l}\theta_{l-j}^{(l)}\nabla\xi^{j},\nabla\xi^{l})-\sum_{l=1}^{k}(\nabla_{\tau}\eta^{j},\xi^{l})+\sum_{l=1}^{k}(\sum_{j=1}^{l}\theta_{l-j}^{(l)}E_{2}^{j},\xi^{l})
≤∑l=1k‖ξl‖​‖∇τηl‖+∑l=1k‖ξl‖​∑j=1lθl−j(l)​‖E2j‖,\displaystyle\leq\sum_{l=1}^{k}\|\xi^{l}\|\|\nabla_{\tau}\eta^{l}\|+\sum_{l=1}^{k}\|\xi^{l}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}\|E_{2}^{j}\|, (3.45)

where the last inequality uses the positive definiteness of (2.8). Inserting (3.44) into (3.45), one has

‖ξk‖2≤‖ξ0‖2+2​∑l=1k‖ξl‖​‖∇τηl‖+2​C11​∑l=1k‖ξl‖​∑j=1lθl−j(l)​(‖ξj−1‖+‖ξj‖+2​CΩ​(ℳ+1)​h2).\displaystyle\|\xi^{k}\|^{2}\leq\|\xi^{0}\|^{2}+2\sum_{l=1}^{k}\|\xi^{l}\|\|\nabla_{\tau}\eta^{l}\|+2C_{11}\sum_{l=1}^{k}\|\xi^{l}\|\sum_{j=1}^{l}\theta_{l-j}^{(l)}\Big{(}\|\xi^{j-1}\|+\|\xi^{j}\|+2C_{\Omega}(\mathcal{M}+1)h^{2}\Big{)}.

Choosing k∗​(0≤k∗≤k)k^{*}(0\leq k^{*}\leq k) such that ‖ξk∗‖=max0≤i≤k⁡‖ξi‖\|\xi^{k^{*}}\|=\max_{0\leq i\leq k}\|\xi^{i}\|. Then the above inequality combining with (2.10) yield

‖ξk∗‖2\displaystyle\|\xi^{k^{*}}\|^{2} ≤‖ξ0‖​‖ξk∗‖+2​‖ξk∗‖​∑l=1k∗‖∇τηl‖+4​C11​‖ξk∗‖​(CΩ​(ℳ+1)​T​h2+∑l=1k∗τl​‖ξl‖).\displaystyle\leq\|\xi^{0}\|\|\xi^{k^{*}}\|+2\|\xi^{k^{*}}\|\sum_{l=1}^{k^{*}}\|\nabla_{\tau}\eta^{l}\|+4C_{11}\|\xi^{k^{*}}\|\Big{(}C_{\Omega}(\mathcal{M}+1)Th^{2}+\sum_{l=1}^{k^{*}}\tau_{l}\|\xi^{l}\|\Big{)}.

Thus, one further has

‖ξk‖≤‖ξ0‖+2​∑l=1k‖∇τηl‖+4​C11​(CΩ​(ℳ+1)​T​h2+∑l=1kτl​‖ξl‖).\displaystyle\|\xi^{k}\|\leq\|\xi^{0}\|+2\sum_{l=1}^{k}\|\nabla_{\tau}\eta^{l}\|+4C_{11}\Big{(}C_{\Omega}(\mathcal{M}+1)Th^{2}+\sum_{l=1}^{k}\tau_{l}\|\xi^{l}\|\Big{)}.

According to (3.36) and (3.7), we find

‖ξk‖\displaystyle\|\xi^{k}\| ≤CΩ​h2​‖u0‖H2+2​CΩ​h2​∑l=1k‖∇τUl‖H2+4​C11​(CΩ​(ℳ+1)​T​h2+∑l=1kτl​‖ξl‖)\displaystyle\leq C_{\Omega}h^{2}\|u^{0}\|_{H^{2}}+2C_{\Omega}h^{2}\sum_{l=1}^{k}\|\nabla_{\tau}U^{l}\|_{H^{2}}+4C_{11}\Big{(}C_{\Omega}(\mathcal{M}+1)Th^{2}+\sum_{l=1}^{k}\tau_{l}\|\xi^{l}\|\Big{)}
≤(ℳ+2​∑l=1k(‖∇τul‖H2+‖∇τel‖H2))​CΩ​h2+4​C11​((ℳ+1)​T​CΩ​h2+∑l=1kτl​‖ξl‖)\displaystyle{\leq(\mathcal{M}+2\sum_{l=1}^{k}(\|\nabla_{\tau}u^{l}\|_{H^{2}}+\|\nabla_{\tau}e^{l}\|_{H^{2}}))C_{\Omega}h^{2}+4C_{11}\Big{(}(\mathcal{M}+1)TC_{\Omega}h^{2}+\sum_{l=1}^{k}\tau_{l}\|\xi^{l}\|\Big{)}} (3.46)
≤(ℳ+2​(ℳ​T+C2+4​C11​(ℳ+1)​T))​CΩ​h2+4​C11​∑l=1kτl​‖ξl‖\displaystyle\leq\Big{(}\mathcal{M}+2(\mathcal{M}T+C_{2}+4C_{11}(\mathcal{M}+1)T)\Big{)}C_{\Omega}h^{2}+4C_{11}\sum_{l=1}^{k}\tau_{l}\|\xi^{l}\|
:=C12​h2+4​C11​∑l=1kτl​‖ξl‖,\displaystyle:=C_{12}h^{2}+4C_{11}\sum_{l=1}^{k}\tau_{l}\|\xi^{l}\|,

where ‖ξ0‖=‖Rh​U0−Uh0‖=‖Rh​u0−u0‖≤CΩ​h2​‖u0‖H2\|\xi^{0}\|=\|R_{h}U^{0}-U_{h}^{0}\|=\|R_{h}u^{0}-u^{0}\|\leq C_{\Omega}h^{2}\|u^{0}\|_{H^{2}} is used. Noting τ≤τ∗⁣∗∗≤1/(8​C11)\tau\leq\tau^{***}\leq 1/(8C_{11}), we have

‖ξk‖≤2​C12​h2+8​C11​∑l=1k−1τl​‖ξl‖.\|\xi^{k}\|\leq 2C_{12}h^{2}+8C_{11}\sum_{l=1}^{k-1}\tau_{l}\|\xi^{l}\|.

Thus, from Lemma 3.1, we arrive at

‖ξk‖≤2​exp⁡(8​C11​T)​C12​h2:=C10​h2.\|\xi^{k}\|\leq 2\exp(8C_{11}T)C_{12}h^{2}:=C_{10}h^{2}.

Hence, for h≤h∗∗h\leq h^{**}, it holds

‖Uhk‖L∞\displaystyle\|U_{h}^{k}\|_{L^{\infty}} ≤‖Rh​Uk‖L∞+‖ξk‖L∞≤‖Rh​Uk‖L∞+CΩ​h−d2​‖ξk‖≤Q.\displaystyle\leq\|R_{h}U^{k}\|_{L^{\infty}}+\|\xi^{k}\|_{L^{\infty}}\leq\|R_{h}U^{k}\|_{L^{\infty}}+C_{\Omega}h^{-\frac{d}{2}}\|\xi^{k}\|\leq Q. (3.47)

Therefore, the estimates (3.41) and (3.42) hold for n=kn=k and the proof is completed.  

4 Unconditionally optimal L2L^{2}-norm error estimate

We now present the unconditionally optimal L2L^{2}-norm error estimate for fully discrete scheme (1.8).

Theorem 4.1.

Assume u​(⋅,t)∈Hr+1​(Ω)​⋂H01​(Ω)u(\cdot,t)\in H^{r+1}(\Omega)\bigcap H_{0}^{1}(\Omega) for any t≥0t\geq 0 and r≥1r\geq 1, and the conditions A1 and A2 hold. Then there exist constants τ∗\tau^{*} and h∗h^{*} such that, when τ<τ∗\tau<\tau^{*} and h<h∗h<h^{*}, the rr-degree finite element system defined in (1.8) owns a unique solution and satisfies

‖un−Uhn‖≤C0∗​(τ2+hr+1),\displaystyle\|u^{n}-U_{h}^{n}\|\leq C_{0}^{*}(\tau^{2}+h^{r+1}), (4.1)

where C0∗C_{0}^{*} is a positive constant independent of hh and τ\tau.

Proof. The error of fully discrete solution and exact solution can be split into the following two parts

‖un−Uhn‖≤‖un−Rh​un‖+‖Rh​un−Uhn‖:=‖ϑn‖+‖ζn‖.\displaystyle\|u^{n}-U_{h}^{n}\|\leq\|u^{n}-R_{h}u^{n}\|+\|R_{h}u^{n}-U_{h}^{n}\|:=\|\vartheta^{n}\|+\|\zeta^{n}\|. (4.2)

Note that the projection error ϑn\vartheta^{n} can be immediately estimated by (3.34) as follows

‖ϑn‖≤CΩ​hs​‖un‖Hs,0≤s≤r+1.\displaystyle\|\vartheta^{n}\|\leq C_{\Omega}h^{s}\|u^{n}\|_{H^{s}},\quad 0\leq s\leq r+1. (4.3)

Thus, we only need to consider ζn\zeta^{n}. Subtracting (1.8) from (1.1), we get the error equation of ζn\zeta^{n}

(𝒟2​ζn,vh)=−(∇ζn,∇vh)−(𝒟2​ϑn,vh)+(E3n,vh)+(Rtn+Rfn,vh),∀vh∈Vh,\displaystyle(\mathcal{D}_{2}\zeta^{n},v_{h})=-(\nabla\zeta^{n},\nabla v_{h})-(\mathcal{D}_{2}\vartheta^{n},v_{h})+(E_{3}^{n},v_{h})+(R_{t}^{n}+R_{f}^{n},v_{h}),\quad\forall v_{h}\in V_{h}, (4.4)

where E3n=f​(un−1)+f′​(un−1)​∇τun−(f​(Uhn−1)+f′​(Uhn−1)​∇τUhn)E_{3}^{n}=f(u^{n-1})+f^{\prime}(u^{n-1})\nabla_{\tau}u^{n}-(f(U_{h}^{n-1})+f^{\prime}(U_{h}^{n-1})\nabla_{\tau}U_{h}^{n}).

Let n=jn=j in (4.4). Multiplying (4.4) by DOC kernels θl−j(l)\theta_{l-j}^{(l)} and summing jj from 1 to ll, one has

(∇τζl,vh)=−(∑j=1lθl−j(l)​∇ζj,∇vh)−(∇τϑl,vh)+(∑j=1lθl−j(l)​E3j,vh)+(∑j=1lθl−j(l)​(Rtj+Rfj),vh),\displaystyle(\nabla_{\tau}\zeta^{l},v_{h})=-(\sum_{j=1}^{l}\theta_{l-j}^{(l)}\nabla\zeta^{j},\nabla v_{h})-(\nabla_{\tau}\vartheta^{l},v_{h})+(\sum_{j=1}^{l}\theta_{l-j}^{(l)}E_{3}^{j},v_{h})+(\sum_{j=1}^{l}\theta_{l-j}^{(l)}(R_{t}^{j}+R_{f}^{j}),v_{h}), (4.5)

where the property (2.5) is used. Taking vh=ζlv_{h}=\zeta^{l} in (4.5), summing ll from 11 to nn and using the inequality (3.34) and Corollary 2.1, one has

∑l=1n(∇τζl,ζl)=−∑l=1n(∑j=1lθl−j(l)​∇ζj,∇ζl)−∑l=1n(∇τϑl,ζl)+∑l=1n(∑j=1lθl−j(l)​(E3j+Rtj+Rfj),ζl)≤∑l=1n‖∇τϑl‖​‖ζl‖+∑l=1n∑j=1lθl−j(l)​(‖E3j‖+‖Rfj‖+‖Rtj‖)​‖ζl‖.\begin{split}\sum_{l=1}^{n}(\nabla_{\tau}\zeta^{l},\zeta^{l})&=-\sum_{l=1}^{n}(\sum_{j=1}^{l}\theta_{l-j}^{(l)}\nabla\zeta^{j},\nabla\zeta^{l})-\sum_{l=1}^{n}(\nabla_{\tau}\vartheta^{l},\zeta^{l})+\sum_{l=1}^{n}(\sum_{j=1}^{l}\theta_{l-j}^{(l)}(E_{3}^{j}+R_{t}^{j}+R_{f}^{j}),\zeta^{l})\\ &\leq\sum_{l=1}^{n}\|\nabla_{\tau}\vartheta^{l}\|\|\zeta^{l}\|+\sum_{l=1}^{n}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|E_{3}^{j}\|+\|R_{f}^{j}\|+\|R_{t}^{j}\|)\|\zeta^{l}\|.\end{split} (4.6)

Noting

‖∇τϑl‖≤CΩ​‖∇τul‖Hr+1​hr+1≤CΩ​hr+1​‖∫tl−1tl∂tu​(s)​d​s‖Hr+1≤CΩ​ℳ​τl​hr+1,\|\nabla_{\tau}\vartheta^{l}\|\leq C_{\Omega}\|\nabla_{\tau}u^{l}\|_{H^{r+1}}h^{r+1}\leq C_{\Omega}h^{r+1}\|\int_{t_{l-1}}^{t_{l}}\partial_{t}u(s)\,\mathrm{d}s\|_{H^{r+1}}\leq C_{\Omega}\mathcal{M}\tau_{l}h^{r+1},

together with the inequality 2​(a−b)​a≥a2−b22(a-b)a\geq a^{2}-b^{2}, we arrive at

‖ζn‖2\displaystyle\|\zeta^{n}\|^{2} ≤‖ζ0‖2+2​∑l=1n∑j=1lθl−j(l)​(‖E3j‖+‖Rfj‖+‖Rtj‖)​‖ζl‖+2​CΩ​ℳ​hr+1​∑l=1nτl​‖ζl‖.\displaystyle\leq\|\zeta^{0}\|^{2}+2\sum_{l=1}^{n}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|E_{3}^{j}\|+\|R_{f}^{j}\|+\|R_{t}^{j}\|)\|\zeta^{l}\|+2C_{\Omega}\mathcal{M}h^{r+1}\sum_{l=1}^{n}\tau_{l}\|\zeta^{l}\|. (4.7)

Thanks to the boundedness of ‖Uhn‖L∞\|U^{n}_{h}\|_{L^{\infty}} in (3.42), the nonlinear term E3nE_{3}^{n} can be estimated by

‖E3n‖\displaystyle\|E_{3}^{n}\| =‖f​(un−1)+f′​(un−1)​∇τun−(f​(Uhn−1)+f′​(Uhn−1)​∇τUhn)‖\displaystyle=\|f(u^{n-1})+f^{\prime}(u^{n-1})\nabla_{\tau}u^{n}-(f(U_{h}^{n-1})+f^{\prime}(U_{h}^{n-1})\nabla_{\tau}U_{h}^{n})\|
≤‖f​(un−1)−f​(Uhn−1)‖+‖(f′​(un−1)−f′​(Uhn−1))​un‖+‖f′​(Uhn−1)​(un−Uhn)‖\displaystyle\leq\|f(u^{n-1})-f(U_{h}^{n-1})\|+\|(f^{\prime}(u^{n-1})-f^{\prime}(U_{h}^{n-1}))u^{n}\|+\|f^{\prime}(U_{h}^{n-1})(u^{n}-U_{h}^{n})\|
+‖(f′​(un−1)−f′​(Uhn−1))​un−1‖+‖f′​(Uhn−1)​(un−1−Uhn−1)‖\displaystyle\quad+\|(f^{\prime}(u^{n-1})-f^{\prime}(U_{h}^{n-1}))u^{n-1}\|+\|f^{\prime}(U_{h}^{n-1})(u^{n-1}-U_{h}^{n-1})\|
≤C13​(‖un−1−Uhn−1‖+‖un−Uhn‖)\displaystyle\leq C_{13}\Big{(}\|u^{n-1}-U_{h}^{n-1}\|+\|u^{n}-U_{h}^{n}\|\Big{)}
≤C13​(‖ζn−1‖+‖ζn‖+‖ϑn−1‖+‖ϑn‖)\displaystyle\leq C_{13}\Big{(}\|\zeta^{n-1}\|+\|\zeta^{n}\|+\|\vartheta^{n-1}\|+\|\vartheta^{n}\|\Big{)}
≤C13​(‖ζn−1‖+‖ζn‖+2​CΩ​ℳ​hr+1),\displaystyle\leq C_{13}\Big{(}\|\zeta^{n-1}\|+\|\zeta^{n}\|+2C_{\Omega}\mathcal{M}h^{r+1}\Big{)}, (4.8)

where the last inequality holds by (3.34) and

C13=2​sup|v|<max⁡{CΩ​ℳ,Q}|f′​(v)|+2​sup|v|<max⁡{CΩ​ℳ,Q}|f′′​(v)|​CΩ​ℳ.C_{13}=2\sup_{|v|<\max\{C_{\Omega}\mathcal{M},Q\}}|f^{\prime}(v)|+2\sup_{|v|<\max\{C_{\Omega}\mathcal{M},Q\}}|f^{\prime\prime}(v)|C_{\Omega}\mathcal{M}.

Inserting (4.8) into (4.7), one has

‖ζn‖2\displaystyle\|\zeta^{n}\|^{2} ≤‖ζ0‖2+2​C13​∑l=1n∑j=1lθl−j(l)​(‖ζj−1‖+‖ζj‖)​‖ζl‖\displaystyle\leq\|\zeta^{0}\|^{2}+2C_{13}\sum_{l=1}^{n}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|\zeta^{j-1}\|+\|\zeta^{j}\|)\|\zeta^{l}\|
+2​∑l=1n∑j=1lθl−j(l)​(‖Rfj‖+‖Rtj‖)​‖ζl‖+2​CΩ​ℳ​(1+2​C13)​hr+1​∑l=1nτl​‖ζl‖.\displaystyle+2\sum_{l=1}^{n}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|R_{f}^{j}\|+\|R_{t}^{j}\|)\|\zeta^{l}\|+2C_{\Omega}\mathcal{M}(1+2C_{13})h^{r+1}\sum_{l=1}^{n}\tau_{l}\|\zeta^{l}\|.

Choosing n∗n^{*} such that ‖ζn∗‖=max0≤l≤n⁡‖ζl‖\|\zeta^{n^{*}}\|=\max_{0\leq l\leq n}\|\zeta^{l}\|. The above inequality yields

‖ζn∗‖2\displaystyle\|\zeta^{n^{*}}\|^{2} ≤‖ζ0‖​‖ζn∗‖+4​C13​∑l=1n∗∑j=1lθl−j(l)​‖ζn∗‖​‖ζl‖\displaystyle\leq\|\zeta^{0}\|\|\zeta^{n^{*}}\|+4C_{13}\sum_{l=1}^{n^{*}}\sum_{j=1}^{l}\theta_{l-j}^{(l)}\|\zeta^{n^{*}}\|\|\zeta^{l}\|
+2​∑l=1n∗∑j=1lθl−j(l)​(‖Rfj‖+‖Rtj‖)​‖ζn∗‖+2​CΩ​ℳ​(1+2​C13)​hr+1​∑l=1n∗τl​‖ζn∗‖.\displaystyle+2\sum_{l=1}^{n^{*}}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|R_{f}^{j}\|+\|R_{t}^{j}\|)\|\zeta^{n^{*}}\|+2C_{\Omega}\mathcal{M}(1+2C_{13})h^{r+1}\sum_{l=1}^{n^{*}}\tau_{l}\|\zeta^{n^{*}}\|.

Eliminating a ‖ζn∗‖\|\zeta^{n^{*}}\| from both sides and using the facts that ‖ζn‖≤‖ζn∗‖\|\zeta^{n}\|\leq\|\zeta^{n^{*}}\| and n∗≤nn^{*}\leq n, we arrive at

‖ζn‖≤‖ζn∗‖\displaystyle\|\zeta^{n}\|\leq\|\zeta^{n^{*}}\| ≤‖ζ0‖+4​C13​∑l=1nτl​‖ζl‖+2​∑l=1n∑j=1lθl−j(l)​(‖Rfj‖+‖Rtj‖)+2​CΩ​ℳ​(1+2​C13)​tn​hr+1\displaystyle\leq\|\zeta^{0}\|+4C_{13}\sum_{l=1}^{n}\tau_{l}\|\zeta^{l}\|+2\sum_{l=1}^{n}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|R_{f}^{j}\|+\|R_{t}^{j}\|)+2C_{\Omega}\mathcal{M}(1+2C_{13})t_{n}h^{r+1}
≤4​C13​∑l=1nτl​‖ζl‖+2​∑l=1n∑j=1lθl−j(l)​(‖Rfj‖+‖Rtj‖)+CΩ​ℳ​(2​T+4​C13​T+1)​hr+1,\displaystyle\leq 4C_{13}\sum_{l=1}^{n}\tau_{l}\|\zeta^{l}\|+2\sum_{l=1}^{n}\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|R_{f}^{j}\|+\|R_{t}^{j}\|)+C_{\Omega}\mathcal{M}(2T+4C_{13}T+1)h^{r+1}, (4.9)

where ‖ζ0‖=‖Rh​u0−Uh0‖=‖Rh​u0−u0‖≤CΩ​hr+1​‖u0‖Hr+1\|\zeta^{0}\|=\|R_{h}u_{0}-U_{h}^{0}\|=\|R_{h}u_{0}-u_{0}\|\leq C_{\Omega}h^{r+1}\|u_{0}\|_{H^{r+1}} is used. By exchanging the order of summation and using identity (2.6), Lemmas 3.2, 3.3 and Proposition 2.1, it holds

2​∑l=1n\displaystyle 2\sum_{l=1}^{n} ∑j=1lθl−j(l)​(‖Rfj‖+‖Rtj‖)=2​∑j=1npn−j(n)​(‖Rfj‖+‖Rtj‖)\displaystyle\sum_{j=1}^{l}\theta_{l-j}^{(l)}(\|R_{f}^{j}\|+\|R_{t}^{j}\|)=2\sum_{j=1}^{n}p^{(n)}_{n-j}(\|R_{f}^{j}\|+\|R_{t}^{j}\|)
=2​∑j=1npn−j(n)​‖Rfj‖+2​∑j=2npn−j(n)​‖Rtj‖+pn−1(n)​‖Rt1‖\displaystyle=2\sum_{j=1}^{n}p^{(n)}_{n-j}\|R_{f}^{j}\|+2\sum_{j=2}^{n}p^{(n)}_{n-j}\|R_{t}^{j}\|+p^{(n)}_{n-1}\|R_{t}^{1}\|
≤(2​Cf​tn+3​tn​ℳ+ℳ)​τ2.\displaystyle\leq(2C_{f}t_{n}+3t_{n}\mathcal{M}+\mathcal{M})\tau^{2}. (4.10)

Thus, inserting (4.10) into (4.9), for τ≤τ∗≤1/(8​C13)\tau\leq\tau^{*}\leq 1/(8C_{13}), we have

‖ζn‖≤8​C13​∑l=1n−1τl​‖ζl‖+2​(2​Cf​T+3​T​ℳ+ℳ)​τ2+2​CΩ​ℳ​(2​T+4​C13​T+1)​hr+1,\displaystyle\|\zeta^{n}\|\leq 8C_{13}\sum_{l=1}^{n-1}\tau_{l}\|\zeta^{l}\|+2(2C_{f}T+3T\mathcal{M}+\mathcal{M})\tau^{2}+2C_{\Omega}\mathcal{M}(2T+4C_{13}T+1)h^{r+1},

which together with Lemma 3.1 implies that

‖ζn‖\displaystyle\|\zeta^{n}\| ≤2​exp⁡(8​C13​T)​((2​Cf​T+3​T​ℳ+ℳ)​τ2+CΩ​ℳ​(2​T+4​C13​T+1)​hr+1)\displaystyle\leq 2\exp(8C_{13}T)\big{(}(2C_{f}T+3T\mathcal{M}+\mathcal{M})\tau^{2}+C_{\Omega}\mathcal{M}(2T+4C_{13}T+1)h^{r+1}\big{)}
≤C14​(hr+1+τ2),\displaystyle\leq C_{14}(h^{r+1}+\tau^{2}), (4.11)

where C14=2​exp⁡(8​C13​T)​max⁡{2​Cf​T+3​T​ℳ+ℳ,CΩ​ℳ​(2​T+4​C13​T+1)}.C_{14}=2\exp(8C_{13}T)\max\{2C_{f}T+3T\mathcal{M}+\mathcal{M},C_{\Omega}\mathcal{M}(2T+4C_{13}T+1)\}. The proof is completed by inserting (4.3) and (4.11) into (4.2) and setting C0∗:=CΩ​ℳ+C14C_{0}^{*}:=C_{\Omega}\mathcal{M}+C_{14}.  

5 Numerical Examples

We now present two examples to investigate the quantitative accuracy of fully discrete scheme (1.8) from two perspectives: (a) the convergence order of numerical scheme (1.8) in time and space; (b) the unconditional convergence by fixing the spacial size hh and refining the temporal size τ\tau. To obtain the variable time steps, we construct the time steps by τk=T​λk/Λ\tau_{k}=T\lambda_{k}/\Lambda for 1≤k≤N1\leq k\leq N, where Λ=∑k=1Nλk\Lambda=\sum_{k=1}^{N}\lambda_{k} and λk\lambda_{k} is randomly drawn from the uniform distribution on (0,1)(0,1). In the simulations, we only use the linear finite element (i.e. r=1r=1), and consider the time steps in two cases:

  • Case (i): the ratios of adjacent time steps satisfy A1, i.e., 0<rk<4.86450<r_{k}<4.8645;

  • Case (ii): the ratios do not satisfy A1, i.e., can be taken large randomly.

Example 5.1. We here consider the computation of the following 2D nonlinear parabolic equation

∂tu=Δ​u+1+u2+g​(𝒙,t).\partial_{t}u=\Delta u+\sqrt{1+u^{2}}+g(\bm{x},t).

In the simulations, we take the final time T=1T=1 and the computational domain Ω=(0,1)2\Omega=(0,1)^{2}. As a benchmark solution, we take an exact solution in the form of u​(𝒙,t)=(1+t3)​x1​(1−x1)2​x2​(1−x2)2u(\bm{x},t)=(1+t^{3})x_{1}(1-x_{1})^{2}x_{2}(1-x_{2})^{2}, and the source term g​(𝒙,t)g(\bm{x},t) can be calculated accordingly.

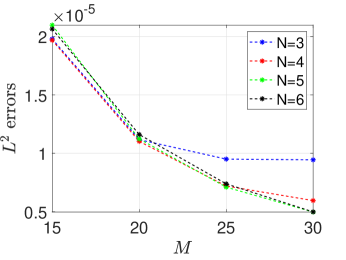
Table 1 shows the spatial L2L^{2}-error by increasing MM and fixing N=104N=10^{4}. Tables 2 and 3 show the temporal L2L^{2}-errors by taking M=NM=N and increasing NN under Cases (i) and (ii) in above, respectively. From Tables 1-3, the second order convergence rates can be observed, which agrees with the results in Theorem 4.1. In addition, The left panel in Figure 1 plots the L2L^{2}-error by fixing NN and increasing MM, which implies that the error estimate is unconditionally stable since the solution does not blowup for any temporal and spatial ratios.

Table 1: Errors and spatial convergence orders with N=104N=10^{4} for Example 5.1

  MM error order rmaxr_{\max} 40 4.2893e-05 – 4.6836 80 8.9895e-06 2.2544 4.8091 160 1.9913e-06 2.1745 4.7541 320 4.6221e-07 2.1071 4.7043  

Table 2: Errors and time convergence orders with 0<rk<4.86450<r_{k}<4.8645 for Example 5.1

  NN error order rmaxr_{\max} 120 3.6800e-06 – 4.2785 240 8.3695e-07 2.1365 4.6672 480 1.9795e-07 2.0800 4.1304 960 4.8114e-08 2.0406 4.2979  

Refer to caption
Refer to caption
Figure 1: To investigate the scheme is unconditionally stable, L2L^{2}-errors are plotted by increasing MM for different given NN: left and right panels for Examples 5.1 and 5.2, respectively.
Table 3: Errors and time convergence orders with rk>0r_{k}>0 for Example 5.1

  NN error order rmaxr_{\max} 120 3.6533e-06 – 21.6746 240 8.3479e-07 2.1297 24.1472 480 1.9783e-07 2.0772 285.448 960 4.7942e-08 2.0449 792.551  


Example 5.2. We now consider a 3D nonlinear parabolic equation

∂tu=Δ​u+u−u3+g​(𝒙,t).\partial_{t}u=\Delta u+u-u^{3}+g(\bm{x},t).

In the simulations, we take the final time T=1T=1 and the computational domain Ω=(0,1)3\Omega=(0,1)^{3}. Again, as a benchmark solution, we take an exact solution in the form of u​(𝒙,t)=(1+t3)​x1​(1−x1)2​x2​(1−x2)2​x3​(1−x3)2u(\bm{x},t)=(1+t^{3})x_{1}(1-x_{1})^{2}x_{2}(1-x_{2})^{2}x_{3}(1-x_{3})^{2}, and the source term g​(𝒙,t)g(\bm{x},t) can be calculated accordingly.

Table 4 shows the spatial L2L^{2}-error by increasing MM and fixing N=103N=10^{3}. Tables 5 and 6 show the temporal L2L^{2}-errors by taking M=NM=N and increasing NN under Cases (i) and (ii) in above, respectively. From Tables 4-6, the second order convergence rates can be observed, which again agrees with the results in Theorem 4.1. The right panel in Figure 1 plots the L2L^{2}-error by fixing NN and increasing MM, which again implies that the error estimate is unconditionally stable since the solution does not blowup for any temporal and spatial ratios.

Table 4: Errors and spatial convergence orders with N=103N=10^{3} for Example 5.2

  MM error order rmaxr_{\max} 6 1.3595e-04 – 4.5317 12 3.3786e-05 2.0086 4.3782 24 8.4315e-06 2.0025 4.3911 48 2.1069e-06 2.0007 4.6375  

Table 5: Errors and time convergence orders with 0<rk<4.86450<r_{k}<4.8645 for Example 5.2

  NN error order rmaxr_{\max} 4 3.0607e-04 – 2.3893 8 7.5914e-05 2.0114 2.2410 16 1.8918e-05 2.0046 2.9583 32 4.7170e-06 2.0038 3.9028  

Table 6: Errors and time convergence orders with rk>0r_{k}>0 for Example 5.2

  NN error order rmaxr_{\max} 4 3.0721e-04 – 2.4017 8 7.5918e-05 2.0167 13.2425 16 1.8929e-05 2.0039 32.1533 32 4.7200e-06 2.0037 25.1107  

6 Conclusions

We have presented the unconditionally optimal error estimate of a linearized variable-time-step BDF2 scheme for nonlinear parabolic equations in conjunction with a Galerkin finite element approximation in space. The rigorous error estimate of 𝒪​(τ2+hr+1)\mathcal{O}(\tau^{2}+h^{r+1}) in the L2L^{2}-norm has been established under mild assumptions on the ratio of adjacent time steps A1 and the maximum time-step size A2. The analysis is based on the recently developed DOC and DCC kernels and the time-space error splitting approach. The techniques of DOC and DCC kernels facilitate the proof of the second order convergence of BDF2 with a new ratio of adjacent time steps, i.e., 0<rk<4.86450<r_{k}<4.8645. The error splitting approach divides the error estimate of numerical solution into the estimates of ‖Un‖H2\|U^{n}\|_{H^{2}} and ‖Rh​Un−Uhn‖L2\|R_{h}U^{n}-U_{h}^{n}\|_{L^{2}}, which circumvents the ratio restriction of time-space sizes, i.e., this is the so-called unconditionally optimal error estimate.

In addition, our error estimate is robust. The robustness here means the error estimate does not require any extra restriction on time steps except the conditions A1 and A2. Meanwhile, we used the first-order BDF1 to calculate the first level solution u1u^{1}, and found that this first-order scheme did not bring the loss of global accuracy of second order. Although a great progress has been made for the second order convergence of variable time-step BDF2 scheme solving nonlinear problems, but most of them use the implicit approximation to the nonlinear terms. As far as we know, it is a pioneer work to present the optimal error estimate for the variable time-step BDF2 scheme with a linearized approximation to nonlinear terms only under the ratio condition 0<rk<4.86450<r_{k}<4.8645 and a mild assumption on maximum time step A2. Numerical examples were provided to verify our theoretical analysis.

Acknowledgements

The research is supported by the National Natural Science Foundation of China (Nos. 11771035 and 12171376), 2020- JCJQ-ZD-029, NSAF U1930402. The numerical calculations in this paper have been done on the supercomputing system in the Supercomputing Center of Wuhan University. JZ would like to thank professor Tao Tang and professor Zhimin Zhang for their valuable discussions on this topic.

7 Appendix

7.1 The proof of Lemma 3.2

Proof. It follows from the Taylor expansion that

‖Rfj‖\displaystyle\|R_{f}^{j}\| =‖(uj−uj−1)2​∫01f′′​(uj−1+s​∇τuj)​(1−s)​ds‖\displaystyle=\|(u^{j}-u^{j-1})^{2}\int_{0}^{1}f^{\prime\prime}(u^{j-1}+s\nabla_{\tau}u^{j})(1-s)\,\mathrm{d}s\|
≤‖uj−uj−1‖⋅‖(uj−uj−1)​∫01f′′​(uj−1+s​∇τuj)​(1−s)​ds‖L∞\displaystyle\leq\|u^{j}-u^{j-1}\|\cdot\|(u^{j}-u^{j-1})\int_{0}^{1}f^{\prime\prime}(u^{j-1}+s\nabla_{\tau}u^{j})(1-s)\,\mathrm{d}s\|_{L^{\infty}}
≤‖∫tj−1tj∂tu​d​t‖⋅‖uj−uj−1‖L∞​‖∫01f′′​(uj−1+s​∇τuj)​(1−s)​ds‖L∞\displaystyle\leq\|\int_{t_{j-1}}^{t_{j}}\partial_{t}u\,\mathrm{d}t\|\cdot\|u^{j}-u^{j-1}\|_{L^{\infty}}\|\int_{0}^{1}f^{\prime\prime}(u^{j-1}+s\nabla_{\tau}u^{j})(1-s)\,\mathrm{d}s\|_{L^{\infty}}
≤ℳ​τj⋅‖∫tj−1tj∂tu​d​t‖L∞​sup|u|≤CΩ​ℳ|f′′​(u)|2\displaystyle\leq\mathcal{M}\tau_{j}\cdot\big{\|}\int_{t_{j-1}}^{t_{j}}\partial_{t}u\,\mathrm{d}t\big{\|}_{L^{\infty}}\frac{\sup_{|u|\leq C_{\Omega}\mathcal{M}}|f^{\prime\prime}(u)|}{2}
≤12​ℳ​τj​sup|u|≤CΩ​ℳ|f′′​(u)|​∫tj−1tj‖∂tu‖L∞​dt≤12​sup|u|≤CΩ​ℳ|f′′​(u)|​CΩ​ℳ2​τj2,\displaystyle\leq\frac{1}{2}\mathcal{M}\tau_{j}\sup_{|u|\leq C_{\Omega}\mathcal{M}}|f^{\prime\prime}(u)|\int_{t_{j-1}}^{t_{j}}\|\partial_{t}u\|_{L^{\infty}}\,\mathrm{d}t\;\leq\frac{1}{2}\sup_{|u|\leq C_{\Omega}\mathcal{M}}|f^{\prime\prime}(u)|{C_{\Omega}}\mathcal{M}^{2}\tau_{j}^{2},

where ‖∂tu‖L∞≤CΩ​‖∂tu‖H2≤CΩ​ℳ\|\partial_{t}u\|_{L^{\infty}}\leq C_{\Omega}\|\partial_{t}u\|_{H^{2}}\leq C_{\Omega}\mathcal{M} is used. The proof is completed.  

7.2 The proof Lemma 3.3

Proof. Recall that the first step value u1u^{1} is computed by BDF1, i.e., Rt1=u1−u0τ1−∂tu​(t1)R_{t}^{1}=\frac{u_{1}-u_{0}}{\tau_{1}}-\partial_{t}u(t_{1}), one has

‖Rt1‖\displaystyle\|R_{t}^{1}\| =‖u1−u0τ1−∂tu​(t1)‖=1τ1​‖∫0t1∂tu​(s)−∂tu​(t1)​d​s‖\displaystyle=\|\frac{u_{1}-u_{0}}{\tau_{1}}-\partial_{t}u(t_{1})\|=\frac{1}{\tau_{1}}\|\int_{0}^{t_{1}}\partial_{t}u(s)-\partial_{t}u(t_{1})\,\mathrm{d}s\|
≤1τ1​∫0t1‖∂tu​(s)−∂tu​(t1)‖​ds≤1τ1​∫0t1∫st1‖∂t​tu​(t)‖​dt​ds≤ℳ2​τ1.\displaystyle\leq\frac{1}{\tau_{1}}\int_{0}^{t_{1}}\|\partial_{t}u(s)-\partial_{t}u(t_{1})\|\,\mathrm{d}s\leq\frac{1}{\tau_{1}}\int_{0}^{t_{1}}\int_{s}^{t_{1}}\|\partial_{tt}u(t)\|\,\mathrm{d}t\,\mathrm{d}s\leq\frac{\mathcal{M}}{2}\tau_{1}.

For j≥2j\geq 2, by using the Taylor’s expansion formula , one produces (also see [19, Theorem 10.5])

Rtj=−1+rj2​τj​∫tj−1tj(t−tj−1)2​∂t​t​tu​δ​t+rj2​(1+rj)​τj−1​∫tj−2tj(t−tj−2)2​∂t​t​tu​δ​t,2≤j≤N.\displaystyle R_{t}^{j}=-\frac{1+r_{j}}{2\tau_{j}}\int_{t_{j-1}}^{t_{j}}(t-t_{j-1})^{2}\partial_{ttt}u\delta t+\frac{r_{j}}{2(1+r_{j})\tau_{j-1}}\int_{t_{j-2}}^{t_{j}}(t-t_{j-2})^{2}\partial_{ttt}u\delta t,\quad 2\leq j\leq N.

Combining with the regularity assumption (2.1) and the ratio condition A1, one derive

‖Rtj‖≤ℳ6​(1+rj)​τj​(2​τj+τj−1)≤32​ℳ​τj​τ.\displaystyle\|R_{t}^{j}\|\leq\frac{\mathcal{M}}{6}(1+r_{j})\tau_{j}(2\tau_{j}+\tau_{j-1})\leq\frac{3}{2}\mathcal{M}\tau_{j}\tau. (7.1)

The proof is completed.  

References

  • [1] J. Becker. A second order backward difference method with variable steps for a parabolic problem. BIT, 34(4):644–662, 1998.
  • [2] W. Chen, X. Wang, Y. Yan, and Z. Zhang. A second order BDF numerical scheme with variable steps for the cahn-hilliard equation. SIAM J. Numer. Anal., 57(1):495–525, 2019.
  • [3] E. Emmrich. Stability and error of the variable two-step BDF for semilinear parabolic problems. J. Appl. Math. Comput., 19:33–55, 2005.
  • [4] R. Fisher. The wave of advance of advantageous genes. Annals of Eugencies, 7:355–369, 1937.
  • [5] R. Grigorieff. Stability of multistep-methods on variable grids. Numer. Math., 42:359–377, 1983.
  • [6] R. Grigorieff. Time discretization of semigroups by the variable two-step BDF method. numerical treatment of differential equations, 121:204–216, 1991.
  • [7] R. Grigorieff. On the variable grid two-step BDF method for parabolic equation. TU, Fachbereich 3, 1995.
  • [8] M. Leroux. Variable stepsize multistep methods for parabolic problems. SIAM J. Numer. Anal., 19:725–741, 1982.
  • [9] B. Li and W. Sun. A new approch to errror analysis of linearized semi-implicit galerkin fems for nonlinear parabolic equations. Int. J. Numer. Anal. Model., 24(1):86–103, 2012.
  • [10] D. Li, H. Liao, J. Wang, W. Sun, and J. Zhang. Analysis of l1-galerkin fems for time- fractional nonlinear parabolic problems. Commun. Comput. Phys., 24(1):86–103, 2018.
  • [11] D. Li, J. Wang, and J. Zhang. Unconditionally convergent l1-galerkin fems for nonlinear time-fractional schrödinger equations. SIAM J. Sci. Comput., 39(1):A3067–A3088, 2017.
  • [12] D. Li, C. Wu, and Z. Zhang. Linearized galerkin fems for nonlinear time fractional parabolic problems with non-smoooth solutions in time direction. J. Sci. Comput., 80:403–419, 2019.
  • [13] H. Liao, B. Ji, and L. Zhang. An adaptive BDF2 implicit time-stepping method for the phase field crystal model. IMA J. Numer. Anal., page draa075, 2020.
  • [14] H. Liao, D. Li, and J. Zhang. Sharp error estimate of the nonuniform l1 formula for reaction- subdiffusion equations. SIAM J. Numer. Anal., 56-2:1112–1133, 2018.
  • [15] H. Liao, X. Song, T. Tang, and T. Zhou. Analysis of the second-order BDF scheme with variable steps for the molecular beam epitaxial model without slope selection. Sci. China Math., 64:887–902, 2021.
  • [16] H. Liao, T. Tang, and T. Zhou. On energy stable, maximum-principle preserving, second-order BDF scheme with variable steps for the allen-cahn equation. SIAM J. Numer. Anal., 58(4):2294–2314, 2020.
  • [17] H. Liao and Z. Zhang. Analysis of adaptive BDF2 scheme for diffusion equations. Math. Comp., 90:1207–1226, 2021.
  • [18] C. Palencia and B. García-Archilla. Stability of multistep methods for sectorial operators in banach spaces. Appl. Numer. Math., 12:503–520, 1993.
  • [19] V. Thomée. Galerkin finite element methods for parabolic problems, second edition. Springer-Verlag, 2006.
  • [20] W. Wang, Y. Chen, and H. Fang. On the variable two-step imex BDF method for parabolic integro-differential equations with nonsmooth initial data arising in finance. SIAM J. Numer. Anal., 57(3):1289–1317, 2019.
  • [21] Y. Zeldovich and D. Frank-Kamenetskii. A theory of thermal propagation of flame, dynamics of curved fronts. Academic Press, pages 131–140, 1988.
  • [22] J. Zhang and C. Zhao. Sharp error estimate of BDF2 scheme with variable time steps for linear reaction-diffusion equations. J. Math., https://doi.org/10.13548/j.sxzz.20211014.001, 41(6):471–488, 2021.
  • [23] J. Zhang and C. Zhao. Sharp error estimate of BDF2 scheme with variable time steps for molecular beam expitaxial models without slop selection. https://doi.org/10.13140/RG.2.2.24714.59842, 41(6):471–488, 2021.