Ultrafast selective mid-infrared sublattice manipulation in the ferrimagnet FeCr₂S₄

Ferrimagnets are materials characterized by sublattices with opposite spin orientation that, differently from antiferromagnets, give a finite net magnetic moment. Although this is typically smaller than for ferromagnets, it does not exclude large responses to externally applied fields. In presence of plasma resonances or intra-atomic d-d transitions, strong magneto-optical responses can be observed [1, 2, 3, 4, 5, 6]. The interaction between the two sublattices is central for the ferrimagnetic alignment, leading to associated magnetic properties. These can be monitored through the magneto-optical Kerr effect (MOKE) both at equilibrium and dynamically through light pulses in a time-resolved approach (TR-MOKE) [7, 8]. The response, however, is typically dependent on the photon energy. This is influenced by the presence of corresponding electronic transitions and the spin alignment. In principle, exciting and probing the material resonantly to intra-atomic transitions involving unfilled shells with unpaired electrons provides a unique pathway, by selectively perturbing or monitoring a single sublattice [9, 10]. However, the energy levels in solids are often of mixed atomic character due to bonding, with various possible transitions superimposed in the energy spectrum. Therefore, a clear spectral separation and localized orbital character are required.

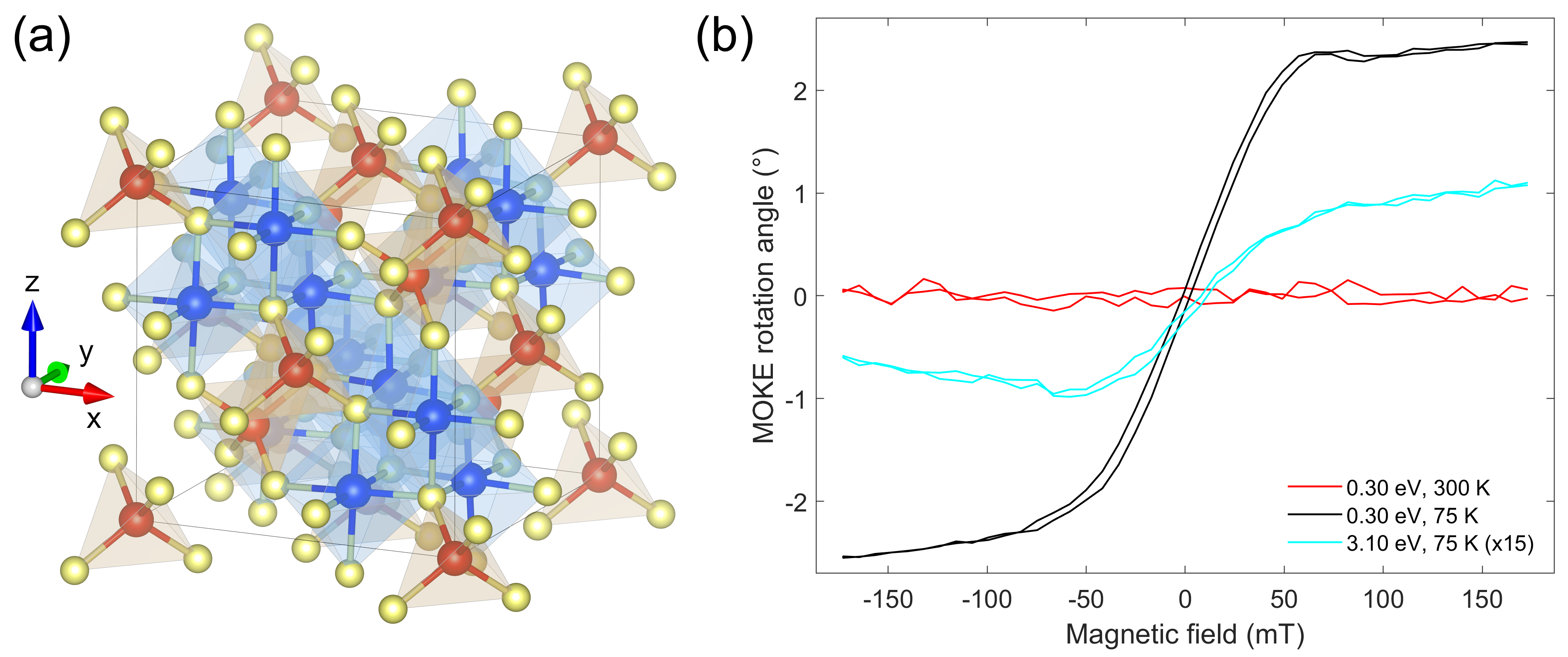
FeCr₂S₄ is a ferrimagnet with a cubic spinel structure (space group Fd$\bar{3}$m) between 65 and 300 K (Fig. 1(a)) [11, 13, 14], with some reports suggesting structural distortions below 65 K [15, 16, 17]. The iron ions (Fe²⁺) are found in tetrahedral sites, while the chromium ones (Cr³⁺) are octahedrally coordinated. A mixed valence configuration for the Fe and Cr ions was excluded by Chen et al. [13]. Recently, the possibility to grow 2D-like crystals with analogous magnetic properties has been demonstrated, making the material attractive for applications in ultrathin devices [18]. The material becomes ferrimagnetic below the ordering temperature $T_{C}$$\approx$170 K. Such alignment is favored by the superexchange interaction between the half-filled Cr $t_{2g}$ states and the half-filled Fe $d$ ones, mediated by the S atoms [19, 20, 21]. This phase transition has been studied through its magnetization, high photon-energy techniques such as x-ray absorption (XAS), x-ray magnetic circular dichroism (XMCD) and resonant inelastic x-ray scattering (RIXS),and magneto-optical response, elucidating together the electronic configuration of the two sublattices [22, 23, 24, 21, 5, 6].

Polar MOKE studies on bulk samples revealed a large, few-degree MOKE rotation and temperature-dependent response around 0.30 eV, corresponding to intra-atomic Fe d-d transitions, which become dipole-active due to the absence of local inversion symmetry at the iron site, leading to Davydov splitting [5, 6]. Around 3.10 eV, the MOKE rotation is about one order of magnitude smaller and it is connected to charge-transfer (CT) transitions between S-3p orbitals and mixed Fe-3d/Cr-3d states [25, 20, 5, 6]. Here the large spectral separation between the Fe d-d transitions and the rest offers an unambiguous scheme to excite or probe a single sublattice. In this work, we performed polar TR-MOKE experiments on single-crystal FeCr₂S₄ samples to study the response of the material on- and off-resonant to the intra-atomic Fe d-d transitions. We show how these different options lead to distinct dynamical responses connected to the reciprocal interaction between the two sublattices and allow us to obtain sublattice-specific information.

The description of the sample growth of our samples was previously reported by Ohgushi et al. [5]. We decided to study the sample keeping its as-grown (111) surface. While the easy axis corresponds to the $\langle 100\rangle$ direction, a mechanical polishing has been reported to cause a marked increase in the coercive field [5, 6]. Such preferential alignment is connected to the temperature-dependent magnetocrystalline anisotropy energy, mainly caused by the Fe sites [26]. The experiments were performed using an amplified Ti:sapphire laser system (Coherent Astrella, photon energy 1.55 eV), pulse duration 100 fs, repetition rate 1 kHz) in combination with an optical parametric amplifier (TOPAS, Light Conversion). Mid-infrared (mid-IR) pulses at 0.30 eV were generated by difference frequency generation between signal and idler through a GaSe crystal, while visible 3.10 eV pulses were obtained by second-harmonic generation through a beta barium borate crystal. In all the presented wavelength settings, we used a s-polarized pump beam arriving with a 2^∘ incident angle to excite the system and a p-polarized probe beam with 7^∘ angle, both with respect to the surface normal. A complete list of the pump and probe spot sizes at the sample position is reported in the Supplemental Material, Sec. I [27]. Using the optical data from Ogasawara et al. [25], we estimate the power reflectivity coefficient (penetration depth in nm) for 0.30, 1.55 and 3.10 eV, to be, in order, 0.33 (197), 0.18 (96), 0.30 (20). See Supplemental Material, Sec. II for a detailed energy dependence [27].

To access the ferrimagnetic phase, we cooled down the sample to 75 K using a cryostat with calcium fluoride windows, having $\approx$93% transmission in the whole investigated photon energy range. To orient the spins, we utilized a single-pole electromagnet, giving a maximum 180 mT DC magnetic field at the sample position. The reflected probe beam was collected and sent to a half waveplate and then split between two orthogonal polarizations using a Wollaston prism. The probe beams were finally collected using Si or HgCdTe detectors depending on the photon energy. The MOKE angle was calculated as reported in Supplemental Material, Sec. I [27].

First of all, we confirmed the previous results by Ohgushi et al. [5], regarding the equilibrium properties. In Fig. 1(b) we report the polar MOKE response from FeCr₂S₄ at 0.30 eV and 3.10 eV through hysteresis cycles. Indeed, the large few-degree mid-IR MOKE rotation at 0.30 eV, connected to the intra-atomic Fe d-d, transitions dwarfs the VIS response at 3.10 eV, linked to interatomic CT transitions S $3p\to$ Fe-3$d$/Cr-3$d$, and is extinguished above the critical temperature $T_{C}$$\approx$170 K.

In the following, we focus on the time-resolved MOKE rotation dynamics, in particular on the out-of-equilibrium signal which is odd with respect to a sign change of the externally applied magnetic field. To obtain it, we acquired each time two datasets, both with a magnetic field modulus of $\approx$170 mT, but with opposite directions with respect to the surface normal, which we call $\theta_{+}$ and $\theta_{-}$. We express the signal as $\Delta(\theta_{+}-\theta_{-})/(\theta_{+}-\theta_{-})$, i.e., the difference between the pumped and unpumped subtractions, between the two rotation angles, with respect to the equilibrium subtraction.

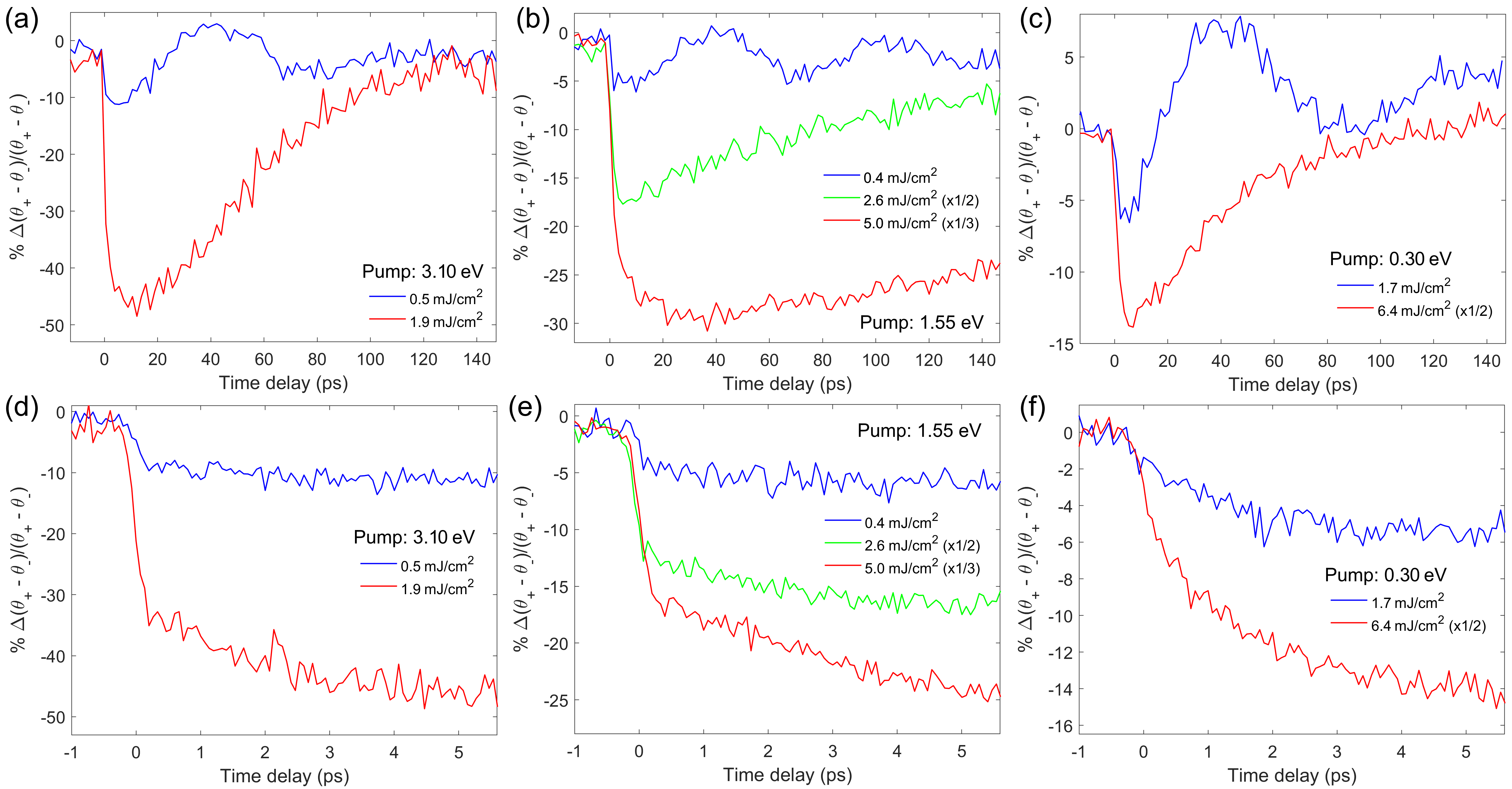
We start by considering the case of non-resonant probing (3.10 eV), i.e., using a photon energy which does not correspond to intratomic d-d transitions of Fe or Cr ions. We explored three distinct time ranges with different time steps for selected incident fluence values (Figs. 2, 4(a)). Three pump photon energies were employed: 0.30 eV, 1.55 eV and 3.10 eV. In all these cases, the probe penetration depth is smaller than, or equal to, the pump one. In Fig. 2, we show in the top row the TR-MOKE rotation dynamics in a 150 ps range around time-zero ($t$=0), i.e., the temporal overlap between pump and probe pulses. A shared characteristic among the three different pump photon energies is the emergence of a 24 GHz oscillation which disappears at higher fluences. In the bottom row, the focus is the dynamics close to time-zero in an 7 ps window. In the non-resonant cases (panels (d) and (e)), a sudden drop occurs at time-zero, followed by a slower dynamics. This last feature is almost flat at the lowest fluences, while a further decrease in the signal occurs and becomes faster (panel (e)) as the excitation energy is increased. A major difference occurs with the pump photon energy resonant to the Fe d-d transitions (panel (f)). Here the dynamics do not exhibit a sharp drop at time-zero, but rather a more gradual decrease to then follow a similar trend as for the non-resonant pumping after about 2 ps. The 0.3 eV pump pulse duration was estimated to be much shorter than this (Supplemental Material, Sec. I [27]). In the larger time delay window (1600 ps, Fig. 4(a)), the response is similar for all the pump photon energies, consisting of a slow recovery after the initial excitation. As the pump fluence is increased (see traces for 1.55 eV), the recovery in the first hundreds of picoseconds becomes first slower, then follows dynamics analogous to the lower fluence.

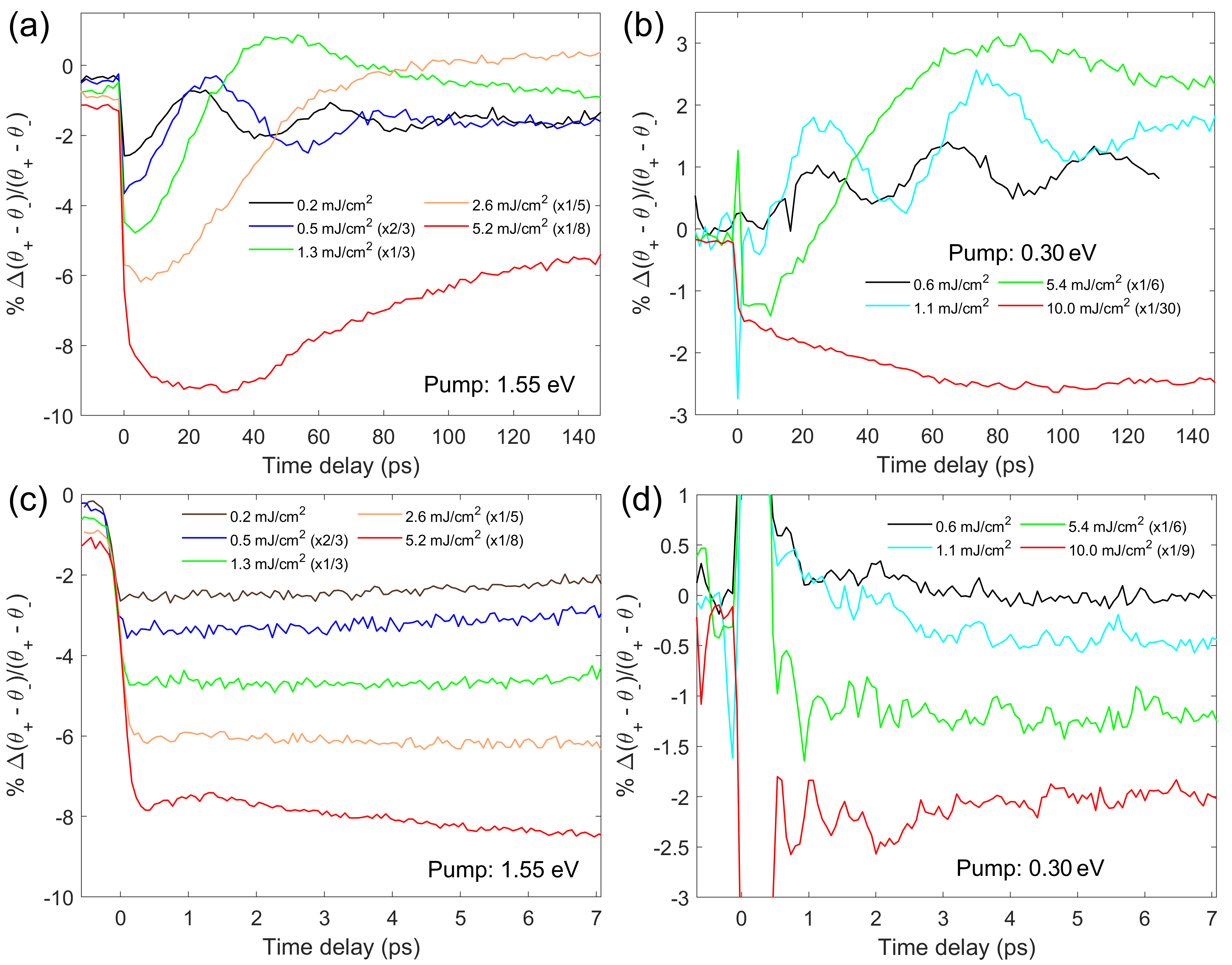
We now turn our attention to the case of probe photon energy resonant to the Fe sublattice d-d transitions (0.30 eV). Again, three time windows were collected, albeit only for two pump photon energies (1.55 eV and 0.30 eV). The reason being the large discrepancy in penetration depth between 3.10 eV and 0.30 eV, around a factor 10, which would have lead to probing a large volume in which the excitation predominantly occurs only in its very first section. The results are reported in Figs. 3 and 4(b),(c). For the 1.55 eV excitation, a small pre-pump pulse was present, which leads to an offset of the signal before time-zero, not observed with a larger time-step as in Fig. 4(b).

In case of degenerate pump and probe photon energies (0.30 eV), it was not possible to fully remove the contribution of pump scattering into the detector, which created some artifacts localized mainly around the first few hundreds of fs after time-zero (Figs. 3(b), (d) and 4(c)). Their identification is described in Supplemental Material, Sec. III.[27].

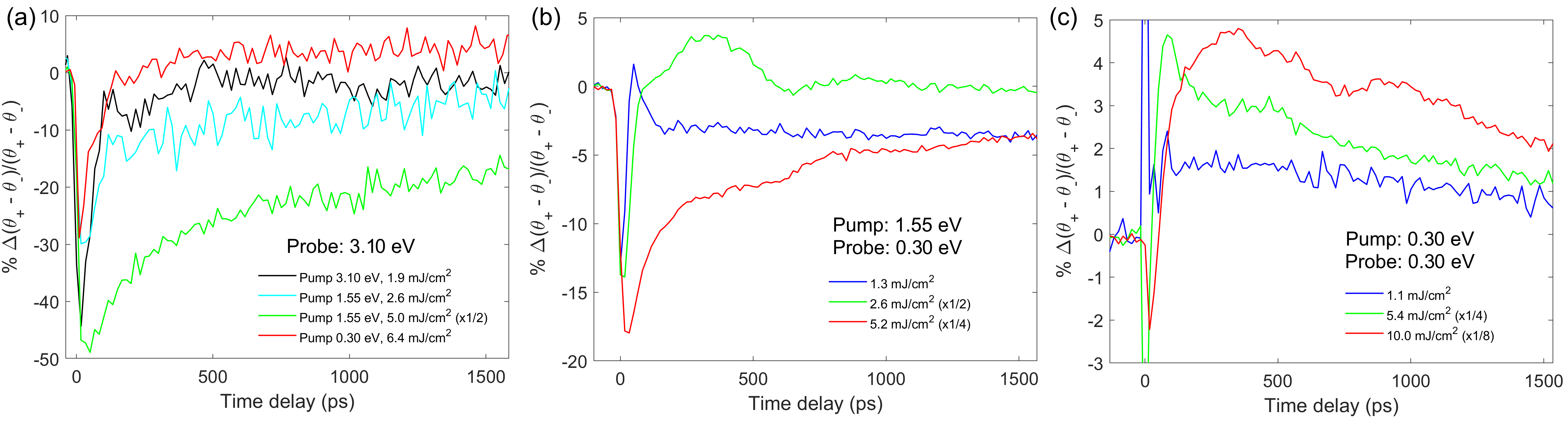
Starting from the 150 ps range (top row, Fig. 3), we observe a similar response to VIS probe: a 24 GHz oscillation is present at the lower fluences, which gradually disappears and is dominated by a strong signal decrease at the highest excitations. Close to time-zero, in the 7 ps window (Figs. 3 (c),(d)) the response is predominantly flat after the excitation. In the case of NIR pump, at the highest fluence, a small bulge, nonetheless clearly above the noise level, was recorded around 1 ps. This is possibly tied to a rapid change in the magneto-optical coefficients due to, e.g. photobleaching [8, 28]. Under mid-IR pump, although limited by pump scattering at time-zero, we do not observe a slow decrease of the out-of-equilibrium signal as in the case of the visible probe: after one picosecond the response is already flat and even shows already a slow recovery at the highest fluences. Combining the data from the 150 ps and the 1600 ps window, Figs. 3 (a),(b) and 4 (b),(c)) respectively, it is clear than the 24 GHz oscillation exhibits a gradual, but strong, red-shift until around 2 GHz at the highest fluences.

The differences among the time dynamics at close fluences and same pump photon energy in Figs. 2, 3, 4 can be attributed to multiple factors. One major contribution comes from the different penetration depth at those photon energies. In fact, the pump transmission is expected to follow an exponentially-decaying profile [29], leading to an accumulation of the absorbed energies primarily over a penetration depth length. This explains, for example, why under a 1.55 eV excitation with the same nominal fluence, the 0.30 eV probe reveals a dynamics which resembles the ones at lower fluence for the 3.10 eV probe. A similar argument applies for the differences among distinct pump photon energies, even after taking into account their reflectivities. However, the dynamics of a material is not simply determined by the absorbed energy, but also by the energy levels and quasi-particles involved. An example is the MOKE dynamics around $t$=0 in Fig. 2(d)-(f). In fact, considering the absorbed excitation energy density, the highest fluence for the 3.10 eV pump in panel (d) corresponds to $9.8\cdot 10^{-6}$ J/m³, while it is $4.3\cdot 10^{-6}$ J/m³ for 1.55 eV excitation in panel (e) and $2.2\cdot 10^{-6}$ J/m³ for 0.30 eV excitation in panel (f). However, even decreasing the pulse energy by a factor 10 for the 1.55 eV case (panel (e)) does not reproduce the slower dynamics of the 0.30 eV one (panel (f)).

As shown for antiferromagnetic iron oxides [10], resonant pumping of Fe d-d transitions can weaken the magnetic interactions by altering the electronic configuration of the sublattices, e.g., transiently making a ferromagnetic alignment more favorable. As discussed in the literature [20, 5, 6], a 3.10 eV probe matches the interatomic CT transitions S $3p\to$ Fe-3$d$/Cr-3$d$ states, sensitive to modifications occurring in both sublattices. Nonetheless, the 0.30 eV excitation does not lead to a slower MOKE dynamics in the case of resonant probe (Fig. 3(c),(d)), where instead we see a fast drop for both pump photon energies. This indicates that the slower response in Fig. 2(f) is likely connected to the interaction between the excited Fe states and the Cr sublattice. Conversely, 1.55 and 3.10 eV photon energies perturb both the two sublattices causing the response to be faster without the need of a slower spin reorganization.

This response is caused by transient modifications in the superexchange coupling between the two sublattices. In particular, in a semiclassical picture of Heisenberg Hamiltonian, we can rewrite the contributions in terms of scalar products between the local spins and effective fields [19]. In our case, these are $\bm{H}^{\mathrm{Fe}}_{\mathrm{ex}}=[12/(g\mu_{\mathrm{B}})]J_{\mathrm{Fe,Cr}}\langle\bm{S}_{\mathrm{Cr}}\rangle$ and $\bm{H}^{\mathrm{Cr}}_{\mathrm{ex}}=[6/(g\mu_{\mathrm{B}})]J_{\mathrm{Fe,Cr}}\langle\bm{S}_{\mathrm{Fe}}\rangle$, where $g$ is the g-factor, $\mu_{\mathrm{B}}$ the Bohr magneton, $J_{\mathrm{Fe,Cr}}$ the exchange interaction between the Fe and Cr atoms and $\langle\bm{S}_{\mathrm{Cr}}\rangle$ ($\langle\bm{S}_{\mathrm{Fe}}\rangle$) the expectation for value for the Cr (Fe) spin vector [25]. An involvement in the mutual interaction of the phonon bath is expected to occur on a longer timescale [30].

The 24 GHz oscillation was previously recorded by Ogasawara et al. and assigned to the procession of the Cr spins [25]. A lack of involvement of the Fe spins was suggested by the absence of oscillations in the ellipticity dynamics probing at 0.5 eV (pump at 1.55 eV), supported by its reported elevated magnetocrystalline anisotropy [26]. However, our results (Fig. 3(a),(b)) show such modulations when probing resonantly to the Fe sublattice (0.30 eV). These experimental results can be reconciled by noting that at 0.5 eV we are at the very edge of the MOKE resonance associated to the Fe d-d transitions [5, 25, 6], therefore a different sensitivity to the oscillation is possible. In the work from Ogasawara et al. [25], an oscillation appears to be present in the datasets at 70 K and 90 K datasets, although comparable to the noise level. Regarding the crystalline anisotropy, although it is predicted to be on the order of a few Tesla at 4 K [25], giving a preferential spin alignment along the $\langle 100\rangle$, it is heavily influenced by temperature [26]. This is also evident from the coercive field which grows as the temperature is lowered [18]. Therefore, we conclude that in our conditions ($T$=75 K), the magnetocrystalline anisotropy, while present, is considerably reduced. Since the oscillation frequency is close to the one observed at low fluences at 3.10 eV (Fig. 2) and 1.9 eV [25], we deduce that the two sublattice are coupled in their precession motion, thanks to the superexchange interaction. No further oscillatory contributions were resolved (see also Supplemental Material, Sec. IV [27]).

A further description of the out-of-equilibrium dynamics is given though hysteresis curves in the Supplemental Material, Sec. V [27]. Additionally, we measured for the highest fluences the equilibrium and time-resolved ellipticity in the different wavelength configurations. These suggest heating effects in the system, which lead to drastic changes in the associated magneto-optical coefficients (Supplemental Material, Sec. VI [27]). Finally in Supplemental Material, Sec. VII [27] we present the non-negligible impact of the external magnetic field on the time-resolved reflectivity of the sample under $T_{C}$.

In summary we have shown that, by selectively pumping the Fe sublattice, we are able to modify dramatically the time scale of the nonequilibrium magnetic response connected to both the Fe and Cr sublattices. We propose that the likely mechanism is a different modification of the superexchange interaction between the sublattices. Moreover, we highlighted the importance of resonant probing by showing how the precession of the spins impacts the MOKE dynamics resonant to the Fe d-d transitions. This approach can be extended to other magnetic materials provided there is a clear spectral separation among the localized energy levels of the atoms.