Ultrafast Dynamics of Coherent Phonon Modes in Excitonic Insulator Ta₂NiSe₅

In a previous report on ultrafast spectroscopy of TNSe [23], the amplitude A₁ and the relaxation time $\tau_{1}$ remain constant up to $\sim$200 K, after which they decrease with increasing temperature. The amplitude A₂ and $\tau_{2}$ exhibited a constant behavior with temperature, except for a jump in the constant value of $\tau_{2}$ above $\sim$200 K. Figure 1b and 1c displays the fitting parameters ($A_{1}$,$A_{2}$) and ($\tau_{1}$,$\tau_{2}$) at different temperatures. The amplitude ($A_{1}$) and the corresponding relaxation time ($\tau_{1}$) of the fast relaxation process, represented by solid red circles, exhibit a constant value till $\sim$250 K, followed by a gradual fall with further increase in temperature, similar to [23]. However, the temperature dependence of A₂ and $\tau_{2}$ shown in Figure 1b and 1c is different from earlier report [23]. The amplitude $A_{2}$ shows a similar temperature dependence as that of A₁. The corresponding relaxation time $\tau_{2}$ shows a systematic fall with increase in temperature. Werdehausen et al. [23] considered the number of photoexcited carriers above the excitonic gap to be directly related to amplitude A₁(T), with their relaxation governed by $\tau_{1}$(T). Both parameters are derived using the Rothwarf-Taylor (RT) model with a temperature-independent excitonic gap [24]. Physically, the RT model incorporates the disintegrating of the excitons into unbounded electrons and holes by the pump pulse. Following the photoexcitation, the excited electrons and holes recombine to form excitons, resulting in the emission of high-frequency phonons (HFPs). The recombination described here corresponds to the fast relaxation process ($A_{1}$, $\tau_{1}$). There are now two possibilities: (a) The HFPs released in this process can either disintegrate another exciton to produce an electron and a hole, or (b) decay into low-frequency phonons (LFP), which are incapable of further excitonic dissociation. As the excitonic insulator to a semiconducting phase transition temperature is approached, the process (a) can instigate an avalanche of free electrons and holes, leading to a bottleneck for them to recombine into an exciton. This phenomenon results in a substantial increase in relaxation time near the transition point[31, 25]. For the process (b) the decay of a high-frequency phonon (HFP) into low-frequency phonons occurs much more rapidly than the creation of a fermion pair[32]. The observed decrease in the fast relaxation time ($\tau_{1}$) as the transition temperature $T_{C}$ is approached (Figure 1c), illustrates the process (b) where the HFP decays into LFPs. In addition to qualitative understanding, acquiring a quantitative estimation of the amplitude and relaxation time with temperature would provide more comprehensive insights.

Utilizing the RT model, the expressions for the amplitude ($A_{1}$) and the corresponding relaxation time ($\tau_{1}$) can be derived, taking into account the temperature-independent gap (excitonic binding energy, $\Delta_{EI}\equiv 2\Delta$)[31, 25, 23].

$\displaystyle A_{1}(T)=\frac{A_{0}/\Delta}{1+Jexp(-\frac{\Delta}{k_{B}T})}$

$\displaystyle\tau_{1}(T)=\frac{1}{K+L\sqrt{\Delta T}exp(-\frac{\Delta}{k_{B}T})}$

(2)

where A₀, J, K, L and $\Delta$ are fitting parameters. The blue dashed curve in Figures 1b and 1c accurately describes the behavior of $A_{1}$ and $\tau_{1}$ respectively till T_C=325 K. Our fitting process gives $\Delta=131$ meV, corresponding to $\Delta_{EI}$ = 262 meV, which aligns closely with the estimated range of 250 to 320 meV[33, 16, 34]. Thus, the Rothwarf-Taylor model effectively describes the condensed phase of excitons in TNSe. When comparing the amplitudes $A_{1}$ and $A_{2}$ (Figure 1b) for T$<$$T_{C}$, $A_{1}$ is one order of magnitude larger than $A_{2}$, suggesting that the carrier dynamics is primarily governed by the quasiparticles recombining into excitons. Consistent with ref. [23], we attribute the slow component in Eq.1, namely $A_{2}$ and $\tau_{2}$, to thermalization of phonons (HFPs). The relaxation time $\tau_{2}$ signifies the process of hot HFPs gradually cooling down by decaying into low-frequency phonons (LFPs). As temperature increases, the expanded phase space available for phonons results in a more rapid cooling process, leading to a decrease in $\tau_{2}$ with temperature. In the semiconductor region, for temperatures T$>$$T_{C}$, the relaxation dynamics are characterized by photoexcited carriers transferring energy to optical phonons, which subsequently relax through low-energy acoustic phonons. The fast relaxation time ($\tau_{1}$) pertains to the cooling of carriers by emission of optical phonons ($<$1 ps), while the slow relaxation time ($\tau_{2}$) relates to further cooling of optical phonons via acoustic phonons ($\sim$10 ps).

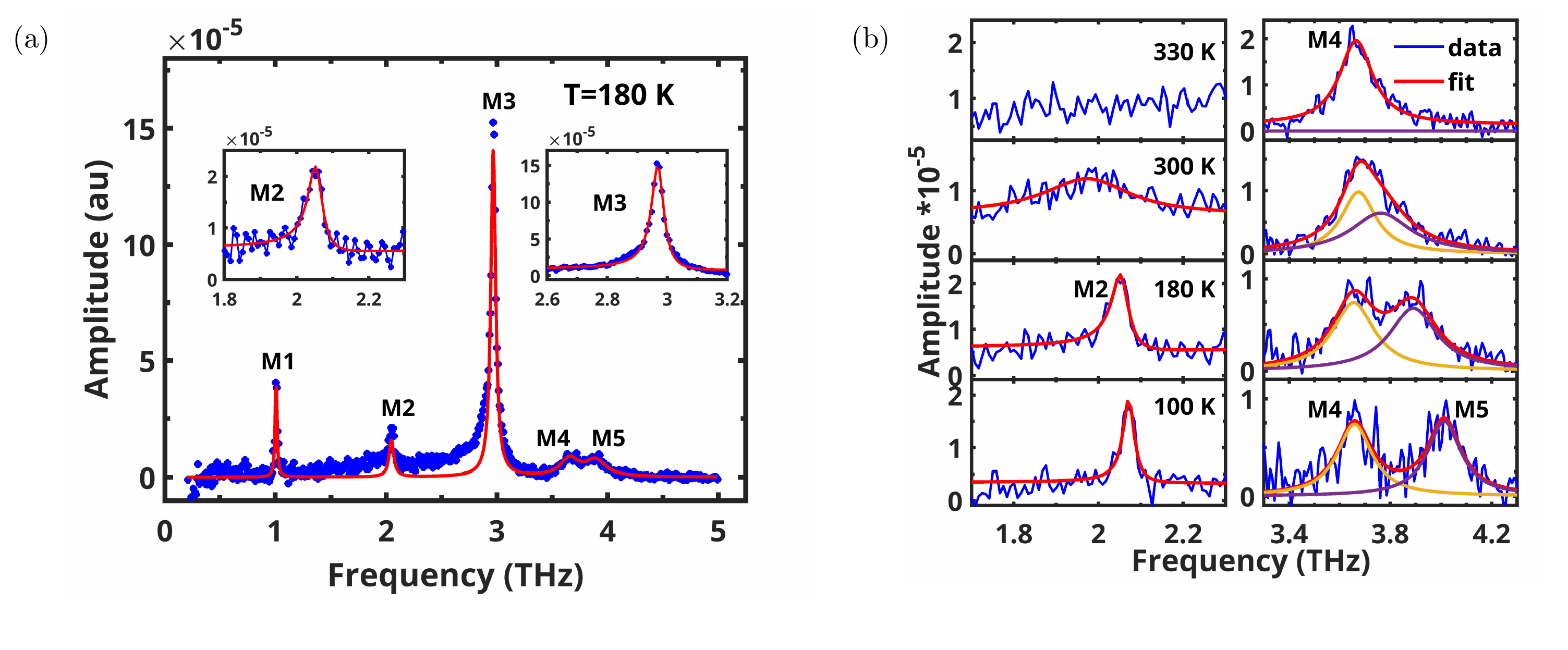
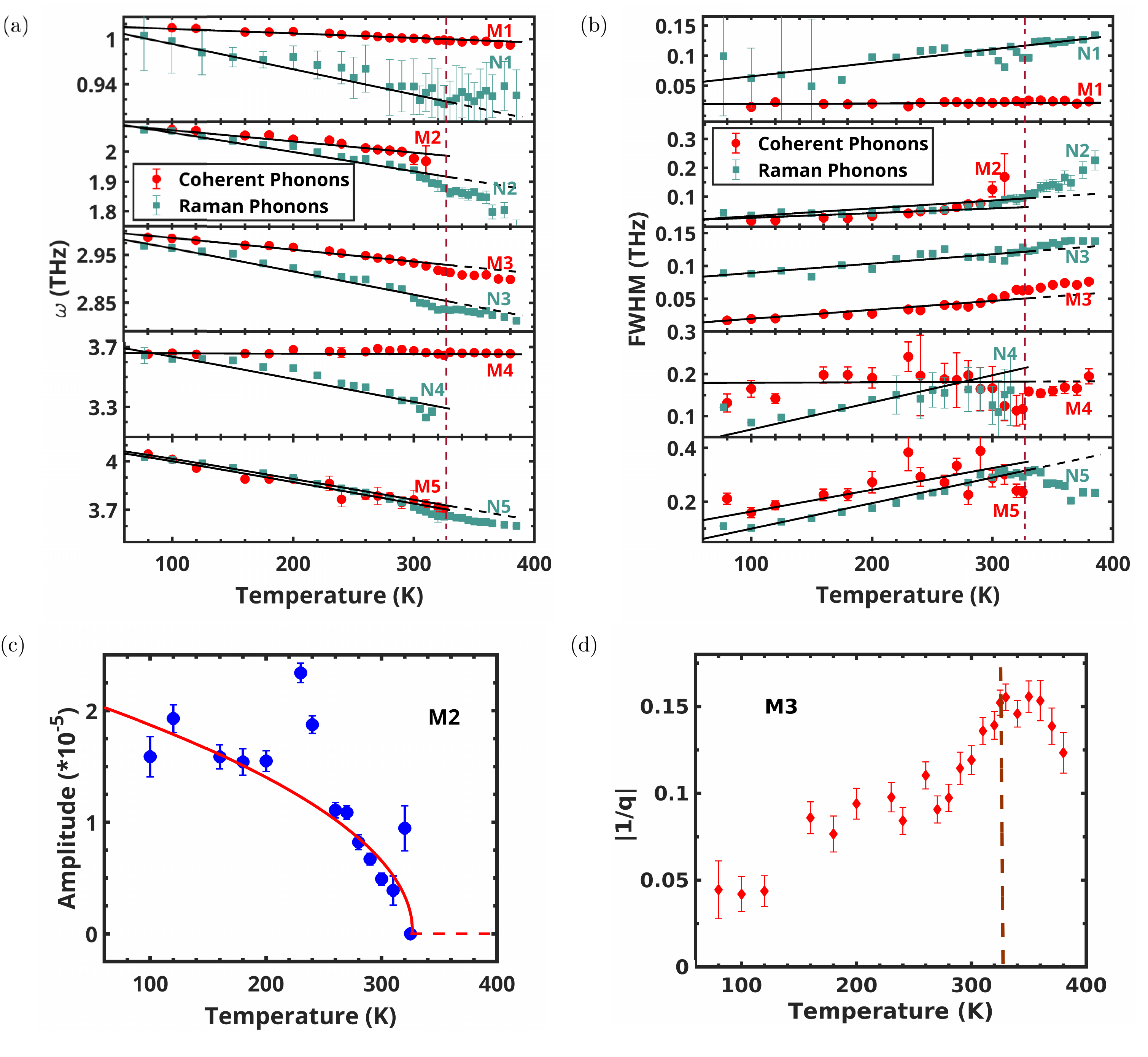
The coherent oscillations observed in the lower panel of Figure 1a allow us to extract coherent phonon modes using the Fast Fourier Transform (FFT). Figure 2a represents the coherent phonon modes, including M1 (1 THZ), M2 (2THz), M3 (3THz), M4 (3.65 THz), and M5 (4.0 THz) depicted by the solid blue circles, is consistent with findings from earlier Raman studies[35, 19]. The phonon modes have been fitted using a sum of Lorentz functions, represented by red solid curve. As can be seen in Figure 2a, modes M1, M4, and M5 were fitted well by Lorentzian functions, while M2 and M3 modes exhibit asymmetric lineshapes and were consequently fitted to the Breit-Wigner-Fano (BWF) lineshape, as illustrated in the insets. The BWF lineshape arising from quantum interference between discrete and continuum transitions is given by $I(\omega)=I_{0}\frac{[1+(\omega-\omega_{F})/q\Gamma]^{2}}{1+[(\omega-\omega_{F})/\Gamma]^{2}}$ where $|1/q|$ represents an asymmetry factor characterizing the coupling strength between the discrete (phonons in this case) and continuous transitions (continuum of photoexcited carriers)[36, 37]. The parameter $\Gamma$ is the broadening parameter, while $\omega_{F}$ corresponds to the uncoupled BWF peak frequency. At the transition temperature $T_{C}$, mode M2 vanishes, while modes M4 and M5 coalesce, as depicted in Figure 2b. Figure 3a and 3b show the peak frequency and full width at half maximum (FWHM) for various modes as a function of temperature. The solid black lines represent the simplistic cubic anharmonicity model for the peak frequency, expressed mathematically as

$$\omega_{cubic}(T)=\omega_{0}-A[1+2n(\omega_{0}/2)]$$

(3)

and for the full width at half maximum (FWHM), presented as

$$\Gamma_{cubic}(T)=\Gamma_{0}+B[1+2n(\omega_{0}/2)]$$

(4)

In this simple anharmonic model, the phonon with frequency $\omega_{0}$ decays into two phonons of equal frequency ($\omega_{0}/2$) [38]. Note that the parameters A and B are both positive. The temperature dependence of mode M3 for $T>T_{C}$ deviates from the extrapolated values of the above model, as is expected for a structural transition.

In the BEC condensate phase of TNSe, a mean-field-like order parameter behavior has been reported for the signal amplitude, represented by the maximum amplitude of $\Delta$R/R [5]. Werdehausen et al. [26] and Mor et al. [35] presented the amplitude of the coherent phonon modes M1 and M4 exhibiting order parameter behavior. In comparison to these phonon modes, we observe the order parameter for the amplitude of the coherent phonon mode M2, as seen by the red line depicting Amplitude $\sim$ A${}_{11}\sqrt{T-T_{C}}$ (Figure 3c). Figure 3d shows the temperature dependence of $|1/q|$ for the M3 mode, displaying that the coupling strength is maximum at $T_{C}$. The coupling strength $|1/q|$ for the M2 mode decreases as T_C is approached, as shown in Figure 6b. The absence of the M2 mode at $T>T_{C}$, along with its order parameter-like trend, suggests that it is coupled to the condensed excitonic phase of TNSe.

While coherent phonon modes offer a plethora of information about TNSe, studying their time evolution can offer insights into the dressing of phonons due to photoexcited carriers, known as birth time [27], and the time evolution of asymmetry of phonon modes. The continuous wavelet transform (CWT) is a tool to describe the temporal evolution of coherent phonons. The oscillatory component of the differential reflectivity (depicted in the bottom section of Figure 1a) is analyzed using continuous wavelet transform (CWT), following [27], utilizing the Morlet mother wavelet as follows [39]:

$$\psi(t/s)=\pi^{-1/4}e^{-t^{2}/2s^{2}+jt/s}\\$$

(5)

The amplitude of the continuous wavelet transform (CWT) for a fixed scaling factor $s$ at a given time $\tau$ is expressed as:

$$CWT(\tau,s)=\frac{1}{\sqrt{|s|}}\int\frac{\Delta R}{R}(t)\psi^{*}(\frac{t-\tau}{s})dt$$

(6)

In simpler terms, the CWT coefficient for a fixed scaling factor $s$ is obtained by taking the Fast Fourier Transform (FFT) of the product of the real-time signal and a Gaussian envelope, where the envelope slides in time with a step size of $\tau$. The CWT spectrogram for TNSe at T = 180 K is illustrated in Figure 4a, presenting the temporal evolution of modes M1 to M5. The time evolution of all the modes is displayed in Figure 4b, with appropriate scaling as indicated in the legends, for better visualization. The inset shows the normalized intensity for the time evolution of modes, highlighting the birth of these quasiparticles, phonons, defined as the time when the intensity of a particular mode reaches its maximum, denoted by $t_{peak}$. It is evident that $t_{peak}$ is approximately the same for all modes except for the strongest mode M3. The observation of higher $t_{peak}$ for the stronger mode is also seen in coherent phonon A${}_{1g}^{1}$ in Bi₂Te₃ [39]. We selected two modes, M2 and M3, with a better signal-to-noise ratio to analyze the evolution of $t_{peak}$ with temperature, as depicted in Figure 4c. For temperatures below $260$ K, mode M2 exhibits a constant value for $t_{peak}$, which then gradually decreases as the transition temperature is approached. The $t_{peak}$ for M3 mode shows a gradual fall with an increase in temperature until reaching the transition temperature $T_{C}$, beyond which it remains constant. With the increase in temperature, the dressing of M3 mode occurs sooner due to the availability of additional phonon phase space. However, the change in slope of $t_{peak}$ for M3 across T_C illustrates that the birth of coherent phonons is affected by the condensate. We want to emphasize that the absolute value of $t_{peak}$ depends on the scaling factor, $s$, and sliding time, $\tau$. We have identified an optimized value for both parameters to facilitate the presentation of CWT analysis. Thus, while the absolute value of $t_{peak}$ may vary, its trend with temperature remained independent of these parameters. Next, we address the asymmetry of the M3 mode through the CWT analysis.

The vertical snippets of the CWT spectrogram (Figure 4a) at various delay times offer insights into the evolution of phonon modes over time. Figure 5a presents the behavior of M3 mode at three distinct time points, t=0 ps, 2 ps, and 6 ps. The asymmetric nature of the M3 mode decreases with time evolution, represented by the black curve. Figure 5b shows the asymmetry parameter $|1/q|$ versus delay time. As time evolves, $|1/q|$ decreases and becomes almost negligible beyond t=4 ps. Hence, it is evident that the asymmetry of the M3 mode arises from its coupling with the photoexcited carriers in the background. As these carriers relax to the ground state, forming excitons, the asymmetry of the M3 mode disappears. Given the diverse temperature-dependent behavior of different coherent phonon modes, it would be valuable to investigate the Raman counterparts of these phonon modes, and compare the results.

There is a total of 45 optical phonons at the Brillouin zone center of Ta₂NiSe₅, among which 21 modes are infrared active [11B_1u+10A_u] and 24 are Raman active [11A_g + 13B_1g] [26]. Figure 6a shows the temperature evolution of the reduced Raman susceptibility $\chi$”$(\omega)$ = Intensity($\omega$)/(n($\omega$)+1), of Ta₂NiSe₅ at a few typical temperatures where n($\omega$) is the Bose-Einstein population factor. We observe 11 modes at 77 K: N1($A_{g}$ at 0.99 THz), N2($B_{1g}$ at 2.01 THz), N3($B_{1g}$ at 3 THz), N4($B_{1g}$ at 3.66 THz), N5($A_{g}$ at 3.99 THz), N6($A_{g}$ at 4.41 THz), N7($A_{g}$ at 5.31 THz), N8($B_{1g}$ at 5.78 THz), N9($B_{1g}$ at 6.50 THz) and N10($B_{1g}$ at 8.78 THz). To distinguish between Raman and coherent phonon modes, the Raman phonon modes are denoted with the letter ‘N’, while the coherent phonon modes are expressed as ‘M’. The symmetry assignments are taken from a recent study (supplementary materials of[26]). Mode marked as L ($B_{1g}$ at 7.10 THz), becomes very weak with increasing temperature and cannot be clearly resolved above 200 K. Loretzian functions were fitted to Raman susceptibility $\chi$”$(\omega)$ to extract the phonon frequencies and full width at half maximum (FWHM) of the Raman modes, except for mode M2, which shows asymmetric lineshape and hence was fitted to BWF lineshape.

We will now comment on the reported Raman results. Yan et al. [19] have reported the merging of N4 and N5 and the disappearance of N6 and L modes beyond T_C of 328 K. In comparison, Kim et al. [3] reported that N5, though absent in unpolarized spectra, is present in polarization-resolved spectra. They showed the presence of all the 11 phonon modes across the transition temperature of 325 K, claiming the electronic origin of the EI transition in TNSe. We observed the presence of the N2 mode across T_C (Figure 6a), in contrast to the disappearance of the coherent M2 mode above T_C. Figure 6a shows the absence of Raman phonon mode N4, but the presence of mode N5 above T_C, whereas in the time-resolved spectroscopy, coherent phonon mode M5 disappears instead of M4, as supported by previous Raman reports [19]. Figures 3a and 3b present the temperature dependence of phonon frequencies ($\omega$) and FWHM ($\Gamma$). The solid black lines are fit to the cubic anharmonic model, Eq. 3 and 4. The deviations from anharmonicity for all the phonon modes for temperatures above T_C depict the structural transition for TNSe. Above T_c, the FWHM of mode N5 shows an anomalous decrease, indicating phonon dynamics influenced by strong electron-phonon coupling (Figure 3b). The increase in the broadening parameter ($\Gamma$) (Figure 3b) and the Fano asymmetry parameter $|1/q|$ with temperature (Figure 6b) reflect the enhanced electron-phonon coupling with temperature. The amplitude of the N2 and N4 modes follows order parameter behavior (Figure 6c), consistent with coherent M2 mode.

The origin of coherent phonons in opaque materials is governed by the mechanism of displacive excitation of coherent phonons (DECP). In this, the pump pulse induces a sudden onset of photoexcited carriers, displacing the equilibrium position of lattice atoms, and consequently, these atoms start oscillating around their new mean position[40, 41]. Figure 3a shows that the mode frequency ($\omega$) for Raman phonons (RP) is less than the coherent phonons (CP) across the temperature range of 80 K to 380 K. Figure 7 (top panel) shows that the ratio of the anharmonicity coefficient (parameter A in Eq.3) of Raman phonons, A_RP to the coherent phonons, A_CP is greater than one for all the phonon modes. Hence, the RPs show more anharmonicity compared to CPs. Additionally, the anharmonic coefficient derived from the FWHM of phonon modes, B (Eq.4) is also more for Raman phonons than for coherent phonons (bottom panel of Figure 7). The comparison of peak frequency and cubic anharmonic strengths for Raman and coherent phonon modes in various materials, such as pyrochlore titanates Dy₂Ti₂O₇ and Gd₂Ti₂O₇ [28], as well as metal Bismuth [42, 43] and semiconductor CsPbCl₃ [44, 45], show similar trend that coherent phonon modes exhibit a weaker anharmonicity compared to corresponding Raman phonons. Further investigation is required to elucidate the underlying mechanisms driving this distinctive behavior of coherent phonons.