Twisting or untwisting graphene twisted nanoribbons without rotation
Abstract
The common sense regarding twisting or untwisting a ribbon is that it requires the application of an external rotation to happen. However, at nanoscale, the application of precise amounts of rotation on a nanoribbon is not a trivial task. Here, the concept of an alternative method to add twist to or remove twist from a twisted graphene nanoribbon (TGNR) without rotation is presented. The method consists of suspending a TGNR on two separate substrates and by changing only their distance, the total amount of twist of the TGNR is shown to change. The possibility to fine-tuning the amount of twist of a TGNR is also shown. The concept is demonstrated through fully atomistic molecular dynamics simulations and numerical calculations of the topological parameters twist and writhe of a TGNR. It is shown that the above process satisfies the so-called linking number theorem of space curves. Besides being experimentally feasible, this concept reveals a new kind of twist to writhe transition phenomenon that is tension-free and does not require controlling neither the nanoribbon end-to-end distance nor its critical twist density.
I Introduction
Graphene nanoribbons (GNRs) have the most of the outstanding properties of pristine graphene and a non-null bandgap that is edge-dependent and inversely proportional to the ribbon width [1, 2, 3]. GNRs have been fabricated by several methods, from top-down to chemical and bottom-up methods [4, 5, 6, 7, 8, 9, 10, 11, 12]. A particularly interesting discovery is the possibility of tuning the bandgap and other electronic and magnetic properties of GNRs by application of twisting along its axis [13, 14, 15, 16, 17, 18, 19, 20]. Electronic, mechanical [21, 22, 23, 24, 25] and thermal [26, 27, 28] properties of twisted GNRs (TGNRs) make them promising and versatile nanostructures for diverse applications.
Fabrication of TGNRs has been reported in the literature. Chamberlain et al. [29] grew TGNRs inside carbon nanotubes from reaction of small sulfur-containing molecules. Cao et al. [30] developed a method to curl GNRs by thermal annealing that was used by Jarrari et al. [31] to show that curled GNRs enhance photocurrent responses. Previously developed methods to bend and twist nanotubes [32] or induce, by laser, changes in GNRs [33], might be useful to fabricate TGNRs.
A ubiquitous phenomenon in filamentary structures is the so-called twist-to-writhe transition (TWT). It consists of releasing the torsional elastic energy accumulated in an initially straight twisted rod by spontaneous curling and coiling. The TWT is shown to happen when the filament twist density reaches a critical value [34, 35, 36, 37]. In turn, the twist density is shown to depend on either the applied tensile stress or filament end-to-end distance [35, 36, 37]. TWT has been shown to obey the conservation of a geometric quantity called the linking number, , of a pair of closed curves or a pair of open curves with extremities prevented from crossing one with respect to the other. Defined as a double Gauss integral along the two curves, is shown to be always an integer number given by half the value of a certain “oriented” way of counting how many times one curve crosses the other [40]. , then, satisfies the Călugăreanu-White-Fuller linking number theorem [34, 38, 39]:
| (1) |
where () is the total twist (writhe) of the filament (filament centerline). Writhe is a geometric quantity related to the non-planarity of a space curve [39, 40, 41].
TWT is observed in conformations of DNA [41, 42, 43, 44, 45], filamentary structures of some bacteria [46, 47, 48], in garden hoses, telephone cords, cables and other engineering structures [45, 49, 50, 51]. It is also present in a wide range of correlated phenomena and applications as in dynamics of stiff polymers [52], coiled artificial muscles made of twisted carbon nanotube yarns [53] or fishing lines [54], helicity in solar active structures [55] and in fluid vortices [56], chemical synthesis of twisted annulene molecules [57], mechanics of knots and tangles [58], collagen fibrils [59], etc.
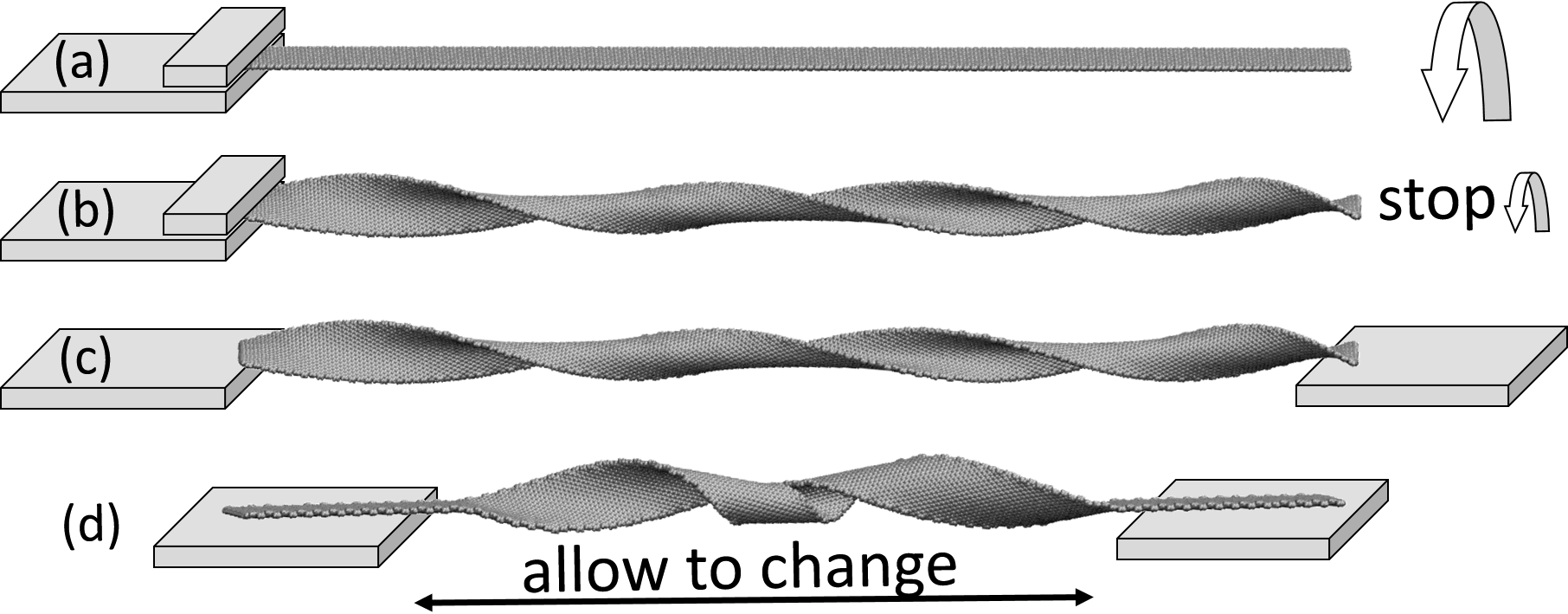
In this Work, a new experimental concept designed to promote and control the interconversion between twist and writhe in a TGNR, without rotation of its extremities, is proposed and computationally demonstrated. Basically, it consists of laying the extremities of a TGNR on two separate substrates, and then allowing the distance between them to vary, within the nanoribbon length (Fig. 1). As these substrates play an essential role on the proposed TWT phenomenon, it is here named substrate induced TWT (SITWT). Although nanoribbons can be subject to regular TWT [60], the proposed interconversion method is innovative because it does not require the TGNR to be neither tensioned (or tension released) nor additionally twisted to reach or exceed the critical twist density.
Section II presents the description of the proposed SITWT method as well as the theory and the computational approach used to calculate and of each configuration of the TGNR, required to demonstrate the SITWT. It also describes the computational methods employed to simulate the SITWT experiment. In Sections III and IV, the results and the conclusions are presented, respectively.
II Methodology
II.1 Description of the proposed SITWT method
An initial amount of turns or torsional strain has to be applied to a GNR in order to produce a TGNR with a given value of (Figs. 1a and 1b). will be conserved as long as the TGNR extremities are prevented from rotation with respect to the ribbon axis (also called the ribbon centerline).
The experiment itself consists of first suspending the TGNR, by laying its two extremities on two separated substrates (Fig. 1c). As the adhesion forces between the nanoribbon and substrates are relatively large, as in graphene-graphene surface interactions [61, 62], it is expected that these forces will themselves prevent the TGNR extremities from rotating or releasing the initial applied torsional strain. The idea of the proposed experiment is, then, to allow the distance between the substrates to vary within the size of the TGNR (Fig. 1d). Variation of this distance leads to variation of the amount of TGNR surface that interacts with the substrates. As the flexural rigidity of nanoribbons are usually low (see for example, that of graphene [63]), van der Waals forces between the nanoribbon and substrates flattens the TGNR parts in touch with the substrates, leading to an overall change of the shape of the suspended part of the TGNR (illustrated in Fig. 1d). Smaller the distance between the substrates, larger the difference in the conformation of the axis (or centerline) of the TGNR from that of a straight twisted ribbon. As a consequence, the writhe, , of the TGNR centerline changes with the substrate distance. As long as the adhesion forces with the substrates keep preventing the TGNR ends from rotation, the linking number theorem, eq. (1), is expected to be satisfied during the movement of the substrates. The theorem, then, predicts that if the writhe, , of the TGNR varies, its total twist, , will vary in order to keep the TGNR unchanged. That is the basis for the experiment of changing the twist, , without applying or removing any amount of rotation to the TGNR extremities.
In order to demonstrate the above SITWT, fully atomistic classical molecular dynamics (MD) simulations of a TGNR suspended on two substrates will be performed. The AIREBO potential [64, 65] and LAMMPS package [66] will be employed to simulate the proposed experiment of moving substrates with suspended TGNRs. Graphite substrates will be considered and modeled as fixed graphene layers. AIREBO is a well-known reactive empirical potential, largely used to study the structure, mechanical and thermal properties of carbon nanostructures [67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77]. Therefore, the MD results for the structure and dynamics of the TGNRs on the moving substrates are expected to really represent real experiments.
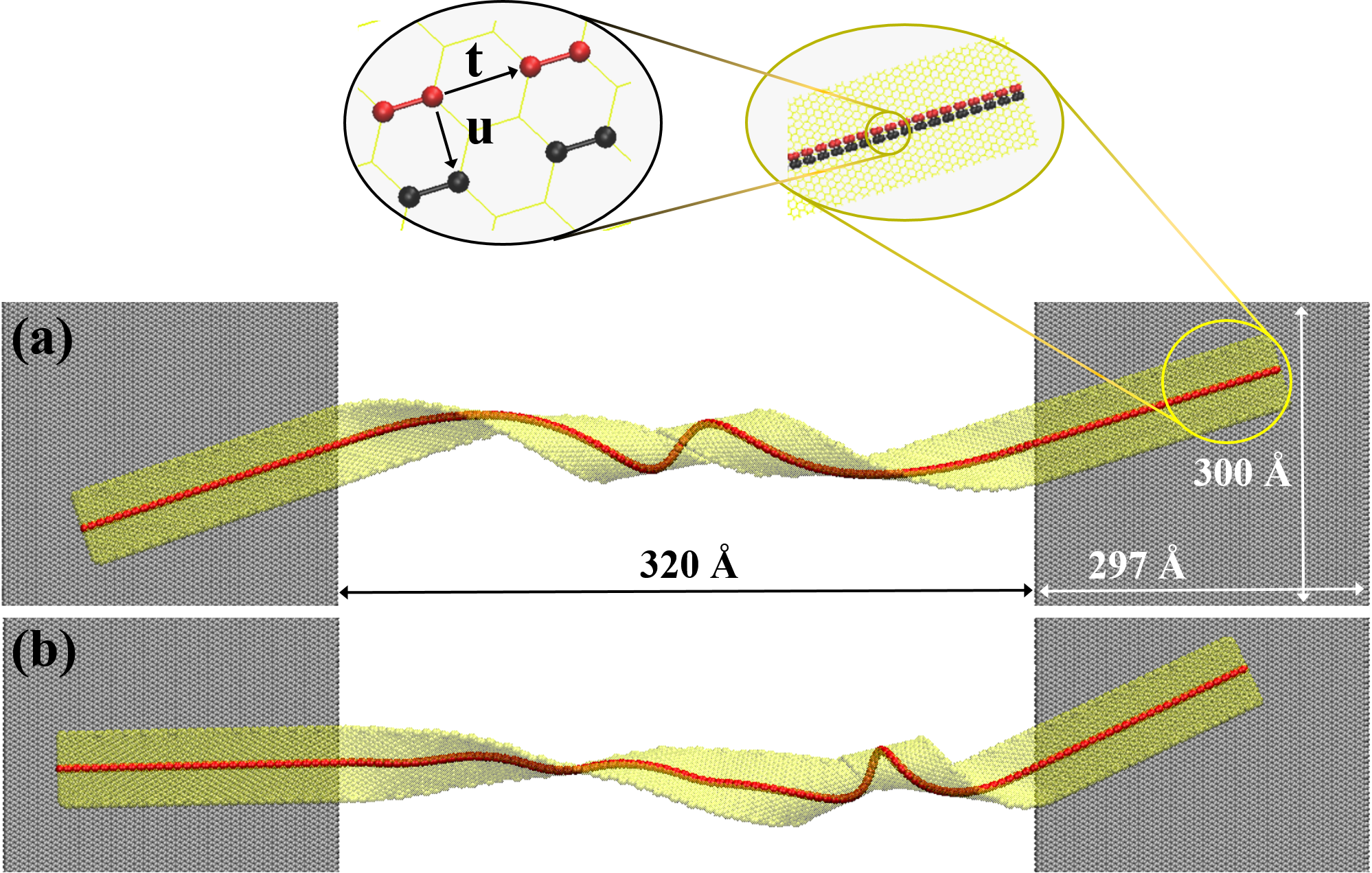
From the MD results, the linking number theorem will be shown to be always satisfied for suspended TGNRs under the present method. To show that, the calculation of and for every configuration of the TGNRs studied here is required. Their summation should be equal to the initially applied to the TGNR, according to eq. (1). In turn, calculations of and require the definition of two space curves corresponding to the TGNR centerline and an adjacent line. As described ahead, these space curves will be discretized based on the positions of two sets of carbon atoms along the TGNR, one at the middle part of the nanoribbon, and the other at about one graphene lattice of distance from the first, on the side, respectively. A piece of the TGNR showing these two sets of atoms is shown in the insets of Fig. 2. In what follows, the details about how these quantities are calculated and the definitions of and are presented.
II.2 Numerical approach for calculating and of TGNRs
Let vectors x and y be identified with the TGNR centerline and an adjacent line bounded to it, as ilustrated by red and black atoms drawn in the insets of Fig. 2, respectively. and can be calculated by [39, 40]:
| (2) |
where and t are the arclength and tangent vector of the TGNR centerline curve x, respectively, and u is a unit vector orthogonal to t, and pointing from x to y. And
| (3) |
While is shown to be always an integer number, and are real numbers that, for closed or end-constrained rods, can varies as long as eq. (1) is satisfied. Eqs. (2) and (3) are defined for closed curves. However, it has been shown [40, 78] that if the tangents at the endpoints of a finite open centerline are coplanar, an imagined coplanar closing curve would contribute with zero to . Similarly, it is possible to think of closing curves for the centerline, x, and its adjancent line, y, that do not cross one to each other, so contributing with zero to the calculation of . In the proposed experiment, the TGNRs are not closed ribbons but the substrates on which its extremities are laid, are coplanar.
All above quantities are discretized according to the following definitions:
| (4a) | |||
| (4b) | |||
| (4c) | |||
| (4d) | |||
| (4e) | |||
| (4f) | |||
| (4g) | |||
where () and are the position of the -esim atom along the centerline (adjacent line) and the number of atoms along the centerline of the TGNR, respectively. For the TGNR studied here, . In eqs. (4) the indices go from 1 to .
II.3 Molecular Dynamics simulations and chosen structures of TGNRs
Every structure was optimized by an energy minimization method based on gradient conjugate implemented in LAMMPS, with energy and force tolerances of and eV/Å, respectively. Thermal fluctuations were simulated using Langevin thermostat, with timestep set to 0.5 fs and thermostat damping factor set in 1 ps.
The set-up of the simulated experiments carried out here is shown in Fig. 2. The nanoribbon chosen to investigate the SITWT phenomenon is an initially straight hydrogen passivated armchair GNR of about 600 Å (33 Å) length (width) to which a total torsional strain of (two full turns) was previously applied. Its initial linking number is, then, . TGNRs in Fig. 2 were drawn in a transparent color in order to facilitate the observation of the shape of their centerlines, highlighted in red. The substrates are modeled as fixed graphene layers.
Fig. 2 shows two different configurations of suspended TGNRs that have the same value of but different values of and (see Table 1). They were obtained from two different pathways as described below and will be considered for the experiment of moving substrates. One of them came from bringing the extremities of the TGNR into contact with two substrates followed by optimization. The structure was, then, simulated for 4 and 8 ns at 300 and 1000 K, respectively, in order to verify its thermal stability under the suspended configuration. Optimization of these structures at the end of the thermal simulations revealed no difference in their corresponding configurations. Fig. 2b shows this optimized structure.
Before proceeding to the dynamical simulations of the moving substrates experiment, I have looked for other possible equilibrium configurations of suspended TGNRs with the same . The recent work by Savin et al. [79], then, came to my knowledge. There, a particular TGNR, also having , was fully laid on a substrate and the final configuration displayed two loop-like structures named by them as twistons. After testing the formation of the same two twistons, I moved the structure to a suspended configuration on two separate substrates, and simulated it by 8 ns at 300 K. Then, the configuration shown in Fig. 2a was found. Further simulation of this structure at 1000 K, made it to become similar to that of Fig. 2b, indicating that they might have similar cohesive energies. In fact, Table 1 shows that the optimized cohesive energies of the structures shown in Figs. 2a and 2b are very close. The files containing the coordinates of the atoms of the structures shown in Fig. 2 are provided in Supplemental Material [80].
III Results
III.1 Test of the numerical calculation of and
The centerline and its adjacent line of the TGNRs considered here possess 285 carbon atoms. Therefore, the eqs. (4a) and (4b) possess 285 coordinates. Before using the discretization of eqs. (2) and (3) to calculate and of the TGNRs, as described and explained in the previous section, the accuracy of the eqs. (4) was tested with two discretized special curves: i) a helical curve closed by straight segments similar to that shown in Fig. 4 of Fuller’s paper [39], and ii) a discretized almost straight TGNR, to which two turns were previously applied (the same structure used to draw the panels (b) and (c) of Fig. 1). According to Fuller, the writhe of a ribbon having that particular centerline curve can be calculated by the formula , where is the helix pitch angle of the helical part of the curve, and is the number of turns. I generated a list of points following the helical curve with , radius = and pitch = , which, from the Fuller’s formula, provides . Using the proposed discretization method, the result for the numerical calculation of writhe of the discretized curve i), with 285 points, is . The second curve (in fact, two curves are needed, the centerline and an adjacent line) was considered for the calculation of the total twist, , since the writhe of a straight curve is zero. of the almost straight -twisted TGNR, whose centerline and adjacent line also have 285 points, was obtained as . Therefore, the estimated uncertainty in the calculations of and using the present method is . Wolfram Mathematica scripts and the data points used to calculate and of curves i) and ii) are provided in Supplemental Material [80].
III.2 and of static TGNRs
Using the above discretization method, and of the structures shown in Fig. 2 were calculated. Table 1 shows the values of , and the sum for these two TGNRs, showing that although they have different values of and , their sum is within the uncertainties of the calculation method. These results confirm the validity of the linking number theorem, eq. (1), and the SITWT. The possibility of performing additional control of the and of the TGNR, while keeping conserved, and the results for the dynamical tests of the SITWT will be shown in the next subsection.
| Fig. 2a | Fig. 2b | |
|---|---|---|
| [eV/atom] | -7.0849 | -7.0848 |
| 0.323 | 0.457 | |
| 1.663 | 1.524 | |
| 1.986 | 1.981 |
The results shown in Table 1 raise an important issue regarding the determination of the total amount of twist of a given TGNR. Although the TGNRs of Fig. 2 initially received a torsional strain of , as soon as the TGNR extremities touched the substrates, its total amount of twist became no longer anymore ( corresponds to ). Besides, although both configurations shown in Fig. 2 have , both have neither nor the same . calculated from eq. (2) represents the real values of the total twist of the nanoribbon. As the electronic properties of GNRs depend on the amount of twist applied to them [13, 14, 15, 31, 19, 20], it is important to know the real value of the twist in order to correctly determine the structure-property relationships in TGNRs. Subsection III.4 shows an example of how to find out the right distance between the substrates on which a TGNR of presents a chosen value of the .
III.3 Dynamical interconvertion of and in TGNRs
In view of the problem mentioned in the previous section and the need for precise determination of the total twist of a TGNR, the present experimental proposal of moving substrates with suspended TGNRs might come in handy. The reason is that by simply controling the substrate distance, the amount of twist of a TGNR can be determined. In order to demonstrate that, I simulated several cycles of movements of the substrates using the structures shown in Figs. 2a and 2b. From these simulations, using the discretization method described in Subsection II.2, , and were calculated as function of time. One cycle of the numerical experiment consists of moving both substrates, one towards the other until almost touching, so “closing” them, then inverting the velocities and moving back to the initial distance, so “opening” them. Each substrate was moved at an absolute speed of 0.2 Å/ps, then the effective approaching or going away speed was 0.4 Å/ps. For an initial maximum distance of 320 Å, one cycle takes 1.6 ns. In the numerical simulations of the experiment, the atoms of the TGNR of Fig. 2a (Fig. 2b) were thermostated at 300 K (1000 K) in order to verify if conditions close to realistic situations influence the results. The atoms of the substrates, however, were not thermostated.
In order to calculate the dependence of and of the TGNRs with time, one frame of the system was collected every 20 ps, or 50 frames were collected per nanosecond. Every frame provides the sets of carbon atoms positions of the TGNR centerline and adjacent line and, from them, the quantities given in eq. (4) were calculated. The summation of and allows for the verification of the linking number theorem and, consequently, once more, the legitimacy of the SITWT.
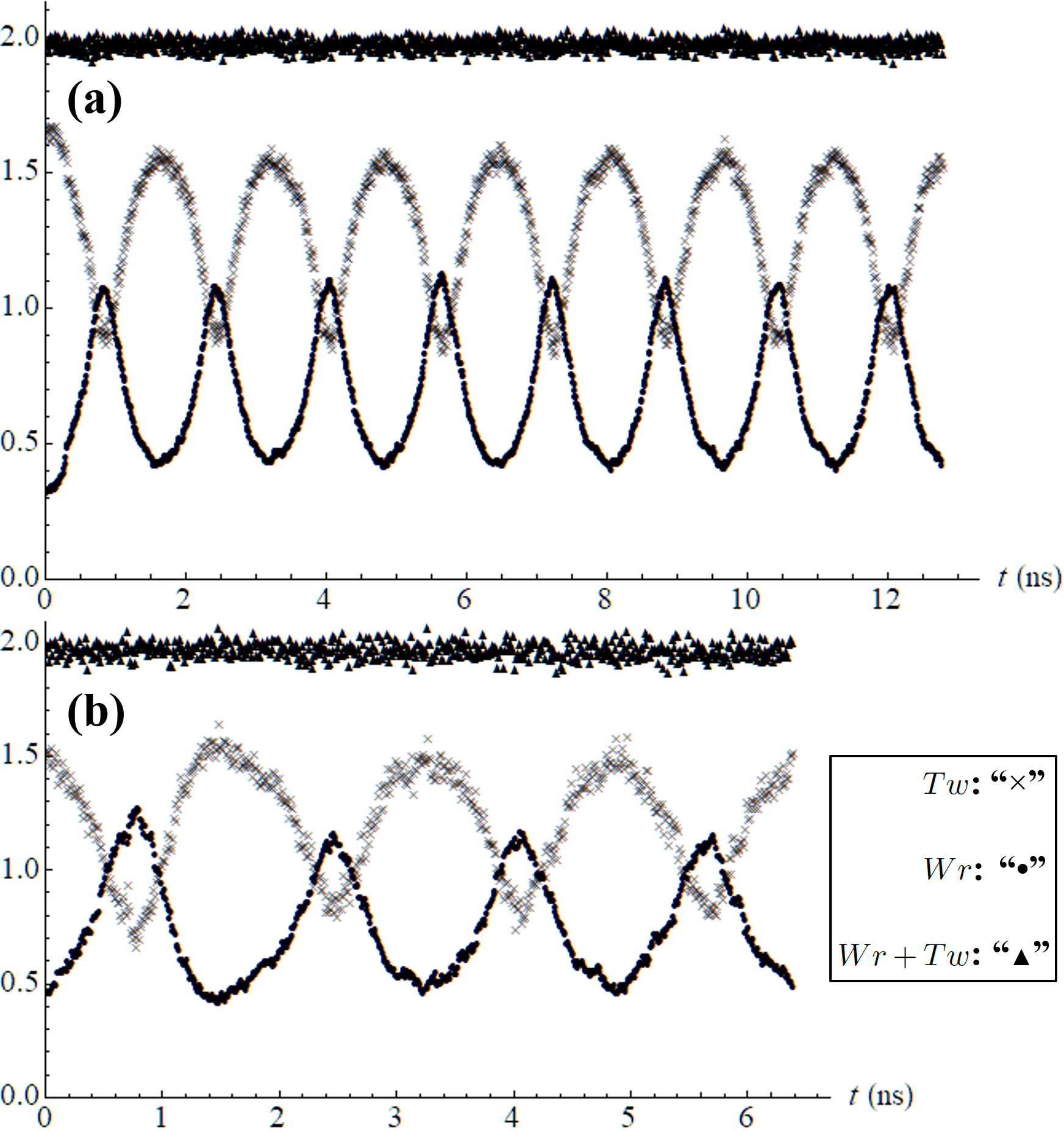
Fig. 3a (3b) shows , and as function of time, during 8 (4) cycles of closing and opening the substrates with the TGNRs of Fig. 2a (2b) simulated at 300 K (1000 K). Fig. 3 shows that and oscillate between minimum and maximum values during the cycles. The maximum (minimum) value of happens for the substrates closed (opened) and contrary for . The rate of changing and is not uniform despite the constancy of the speed of moving substrates. The rate increases (decreases) when the substrates get closed (far) one to each other, what suggests that longer the suspended TGNR easier to fine-tune its total twist. Movies from S1 to S4 in Supplemental Material [80] show upper and lateral views of one cycle of the experiment with both the TGNRs shown in Fig. 2. The movies allow to see the change of the centerline as the substrates get closed and go away.
Fig. 3, then, demonstrates the possibility of controlling the amount of total twist of a TGNR by just changing the distance between the substrates on which its ends are laid. The results for along the time show that the linking number theorem, eq. (1), is satisfied within thermal fluctuations and uncertainties that come from the discrete method of calculating and .
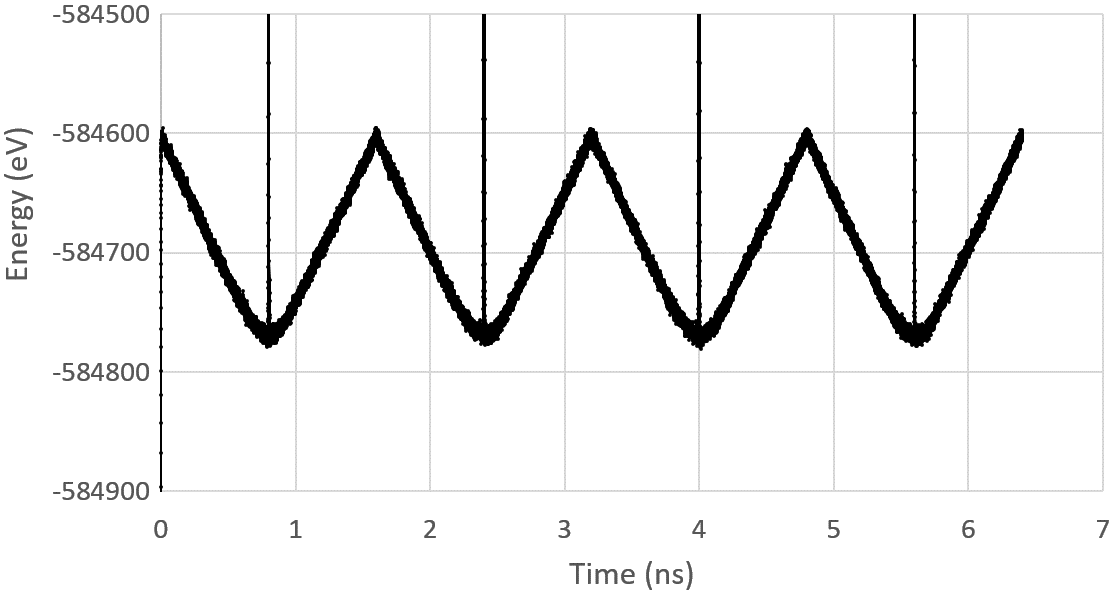
Fig. 4 displays the energy of the whole system during 4 cycles of movement of the substrates with the TGNR of Fig. 2a simulated at 300 K. The energy decreases with the increase of the contact between the TGNR and substrates (increased adhesion), and back. The cusps in Fig. 4 represent the subtle increase of the energy of the system because the simulation allowed the substrates to be almost in full contact. The rate of variation of the energy with the time, calculated from the inclination of the curve in Fig. 4, is nW. It provides an estimate for the external power necessary to carry out the SITWT process. Assuming the force, , needed to move the substrates is approximately constant, using the equation , with Å/ps, it is found that nN. This value of force is within the range of actuation of AFM microscopes [81].
III.4 Example of determination of the distance between substrates to reach a chosen
From Fig. 3 we see that the range of variation of the total twist of the initially applied 2 turns (or 4) TGNR is . To ilustrate the possibility of chosing and determining the total amount of twist of the TGNR, within uncertainties of the method, let us find out the distance, , between the substrates, such that has the chosen value. Suppose the desired value of the total twist of the TGNR is . Based on the present conditions of MD simulations,
| (5) |
where Å/ps is the simulated speed of approaching or moving away the substrates. Taking the value of ps, that corresponds to in Fig. 3a, we obtain Å.
Applications, other than controlling the electronic properties of the TGNR, are the possibility of tunning thermal transport and mechanical properties of TGNRs by fixing their amount of twist. As the writhe of a suspended TGNR varies with the distance between the substrates in the present SITWT method, any physical property that depends on ribbon shape can be also controlled by controlling the substrate distance. These options expand the range of possible applications of suspended TGNRs.
IV Conclusions
In summary, a method to adjust and determine the amount of twist of a previously twisted GNR without the need of applying additional rotation is presented and computationally demonstrated. The method reveals the concept of a tension-free, ends-rotation-free, substrate induced twist to writhe transition in twisted nanoribbons. The method relies on the adhesion forces between the extremities of the twisted nanoribbon and the substrates, and on the relatively low flexural rigidity of the ribbon. The total twist, , writhe, , and the sum were numerically calculated for several configurations of suspended TGNRs, obtained from MD simulations. In particular, the sum was compared to the value of initially ascribed to the TGNR (). The results were shown to satisfy the linking number theorem, eq. (1), within the uncertainties of the methods and thermal fluctuations. Estimates for the power and force needed to move the substrates were presented based on the MD results. An application of the method to the controlling of the total amount of twist of a TGNR was also presented. The advantage of such a method is the possibility of fine-tunning the total twist of a TGNR by simply moving the substrates on which its extremities are laid. This method, then, might be useful for experimentalists to manipulate TGNRs. It was also shown that temperature does not affect the SITWT phenomenon, so the experiment can be performed at different temperatures. I hope this work motivates the development of new experiments and applications of twisted nanoribbons.
Acknowledgements.
I thank the Brazilian Agency CNPq for grant 311587/2018-6 and São Paulo Research Foundation (FAPESP) for the grant #2020/02044-9. This research also used the computing resources and assistance of the John David Rogers Computing Center (CCJDR) in the Institute of Physics “Gleb Wataghin”, University of Campinas.References
- [1] Y. -W. Son, M. L. Cohen, and S. G. Louie, Energy Gaps in Graphene Nanoribbons, Phys. Rev. Lett. 97, 216803 (2006).
- [2] M. Y. Han, B. Özyilmaz, Y. Zhang, and P. Kim, Energy Band-Gap Engineering of Graphene Nanoribbons, Phys. Rev. Lett. 98, 206805 (2007).
- [3] L. Yang, C. -H. Park, Y. -W. Son, M. L. Cohen, and S. G. Louie, Quasiparticle Energies and Band Gaps in Graphene Nanoribbons, Phys. Rev. Lett. 99, 186801 (2007).
- [4] X. Li, X. Wang, L. Zhang, S. Lee, and H. Dai, Chemically Derived, Ultrasmooth Graphene Nanoribbon Semiconductors, Science 319, 1229 (2008).
- [5] S. S. Datta, D. R. Strachan, S. M. Khamis, and A. T. Charlie Johnson, Crystallographic Etching of Few-Layer Graphene, Nano Lett. 8, 1912 (2008).
- [6] L. Tapasztó, G. Dobrik, P. Lambin, and L. P. Biro, Tailoring the atomic structure of graphene nanoribbons by scanning tunnelling microscope lithography, Nat. Nanotechnology 3, 397 (2008).
- [7] J. Campos-Delgado, J. M. Romo-Herrera, X. Jia, D. A. Cullen, H. Muramatsu, Y. A. Kim, T. Hayashi, Z. Ren, D. J. Smith, Y. Okuno, T. Ohba, H. Kanoh, K. Kaneko, M. Endo, H. Terrones, M. S. Dresselhaus, and M. Terrones, Bulk Production of a New Form of sp2 Carbon: Crystalline Graphene Nanoribbons, Nano Lett. 8, 2773 (2008).
- [8] D. V. Kosynkin, A. L. Higginbotham, A. Sinitskii, J. R. Lomeda, A. Dimiev, B. K. Price, and J. M. Tour, Longitudinal unzipping of carbon nanotubes to form graphene nanoribbons, Nature 458, 872 (2009).
- [9] J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen, and R. Fasel, Atomically precise bottom-up fabrication of graphene nanoribbons, Nature 466, 470 (2010).
- [10] H. Sakaguchi, S. Song, T. Kojima, and T. Nakae, Homochiral polymerization-driven selective growth of graphene nanoribbons, Nat. Chemistry 9, 57 (2017).
- [11] A. J. Way, R. M. Jacobberger, and M. S. Arnold, Seed-Initiated Anisotropic Growth of Unidirectional Armchair Graphene Nanoribbon Arrays on Germanium, Nano Lett. 18, 898 (2018).
- [12] Z. Hao, H. Zhang, Z. Ruan, C. Yan, J. Lu, and J. Cai, Tuning the Electronic Properties of Atomically Precise Graphene Nanoribbons by Bottom-Up Fabrication, ChemNanoMat 6, 493 (2020).
- [13] A. Sadrzadeh, M. Hua and B. I. Yakobson, Electronic properties of twisted armchair graphene nanoribbons, Appl. Phys. Lett. 99, 013102 (2011).
- [14] P. Koskinen, Electromechanics of twisted graphene nanoribbons, Appl. Phys. Lett. 99, 013105 (2011).
- [15] G. P. Tang, J. C. Zhou, Z. H. Zhang, X. Q. Deng, and Z. Q. Fan, Altering regularities of electronic transport properties in twisted graphene nanoribbons, Appl. Phys. Lett. 101, 023104 (2012).
- [16] H. Li, N. Al-Aqtash, L. Wang, R. Qin, Q. Liu, J. Zheng, W. -N. Mei, R. F. Sabirianov, Z. Gao, and J. Lu, Electromechanical switch in metallic graphene nanoribbons via twisting, Physica E 44, 2021 (2012).
- [17] S. -Y. Yue, Q. -B. Yan, Z. -G. Zhu, H. -J. Cui, Q. -R. Zheng, and G. Su, First-principles study on electronic and magnetic properties of twisted graphene nanoribbon and Möbius strips, Carbon 71, 150 (2014).
- [18] J. Jia, D. Shi, X. Feng, and G. Chen, Electromechanical properties of armchair graphene nanoribbons under local torsion, Carbon 76, 54 (2014).
- [19] D. -B. Zhang, G. Seifert, and K. Chang, Strain-Induced Pseudomagnetic Fields in Twisted Graphene Nanoribbons, Phys. Rev. Lett. 112, 096805 (2014).
- [20] M. Saiz-Bretín, F. Domínguez-Adame, and A. V. Malyshev, Twisted graphene nanoribbons as nonlinear nanoelectronic devices, Carbon 149, 587 (2019).
- [21] S. Cranford, and M. J. Buehler, Twisted and coiled ultralong multilayer graphene ribbons, Modelling Simul. Mater. Sci. Eng. 19, 054003 (2011).
- [22] E. Dontsova, and T. Dumitrică, Nanomechanics of Twisted Mono- and Few-Layer Graphene Nanoribbons, J. Phys. Chem. Lett. 4, 2010 (2013).
- [23] E. M. Diniz, Self-reconstruction and predictability of bonds disruption in twisted graphene nanoribbons, Appl. Phys. Lett. 104, 083119 (2014).
- [24] D. Xia, Q. Li, Q. Xue, C. Liang, and M. Dong, Super flexibility and stability of graphene nanoribbons under severe twist, Phys. Chem. Chem. Phys. 18, 18406 (2016).
- [25] A. V. Savina, E. A. Korznikova, and S. V. Dmitriev, Improving bending rigidity of graphene nanoribbons by twisting, Mechanics of Materials 137, 103123 (2019).
- [26] X. Wei, G. Guo, T. Ouyang, and H. Xiao, Tuning thermal conductance in the twisted graphene and gamma graphyne nanoribbons, Appl. Phys. Lett. 115, 154313 (2014).
- [27] A. Antidormi, M. Royo, and R. Rurali, Electron and phonon transport in twisted graphene nanoribbons, J. Phys. D: Appl. Phys. 50, 234005 (2017).
- [28] A. V. Savin, E. A. Korznikova, A. M. Krivtsov, and S. V. Dmitriev, Longitudinal stiffness and thermal conductivity of twisted carbon nanoribbons, European Journal of Mechanics / A Solids 80, 103920 (2020).
- [29] T. W. Chamberlain, J. Biskupek, G. A. Rance, A. Chuvilin, T. J. Alexander, E. Bichoutskaia, U. Kaiser, and A. N. Khlobystov, Size, Structure, and Helical Twist of Graphene Nanoribbons Controlled by Confinement in Carbon Nanotubes, ACS Nano 6, 3943 (2012).
- [30] Y. Cao, R. L. Flores, and Y. -Q. Xu, Curling graphene ribbons through thermal annealing, Appl. Phys. Lett. 103, 183103 (2013).
- [31] Z. Jarrahi, Y. Cao, T. Hong, Y. S. Puzyrev, B. Wang, J. Lin, A. H. Huffstutter, S. T. Pantelides, and Y. -Q. Xu, Enhanced photoresponse in curled graphene ribbons, Nanoscale 5, 12206 (2013).
- [32] Y. -Q. Xu, A. Barnard, and P. L. McEuen, Bending and Twisting of Suspended Single-Walled Carbon Nanotubes in Solution, Nano Lett. 9, 1609 (2009).
- [33] X. Zhang, T. S. Walmsley, and Y. -Q. Xu, In situ monitoring of electrical and optoelectronic properties of suspended graphene ribbons during laser-induced morphological changes,, Nanoscale Adv. 2, 4034 (2020).
- [34] F. B. Fuller, The Writhing Number of a Space Curve, Proc. Natl. Acad. Sci. 68, 815 (1971).
- [35] A. Goriely and M. Tabor, The Nonlinear Dynamics of Filaments, Nonlinear Dynamics 21, 101 (2000).
- [36] A. F. da Fonseca, C. P. Malta, and D. S. Galvão, Elastic properties of nanowires, J. Appl. Phys. 99, 094310 (2006).
- [37] N. Charles, M. Gazzola and L. Mahadevan, Topology, Geometry, and Mechanics of Strongly Stretched and Twisted Filaments: Solenoids, Plectonemes, and Artificial Muscle Fibers, Phys. Rev. Lett. 123, 208003 (2019).
- [38] G. Călugăreanu, Sur les classes d’isotopie des noeuds tridimensionnels et leurs invariants, Czechoslovak Math. J. 11, 588 (1961).
- [39] F. B. Fuller, Decomposition of the linking number of a closed ribbon: A problem from molecular biology, Proc. Natl. Acad. Sci. 75, 3557 (1978).
- [40] M. A. Berger and C. Prior, The writhe of open and closed curves, J. Phys. A: Math. Gen. 39, 8321 (2006).
- [41] K. Klenin and J. Langowski, Computation of writhe in modeling of supercoiled DNA. Biopolymers, 54, 307 (2000).
- [42] Y. Yang, I. Tobias and W. K. Olson, Finite element analysis of DNA supercoiling, J. Chem. Phys. 98, 1673 (1993).
- [43] W. R. Bauer, R. A. Lund and J. H. White, Twist and writhe of a DNA loop containing intrinsic bends, Proc. Natl. Acad. Sci. 90, 833 (1993).
- [44] M. Barbi, J. Mozziconacci, J. -M. Victor, H. Wong, and C. Lavelle, On the topology of chromatin fibres, Interface Focus 2, 546 (2012).
- [45] A. Fathizadeh, H. Schiessel and Ejtehadi M. R., Molecular dynamics simulation of supercoiled DNA rings, Macromolecules 48, 164 (2015).
- [46] N. H. Mendelson, Bacterial Growth and Division: Genes, Structures, Forces, and Clocks, Microbiol. Rev. 46, 341 (1982).
- [47] N. H. Mendelson, Helical growth of Bacillus subtilis: A new model of cell growth, Proc. Natl. Acad. Sci. 73, 1740 (1976).
- [48] R. E. Goldstein, T. R. Powers, and C. H. Wiggins, Viscous Nonlinear Dynamics of Twist and Writhe, Phys. Rev. Lett. 80, 5232 (1998).
- [49] E. E. Zajac, Stability of Two Planar Loop Elasticas, ASME J. Appl. Mech. 29, 136 (1962).
- [50] Y. Sun and J. W. Leonard, Dynamics of ocean cables with local low-tension regions, Ocean Eng. 25, 443 (1997).
- [51] S. Goyal, N. C. Perkins, and C. L. Lee, Nonlinear dynamics and loop formation in Kirchhoff rods with implications to the mechanics of DNA and cables, Journal of Computational Physics 209, 371 (2005)
- [52] A. C. Maggs, Twist and Writhe Dynamics of Stiff Polymers, Phys. Rev. Lett. 85, 5472 (2000).
- [53] M. D. Lima, N. Li, M. J. de Andrade, S. Fang, J. Oh, G. M. Spinks, M. E. Kozlov, C. S. Haines, D. Suh, J. Foroughi, S. J. Kim, Y. Chen, T. Ware, M. K. Shin, L. D. Machado, A. F. Fonseca, J. D. W. Madden, W. E. Voit, D. S. Galvão, R. H. Baughman, Electrically, Chemically, and Photonically Powered Torsional and Tensile Actuation of Hybrid Carbon Nanotube Yarn Muscles, Science 338, 928 (2012).
- [54] C. S. Haines, M. D. Lima, N. Li, G. M. Spinks, J. Foroughi, J. D. W. Madden, S. H. Kim, S. Fang, M. J. de Andrade, F. Göktepe, Ö. Göktepe, S. M. Mirvakili, S. Naficy, X. Lepró, J. Oh, M. E. Kozlov, S. J. Kim, X. Xu, B. J. Swedlove, G. G. Wallace, and R. H. Baughman, Artificial Muscles from Fishing Line and Sewing Thread, Science 343, 868 (2014).
- [55] A. A. Pevtsov, M A. Berger, A. Nindos, A. A. Norton, and L. van Driel-Gesztelyi, Magnetic Helicity, Tilt, and Twist, Space Science Reviews 186, 285 (2014)
- [56] M. W. S., W. M. van Rees, H. Kedia, D. Kleckner, and W. T. M. Irvine, Complete measurement of helicity and its dynamics in vortex tubes, Science 357, 487 (2017).
- [57] G. R. Schaller, F. Topić, K. Rissanen, Y. Okamoto, J. Shen, and R. Herges, Design and synthesis of the first triply twisted Möbius annulene, Nat. Chem. 6, 608 (2014).
- [58] V. P. Patil, J. D. Sandt, M. Kolle, and J. Dunkel, Topological mechanics of knots and tangles, Science 367, 71 (2020).
- [59] C. Peacock, E. Lee, T. Beral, R. Cisek, D. Tokarz, and L. Kreplak, Buckling and torsional instabilities of a nanoscale biological rope bound to an elastic substrate, ACS Nano 14, 12877 (2020).
- [60] A. Shahabi, H. Wang, and M. Upmanyu, Shaping van der Waals nanoribbons via torsional constraints: scrolls, folds and supercoils, Sci. Rep. 4, 7004 (2014).
- [61] J. Annett and G. L. W. Cross, Self-assembly of graphene ribbons by spontaneous self-tearing and peeling from a substrate, Nature 535, 271 (2016).
- [62] A. F. Fonseca and D. S. Galvão, Self-tearing and self-peeling of folded graphene nanoribbons, Carbon 143, 230 (2019).
- [63] D. -B. Zhang, E. Akatyeva and T. Dumitrică, Bending Ultrathin Graphene at the Margins of Continuum Mechanics, Phys. Rev. Lett. 106, 255503 (2011).
- [64] D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni, and S. B. Sinnott, A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons, J. Phys.: Condens. Matter 14, 783 (2002).
- [65] S. J. Stuart, A. B. Tutein, and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys. 112, 6472 (2000).
- [66] S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comp. Phys. 117, 1 (1995).
- [67] B. I. Yakobson, C. J. Brabec, and J. Bernholc, Nanomechanics of carbon tubes: instabilities beyond linear response, Phys. Rev. Lett. 76, 2511 (1996).
- [68] A. Garg and S. B. Sinnott, Molecular dynamics of carbon nanotubule proximal probe tip-surface contacts, Phys. Rev. B 60, 13786 (1999).
- [69] D. Srivastava, C. Wei, and K. Cho, Nanomechanics of carbon nanotubes and composites, Appl. Mech. Rev. 56, 215-230 (2003).
- [70] V. R. Coluci, N. M. Pugno, S. O. Dantas, D. S. Galvão, and A. Jorio, Atomistic simulations of the mechanical properties of ’super’ carbon nanotubes, Nanotechnology 18, 335702 (2007).
- [71] S. A. Hernandez and A. F. Fonseca, Anisotropic elastic modulus, high Poisson’s ratio and negative thermal expansion of graphynes and graphdiynes, Diamond & Related Materials 77, 57 (2017).
- [72] R. R. Del Grande, A. F. Fonseca, R. B. Capaz, Energy barriers for collapsing large-diameter carbon nanotubes, Carbon 159, 161 (2020).
- [73] E. Gao, R. Li, and R. H. Baughman, Predicted confinement-enhanced stability and extraordinary mechanical properties for carbon nanotube wrapped chains of linear carbon, ACS Nano 14, 17071 (2020).
- [74] A. F. Fonseca, and D. S. Galvão, Graphene-based nanoscale version of da Vinci’s reciprocal structures, Computational Materials Science 187, 110105 (2021).
- [75] M. Neek-Amal, and F. M. Peeters, Lattice thermal properties of graphane: thermal contraction, roughness, and heat capacity, Phys. Rev. B 83, 235437 (2011).
- [76] N. C. B. Mostério, and A. F. Fonseca, Thermal expansion behavior of holes in graphene nanomeshes, Phys. Rev. B 89, 195437 (2014).
- [77] T. E. Cantuario and A. F. Fonseca, High performance of carbon nanotube refrigerators, Annalen der Physik 531, 1800502 (2019).
- [78] G. H. M. van der Heijden, S. Neukirch, V. G. A. Goss, and J. M. T. Thompson, Instability and self-contact phenomena in the writhing of clamped rods, Int. J. Mech. Sciences 45, 161 (2003).
- [79] A. V. Savin, E. A. Korznikova, and S. V. Dmitriev, Twistons in graphene nanoribbons on a substrate, Phys. Rev. B 102, 245432 (2020).
- [80] See Supplemental Material at … for: atom coordinates files of the structures shown in Fig. 2; two Wolfram Mathematica scripts containing the calculation of the writhe of a discrete helical curve and the twist of an almost straight TGNR, before laying it on the substrates. The scripts contain the numerical calculation of and ; four movies showing upper and lateral views, respectively, of one cycle of the movement of the graphite substrates reducing the suspended size of the TGNRs of Fig. 2 and back. The colors of the structures in the movies are the same as explained in Fig. 2.
- [81] D. Rugar and P. Hansma, Atomic Force Microscopy, Physics Today 43, 23 (1990).