Twist polynomials of delta-matroids

Qi Yan
School of Mathematics
China University of Mining and Technology
P. R. China
Xian’an Jin¹¹1Corresponding author.
School of Mathematical Sciences
Xiamen University
P. R. China
Email:[email protected]; [email protected]

Abstract

Recently, Gross, Mansour and Tucker introduced the partial duality polynomial of a ribbon graph and posed a conjecture that there is no orientable ribbon graph whose partial duality polynomial has only one non-constant term. We found an infinite family of counterexamples for the conjecture and showed that essentially these are the only counterexamples. This is also obtained independently by Chumutov and Vignes-Tourneret and they posed a problem: it would be interesting to know whether the partial duality polynomial and the related conjectures would make sence for general delta-matroids. In this paper, we show that partial duality polynomials have delta-matroid analogues. We introduce the twist polynomials of delta-matroids and discuss its basic properties for delta-matroids. We give a characterization of even normal binary delta-matroids whose twist polynomials have only one term and then prove that the twist polynomial of a normal binary delta-matroid contains non-zero constant term if and only if its intersection graph is bipartite.

keywords:

delta-matroid, binary, twist, polynomial

MSC:

[2020] 05B35, 05C10, 05C31

1 Introduction

For any ribbon graph $G$ , there is a natural dual ribbon graph $G^{*}$ , also called geometric dual. Chmutov [4] introduced an extension of geometric duality called partial duality. Roughly speaking, a partial dual $G^{A}$ is obtained by forming the geometric dual with respect to only a subset $A\subseteq E(G)$ of a ribbon graph $G$ .

In [10], Gross, Mansour and Tucker introduced the enumeration of the partial duals $G^{A}$ of a ribbon graph $G$ , by Euler genus $\varepsilon$ , over all edge subsets $A\subseteq E(G)$ . The associated generating functions, denoted as ${}^{\partial}\varepsilon_{G}(z)$ , are called partial duality polynomials of $G$ . They formulated the following conjecture.

Conjecture 1.

[10] There is no orientable ribbon graph having a non-constant partial duality polynomial with only one non-zero coefficient.

The conjecture is not true. In [13] we found an infinite family of counterexamples. Furthermore, we [14] proved that essentially these are the only counterexamples. This is also obtained independently by Chumutov and Vignes-Tourneret in [5] and they also posed the following question:

Question 2.

[5] Ribbon graphs may be considered from the point of view of delta-matroid. In this way the concepts of partial duality and genus can be interpreted in terms of delta-matroids [6, 7]. It would be interesting to know whether the partial duality polynomial and the related conjectures would make sence for general delta-matroids.

In this paper, we show that partial duality polynomials have delta-matroid analogues. We introduce the twist polynomials of delta-matroids and discuss its basic properties and consider Conjecture 1 for delta-matroids. We give a characterization of even normal binary delta-matroids whose twist polynomials have only one term and then prove that the twist polynomial of a normal binary delta-matroid contains non-zero constant term if and only if its intersection graph is bipartite.

2 Preliminaries

2.1 Delta-matroids

A set system is a pair $D=(E,\mathcal{F})$ , where $E$ or $E(D)$ , is a finite set, called the ground set, and $\mathcal{F}$ , or $\mathcal{F}(D)$ , is a collection of subsets of $E$ , called feasible sets. A set system $D$ is proper if $\mathcal{F}\neq\emptyset$ and $D$ is trivial if $E=\emptyset$ .

As introduced by Bouchet in [1], a delta-matroid is a proper set system $D=(E,\mathcal{F})$ for which satisfies the symmetric exchange axiom: for all triples $(X,Y,u)$ with $X,Y\in\mathcal{F}$ and $u\in X\Delta Y$ , there is a $v\in X\Delta Y$ (possibly $v=u$ ) such that $X\Delta\{u,v\}\in\mathcal{F}$ . Here $X\Delta Y=(X\cup Y)\backslash(X\cap Y)$ is the usual symmetric difference of sets.

Let $D=(E,\mathcal{F})$ be a delta-matroid. If for any $A_{1},A_{2}\in\mathcal{F}$ , we have $|A_{1}|=|A_{2}|$ . Then $D$ is said to be a matroid and we refer to $\mathcal{F}$ as its bases. If a set system forms a matroid $M$ , then we usually denote $M$ by $(E,\mathcal{B})$ . The rank function of $M$ takes any subset $A\subseteq E(M)$ to the number

\max\{|A\cap B|:B\in\mathcal{B}\}.

This is written as $r_{M}(A)$ . We say that the rank of $M$ , written $r(M)$ , is equal to $|B|$ for any $B\in\mathcal{B}(M)$ . It is clear that the rank function of a matroid $M$ on a set $E$ has the following properties [12]:

1.

If $X\subseteq Y\subseteq E$ , then $r_{M}(X)\leq r_{M}(Y)$ ;
2.

If $X$ and $Y$ are subsets of $E$ , then

$r_{M}(X\cup Y)+r_{M}(X\cap Y)\leq r_{M}(X)+r_{M}(Y).$

The nullity of $A$ , written $n_{M}(A)$ , is $|A|-r_{M}(A)$ .

Bouchet [2] defined an analogue of the rank function for delta-matroids. Let $D=(E,\mathcal{F})$ be a delta-matroid. For $A\subseteq E$ , define

\rho_{D}(A):=|E|-min\{|A\Delta F|:F\in\mathcal{F}\}.

A delta-matroid is even if for every pair $F$ and $\widetilde{F}$ of its feasible sets $|F\Delta\widetilde{F}|$ is even. Otherwise, we call the delta-matroid odd. A delta-matroid is normal if the empty set is feasible.

For a delta-matroid $D=(E,\mathcal{F})$ , let $\mathcal{F}_{max}(D)$ and $\mathcal{F}_{min}(D)$ be the collection of maximum and minimum cardinality feasible sets of $D$ , respectively. Bouchet [3] showed that the set systems $D_{max}=(E,\mathcal{F}_{max})$ and $D_{min}=(E,\mathcal{F}_{min})$ are matroids. The width of $D$ , denote by $w(D)$ , is defined by

w(D):=r(D_{max})-r(D_{min}).

Particularly, $D$ is a matroid if and only if $w(D)=0$ .

A fundamental operation on delta-matroids, introduced by Bouchet in [1], is the twist. Let $D=(E,\mathcal{F})$ be a set system. For $A\subseteq E$ , the twist of $D$ with respect to $A$ , denoted by $D*A$ , is given by

(E,\{A\Delta X:X\in\mathcal{F}\}).

The dual of $D$ , written $D^{*}$ , is equal to $D*E$ . Using the identity

(A\Delta C)\Delta(B\Delta C)=A\Delta B,

it is straightforward to show that the twist of a delta-matroid is a delta-matroid [1]. Note that being even is preserved under taking twists.

Definition 3.

The twist polynomial of any delta-matroid $D=(E,\mathcal{F})$ is the generating function

{}^{\partial}w_{D}(z):=\sum_{A\subseteq E}z^{w(D*A)}

that enumerates all twists of $D$ by width.

Definition 4.

[7] For delta-matroids $D=(E,\mathcal{F})$ and $\widetilde{D}=(\widetilde{E},\widetilde{\mathcal{F}})$ with $E\cap\widetilde{E}=\emptyset$ , the direct sum of $D$ and $\widetilde{D}$ , written $D\oplus\widetilde{D}$ , is the delta-matroid defined as

D\oplus\widetilde{D}:=(E\cup\widetilde{E},\{F\cup\widetilde{F}:F\in\mathcal{F}~{}\text{and}~{}\widetilde{F}\in\widetilde{\mathcal{F}}\}).

A delta-matroid is disconnected if it can be written as $D\oplus\widetilde{D}$ for some non-trivial delta-matroids $D$ and $\widetilde{D}$ , and connected otherwise.

Let $D=(E,\mathcal{F})$ be a proper set system. An element $e\in E$ contained in every feasible set of $D$ is said to be a coloop, while an element $e\in E$ contained in no feasible set of $D$ is said to be a loop.

Let $D=(E,\mathcal{F})$ be a proper set system and $e\in E$ . Then $D$ delete by $e$ , denoted $D\backslash e$ , is defined as $D\backslash e:=(E\backslash e,\mathcal{F}^{\prime})$ , where

\mathcal{F}^{\prime}:=\left\{\begin{array}[]{ll}\{F:F\in\mathcal{F},F\subseteq E\backslash e\},&\text{if $e$ is not a coloop}\\ \{F\backslash e:F\in\mathcal{F}\},&\text{if $e$ is a coloop}.\end{array}\right.

Bouchet [1] has shown that the order in which deletions are performed does not matter. Let $A\subseteq E$ . We define $D\setminus A$ as the result of deleting every element of $A$ in any order. The restriction of $D$ to $A$ , written $D|_{A}$ , is the delta-matroid $D\setminus(E\backslash A)$ . Throughout the paper, we will often omit the set brackets in the case of a single element set. For example, we write $D*e$ instead of $D*\{e\}$ , or $D|_{e}$ instead of $D|_{\{e\}}$ .

2.2 Ribbon graphs

We give a brief review of ribbon graphs referring the reader to [8, 9] for further details.

Definition 5 ([9]).

A ribbon graph $G=(V(G),E(G))$ is a (possibly non-orientable) surface with boundary represented as the union of two sets of discs, a set $V(G)$ of vertices, and a set $E(G)$ of edges such that

1.

The vertices and edges intersect in disjoint line segments;
2.

Each such line segment lies on the boundary of precisely one vertex and precisely one edge;
3.

Every edge contains exactly two such line segments.

A bouquet is a ribbon graph with only one vertex. An edge $e$ of a ribbon graph is a loop if it is incident with exactly one vertex. A loop is non-orientable if together with its incident vertex it forms a Möbius band, and is orientable otherwise. A signed rotation of a bouquet is a cyclic ordering of the half-edges at the vertex and if the edge is an orientable loop, then we give the same sign $+$ to the corresponding two half-edges, and give the different signs (one $+$ , the other $-$ ) otherwise. The sign $+$ is always omitted. See Figure 1 for an example.

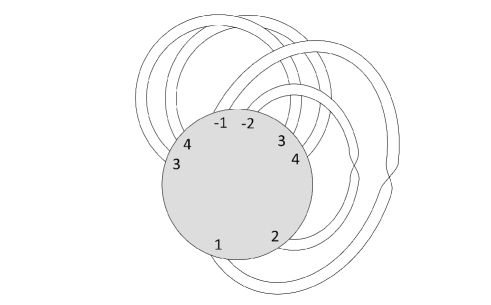
Refer to caption — Figure 1: The signed rotation of the bouquet is $(-1,-2,3,4,2,1,3,4)$ .

Definition 6.

[7] Let $G=(V,E)$ be a ribbon graph and let

\mathcal{F}:=\{F\subseteq E(G):\text{$F$ is the edge set of a spanning quasi-tree of $G$}\}.

We call $D(G)=:(E,\mathcal{F})$ the delta-matroid of $G$ .

2.3 Binary and intersection graphs

For a finite set $E$ , let $C$ be a symmetric $|E|$ by $|E|$ matrix over $GF(2)$ , with rows and columns indexed, in the same order, by the elements of $E$ . Let $C[A]$ be the principal submatrix of $C$ induced by the set $A\subseteq E$ . We define the set system $D(C)=(E,\mathcal{F})$ with

\mathcal{F}:=\{A\subseteq E:C[A]\mbox{ is non-singular}\}.

By convention $C[\emptyset]$ is non-singular. Then $D(C)$ is a delta-matroid [2]. A delta-matroid is said to be binary if it has a twist that is isomorphic to $D(C)$ for some symmetric matrix $C$ over $GF(2)$ .

Let $D=(E,\mathcal{F})$ be a delta-matroid. If $D=D(C)$ for some symmetric matrix $C$ over $GF(2)$ , that is, $D$ is a normal binary delta-matroid, then we can get $C$ as following [11]:

1.

Set $C_{v,v}=1$ if and only if $\{v\}\in\mathcal{F}$ . This determines the diagonal entries of $C$ ;
2.

Set $C_{u,v}=1$ if and only if $\{u\},\{v\}\in\mathcal{F}$ but $\{u,v\}\notin\mathcal{F}$ , or $\{u,v\}\in\mathcal{F}$ but $\{u\}$ and $\{v\}$ are not both in $\mathcal{F}$ . Then the feasible sets of size two determine the off-diagonal entries of $C$ .

Let $D=(E,\mathcal{F})$ be a normal binary delta-matroid. Then there exists a symmetric $|E|$ by $|E|$ matrix $C$ over $GF(2)$ such that $D=D(C)$ . The intersection graph $G_{D}$ of $D$ is the graph with vertex set $E$ and in which two vertices $u$ and $v$ of $G_{D}$ are adjacent if and only if $C_{u,v}=1$ . Recall that a looped simple graph is a graph obtained from a simple graph by adding (exactly) one loop to some of its vertices. If $D$ is odd, then $G_{D}$ is a looped simple graph, and if $D$ is even, then $G_{D}$ is a simple graph. Note that $D$ is connected if and only if $G_{D}$ is connected.

Conversely, the adjacency matrix $A(G)$ of a looped simple graph $G$ is the matrix over $GF(2)$ whose rows and columns correspond to the vertices of $G$ ; and where, $A(G)_{u,v}=1$ if and only if $u$ and $v$ are adjacent in $G$ and $A(G)_{u,u}=1$ if and only if there is a loop at $u$ . Let $D$ be a normal binary delta-matroid. It obvious that $D=D(A(G_{D}))$ .

3 Main results

Proposition 7.

Let $D=(E,\mathcal{F})$ and $\widetilde{D}=(\widetilde{E},\widetilde{\mathcal{F}})$ be two delta-matroids and $A\subseteq E$ . Then

1.

${}^{\partial}w_{D}(1)=2^{|E|}$ ;
2.

${}^{\partial}w_{D}(z)=~{}^{\partial}w_{D*A}(z);$
3.

${}^{\partial}w_{D\oplus\widetilde{D}}(z)=~{}^{\partial}w_{D}(z)~{}^{\partial}w_{\widetilde{D}}(z).$

Proof.

For (1), the evaluation ${}^{\partial}w_{D}(1)$ counts the total number of twists, which is $2^{|E|}$ . For (2), this is because the sets of all twists of $D$ and $D*A$ are the same. For (3), the underlying phenomenon is the additivity of width over the direct sum. It follows immediately that for any subset $B\subseteq E\cup\widetilde{E}$ , we have

(D\oplus\widetilde{D})*B=D*(B\cap E)\oplus\widetilde{D}*(B\cap\widetilde{E}),

from which formula (3) follows. ∎

Remark 8.

By Proposition 7, we can observe that analyzing the twist polynomials of all delta-matroids is equivalent to analyzing normal delta-matroids. Consequently, it is natural to focus on normal delta-matroids.

Lemma 9.

[7] Let $G=(V,E)$ be a ribbon graph, $A\subseteq E$ and $e\in E$ . Then $D(G^{A})=D(G)*A$ and $\varepsilon(G)=w(D(G))$ .

Lemma 10.

Let $G=(V,E)$ be a ribbon graph. Then ${}^{\partial}w_{D(G)}(z)=~{}^{\partial}\varepsilon_{G}(z)$ .

Proof.

By Lemma 9, for any $A\subseteq E$ ,

w(D(G)*A)=w(D(G^{A}))=\varepsilon(G^{A}).

Hence ${}^{\partial}w_{D(G)}(z)=~{}^{\partial}\varepsilon_{G}(z)$ . ∎

Theorem 11.

If two normal binary delta-matroids $D$ and $\widetilde{D}$ have the same intersection graph, then ${}^{\partial}w_{D}(z)=~{}^{\partial}w_{\widetilde{D}}(z)$ .

Proof.

Since $G_{D}=G_{\widetilde{D}}$ , $D=D(A_{G_{D}})$ and $\widetilde{D}=D(A_{G_{\widetilde{D}}})$ , it follows that $D=\widetilde{D}$ . Therefore ${}^{\partial}w_{D}(z)=~{}^{\partial}w_{\widetilde{D}}(z)$ . ∎

Theorem 12.

Let $B$ and $\widetilde{B}$ be two bouquets. If $G_{D(B)}=G_{D(\widetilde{B})}$ , then ${}^{\partial}\varepsilon_{B}(z)={{}^{\partial}}\varepsilon_{\widetilde{B}}(z)$ .

Proof.

If $G_{D(B)}=G_{D(\widetilde{B})}$ , then $D(B)=D(\widetilde{B})$ . For any $A\subseteq E(B)$ , we denoted its corresponding subset of $E(\widetilde{B})$ by $\widetilde{A}$ . By Lemma 9,

D(B^{A})=D(B)*A=D(\widetilde{B})*\widetilde{A}=D(\widetilde{B}^{\widetilde{A}}).

We have $w(D(B^{A}))=w(D(\widetilde{B}^{\widetilde{A}}))$ . Since $w(D(B^{A}))=\varepsilon(B^{A})$ and $w(D(\widetilde{B}^{\widetilde{A}}))=\varepsilon(\widetilde{B}^{\widetilde{A}})$ , it follows that $\varepsilon(B^{A})=\varepsilon(\widetilde{B}^{\widetilde{A}}).$ Thus ${}^{\partial}\varepsilon_{B}(z)=~{}^{\partial}\varepsilon_{\widetilde{B}}(z).$ ∎

Lemma 13.

[13] Let $B_{t}$ be a bouquet with the signed rotation

(1,2,3,...,t,1,2,3,...,t).

We have

{}^{\partial}\varepsilon_{B_{t}}(z)=\left\{\begin{array}[]{ll}2^{t}z^{t-1},&\mbox{if}~{}t~{}\mbox{is odd}\\ 2^{t-1}z^{t}+2^{t-1}z^{t-2},&\mbox{if}~{}t~{}\mbox{is even.}\end{array}\right.

Proposition 14.

Let $D$ be a normal binary delta-matroid and let $v$ be the number of vertices of $G_{D}$ . If $G_{D}$ is a complete graph, then

{}^{\partial}w_{D}(z)=\left\{\begin{array}[]{ll}2^{v}z^{v-1},&\text{if $v$ is odd}\\ 2^{v-1}z^{v}+2^{v-1}z^{v-2},&\text{if $v$ is even}.\end{array}\right.

Proof.

By Theorem 11, we just need to find a normal binary delta-matroid $\widetilde{D}$ such that $G_{\widetilde{D}}=G_{D}$ and the evaluation ${}^{\partial}w_{\widetilde{D}}(z)$ is easy to obtained. Let $B_{v}$ be a bouquet with the signed rotation $(1,2,3,...,v,1,2,3,...,v).$ Obviously, $G_{D(B_{v})}=G_{D}=K_{v}$ . By Lemma 10 and Theorem 11,

{}^{\partial}w_{D}(z)=~{}^{\partial}w_{D(B_{v})}(z)=~{}^{\partial}\varepsilon_{B_{v}}(z).

Therefore ${}^{\partial}w_{D}(z)$ can be obtained by Lemma 13. ∎

Theorem 15.

Let $D=(E,\mathcal{F})$ be a delta-matroid. Then ${}^{\partial}w_{D}(z)=k$ for some integer $k$ if and only if $|\mathcal{F}|=1$ .

Proof.

The sufficiency is straightforward. To prove the necessity, suppose that $|\mathcal{F}|\geq 2$ , then there exist $A_{1},A_{2}\in\mathcal{F}$ such that $A_{1}\neq A_{2}$ . Since ${}^{\partial}w_{D}(z)=k$ , we have $w(D)=0$ . Thus $|A_{1}|=|A_{2}|$ . Then for any $x\in A_{1}\backslash A_{2}$ we have $A_{1}\backslash x,A_{2}\cup x\in\mathcal{F}(D*x)$ . Obviously, $|A_{1}\backslash x|\neq|A_{2}\cup x|$ , a contradiction, since $~{}^{\partial}w_{D}(z)=~{}^{\partial}w_{D*x}(z)=k$ by Proposition 7. ∎

Lemma 16.

[7] Let $D=(E,\mathcal{F})$ be a delta-matroid and $A\subseteq E$ . Then

w(D|_{A})=\rho_{D}(A)-r_{D_{min}}(A)-n_{D_{min}}(E)+n_{D_{min}}(A).

Lemma 17.

Let $D=(E,\mathcal{F})$ be a normal delta-matroid and $A\subseteq E$ . Then

w(D*A)=w(D|_{A})+w(D|_{A^{c}}).

Proof.

Since $D$ is a normal delta-matroid, it follows that $D_{min}=(E,\{\emptyset\})$ . We have $r_{D_{min}}(A)=r_{D_{min}}(A^{c})=0$ , $n_{D_{min}}(E)=|E|,n_{D_{min}}(A)=|A|$ and $n_{D_{min}}(A^{c})=|A^{c}|$ . Then by Lemma 16,

			$\displaystyle w(D\|_{A})+w(D\|_{A^{c}})$
		$\displaystyle=$	$\displaystyle\rho_{D}(A)-r_{D_{min}}(A)-n_{D_{min}}(E)+n_{D_{min}}(A)+$
			$\displaystyle\rho_{D}(A^{c})-r_{D_{min}}(A^{c})-n_{D_{min}}(E)+n_{D_{min}}(A^{c})$
		$\displaystyle=$	$\displaystyle\rho_{D}(A)+\rho_{D}(A^{c})-\|E\|$
		$\displaystyle=$	$\displaystyle\|E\|-min\{\|A\Delta F\|:F\in\mathcal{F}\}+$
			$\displaystyle\|E\|-min\{\|A^{c}\Delta F\|:F\in\mathcal{F}\}-\|E\|$
		$\displaystyle=$	$\displaystyle\|E\|-min\{\|A^{c}\Delta F\|:F\in\mathcal{F}\}-min\{\|A\Delta F\|:F\in\mathcal{F}\}$
		$\displaystyle=$	$\displaystyle\|E\|-r((DA^{c})_{min})-r((DA)_{min})$
		$\displaystyle=$	$\displaystyle\|E\|-r((DA)^{}_{min})-r((D*A)_{min})$
		$\displaystyle=$	$\displaystyle r((DA)_{max})-r((DA)_{min})=w(D*A).$

∎

Remark 18.

This is not right for non-normal delta-matroids. For example, let $D=(\{1,2\},\{\{1\},\{2\}\})$ . It is easy to check that $D*1=(\{1,2\},\{\emptyset,\{1,2\}\})$ , $D|_{1}=(\{1\},\{\{1\}\})$ and $D|_{2}=(\{2\},\{\{2\}\})$ . Obviously, $w(D*1)=2$ and $w(D|_{1})=w(D|_{2})=0$ . Note that $w(D*1)\neq w(D|_{1})+w(D|_{2})$ .

Theorem 19.

Let $D=(E,\mathcal{F})$ be a binary normal delta-matroid. Then ${}^{\partial}w_{D}(z)$ contains non-zero constant term if and only if $G_{D}$ is a bipartite graph.

Proof.

Since ${}^{\partial}w_{D}(z)$ contains non-zero constant term, it follows that $D$ is a twist of a matroid. On account of the property that twist preserving evenness, we have that $D$ is even and hence $G_{D}$ is a simple graph. Suppose that $G_{D}$ is not bipartite. Then $G_{D}$ contains an odd cycle $P$ of length more than or equal to 3. We denote by $A$ the subset of $E$ corresponding to the vertices of $P$ . It is obvious that deleting can not increase the width. Then for any subset $B$ of $E$ , we have $w(D|_{B\cap A})\leq w(D|_{B})$ and $w(D|_{B^{c}\cap A})\leq w(D|_{B^{c}})$ . Since $D$ is a normal binary delta-matroid, we know that $D=D(C)$ for some symmetric matrix $C$ over $GF(2)$ . Note that there are $e,f\in B\cap A$ or $e,f\in B^{c}\cap A$ such that

C[\{e,f\}]=\bordermatrix{&e&f\cr e&0&1\cr f&1&0\cr}.

Then

w(D|_{B})+w(D|_{B^{c}})\geq w(D|_{B\cap A})+w(D|_{B^{c}\cap A})>0.

Thus by Lemma 17 $w(D*B)=w(D|_{B})+w(D|_{B^{c}})>0,$ a contradiction.

Conversely, if $G_{D}$ is bipartite and non-trivial, then its vertex set can be partitioned into two subsets $X$ and $Y$ so that every edge of $G_{D}$ has one end in $X$ and the other end in $Y$ . For these two subsets $X$ and $Y$ of the vertex set of $G_{D}$ , we denoted these two corresponding subset of $E$ also by $X$ and $Y$ . Obviously, $X\cup Y=E$ , $X\cap Y=\emptyset$ and $w(D|_{X})=w(D|_{Y})=0.$ Thus $w(D*X)=w(D|_{X})+w(D|_{Y})=0$ by Lemma 17. Hence ${}^{\partial}w_{D}(z)$ contains non-zero constant term. ∎

Theorem 20.

Let $D=(E,\mathcal{F})$ be a connected even normal binary delta-matroid. Then ${}^{\partial}w_{D}(z)=mz^{k}$ if and only if $G_{D}$ is a complete graph of odd order.

Proof.

The sufficiency is easily verified by Proposition 14. For necessity,

D=\left\{\begin{array}[]{ll}(\{e\},\{\emptyset\}),&\text{if $|E|=1$}\\ (\{e,f\},\{\emptyset,\{e,f\}\}),&\text{if $|E|=2$}.\end{array}\right.

Then the result is easily verified when $|E|\in\{1,2\}$ . Assume that $|E|\geq 3$ . Let $e,f,g\in E$ . We consider three claims:

Claim 1. If $\{e,f\}\in\mathcal{F}$ , we have $r_{{D^{*}}_{min}}(\{e,f\})=1$ and $r_{{D^{*}}_{min}}(e)=1$ .

Proof of Claim 1. For any $A\in\mathcal{F}_{max}$ , we observe that $A\cap\{e,f\}\neq\emptyset$ . Otherwise, $\emptyset,A\cup\{e,f\}\in\mathcal{F}(D*\{e,f\})$ . Since $\{e,f\}\in\mathcal{F}$ , it follows that $\emptyset\in\mathcal{F}(D*\{e,f\})$ . Then $w(D*\{e,f\})>w(D)$ , this contradicts ${}^{\partial}w_{D}(z)=mz^{k}$ . Furthermore, we observe that there exists $B\in\mathcal{F}_{max}$ such that $e\notin B$ . Otherwise, $r(D*e_{max})=r(D_{max})-1$ . Since $e\notin\mathcal{F}$ and $\emptyset\in\mathcal{F}$ , we have $r(D*e_{min})=1$ . Then $w(D*e)=w(D)-2$ , this also contradicts ${}^{\partial}w_{D}(z)=mz^{k}$ . Consequently, for any $A\in{\mathcal{F}^{*}}_{min}$ , $A\cap\{e,f\}\neq\{e,f\}$ and there exists $B\in{\mathcal{F}^{*}}_{min}$ such that $e\in B$ . Thus $r_{{D^{*}}_{min}}(\{e,f\})=1$ and $r_{{D^{*}}_{min}}(e)=1$ .

Claim 2. If $\{e,f\}\notin\mathcal{F}$ , we have $r_{{D^{*}}_{min}}(\{e,f\})=2$ .

Proof of Claim 2. There exists $A\in\mathcal{F}_{max}$ such that $\{e,f\}\cap A=\emptyset$ . Otherwise, $r(D*\{e,f\}_{max})\leq r(D_{max})$ . Since $\{e,f\}\notin\mathcal{F}$ and $\emptyset\in\mathcal{F}$ , we have $r(D*\{e,f\}_{min})=2$ . Then $w(D*\{e,f\})\leq w(D)-2$ , a contradiction. Consequently, there exists $A\in{\mathcal{F}^{*}}_{min}$ such that $\{e,f\}\in A$ . Thus $r_{{D^{*}}_{min}}(\{e,f\})=2$ .

Claim 3. $E$ does not contain $e,f,g$ such that $\{e,f\},\{e,g\}\in\mathcal{F}$ and $\{f,g\}\notin\mathcal{F}$ .

Proof of Claim 3. Assume that Claim 3 is not true. Since $\{e,f\},\{e,g\}\in\mathcal{F}$ , it follows that $r_{{D^{*}}_{min}}(\{e,f\})=1$ and $r_{{D^{*}}_{min}}(\{e,g\})=1$ by Claim 1. Then

			$\displaystyle r_{{D^{}}_{min}}(\{e,f\}\cup\{e,g\})+r_{{D^{}}_{min}}(\{e,f\}\cap\{e,g\})$
		$\displaystyle=$	$\displaystyle r_{{D^{}}_{min}}(\{e,f,g\})+r_{{D^{}}_{min}}(e)$
		$\displaystyle\leq$	$\displaystyle r_{{D^{}}_{min}}(\{e,f\})+r_{{D^{}}_{min}}(\{e,g\})$
		$\displaystyle=$	$\displaystyle 2.$

Hence $r_{{D^{*}}_{min}}(\{e,f,g\})\leq 1$ . Since $\{f,g\}\notin\mathcal{F}$ , we have $r_{{D^{*}}_{min}}(\{f,g\})=2$ by Claim 2. But

r_{{D^{*}}_{min}}(\{f,g\})\leq r_{{D^{*}}_{min}}(\{e,f,g\})\leq 1,

a contradiction.

Suppose that $G_{D}$ is not a complete graph. Note that $G_{D}$ is connected. Then there is a vertex set $v_{e},v_{f},v_{g}$ of $G_{D}$ such that the induced subgraph $G_{D}(\{v_{e},v_{f},v_{g}\})$ is a 2-path. We may assume without loss of generality that the degree of $v_{e}$ is 2 in $G_{D}(\{v_{e},v_{f},v_{g}\})$ . Since $D$ is a normal binary delta-matroid, we know that $D=D(C)$ for some symmetric matrix $C$ over $GF(2)$ . Then

C[\{e,f,g\}]=\bordermatrix{&e&f&g\cr e&0&1&1\cr f&1&0&0\cr g&1&0&0\cr}.

Thus $\{e,f\},\{e,g\}\in\mathcal{F}$ and $\{f,g\}\notin\mathcal{F}$ , this contradicts Claim 3. Therefore $G_{D}$ is a complete graph. ∎

Corollary 21.

Let $D=(E,\mathcal{F})$ be an even normal binary delta-matroid. Then ${}^{\partial}w_{D}(z)=mz^{k}$ if and only if each connected component of $G_{D}$ is a complete graph of odd order.

Proof.

The proof is straightforward by Proposition 7 and Theorem 20. ∎

Acknowledgements

This work is supported by NSFC (No. 11671336) and the Fundamental Research Funds for the Central Universities (Nos. 20720190062, 2021QN1037).

References

[1] A. Bouchet, Greedy algorithm and symmetric matroids, Math. Program. 38 (1987) 147–159.
[2] A. Bouchet, Representability of $\Delta$ -matroids, Colloq. Math. Soc. J $\acute{a}$ nos Bolyai (1987) 167–182.
[3] A. Bouchet, Maps and delta-matroids, Discrete Math. 78 (1989) 59–71.
[4] S. Chmutov, Generalized duality for graphs on surfaces and the signed Bollobás-Riordan polynomial, J. Combin. Theory Ser. B 99 (2009) 617–638.
[5] S. Chmutov and F. Vignes-Tourneret, On a conjecture of Gross, Mansour and Tucker, European J. Combin. 97 (2021) 103368.
[6] C. Chun, I. Moffatt, S. D. Noble and R. Rueckriemen, On the interplay between embedded graphs and delta-matroids, Proc. London Math. Soc. 118 (2019) 3: 675–700.
[7] C. Chun, I. Moffatt, S. D. Noble and R. Rueckriemen, Matroids, delta-matroids and embedded graphs, J. Combin. Theory Ser. A 167 (2019) 7–59.
[8] J. A. Ellis-Monaghan and I. Moffatt, Twisted duality for embedded graphs, Trans. Amer. Math. Soc. 364 (2012) 1529–1569.
[9] J. A. Ellis-Monaghan and I. Moffatt, Graphs on surfaces, Springer New York, 2013.
[10] J. L. Gross, T. Mansour and T. W. Tucker, Partial duality for ribbon graphs, I: Distributions, European J. Combin. 86 (2020) 103084.
[11] I. Moffatt, Surveys in Combinatorics, 2019: Delta-matroids for graph theorists, 2019.
[12] J. Oxley, Matroid theory, 2nd edn, Oxford University Press, New York, 2011.
[13] Q. Yan and X. Jin, Counterexamples to a conjecture by Gross, Mansour and Tucker on partial-dual genus polynomials of ribbon graphs, European J. Combin. 93 (2021) 103285.
[14] Q. Yan and X. Jin, Partial-dual genus polynomials and signed intersection graphs, Preprint arXiv:math.CO/2102.01823.