Tunneling conductance of -wave superconductor
Abstract
We theoretically investigate the tunneling conductance of the -wave superconductor that has recently been proposed to be realized at the (110) surface of a high- cuprate superconductor. Utilizing the quasiclassical Eilenberger theory, we obtain the self-consistent pair potentials and the differential conductance of the normal-metal/-wave superconductor junction. We demonstrate that the zero-bias peak of a -wave superconductor is robust against the spin-triplet -wave surface subdominant order, even though it is fragile against the spin-singlet -wave one. Comparing our numerical results with experimental results, we conclude that the spin-triplet -wave surface subdominant order is feasible.
I Introduction

Unconventional superconductors (SCs) can host surface bound states, the Andreev bound states (ABSs), forming a zero-energy flat band Buchholtz and Zwicknagl (1981); Hara and Nagai (1986); Hu (1994); Matsumoto and Shiba (1995a); Kashiwaya and Tanaka (2000); Löfwander et al. (2001). The zero-energy ABSs can be observed as a zero-bias conductance peak (ZBCP) in the quasiparticle tunneling spectra of the junctions of a normal metal and a high- cuprate (i.e., a spin-singlet -wave SC) Tanaka and Kashiwaya (1995); Kashiwaya et al. (1995a, 1998); Covington et al. (1997); Alff et al. (1997); Wei et al. (1998); Biswas et al. (2002); Chesca et al. (2008); Bouscher et al. (2020); Saadaoui et al. (2013). In addition, the ABSs induce a Josephson current with a low-temperature anomaly Tanaka and Kashiwaya (1996, 1997); Barash et al. (1996) and a paramagnetic Meissner current Higashitani (1997); Barash et al. (2000); Tanaka et al. (2005); Asano et al. (2011); Yokoyama et al. (2011); Suzuki and Asano (2014); Higashitani (2014); Suzuki and Asano (2015); Espedal et al. (2016); Lee et al. (2017). The origin of the ABSs has been clarified from the view point of the topological invariant defined using the bulk Hamiltonian Sato et al. (2011).
The zero-energy ABSs may be fragile against perturbations because of the high degeneracy of the flat band. The surface -wave subdominant order originating this instability was proposed Matsumoto and Shiba (1995b); Kuboki and Sigrist (1996) in 1995. Theoretically, the subdominant -wave component splits the zero-energy peak in the local density of states (LDOS) Kashiwaya et al. (1995b); Tanuma et al. (1999, 2001a) and gives rise to a spontaneous surface current by breaking the time reversal symmetry (TRS) Matsumoto and Shiba (1995c). In experiments, however, neither such peak splitting nor TRS breaking has been observed Kashiwaya et al. (1995a, 1998); Alff et al. (1997); Wei et al. (1998); Biswas et al. (2002); Chesca et al. (2008); Bouscher et al. (2020); Saadaoui et al. (2013), except for a few cases Covington et al. (1997); Fogelström et al. (1997); Krupke and Deutscher (1999). More seriously, the induced -wave pair potential requires an on-site attractive interaction, in contradiction to the strong repulsive interaction in the cuprate. The instability of the ABSs is not still conclusive, even though other possibilities have been pointed out, such as surface ferromagnetism Potter and Lee (2014), spin density wave Honerkamp and Sigrist (1998), staggered flux phase Kuboki (2014, 2015), and translational symmetry breaking Vorontsov (2009); Higashitani and Miyawaki (2015); Miyawaki and Higashitani (2015, 2017); Håkansson et al. (2015); Holmvall et al. (2018); Miyawaki and Higashitani (2018); Holmvall et al. (2019).
The spin-triplet -wave subdominant order has recently been proposed using the finite-size two-dimensional Hubbard model with the random-phase approximation Matsubara and Kontani (2020a). The ferromagnetic fluctuation caused by the ABSs can stabilize such a -wave subdominant order, which breaks the TRS Matsubara and Kontani (2020b). The obtained -wave pairing shows different properties compared with those of the -wave: there is no clear zero-energy splitting in the LDOS and no spontaneous surface current. Although a number of papers have studied the -wave state Matsumoto and Shiba (1995b, c); Tanuma et al. (1999, 2001a), the unique properties of the -wave state have not yet been clarified. In particular, the mixture of the spin-singlet and spin-triplet pairs would cause non-trivial phenomena.
We here study the conductance spectra of the normal-metal/-wave SC junctions with a subdominant -wave pair potential at the interface and compare the results with those for the well-known -wave superconducting junction. We consider a ballistic planar junction, as shown in Fig. 1, where the barrier potential is present at the interface. Utilizing the quasiclassical Eilenberger formalism, we obtain the differential conductance using the pair potential obtained by solving the self-consistency equation. The calculated results show that the ZBCP of the -wave SC can survive under the spin-triplet -wave subdominant pair potential, even though it is fragile against the spin-singlet -wave subdominant pair potential. From the spin-resolved conductance spectra, we show that the transport properties of the -wave junction strongly depend on the spin of an injected electron because of the coexistence of the spin-triplet and singlet pairs near the interface.
We also investigate whether the ZBCP can survive, even if the -wave surface attractive potential is short-range and strong, as pointed out in Ref. Matsubara and Kontani, 2020a. The ZBCP is demonstrated to be robust even against such a short-range attractive potential. Comparing our results with experimental data, we conclude that our results, which take the subdominant -wave order into account phenomenologically, support recent theoretical predictions based on microscopic calculations.
II Model and formulation
We consider the ballistic normal-metal/-wave SC junction shown in Fig. 1, where the SC and the normal-metal (N) occupy and respectively. In a ballistic SC, Green’s function obeys the Eilenberger equation Eilenberger (1968):
| (1) | |||
| (4) |
where and are the normal and anomalous Green’s functions, is the component of the Fermi velocity , is the Matsubara frequency with the integer , the direction of the momentum is characterized by the angle (, and with and ), , and (, , or ) are the Pauli matrices in the particle-hole space. In this study, the symbols and denotes the matrices in the particle–hole and spin space, respectively. The pair-potential matrix is defined as
| (9) |
where we have omitted the index . The spin structure of the pair potential is parametrized as
| (12) |
where (, , and ) is the amplitude of the -wave pair potential and (, , or ) are the Pauli matrices in spin space. The momentum dependence of the pair potentials are given by
| (13) | ||||
| (14) | ||||
| (15) |
The pair potentials are determined by the self-consistency equation:
| (16) |
where the angular brackets means the angle average on the Fermi surface: and is the cutoff integer which is decided by the relation with being the cutoff energy. The attractive potential depends on the pairing symmetry:
| (20) |
The coupling constant is
| (21) |
where is the effective critical temperature. Namely, the ratio and characterize the amplitude of the subdominant pair potential.
The microscopic theoriesMatsubara and Kontani (2020a, b) suggest that the attractive potential for the -wave channel may be short-range. To model such a short-range potential, we introduce the spatial-dependent attractive potential as
| (22) |
where is the decay parameter which characterizes the length scale of the attractive potential. Replacing in Eq. (16) by , we can self-consistently calculate the subdominant pair potential under the short-range attractive potential.
When the pair-potential matrix does not have the diagonal component as in Eq. (12), the Eilenberger equation can be decomposed into two ones:
| (23) |
The spin-reduced Green’s function and the pair potential are defined as
| (28) | |||
| (33) |
where we omit the direction index and the index and means the outer and inner components in the Nambu space respectively. Hereafter we make the index explicit only when necessary. Using the Riccati parametrization Schopohl and Maki (1995); Eschrig (2000, 2009), the quasiclassical Green’s functions can be expressed as
| (36) |
where and are the so-called Riccati amplitudes. The Riccati amplitudes obey the following Riccati-type differential equations:
| (37) | |||
| (38) | |||
| (39) | |||
| (40) |
The Eilenberger equation is supplemented by the boundary conditions Ashida et al. (1989); Nagato et al. (1993); Eschrig (2000); Tanuma et al. (2001b); Hirai et al. (2003); Eschrig (2009). The boundary conditions at the N/SC interface are given by:
| (41) |
where is the reflection probability amplitude and .
II.1 Real-energy representation
In order to discuss the quantities depending on the energy, we need the Green’s function in the real-frequency representation. The Green’s function in the real-energy space can be obtained by the analytic continuation; . In this case, the Riccati amplitudes are also converted as
| (42) |
From the Riccati amplitude , we can directly calculate the angle-resolved conductance as a function of and :
| (43) |
where , , , is the bias voltage applied to the junction and . The conductance in the normal state is obtained by solving the scattering problem: , where we assume the potential barrier with being the delta function.
The total conductance is defined as
| (44) | |||
| (45) |
where is the angle-resolved differential conductance. The conductances and correspond to those to up-spin and down-spin injections, respectively. It is convenient to introduce the normalized conductance with .
The local density of states (LDOS) can be obtained from the quasiclassical Green’s function. The LDOS is given by
| (46) |
In quasiclassical theory, the LDOS is normalized by its normal-state value.
III Results
III.1 Differential conductance



The differential conductance for the - and -wave junctions are shown in Figs. 2(a) and 2(b), respectively, where the magnified figures are shown in Figs. 2(c) and 2(d) and the pair potentials are determined self-consistently (see Appendix for details). Throughout this paper, the temperature and cutoff-energy are set to and . Figure 2 shows that the ZBCP is robust against the - wave subdominant component but fragile against the -wave component. In the case, the ZBCP survives even when . With increasing , the ZBCP becomes broader where the peak width is roughly characterized by . When , Two peaks seem to overlap at : sharper one and broader one. In the case, the ZBCP is fragile against the subdominant pair potential as shown in Fig. 2(b). In the presence of the -wave pair potential, the ZBCP is split into two peaks, where distance between two peaks are characterised by . This result is consistent with Ref.Matsumoto and Shiba, 1995b, c.
We explain the origin of the sharp and narrow peaks for the -wave junction by analyzing the injected-spin dependence of . The conductance for the up-spin and down-spin injections are shown in Fig. 3(a) and 3(b), respectively, where the parameters are set to the same values used in Fig. 2. The center of the zero-energy peak for the up-spin (down-spin) injection shifts from to a finite positive (negative) energy, where the peak becomes broader simultaneously. Although the peak center moves from the zero bias, the zero-energy conductance always has an amplitude larger than the unity independent of the injected spin. Therefore, the ZBCP of the total conductance [Fig. 2(a)] does not disappear but becomes thicker by the subdominant -wave order parameter. The spin-resolved conductance for the -wave junction (not shown) does not depend on the injected spin because both of the - and -wave pairs are spin singlet.
The angle-resolved differential conductance are shown in Fig. 4, where the pairing symmetry is assumed -wave in (a) and (b), -wave in (c), and pure -wave in (d). The injected spin is assumed up in Figs. 4(a), 4(c) 4(d), whereas down in Fig. 4(b), where the conductance for the - and pure -wave junctions does not depend on the injected spin. In the absence of a subdominant pair potential, the angle-resolved conductance has a peak at the zero bias voltage (i.e., ) independent of , [see Fig. 4(d)].
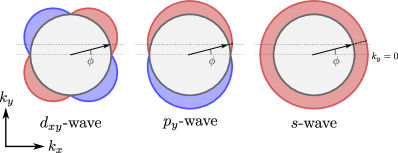
In the presence of the -wave subdominant component, the in-gap conductance peak changes from a flat band to the V [inverted V] shape for up-spin [down-spin] injection, as shown in Fig. 4(a) [Fig. 4(b)]. However, the in-gap peak around stay around because the -wave component has nodes at (see Fig. 5). As a result, for both spin injections, the zero-energy conductance have relatively large amplitude and the ZBCP in the total conductance can survive even with the -wave subdominant component
In the -wave case, the in-gap conductance changes from the flat band to a s-shaped one as shown in Fig. 4(c), where the conductance does not depend on the injected spin. Even around , the ABSs are lifted from because the -wave pair potential does not have any node on the Fermi surface (see Fig. 5). Reflecting this nodeless structure, the slope of the in-gap conductance peak around is much larger than those for the -wave junction. As a result, the conductance at of the -wave junction is greatly reduced by the subdominant component.

Contrary to the differential conductance, the LDOS reflects the splitting of the zero-energy peak owing to the subdominant pair potential. The LDOS at the interface of the - and -wave junctions are shown in Figs. 6(a) and 6(b). Comparing Figs. 6(a) and 2(a), we see that the zero-energy peak splits even in the -wave junction, where the ZBCP does not split. The zero-energy peak moves to . In , the surface state with the small angle (i.e., ) contributes more than those with large angles (i.e., ) because the conductance represents the electric current flowing in the -direction; the more perpendicular injection has the more contribution to the conductance (see the factor in the angle integration in Eq. 44). On the other hand, the LDOS is not directly related to the transport. Thus, the channels with large angles also contribute to the LDOS. Although there are two high peaks in the LDOS of the -wave junction, a sharp but low peak appears at . The origin of this low peak is the same as in the conductance. The center of the LDOS peaks shift to the positive or negative side depending on the spin. However, the LDOS for both spin have a relatively large amplitude at and make a zero-energy peak in the total LDOS.
The spontaneous edge currents in the - and -wave SCs are explained in Appendix B with focusing on the symmetry of the quasiclassical Green’s function. The spontaneous current is absent (present) in the -wave (-wave) SC.
III.2 Barrier-strength dependence

The differential conductance in the presence of a subdominant component depends on the strength of the barrier potential Tanuma et al. (2001c). The evolution of the ZBCP is shown in Figs. 7(a) and 7(b), where the - and -wave superconductor assumed in Figs. 7(a), and 7(b) respectively. The barrier potential changes asfollows: , , , , and . Effective critical temperature for the subdominant components are set to . The ZBCP for the -wave junction is present regardless of the strength of the barrier parameter . We have confirmed that the ZBCP does not split under even higher barrier potentials. In general, the position of the midgap conductance peak is not influenced by the barrier parameter . The larger barrier just results in the sharper spectra. Therefore, the low-angle contribution as discussed above can survive even with a large barrier potential.
The zero-bias conductance for the -wave is more sensitive to the barrier potential than that for that for the -wave junction. The amplitude of the zero-bias conductance reduces significantly with increasing . Even with a rather small barrier potential (e.g., ), the two peaks appear at , which corresponds to the amplitude of the subdominant -wave pair potential. Namely, the split peak would be observed more frequently in high- superconductor junctions if the -wave subdominant order is realized.
The barrier-potential dependence of the pair potentials for the - and -wave junctions are shown in Figs. 7(c) and 7(d), where the - and -wave subdominant components are shown in the insets. The barrier potential is set to , , , and . The dominant -wave pair potential is not strongly depend on . Their profiles for are almost the same regardless the pairing symmetry of the subdominant components. The amplitudes of both of the subdominant - and -wave pair potentials increase with an increase in . The larger generates the more subdominant components reflecting the parity mixing by the inversion symmetry breaking.
III.3 Effects of short decay length

The microscopic calculationsMatsubara and Kontani (2020a, b) indicates that the -wave attractive interaction may be very strong in the very vicinity of the interface. The decay length of surface -wave component may be much shorter than the superconducting coherence length and may be larger than . Such a short-range strong attractive interaction can be modeled by increasing , and by introducing the decay parameter [see Eq. (22)]: The differential conductance and pair potentials with a short-range strong attractive potential is shown in Figs. 8(a) and 8(b). The results show that the ZBCP is not split by the subdominant pair potential even when the attractive potential is much larger than that for the dominant -wave. With increasing decay parameter, the ZBCP becomes broader because the influences from the subdominant potential becomes larger.
IV Discussion
We have confirmed that our conclusions on the ZECP do not depend on the details of the potential at the interface. We have replaced the -function insulating barrier with the rectangular one. The results with the rectangular potential (not shown) are qualitatively the same as those with the -function one [e.g., Fig. 7(a)]; the ZBCP of the -wave junction does not split. Therefore, our conclusions are valid even when the interface potential has a finite width (i.e., more realistic model than the -function barrier model).
The conductance spectra of cuprate superconductors observed in experiments to date have a peak at the zero energy Kashiwaya et al. (1995a, 1998); Alff et al. (1997); Wei et al. (1998); Biswas et al. (2002); Chesca et al. (2008); Bouscher et al. (2020), even though several experiments have reported splitting of the ZBCP Covington et al. (1997); Fogelström et al. (1997); Krupke and Deutscher (1999). Our theoretical study, where the -wave surface attractive interaction is phenomenologically taken into account, demonstrates that the -wave subdominant pair potential does not split the zero-bias peak. In particular, our results show that the microscopic theory Matsubara and Kontani (2020a, b) can be consistent with experimental results obtained to date.
The conductance spectrum of a -wave junction depends on the spin of the injected particle because of the mixture of the -wave spin-triplet and -wave spin-singlet pairs. Replacing the normal-metal electrode with a ferromagnetic metal will provide useful information for detecting the surface subdominant pair potential. Investigating how the - and -wave subdominant pair potentials modify the conductance spectra would be interesting.
In this paper, we have studied the transport property of the -wave junction in the ballistic limit by calculating the tunneling conductance. The induced -wave pair, however, is more fragile against impurity scatterings than are -wave pairs Suzuki and Asano (2015); Yamada et al. (1996); Poenicke et al. (1999); Zare et al. (2008); Suzuki and Asano (2016). Thus, in the presence of disorder, the differential conductance of the - and -wave junctions may be different. Clarifying the effect of disorder would be important for applying our theory to experimental results.
V Conclusion
We have theoretically studied the conductance spectroscopy of normal-metal/-wave superconductor junctions with the spin-triplet -wave subdominant order at the interface utilizing the quasiclassical Eilenberger formalism. We have considered the ballistic junction, where a -function-type insulating barrier exists at the interface. The conductance spectra are calculated using the self-consistent pair potentials.
The calculated conductance spectra show that the ZBCP originating from the -wave pair potential is not split by the -wave subdominant pair potential at the interface, in contrast to the -wave subdominant component, which is known to split the ZBCP. The -wave pair potential has nodes at , which does not affect the zero-energy states around . The contributions from these channels form the ZBCP in the conductance spectra, even in the presence of the -wave subdominant pair potential.
In addition, we have studied the effect of the -wave subdominant pair potential on the dispersion of the surface states of the -wave SC. The -wave subdominant component changes the zero-energy flat band formed with the Andreev bound states to a V-shape or inverted V-shape, depending on the spin subspace. The spin-subspace dependence stems from the coexistence of the spin-singlet and spin-triplet pair potentials near the interface.
Acknowledgements.
The authors would like to thank S. Matsubara, S. Kashiwaya, H. Kontani, and Y. Maeno for the useful discussions. This work was supported by Grants-in-Aid from JSPS for Scientific Research on Innovative Areas “Topological Materials Science” (KAKENHI Grant Numbers JP15H05851, JP15H05852, JP15H05853 and JP15K21717), Scientific Research (A) (KAKENHI Grant No. JP20H00131), Scientific Research (B) (KAKENHI Grant Numbers JP18H01176 and JP20H01857), Japan-RFBR Bilateral Joint Research Projects/Seminars number 19-52-50026, and the JSPS Core-to-Core program “Oxide Superspin” international network.Appendix A Profile of the pair potential
The profiles of the pair potentials of the - and -wave junctions are shown in Fig. 9(a) and 9(b), respectively. The pair potentials are normalised by that in a homogeneous -wave superconductor (i.e., ). The parameters are set to the same values used in Fig. 2. The amplitude of the subdominant pair potential depends on the effective critical temperature and . The The -wave subdominant pair potential is slightly larger than the -wave one. The subdominant component affects slightly on the -wave dominant component. However, the effect is negligible.

Appendix B Spontaneous charge current
The Eilenberger equation (1) can be rewritten as
| (47) | |||
| (50) |
where . In this section, we make explicit only when necessary. The current density in the -direction can be obtained from the Green’s function:
| (51) |
where is the charge of a quasiparticle, , and . Using the basic symmetry of the Green’s function , we can reduce the current density into the form
| (52) | ||||
| (53) |
where . In Eq. (53), we have divided the interval of integration into two regions.
The matrices for the -wave SC can be written as
| (56) |
which satisfies the symmetry relation
| (57) |
This relation means that the Green’s function has the symmetry in the particle-hole space , meaning that
| (58) |
Substituting Eq. (58) into (53), we can demonstrate that no spontaneous current flows at a surface of a -wave SC without a subdominant pair potential.
The matrices for the - and -wave SCs can be written as
| (61) | ||||
| (64) |
We can show that the matrix satisfies Eq. (57), whereas does not due to . Namely, we can demonstrate that no spontaneous charge current flows in the -wave case, whereas the current flows spontaneously in the -wave case.
References
- Buchholtz and Zwicknagl (1981) L. J. Buchholtz and G. Zwicknagl, Phys. Rev. B 23, 5788 (1981).
- Hara and Nagai (1986) J. Hara and K. Nagai, Prog. Theor. Phys. 76, 1237 (1986).
- Hu (1994) C. R. Hu, Phys. Rev. Lett. 72, 1526 (1994).
- Matsumoto and Shiba (1995a) M. Matsumoto and H. Shiba, J. Phys. Soc. Jpn 64, 1703 (1995a).
- Kashiwaya and Tanaka (2000) S. Kashiwaya and Y. Tanaka, Rep. Prog. Phys. 63, 1641 (2000).
- Löfwander et al. (2001) T. Löfwander, V. S. Shumeiko, and G. Wendin, Supercond. Sci. Technol. 14, R53 (2001).
- Tanaka and Kashiwaya (1995) Y. Tanaka and S. Kashiwaya, Phys. Rev. Lett. 74, 3451 (1995).
- Kashiwaya et al. (1995a) S. Kashiwaya, Y. Tanaka, M. Koyanagi, H. Takashima, and K. Kajimura, Phys. Rev. B 51, 1350 (1995a).
- Kashiwaya et al. (1998) S. Kashiwaya, Y. Tanaka, N. Terada, M. Koyanagi, S. Ueno, L. Alff, H. Takashima, Y. Tanuma, and K. Kajimura, J. Phys. Chem. Solid 59, 2034 (1998).
- Covington et al. (1997) M. Covington, M. Aprili, E. Paraoanu, L. H. Greene, F. Xu, J. Zhu, and C. A. Mirkin, Phys. Rev. Lett. 79, 277 (1997).
- Alff et al. (1997) L. Alff, H. Takashima, S. Kashiwaya, N. Terada, H. Ihara, Y. Tanaka, M. Koyanagi, and K. Kajimura, Phys. Rev. B 55, R14757 (1997).
- Wei et al. (1998) J. Y. T. Wei, N.-C. Yeh, D. F. Garrigus, and M. Strasik, Phys. Rev. Lett. 81, 2542 (1998).
- Biswas et al. (2002) A. Biswas, P. Fournier, M. M. Qazilbash, V. N. Smolyaninova, H. Balci, and R. L. Greene, Phys. Rev. Lett. 88, 207004 (2002).
- Chesca et al. (2008) B. Chesca, H. J. H. Smilde, and H. Hilgenkamp, Phys. Rev. B 77, 184510 (2008).
- Bouscher et al. (2020) S. Bouscher, Z. Kang, K. Balasubramanian, D. Panna, P. Yu, X. Chen, and A. Hayat, Journal of Physics: Condensed Matter 32, 475502 (2020).
- Saadaoui et al. (2013) H. Saadaoui, Z. Salman, T. Prokscha, A. Suter, H. Huhtinen, P. Paturi, and E. Morenzoni, Phys. Rev. B 88, 180501 (2013).
- Tanaka and Kashiwaya (1996) Y. Tanaka and S. Kashiwaya, Phys. Rev. B 53, R11957 (1996).
- Tanaka and Kashiwaya (1997) Y. Tanaka and S. Kashiwaya, Phys. Rev. B 56, 892 (1997).
- Barash et al. (1996) Y. S. Barash, H. Burkhardt, and D. Rainer, Phys. Rev. Lett. 77, 4070 (1996).
- Higashitani (1997) S. Higashitani, J. Phys. Soc. Jpn. 66, 2556 (1997).
- Barash et al. (2000) Y. S. Barash, M. S. Kalenkov, and J. Kurkijärvi, Phys. Rev. B 62, 6665 (2000).
- Tanaka et al. (2005) Y. Tanaka, Y. Asano, A. Golubov, and S. Kashiwaya, Phys. Rev. B 72, 140503(R) (2005).
- Asano et al. (2011) Y. Asano, A. A. Golubov, Y. V. Fominov, and Y. Tanaka, Phys. Rev. Lett. 107, 087001 (2011).
- Yokoyama et al. (2011) T. Yokoyama, Y. Tanaka, and N. Nagaosa, Phys. Rev. Lett. 106, 246601 (2011).
- Suzuki and Asano (2014) S.-I. Suzuki and Y. Asano, Phys. Rev. B 89, 184508 (2014).
- Higashitani (2014) S. Higashitani, J. Phys. Soc. Jpn. 83, 075002 (2014).
- Suzuki and Asano (2015) S.-I. Suzuki and Y. Asano, Phys. Rev. B 91, 214510 (2015).
- Espedal et al. (2016) C. Espedal, T. Yokoyama, and J. Linder, Phys. Rev. Lett. 116, 127002 (2016).
- Lee et al. (2017) S.-P. Lee, R. M. Lutchyn, and J. Maciejko, Phys. Rev. B 95, 184506 (2017).
- Sato et al. (2011) M. Sato, Y. Tanaka, K. Yada, and T. Yokoyama, Phys. Rev. B 83, 224511 (2011).
- Matsumoto and Shiba (1995b) M. Matsumoto and H. Shiba, J. Phys. Soc. Jpn. 64, 3384 (1995b).
- Kuboki and Sigrist (1996) K. Kuboki and M. Sigrist, J. Phys. Soc. Jpn. 65, 361 (1996).
- Kashiwaya et al. (1995b) S. Kashiwaya, Y. Tanaka, M. Koyanagi, H. Takashima, and K. Kajimura, J. Phys. Chem. Solids 56, 1721 (1995b).
- Tanuma et al. (1999) Y. Tanuma, Y. Tanaka, M. Ogata, and S. Kashiwaya, Phys. Rev. B 60, 9817 (1999).
- Tanuma et al. (2001a) Y. Tanuma, Y. Tanaka, and S. Kashiwaya, Phys. Rev. B 64, 214519 (2001a).
- Matsumoto and Shiba (1995c) M. Matsumoto and H. Shiba, J. Phys. Soc. Jpn. 64, 4867 (1995c).
- Fogelström et al. (1997) M. Fogelström, D. Rainer, and J. A. Sauls, Phys. Rev. Lett. 79, 281 (1997).
- Krupke and Deutscher (1999) R. Krupke and G. Deutscher, Phys. Rev. Lett. 83, 4634 (1999).
- Potter and Lee (2014) A. C. Potter and P. A. Lee, Phys. Rev. Lett. 112, 117002 (2014).
- Honerkamp and Sigrist (1998) C. Honerkamp and M. Sigrist, J. Low Temp. Phys. 111, 895 (1998).
- Kuboki (2014) K. Kuboki, J. Phys. Soc. Jpn. 83, 125001 (2014).
- Kuboki (2015) K. Kuboki, J. Phys. Soc. Jpn. 84, 064706 (2015).
- Vorontsov (2009) A. B. Vorontsov, Phys. Rev. Lett. 102, 177001 (2009).
- Higashitani and Miyawaki (2015) S. Higashitani and N. Miyawaki, J. Phys. Soc. Jpn. 84, 033708 (2015).
- Miyawaki and Higashitani (2015) N. Miyawaki and S. Higashitani, Phys. Rev. B 91, 094511 (2015).
- Miyawaki and Higashitani (2017) N. Miyawaki and S. Higashitani, J. Low Temp. Phys. 187, 545 (2017).
- Håkansson et al. (2015) M. Håkansson, T. Löfwander, and M. Fogelström, Nat. Phys. 11, 755 (2015).
- Holmvall et al. (2018) P. Holmvall, T. Lofwander, and M. Fogelstrom, Journal of Physics: Conference Series 969, 012037 (2018).
- Miyawaki and Higashitani (2018) N. Miyawaki and S. Higashitani, Phys. Rev. B 98, 134516 (2018).
- Holmvall et al. (2019) P. Holmvall, A. B. Vorontsov, M. Fogelström, and T. Löfwander, Phys. Rev. B 99, 184511 (2019).
- Matsubara and Kontani (2020a) S. Matsubara and H. Kontani, Phys. Rev. B 101, 075114 (2020a).
- Matsubara and Kontani (2020b) S. Matsubara and H. Kontani, Phys. Rev. B 101, 235103 (2020b).
- Eilenberger (1968) G. Eilenberger, Z. Phys. 214, 195 (1968).
- Schopohl and Maki (1995) N. Schopohl and K. Maki, Phys. Rev. B 52, 490 (1995).
- Eschrig (2000) M. Eschrig, Phys. Rev. B 61, 9061 (2000).
- Eschrig (2009) M. Eschrig, Phys. Rev. B 80, 134511 (2009).
- Ashida et al. (1989) M. Ashida, S. Aoyama, J. Hara, and K. Nagai, Phys. Rev. B 40, 8673 (1989).
- Nagato et al. (1993) Y. Nagato, K. Nagai, and J. Hara, J. Low Temp. Phys. 93, 33 (1993).
- Tanuma et al. (2001b) Y. Tanuma, Y. Tanaka, and S. Kashiwaya, Phys. Rev. B 64, 214519 (2001b).
- Hirai et al. (2003) T. Hirai, Y. Tanaka, N. Yoshida, Y. Asano, J. Inoue, and S. Kashiwaya, Phys. Rev. B 67, 174501 (2003).
- Tanuma et al. (2001c) Y. Tanuma, K. Kuroki, Y. Tanaka, and S. Kashiwaya, Phys. Rev. B 64, 214510 (2001c).
- Yamada et al. (1996) K. Yamada, Y. Nagato, S. Higashitani, and K. Nagai, J. Phys. Soc. Jpn. 65, 1540 (1996).
- Poenicke et al. (1999) A. Poenicke, Y. S. Barash, C. Bruder, and V. Istyukov, Phys. Rev. B 59, 7102 (1999).
- Zare et al. (2008) A. Zare, A. Markowsky, T. Dahm, and N. Schopohl, Phys. Rev. B 78, 104524 (2008).
- Suzuki and Asano (2016) S.-I. Suzuki and Y. Asano, Phys. Rev. B 94, 155302 (2016).