Tunable second-order Josephson response in altermagnets
Abstract
We study the influence of external electric and Zeeman fields on the Josephson response in a planar superconductor/altermagnet/superconductor junction. Remarkably, we discover that the current-phase relation can be forward- or backward-skewed due to significant second-order Josephson response. It decisively depends on the altermagnetic field strength. Such a second-order Josephson response can be measured directly by double SQUID devices. Additionally, the skewness can be effectively manipulated by electric gating. Furthermore, we reveal two additional impacts of external fields on the Josephson current: (i) Fields can induce 0- transitions. (ii) Fields can substantially enhance the critical current. Our study opens a new avenue for exploring the second-order Josephson response in altermagnets.
Introduction.—Altermagnism is a newly discovered magnetic phase categorized by spin-group symmetries [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. It is an unconventional collinear antiferromagnet, where opposite spins at different sublattices are related by crystal rotation or reflection symmetry [1, 2], in contrast to classical antiferromagnets, where the spins are related via inversion or lattice translation symmetry. Hence, the combined time-reversal and translation (or inversion) symmetry is broken in altermagnets, leading to anisotropic spin-split energy bands in momentum space. This phenomenon has been predicted in various candidate materials [11, 7, 8, 6, 12, 2, 9, 13, 1, 14, 15, 16], such as RuO2 [11, 7, 8], MnTe [2, 14], CrSb [2, 15], FeSb2 [12, 2], Mn5Si3 [13], and CrNb4S8 [15], and confirmed experimentally in Mn5Si3 [17], MnTe [18, 19, 20, 21] and CrSb [22, 23, 24]. One notable feature of altermagnets is spin-momentum locking, protected by spin groups [2, 1, 25]. Similar spin-momentum locking can be achieved by twisting antiferromagnetic bilayers [26, 27, 28, 29]. In these systems, the altermagnetic field strength (AFS) depends crucially on the twist angle.
Recently, the interplay of altermagnetism and superconductivity has triggered intensive interest [30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40] due to its potential for uncovering novel phenomena and applications in superconducting spintronics and quantum computing. Particularly, Andreev reflection has been investigated at superconductor/altermagnet interfaces [32, 33, 34] and proposed to function as a memory device [41]. Altermagnetic Josephson junctions (AMJJs), such as superconductor/altermagnet/superconductor junctions, have been predicted to exhibit 0- transitions by modulating the junction length despite the vanishing net magnetization [35, 36, 37]. It has further been suggested that AMJJs support the formation of -junctions [42] and exhibit the superconducting diode effect [43, 44].
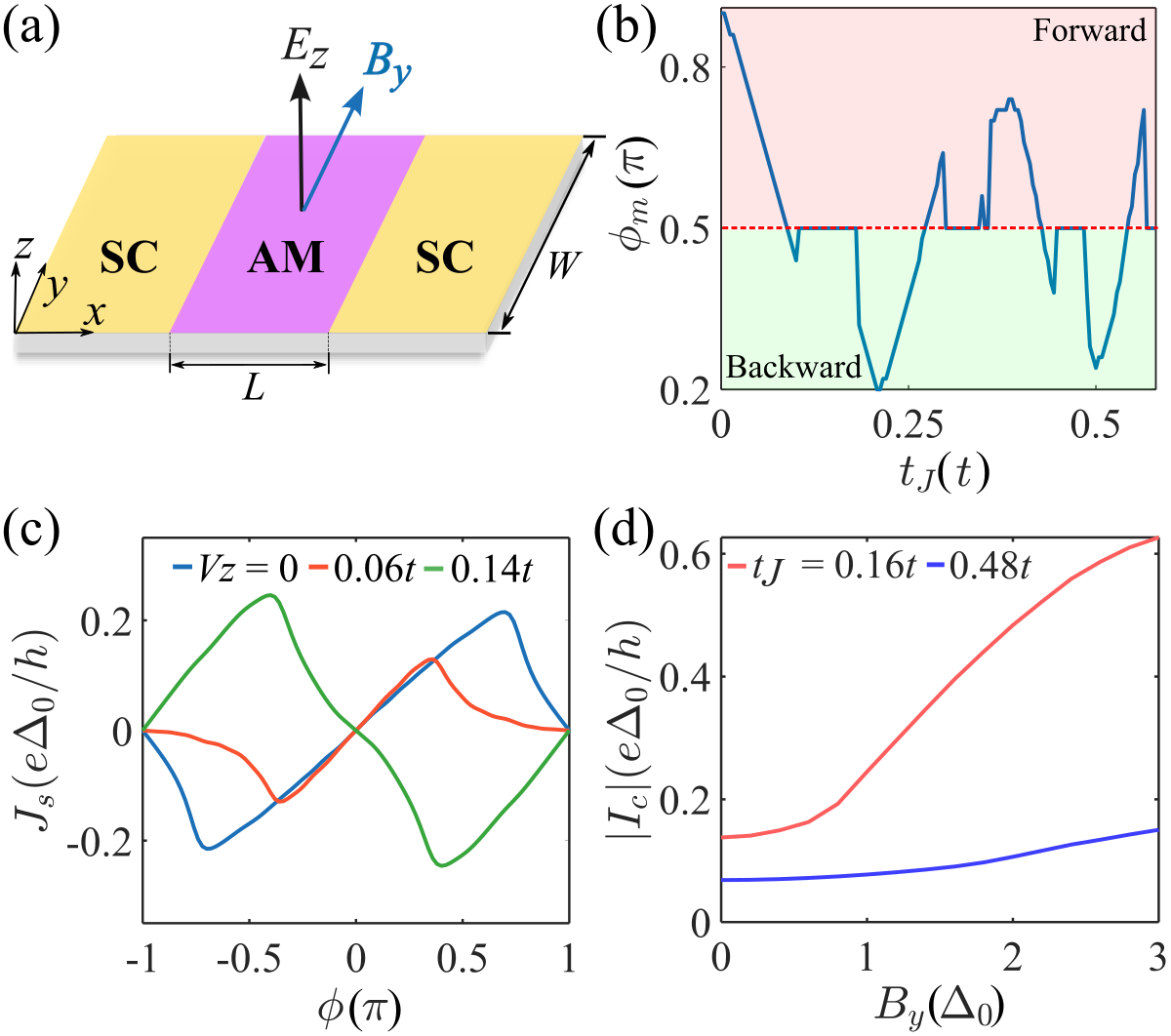
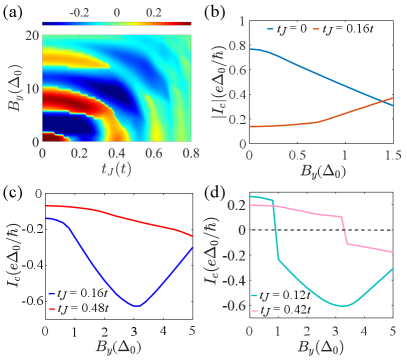
In this Letter, we study the effects of external electric or Zeeman fields on the Josephson response of AMJJs as shown in Fig. 1(a). We find that the current-phase relation (CPR) can be either forward or backward-skewed due to a large second-order Josephson response, which can be detected by double SQUID measurements [45]. The skewness changes with AFS parameter [Fig. 1(b)]. Near 0- transitions [plateau in Fig. 1(b)], supercurrent reversal emerges as the second-order Josephson response dominates. When an electric field is applied to the altermagnetic region, for significant AFS, the critical current starts to oscillate around zero, leading to - transitions. Interestingly, the magnitude of the critical current can be enhanced [Fig. 1(c)]. Moreover, external electric fields can also modify the CPR skewness [Fig. 1(c)]. Notably, the magnitude of the critical current can be substantially enhanced with increasing field strength for in-plane Zeeman fields [Fig. 1(d)]. Finally, we reveal that the Zeeman field can induce 0- transitions in AMJJs.
Model.—The altermagnet manifests non-relativistic spin splitting while having zero net magnetization, enforced by magnetic rotational symmetry. To model this, we consider the following tight-binding Hamiltonian with -wave symmetry on a square lattice [13, 1]
| (1) |
where is the 2D momentum, and are Pauli and identity matrices for spin, respectively. The first term in Eq. (1) represents the normal kinetic energy and the second term parameterized by describes the altermagnetic order. The model obeys spin symmetry, i.e., a combination of four-fold rotation in real space and two-fold rotation in spin space, which enforces -wave planar magnetism in momentum space. Notably, there exist several candidate materials with -wave planar altermagnetism, such as KRu4O8, La2CuO4 and FeSb2 [2, 1]. Transforming into real space, the Hamiltonian becomes
| (2) |
where and is the electron annihilation operator at site with spin , () is the unit vector in the () direction, and and are the hopping matrices in the and directions, respectively.
We consider planar Josephson junctions constructed by sandwiching the altermagnet with two conventional -wave superconductors, as depicted in Fig. 1(a). The junction length and width are and , respectively. This setup can be described by the Bogoliubov-de-Gennes Hamiltonian
| (3) |
where the position-dependent pairing potential is defined as with being the superconducting phase difference between the superconductors, the pairing potential, the Heaviside function, and the sign function. The chemical potential is with and being the chemical potentials in the altermagnetic and superconducting regions, respectively. , given by Eq. (2), has finite in the altermagnetic region () while in the superconducting regions (). To obtain the Josephson supercurrent, we adopt the recursive Green’s function approach [46, 47]. For convenience, periodic boundary conditions are applied along the direction. For concreteness, we set parameters , , , , and temperature throughout the paper unless specified differently.
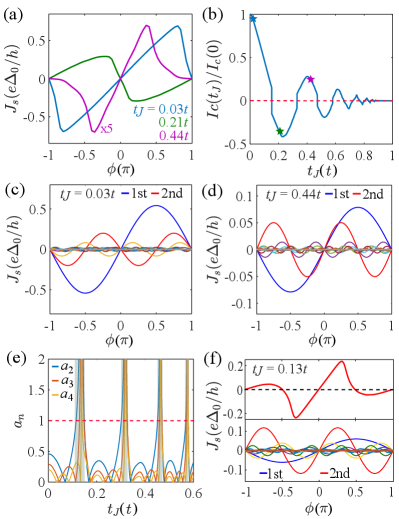
Altermagnetism induced tunable CPR skewness.—We first analyze the response of the Josephson current by changing AFS . Figure 2(a) presents several typical CPRs for various . All the CPRs are -periodic, i.e., , and odd in the phase difference , i.e., , due to inversion symmetry of the junction. The supercurrent generally has either one maximum or minimum in the positive phase region , which we define as the critical current . When the first harmonic dominates (e.g., in case of low-transparent junction interfaces), the supercurrent has a sinusoidal form . Thus, the maximum or minimum is located at . However, when the junction interfaces become more transparent, higher harmonics contribute, leading to skewed CPRs. The supercurrent is essentially determined by the derivative of the free energy of the junction to the phase difference , . For positive , the ground state (corresponding to the free energy minimum) of the junction occurs at . In contrast, for negative , the ground state occurs at . In Fig. 2(b), we calculate as a function of . We observe that oscillates around zero as increases. Similar results have been reported in a recent preprint exploiting complementary theoretical methods [42]. These oscillations indicate that the AMJJ undergoes 0- transitions [Fig. 2(a)]. They can be attributed to the proximity-induced finite-momentum pairing correlations in the altermagnet [35]. The amplitude of first quickly decreases as the altermagnetism is turned on. Then, it oscillates with a reduced amplitude and finally vanishes for . Note that is different from material to material and may be varied, e.g., by the twist angle in twisted bilayer platforms [26, 27, 28, 29].
Altermangetism can not only induce 0- transitions but also significantly affect the skewness of CPR where the impact of the second-order Josephson response is vital. The CPR dominated by the first harmonic term has the form . A skewed CPR implies the presence of pronounced higher harmonic contributing to the supercurrent, resulting in a non-sinusoidal form [48]. The skewness can be characterized by the deviation of the maximum/minimum position of from , i.e., . A positive indicates a forward-skewed CPR, while a negative corresponds to a backward-skewed CPR. In Fig. 1(b), we calculate the skewness of CPR as a function of AFS . Strikingly, the CPR can be either forward- (pink area) or backward-skewed (green area). Examples of CPRs with forward and backward skewness are explicitly shown in Fig. 2(a). When the transparency of the junction changes because of the presence of altermagnetism, the second-order Josephson response can not be ignored, leading to the non-sinusoidal form of Josephson supercurrent with . Note that the skewness of CPR is primarily dictated by the sign of the second harmonic term. Using 0-junction () as an example, for a negative second harmonic term, the CPR is forward-skewed with as illustrated in Figs. 2(a) and 2(c) with and . For a positive second harmonic term, the CPR is backward-skewd with as shown in Figs. 2(a) and 2(d) with and . A similar ratio of has recently been observed in planar Josephson junctions based on Al/InAs-quantum wells [49]. The second-order Josephson response in AMJJs can be detected in SQUID devices or in tunnel junctions [45, 50]. More details on the skewness analysis can be found in the Supplemental Material (SM) [51]. Notably, the skewness can be as large as . This particular feature of tunable skewness of CPRs in AMJJs may be exploited to realize a large Josephson diode effect, e.g, in supercurrent interferometers [52]. We also note that multiple maxima may appear in the CPR due to dominant higher harmonics. Figure 2(e) shows the higher harmonic contribution compared to the first harmonic as a function of AFS with representing the amplitude of th harmonic and . When higher harmonics are dominant (), as illustrated in the grey shaded area in Fig. 2(e), the AMJJ turns into a -Josephson junction. An example for dominant second-order Josephson response is shown in Fig. 2(f). In these cases, the skewness is not clearly defined. Thus, we exclude them in Fig. 1(b). We emphasize that the tunable second-order Josephson response is important in applications as it enhances the robustness of superconducting quantum bits [45].
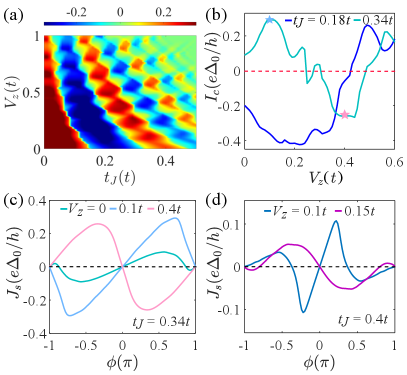
Tuning CPR skewness and critical current by gating.—Now, we investigate the influence of an external gate potential on the Josephson current. Figure 3(a) shows the critical current of the AMJJ as functions of AFS and gate potential for . For small (i.e., ), is always positive with only slight oscillations. These oscillations appear due to Fabry-Pérot interferences. Thus, there is no 0- transition. As increases, we observe transitions alongside a tilted interference pattern. The larger , the more inclined the interference pattern becomes, as illustrated in the phase diagram in Fig. 3(a). Hence, oscillates around zero with increasing for stronger AFS (i.e., ). Figure 3(b) presents as a function of for and . This plot demonstrates the switching of the AMJJ between 0 and junctions by changing the gate potential, as illustrated in Fig. 3(c). Meanwhile, the magnitude of is substantially enhanced for a wide range of gate potential, as shown in Fig. 3(b). Notably, the critical current can be enhanced by a factor 3 before the 0- transition occurs for , as illustrated in Fig. 3(b). The corresponding CPRs are displayed in Fig. 3(c). The observed enhancement is primarily governed by finite-momentum pairing, depending on both the gate potential and the AFS [35]. Furthermore, the skewness of CPR can also be manipulated by electric gating. For instance, the CPR changes from forward- to backward-skewed, as shown in Fig. 1(c). Additionally, a 0-junction can be transformed into a - or -junction by adjusting the gate potential, as illustrated in Figs. 1(c) and 3(d). Gate-tunable -junctions, shown in Fig. 3(d), have previously been reported in Ref. [42]. These gate-tunable characteristics of AMJJs enrich their potential applications in superconducting circuits and spintronics.
Enhancement of supercurrent by Zeeman fields.—Now, we discuss the influence of an in-plane magnetic field on the supercurrent in AMJJs, modeled by by the Zeeman term . The particular in-plane direction of the magnetic field does not matter qualitatively for our results. Figure 4(a) illustrates the phase diagram of the AMJJ against and . The stripes bend downward as grows. This demonstrates the competition between altermagnetism and Zeeman effect. Strikingly, this competition gives rise to the enhancement of the critical current as shown in Figs. 1(d) and 4(b). In absence of altermagnetism (), the critical current decreases as the Zeeman field increases, illustrated by the blue line in Fig.4(b). However, the critical current can be monotonically enhanced when both altermagnetism and Zeeman field are present, as illustrated in Fig. 1(d) and the orange line in Fig. 4(b). Moreover, the magnitude of the critical current increases monotonically for large AFS as shown in Fig. 4(c) for . Nevertheless, it first increases then decreases for small AFS, illustrated in Fig. 4(c) for . To reach substantial ratios of , we envision that type-II superconductors, such as Nb and MoRe [53, 54], form the AMJJs with an altermagnet with large g-factor as the weak link.
The enhancement of the critical current in the presence of an exchange field is uncommon because the critical current generally decreases with increasing field strength in both ferromagnetic [55] and altermagnetic [Fig. 2(b)] Josephson junctions. Nevertheless, in a superconductor/ferromagnet bilayer separated by an insulating film, the critical current can also be enhanced when the exchange fields in the two ferromagnets are anti-parallel, resulting in no net magnetization [56]. Notably, the mechanism underlying the enhancement of the critical current in AMJJs differs from this scenario, as AMJJs exhibit net magnetization in presence of Zeeman fields. This phenomenon is a characteristic signature of altermagnetic superconducting heterostructures.
Another impact of Zeeman fields on AMJJs is that it induces 0- transitions. - transitions emerge as changes as shown in Fig. 4(d). These oscillations stem from the Fermi surface spin splitting by the Zeeman field. For an AFS less than , the AMJJ transforms from 0-junction () to -junction () for , as shown in Fig. 4(a) and the cyan line in Fig. 4(d). Additionally, it needs larger Zeeman field to induce 0- transition for large AFS as shown in Fig. 4(d).
Conclusion.—We investigate the influence of external electric and Zeeman fields on AMJJs. We reveal that changing the AFS significantly alters the second-order Josephson response, enabling both forward- and backward-skewed CPRs in the junction. Applying either an electric or a Zeeman field can also significantly enhance the magnitude of the critical current across the junction. Remarkably, 0- transitions can be controlled by either electric gating or Zeeman fields. Moreover, we discover that the second-order Josephson response can be manipulated by electric gating.
Acknowledgements.
We thank Charles Gould, Lun-Hui Hu, Kristian Mæland, Martin Stehno and Shun Tamura for valuable discussions. This work was supported by the Würzburg-Dresden Cluster of Excellence ct.qmat (Project-id 390858490), the DFG (SFB 1170), and the Bavarian Ministry of Economic Affairs, Regional Development and Energy for financial support within the High-Tech Agenda Project “Bausteine für das Quanten Computing auf Basis topologischer Materialen”. S.B.Z. acknowledges the support of the start-up fund at HFNL, the Innovation Program for Quantum Science and Technology (Grant No. 2021ZD0302800), and Anhui Initiative in Quantum Information Technologies (Grant No. AHY170000).Note added.—During finalizing the manuscript, we became aware of a related preprint [42], which partially overlaps with our work but puts emphasis on Josephson junctions.
References
- Šmejkal et al. [2022a] L. Šmejkal, J. Sinova, and T. Jungwirth, “Emerging Research Landscape of Altermagnetism”, Phys. Rev. X 12, 040501 (2022a).
- Šmejkal et al. [2022b] L. Šmejkal, J. Sinova, and T. Jungwirth, “Beyond Conventional Ferromagnetism and Antiferromagnetism: A Phase with Nonrelativistic Spin and Crystal Rotation Symmetry”, Phys. Rev. X 12, 031042 (2022b).
- Wu et al. [2007] C. Wu, K. Sun, E. Fradkin, and S.-C. Zhang, “Fermi liquid instabilities in the spin channel”, Phys. Rev. B 75, 115103 (2007).
- Naka et al. [2019] M. Naka, S. Hayami, H. Kusunose, Y. Yanagi, Y. Motome, and H. Seo, “Spin current generation in organic antiferromagnets”, Nat. Commun. 10, 4305 (2019).
- Shao et al. [2021] D.-F. Shao, S.-H. Zhang, M. Li, C.-B. Eom, and E. Y. Tsymbal, “Spin-neutral currents for spintronics”, Nat. Commun. 12, 7061 (2021).
- Hayami et al. [2019] S. Hayami, Y. Yanagi, and H. Kusunose, “Momentum-Dependent Spin Splitting by Collinear Antiferromagnetic Ordering”, J. Phys. Soc. Jpn. 88, 123702 (2019).
- Ahn et al. [2019] K.-H. Ahn, A. Hariki, K.-W. Lee, and J. Kuneš, “Antiferromagnetism in RuO2 as -wave Pomeranchuk instability”, Phys. Rev. B 99, 184432 (2019).
- Šmejkal et al. [2020] L. Šmejkal, R. González-Hernández, T. Jungwirth, and J. Sinova, “Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets”, Science Advances 6, eaaz8809 (2020).
- Yuan et al. [2020] L.-D. Yuan, Z. Wang, J.-W. Luo, E. I. Rashba, and A. Zunger, “Giant momentum-dependent spin splitting in centrosymmetric low- antiferromagnets”, Phys. Rev. B 102, 014422 (2020).
- [10] L. Bai, W. Feng, S. Liu, L. Šmejkal, Y. Mokrousov, and Y. Yao, “Altermagnetism: Exploring new frontiers in magnetism and spintronics”, arXiv:2406.02123 .
- Berlijn et al. [2017] T. Berlijn, et al., “Itinerant Antiferromagnetism in RuO2”, Phys. Rev. Lett. 118, 077201 (2017).
- Mazin et al. [2021] I. I. Mazin, K. Koepernik, M. D. Johannes, R. González-Hernández, and L. Šmejkal, “Prediction of unconventional magnetism in doped FeSb2”, P. Natl. Acad. Sci. Usa. 118, e2108924118 (2021).
- Šmejkal et al. [2022c] L. Šmejkal, A. B. Hellenes, R. González-Hernández, J. Sinova, and T. Jungwirth, “Giant and Tunneling Magnetoresistance in Unconventional Collinear Antiferromagnets with Nonrelativistic Spin-Momentum Coupling”, Phys. Rev. X 12, 011028 (2022c).
- Mazin [2023] I. I. Mazin, “Altermagnetism in mnte: Origin, predicted manifestations, and routes to detwinning”, Phys. Rev. B 107, L100418 (2023).
- Guo et al. [2023] Y. Guo, H. Liu, O. Janson, I. C. Fulga, J. van den Brink, and J. I. Facio, “Spin-split collinear antiferromagnets: A large-scale ab-initio study”, Materials Today Physics 32, 100991 (2023).
- [16] Z. Lin, et al., “Observation of Giant Spin Splitting and d-wave Spin Texture in Room Temperature Altermagnet RuO2”, arXiv:2402.04995 .
- Reichlova et al. [2024] H. Reichlova, et al., “Observation of a spontaneous anomalous Hall response in the Mn5Si3 d-wave altermagnet candidate”, Nat. Commun. 15, 4961 (2024).
- Krempaský et al. [2024] J. Krempaský, et al., “Altermagnetic lifting of Kramers spin degeneracy”, Nature 626, 517 (2024).
- Lee et al. [2024] S. Lee, et al., “Broken Kramers Degeneracy in Altermagnetic MnTe”, Phys. Rev. Lett. 132, 036702 (2024).
- Osumi et al. [2024] T. Osumi, S. Souma, T. Aoyama, K. Yamauchi, A. Honma, K. Nakayama, T. Takahashi, K. Ohgushi, and T. Sato, “Observation of a giant band splitting in altermagnetic MnTe”, Phys. Rev. B 109, 115102 (2024).
- [21] N. N. Orlova, A. A. Avakyants, A. V. Timonina, N. N. Kolesnikov, and E. V. Deviatov, “Crossover from relativistic to non-relativistic net magnetization for MnTe altermagnet candidate”, arxiv:2403.15348 .
- Reimers et al. [2024] S. Reimers, et al., “Direct observation of altermagnetic band splitting in CrSb thin films”, Nat. Commun. 15, 2116 (2024).
- [23] J. Ding, et al., “Large band-splitting in -wave type altermagnet CrSb”, arxiv:2405.12687 .
- [24] G. Yang, et al., “Three-dimensional mapping and electronic origin of large altermagnetic splitting near Fermi level in CrSb”, arXiv:2405.12575 .
- Liu et al. [2022] P. Liu, J. Li, J. Han, X. Wan, and Q. Liu, “Spin-Group Symmetry in Magnetic Materials with Negligible Spin-Orbit Coupling”, Phys. Rev. X 12, 021016 (2022).
- He et al. [2023] R. He, D. Wang, N. Luo, J. Zeng, K.-Q. Chen, and L.-M. Tang, “Nonrelativistic Spin-Momentum Coupling in Antiferromagnetic Twisted Bilayers”, Phys. Rev. Lett. 130, 046401 (2023).
- [27] S. Sheoran and S. Bhattacharya, “Nonrelativistic spin splittings and altermagnetism in twisted bilayers of centrosymmetric antiferromagnets”, arxiv:2310.19395 .
- [28] Y. Liu, J. Yu, and C.-C. Liu, “Twisted Magnetic Van der Waals Bilayers: An Ideal Platform for Altermagnetism”, arxiv:2404.17146 .
- [29] S. Zeng and Y.-J. Zhao, “Bilayer stacking A-type altermagnet: A general approach to generating two-dimensional altermagnetism”, arXiv:2407.15097 .
- Zhu et al. [2023] D. Zhu, Z.-Y. Zhuang, Z. Wu, and Z. Yan, “Topological superconductivity in two-dimensional altermagnetic metals”, Phys. Rev. B 108, 184505 (2023).
- Wei et al. [2024] M. Wei, L. Xiang, F. Xu, L. Zhang, G. Tang, and J. Wang, “Gapless superconducting state and mirage gap in altermagnets”, Physical Review B 109, L201404 (2024).
- Sun et al. [2023] C. Sun, A. Brataas, and J. Linder, “Andreev reflection in altermagnets”, Phys. Rev. B 108, 054511 (2023).
- Papaj [2023] M. Papaj, “Andreev reflection at the altermagnet-superconductor interface”, Phys. Rev. B 108, L060508 (2023).
- [34] Y. Nagae, A. P. Schnyder, and S. Ikegaya, “Spin-polarized Specular Andreev Reflections in Altermagnets”, arxiv:2403.07117 .
- Zhang et al. [2024a] S.-B. Zhang, L.-H. Hu, and T. Neupert, “Finite-momentum Cooper pairing in proximitized altermagnets”, Nat. Commun. 15, 1801 (2024a).
- Ouassou et al. [2023] J. A. Ouassou, A. Brataas, and J. Linder, “Dc Josephson Effect in Altermagnets”, Phys. Rev. Lett. 131, 076003 (2023).
- Beenakker and Vakhtel [2023] C. W. J. Beenakker and T. Vakhtel, “Phase-shifted Andreev levels in an altermagnet Josephson junction”, Phys. Rev. B 108, 075425 (2023).
- Sumita et al. [2023] S. Sumita, M. Naka, and H. Seo, “Fulde-Ferrell-Larkin-Ovchinnikov state induced by antiferromagnetic order in -type organic conductors”, Phys. Rev. Res. 5, 043171 (2023).
- Chakraborty and Black-Schaffer [2024] D. Chakraborty and A. M. Black-Schaffer, “Zero-field finite-momentum and field-induced superconductivity in altermagnets”, Phys. Rev. B 110, L060508 (2024).
- Cheng and Sun [2024] Q. Cheng and Q. Sun, “Orientation-dependent Josephson effect in spin-singlet superconductor/altermagnet/spin-triplet superconductor junctions”, Phys. Rev. B 109, 024517 (2024).
- Giil and Linder [2024] H. G. Giil and J. Linder, “Superconductor-altermagnet memory functionality without stray fields”, Phys. Rev. B 109, 134511 (2024).
- [42] B. Lu, K. Maeda, H. Ito, K. Yada, and Y. Tanaka, “ Josephson junction induced by altermagnetism”, arxiv:2405.10656 .
- Banerjee and Scheurer [2024] S. Banerjee and M. S. Scheurer, “Altermagnetic superconducting diode effect”, Phys. Rev. B 110, 024503 (2024).
- [44] D. Chakraborty and A. M. Black-Schaffer, “Perfect superconducting diode effect in altermagnets”, arXiv:2408.07747 .
- Messelot et al. [2024] S. Messelot, N. Aparicio, E. de Seze, E. Eyraud, J. Coraux, K. Watanabe, T. Taniguchi, and J. Renard, “Direct measurement of a current phase relation in a graphene superconducting quantum interference device”, Phys. Rev. Lett. 133, 106001 (2024).
- Furusaki [1994] A. Furusaki, “DC Josephson effect in dirty SNS junctions: Numerical study”, Physica B: Condensed Matter 203, 214 (1994).
- Asano [2001] Y. Asano, “Numerical method for dc Josephson current between d-wave superconductors”, Phys. Rev. B 63, 052512 (2001).
- Golubov et al. [2004] A. A. Golubov, M. Y. Kupriyanov, and E. Il’ichev, “The current-phase relation in Josephson junctions”, Rev. Mod. Phys. 76, 411 (2004).
- Zhang et al. [2024b] P. Zhang, et al., “Large second-order Josephson effect in planar superconductor-semiconductor junctions”, SciPost Physics 16, 030 (2024b).
- Willsch et al. [2024] D. Willsch, et al., “Observation of Josephson harmonics in tunnel junctions”, Nat. Phys. 20, 815 (2024).
- [51] See Supplemental Material for more details .
- Souto et al. [2022] R. S. Souto, M. Leijnse, and C. Schrade, “Josephson diode effect in supercurrent interferometers”, Phys. Rev. Lett. 129, 267702 (2022).
- Li et al. [2021] C.-Z. Li, A.-Q. Wang, C. Li, W.-Z. Zheng, A. Brinkman, D.-P. Yu, and Z.-M. Liao, “Topological transition of superconductivity in dirac semimetal nanowire josephson junctions”, Phys. Rev. Lett. 126, 027001 (2021).
- Mandal et al. [2024] P. Mandal, S. Mondal, M. P. Stehno, S. Ilić, F. S. Bergeret, T. M. Klapwijk, C. Gould, and L. W. Molenkamp, “Magnetically tunable supercurrent in dilute magnetic topological insulator-based Josephson junctions”, Nat. Phys. , 1 (2024).
- Ryazanov et al. [2001] V. V. Ryazanov, V. A. Oboznov, A. Y. Rusanov, A. V. Veretennikov, A. A. Golubov, and J. Aarts, “Coupling of two superconductors through a ferromagnet: Evidence for a junction”, Phys. Rev. Lett. 86, 2427 (2001).
- Bergeret et al. [2001] F. S. Bergeret, A. F. Volkov, and K. B. Efetov, “Enhancement of the Josephson Current by an Exchange Field in Superconductor-Ferromagnet Structures”, Phys. Rev. Lett. 86, 3140 (2001).
Supplemental Material
In the following, we derive the real space lattice model and introduce the recursive Green’s function approach. Additionally, we analyse the sknewness change by a simple model.
SI Model
We use the following continuum model [13, 1]
| (S1) |
By substituting with and , we map the continuum model to a square lattice, which reads
| (S2) |
Ignoring the energy shift and substituting and , we obtain the lattice model in the main text. After Fourier transformation, we arrive at the real space Hamiltonian with periodic boundary condition along -direction as
| (S3) |
SII Recursive Green’s function approach
We calculate the Josephson current exploiting the recursive Green’s function approach [46, 47]. Since we assume translation symmetry along -direction, is a good quantum number. The planar Josephson junction we study is a quasi-1D system along -direction. In the calculation, we put the Boltzmann constant . The number of points is 500.
Employing the lattice model in the main text, the dc Josephson current can be calculated as
| (S4) |
where is the Green’s function in Nambu space, is the third Pauli matrix in particle-hole space, is the Matsubara frequency, and is the hopping matrix. The Nambu Green’s function for each Matsubara frequency and momentum can be obtained by the iterative method
| (S5) |
where is a unit matrix, is the on-site energy matrix, and is the hopping matrix between two neighbouring sites. The superconducting leads are modeled using self-energy terms attached to the altermagnetic region. The self-energy terms incorporate the superconducting gap and the phase difference between the superconductors. By attaching the superconductor to the altermagnetic region, the Green’s function of the connected system can be obtained as
| (S6) |
By substituting the above two equations into Eq.(S4) for each Matsubara frequency and then summing over them, we obtain the dc Josephson current.
SIII Skewness analysis
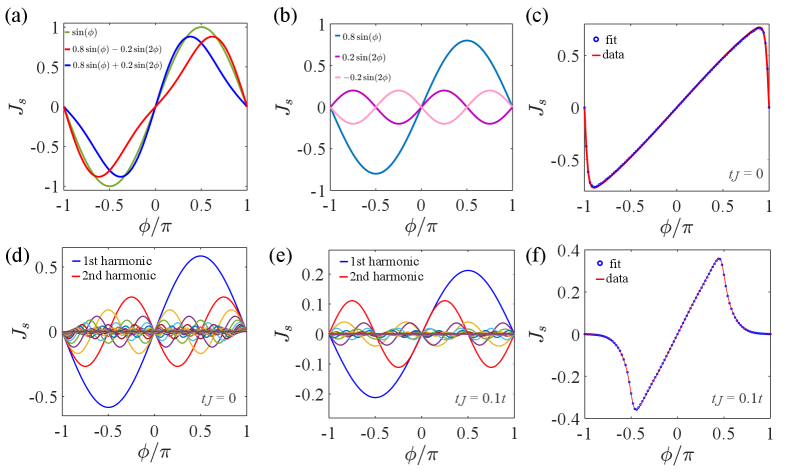
In the main text, we show that the skewness varies as the altermagnetic field strength grows (Fig.1 in the main text). Here, we propose a simple model to simulate the skewness change. The sinusoidal form of the Josephson supercurrent reads with the critical current, shown in Fig. S1(a). When the transparency of the junction changes because of the introduction of altermagnetism, the second harmonic contribution can not be ignored leading to the nonsinusoidal form of Josephson supercurrent with . For the case with negative second harmonic term, the skewness is forward with as illustrated in Fig. S1(a). For the case with positive second harmonic term, the skewness is backward with . The first harmonic and second harmonic terms are depicted in Fig. S1(b). The nonsinusoidal behavior without altermagnetism () can be captured by expressing the CPR as Fourier series [48]
| (S7) |
where is an integer, and . It is illustrated in Figs. S1 (c)-(d) with . When the altermagnetism is introduced, the higher harmonic terms change sign. For instance, as the sign of the second harmonic term () changes from minus to plus the skewness of the CPR becomes backward as illustrated in Figs. S1 (e)-(f) with .