Tunable planar Josephson junctions driven by time-dependent spin-orbit coupling

In the push to implement beyond-CMOS applications, Josephson junctions (JJs) have found their broad use due to their high-speed switching, low-power dissipation, and intrinsic nonlinearities[1, 2]. In addition to the well-established role of JJs as the key elements for superconducting electronics and superconducting qubits[1, 2, 3, 4, 5, 6], there is a growing interest in tailoring their spin-dependent properties to enable dissipationless spin currents, cryogenic memory[7, 9, 10, 11, 12, 13, 8, 14], and fault-tolerant quantum computing[15, 16, 17, 18, 19, 20, 21, 22]. The role of spin-orbit coupling (SOC) has been extensively studied in the normal-state properties and recognized for its importance in spintronics[23, 24, 25]. However, the superconducting analogs of the SOC-related effects remain to be understood. They might even be important when their normal-state counterparts are negligibly small[26, 27, 28, 29, 30, 31, 32]. Motivated by the recent progress in gate-controlled SOC in planar JJs based on a two-dimensional electron gas (2DEG)[33, 34, 35], we reveal how time-dependent SOC tunes many of their key properties and offers an unexplored mechanism to drive JJs.

A common description of a JJ circuit, is given by a Josephson element, resistor, and capacitor connected in parallel, using the resistively and capacitively shunted junction (RSCJ)[1] model. The bias current through the junction, $i$, is the sum of the supercurrent and the quasiparticle current flowing in the resistor and capacitor. The supercurrent is usually assumed as $I(\varphi)=I_{c}\sin(\varphi+\varphi_{0})$, where $I_{c}$ is the maximum supercurrent, $\varphi$ is the phase difference between the superconducting regions, and the anomalous phase, $\varphi_{0}\neq 0,\pi$, arises from the broken time-reversal and inversion symmetries[37, 38, 39, 40, 41, 42, 43].

For a ballistic JJ depicted in Fig. 1(a), the interplay between SOC and the effective Zeeman field ${\bf h}$, yields a more complex current-phase relation (CPR) than $I(\varphi)$ given above, such that for a generalized RSCJ model

where $\tau=\omega_{p}t$ is a dimensionless time, expressed using the JJ plasma frequency, $\omega_{p}=\sqrt{2\pi I_{c}/\Phi_{0}C}$, $\Phi_{0}=h/2e$ is the magnetic flux quantum, and $C$ is the capacitance. The damping of this nonlinear oscillator is characterized by the Stewart-McCumber parameter, $\beta_{c}=2\pi I_{c}CR^{2}/\Phi_{0}$, where $R$ is the resistance[44, 45] and $Q=\sqrt{\beta_{c}}$ is the quality factor. The generalized CPR can be modified by the chemical potential $\mu$, and ${\bf h}$, arising from the applied magnetic field or magnetic proximity effect[46]. Since $h_{z}$ does not induce $\varphi_{0}$[47, 48] and only produces CPR reversals, we focus on $h_{z}=0$ [Fig.  1(a)]. The CPR can also be tuned by the Rashba SOC, illustrated in Fig. 1(a), which is parametrized by its strength $\alpha$, in the Hamiltonian, $H_{\mathrm{so}}=\alpha(\bf\sigma\times{\bf p})\cdot{\bf\hat{z}}$. Here, $\bf\sigma$ is the Pauli matrix vector, and $\bf p$ is the in-plane momentum, for 2DEG with the inversion symmetry broken along the $z$-direction[49].

While quasistatic gate-tunable changes in SOC and $\varphi_{0}$ have been demonstrated in 2DEG-based JJs[33, 34], the implications of dynamically tuned SOC on the CPR remain unexplored. For a conventional CPR without any $\varphi_{0}$, Eq. (1) has a mechanical analog with a driven and damped pendulum, in which $\varphi$ becomes the displacement angle[44, 45]. A JJ driven by $i$ is equivalent to the pendulum displaced by an external torque from its stable equilibrium, determined by the gravitational acceleration $\bf g$, while $\omega_{p}$ determines the oscillation frequency around a stable equilibrium point[1].

Instead of using $i$, Fig. 1(b) suggests an entirely different way to drive the pendulum: By changing the orientation of the effective $\bf g^{\prime}$ and the new equilibrium, resulting from the interplay of the static $\bf h$ and time-dependent $\alpha$. With JJ advances and gate changes exceeding the gigahertz range[3], there is a tantalizing prospect for dynamically controlled CPR by time-dependent SOC. Unlike assuming a specific relation, $I(\varphi)=I_{c}\sin(\varphi+\varphi_{0})$, the CPR can have a more general and anharmonic form which should be obtained microscopically. To this end, a single-particle Hamiltonian, $H({\bf p})={\bf p}^{2}/2m^{*}+{\bf\sigma}\cdot{\bf h}+H_{\mathrm{so}}({\bf p})$, where $m^{*}$ is the effective mass, can be used to solve a BCS model of superconductivity, given by the effective Hamiltonian

where $\hat{\Delta}$ is a $2\times 2$ superconducting gap in spin space[47].

After diagonalizing the resulting Bogoliubov–de Gennes equations, ${\cal H}\hat{\psi}=E\hat{\psi}$, where $\hat{\psi}$ is the four-component wave function for quasiparticle states with energy $E$, we match the wave functions and generalized velocities at interfaces ($x=0,d$), shown in Fig. 1(a). This allows us to obtain the ground-state JJ energy $E_{\mathrm{GS}}$, together with the corresponding CPR, using charge conservation and the quantum definition of current[47, 47]. The CPR is related to the JJ energy: $I(\varphi)\propto\partial E_{\mathrm{GS}}/\partial\varphi$[50].

Our numerical findings are illustrated for the JJ depicted in Fig. 1(a). The normal region ($N$) has a length $L=0.3\xi_{S}$ and a width $W=10L$, such that lengths are normalized by $\xi_{\text{S}}=\hbar/\sqrt{2m^{*}\Delta}$, where $\Delta$ is the superconducting gap in $S$. The energies are normalized by $\Delta$ and the supercurrent $I_{0}=2|e\Delta|/\hbar$, where $e$ is the electron charge and $|e\Delta|/\hbar$ is the maximum supercurrent in a single-channel short $S$-$N$-$S$ JJ[50].

To explore the tunability of CPRs and JJ energies with SOC, we focus on the parameters for high-quality epitaxial InAs-Al based JJs, $\Delta_{\text{Al}}=0.2\,$meV, with a $g$-factor of 10 for InAs, while its $m^{*}$ is $0.03\,$ times the electron mass[33, 34]. In these JJs the gate control of Rashba SOC and thus its magnitude in the range $\alpha\in(0,\,180\,\text{meV\AA}$) has been demonstrated[33, 34]. In Fig. 2, at $h_{x}=(2/3)\Delta\approx 450\,$mT, we assume gate control process that primarily changes $\alpha$, not $\mu$. Experimentally, this could be realized with dual-gate schemes[51] to independently tune the carrier density and the electric field, ${\bf E}$. However, for a continuous change of $\alpha$, we are unaware that even in a static case the calculated CPR and $E_{\mathrm{GS}}$ are given.

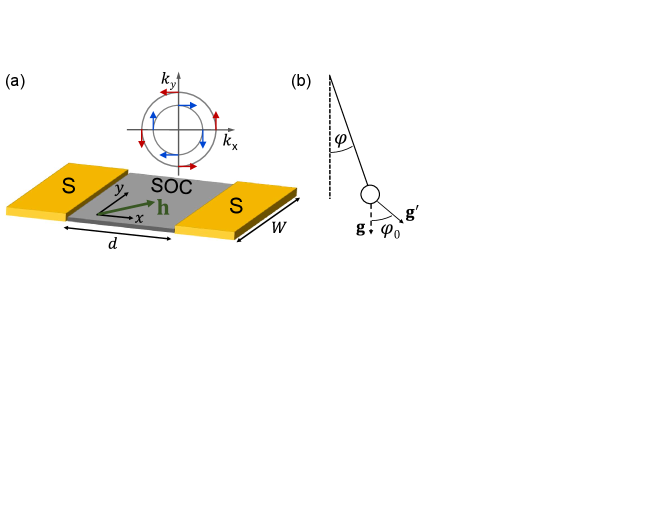
In Fig. 2(a), for $\mu=\Delta$, the anharmonic CPR changes significantly with $\alpha$. There is a competition between $\sin\varphi$ and the next harmonic, $\sin 2\varphi$, resulting in $I(-\varphi)=-I(\varphi)$. However, there is no spontaneous current, $I(\varphi=0)\equiv 0$, only $I_{c}$ reversal with $\alpha$. Such a continuous and symmetric 0–$\pi$ transition is well studied without SOC in S/ferromagnet/S JJs due to the changes in the effective magnetization, temperature, or the thickness of the magnetic region[52, 53, 54, 55, 56, 57, 58, 59, 60]. The corresponding JJ energy landscape in Fig. 2(b), shifted such that its overall minimum value is 0, corroborates this SOC evolution. By increasing $\alpha$ from 0 to 200 meVÅ, the minimum in $E_{\mathrm{GS}}$ changes from $\varphi=0$ to $\pi$, and then goes back to $0$. A gray trace indicates that by increasing $\alpha$ in a smaller range, the JJ minimum can transition from $\varphi=0$ to approximately $\pi/2$.

While we use an exact (complete) CPR with its anharmonicities, their prior descriptions have often relied on an approximate simple harmonic expansion ($\sin n\varphi,\,\cos n\varphi$)[61, 62]. However, this approach is not very efficient with SOC. Instead, it is better to use a compact form where only a small number of terms gives a more accurate description[47]

where $\tau_{n}^{\sigma}$ is the JJ transparency for spin channel $\sigma$ and the phase shifts $\varphi_{0n}$ are additional fitting parameters. This description includes the anomalous Josephson effect $I(\varphi=0)\neq 0$, revisited in JJ diode effects[63, 64, 65, 66, 67]. For a simple picture of a single anomalous phase[47, 48].

therefore vanishing in Fig.  2, where ${\bf h}=h_{x}\hat{x}$.

A quasistatic gate-controlled SOC suggests that more important opportunities are available using fast gate changes, compatible with the advances in JJ circuits[3]. However, the implications of gigahertz changes in SOC and a different mechanism to drive JJ, as sketched in Fig. 1(b), remain unexplored. To obtain the resulting JJ dynamics we use Eq. (1) with $i\equiv 0$, where the driving arises from $\alpha=\alpha(t)$, viewed as a time-dependent effective ${\bf g^{\prime}}$.

Some guidance as to what to expect for JJ dynamics can be given from the InAs-Al samples, where, in addition to the previous range of $\alpha$, $I_{c}\sim 4\,\mathrm{\mu A}$, $R\sim 100\,\Omega$, and $C\sim 15\,\mathrm{fF}$, leading to $\omega_{p}\sim 900\,\mathrm{GHz}$ and the damping $\beta_{c}\sim 1$, which is also suitable for the rapid single-flux quantum (RSFQ) applications[1, 4]. We keep $h_{x}=(2/3)\Delta$.

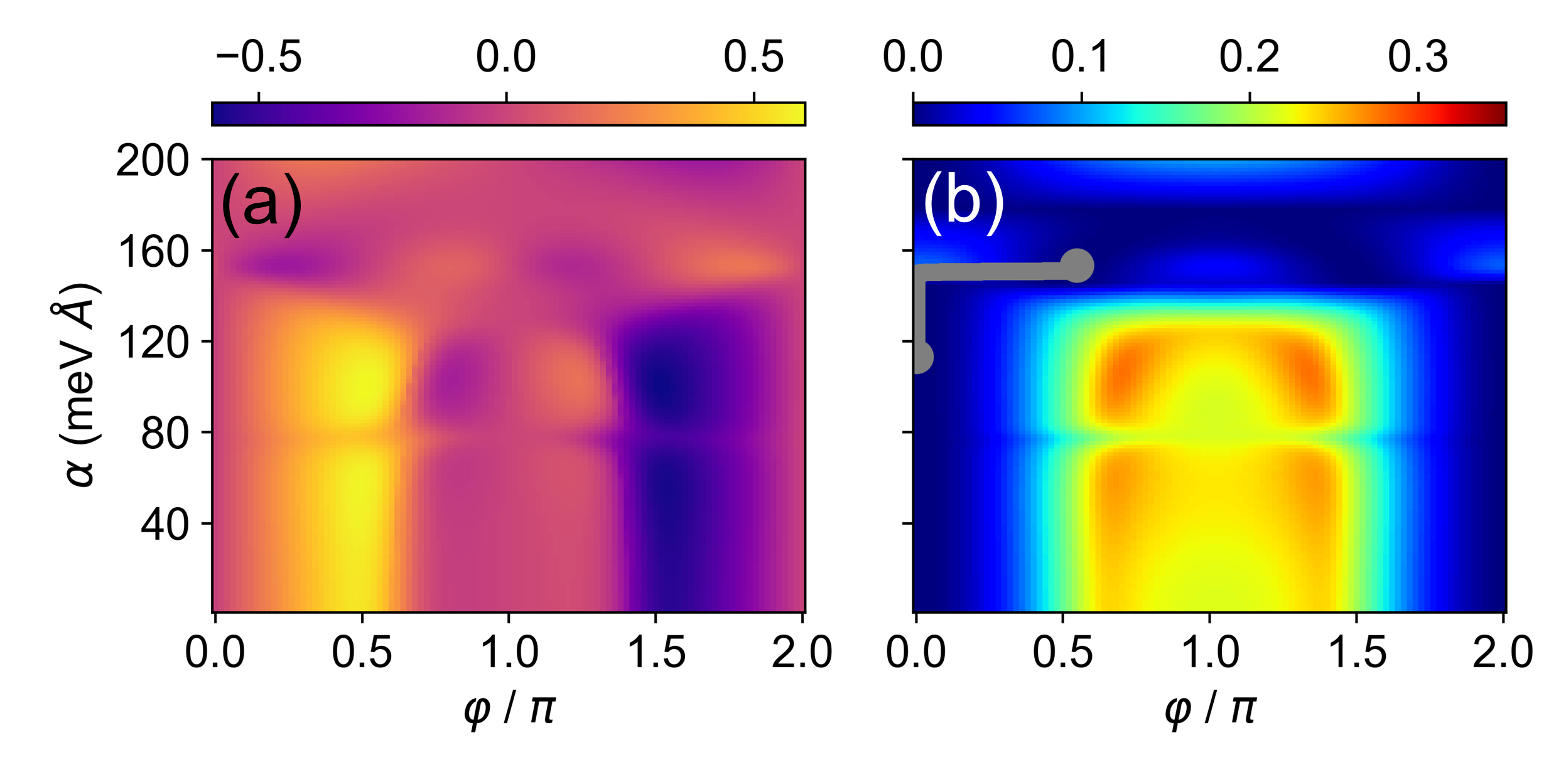
The JJ dynamics are driven by a simple linear variation of $\alpha(t)$ from the gate-controlled ${\bf E}$, as shown in Fig. 3(a). We first consider in Fig. 3(b) the reduction of $\omega_{p}$, from 1000 GHz (similar to InAs-Al JJs[33]) to 10 GHz (much faster than the $\alpha(t)$ variation), at $\beta_{c}=1$. The results reveal a strong delay in the onset in the $\varphi=0$ to approximately $\pi/2$ transition, which is indicated from the static picture in Fig. 2(b). Simultaneously, the time for the $\varphi=0$ to approximately $\pi/2$ transition is increased by an order of magnitude.

We next examine, in the inset of Fig. 3(b), the influence of reducing $\beta_{c}$ from the underdamped and critical ($\beta_{c}=10$ and 1) to the overdamped ($\beta_{c}=0.1$) regime, at $\omega_{p}=1000\,$GHz. In addition to the phase-oscillation damping, consistent with the pendulum model in Fig. 1(b), we also see a delay in the $\varphi=0$ to approximately $\pi/2$ transition and its growth, the trends noted from reducing $\omega_{p}$.

Finally, in Fig. 3(c), the $\varphi=0$ to approximately $\pi/2$ transition occurs first for the slower $\alpha(t)$ variation, but takes approximately the same time as the faster gigahertz $\alpha(t)$ variation. This is encouraging for various applications, since (i) ${\bf E}$ control of SOC allows tailoring of the onset of the transition between different states, (ii) a high-frequency switching between different equilibrium states and driving JJs is not limited by the characteristic times for the ${\bf E}$ variation. $\alpha(t)$ changes at 0.2 GHz give an order-of-magnitude faster transition between the stable phases.

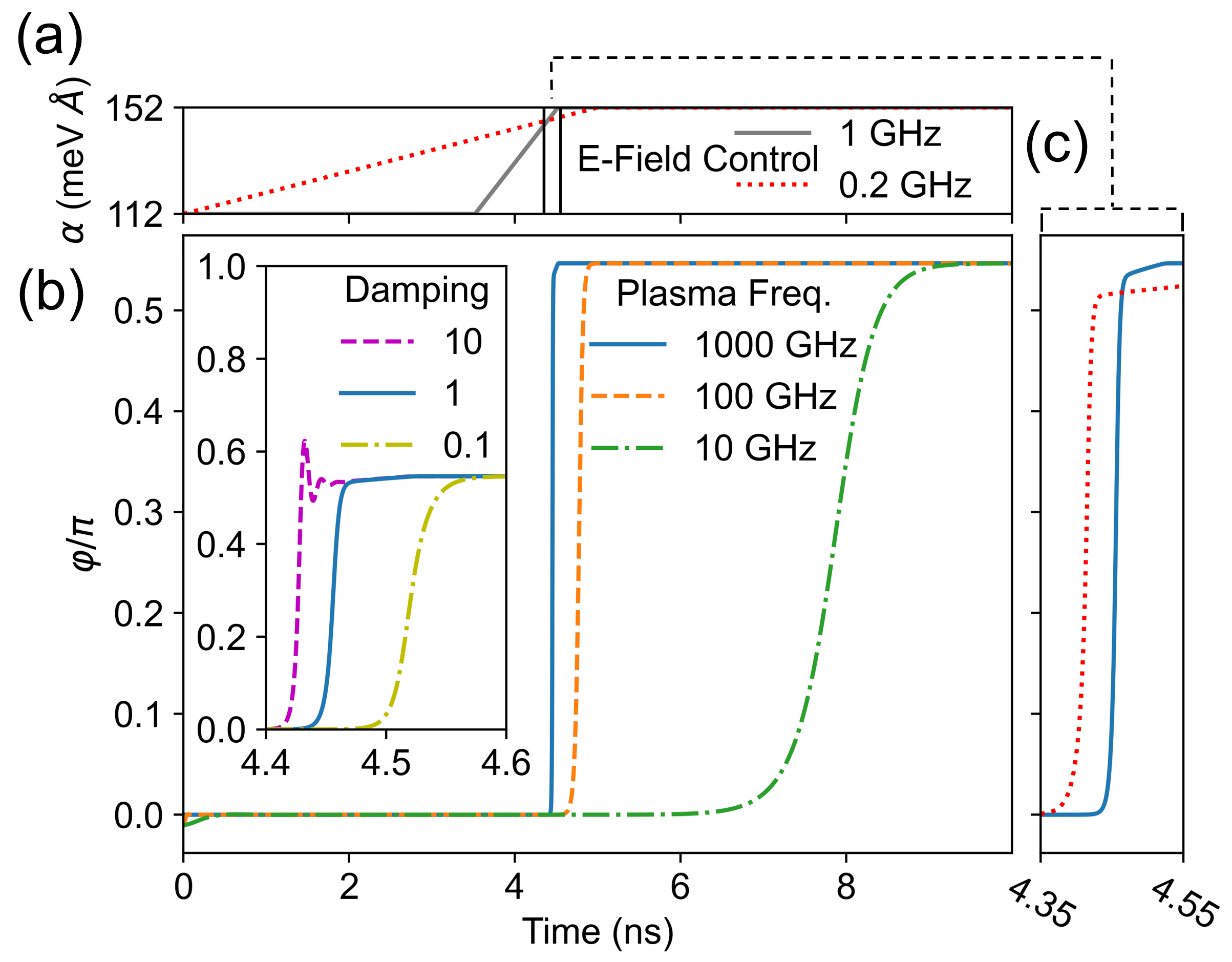
While the ${\bf E}$ control of $\alpha$ and the evolution of the $E_{\text{GS}}$ minima in Fig. 2 largely determine the JJ dynamics in Fig. 3, it helps to identify other opportunities for SOC-driven JJs. In Fig. 4, we consider $\omega_{p}=10\,$GHz and a triangularlike $\alpha(t)$ at $\mu=10\Delta$. For an underdamped regime, $\beta_{c}=10$, the pendulum analogy from Fig. 1(b) explains the phase evolution of the gray trajectory from Fig. 4(a), also reproduced in Fig. 4(c). By increasing $\alpha$ to the maximum at $192\,\text{meV\AA}$, the pendulum is at an unstable position and will swing toward the $\varphi=0$ minimum (equivalently shown as $\varphi=2\pi$), implying that ${\bf g^{\prime}}$ points vertically down. With small damping (gray trajectory), the pendulum passes the equilibrium point, even when, with $\alpha<80\,$meVÅ, the equilibrium and the overall minimum shift to $\varphi=\pi$, with ${\bf g^{\prime}}$ vertically up. Eventually, with damping it reaches the $\varphi=\pi$ minimum.

For critical damping, with the same starting point [see also Fig. 4(c)], the brown trajectory reveals a very different evolution with $\alpha$. Instead at the overall $E_{\text{GS}}$ minimum $\varphi=\pi$, for $\alpha=0$, the phase is locked at the local minimum $\varphi=0$. With a stronger damping, the $\varphi$ oscillations are insufficient to overcome the SOC-dependent barrier which, for $\alpha=0$, separates the local minimum at $\varphi=\pi$ from the global one at $\varphi=2\pi$. The tunability of the SOC-controlled energy landscape alone does not fully determine the generalized CPRs. The influence of the JJ circuit parameters can enable different $\varphi$ transitions.

In the above discussion, the tunability of CPRs and $E_{\text{GS}}$ does not exploit the anomalous Josephson effect[37, 38, 39, 40, 70], which can be understood in analogy to ${\bf g^{\prime}}$ pointing sideways and therefore, breaking the symmetry from Figs. 2-4 and $I(-\varphi)\neq-I(\varphi)$. This situation can be simply realized by rotating $\bf h$ along the $y$ axis, while we retain all the other parameters from Fig. 2(a). The resulting CPR in Fig. 5(a) confirms that the JJ supercurrent is driven not only by $\varphi$ but also by $\varphi_{0}$, which is responsible for the stated symmetry breaking and, equivalently, the tilted ${\bf g^{\prime}}$. As for SOC cubic in ${\bf k}$[47], there is a strong anharmonic behavior and the expected diode effect, where the sign and magnitude of the supercurrent depend on the polarity of the applied bias [34].

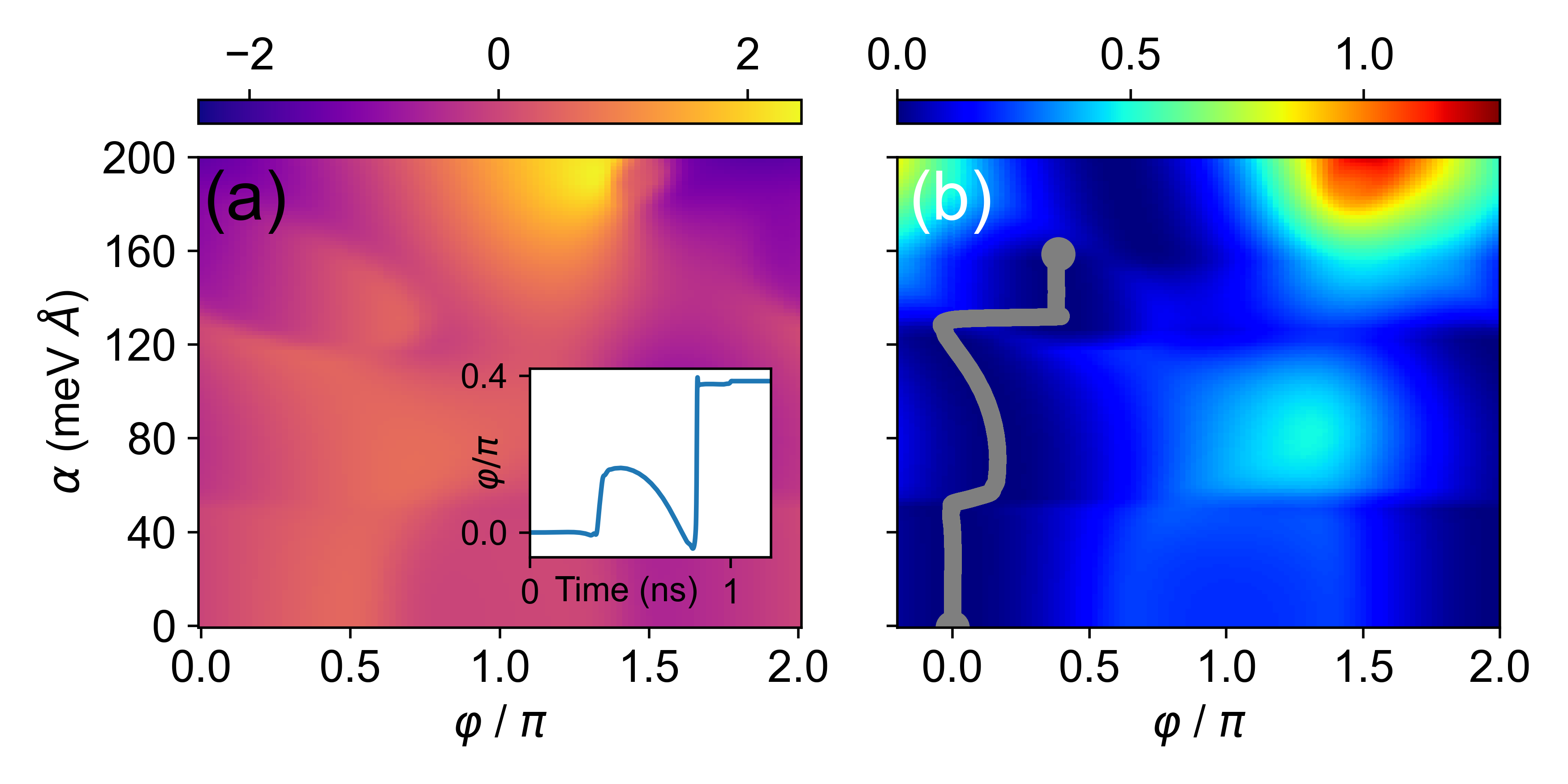
The implications of the combined broken time-reversal and inversion symmetries, responsible for the anomalous Josephson effect, are further illustrated in Fig. 5(b), which shows the SOC-tunable $E_{\text{GS}}$, single valued for the gray path, and leading to the time-dependent diode effect. This behavior is qualitatively different from the doubly degenerate $\varphi_{0}$ state in Fig. 2(b), which results from the second-harmonic generation in the CPR.

Even with a moderate $h_{y}\approx 450\,$mT for InAs based JJs, with increasing $\alpha(t)$ we see an evolution of the single global minimum and thus the changes in the corresponding values of $\varphi_{0}$ from $\varphi=0$ to approximately $3\pi/4$, in good agreement with the measured values[33]. This suggests that at a larger ${\bf h}$, for example, in In(As,Sb) with a much larger $g$ factor[35], it may be possible to fully control the tilt angle of ${\bf g^{\prime}}$ and simply swap between $0$ and $\pi$ states in JJs, further controlling how the JJ dynamics are driven.

The same geometry in Al-InAs JJs at a larger $h_{y}$ has been experimentally shown to also support topological superconductivity[34]. This is important for several reasons, beyond hosting Majorana bound states[16]. The resulting topological superconductivity is associated with equal-spin $p$-wave superconductivity which could offer gate-controlled dissipationless spin currents, a key element for superconducting spintronics[7, 8]. Such spin-triplet supercurrents could be extended over a long range[71] and could overcome the usual competition between superconductivity and ferromagnetism. A transition to topological superconductivity is accompanied by an extra phase jump, of approximately $\pi$[72, 73]. Such a $\pi$ jump in Al-InAs JJs has been observed at $h_{y}\approx 600\,$mT[34], an effective field about 25 times smaller, than expected for the $0–\pi$ transition

for a spin-polarized system in the absence of SOC[74], where $v_{\mathrm{F}}$ is the Fermi velocity, $\mu_{\mathrm{B}}$ the Bohr magneton, and $L$ the JJ length. Therefore, SOC plays a crucial role in understanding various transitions and, at larger $h_{y}$, the range of an effective $\varphi_{0}$ could exceed $2\pi$[34] and support $2\pi$ pendulum rotation from Fig. 1(b), as used in RSFQ logic and memory[1, 4]. Therefore, in addition to the prospect of fault-tolerant quantum computing, the search for topological superconductivity also offers a promising platform for superconducting electronics and spintronics.

Without previous studies on SOC-driven JJ dynamics, we focus on a simple model and do not consider time-dependent magnetic fields[75] or noise[76]. A more general description could simultaneously include the role of changing $\mu$ and other SOC forms, linear and cubic in ${\bf k}$, shown to give different routes to topological superconductivity and control of Majorana states[47, 77, 78, 79]. However, we expect that our focus only on linearized Rashba SOC, easily tunable by ${\bf E}$ field[33, 34], already clarifies its important role in JJ dynamics. With changing SOC, there are further opportunities for gate-controlled Majorana states and the probing of their non-Abelian statistics[80, 81] or an added tunability in the implementation of superconducting qubits[3, 82, 83]. This would extend the previously studied qubit tunability by voltage or flux[3, 84] as well as the use of $\pi$-phase states for an improved qubit operation[85, 86].