TSC-PCAC: Voxel Transformer and Sparse Convolution Based Point Cloud Attribute Compression for 3D Broadcasting
Abstract
Point cloud has been the mainstream representation for advanced 3D applications, such as virtual reality and augmented reality. However, the massive data amounts of point clouds is one of the most challenging issues for transmission and storage. In this paper, we propose an end-to-end voxel Transformer and Sparse Convolution based Point Cloud Attribute Compression (TSC-PCAC) for 3D broadcasting. Firstly, we present a framework of the TSC-PCAC, which includes Transformer and Sparse Convolutional Module (TSCM) based variational autoencoder and channel context module. Secondly, we propose a two-stage TSCM, where the first stage focuses on modeling local dependencies and feature representations of the point clouds, and the second stage captures global features through spatial and channel pooling encompassing larger receptive fields. This module effectively extracts global and local inter-point relevance to reduce informational redundancy. Thirdly, we design a TSCM based channel context module to exploit inter-channel correlations, which improves the predicted probability distribution of quantized latent representations and thus reduces the bitrate. Experimental results indicate that the proposed TSC-PCAC method achieves an average of 38.53%, 21.30%, and 11.19% bitrate reductions on datasets 8iVFB, Owlii, 8iVSLF, Volograms, and MVUB compared to the Sparse-PCAC, NF-PCAC, and G-PCC v23 methods, respectively. The encoding/decoding time costs are reduced 97.68%/98.78% on average compared to the Sparse-PCAC. The source code and the trained TSC-PCAC models are available at https://github.com/igizuxo/TSC-PCAC.
Index Terms:
Point cloud compression, voxel transformer, sparse convolution, variational autoencoder, channel context module.I Introduction
With the development of information technology, the demands for more realistic visual entertainment have been rising continuously and rapidly. 3D visual application has emerged as a pivotal trend nowadays as it provides 3D depth perception and immersive visual experience. Point cloud has come into prominence as an indispensable form of expression within the realm of 3D vision, which has wide applications in entertainment, medical imaging, engineering, navigation and autonomous vehicles. However, a high-quality large-scale point cloud at one instant contains millions of points, where each point consists of 3D geometry and high dimensional attributes, such as color, transparency, reflectance and so on. These massive data poses great challenges for transmission and broadcasting, which hinders the widespread application of point clouds. Therefore, there is a pressing demand for point cloud compression that can substantially reduce the size of point cloud data. Nevertheless, unlike images where elements are densely and regularly distributed in 2D plane, 3D point cloud is irregular and sparse, leading to irregular 3D patterns and low correlations between neighboring points. These inherent characteristics pose substantial challenges to point cloud compression.
To compress the point cloud effectively, the Moving Picture Expert Group (MPEG) has proposed two traditional point cloud compression methods, i.e., Geometry-based Point Cloud Compression (G-PCC) [1] and Video-based Point Cloud Compression (V-PCC) [2]. The G-PCC directly encodes point clouds with an octree structure in 3D space. On the other hand, V-PCC projects the 3D point clouds into 2D images, which are then encoded using conventional codecs in 2D space, such as High Efficiency Video Coding (HEVC) and the latest Versatile Video Coding (VVC). In addition to traditional compression methods, given the remarkable achievements in deep learning-based image compression technologies [3], many researchers have recently started exploring the potential of deep learning-based point cloud compression techniques including geometry and attribute [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]. Despite some achievements in geometry compression, in terms of attribute compression, point-based compression methods have difficulty leveraging excellent feature extraction operators, such as convolution, or voxel-based compression networks are solely composed of convolution stacks [11, 12]. These could potentially lead to the network struggling to remove redundancy among highly correlated voxels, resulting in suboptimal compression efficiency.
In this paper, we propose a Transformer and Sparse Convolution based Point Cloud Attribute Compression (TSC-PCAC) to improve the coding efficiency. Main contributions are
-
•
We propose a deep learning based point cloud attribute compression framework, called TSC-PCAC, which combines the Transformer and Sparse Convolutional Module (TSCM) based autoencoder and a TSCM optimized channel context module to improve compression efficiency.
-
•
We propose a two-stage TSCM that jointly models global and local features to reduce data redundancy. The first stage focuses on capturing the dependencies and feature representations of local regions of the point clouds, while the second stage captures global features by combining spatial and channel pooling operations.
-
•
We design a channel context module based upon the TSCM, which divides quantified latent representations into multiple groups. It improves prediction accuracies of probability distributions by leveraging decoded groups.
The paper is organized as follows. Section II presents the related work. Section III presents motivations and the proposed TSC-PCAC. Section IV presents the experimental results and analysis. Finally, Section V draws the conclusions.
II Related Work
II-A Traditional Point Cloud Compression
Traditional point cloud compression methods are mainly divided into two categories: octree based and projection based. Octree can efficiently and losslessly represent point clouds, where adjacent nodes exhibit high spatial correlation for point cloud compression. G-PCC [1] employs an octree-based compression method. The attribute compression of G-PCC integrates three key compression methods, which are Region-Adaptive Hierarchical Transform (RAHT) [15], predictive transform, and lifting transform [16]. RAHT is a variant of the Haar wavelet transform, using lower octree levels to predict values at the next level. Predictive transform generates different levels of detail based on distance and performs encoding using the order of detailed levels. Lifting transform is performed on top of predictive transform with an additional updating operation [17, 18]. Pavez et al. [19] utilized a Regionally Adaptive Graph Fourier Transform (RAGFT) to obtain low-pass and high-pass coefficients, and then used the decoded low-pass coefficients to predict the high-pass coefficients. Gao et al. [20] exploited the statistical correlation between color signals to construct the Laplace matrix, which overcame the interdependence between graph transform and entropy coding and improved the coding efficiency. V-PCC is a projection-based compression method. It divides the point cloud sequences into 3D patches and projects them into 2D geometry and attribute videos, which are then smoothed and compressed by the conventional 2D codecs. Zhang et al. [21] proposed a perceptually weighted Rate-Distortion (RD) optimization scheme for V-PCC, where perceptual distortion of point clouds [22] was considered in objectives of attribute and geometry video encoding. These are traditional coding schemes exploiting spatial-temporal correlations, symbol and visual redundancies.
II-B Learning-based Image Compression
Deep learning and neural networks have achieved great success in solving vision tasks [23, 24, 25]. Learning-based image compression [26, 3, 27, 28, 29, 30] has been hotspot in recent years, which has surpassed the traditional image compression methods, such as JPEG2000 and VVC Intra coding. The framework of learned image compression mainly transforms an image into a compact representation, which then undergoes quantization and entropy encoding for transmission. At the decoder side, the output image is synthesized from the decoded compact representation from entropy decoded bit stream. The entire end-to-end compression framework is optimized using RD loss as the objective function [26]. Ballé et al. [26] applied a hyper-prior module into the Variational AutoEncoder (VAE) compression framework. Minnen et al. [30] proposed a context module exploiting autoregressive and hierarchical priors to improve compression efficiency, which was further extended to model channel-wise context [29]. Tang et al. [27] utilized graph attention mechanism and asymmetric convolution to capture long-distance dependencies. Zou et al. [28] proposed to combine local perceptual attention mechanism with global-related feature learning. Then, a window-based image compression was proposed to exploit spatial redundancies. Liu et al. [3] proposed a mixed transformer-Convolutional Neural Network (CNN) module, which was incorporated to optimize channel context module for learned image compression. However, unlike the regular distributed 2D image, a point cloud is dispersed in 3D space in an unstructured and sparse manner. These 2D image compression methods cannot be directly applied to encode 3D point clouds.
II-C Learning-based Point Cloud Compression
To compress point clouds effectively, a number of learning-based compression methods have been proposed, which are categorized into learned geometry and attribute compression.
Generally, end-to-end learned Point Cloud Geometry Compression (PCGC) can be categorized into point-based methods [4, 5] and voxel-based methods [6, 7, 8]. The point-based methods process point clouds in 3D perspective. Huang et al. [4] developed a hierarchical autoencoder that incorporated multi-scale losses to achieve detailed reconstruction. Gao et al. [5] utilized local graphs for extracting neighboring features and employed attention-based methods for down-sampling points. These point-based methods struggle to efficiently aggregate spatial information. Voxel-based methods require an initial voxelization of point clouds before input to the compression network. Song et al. [31] designed a grouping context structure and a hierarchical attention module for the entropy model of octrees, which supported parallel decoding. Wang et al. [8] extended the Inception-Resnet block [32] to 3D domain, and then incorporated it into the VAE based compression network to address the gradient vanishing problem from going deeper. However, the employed dense convolution required intensive computations and large memory, which were unaffordable in processing large-scale point clouds. Wang et al. [6] introduced sparse convolution to accelerate computations and reduce memory cost. Additionally, a hierarchical reconstruction method was proposed to enhance compression performance. Liu et al. [7] introduced local attention mechanisms in PCGC, which achieved promising coding efficiency and demonstrated the potential of attention mechanisms. Qi et al. [33] proposed a variable rate PCGC framework to realize multiple rates by tuning the features. Akhtar et al. [34] proposed to predict a latent potential representation of the current frame from those of previous frames by using a generalized sparse convolution. Zhou et al. [35] proposed using transformers to capture temporal context information and reduce temporal redundancy. They also used a multi-scale approach to capture the temporal correlations of multi-frame point clouds over both short and long ranges. These methods are proposed to encode the point cloud geometry. However, the point cloud attribute is attached to the geometry, which is significantly different from the geometry.
To compress the point cloud attribute effectively, a number of Point Cloud Attribute Compression (PCAC) methods were developed, which can be categorized as lossless [9, 10] and lossy compression [11, 12, 13, 14, 36]. In lossless compression, Nguyen et al. [10] constructed the context information between the color channels to reduce redundancy among RGB components. Wang et al. [9] generated multi-scale attribute tensor and encoded the current scale attribute conditioned on lower scale attribute. In addition, it further reduced spatial and channel redundancy by grouping spatial and color channels. However, lossless compression can hardly achieve high compression ratio, which motivates lossy compression. In lossy compression, Isik et al. [36] modeled point cloud attribute as a volumetric function and then compressed the parameters of the volumetric function to achieve attribute compression. However, fitting the function leads to high coding time complexity. Fang et al. [13] employed the RAHT for initial encoding and designed a learning-based approach to estimate entropy. Pinheiro et al. [14] proposed a Normalized Flow Point Cloud Attribute Compression (NF-PCAC) method. It incorporated strictly reversible modules to improve the reversibility of data reconstruction, which extended the upper bound of coding performance. Similarly, Lin et al. [37] utilized the normalized flow paradigm by proposing the Augmented Normalizing Flow (ANF) model, in which additional adjustment variables were introduced. Zhang et al. [38] used two-stage coding, the point cloud was roughly coded using G-PCC in the first stage and it was augmented with a network in the second stage.
There are two more advanced PCAC methods based on the VAE framework, which are the Deep PCAC (Deep-PCAC) [11] and the Sparse convolution-based PCAC (Sparse-PCAC) [12]. In Deep-PCAC, a PointNet++ [39] based feature extraction was proposed to provide a larger receptive field for aggregating neighboring features. However, since the Deep-PCAC processes irregular points directly, it cannot utilize convolution operators on regular voxels to extract local features[32]. The latter Sparse-PCAC processed voxelized point clouds, which used convolution to aggregate neighboring features and sparse convolution to reduce the computation and memory requirements [40]. However, Sparse-PCAC used stacked convolutional layers with fixed kernel weights, degrading the model’s ability of focusing highly relevant voxels.
III The proposed TSC-PCAC
III-A Motivations and Analysis
Point cloud is sparsely distributed in 3D space, which suits for sparse processing in neighboring feature extraction. In addition, attention mechanisms that can capture correlations between voxels are also applicable to the point cloud compression. Therefore, the properties of sparse convolution and local attention are analyzed for the attribute coding.
III-A1 Importance of Sparse Convolution
Dealing with large-scale dense point clouds requires a large number of parameters and computational cost of 3D convolutional networks, which is challenging in constructing effective compression networks for large-scale point clouds. Sparse convolution is effective in reducing the computational complexity by exploiting the sparse and vacant points in point clouds. The general representation of 3D convolution is
| (1) |
where represents the output feature at 3D spatial coordinate and represents the input feature at the position , where is an offset of in 3D space. represents the convolution kernel weight corresponding to offset .





For spatial scale-invariant dense convolution, is an offset selected from the list of offsets in a 3D hypercube with center , where is the size of one dimension of the convolution kernel. More intuitively, Fig. 1 illustrates the difference between sparse convolution and dense convolution. For a convolution operation with kernel size , dense convolution stores both occupied and vacant voxels. During the convolution, it acts on all 27 voxels covered by the convolution kernel. However, for spatial scale-invariant sparse convolution, is an offset selected from the set of offsets , which is defined as the set of offsets from the current center that exists in the set . are predefined input coordinates of sparse tensors that only include occupied voxels. As depicted in Fig. 1, sparse convolution only stores and acts on the occupied voxels [40]. In addition, sparse convolution does not perform convolution with vacant voxels at the center. Compared with the dense convolution, sparse convolution significantly reduces the memory cost and computational complexity, which enables the design of more powerful compression networks for large-scale point clouds.

III-A2 Importance of Local Attention
Fig. 2 shows the learned weights of the convolution kernels in point cloud processing. There is only one set of weights in each convolution of CNN and it traverses the entire point cloud using a sliding convolution kernel to extract features, which leads to learn a universal convolution kernel for different point cloud regions. Obviously, the properties of the regions/voxels vary from regions. Therefore, it is not the optimal solution to treat all voxels equally regardless of the region contents. In contrast, the self-attention in transformer uses the input to compute the attention matrix and model the dependencies of different voxels [41]. As shown in Fig. 2, local attention operator in transformers computes the attention weights of the input voxels with respect to other voxels, which is able to capture correlations between voxels. In this case, the correlations between voxels are captured using the self-attention, which is to model the redundancy between voxels and reduce the coding bitrate. Moreover, comparing with the convolution, transformer utilizes self-attention mechanisms to establish mutual dependencies between voxels, which enhances the capability of feature representation. However, transformer lacks an effective inductive bias, compromising the generalization performance, especially in 3D point cloud processing. Combining transformer with sparse convolution can improve the capabilities of feature representation and generalization.
III-B Framework of the TSC-PCAC
Given a point cloud , a learned point cloud compression framework to encode and decode can be expressed as
| (2) |
where and represent the point cloud encoder and decoder, respectively. and respectively represent arithmetic encoder and decoder. and represent the source and the reconstructed point clouds, respectively. and represent the compact latent representations after quantization and the bitstream containing the information. is a quantization operation.
A point cloud consists of geometry and attribute , i.e., . Since attribute attaches to geometry and is compressed after geometry [2, 1]. Eq.(2) is rewritten as
| (3) |
where and represent the reconstructed point cloud geometry and attribute. and represent the quantified latent representations of geometry and attribute. and represent point cloud geometry encoder and decoder. and represent the point cloud attribute encoder and decoder. and represent the bitstream containing the and information. Attribute is on the basis of geometry , thus geometry is compressed before the attribute, and then the attribute is compressed with the reconstructed geometry information as an input.
In this work, suppose that point cloud geometry has already been compressed, we focus on optimizing the PCAC. Consequently, our goal is to optimize and , as well as the entropy model required in arithmetic codec while encoding and decoding . We propose an efficient TSC-PCAC framework based on the VAE, as shown in Fig. 3, in which TSCM and a TSCM based context module are proposed to improve the point cloud coding. The TSC-PCAC combines the inductive bias capabilities and memory-saving advantages of sparse convolution, and also leverages the ability of transformers in capturing correlations between voxels. The TSC-PCAC consists of a pair of learning-based encoder/decoder and a pair of entropy model, which is
| (4) |
where and are the original and quantized latent representations of attribute, respectively. and are TSCM-optimized attribute encoder and decoder with parameters and , respectively. represents the entropy model for . The mean and scale from the entropy model are used for the arithmetic codec and . Specifically, the entropy model consists of a hyper-prior encoder-decoder and context module. In estimating the probability distribution of , the initial mean and scale are firstly achieved by a hyper-prior encoder-decoder, and then refined by a context module. The TSCM based channel context model and entropy coding can be represented as
| (5) |
where represent the bitstream containing the quantized hyperprior representations information. and represent the hyperprior encoder and decoder with parameters and , respectively. and represent initial mean and scale of . denotes the TSCM based channel context module with parameters , which establishes relationships between channels to provide contextual information for higher compression efficiency.
To enhance the network’s capability of allocating more importance to voxels with higher relevance and obtaining a compact representation, TSCM blocks are placed in the encoder and decoder . Specifically, due to memory constraints, only two TSCM blocks are used in the encoder and decoder. Similarly, one TSCM block is employed in the hyper-prior encoder and decoder. Since the attribute is attached to geometry, the geometry information is utilized in the entire process of attribute coding, shown as gray arrows in Fig. 3. For simplicity, geometry variables are not explicitly indicated in subsequent diagrams.


III-C Architecture of TSCM
Transformer models the correlations dependencies between voxels through the self-attention mechanism, which has the potential to enable the network to focus on voxels of higher relevance. However, it may reduce the generalization ability. Convolution, on the other hand, has a strong inductive bias and can achieve excellent generalization ability. Combining convolution and transformer can gain their advantages. However, when using the transformer to process large-scale color point clouds that contain millions of points, global attention is able to capture long-range dependencies at the cost of the unaffordable memory, while local attention reduces the memory cost at the cost of reducing the receptive field. To take the advantages of these methods, we propose a two-stage TSCM, which consists of local attention based transformer [41], residual block, and voxel-based global block to increase the receptive field.
Fig. 4 shows the structure of the proposed TSCM. In the first stage, residual block and local attention based transformer are utilized to extract local features. To take advantage of these features, we use a dual-branch structure to extract features separately and fused by concatenation. Specifically, an input performs sparse convolution with a kernel size of 1 and splits along the channel dimension, resulting in and . They are used as inputs for the local attention-based transformer and residual block, respectively. The output is then concatenated to restore the feature channel to the original dimension, i.e., 128. This fusion combines both two types of features to form local features , which captures interdependencies among voxels and has effective inductive bias. These features are the output of the first stage and the input of the second stage.
In the second stage, to alleviate the computation/memory cost and achieve the global features, the residual block and the voxel-based global block are employed. The global block in [42] uses linear layers and global pooling to extract and sharpen global features. To further capture spatial neighboring redundancy, voxel-based global block is proposed by replacing the linear layer in global block with convolutional layers. Specifically, and are input to the voxel-based global block and residual block, respectively. The voxel-based global block is shown in Fig. 4. It utilizes global pooling to extract global spatial features and global channel features . and undergo matrix multiplication to obtain global spatial-channel features . Subsequently, the global spatial-channel features are subtracted from the input features of voxel-based global block to obtain sharpened global spatial-channel features. The outputs of the voxel-based global block and residual block are concatenated to restore the feature channel to the original dimension. This fusion combines both two types of features to form global features with a large receptive field and inductive bias capabilities.
In TSCM, the integration of these two stages effectively captures both global and local inter-point relevance for reducing data redundancy. We use both the residual block and the transformer with local self-attention to extract local features and correlations. Meanwhile, the global features are obtained through channel and spatial pooling within voxel-based global blocks. Finally, the features of TSCM are output as .
III-D TSCM based Channel Context Module
In the Sparse-PCAC, the context module is a per-voxel context network, which processes voxels sequentially. While dealing with large-scale point clouds, this sequential processing leads to extremely high encoding and decoding delays. We propose a TSCM based channel context module to improve the network prediction probability distribution by constructing contextual information over quantized latent representations. Features are processed sequentially along the channel dimension instead of voxels, which reduces the sequential number.
The architecture of the proposed TSCM based channel context module is illustrated in Fig. 5, where the hyper-prior module is detailed in Fig. 3. represents the latent representation of the -th quantized slice, while represents the latent representation of the -th slice with the addition of quantization error estimation, where . represents the number of equal divisions in the channel. Besides the mean and scale, we also employ a module to predict quantization error. Specifically, the channel context module processes each slice sequentially by dividing the quantized latent representation proportionally into slices along the channel. Predicting the mean of each slice depends on the previously decoded slices and the initial mean value. Similar process is applied to predict the scale. Since the obtained probability distribution can be used to decode the current slice, the quantization error can be predicted from the decoded current slice. It is worth noting that the network architectures for predicting the mean, scale, and quantization error are the same. So, we use the term ‘TSCM based Transform’ for these three cases.


The detailed structure of the TSCM based transform is depicted in Fig. 5, where inputs are concatenated and processed through sparse convolutions and TSCM block. Due to the computational complexity of TSCM, we reduce the number of feature channels to 32. The mathematical expressions of obtaining the scale , mean , and quantization error are
| (6) |
where and represent the refined mean and scale of . is the estimated quantization error. denotes the refined latent representation of group , i.e., . indicates a set of where is smaller than , . is the ‘TSCM based Transform’ learning parameters of slices, which are , , and , respectively. The mean and scale of -th group are utilized for entropy encoding and decoding of the current group’s . The quantization error predicted for each group is then employed to refine . Based on Eq. 6 and Fig.5, the mean , scale , and quantization error can be predicted by the TSCM based transform, which improve the channel context module in entropy coding.
III-E Loss Function
The overall objective of point cloud compression is to minimize the distortion of the reconstructed point cloud at a given bitrate constraint. As a point cloud consists of geometry and attribute, the objective is to minimize
| (7) |
where and are distortion measurements. and represent the bitrate required for transmitting the quantized attribute and geometry latent representations, and . Due to the hyper-codec, the total bit rate includes the rate of hyper-prior feature, i.e., . The trade-off between distortion and bitrate is controlled by and . Furthermore, in this paper, we focus on the PCAC and assume the geometry information is shared and fixed at the encoder and decoder sides, Therefore, the objective for attribute coding is simplified to minimize
| (8) |
In this paper, uses Mean Squared Error (MSE) loss in the YUV color space.
IV Experimental Results and Analyses
IV-A Experimental Settings















| PC | TSC-PCAC vs Sparse-PCAC | TSC-PCAC vs NF-PCAC | TSC-PCAC vs GPCC v23 | ||||
| BD-BR(%) | BD-PSNR(dB) | BD-BR(%) | BD-PSNR(dB) | BD-BR(%) | BD-PSNR(dB) | ||
| Soldier | -35.09 | 1.73 | -24.96 | 1.10 | -8.08 | 0.22 | |
| Redandblack | -30.12 | 1.17 | -19.13 | 0.59 | 22.44 | -0.83 | |
| Dancer | -49.11 | 2.35 | -29.61 | 1.25 | -9.30 | 0.26 | |
|
-50.14 | 2.18 | -25.68 | 1.04 | -3.72 | 0.06 | |
| Phil | -33.65 | 1.48 | -22.05 | 0.77 | -4.33 | 0.02 | |
| Boxer | -44.00 | 2.01 | -23.97 | 0.85 | -2.43 | 0.07 | |
| Thaidancer | -32.67 | 1.15 | -19.54 | 0.54 | 28.01 | -1.28 | |
| Rafa | -35.93 | 1.58 | -12.85 | 0.47 | 18.75 | -0.67 | |
| Sir Frederick | -35.47 | 1.78 | -13.22 | 0.61 | 7.58 | -0.31 | |
| Andrew* | -37.26 | 1.44 | -9.44 | 0.34 | -53.07 | 2.46 | |
| David* | -50.57 | 2.57 | -21.52 | 0.82 | -0.63 | 0.01 | |
| Exerciese* | -45.76 | 1.40 | -30.18 | 0.94 | -14.63 | 0.34 | |
| Longdress* | -30.87 | 1.24 | -18.38 | 0.55 | -21.43 | 0.62 | |
| Loot* | -39.88 | 2.19 | -11.24 | 0.48 | -14.39 | 0.58 | |
| Model* | -44.87 | 1.77 | -24.91 | 1.02 | -18.72 | 0.54 | |
| Sarah* | -54.00 | 2.39 | -26.13 | 0.86 | 0.12 | -0.30 | |
| Average | -36.62 | 1.66 | -22.27 | 0.85 | 1.26 | -0.11 | |
| Average* | -38.53 | 1.72 | -21.30 | 0.80 | -11.19 | 0.34 | |
IV-A1 Coding Methods
Four point cloud compression methods were compared with the proposed TSC-PCAC, including Deep-PCAC [11], Sparse-PCAC [12], NF-PCAC [14] and G-PCC v23. For a fair comparison, we retrained the Sparse-PCAC and NF-PCAC models according to the training conditions of TSC-PCAC. As for the Deep-PCAC model, since the authors have provided pre-trained models, we used them to obtain coding results. The G-PCC encoding settings were configured with default settings for dense point clouds and the attribute encoding mode was RAHT. Quantization Parameters (QP) followed the default settings of Common Test Conditions (CTCs) [43].
IV-A2 Quality Metrics
Peak Signal-to-Noise Ratio (PSNR) was used as the quality metric for distortion measurement [44], and the rate was measured in bit per point (). We also used Bjøntegaard Delta bitrate (BD-BR) to evaluate the coding performance. Additionally, we used Bjøntegaard Delta PSNR (BD-PSNR) to compare the reconstruction quality of different codecs[45]. It’s worth noting that the PSNR of attribute in the paper is calculated from the luminance component and the geometry is losslessly coded.
IV-A3 Databases
The dataset utilized consists of 8iVFB [46], Owlii [47], 8iVSLF [48], Volograms [49], and MVUB [50]. We selected the Longdress, Loot, Exercise, Model, Andrew, Sarah, and David point cloud sequences for training, and selected Redandblack, Soldier, Basketball Player, Dancer, Thaidancer, Boxer, Rafa, Sir Frederick and Phil point cloud sequences for testing. Longdress, Loot, Soldier, and Redandblack are from 8iVFB. Andrew, Sarah, David, and Phil are from MVUB. Exercise, Model, Basketball Player and Dancer are from Owlii. Rafa and Sir Frederick are from Volograms. Thaidancer and Boxer are from 8iVSLF. For Boxer and Thaidancer, following [51], we quantified them to 10-bit. For Rafa and Sir Frederick, we sampled them from mesh data to dense colored point cloud sequences with a precision of 10-bit. For the sequences of MVUB, we used point cloud sequences with a precision of 10-bit.
IV-A4 Training Settings
To reduce the data volume and accelerate training, the point clouds are resampled. Specifically, cluster centers of a point cloud with points were obtained by farthest point sampling, where . Then, we used the k-Nearest Neighbor (kNN) algorithm to cluster the surrounding 100,000 points on cluster centers. Resampling was applied to the first 100 frames of each point cloud sequence in the training set. The point clouds in the testing set were not resampled. To further validate the compression performance, we included more test sequences where the previous frames are used as training and the rest subsequent frames are used as testing data. Their coding results were marked with ‘*’. We set as 400, 1000, 4000, 8000, and 16000 to obtain different bitrate points. For efficient training, we first trained a model with as 16000. We then fine-tuned the model 50 epochs at a learning rate of to obtain different models at different values of . During the training, we found that it was easier to train the model without the channel context module first and then jointly train it. Considering the trade-off between coding performance and computational complexity, we set the number of channel divisions in the channel context module as 8. All the experiments were conducted on a workstation with an Intel Core i9-10900 CPU and an NVIDIA GeForce RTX 3090 GPU.












IV-B Coding Efficiency Evaluation
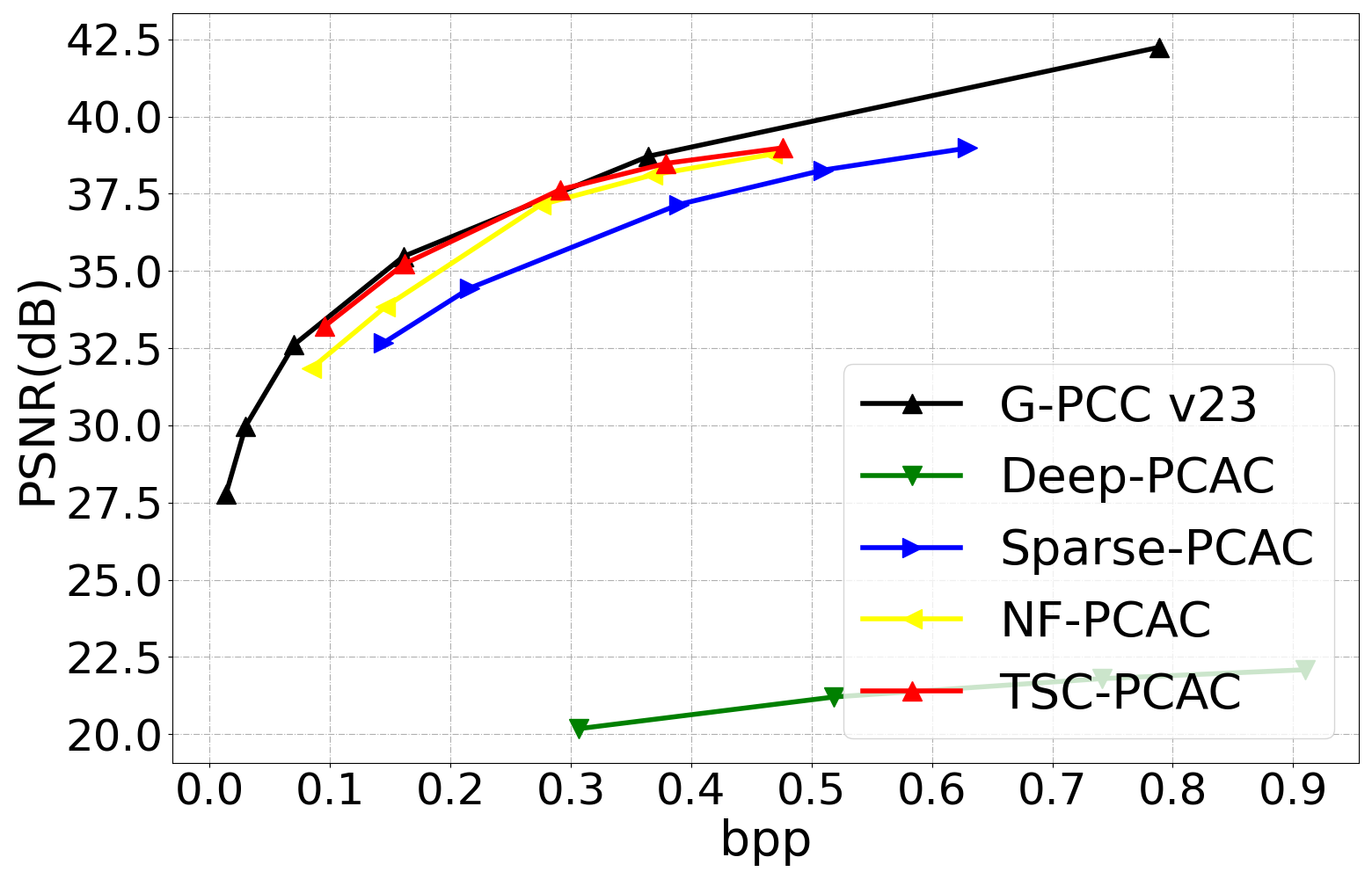
Fig. 6 illustrates the coding performance comparison of Deep-PCAC, Sparse-PCAC, G-PCC, NF-PCAC and TSC-PCAC, where the vertical-axis is PSNR and the horizontal-axis is bit rate in terms of . It can be observed that the Sparse-PCAC significantly outperforms the Deep-PCAC, but it is worse than the G-PCC in the majority of point clouds. NF-PCAC has higher compression efficiency than Sparse-PCAC. As for the proposed TSC-PCAC, it outperforms the NF-PCAC by a large margin in all point clouds. Our TSC-PCAC achieves the best performance on most test point clouds, such as Soldier and Dancer. However, it ranks second behind G-PCC v23 on a few point clouds such as Thaidancer and Redandblack.
Table I presents the quantitative BD-BR and BD-PSNR comparisons. ‘Average’ is the average value over 9 point clouds, while the ‘Average*’ is the average result over all including point clouds marked with ‘*’. It can be observed that, excluding the point clouds marked with ‘*’, the proposed TSC-PCAC achieves bit-rate savings ranging from 30.12% to 50.14%, and 36.62% on average compared to the Sparse-PCAC. In terms of BD-PSNR, our method achieves BD-PSNR gain ranging from 1.15 dB to 2.35 dB, and 1.66 dB on average, which is significant. While including the seven point clouds marked with ‘*’, the proposed TSC-PCAC achieves bit rate savings ranging from 30.87% to 54.00%, and 38.53% on average as compared with the Sparse-PCAC. Meanwhile, the proposed TSC-PCAC achieves an average of 1.72 dB BD-PSNR gain. Compared to NF-PCAC, TSC-PCAC achieves bitrate savings ranging from 12.85% to 29.61%, and 22.27% on average. In terms of BD-PSNR, it achieves from 0.47 dB to 1.25 dB and 0.85 dB on average. While including point clouds marked with ‘*’, the proposed TSC-PCAC achieves an average of 21.30% bitrate saving and 0.80 dB BD-PSNR gain, which is significantly superior to the NF-PCAC.
As compared to the G-PCC v23, the proposed TSC-PCAC saves bitrate up to 53.07% across different point clouds. However, as shown in Fig. 6 and Table I, the proposed TSC-PCAC increases the BD-BR by 28.01% for the Thaidancer. This is mainly because the geometry and color attribute of Thaidancer are relatively complex, and it has low PSNR value even at higher bit rates. These characteristics do not align with the training set, which primarily consists of point clouds with relatively simple color attributes. Therefore, TSC-PCAC exhibits better compression performance for simpler-colored point clouds like basketball player and dancer. Increasing more colorful point clouds to training set may improve coding the complex sequences. The TSC-PCAC is inferior to G-PCC v23 with bitrate increasing of 1.26% on average. As we include the seven point clouds marked with ‘*’, the proposed TSC-PCAC achieves an average of 11.19% bit rate saving and 0.34 dB BD-PSNR gain, which proves the effectiveness of the proposed TSC-PCAC. The TSC-PCAC achieves coding gains for most point clouds and is capable of learning from the first few frames to enhance coding the subsequent frames.
| PC | Deep-PCAC | Sparse-PCAC | GPCC v23 | NF-PCAC | TSC-PCAC | |||||
| Enc. time | Dec. time | Enc. time | Dec. time | Enc. time | Dec. time | Enc. time | Dec. time | Enc. time | Dec. time | |
| Soldier | 28.26 | 23.77 | 66.78 | 294.57 | 5.53 | 4.95 | 1.99 | 2.45 | 1.62 | 4.49 |
| Redandblack | 17.89 | 14.88 | 43.44 | 151.94 | 3.70 | 3.31 | 1.37 | 1.67 | 1.41 | 3.39 |
| Dancer | 80.02 | 69.67 | 156.90 | 1135.91 | 13.40 | 12.08 | 4.45 | 5.48 | 2.85 | 9.79 |
| Basketball Player | 91.21 | 79.68 | 173.35 | 1364.30 | 14.82 | 13.37 | 4.85 | 5.98 | 3.14 | 10.66 |
| Phil | 40.33 | 33.99 | 70.66 | 323.55 | 7.38 | 6.62 | 2.53 | 3.09 | 1.87 | 5.54 |
| Boxer | 25.41 | 21.30 | 60.92 | 247.24 | 5.04 | 4.51 | 1.74 | 2.15 | 1.46 | 3.77 |
| Thaidancer | 16.24 | 13.42 | 37.86 | 122.97 | 3.34 | 2.99 | 1.45 | 1.76 | 1.30 | 3.22 |
| Rafa | 21.84 | 18.44 | 48.19 | 166.93 | 4.30 | 3.84 | 1.63 | 1.99 | 1.55 | 4.01 |
| Sir Frederick | 24.58 | 20.74 | 53.60 | 197.20 | 4.76 | 4.25 | 1.61 | 2.01 | 1.50 | 3.87 |
| Andrew* | 34.54 | 29.51 | 58.95 | 239.06 | 6.53 | 5.85 | 2.33 | 2.77 | 1.65 | 4.40 |
| David* | 54.83 | 46.92 | 93.58 | 473.10 | 9.52 | 8.55 | 3.19 | 3.86 | 2.22 | 7.41 |
| Exerciese* | 75.59 | 65.15 | 148.08 | 1062.44 | 12.80 | 11.52 | 3.60 | 4.69 | 2.44 | 7.85 |
| Longdress* | 20.03 | 16.60 | 48.87 | 178.55 | 4.10 | 3.67 | 1.60 | 1.94 | 1.54 | 4.17 |
| Loot* | 19.91 | 16.60 | 47.90 | 169.38 | 4.03 | 3.62 | 1.46 | 1.80 | 1.34 | 3.12 |
| Model* | 71.52 | 62.81 | 141.21 | 958.28 | 12.40 | 11.16 | 4.05 | 5.11 | 2.90 | 9.87 |
| Sarah* | 36.40 | 30.94 | 63.85 | 268.69 | 6.74 | 6.07 | 1.97 | 2.46 | 1.59 | 4.13 |
| Average* | 41.16 | 35.28 | 82.13 | 459.63 | 7.40 | 6.65 | 2.49 | 3.08 | 1.90 | 5.61 |
IV-C Visual Quality Evaluation
In addition, visual quality comparisons were performed to validate the effectiveness of TSC-PCAC. Fig. 7 illustrates the visual quality comparison of the compressed point clouds from five different encoding methods across two test sequences. Figs. 7 to 7 display the enlarged images reconstructed by each encoding method for Redandblack. To ensure fair comparisons, examples with similar bpp were selected. The face of Redandblack reconstructed from G-PCC v23, showed in Fig. 7, exhibits noticeable block artifacts when compared to the original. The bitrate and PSNR for the reconstruction are 0.102 and 33.10 dB. In contrast, bitrate and PSNR of the point clouds reconstructed by the Sparse-PCAC shown in Fig. 7 and NF-PCAC shown in Fig. 7 are 0.143 and 31.75 dB, and 0.116 and 32.21 dB, respectively. The reconstructed point clouds appear smoother with a lower PSNR. The reconstructed point cloud of our TSC-PCAC is presented in Fig. 7 with bitrate and PSNR of 0.132 and 33.24 dB. Compared with those from the Sparse-PCAC and NF-PCAC, it exhibits a lower bit rate and higher PSNR. Additionally, in terms of visual quality, it can be observed that TSC-PCAC is smoother and offers better visual quality. Similar results can be found for Soldier from Figs. 7 to Fig. 7. The visual results further validate the superiority of TSC-PCAC for Redandblack and Soldier sequences comparing with Sparse-PCAC, NF-PCAC and G-PCC v23 methods.



IV-D Computational Complexity Evaluation
We also evaluated the computational complexity of TSC-PCAC on all the testing point clouds. We processed each point cloud sequentially using a single GPU and the operating system was Ubuntu 22.04. For G-PCC, the encoding and decoding time for each point cloud corresponds to the average time required to encode and decode using different QP settings, while for the learned methods, it corresponds to the average time required to encode and decode using networks with different values.
| Methods | Sparse-PCAC | NF-PCAC | TSC-PCAC |
| Parameter | 15.88M | 51.16M | 23.62M |
| Memory | 4.75GB | 16.69GB | 5.58GB |
| Y Enc. | 0.11s | 1.10s | 0.20s |
| Y Entropy Enc. | 82.02s | 1.39s | 1.70s |
| Total Enc. | 82.13s | 2.49s | 1.90s |
| Y Entropy Dec. | 459.29s | 1.13s | 5.16s |
| Y Dec. | 0.34s | 1.95s | 0.45s |
| Total Dec. | 459.63s | 3.08s | 5.61s |
From Table II, it can be observed that Deep-PCAC and Sparse-PCAC have relatively long total encoding/decoding time, which are 41.16s/35.28s and 82.13s/459.63s, respectively. The furthest point sampling in the network results in longer encoding and decoding time for Deep-PCAC. For Sparse-PCAC, the sequential processing of the voxel context module results in longer encoding and decoding time. This issue becomes particularly severe when processing denser point clouds, such as Basketball Player and Dancer, where the decoding time can exceed a thousand seconds. For NF-PCAC, the average encoding/decoding time is 2.49s/3.08s. For G-PCC v23, the encoding/decoding time ranges from 3.34s/2.99s to 14.82s/13.37s, with an average of 7.40s/6.65s. The encoding/decoding time of TSC-PCAC ranges from 1.30s/3.22s to 3.14s/10.66s, with an average of 1.90s/5.61s. TSC-PCAC reduces encoding/decoding time by 97.68%/98.78%, 23.74%/-82.22% and 74.33%/15.66% on average as compared with the Sparse-PCAC, NF-PCAC and G-PCC v23. Note that the encoding and decoding of G-PCC were performed on CPU, while learning-based methods were performed on the GPU+CPU platform.
We also analyze the computational complexity for the modules of learned compression methods. Table III illustrates the network parameters, memory consumption in testing, the encoding and decoding time. ‘Y Enc.’ and ‘Y Dec.’ represent the average computing time of encoder and decoder . Firstly, the parameter counts for Sparse-PCAC, TSC-PCAC, and NF-PCAC are 15.88M, 23.62M, and 51.16M respectively. NF-PCAC has the largest number of network parameters while Sparse-PCAC has the smallest. Secondly, the encoder and decoder runtime for Sparse-PCAC is the shortest, while NF-PCAC takes the longest. However, the encoding/decoding time of Sparse-PCAC and TSC-PCAC are longer compared to NF-PCAC because of the context modules. Sparse-PCAC employed the voxel context module performing autoregression in spatial dimensions, while our TSC-PCAC utilizes the channel context module performing autoregression in channel dimensions. Thus, TSC-PCAC greatly reduces the number of autoregression steps. This results in longest entropy encoding/decoding time for Sparse-PCAC, moderate for TSC-PCAC, and shortest for NF-PCAC, which are 82.02s/459.29s, 1.70s/5.16s, and 1.39s/1.13s, respectively. Finally, the average total encoding time of the TSC-PCAC is 1.90s, which is the shortest among all schemes. The average total decoding time of the TSC-PCAC is 5.61s, which is in the second place and a little longer than that of the NF-PCAC, i.e., 3.08s.
IV-E Ablation Study for TSC-PCAC
Ablation studies were performed to validate the effectiveness of the TSCM, the TSCM based channel context module, and the voxel-based global module. ‘TSCM w/o transformer’ represents the transformer in TSCM is replaced with residual block, ‘TSCM w/o global block’ represents the global block in TSCM is replaced with residual block, and ‘TSCM w/o both’ represents the global block and transformer in TSCM are replaced with residual block. ‘Point-based Global block’ indicates the TSCM that uses the global block from [42].
Table IV show the BD-BR and BD-PSNR gains achieved by the TSC-PCAC using different coding modules compared to the baseline Sparse-PCAC. Firstly, TSCM without Transformer achieves an average of 27.47% bitrate saving and an average of 1.19 dB PSNR gain. If without both transformer and global block, the TSC-PCAC achieves an average bitrate saving of 28.38% and 1.23 dB PSNR gain. As for the TSCM w/o Global block consisting of only residual blocks and the transformer, it achieves an average of 36.09% bitrate savings. Secondly, to evaluate the effectiveness of using the TSCM, we replaced TSCM in the channel context module with two convolutional layers, denoted as ‘context module w/o TSCM’. The channel context module using conventional convolutions has larger parameters than that using TSCM. It is also found in Table IV that if removing TSCM from the channel context, only 32.16% bitrate on average can be saved. Thirdly, to validate the effectiveness of using voxel-based global block in the TSC-PCAC, we replaced the voxel-based global block with point-based global block [42] in TSCM, and it is able to achieve an average of 36.89% bit rate reduction. Finally, the overall TSC-PCAC achieves an average of 38.53% bitrate saving, which is the best. Fig. 8 shows the coding performance comparison of the ablation studies in TSC-PCAC, where the TSC-PCAC is the best for Basketball Player, Redandblack and average of all sequences. These results prove the effectiveness of each module in TSC-PCAC, including transformer and global block in TSCM, voxel-based global block and TSCM based channel context module.
| Methods | Methods vs Sparse-PCAC | |
| BD-BR(%) | BD-PSNR(dB) | |
| Context w/o TSCM | -32.16 | 1.41 |
| TSCM w/o Transformer | -27.47 | 1.19 |
| TSCM w/o both | -28.38 | 1.23 |
| TSCM w/o Global block | -36.09 | 1.60 |
| Point-based Global block | -36.89 | 1.62 |
| TSC-PCAC | -38.53 | 1.72 |
V Conclusions
In this paper, we propose a voxel Transformer and Sparse Convolution-based Point Cloud Attribute Compression (TSC-PCAC) for point cloud broadcasting, where an efficient Transformer and Sparse Convolution Module (TSCM) and TSCM based channel context module are developed to improve the attribute coding efficiency. The TSCM integrates local dependencies and global spatial-channel features for point clouds, modeling local correlations among voxels and capturing global features to remove redundancy. Furthermore, the TSCM based channel context module exploits inter-channel correlations to improve the predicted probability distribution of quantized latent representations. The TSC-PCAC achieves an average of 38.53%, 21.30%, and 11.19% bit rate reductions as compared with the Sparse-PCAC, NF-PCAC and G-PCC v23. Meanwhile, it maintains low encoding/decoding complexity. Overall, the proposed TSC-PCAC is effective for point cloud attribute coding.
The deep learning based Sparse-PCAC, NF-PCAC, and TSC-PCAC are for attribute coding only and require to be trained multiple times for different rate points. In future, we will investigate deep networks for higher compression ratio, as well as joint geometry and attribute coding.
References
- [1] K. Mammou, P. A. Chou, D. Flynn, M. Krivokuća, O. Nakagami, and T. Sugio, G-PCC codec description v2, document ISO/IEC JTC1/SC29/WG11 N18189, 2019.
- [2] K. Mammou, A. M. Tourapis, D. Singer, and Y. Su, Video-based and hierarchical approaches point cloud compression, document ISO/IEC JTC1/SC29/WG11 m41649, Macau, China, 2017.
- [3] J. Liu, H. Sun, and J. Katto, “Learned image compression with mixed transformer-cnn architectures,” in Proc. IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2023, pp. 14 388–14 397.
- [4] T. Huang and Y. Liu, “3d point cloud geometry compression on deep learning,” in Proc. ACM Int. Conf. Multimedia, 2019, pp. 890–898.
- [5] L. Gao, T. Fan, J. Wan, Y. Xu, J. Sun, and Z. Ma, “Point cloud geometry compression via neural graph sampling,” in Proc. IEEE Int. Conf. Image Process. (ICIP), 2021, pp. 3373–3377.
- [6] J. Wang, D. Ding, Z. Li, and Z. Ma, “Multiscale point cloud geometry compression,” in Proc. Data Compress. Conf. (DCC), 2021, pp. 73–82.
- [7] G. Liu, J. Wang, D. Ding, and Z. Ma, “Pcgformer: Lossy point cloud geometry compression via local self-attention,” in Proc. IEEE Int. Conf. Visual Commun. Image Process. (VCIP), 2022, pp. 1–5.
- [8] J. Wang, H. Zhu, H. Liu, and Z. Ma, “Lossy point cloud geometry compression via end-to-end learning,” IEEE Trans. Circuits Syst. Video Technol., vol. 31, no. 12, pp. 4909–4923, 2021.
- [9] J. Wang, D. Ding, and Z. Ma, “Lossless point cloud attribute compression using cross-scale, cross-group, and cross-color prediction,” in Proc. Data Compress. Conf. (DCC), 2023, pp. 228–237.
- [10] D. T. Nguyen and A. Kaup, “Lossless point cloud geometry and attribute compression using a learned conditional probability model,” IEEE Trans. Circuits Syst. Video Technol., vol. 33, no. 8, pp. 4337–4348, 2023.
- [11] X. Sheng, L. Li, D. Liu, Z. Xiong, Z. Li, and F. Wu, “Deep-pcac: An end-to-end deep lossy compression framework for point cloud attributes,” IEEE Trans. Multimedia, vol. 24, pp. 2617–2632, 2021.
- [12] J. Wang and Z. Ma, “Sparse tensor-based point cloud attribute compression,” in Proc. IEEE Int. Conf. Multimed. Inf. Process. Retr. (MIPR), 2022, pp. 59–64.
- [13] G. Fang, Q. Hu, H. Wang, Y. Xu, and Y. Guo, “3dac: Learning attribute compression for point clouds,” in Proc. IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2022, pp. 14 799–14 808.
- [14] R. B. Pinheiro, J.-E. Marvie, G. Valenzise, and F. Dufaux, “Nf-pcac: Normalizing flow based point cloud attribute compression,” in Proc. IEEE Int. Conf. Acoust., Speech Signal Process. (ICASSP), 2023, pp. 1–5.
- [15] R. L. De Queiroz and P. A. Chou, “Compression of 3d point clouds using a region-adaptive hierarchical transform,” IEEE Trans. Image Process., vol. 25, no. 8, pp. 3947–3956, 2016.
- [16] C. Cao, M. Preda, V. Zakharchenko, E. S. Jang, and T. Zaharia, “Compression of sparse and dense dynamic point clouds—methods and standards,” Proc. IEEE, vol. 109, no. 9, pp. 1537–1558, 2021.
- [17] D. Graziosi, O. Nakagami, S. Kuma, A. Zaghetto, T. Suzuki, and A. Tabatabai, “An overview of ongoing point cloud compression standardization activities: Video-based (v-pcc) and geometry-based (g-pcc),” APSIPA Trans. Signal Inf. Proc., vol. 9, p. e13, 2020.
- [18] M. Yang, Z. Luo, M. Hu, M. Chen, and D. Wu, “A comparative measurement study of point cloud-based volumetric video codecs,” IEEE Trans. Broadcast., vol. 69, no. 3, pp. 715–726, 2023.
- [19] E. Pavez, A. L. Souto, R. L. De Queiroz, and A. Ortega, “Multi-resolution intra-predictive coding of 3d point cloud attributes,” in Proc. IEEE Int. Conf. Image Process. (ICIP), 2021, pp. 3393–3397.
- [20] P. Gao, L. Zhang, L. Lei, and W. Xiang, “Point cloud compression based on joint optimization of graph transform and entropy coding for efficient data broadcasting,” IEEE Trans. Broadcast., vol. 69, no. 3, pp. 727–739, 2023.
- [21] Y. Zhang, K. Ding, N. Li, H. Wang, X. Huang, and C.-C. J. Kuo, “Perceptually weighted rate distortion optimization for video-based point cloud compression,” IEEE Trans. Image Process., vol. 32, pp. 5933–5947, 2023.
- [22] X. Wu, Y. Zhang, C. Fan, J. Hou, and S. Kwong, “Subjective quality database and objective study of compressed point clouds with 6dof head-mounted display,” IEEE Trans. Circuits Syst. Video Technol., vol. 31, no. 12, pp. 4630–4644, 2021.
- [23] Q. Liang, Z. He, M. Yu, T. Luo, and H. Xu, “Mfe-net: A multi-layer feature extraction network for no-reference quality assessment of 3-d point clouds,” IEEE Trans. Broadcast., vol. 70, no. 1, pp. 265–277, 2024.
- [24] Y. Zhang, H. Liu, Y. Yang, X. Fan, S. Kwong, and C. C. J. Kuo, “Deep learning based just noticeable difference and perceptual quality prediction models for compressed video,” IEEE Trans. Circuits Syst. Video Technol., vol. 32, no. 3, pp. 1197–1212, 2022.
- [25] J. Xing, H. Yuan, R. Hamzaoui, H. Liu, and J. Hou, “Gqe-net: a graph-based quality enhancement network for point cloud color attribute,” IEEE Trans. Image Process., vol. 32, pp. 6303–6317, 2023.
- [26] J. Ballé, D. Minnen, S. Singh, S. J. Hwang, and N. Johnston, “Variational image compression with a scale hyperprior,” in Proc. Int. Conf. Learn. Represent., 2018, pp. 1–23.
- [27] Z. Tang, H. Wang, X. Yi, Y. Zhang, S. Kwong, and C.-C. J. Kuo, “Joint graph attention and asymmetric convolutional neural network for deep image compression,” IEEE Trans. Circuits Syst. Video Technol., vol. 33, no. 1, pp. 421–433, 2022.
- [28] R. Zou, C. Song, and Z. Zhang, “The devil is in the details: Window-based attention for image compression,” in Proc. IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2022, pp. 17 492–17 501.
- [29] D. Minnen and S. Singh, “Channel-wise autoregressive entropy models for learned image compression,” in Proc. IEEE Int. Conf. Image Process. (ICIP), 2020, pp. 3339–3343.
- [30] D. Minnen, J. Ballé, and G. D. Toderici, “Joint autoregressive and hierarchical priors for learned image compression,” Proc. Adv. Neural Inf. Process. Syst., pp. 10 794–10 803, 2018.
- [31] R. Song, C. Fu, S. Liu, and G. Li, “Efficient hierarchical entropy model for learned point cloud compression,” in CVPR, 2023, pp. 14 368–14 377.
- [32] C. Szegedy, S. Ioffe, V. Vanhoucke, and A. Alemi, “Inception-v4, inception-resnet and the impact of residual connections on learning,” in Proc. AAAI Conf. Artif. Intell., no. 1, 2017, pp. 4278–4284.
- [33] Z. Qi and W. Gao, “Variable-rate point cloud geometry compression based on feature adjustment and interpolation,” in Proc. Data Compress. Conf. (DCC). IEEE, 2024, pp. 63–72.
- [34] A. Akhtar, Z. Li, and G. Van der Auwera, “Inter-frame compression for dynamic point cloud geometry coding,” IEEE Trans. Image Process., vol. 33, pp. 584–594, 2024.
- [35] Y. Zhou, X. Zhang, X. Ma, Y. Xu, K. Zhang, and L. Zhang, “Dynamic point cloud compression with spatio-temporal transformer-style modeling,” in Proc. Data Compress. Conf. (DCC). IEEE, 2024, pp. 53–62.
- [36] B. Isik, P. A. Chou, S. J. Hwang, N. Johnston, and G. Toderici, “Lvac: Learned volumetric attribute compression for point clouds using coordinate based networks,” Front. Sig. Proc., vol. 2, p. 1008812, 2022.
- [37] T.-P. Lin, M. Yim, J.-C. Chiang, W.-H. Peng, and W.-N. Lie, “Sparse tensor-based point cloud attribute compression using augmented normalizing flows,” APSIPA Trans. Signal Inf. Proc., pp. 1739–1744, 2023.
- [38] J. Zhang, J. Wang, D. Ding, and Z. Ma, “Scalable point cloud attribute compression,” IEEE Trans. Multimedia, 2023.
- [39] C. R. Qi, L. Yi, H. Su, and L. J. Guibas, “Pointnet++: Deep hierarchical feature learning on point sets in a metric space,” Proc. Adv. Neural Inf. Process. Syst., pp. 5105–5114, 2017.
- [40] C. Choy, J. Gwak, and S. Savarese, “4d spatio-temporal convnets: Minkowski convolutional neural networks,” in Proc. IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2019, pp. 3075–3084.
- [41] T. Zhao, N. Zhang, X. Ning, H. Wang, L. Yi, and Y. Wang, “Codedvtr: Codebook-based sparse voxel transformer with geometric guidance,” in Proc. IEEE Conf. Comput. Vis. Pattern Recog. (CVPR), 2022, pp. 1435–1444.
- [42] S. Qiu, S. Anwar, and N. Barnes, “Pnp-3d: A plug-and-play for 3d point clouds,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 45, no. 1, pp. 1312–1319, 2021.
- [43] P. A. C. Sebastian Schwarz and I. Sinharoy, Common test conditions for point cloud compression, ISO/IEC JTC1/SC29/WG11 N18474, 2018.
- [44] D. Tian, H. Ochimizu, C. Feng, R. Cohen, and A. Vetro, Updates and Integration of Evaluation Metric Software for PCC, document ISO/IEC JTC1/SC29/WG11 MPEG2016/M40522, 2017.
- [45] G. Bjontegaard, Calculation of average PSNR differences between RD-curves, document VCEG-M33, 2001.
- [46] E. d’Eon, B. Harrison, T. Myers, and P. A. Chou, 8i Voxelized Full Bodies-a Voxelized Point Cloud Dataset, document ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) WG11M40059/WG1M74006, 2017.
- [47] Y. Xu, Y. Lu, and Z. Wen, “Owlii Dynamic human mesh sequence dataset,” document ISO/IEC JTC1/SC29/WG11 M41658, 2017.
- [48] M. Krivokuca, P. A. Chou, and P. Savill, 8i Voxelized Surface Light Field (8iVSLF) Dataset, document ISO/IEC JTC1/SC29/WG11 MPEG, m42914, 2018.
- [49] R. Pagés, K. Amplianitis, J. Ondrej, E. Zerman, and A. Smolic, Volograms & V-SENSE Volumetric Video Dataset, document ISO/IEC JTC1/SC29/WG07 MPEG2021/m56767, 2021.
- [50] C. Loop, Q. Cai, S. O. Escolano, and P. A. Chou, Microsoft Voxelized Upper Bodies-a Voxelized Point Cloud Dataset, document ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) m38673/M72012, 2016.
- [51] D. T. Nguyen, M. Quach, G. Valenzise, and P. Duhamel, “Lossless coding of point cloud geometry using a deep generative model,” IEEE Trans. Circuits Syst. Video Technol., vol. 31, no. 12, pp. 4617–4629, 2021.