Truncated Beam Sweeping for Spatial Covariance Matrix Reconstruction in Hybrid Massive MIMO

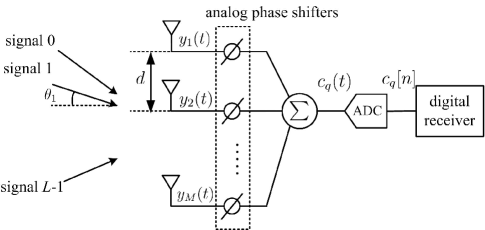
As in Fig. 1, consider a hybrid massive MIMO receiver composed of a uniform linear array (ULA) with $M$ antennas. To simplify the symbol notation, a single RF chain is considered in this paper even though the proposed approach can be also used in the case of multiple RF chains, as in [12].

For a general model, patterns of antenna elements in the array should be taken into account. Since all elements in the ULA are the same, all antenna elements can share a common antenna pattern $g(\theta)$ where $\theta$ indicates the DOA. Therefore, if denote $y_{m}(t)$ to be the received signal on the $m$-th antenna with $m=0,1,\cdots,M-1$, then the received signal vector $\boldsymbol{y}(t)=[y_{0}(t),y_{1}(t),\cdots,y_{M-1}(t)]^{\mathrm{T}}$ can be represented as

where $x_{l}(t)$’s ($l=0,1,\cdots,L-1)$ are $L$ signals impinging from far field onto the array, $\theta_{l}$ is the DOA of $x_{l}(t)$, and $\boldsymbol{z}(t)$ denotes the additive Gaussian noise vector with $\mathrm{E}\{\boldsymbol{z}(t)\boldsymbol{z}^{\mathrm{H}}(t)\}=N_{0}\boldsymbol{I}$ with $N_{0}$ and $\boldsymbol{I}$ being the noise power and an identity matrix, respectively. In (1), $\boldsymbol{a}(\theta_{l})$ is the $M\times 1$ steering vector with the $m$-th entry given by $a_{m}(\theta_{l})=e^{j2\pi\cdot\frac{d}{\lambda}\cdot\sin\theta_{l}\cdot m},$ where $d=0.5\lambda$ is the antenna distance and $\lambda$ is the wave length. If assuming $L$ signals are mutually independent with zero means and the power of the $l$-th signal is $\mathrm{E}\{|x_{l}(t)|^{2}\}=\sigma_{l}^{2}$, then the SCM, $\boldsymbol{R}=\mathrm{E}\{\boldsymbol{y}(t)\boldsymbol{y}^{\mathrm{H}}(t)\}$, can be obtained as

Note that the signal model in (1) can be also used even in the presence of mutual coupling among antennas. As in [15], most antenna elements in a long ULA can see the same neighboring environments, and therefore an average antenna pattern, which is common to all antennas, can be employed to describe the mutual coupling effect. However, due to mutual coupling, the average antenna pattern $g(\theta)$ may deviate from the one designed for the single antenna case. Active measurement can be used in this case to figure out the practical $g(\theta)$.

Denote $\boldsymbol{y}[n]=\boldsymbol{y}(nT_{s})$ to be the sample of received signal where $T_{s}$ denotes the sampling period. If all entries of $\boldsymbol{y}[n]$ are available to the digital receiver, then SCM in (2) can be estimated using the sample average approach, that is [9]

where $N$ denotes the number of samples. In this approach, received signals at all antennas should be sent via RF chains to the digital receiver. In hybrid massive MIMO, however, Fig. 1 shows that only the combination of the entries of $\boldsymbol{y}[n]$ can be seen by the digital receiver because there is only one RF chain. As a consequence, the sample average approach in (3) cannot be used in hybrid massive MIMO systems.

To address this issue, we have developed basic BSA for SCM reconstruction in hybrid massive MIMO with single RF chain [10]. Then, the basic BSA has been improved in [12] to handle the case of multiple RF chains. A careful selection of predetermined DOAs has also been presented in [12] so that the computational complexity can be greatly reduced.

In spite of the success in SCM reconstruction, the weakness of BSA is obvious because it needs a large number of beam sweeping operations and the algorithm delay caused by beam sweeping can be significant. Although fully-connected hybrid structure can be used to reduce algorithm delay [14], that approach is unavailable in the cases of single RF chain or sub-connected hybrid structure. To overcome this issue, a truncated BSA is proposed as we will show in Section III.

As in [10], define $\{\theta^{(0)},\theta^{(1)},\cdots,\theta^{(Q-1)}\}$ to be a set of predetermined DOAs. The analog beamformers switch the beam directions to the predetermined DOAs in turn. For the $q$-th beam, the combination of the received signals can be represented by $c_{q}(t)=\boldsymbol{a}^{\mathrm{H}}(\theta^{(q)})\boldsymbol{y}(t)$. From Fig. 1, the signal combination is sampled before send to the receiver, and thus the samples of the signal combination can be given by

Denote $P_{q}=\mathrm{E}(|c_{q}[n]|^{2})$ to be the statistical power of $c_{q}[n]$. Using sample average, an estimation of $P_{q}$ can be obtained as

Using $\mathrm{vec}(\cdot)$ operator to (5), $\widehat{P}_{q}$ can be rewritten as $\widehat{P}_{q}=\boldsymbol{a}_{q}^{\mathrm{T}}\widehat{\boldsymbol{r}}$ where $\widehat{\boldsymbol{r}}=\mathrm{vec}(\widehat{\boldsymbol{R}})$ and $\boldsymbol{a}_{q}=\boldsymbol{a}(\theta^{(q)})\otimes\boldsymbol{a}^{*}(\theta^{(q)})$ with $\otimes$ indicating Kronecker product. If taking all $Q$ predetermined DOAs into account, we can derive that

where $\widehat{\boldsymbol{p}}=(\widehat{P}_{0},\widehat{P}_{1},\cdots,\widehat{P}_{Q-1})^{\mathrm{T}}$ contains the estimated power on all predetermined beams and $\boldsymbol{A}=(\boldsymbol{a}_{0},\boldsymbol{a}_{1},\cdots,\boldsymbol{a}_{Q-1})^{\mathrm{T}}$. As in [10], unknown $\widehat{\boldsymbol{r}}$ can be obtained by solving (6) so that the desired SCM can be reconstructed as $\widehat{\boldsymbol{R}}=\mathrm{unvec}(\widehat{\boldsymbol{r}})$.

Direct solution of (6) suffers from high complexity due to matrix inverse. To avoid this issue, a low-complexity BSA is investigated in [12]. In this approach, (6) is converted to

where $\boldsymbol{B}=(\boldsymbol{b}_{0},\boldsymbol{b}_{1},\cdots,\boldsymbol{b}_{Q-1})^{\mathrm{T}}$ with $\boldsymbol{b}_{q}$ being a $(2M-1)\times 1$ vector given by

and $\widehat{\boldsymbol{\gamma}}=(\widehat{\gamma}[1-M],\cdots,\widehat{\gamma}[M-1])^{\mathrm{T}}$ corresponds to $2M-1$ non-repeated entries in $\boldsymbol{R}$ with $\widehat{\gamma}[m-n]$ being the $(m,n)$-th entry of $\widehat{\boldsymbol{R}}$, that is, $\widehat{\gamma}[m-n]=[\widehat{\boldsymbol{R}}]_{m,n}$. If the predetermined DOAs are selected as $\theta^{(q)}=2\mathrm{arcsin}(-1+2q/Q)$, then the number of predetermined DOAs can be determined as $Q=2M-1$ and $\boldsymbol{B}^{\mathrm{H}}\boldsymbol{B}$ becomes a diagonal matrix $\boldsymbol{\Delta}$ with the $m$-th $(m=0,1,\cdots,2M-2)$ diagonal entry given by

Therefore, unknown $\widehat{\boldsymbol{\gamma}}$ can be obtained as

where matrix inverse has been avoided. The desired SCM can be then reconstructed using the estimations of the entries contained in $\widehat{\boldsymbol{\gamma}}$.

In [10] and [12], omni-directional antenna elements are implicitly assumed, and therefore full beam sweeping has to be adopted where power estimation in (5) is conducted for each predetermined DOA. Actually, full beam sweeping can be approximated by a truncated beam sweeping if we exploit the antenna pattern $g(\theta)$.

To this end, we assume the number of samples is large enough. Then, the sample average in (5) can be replaced by the statistical average and thus

Substitute (2) into (17), we have

When the number of antennas is large, the feature of $\mathrm{sinc}(\cdot)$ function in (III-B) indicates that only arriving signals with DOAs close to $\theta^{(q)}$ can cause significant contribution to $P_{q}$. Therefore, if the antenna pattern $g(\theta)$ has very weak response for DOAs that are far from the normal direction, the summarization term in (III-B) can be approximated by zero when $\theta^{(q)}$ is far from the normal direction. The mathematical observation in above also coincides with the following physical intuition: as the overall array response $g(\theta)\boldsymbol{a}(\theta)$ is scaled by $g(\theta)$, the received power could be very weak if we point the beam to a direction that is far from the normal direction.

Inspired by the above observation, the full beam sweeping in (5) can be approximated by the following truncated beam sweeping operation

In (19), $\mathcal{S}=\{q|\left\lceil T/2\right\rceil\leq q<Q-\lfloor T/2\rfloor\}$ where $T$ is an integer ($0\leq T\leq Q-1$) indicating the number of truncated predetermined DOAs with $\left\lceil\cdot\right\rceil$ and $\left\lfloor\cdot\right\rfloor$ indicating round up and down to the nearest integers, and $\overline{\mathcal{S}}$ is the complementary set of ${\mathcal{S}}$. It means in (19) that power estimation is only need for $\theta^{(q)}$’s that are close to the normal direction, while a predetermined constant can be used instead for $\theta^{(q)}$’s that are far from the normal direction. Since only $Q-T$ predetermined DOAs needs power estimation, truncated beam sweeping operation can be accelerated when $T>0$, at the cost of negligible performance reduction as will be shown in Section IV.

Once the truncated sweeping results in (19) are available, they can be used in (16) to reconstruct the desired SCM.

To evaluate the performance reduction caused by truncation, define $\|\widehat{\boldsymbol{R}}-\boldsymbol{R}\|_{\mathrm{F}}^{2}$ to be the squared-error (SE) between desired SCM and reconstructed SCM. Then, we can obtain

where $\gamma[m-n]=[\boldsymbol{R}]_{m,n}$. Recalling that $\boldsymbol{R}$ have $2M-1$ non-repeated entries in total, (21) can be rewritten as

where we have used the identity in (15) for the second equation. In (IV-A), $\boldsymbol{\gamma}=({\gamma}[1-M],\cdots,{\gamma}[M-1])^{\mathrm{T}}$ contains $2M-1$ non-repeated entries in $\boldsymbol{R}$. If denote $\boldsymbol{p}=({P}_{0},{P}_{1},\cdots,{P}_{Q-1})^{\mathrm{T}}$, then we can derive, similar to (7) and (16), that $\boldsymbol{B}{\boldsymbol{\gamma}}={\boldsymbol{p}}$ and ${\boldsymbol{\gamma}}=\boldsymbol{\Delta}^{-1}\boldsymbol{B}^{\mathrm{H}}{\boldsymbol{p}}$. Using this identities and (16), (IV-A) can be rewritten as

To simplify the expression $\boldsymbol{B}\boldsymbol{\Delta}^{-1}\boldsymbol{B}^{\mathrm{H}}$, consider that

Since $\boldsymbol{B}^{\mathrm{H}}\boldsymbol{B}=\boldsymbol{\Delta}$, (24) can be rewritten as $\boldsymbol{B}\boldsymbol{\Delta}^{-1}\boldsymbol{B}^{\mathrm{H}}\boldsymbol{B}=\boldsymbol{B}$ or equivalently

where $\boldsymbol{O}$ is a $(2M-1)\times(2M-1)$ all zero matrix. Recalling that $2M-1=\mathrm{Rank}(\boldsymbol{B}^{\mathrm{H}}\boldsymbol{B})\leq\mathrm{Rank}(\boldsymbol{B})\leq 2M-1$, $\boldsymbol{B}$ is therefore a non-singular matrix and equation $\boldsymbol{X}\boldsymbol{B}=\boldsymbol{O}$ has only one solution $\boldsymbol{X}=\boldsymbol{O}$. Therefore, it shows in (25) that

As a result, we have

Then, using (III-B) and the assumption in (20), (27) can be obtained as

It shows in (28) that the $l$-th received signal can contribute to the SE only when $q_{l}\in\overline{\mathcal{S}}$. As a result, performance reduction due to truncated beam sweeping can be ignored because $g(\theta^{(q_{l})})$ is very small if $q_{l}\in\overline{\mathcal{S}}$.

To evaluate the impact of antenna patterns on the performance, asymptotical analysis is used. In this case, the number of samples is finite, and thus mean-SE (MSE) should be used instead. $T=0$ is considered so that no truncation is employed. In addition to the assumption in (20), we also assume that $x_{l}[n]=x_{l}(nT_{s})\sim\mathrm{CN}(0,\sigma_{l}^{2})$.

Under this situations, from (27), we can obtain

Since $\mathrm{E}(\widehat{\boldsymbol{R}})=\boldsymbol{R}$, we have

Then, substitute (1) into the first term in the right-side of (IV-B), and after a long and tedious mathematical procedure, we obtain

where we have used the identity $\mathrm{E}(x_{1}x_{2}x_{3}x_{4})=\mathrm{E}(x_{1}x_{2})\mathrm{E}(x_{3}x_{4})+\mathrm{E}(x_{1}x_{3})\mathrm{E}(x_{2}x_{4})+\mathrm{E}(x_{1}x_{4})\mathrm{E}(x_{2}x_{3})$ for general Gaussian random variables $x_{1},x_{2},x_{3},x_{4}$[16].

Then, with the assumption in (20), (IV-B) is simplified as

The MSE in (29) can be therefore obtained as

Following insights can be obtained from (IV-B): Fist, due to the antenna pattern $g(\theta)$, arriving signals with DOAs close to the normal direction contribute more to the MSE than the ones with DOAs far from the normal direction. This observation can justify the truncated BSA because lost of sweeping results at predetermined DOAs far from normal direction has little impact on the performance. Second, the MSE can vanish as the increasing of $N$, which coincides with the intuition and the simulation results in [10] and [12].