Trineutron resonances in the SS-HORSE extension of the no-core shell model
Abstract
The SS-HORSE–NCSM method is generalized to the case of democratic decay into an odd number of fragments. This method is applied to the search for resonances in three-neutron system (trineutron) using ab initio no-core shell model calculations with realistic nucleon-nucleon () potentials. The and strongly overlapping resonances are predicted when softened interactions are used and are preferred over the case where bare interactions of the chiral effective field theory are used with no resonance obtained.
I Introduction
In this paper, we develop and apply an ab initio method of calculating the democratic decay of light nuclei into an odd number of fragments within the no-core shell model (NCSM) Barrett_ProgrPartNuclPhys_2013 . Such an approach is of a current interest for the studies of neutron-excess light nuclei and, in particular, Borromean neutron-excess nuclei near and beyond the neutron drip line.
We apply this method to the search for resonant states in the three-neutron system (trineutron). There is an increasing interest in theoretical and experimental investigations of multi-neutron systems following the experimental observation of the tetraneutron resonance Kisamori ; Duer_Nature_2022 . By studying the multi-neutron systems we can sensitively probe the interaction between neutrons for details that are not available from neutron-neutron scattering experiments.
The first experimental investigations of the three-neutron system were published in the 1960s. In particular, the bound trineutron search failed in the studies of the 3H(,) reaction in Ref. Ajdacic_PhysRevLett_1965 . A comprehensive description of the history of trineutron experimental searches can be found in reviews of Refs. Kezerashvili_arXiv_2016 ; Marques_EurPhysJA_2021 . The main conclusion of all experiments is the exclusion of the bound trineutron. At the same time, the existence of a resonant trineutron state is not ruled out.
References Kezerashvili_arXiv_2016 ; Marques_EurPhysJA_2021 present also the history of theoretical investigations of the three-neutron system. Among those we note the recent studies based on realistic interactions Hiyama_PhysRevC_2016 ; Gandolfi ; Deltuva_PhysRevC_2018 ; Li_PhysRevC_2019 . The resonant trineutron has not been found in Refs. Hiyama_PhysRevC_2016 ; Deltuva_PhysRevC_2018 . The binding energy of three neutrons confined by an external potential (trap) has been extrapolated in Ref. Gandolfi to the case of the vanishing trap to estimate the trineutron resonance energy (without any estimation for the resonance width). The obtained resonance energy of MeV is close to the result of Ref. Li_PhysRevC_2019 where the trineutron resonance is predicted by the calculations in the ab initio no-core Gamow shell model at the energy of MeV with the width of MeV.
In this work we will extend our SS-HORSE–NCSM approach Shirokov_PhysRevC_2016 ; Mazur_PhysPartNucl_2017 ; Blokhintsev_YaF_2017_1 ; Blokhintsev_YaF_2017_2 ; Shirokov_PhysRevC_2018 ; Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 that generalizes the NCSM to the description of continuum spectrum states. The advantage of the SS-HORSE–NCSM is that the scattering phase shifts are computed by simple analytical expressions at the NCSM eigenenergies and there is no need in additional numerical challenges for no-core systems as compared to other continuum generalizations of NCSM like the NCSM with continuum (NCSMC) NCSMC or the no-core Gamow shell model GSM ; Li_PhysRevC_2019 . Next the matrix is parametrized and the resonant energies and widths are obtained by a numerical location of the -matrix poles. Recently this method has been successfully applied to the description of resonant states in 5He Shirokov_PhysRevC_2016 , 5Li Shirokov_PhysRevC_2018 , 7He Mazur_PhysRevC_2022 , and 9Li Mazur_PhysAtNucl_2022 with JISP16 Shirokov_PhysLettB_2007 and Daejeon16 Shirokov_PhysLettB_2016 realistic interactions in the channels of elastic scattering of protons in the case of 5Li or neutrons in all other nuclei by the remaining nuclear fragment in the ground and sometimes in excited states. This method has been also generalized to the case of four-body democratic decays and applied to the description of resonances in the tetraneutron Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 and in the 7He nucleus in the channel of four-body decay into 4He and three neutrons Mazur_PhysRevC_2022 . In short, we have previously applied the SS-HORSE–NCSM approach up to now only to the decay channels with an even number of fragments.
On the other hand, the SS-HORSE–NCSM has been applied to the hypernuclear system in Ref. Htun_PhysRevC_2022 , a three-body decay, for the first time. The distinction from Refs. Shirokov_PhysRevC_2016 ; Mazur_PhysPartNucl_2017 ; Blokhintsev_YaF_2017_1 ; Blokhintsev_YaF_2017_2 ; Shirokov_PhysRevC_2018 ; Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 is that Ref. Htun_PhysRevC_2022 did not search for the -matrix poles but extracted the resonance parameters from the slope of the phase shifts of the true three-body () scattering.
In this paper we generalize the technique of locating the -matrix poles proposed in Refs. Shirokov_PhysRevC_2016 ; Mazur_PhysPartNucl_2017 ; Blokhintsev_YaF_2017_1 ; Blokhintsev_YaF_2017_2 ; Shirokov_PhysRevC_2018 ; Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 to the case of democratic decay into an odd number of fragments. We construct a family of parametrizations of the scattering matrix in a minimal approximation to enable the possibility of the -matrix pole search.
The structure of the paper is the following. We discuss the scattering, the structure of the respective matrix and the generalization of the SS-HORSE–NCSM approach to the case of the democratic decay into an odd number of fragments using minimal approximations in Sec. II. We apply the developed method to the search of resonances in the three-neutron system based on the NCSM calculations with various realistic interactions in Sec. III. The conclusions are presented in Sec. IV.
II SS-HORSE–NCSM method for democratic decay into odd number of fragments
We make use of the version of the -matrix formalism Heller_PhysRevA_1974 ; Yamani_JMathPhys_1975 in scattering theory utilizing the harmonic oscillator basis, which is also known as HORSE Bang_AnnPhys_2000 , for the generalization of the NCSM to the case of the continuum spectrum. The essence of the HORSE formalism is the division of the many-body Hilbert space into a finite-dimensional oscillator subspace where both the potential energy of the interactions between particles and their kinetic energy are taken into account ( space) and the remaining infinite-dimensional subspace where only the kinetic energy is retained and the interaction is neglected ( space). The space conventionally includes all many-body states with oscillator excitation quanta, which do not exceed some certain number . This definition is well matched with the NCSM where is used to restrict the model space.
We use a generalization of the HORSE formalism to the case of the true many-body () scattering developed in Ref. Zaytsev_TeorMatFiz_1998 to describe states in the many-body continuum. The version of HORSE for scattering utilizes the ideas of the method of hyperspherical harmonics (HH) (see, e. g., Refs. Jibuti ; HHbook ), which was widely used in studies of various atomic and nuclear systems, in particular, of the trineutron Dzhibuti_SovJNuclPhys264_1984 ; Dzhibuti_SovJNuclPhys700_1984 ; Jibuti_NuclPhysA_1985 ; Dzhibuti_SovJNuclPhys_1985 ; Kezerashvili_Preprint_1993 .
In the case of continuum states, the HH method is an adequate tool for the description of the so-called democratic decays of an -body system when no subgroup of the particles has a bound state. This condition appears to be satisfied for the trineutron or tetraneutron. The wave function dependence on the “democratic” hyperradius,
| (1) |
is of a primary importance within the HH approach. Here are the individual neutron coordinates and is the center-of-mass coordinate. The remaining degrees of freedom are described by hyperspherical functions depending on some set of angles on the -dimensional sphere coupled with neutron spins and a function describing the center-of-mass motion. Both the hyperspherical and the hyperradial functions are characterized by the hypermomentum and some other quantum numbers distinguishing different states with the same hypermomentum, which are of no interest for us in this research. For the states of a definite total angular momentum and parity, , where generally is integer, and in the case of trineutron natural (negative) parity states with or 1/2.
In the HH approach, the Schrödinger equation takes the form of a set of coupled equations, which is equivalent to a set of equations describing a multichannel scattering with the same threshold in all channels. Each of the equations includes a centrifugal term , where the effective orbital momentum Zaytsev_TeorMatFiz_1998
| (2) |
We note that the NCSM calculations performed in the space utilize a complete set of HH with . However, in the space, which is associated with the long-range behavior of the wave functions, the HH with are suppressed by the high centrifugal barrier. Therefore, we utilize the democratic decay minimal approximation that implies retaining only one HH with in the -space. So, the wave function is characterized by a single phase shift of scattering. This phase shift can be calculated using NCSM eigenenergies obtained with given values of and the NCSM oscillator basis parameter within the SS-HORSE–NCSM approach as Shirokov_PhysRevLett_2016
| (3) |
where is the minimal number of oscillator quanta allowed by the Pauli principle, and are regular and irregular solutions for a free motion in the HORSE formalism, which explicit analytical expressions can be found in Ref. Zaytsev_TeorMatFiz_1998 . Note, and depend on the oscillator parameter .
The accuracy of the approximation retaining the single lowest HH in the space was confirmed in the studies of three-body democratic decays in Refs. Lurie_IzvRossAkadNaukSerFiz_1993 ; Lurie_IzvRossAkadNaukSerFiz_1997 ; Lurie_AnnPhys_2004 ; Lurie_Jmatrix_book . We also used the minimal approximation for the democratic decay in investigations of the four-neutron system Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 .
The matrix is related to the phase shift ,
| (4) |
To study the matrix analytical properties, it is more convenient to analyze it as a function of the momentum instead of the energy ,
| (5) |
where is total mass of the system.
In the case of even , is integer, and the matrix analytical properties are similar to those of two-body scattering. In particular Baz ; Newton ,
| (6) |
and
| (7) |
which are crucial for the -matrix parametrization. The parameterized matrix can be analytically continued to the complex plane for the search of its poles associated with resonant and bound states. This technique has been used to estimate the energy and width of the resonant state in the tetraneutron Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 .
Analytical properties of the matrix become more complicated in case of an odd due to a half-integer value of the effective angular momentum as follows from Eq. (2). The -matrix properties in the case of arbitrary non-integer angular momentum are discussed in Ref. Newton . In this case Eq. (6) is generalized to
| (8) |
which holds for any complex value of . As a result, for a half-integer we have
| (9) |
Note that Eq. (7) is valid for any real value of angular momentum. We attribute properties (7) and (9) to the matrix in the case of an odd .
The matrix has multiple sheets and its properties are complicated in the case of a non-integer angular momentum. The matrix can be expressed as Alfaro
| (10) |
where has the following property:
| (11) |
Equation (10) cannot be used directly in the case of a half-integer : according to Ref. Alfaro , in this case we have an uncertainty of the type that should be resolved using the L’Hôpital’s theorem considering as a continuous variable and investigate the limit to obtain
| (12) |
where and is a real-valued momentum needed to make dimensionless the argument of in the denominator. We note that our final results for the -matrix poles are independent of . Using Eqs. (4) and (12), it is easy to deduce
| (13) |
The phase shift is a real-valued function for real . Therefore it is convenient to introduce a real-valued at real function
| (14) |
It is easy to show that , that leads to the following symmetry property of the function :
| (15) |
The matrix and phase shift are expressed in terms of as
| (16) |
| (17) |
The expression (16) satisfies the properties of Eqs. (7) and (9).
Due to Eq. (15), the function can be parameterized as a series expansion in even powers of ,
| (18) |
We note that the value of is arbitrary. Redefining results in a redefinition of parameters () in Eq. (18) such that the matrix defined by Eq. (16) remains unchanged.
The parametrization (18) provides for an estimation of the phase-shift behavior in the limit . For example, for the three-body problem (), supposing that , we obtain from Eq. (17):
| (19) |
This behavior is in line with the analysis presented in Ref. Jibuti justifying the parameterization (18).
Following the ideas of the SS-HORSE–NCSM approach Shirokov_PhysRevC_2016 ; Mazur_PhysPartNucl_2017 ; Blokhintsev_YaF_2017_1 ; Blokhintsev_YaF_2017_2 ; Shirokov_PhysRevC_2018 ; Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 , we can obtain the parameters of the expansion (18) by calculating a set of the phase shifts using Eq. (3) at the NCSM eigenenergies obtained with a chosen and a set of the values, and next parameterize this set of by means of Eqs. (17) and (18) (see the next section for more details). To calculate energies and widths of resonances, we locate the -matrix poles by searching for zeros of the denominator in the right-hand side of Eq. (16), which is equivalent to solving numerically in the complex plane equation
| (20) |
using the technique suggested in Ref. Shirokov_PhysRevC_2018 or the Newton–Raphson method (see, e. g., Ref. Rakityansky ).
III Trineutron
The above method is applied to the search of resonances in the three-neutron system. We use various realistic interactions, the same as employed in our analysis of the tetraneutron Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 . We utilize the MFDn code Maris_ProcComputSci_2010 ; Aktulga_ConcurComputPractExper_2014 to perform the NCSM calculations with ranging from 4–20 and spanning from 2–50 MeV.
The results for the ground-state energy obtained with the Daejeon16 Shirokov_PhysLettB_2016 interaction, are shown in the top panel of Fig. 1. The phase shifts at the NCSM eigenenergies obtained using Eq. (3) are presented in the bottom panel. It is seen that the phase shifts tend to the same smooth resonance-like curve as is increasing demonstrating a convergence of the phase shift calculations.
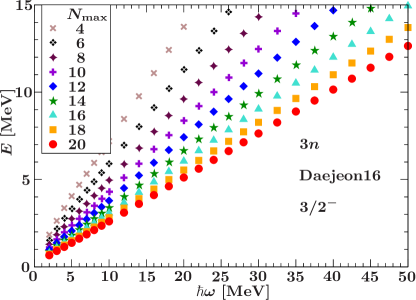
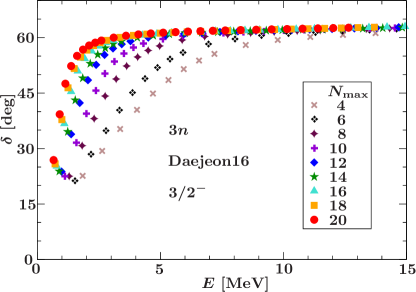
We parametrize the function for each individual value of used in the NCSM calculations of the trineutron ground-state energies. For a given , we use a set of parameters defining to find the energies by solving the equation
| (21) |
for each value of used in the respective NCSM calculations. Here and . To find the optimal values of , we minimize the function
| (22) |
where is the number of the NCSM energies obtained with the same and the same as each of the respective energies , , and is the weight increasing the importance of states with smaller corresponding to energies closer to the resonance region.
The quality of the fits can be estimated by the r.m.s. deviation
| (23) |
In our case we get approximately the same r.m.s. deviations obtained with five () or six () parameters in Eq. (18), which are, however, significantly smaller than the r.m.s. deviations obtained with four parameters (). Energies and widths obtained by locating the -matrix poles using Eq. (20) and the NCSM results from calculations with , 18, 20 and parametrizations with and 5 together with the respective values are presented in Table 1.
| 16 | 18 | 20 | 16 | 18 | 20 | |
|---|---|---|---|---|---|---|
| 4 | 4 | 4 | 5 | 5 | 5 | |
| , MeV | 0.560 | 0.508 | 0.483 | 0.607 | 0.537 | 0.481 |
| , MeV | 1.458 | 1.152 | 0.924 | 1.524 | 1.176 | 0.963 |
| , keV | 3.3 | 3.9 | 2.5 | 2.7 | 2.0 | 1.8 |
Fits of the phase shifts in the state with six parameters in Eq. (18) () are presented by solid curves in Fig. 2. The phase shifts at the NCSM eigenenergies obtained by Eq. (3) and used for the fitting are shown by symbols in Fig. 2. The trineutron resonance energy and width obtained by locating the -matrix pole based on the NCSM calculation with and fit with are adopted as the final result presented in the Table 2 together with their uncertainties estimated as deviations of results obtained with , 20 and , 5 from the final result.
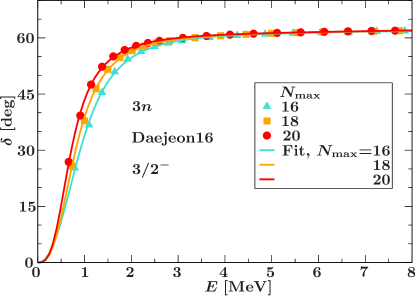
It is interesting that we obtain in the trineutron NCSM calculations the state very close to the lowest state. We perform the same analysis of the trineutron resonance. The phase shifts are very close to those in the state and the obtained resonance energy and width are presented in Table 2. It is seen that the and resonance energies and widths are the same within the uncertainty estimations and these resonances completely overlap.
We employ the same technique to search for resonances with other soft interactions, in particular, with Idaho N3LO Entem_PhysRevC_2003 softened by the similarity renormalization group (SRG) transformation Glazek_PhysRevD_1993 ; Wegner_AnnPhys_1994 with the flow parameter fm-1 and JISP16 Shirokov_PhysLettB_2007 . The respective results are also presented in the Table 2. Note, in these cases the and resonance also degenerate and strongly overlap.
| Interaction | ||||
|---|---|---|---|---|
| Daejeon16 | 0.48(6) | 0.96(21) | 0.48(8) | 0.96(17) |
| JISP16 | 0.35(8) | 0.70(9) | 0.35(11) | 0.67(22) |
| N3LO, SRG, fm-1 | 0.34(8) | 0.70(19) | 0.35(9) | 0.68(16) |
We also have analyzed the trineutron resonance with bare realistic interactions derived in chiral effective field theory: Idaho N3LO and LENPIC N4LO semi-local coordinate space interaction Epelbaum_PhysRevLett_2015 with regulator fm. In these cases, the phase shifts do not demonstrate a resonant behavior. Due to the almost complete degeneracy of the and states, these interactions also do not support the resonance.
We obtained Shirokov_AIPConfProc_2018 a -matrix pole at negative imaginary momentum in the tetraneutron calculations with the Idaho N3LO interaction, which corresponds to a virtual state at the energy of keV. It is easy to prove, that the -matrix for an odd number of fragments does not allow -matrix poles at the negative imaginary half-axis of momentum. Therefore, a virtual state is prohibited in the trineutron treated as a democratic decaying system.
IV Summary and conclusions
We suggest an extension of the SS-HORSE–NCSM method to a democratic decay into odd number of fragments. The first application of this method is the analysis of the resonant trineutron state.
We conclude that the soft interactions that we investigated predict two low-lying nearly degenerate overlapping trineutron resonances with spin-parities and . On the other hand, these resonances are not supported by bare interactions of chiral effective field theory. We do not include interaction in our calculations, which has yet to be designed for three-nucleon systems with isospin .
We argue that the Daejeon16 interaction is preferable for the trineutron studies since it originates from the chiral effective field theory and is fitted to stable light nuclei up to 16O by phase-equivalent off-shell variations, which effectively mimic effects of forces. The JISP16 interaction, which was also fitted to light nuclei by off-shell variations, leads to similar trineutron results as well as the SRG-evolved Idaho N3LO interaction.
We predict two overlapping trineutron resonances with spin-parities and with nearly exactly the same energies and widths : MeV and MeV obtained in calculations with the Daejeon16 and MeV and MeV obtained in calculations with the JISP16 and SRG-evolved N3LO interactions.
Our results are in line with the conclusions of Refs. Gandolfi ; Li_PhysRevC_2019 predicting the trineutron resonance at lower energy than the tetraneutron resonance Shirokov_PhysRevLett_2016 ; Shirokov_AIPConfProc_2018 . However, in our calculations we obtain the trineutron resonance at lower energies as compared to MeV in Ref. Li_PhysRevC_2019 and MeV in Ref. Gandolfi . Meanwhile, its width obtained with the Daejeon16 interaction is in agreement with MeV proposed in Ref. Li_PhysRevC_2019 . We note that Refs. Gandolfi ; Li_PhysRevC_2019 do not specify the spin-parity of the predicted trineutron resonance.
Note added in proof. Recently, a new unsuccessful experimental attempt to find the trineutron and triproton resonances in the reactions 3H(,3He) and 3He(3He,) was published in Ref. Miki_PhysRevLett_2024 .
Acknowledgments
The work of I. A. M. is supported by the Institute for Basic Science (IBS-R031-D1). The work of M. K. E. and A. I. M. is supported by the Ministry of Science and Higher Education of Russian Federation (project No. FEME-2024-0005). The work of I. J. S. is supported by the National Research Foundation of Korea (NRF) funded by Ministry of Science and ICT (2013M7A1A1075764). A. M. S. is thankful to the Chinese Academy of Sciences President’s International Fellowship Initiative Program (Grant No. 2023VMA0013) which supported his visits to the Institute of Modern Physics, Chinese Academy of Sciences in Lanzhou, China, where a part of this work was performed and acknowledges the hospitality of Chinese colleagues during these visits. The work of J. P. V. is supported by the U.S. Department of Energy, Division of Nuclear Physics, Grant No. DE-SC0023692.
References
- (1) B. R. Barrett, P. Navrátil, and J. P. Vary, Prog. Part. Nucl. Phys. 69, 131 (2013).
- (2) K. Kisamori et al., Phys. Rev. Lett. 116, 052501 (2016).
- (3) M. Duer et al., Nature 606, p. 678 (2022).
- (4) V. Ajdačić, M. Cerineo, B. Lalović, G. Paić, I. Šlaus, and P. Tomaš, Phys. Rev. Lett. 14, 444 (1965).
- (5) R. Kezerashvili, in Fission and Properties of Neutron-Rich Nuclei (World Scientific, Singapore, 2017), p. 403.
- (6) F. M. Marqués and J. Carbonell, Eur. Phys. J. A 57, 105 (2021).
- (7) E. Hiyama, R. Lazauskas, J. Carbonell, M. Kamimura, Phys. Rev. C 93, 044004 (2016).
- (8) S. Gandolfi, H.-W. Hammer, P. Klos, J. E. Lynn, and A. Schwenk, Phys. Rev. Lett. 118, 232501 (2017).
- (9) A. Deltuva, Phys. Rev. C 97, 034001 (2018).
- (10) J. G. Li, N. Michel, B. S. Hu, W. Zuo, and F. R. Xu, Phys. Rev. C 100, 054313 (2019).
- (11) A. M. Shirokov, A. I. Mazur, I. A. Mazur, and J. P. Vary, Phys. Rev. C 94, 064320 (2016).
- (12) I. A. Mazur, A. M. Shirokov, A. I. Mazur, and J. P. Vary, Phys. Part. Nucl. 48, 84 (2017).
- (13) L. D. Blokhintsev, A. I. Mazur, I. A. Mazur, D. A. Savin, and A. M. Shirokov, Yad. Fiz. 80, 102 (2017); Phys. Atom. Nucl. 80, 226 (2017).
- (14) L. D. Blokhintsev, A. I. Mazur, I. A. Mazur, D. A. Savin, and A. M. Shirokov, Yad. Fiz. 80, 619 (2017); Phys. Atom. Nucl. 80, 1093 (2017).
- (15) A. M. Shirokov, A. I. Mazur, I. A. Mazur, E. A. Mazur, I. J. Shin, Y. Kim, L. D. Blokhintsev, and J. P. Vary, Phys. Rev. C 98, 044624 (2018).
- (16) A. M. Shirokov, G. Papadimitriou, A. I. Mazur, I. A. Mazur, R. Roth, and J. P. Vary, Phys. Rev. Lett. 117, 182502 (2016).
- (17) A. M. Shirokov, Y. Kim, A. I. Mazur, I. A. Mazur, I. J. Shin, and J. P. Vary, AIP Conf. Proc. 2038, 020038 (2018).
- (18) P. Navrátil, S. Quaglioni, G. Hupin, C. Romero-Redondo, and A. Calci, Phys. Scr. 91, 053002 (2016).
- (19) G. Papadimitriou, J. Rotureau, N. Michel, M. Płoszajczak, and B. R. Barrett, Phys. Rev. C 88, 044318 (2013).
- (20) I. A. Mazur, I. J. Shin, Y. Kim, A. I. Mazur, A. M. Shirokov, P. Maris, and J. P. Vary, Phys. Rev. C 106, 064320 (2022).
- (21) I. A. Mazur, A. I. Mazur, V. A. Kulikov, A. M. Shirokov, I. J. Shin, Y. Kim, P. Maris, and J. P. Vary, Yad. Fiz. 86, 104 (2023); Phys. At. Nucl. 85, 823 (2022).
- (22) A. M. Shirokov, J. P. Vary, A. I. Mazur, and T. A. Weber, Phys. Lett. B 644, 33 (2007); a Fortran code generating the JISP16 matrix elements is available at http://lib.dr.iastate.edu/energy_datasets/2/.
- (23) A. M. Shirokov, I. J. Shin, Y. Kim, M. Sosonkina, P. Maris, and J. P. Vary, Phys. Lett. B 761, 87 (2016); a Fortran code generating the Daejeon16 matrix elements is available at http://lib.dr.iastate.edu/energy_datasets/1/.
- (24) T. Y. Htun and Y. Yan, Phys. Rev. C 105, 064001 (2022).
- (25) E. J. Heller and H. A. Yamani, Phys. Rev. A 9, 1201 (1974).
- (26) H. A. Yamani and L. Fishman, J. Math. Phys. 16, 410 (1975).
- (27) J. M. Bang, A. I. Mazur, A. M. Shirokov, Yu. F. Smirnov, and S. A. Zaytsev, Ann. Phys. (NY) 280, 299 (2000).
- (28) S. A. Zaitsev, Yu. F. Smirnov, and A. M. Shirokov, Teor. Mat. Fiz. 117, 227 (1998); Theor. Math. Phys. 117, 1291 (1998).
- (29) R. I. Jibuti and N. B. Krupennikova, The Method of Hyperspherical Functions in the Quantum Mechanics of Few Bodies [in Russian] (Metsniereba, Tbilisi, 1984).
- (30) J. E. Avery and J. S. Avery, Hyperspherical Harmonics and Their Physical Applications (World Scientific, Singapore, 2018).
- (31) R. I. Dzhibuti and R. Ya. Kezerashvili, Sov. J. Nucl. Phys. 39, 264 (1984).
- (32) R. I. Dzhibuti and R. Ya. Kezerashvili, Sov. J. Nucl. Phys. 39, 700 (1984).
- (33) R. I. Jibuti and R. Ya. Kezerashvili, Nucl. Phys. A437, 687 (1985).
- (34) R. I. Dzhibuti and R. Ya. Kezerashvili, Sov. J. Nucl. Phys. 40, 443 (1985).
- (35) R. Ya. Kezerashvili, preprint IFUP-TH 24/93, 1993.
- (36) Yu. A. Lurie, Yu. F. Smirnov, and A. M. Shirokov, Izv. Ross. Akad. Nauk, Ser. Fiz. 57, 193 (1993) [Bull. Russ. Acad. Sci., Phys. Ser. 57, 943 (1993)].
- (37) Yu. A. Lurie and A. M. Shirokov, Izv. Ross. Akad. Nauk, Ser. Fiz. 61, 2121 (1997) [Bull. Russ. Acad. Sci., Phys. Ser. 61, 1665 (1997)].
- (38) Yu. A. Lurie and A. M. Shirokov, Ann. Phys. (NY) 312, 284 (2004).
- (39) Yu. A. Lurie and A. M. Shirokov, in The J-Matrix Method. Developments and Applications, edited by A. D. Alhaidari, H. A. Yamani, E. J. Heller, and M. S. Abdelmonem (Springer, New York, 2008), p. 183.
- (40) A. I. Baz’, Ya. B. Zel’dovich, and A. M. Perelomov, Scattering, Reactions and Decay in Non-relativistic Quantum Mechanics (Israel Program for Scientific Translation, Jerusalem, 1969).
- (41) R. G. Newton, Scattering Theory of Waves and Particles, 2nded. (Springer-Verlag, New York, 1982).
- (42) V. de Alfaro and T. Regge, Potential Scattering (North-Holland, Amsterdam, 1965).
- (43) S. A. Rakityansky, Jost Functions in Quantum Mechanics. A Unified Approach to Scattering, Bound, and Resonant State Problems (Springer Nature, Cham, 2022).
- (44) P. Maris, M. Sosonkina, J. P. Vary, E. G. Ng, and C. Yang, Proc. Comput. Sci. 1, 97 (2010).
- (45) H. M. Aktulga, C. Yang, E. G. Ng, P. Maris, and J. P. Vary, Concur. Comput. Pract. Exper. 26, 2631 (2014).
- (46) D.R. Entem, R. Machleidt, Phys. Rev. C 68 (2003) 041001(R).
- (47) S. D. Glazek and K. G. Wilson, Phys. Rev. D 48, 5863 (1993).
- (48) F. Wegner, Ann. Phys. (NY) 506, 77 (1994).
- (49) E. Epelbaum, H. Krebs, and U.-G. Meißner Phys. Rev. Lett. 115, 122301 (2015).
- (50) K. Miki et al. (RIBF-SHARAQ11 Collaboration and RCNP-E502 Collaboration), Phys. Rev. Lett. 133, 012501 (2024).